2.2 : La limite d'une fonction
- Page ID
- 197993
- Décrivez la limite d'une fonction à l'aide d'une notation correcte.
- Utilisez un tableau de valeurs pour estimer la limite d'une fonction ou pour identifier les cas où la limite n'existe pas.
- Utilisez un graphique pour estimer la limite d'une fonction ou pour identifier les cas où la limite n'existe pas.
- Définissez des limites unilatérales et fournissez des exemples.
- Expliquez la relation entre les limites unilatérales et bilatérales.
- Décrivez une limite infinie à l'aide d'une notation correcte.
- Définissez une asymptote verticale.
Le concept de limite ou de processus limitant, essentiel à la compréhension du calcul, existe depuis des milliers d'années. En fait, les premiers mathématiciens ont utilisé un processus de limitation pour obtenir des approximations de plus en plus précises des zones des cercles. Pourtant, la définition officielle d'une limite, telle que nous la connaissons et la comprenons aujourd'hui, n'est apparue qu'à la fin du XIXe siècle. Nous commençons donc notre quête pour comprendre les limites, comme l'ont fait nos ancêtres mathématiques, en utilisant une approche intuitive. À la fin de ce chapitre, forts d'une compréhension conceptuelle des limites, nous examinons la définition formelle d'une limite.
Nous commençons notre exploration des limites en examinant les graphes des fonctions
- \(f(x)=\dfrac{x^2−4}{x−2}\),
- \(g(x)=\dfrac{|x−2|}{x−2}\), et
- \(h(x)=\dfrac{1}{(x−2)^2}\),
qui sont illustrés dans la figure\(\PageIndex{1}\). Concentrons en particulier notre attention sur le comportement de chaque graphique à l'emplacement et aux alentours\(x=2\).
Chacune des trois fonctions n'est pas définie à\(x=2\), mais si nous faisons cette déclaration et aucune autre, nous donnons une image très incomplète de la façon dont chaque fonction se comporte à proximité de\(x=2\). Pour exprimer le comportement de chaque graphe de manière\(2\) plus complète, nous devons introduire le concept de limite.
Définition intuitive d'une limite
Examinons d'abord de plus près le\(f(x)=(x^2−4)/(x−2)\) comportement de la fonction\(x=2\) dans Figure\(\PageIndex{1}\). En tant que valeurs d'\(x\)approche\(2\) de part et d'autre de\(2\), les valeurs d'\(y=f(x)\)approche\(4\). Mathématiquement, nous disons que la limite\(f(x)\) des\(x\) approches\(2\) est\(4\). Symboliquement, nous exprimons cette limite comme suit :
\(\displaystyle \lim_{x \to 2} f(x)=4\).
À partir de ce bref aperçu informel d'une limite, commençons à développer une définition intuitive de la limite. Nous pouvons considérer que la limite d'une fonction à un nombre\(a\) est le nombre réel\(L\) que les valeurs fonctionnelles abordent sous le nom d'approche\(x\) -values\(a\), à condition qu'un tel nombre réel\(L\) existe. Exprimée plus attentivement, nous avons la définition suivante :
\(f(x)\)Soit une fonction définie à toutes les valeurs d'un intervalle ouvert contenant\(a\), à l'exception éventuelle de\(a\) elle-même, et\(L\) soit un nombre réel. Si toutes les valeurs de la fonction s'\(f(x)\)approchent du nombre\(L\) réel lorsque les valeurs d'\(x(≠a)\)approchent le nombre\(a\), alors nous disons que la limite des\(f(x)\)\(x\) approches\(a\) est\(L\). (Plus succinct, au fur et à mesure que l'on\(x\) s'en\(f(x)\) rapproche\(a\), qu'on s'en rapproche et qu'on reste proche de\(L\) Symboliquement, nous exprimons cette idée comme
\[\lim_{x \to a} f(x)=L. \label{limit} \]
Nous pouvons estimer les limites en construisant des tableaux de valeurs fonctionnelles et en examinant leurs graphiques. Ce processus est décrit dans la stratégie de résolution de problèmes suivante.
1. Pour évaluer\(\displaystyle \lim_{x \to a} f(x)\), nous commençons par compléter un tableau de valeurs fonctionnelles. Nous devons choisir deux ensembles de\(x\) valeurs : un ensemble de valeurs proches\(a\) et inférieures à\(a\), et un autre ensemble de valeurs proches\(a\) et supérieures à\(a\). Le tableau\(\PageIndex{1}\) montre à quoi peuvent ressembler vos tables.
| \(x\) | \(f(x)\) | \(x\) | \(f(x)\) |
|---|---|---|---|
| \ (x \) » style="text-align:center ; « >\(a-0.1\) | \ (f (x) \) » style="text-align:center ; « >\(f(a-0.1)\) | \ (x \) » style="text-align:center ; « >\(a+0.1\) | \ (f (x) \) » style="text-align:center ; « >\(f(a+0.1)\) |
| \ (x \) » style="text-align:center ; « >\(a-0.01\) | \ (f (x) \) » style="text-align:center ; « >\(f(a-0.01)\) | \ (x \) » style="text-align:center ; « >\(a+0.01\) | \ (f (x) \) » style="text-align:center ; « >\(f(a+0.01)\) |
| \ (x \) » style="text-align:center ; « >\(a-0.001\) | \ (f (x) \) » style="text-align:center ; « >\(f(a-0.001)\) | \ (x \) » style="text-align:center ; « >\(a+0.001\) | \ (f (x) \) » style="text-align:center ; « >\(f(a+0.001)\) |
| \ (x \) » style="text-align:center ; « >\(a-0.0001\) | \ (f (x) \) » style="text-align:center ; « >\(f(a-0.0001)\) | \ (x \) » style="text-align:center ; « >\(a+0.0001\) | \ (f (x) \) » style="text-align:center ; « >\(f(a+0.0001)\) |
| \ (f (x) \) » rowspan="1" style="text-align:center ; ">Utilisez des valeurs supplémentaires si nécessaire. | \ (f (x) \) » rowspan="1" style="text-align:center ; ">Utilisez des valeurs supplémentaires si nécessaire. | ||
2. Examinons ensuite les valeurs de chacune des\(f(x)\) colonnes et déterminons si les valeurs semblent s'approcher d'une valeur unique lorsque nous descendons chaque colonne. Dans nos colonnes, nous examinons la séquence\(f(a−0.1)\),,\(f(a−0.01)\)\(f(a−0.001)\),\(f(a−0.0001)\), et ainsi de suite\(f(a+0.1), \;f(a+0.01), \;f(a+0.001), \;f(a+0.0001)\), et ainsi de suite. (Remarque : bien que nous ayons choisi les\(x\) valeurs\(a±0.1, \;a±0.01, \;a±0.001, \;a±0.0001\) -, etc., et que ces valeurs fonctionneront probablement presque à chaque fois, il se peut que nous devions modifier nos choix dans de très rares cas.)
3. Si les deux colonnes s'approchent d'une\(y\) valeur commune\(L\), nous indiquons\(\displaystyle \lim_{x \to a}f(x)=L\). Nous pouvons utiliser la stratégie suivante pour confirmer le résultat obtenu à partir du tableau ou comme méthode alternative pour estimer une limite.
4. À l'aide d'une calculatrice graphique ou d'un logiciel informatique qui nous permet de tracer des fonctions, nous pouvons tracer la fonction\(f(x)\) en nous assurant que les valeurs fonctionnelles de\(f(x)\) for\(x\) -values near\(a\) se trouvent dans notre fenêtre. Nous pouvons utiliser la fonction de traçage pour nous déplacer le long du graphique de la fonction et observer la\(y\) lecture de la valeur à mesure que les\(x\) valeurs s'approchent\(a\). Si les\(y\) valeurs s'approchent\(L\) comme nos\(x\) valeurs s'approchent\(a\) des deux côtés, alors\(\displaystyle \lim_{x \to a}f(x)=L\). Il se peut que nous devions zoomer sur notre graphique et répéter ce processus plusieurs fois.
Nous appliquons cette stratégie de résolution de problèmes pour calculer une limite dans les exemples\(\PageIndex{1A}\) et\(\PageIndex{1B}\).
Évaluez\(\displaystyle \lim_{x \to 0}\frac{\sin x}{x}\) à l'aide d'un tableau de valeurs fonctionnelles.
Solution
Nous avons calculé les valeurs de\(f(x)=\dfrac{\sin x}{x}\) pour les valeurs\(x\) répertoriées dans le tableau\(\PageIndex{2}\).
| \(x\) | \(\frac{\sin x}{x}\) | \(x\) | \(\frac{\sin x}{x}\) |
|---|---|---|---|
| \ (x \) » style="text-align:center ; « >-0.1 | \ (\ frac {\ sin x} {x} \) » style="text-align:center ; « >0.998334166468 | \ (x \) » style="text-align:center ; « >0,1 | \ (\ frac {\ sin x} {x} \) » style="text-align:center ; « >0.998334166468 |
| \ (x \) » style="text-align:center ; « >-0,01 | \ (\ frac {\ sin x} {x} \) » style="text-align:center ; « >0.999983333417 | \ (x \) » style="text-align:center ; « >0,01 | \ (\ frac {\ sin x} {x} \) » style="text-align:center ; « >0.999983333417 |
| \ (x \) » style="text-align:center ; « >-0.001 | \ (\ frac {\ sin x} {x} \) » style="text-align:center ; « >0.999999833333 | \ (x \) » style="text-align:center ; « >0,001 | \ (\ frac {\ sin x} {x} \) » style="text-align:center ; « >0.999999833333 |
| \ (x \) » style="text-align:center ; « >-0,0001 | \ (\ frac {\ sin x} {x} \) » style="text-align:center ; « >0.999999998333 | \ (x \) » style="text-align:center ; « >0,0001 | \ (\ frac {\ sin x} {x} \) » style="text-align:center ; « >0.999999998333 |
Remarque : Les valeurs de ce tableau ont été obtenues à l'aide d'une calculatrice et en utilisant tous les emplacements indiqués dans les résultats de la calculatrice.
Lorsque nous lisons chaque\(\dfrac{\sin x}{x}\) colonne, nous constatons que les valeurs de chaque colonne semblent s'approcher d'une. Il est donc assez raisonnable de conclure que\(\displaystyle \lim_{x\to0}\frac{\sin x}{x}=1\). Un graphique généré par une calculatrice ou par ordinateur\(f(x)=\dfrac{\sin x}{x}\) serait similaire à celui de la figure\(\PageIndex{2}\), et il confirme notre estimation.
![Un graphique de f (x) = sin (x) /x sur l'intervalle [-6, 6]. La fonction de courbure possède une intersection y à x=0 et une intersection x à y=pi et y=-pi.](https://math.libretexts.org/@api/deki/files/7963/imageedit_1_8651812985.png)
Évaluez\(\displaystyle \lim_{x\to4}\frac{\sqrt{x}−2}{x−4}\) à l'aide d'un tableau de valeurs fonctionnelles.
Solution
Comme précédemment, nous utilisons un tableau (dans ce cas, un tableau\(\PageIndex{3}\)) pour répertorier les valeurs de la fonction pour les valeurs données de\(x\).
| \(x\) | \(\frac{\sqrt{x}−2}{x−4}\) | \(x\) | \(\frac{\sqrt{x}−2}{x−4}\) |
|---|---|---|---|
| \ (x \) » style="text-align:center ; « >3,9 | \ (\ frac {\ sqrt {x} −2} {x−4} \) » style="text-align:center ; « >0.251582341869 | \ (x \) » style="text-align:center ; « >4.1 | \ (\ frac {\ sqrt {x} −2} {x−4} \) » style="text-align:center ; « >0.248456731317 |
| \ (x \) » style="text-align:center ; « >3,99 | \ (\ frac {\ sqrt {x} −2} {x−4} \) » style="text-align:center ; « >0.25015644562 | \ (x \) » style="text-align:center ; « >4.01 | \ (\ frac {\ sqrt {x} −2} {x−4} \) » style="text-align:center ; « >0,24984394501 |
| \ (x \) » style="text-align:center ; « >3,999 | \ (\ frac {\ sqrt {x} −2} {x−4} \) » style="text-align:center ; « >0,250015627 | \ (x \) » style="text-align:center ; « >4,001 | \ (\ frac {\ sqrt {x} −2} {x−4} \) » style="text-align:center ; « >0.249984377 |
| \ (x \) » style="text-align:center ; « >3,9999 | \ (\ frac {\ sqrt {x} −2} {x−4} \) » style="text-align:center ; « >0,250001563 | \ (x \) » style="text-align:center ; « >4.0001 | \ (\ frac {\ sqrt {x} −2} {x−4} \) » style="text-align:center ; « >0.249998438 |
| \ (x \) » style="text-align:center » ; « >3,99999 | \ (\ frac {\ sqrt {x} −2} {x−4} \) » style="text-align:center ; « >0,25000016 | \ (x \) » style="text-align:center ; « >4.00001 | \ (\ frac {\ sqrt {x} −2} {x−4} \) » style="text-align:center ; « >0.24999984 |
Après avoir examiné ce tableau, nous constatons que les valeurs fonctionnelles inférieures à 4 semblent diminuer vers 0,25 alors que les valeurs fonctionnelles supérieures à 4 semblent augmenter vers 0,25. Nous en concluons que\(\displaystyle \lim_{x\to4}\frac{\sqrt{x}−2}{x−4}=0.25\). Nous confirmons cette estimation à l'aide du graphique de la\(f(x)=\dfrac{\sqrt{x}−2}{x−4}\) figure\(\PageIndex{3}\).
![Un graphique de la fonction f (x) = (sqrt (x) — 2)/(x-4) sur l'intervalle [0,8]. Il y a un cercle ouvert sur la fonction à x=4. La fonction se courbe de façon asymptotique vers l'axe x et l'axe y dans le premier quadrant.](https://math.libretexts.org/@api/deki/files/7964/imageedit_5_9266726966.png)
Estimation\(\displaystyle \lim_{x \to 1} \frac{\frac{1}{x}−1}{x−1}\) à l'aide d'un tableau de valeurs fonctionnelles. Utilisez un graphique pour confirmer votre estimation.
- Allusion
-
Utilisez 0,9, 0,99, 0,999, 0,9999, 0,99999 et 1,1, 1,01, 1,001, 1,0001, 1,0001, 1,00001 comme valeurs de table.
- Réponse
-
\[\lim_{x\to1}\frac{\frac{1}{x}−1}{x−1}=−1\nonumber \]
À ce stade, nous voyons dans\(\PageIndex{1A}\) les exemples\(\PageIndex{1b}\) qu'il peut être tout aussi facile, sinon plus facile, d'estimer la limite d'une fonction en inspectant son graphique que d'estimer la limite à l'aide d'un tableau de valeurs fonctionnelles. Dans l'exemple\(\PageIndex{2}\), nous évaluons une limite exclusivement en regardant un graphique plutôt qu'en utilisant un tableau de valeurs fonctionnelles.
\(g(x)\)Comme indiqué dans la figure\(\PageIndex{4}\), évaluez\(\displaystyle \lim_{x\to−1}g(x)\).
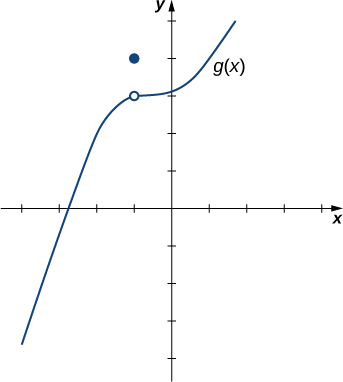
Solution :
Malgré le fait que\(g(−1)=4\), lorsque les\(x\) valeurs s'approchent\(−1\) de chaque côté, les\(g(x)\) valeurs s'approchent\(3\). Par conséquent,\(\displaystyle \lim_{x\to−1}g(x)=3\). Notez que nous pouvons déterminer cette limite sans même connaître l'expression algébrique de la fonction.
Sur la base de l'exemple\(\PageIndex{2}\), nous faisons l'observation suivante : il est possible que la limite d'une fonction existe en un point et que la fonction soit définie à ce point, mais la limite de la fonction et la valeur de la fonction au point peuvent être différentes.
Utilisez le graphique de\(h(x)\) la figure\(\PageIndex{5}\) pour évaluer\(\displaystyle \lim_{x \to 2}h(x)\), si possible.
![Un graphe de la fonction h (x), qui est une parabole représentée graphiquement sur [-2,5, 5]. Il existe un cercle ouvert où le sommet doit se trouver au point (2, -1).](https://math.libretexts.org/@api/deki/files/7966/imageedit_13_2727890618.png)
- Allusion
-
À quelle\(y\) valeur s'approche la fonction selon l'approche\(x\) -values\(2\) ?
- Solution
-
\(\displaystyle \lim_{x \to 2}h(x)=−1.\)
L'examen d'un tableau de valeurs fonctionnelles ou du graphe d'une fonction nous donne un aperçu utile de la valeur de la limite d'une fonction à un point donné. Cependant, ces techniques reposent trop sur des conjectures. Nous devons à terme développer des méthodes alternatives d'évaluation des limites. Ces nouvelles méthodes sont de nature plus algébrique et nous les explorerons dans la section suivante ; toutefois, à ce stade, nous introduisons deux limites spéciales qui sont à la base des techniques à venir.
\(a\)Soyons un nombre réel et\(c\) une constante.
- \(\displaystyle \lim_{x \to a}x=a\)
- \(\displaystyle \lim_{x \to a}c=c\)
Nous pouvons faire les observations suivantes à propos de ces deux limites.
- Pour la première limite, observez qu'à mesure que l'on\(x\) approche\(a\), il en va de même\(f(x)\), parce que\(f(x)=x\). Par conséquent,\(\displaystyle \lim_{x \to a}x=a\).
- Pour la deuxième limite, considérez le tableau\(\PageIndex{4}\).
| \(x\) | \(f(x)=c\) | \(x\) | \(f(x)=c\) |
|---|---|---|---|
| \ (x \) » style="text-align:center ; « >\(a-0.1\) | \ (f (x) =c \) » style="text-align:center ; « >\(c\) | \ (x \) » style="text-align:center ; « >\(a+0.1\) | \ (f (x) =c \) » style="text-align:center ; « >\(c\) |
| \ (x \) » style="text-align:center ; « >\(a-0.01\) | \ (f (x) =c \) » style="text-align:center ; « >\(c\) | \ (x \) » style="text-align:center ; « >\(a+0.01\) | \ (f (x) =c \) » style="text-align:center ; « >\(c\) |
| \ (x \) » style="text-align:center ; « >\(a-0.001\) | \ (f (x) =c \) » style="text-align:center ; « >\(c\) | \ (x \) » style="text-align:center ; « >\(a+0.001\) | \ (f (x) =c \) » style="text-align:center ; « >\(c\) |
| \ (x \) » style="text-align:center ; « >\(a-0.0001\) | \ (f (x) =c \) » style="text-align:center ; « >\(c\) | \ (x \) » style="text-align:center ; « >\(a+0.0001\) | \ (f (x) =c \) » style="text-align:center ; « >\(c\) |
Notez que pour toutes les valeurs de\(x\) (qu'elles soient proches ou non\(a\)), les valeurs\(f(x)\) restent constantes à\(c\). Nous n'avons pas d'autre choix que de conclure\(\displaystyle \lim_{x \to a}c=c\).
L'existence d'une limite
Lorsque nous examinons la limite dans l'exemple suivant, gardez à l'esprit que pour que la limite d'une fonction existe à un point, les valeurs fonctionnelles doivent s'approcher d'une seule valeur réelle à ce point. Si les valeurs fonctionnelles ne s'approchent pas d'une valeur unique, la limite n'existe pas.
Évaluez\(\displaystyle\lim_{x \to 0}\sin(1/x)\) à l'aide d'un tableau de valeurs.
Solution
Le tableau\(\PageIndex{5}\) répertorie les valeurs de la fonction\(\sin(1/x)\) pour les valeurs données de\(x\).
| \(x\) | \(\sin(1/x)\) | \(x\) | \(\sin(1/x)\) |
|---|---|---|---|
| \ (x \) » style="text-align:center ; « >-0.1 | \ (\ sin (1/x) \) » style="text-align:center ; « >0.544021110889 | \ (x \) » style="text-align:center ; « >0,1 | \ (\ sin (1/x) \) » style="text-align:center ; « >−0.544021110889 |
| \ (x \) » style="text-align:center ; « >-0,01 | \ (\ sin (1/x) \) » style="text-align:center ; « >0.50636564111 | \ (x \) » style="text-align:center ; « >0,01 | \ (\ sin (1/x) \) » style="text-align:center ; « >−0.50636564111 |
| \ (x \) » style="text-align:center ; « >-0.001 | \ (\ sin (1/x) \) » style="text-align:center ; « >−0.8268795405312 | \ (x \) » style="text-align:center ; « >0,001 | \ (\ sin (1/x) \) » style="text-align:center ; « >0.8268795405312 |
| \ (x \) » style="text-align:center ; « >-0,0001 | \ (\ sin (1/x) \) » style="text-align:center ; « >0.305614388888 | \ (x \) » style="text-align:center ; « >0,0001 | \ (\ sin (1/x) \) » style="text-align:center ; « >−0.305614388888 |
| \ (x \) » style="text-align:center ; « >-0,00001 | \ (\ sin (1/x) \) » style="text-align:center ; « >−0.035748797987 | \ (x \) » style="text-align:center ; « >0,00001 | \ (\ sin (1/x) \) » style="text-align:center ; « >0.035748797987 |
| \ (x \) » style="text-align:center ; « >-0.000001 | \ (\ sin (1/x) \) » style="text-align:center ; « >0.349993504187 | \ (x \) » style="text-align:center ; « >0,000001 | \ (\ sin (1/x) \) » style="text-align:center ; « >−0.349993504187 |
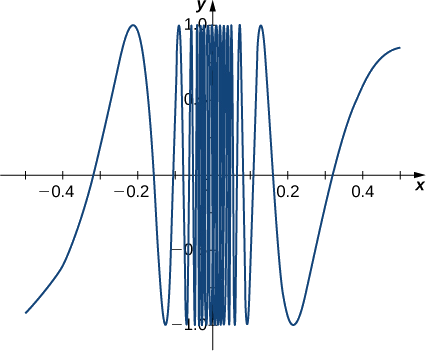
Après avoir examiné le tableau des valeurs fonctionnelles, nous pouvons constater que les\(y\) valeurs -ne semblent pas s'approcher d'une seule valeur. Il semble que la limite n'existe pas. Avant de tirer cette conclusion, adoptons une approche plus systématique. Prenez la séquence de\(x\) valeurs -suivante qui approche\(0\) :
\[\frac{2}{π},\;\frac{2}{3π},\;\frac{2}{5π},\;\frac{2}{7π},\;\frac{2}{9π},\;\frac{2}{11π},\;….\nonumber \]
Les\(y\) valeurs -correspondantes sont
\[1,\;-1,\;1,\;-1,\;1,\;-1,\;....\nonumber \]
À ce stade, nous pouvons en effet conclure que\(\displaystyle \lim_{x \to 0} \sin(1/x)\) cela n'existe pas. (Les mathématiciens abrévent souvent « n'existe pas » en DNE. Ainsi, nous écririons\(\displaystyle \lim_{x \to 0} \sin(1/x)\) DNE.) Le graphique de\(f(x)=\sin(1/x)\) est illustré dans la figure\(\PageIndex{6}\) et donne une image plus claire du comportement\(\sin(1/x)\) des\(x\) approches\(0\). Vous pouvez voir que cela\(\sin(1/x)\) oscille de plus en plus fortement entre\(−1\) et à\(1\) mesure que l'on\(x\) approche\(0\).
Utilisez un tableau de valeurs fonctionnelles pour évaluer\(\displaystyle \lim_{x \to 2}\frac{∣x^2−4∣}{x−2}\), si possible.
- Allusion
-
Utilisez\(x\) les valeurs -1,9, 1,99, 1,999, 1,9999, 1,99999 et 2,1, 2,01, 2,001, 2,0001, 2,00001, 2,00001 dans votre tableau.
- Réponse
-
\(\displaystyle \lim_{x \to 2}\frac{∣x^2−4∣}{x−2}\)n'existe pas.
Limites unilatérales
Parfois, indiquer que la limite d'une fonction n'existe pas à un point ne nous fournit pas suffisamment d'informations sur le comportement de la fonction à ce point précis. Pour voir cela, nous allons maintenant revenir sur la fonction\(g(x)=|x−2|/(x−2)\) introduite au début de la section (voir Figure\(\PageIndex{1}\) (b)). Lorsque nous sélectionnons des valeurs\(x\) proches de\(2\),\(g(x)\) ne s'approche pas d'une seule valeur, de sorte que la limite lorsque nous\(x\) approchons\(2\) n'existe pas, c'est-à-dire\(\displaystyle \lim_{x \to 2}g(x)\) DNE. Cependant, cette déclaration à elle seule ne nous donne pas une image complète du comportement de la fonction autour de la\(x\) valeur\(2\). Pour fournir une description plus précise, nous introduisons l'idée d'une limite unilatérale. Pour toutes les valeurs situées à gauche de\(2\) (ou du côté négatif de\(2\)),\(g(x)=−1\). Ainsi, à mesure que l'on\(x\)\(2\) s'approche par la gauche, on\(g(x)\) approche\(−1\). Mathématiquement, nous disons que la limite à mesure que l'on\(x\) s'approche\(2\) de la gauche est\(−1\). Symboliquement, nous exprimons cette idée comme
\[\lim_{x \to 2^−}g(x)=−1. \nonumber \]
De même, lorsque l'on\(x\) s'approche\(2\) par la droite (ou par le côté positif), on\(g(x)\) s'approche\(1\). Symboliquement, nous exprimons cette idée comme
\[\lim_{x \to 2^+}g(x)=1.\nonumber \]
Nous pouvons maintenant présenter une définition informelle des limites unilatérales.
Nous définissons deux types de limites unilatérales.
Limite depuis la gauche :
\(f(x)\)Soit une fonction définie à toutes les valeurs d'un intervalle ouvert du formulaire\((z,a)\), et\(L\) soit un nombre réel. Si les valeurs de la fonction se\(f(x)\) rapprochent du nombre réel lorsque\(L\) les valeurs de\(x\) (où\(x<a\)) s'approchent du nombre\(a\), alors nous disons que\(L\) c'est la limite\(a\) des\(f(x)\)\(x\) approches par la gauche. Symboliquement, nous exprimons cette idée comme
\[\lim_{x \to a^−}f(x)=L. \nonumber \]
Limite depuis la droite :
\(f(x)\)Soit une fonction définie à toutes les valeurs d'un intervalle ouvert du formulaire\((a,c)\), et\(L\) soit un nombre réel. Si les valeurs de la fonction se\(f(x)\) rapprochent du nombre réel lorsque\(L\) les valeurs de\(x\) (où\(x>a\)) s'approchent du nombre\(a\), alors nous disons que\(L\) c'est la limite\(a\) des\(f(x)\)\(x\) approches par la droite. Symboliquement, nous exprimons cette idée comme
\[\lim_{x \to a^+}f(x)=L. \nonumber \]
Pour la fonction\(f(x)=\begin{cases}x+1, & \text{if }x<2\\ x^2−4, & \text{if }x≥2\end{cases}\), évaluez chacune des limites suivantes.
- \(\displaystyle \lim_{x \to 2^−}f(x)\)
- \(\displaystyle \lim_{x \to 2^+}f(x)\)
Solution
Nous pouvons à nouveau utiliser des tables de valeurs fonctionnelles. Observez dans le tableau\(\PageIndex{6}\) que pour les valeurs\(x\) inférieures à\(2\), nous utilisons\(f(x)=x+1\) et pour les valeurs\(x\) supérieures à\(2\), nous utilisons\(f(x)=x^2−4.\)
| \(x\) | \(f(x)=x+1\) | \(x\) | \(f(x)=x^2-4\) |
|---|---|---|---|
| \ (x \) » style="text-align:center ; « >1,9 | \ (f (x) =x+1 \) » style="text-align:center ; « >2,9 | \ (x \) » style="text-align:center ; « >2.1 | \ (f (x) =x^2-4 \) » style="text-align:center ; « >0,41 |
| \ (x \) » style="text-align:center ; « >1,99 | \ (f (x) =x+1 \) » style="text-align:center ; « >2,99 | \ (x \) » style="text-align:center ; « >2.01 | \ (f (x) =x^2-4 \) » style="text-align:center ; « >0,0401 |
| \ (x \) » style="text-align:center ; « >1.999 | \ (f (x) =x+1 \) » style="text-align:center ; « >2,999 | \ (x \) » style="text-align:center ; « >2,001 | \ (f (x) =x^2-4 \) » style="text-align:center ; « >0,004001 |
| \ (x \) » style="text-align:center ; « >1,9999 | \ (f (x) =x+1 \) » style="text-align:center ; « >2,9999 | \ (x \) » style="text-align:center ; « >2.0001 | \ (f (x) =x^2-4 \) » style="text-align:center ; « >0.00040001 |
| \ (x \) » style="text-align:center ; « >1.99999 | \ (f (x) =x+1 \) » style="text-align:center ; « >2,99999 | \ (x \) » style="text-align:center ; « >2.00001 | \ (f (x) =x^2-4 \) » style="text-align:center ; « >0,0000400001 |
Sur la base de ce tableau, nous pouvons conclure que a.\(\displaystyle \lim_{x \to 2^−}f(x)=3\) et b.\(\displaystyle \lim_{x \to 2^+}f(x)=0\) Par conséquent, la limite (bilatérale) de\(f(x)\) n'existe pas à\(x=2\). La figure\(\PageIndex{7}\) montre un graphique de ces limites\(f(x)\) et renforce notre conclusion à ce sujet.
Utilisez un tableau de valeurs fonctionnelles pour estimer les limites suivantes, si possible.
- \(\displaystyle \lim_{x→2^−}\frac{∣x^2−4∣}{x−2}\)
- \(\displaystyle \lim_{x→2^+}\frac{∣x^2−4∣}{x−2}\)
- Allusion
-
Utilisez\(x\) les valeurs -1,9, 1,99, 1,999, 1,9999, 1,99999 pour estimer\(\displaystyle \lim_{x→2^−}\frac{∣x^2−4∣}{x−2}\).
Utilisez\(x\) les valeurs -2.1, 2,01, 2,001, 2,0001, 2,00001 pour estimer\(\displaystyle \lim_{x→2^+}\frac{∣x^2−4∣}{x−2}.\)
(Ces tableaux sont disponibles à la suite d'un problème précédent de Checkpoint.)
- Solution a
-
un.\(\displaystyle \lim_{x→2^−}\frac{∣x^2−4∣}{x−2}=−4\)
- Solution b
-
\(\displaystyle \lim_{x→2^+}\frac{∣x^2−4∣}{x−2}=4\)
Examinons maintenant la relation entre la limite d'une fonction en un point et les limites depuis la droite et la gauche à ce point. Il semble clair que si la limite de droite et la limite de gauche ont une valeur commune, alors cette valeur commune est la limite de la fonction à ce point. De même, si la limite de gauche et la limite de droite prennent des valeurs différentes, la limite de la fonction n'existe pas. Ces conclusions sont résumées dans la note.
\(f(x)\)Soit une fonction définie à toutes les valeurs d'un intervalle ouvert contenant\(a\), à l'exception éventuelle de\(a\) elle-même, et\(L\) soit un nombre réel. Ensuite,
\[\lim_{x \to a}f(x)=L \nonumber \]
si et seulement si\(\displaystyle \lim_{x \to a^−}f(x)=L\) et\(\displaystyle \lim_{x \to a^+} f(x)=L\).
Limites infinies
L'évaluation de la limite d'une fonction à un point ou l'évaluation de la limite d'une fonction de la droite et de la gauche à un point nous aide à caractériser le comportement d'une fonction autour d'une valeur donnée. Comme nous le verrons, nous pouvons également décrire le comportement de fonctions qui n'ont pas de limites finies.
Nous allons maintenant examiner\(h(x)=1/(x−2)^2\) la troisième et dernière fonction présentée au début de cette section (voir Figure\(\PageIndex{1}\) (c)). Sur son graphique, nous voyons qu'à mesure que les valeurs de\(x\) s'approchent\(2\), les valeurs de\(h(x)=1/(x−2)^2\) deviennent de plus en plus grandes et, en fait, deviennent infinies. Mathématiquement, nous disons que la limite de l'\(h(x)\)\(x\)approche\(2\) est l'infini positif. Symboliquement, nous exprimons cette idée comme
\[\lim_{x \to 2}h(x)=+∞. \nonumber \]
Plus généralement, nous définissons des limites infinies comme suit :
Nous définissons trois types de limites infinies.
Limites infinies à partir de la gauche :\(f(x)\) Soit une fonction définie à toutes les valeurs dans un intervalle ouvert du formulaire\((b,a)\).
i. Si les valeurs d'\(f(x)\)augmentation sans limite lorsque les valeurs de\(x\) (où\(x<a\)) se rapprochent du nombre\(a\), alors nous disons que la limite à mesure que l'on\(x\) s'approche\(a\) de la gauche est une infinité positive et nous écrivons\[\lim_{x \to a^−}f(x)=+∞. \nonumber \]
ii. Si les valeurs de\(f(x)\) décroissent sans limite lorsque les valeurs de\(x\) (où\(x<a\)) s'approchent du nombre\(a\), alors nous disons que la limite à mesure que l'on\(x\) s'approche\(a\) de la gauche est une infinité négative et nous écrivons\[\lim_{x \to a^−}f(x)=−∞. \nonumber \]
Limites infinies à partir de la droite :\(f(x)\) Soit une fonction définie à toutes les valeurs dans un intervalle ouvert du formulaire\((a,c)\).
i. Si les valeurs d'\(f(x)\)augmentation sans limite lorsque les valeurs de\(x\) (où\(x>a\)) s'approchent du nombre\(a\), alors nous disons que la limite à mesure que l'on\(x\) s'approche\(a\) de la droite est une infinité positive et nous écrivons\[\lim_{x \to a^+}f(x)=+∞. \nonumber \]
ii. Si les valeurs de\(f(x)\) décroissent sans limite lorsque les valeurs de\(x\) (où\(x>a\)) s'approchent du nombre\(a\), alors nous disons que la limite à mesure que l'on\(x\) s'approche\(a\) de la droite est une infinité négative et nous écrivons\[\lim_{x \to a^+}f(x)=−∞. \nonumber \]
Limite infinie bilatérale :\(f(x)\) À définir pour tous\(x≠a\) dans un intervalle ouvert contenant\(a\)
i. Si les valeurs d'\(f(x)\)augmentation sans limite lorsque les valeurs de\(x\) (où\(x≠a\)) s'approchent du nombre\(a\), alors nous disons que la limite à l'\(x\)approche\(a\) est une infinité positive et nous écrivons\[\lim_{x \to a} f(x)=+∞. \nonumber \]
ii. Si les valeurs de\(f(x)\) décroissent sans limite lorsque les valeurs de\(x\) (où\(x≠a\)) s'approchent du nombre\(a\), alors nous disons que la limite à l'\(x\)approche\(a\) est négative de l'infini et nous écrivons\[\lim_{x \to a}f(x)=−∞. \nonumber \]
Il est important de comprendre que lorsque nous écrivons des instructions telles que\(\displaystyle \lim_{x \to a}f(x)=+∞\) ou que\(\displaystyle \lim_{x \to a}f(x)=−∞\) nous décrivons le comportement de la fonction, telle que nous venons de la définir. Nous ne prétendons pas qu'il existe une limite. Pour que la limite d'une fonction\(f(x)\) existe\(a\), elle doit s'approcher d'un nombre réel à\(L\) mesure que l'on\(x\) s'approche\(a\). Cela dit, si, par exemple\(\displaystyle \lim_{x \to a}f(x)=+∞\), nous écrivons toujours\(\displaystyle \lim_{x \to a}f(x)=+∞\) plutôt que du\(\displaystyle \lim_{x \to a}f(x)\) DNE.
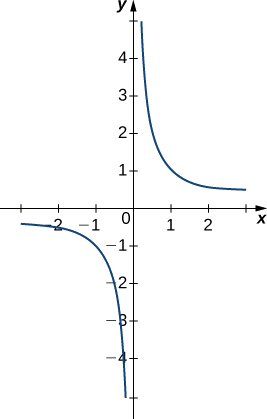
Évaluez chacune des limites suivantes, si possible. Utilisez un tableau de valeurs fonctionnelles et un graphique\(f(x)=1/x\) pour confirmer votre conclusion.
- \(\displaystyle \lim_{x \to 0^−} \frac{1}{x}\)
- \(\displaystyle \lim_{x \to 0^+} \frac{1}{x}\)
- \( \displaystyle \lim_{x \to 0}\frac{1}{x}\)
Solution
Commencez par créer un tableau de valeurs fonctionnelles.
| \(x\) | \(\dfrac{1}{x}\) | \(x\) | \(\dfrac{1}{x}\) |
|---|---|---|---|
| \ (x \) » style="text-align:center ; « >-0.1 | \ (\ dfrac {1} {x} \) » style="text-align:center ; « >-10 | \ (x \) » style="text-align:center ; « >0,1 | \ (\ dfrac {1} {x} \) » style="text-align:center ; « >10 |
| \ (x \) » style="text-align:center ; « >-0,01 | \ (\ dfrac {1} {x} \) » style="text-align:center ; « >-100 | \ (x \) » style="text-align:center ; « >0,01 | \ (\ dfrac {1} {x} \) » style="text-align:center ; « >100 |
| \ (x \) » style="text-align:center ; « >-0.001 | \ (\ dfrac {1} {x} \) » style="text-align:center ; « >-1000 | \ (x \) » style="text-align:center ; « >0,001 | \ (\ dfrac {1} {x} \) » style="text-align:center ; « >1000 |
| \ (x \) » style="text-align:center ; « >-0,0001 | \ (\ dfrac {1} {x} \) » style="text-align:center ; « >-10 000 | \ (x \) » style="text-align:center ; « >0,0001 | \ (\ dfrac {1} {x} \) » style="text-align:center ; « >10 000 |
| \ (x \) » style="text-align:center ; « >-0,00001 | \ (\ dfrac {1} {x} \) » style="text-align:center ; « >-100 000 | \ (x \) » style="text-align:center ; « >0,00001 | \ (\ dfrac {1} {x} \) » style="text-align:center ; « >100 000 |
| \ (x \) » style="text-align:center ; « >-0.000001 | \ (\ dfrac {1} {x} \) » style="text-align:center ; « >-1 000 000 | \ (x \) » style="text-align:center ; « >0,000001 | \ (\ dfrac {1} {x} \) » style="text-align:center ; « >1 000 000 |
a. Les valeurs de\(1/x\) diminution sans limite à mesure que l'on\(x\) s'approche\(0\) de la gauche. Nous concluons que
\[\lim_{x \to 0^−}\frac{1}{x}=−∞.\nonumber \]
b. Les valeurs d'\(1/x\)augmentation sans limite à mesure que l'on\(0\) se\(x\) rapproche de la droite. Nous concluons que
\[\lim_{x \to 0^+}\frac{1}{x}=+∞. \nonumber \]
c. Comme nous\(\displaystyle \lim_{x \to 0^+}\frac{1}{x}=+∞\) avons\(\displaystyle \lim_{x \to 0^−}\frac{1}{x}=−∞\) des valeurs différentes, nous concluons que
\[\lim_{x \to 0}\frac{1}{x}\quad\text{DNE.} \nonumber \]
Le graphique de\(f(x)=1/x\) la figure\(\PageIndex{8}\) confirme ces conclusions.
Évaluez chacune des limites suivantes, si possible. Utilisez un tableau de valeurs fonctionnelles et un graphique\(f(x)=1/x^2\) pour confirmer votre conclusion.
- \(\displaystyle \lim_{x \to 0^−}\frac{1}{x^2}\)
- \(\displaystyle \lim_{x \to 0^+}\frac{1}{x^2}\)
- \(\displaystyle \lim_{x \to 0}\frac{1}{x^2}\)
Limites infinies à partir d'entiers positifs
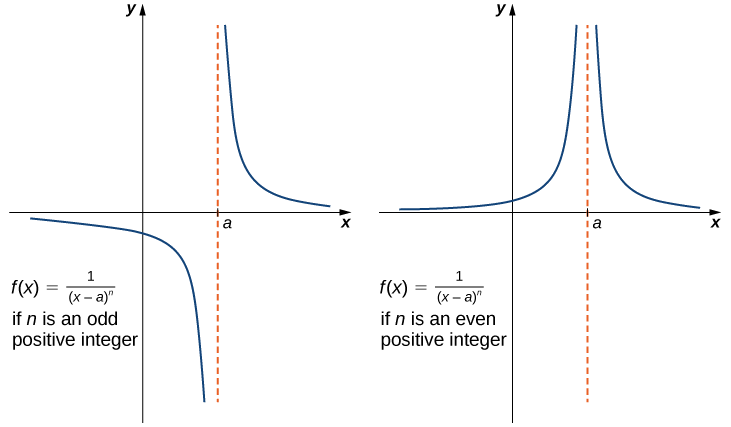
Si\(n\) est un entier pair positif, alors
\[\lim_{x \to a}\frac{1}{(x−a)^n}=+∞.\label{infLim1} \]
Si\(n\) est un entier impair positif, alors
\[\lim_{x \to a^+}\frac{1}{(x−a)^n}=+∞\label{infLim2} \]
et
\[\lim_{x \to a^−}\frac{1}{(x−a)^n}=−∞.\label{infLim3} \]
Nous devons également souligner que dans les graphes de\(f(x)=1/(x−a)^n\), les points du graphique dont les\(x\) coordonnées sont très proches de\(a\) sont très proches de la ligne verticale\(x=a\). C'est-à-dire qu'à mesure que l'on\(x\) approche\(a\), les points du graphique de\(f(x)\) sont plus proches de la droite\(x=a\). La droite\(x=a\) est appelée asymptote verticale du graphe. Nous définissons formellement une asymptote verticale comme suit :
\(f(x)\)Soyons une fonction. Si l'une des conditions suivantes est remplie, la ligne\(x=a\) est une asymptote verticale de\(f(x)\).
\[\lim_{x \to a^−}f(x)=+∞ \nonumber \]
\[\lim_{x \to a^−}f(x)=−∞ \nonumber \]
\[\lim_{x \to a^+}f(x)=+∞ \nonumber \]
\[\lim_{x \to a^+}f(x)=−∞ \nonumber \]
\[\lim_{x \to a}f(x)=+∞ \nonumber \]
\[\lim_{x \to a}f(x)=−∞ \nonumber \]
Évaluez chacune des limites suivantes à l'aide des équations \ ref {InFlim1}, \ ref {InFlim2} et \ ref {InFlim3} ci-dessus. Identifiez toutes les asymptotes verticales de la fonction\(f(x)=1/(x+3)^4.\)
- \(\displaystyle \lim_{x \to −3^−}\frac{1}{(x+3)^4}\)
- \(\displaystyle \lim_{x \to −3^+}\frac{1}{(x+3)^4}\)
- \(\displaystyle \lim_{x \to −3}\frac{1}{(x+3)^4}\)
Solution
Nous pouvons utiliser directement les équations ci-dessus.
- \(\displaystyle \lim_{x \to −3^−}\frac{1}{(x+3)^4}=+∞\)
- \(\displaystyle \lim_{x \to −3^+}\frac{1}{(x+3)^4}=+∞\)
- \(\displaystyle \lim_{x \to −3}\frac{1}{(x+3)^4}=+∞\)
La fonction\(f(x)=1/(x+3)^4\) possède une asymptote verticale de\(x=−3\).
Évaluez chacune des limites suivantes. Identifiez toutes les asymptotes verticales de la fonction\(f(x)=\dfrac{1}{(x−2)^3}\).
- \(\displaystyle \lim_{x→2^−}\frac{1}{(x−2)^3}\)
- \(\displaystyle \lim_{x→2^+}\frac{1}{(x−2)^3}\)
- \(\displaystyle \lim_{x→2}\frac{1}{(x−2)^3}\)
- Répondez à une
-
\(\displaystyle \lim_{x→2^−}\frac{1}{(x−2)^3}=−∞\)
- Réponse b
-
\(\displaystyle \lim_{x→2^+}\frac{1}{(x−2)^3}=+∞\)
- Réponse c
-
\(\displaystyle \lim_{x→2}\frac{1}{(x−2)^3}\)FAIT. La ligne\(x=2\) est l'asymptote verticale de\(f(x)=1/(x−2)^3.\)
Dans l'exemple suivant, nous utilisons notre connaissance des différents types de limites pour analyser le comportement d'une fonction à différents points.
Utilisez le graphique de\(f(x)\) la figure\(\PageIndex{10}\) pour déterminer chacune des valeurs suivantes :
- \(\displaystyle \lim_{x \to −4^−}f(x)\);\(\displaystyle \lim_{x \to −4^+}f(x)\) ;\(\displaystyle \lim_{x→−4}f(x);\;f(−4)\)
- \(\displaystyle \lim_{x \to −2^−}f(x\))\(\displaystyle \lim_{x \to −2^+}f(x)\) ;\(\displaystyle \lim_{x→−2}f(x);\;f(−2)\)
- \( \displaystyle \lim_{x \to 1^−}f(x)\);\(\displaystyle \lim_{x \to 1^+}f(x)\) ;\(\displaystyle \lim_{x \to 1}f(x);\;f(1)\)
- \( \displaystyle \lim_{x \to 3^−}f(x)\);\(\displaystyle \lim_{x \to 3^+}f(x)\) ;\(\displaystyle \lim_{x \to 3}f(x);\;f(3)\)
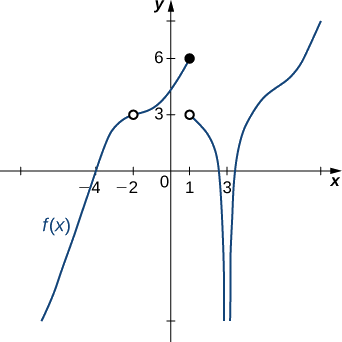
Solution
En utilisant les définitions ci-dessus et le graphique à titre de référence, nous arrivons aux valeurs suivantes :
- \(\displaystyle \lim_{x \to −4^−}f(x)=0\);\(\displaystyle \lim_{x \to −4^+}f(x)=0\) ;\(\displaystyle \lim_{x \to −4}f(x)=0;\;f(−4)=0\)
- \(\displaystyle \lim_{x \to −2^−}f(x)=3\);\(\displaystyle \lim_{x \to −2^+}f(x)=3\) ;\(\displaystyle \lim_{x \to −2}f(x)=3;\;f(−2)\) n'est pas défini
- \(\displaystyle \lim_{x \to 1^−}f(x)=6\)\(\displaystyle \lim_{x \to 1^+}f(x)=3\);\(\displaystyle \lim_{x \to 1}f(x)\) TERMINÉ ;\(f(1)=6\)
- \(\displaystyle \lim_{x \to 3^−}f(x)=−∞\);\(\displaystyle \lim_{x \to 3^+}f(x)=−∞\) ;\(\displaystyle \lim_{x \to 3}f(x)=−∞\) ;\(f(3)\) n'est pas défini
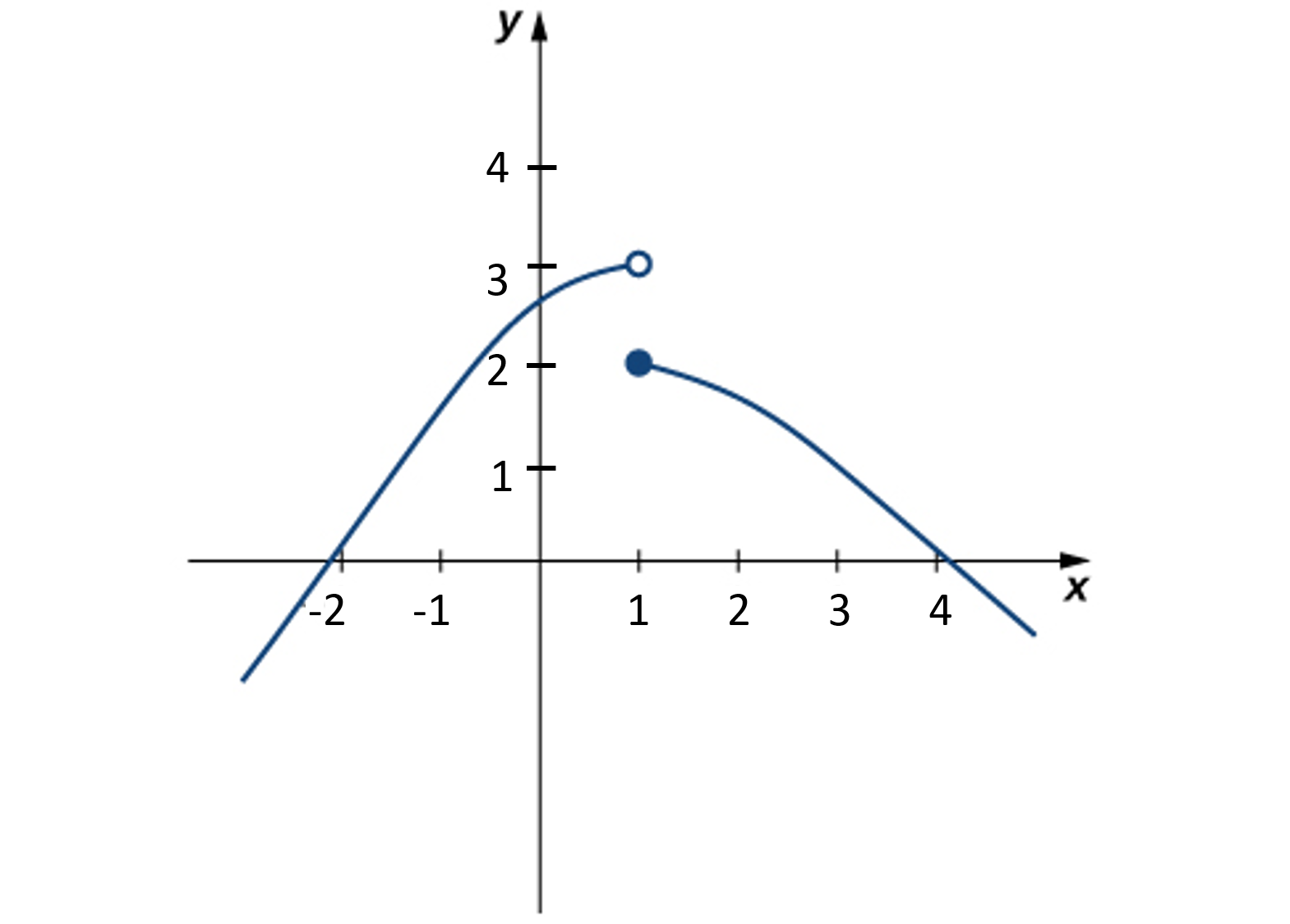
\(\displaystyle\lim_{x \to 1}f(x)\)Évaluez\(f(x)\) comme indiqué ici :
- Allusion
-
Comparez la limite depuis la droite avec la limite depuis la gauche.
- Réponse
-
\(\displaystyle\lim_{x \to 1}f(x)\)n'existe pas
Dans l'ouverture du chapitre, nous avons expliqué brièvement comment Albert Einstein a montré qu'il existe une limite à la vitesse à laquelle un objet peut se déplacer. D'après l'équation d'Einstein pour la masse d'un objet en mouvement
\[m=\dfrac{m_0}{\sqrt{1−\frac{v^2}{c^2}}}, \nonumber \]
quelle est la valeur de cette borne ?

Solution
Notre point de départ est l'équation d'Einstein pour la masse d'un objet en mouvement,
\[m=\dfrac{m_0}{\sqrt{1−\frac{v^2}{c^2}}}, \nonumber \]
où\(m_0\) est la masse de l'objet au repos,\(v\) sa vitesse et\(c\) la vitesse de la lumière. Pour voir comment la masse change à haute vitesse, nous pouvons représenter graphiquement le rapport\(m/m_0\) des masses en fonction du rapport des vitesses\(v/c\) (Figure\(\PageIndex{13}\)).
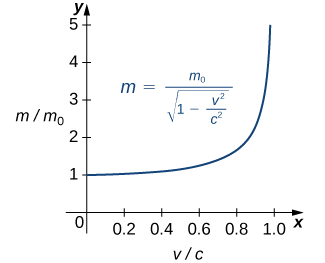
Nous pouvons voir que lorsque le rapport des vitesses approche de 1, c'est-à-dire lorsque la vitesse de l'objet s'approche de la vitesse de la lumière, le rapport des masses augmente sans limite. En d'autres termes, la fonction possède une asymptote verticale à\(v/c=1\). Nous pouvons essayer quelques valeurs de ce ratio pour tester cette idée.
| \(v/c\) | \(\sqrt{1-\frac{v^2}{c^2}}\) | \(m/m_o\) |
|---|---|---|
| \ (v/c \) » style="text-align:center » ; « >0,99 | \ (\ sqrt {1- \ frac {v^2} {c^2}} \) » style="text-align:center ; « >0,1411 | \ (m/m_o \) » style="text-align:center » ; « >7,089 |
| \ (v/c \) » style="text-align:center » ; « >0,999 | \ (\ sqrt {1- \ frac {v^2} {c^2}} \) » style="text-align:center ; « >0.0447 | \ (m/m_o \) » style="text-align:center » ; « >22,37 |
| \ (v/c \) » style="text-align:center » ; « >0,9999 | \ (\ sqrt {1- \ frac {v^2} {c^2}} \) » style="text-align:center ; « >0,0141 | \ (m/m_o \) » style="text-align:center » ; >70,7 |
Ainsi, selon le tableau\(\PageIndex{8}\) :, si un objet d'une masse de 100 kg se déplace à 0,9999c, sa masse devient 7071 kg. Comme aucun objet ne peut avoir une masse infinie, nous concluons qu'aucun objet ne peut se déplacer à une vitesse égale ou supérieure à celle de la lumière.
Concepts clés
- Un tableau de valeurs ou un graphique peuvent être utilisés pour estimer une limite.
- Si la limite d'une fonction à un point n'existe pas, il est toujours possible que les limites de gauche et de droite à ce point existent.
- Si les limites d'une fonction à gauche et à droite existent et sont égales, alors la limite de la fonction est cette valeur commune.
- Nous pouvons utiliser des limites pour décrire le comportement infini d'une fonction à un point.
Équations clés
- Définition intuitive de la limite
\(\displaystyle \lim_{x \to a}f(x)=L\)
- Deux limites importantes
\(\displaystyle \lim_{x \to a}x=a \qquad \lim_{x \to a}c=c\)
- Limites unilatérales
\(\displaystyle \lim_{x \to a^−}f(x)=L \qquad \lim_{x \to a^+}f(x)=L\)
- Des limites infinies depuis la gauche
\(\displaystyle \lim_{x \to a^−}f(x)=+∞ \qquad \lim_{x \to a^−} f(x)=−∞\)
- Des limites infinies depuis la droite
\(\displaystyle \lim_{x \to a^+}f(x)=+∞ \qquad \lim_{x \to a^+} f(x)=−∞\)
- Limites infinies bilatérales
\(\displaystyle \lim_{x \to a}f(x)=+∞\):\(\displaystyle \lim_{x \to a^−}f(x)=+∞\) et\(\displaystyle \lim_{x \to a^+} f(x)=+∞\)
\(\displaystyle \lim_{x \to a}f(x)=−∞\):\(\displaystyle \lim_{x \to a^−}f(x)=−∞\) et\(\displaystyle \lim_{x \to a^+} f(x)=−∞\)
Lexique
- limite infinie
- Une fonction a une limite infinie à un point\(a\) si elle augmente ou diminue sans limite à mesure qu'elle approche\(a\)
- définition intuitive de la limite
- Si toutes les valeurs de la fonction se\(f(x)\) rapprochent du nombre réel\(L\) comme les valeurs de l'\(x(≠a)\)approche a,\(f(x)\) s'approche de L
- limite unilatérale
- Une limite unilatérale d'une fonction est une limite prise à gauche ou à droite
- asymptote verticale
- Une fonction possède une asymptote verticale à\(x=a\) si la limite à mesure que l'on s'\(x\)approche\(a\) de la droite ou de la gauche est infinie



Suivez les procédures décrites dans Example\(\PageIndex{5}\).
un\(\displaystyle \lim_{x \to 0^−}\frac{1}{x^2}=+∞\) ;.
b.\(\displaystyle \lim_{x \to 0^+}\frac{1}{x^2}=+∞\) ;
c.\(\displaystyle \lim_{x \to 0}\frac{1}{x^2}=+∞\)
Il est utile de souligner que les fonctions de la forme\(f(x)=1/(x−a)^n\), où n est un entier positif, ont des limites infinies lorsqu'elles s'\(x\)\(a\)approchent de la gauche ou de la droite (Figure\(\PageIndex{9}\)). Ces limites sont résumées dans les définitions ci-dessus.