13.4 : Les séries et leurs notations
- Page ID
- 194885
- Utilisez la notation de sommation.
- Utilisez la formule pour la somme des premiers\(n\) termes d'une série arithmétique.
- Utilisez la formule pour la somme des premiers\(n\) termes d'une série géométrique.
- Utilisez la formule pour obtenir la somme d'une série géométrique infinie.
- Résolvez les problèmes de rente.
Un couple décide de créer un fonds universitaire pour leur fille. Ils prévoient d'investir\($50\) dans le fonds chaque mois. Le fonds verse des intérêts\(6\%\) annuels, composés mensuellement. Combien d'argent auront-ils économisé lorsque leur fille sera prête à entrer à l'université dans des\(6\) années ? Dans cette section, nous allons apprendre comment répondre à cette question. Pour ce faire, nous devons prendre en compte le montant d'argent investi et le montant des intérêts perçus.
Utilisation de la notation de sommation
Pour connaître le montant total du fonds du collège et la somme des montants déposés, il faut additionner les montants déposés chaque mois et les montants gagnés mensuellement. La somme des termes d'une séquence s'appelle une série. Prenons, par exemple, les séries suivantes.
\(3+7+11+15+19+ \ldots \nonumber \)
La somme\(n^{th}\) partielle d'une série est la somme d'un nombre fini de termes consécutifs commençant par le premier terme. La notation\(S_n\) représente la somme partielle.
\[\begin{align} S_1 &= 3 \nonumber \\ S_2 &= 3+7=10 \nonumber \\ S_3 &= 3+7+11=21 \nonumber \\ S_4 &= 3+7+11+15 =36 \nonumber \end{align} \nonumber\]
La notation par sommation est utilisée pour représenter des séries. La notation de sommation est souvent connue sous le nom de notation sigma car elle utilise la lettre majuscule grecque sigma\(\sum\),, pour représenter la somme. La notation par sommation inclut une formule explicite et spécifie le premier et le dernier terme de la série. Une formule explicite pour chaque terme de la série est donnée à droite du sigma. Une variable appelée indice de sommation est écrite sous le sigma. L'indice de sommation est égal à la limite inférieure de la sommation, qui est le nombre utilisé pour générer le premier terme de la série. Le nombre au-dessus du sigma, appelé limite supérieure de la sommation, est le nombre utilisé pour générer le dernier terme d'une série.
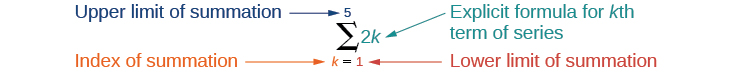
Si nous interprétons la notation donnée, nous voyons qu'elle nous demande de trouver la somme des termes de la série\(a_k=2k\) pour\(k=1\) through\(k=5\). Nous pouvons commencer par remplacer les termes de cette série\(k\) et les énumérer.
\[\begin{align}a_1 &=2(1)=2 \nonumber \\ a_2 &=2(2)=4 \nonumber \\ a_3 &= 2(3)=6 \nonumber \\ a_4 &= 2(4)=8 \nonumber \\ a_5 &= 2(5)=10 \nonumber \end{align} \nonumber\]
Nous pouvons trouver la somme des séries en ajoutant les termes :
\[\sum_{k=1}^{5}2k=2+4+6+8+10=30 \nonumber\]
La somme des premiers\(n\) termes d'une série peut être exprimée en notation de sommation comme suit :
\[\sum_{k=1}^{n}a_k\]
Cette notation nous indique de trouver la somme\(a_k\) de\(k=1\) à\(k=n\).
\(k\)est appelé indice de sommation,\(1\) est la limite inférieure de la sommation et\(n\) est la limite supérieure de la sommation.
Non La limite inférieure de la sommation peut être n'importe quel nombre, mais elle\(1\) est fréquemment utilisée. Nous examinerons des exemples avec des limites de sommation inférieures autres que\(1\).
- Déterminez la limite inférieure de la sommation.
- Déterminez la limite supérieure de la sommation.
- Remplacez chaque valeur\(k\) comprise entre la limite inférieure et la limite supérieure dans la formule.
- Ajoutez pour trouver la somme.
Évaluer
\(\sum_{k=3}^{7}k^2\)
Solution
Selon la notation, la limite inférieure de la sommation est\(3\) et la limite supérieure est\(7\). Nous devons donc trouver la somme\(k^2\) de\(k=3\) à\(k=7\). Nous trouvons les termes de la série en les substituant\(k=3, 4, 5, 6,\) et\(7\) dans la fonction\(k^2\). Nous ajoutons les termes pour trouver la somme.
\[\begin{align}\sum_{k=3}^{7}k^2 &= 3^2+4^2+5^2+6^2+7^2 \nonumber \\[4pt] &= 9+16+25+36+49 \nonumber \\[4pt] &= 135 \nonumber \end{align} \nonumber\]
Évaluer
\(\sum_{k=2}^{5}(3k–1)\)
- Réponse
-
\(38\)
Utilisation de la formule pour les séries arithmétiques
Tout comme nous avons étudié des types particuliers de séquences, nous examinerons des types particuliers de séries. Rappelez-vous qu'une séquence arithmétique est une séquence dans laquelle la différence entre deux termes consécutifs est la différence commune,\(d\). La somme des termes d'une suite arithmétique est appelée série arithmétique. On peut écrire la somme des premiers\(n\) termes d'une série arithmétique comme suit :
\[S_n=a_1+(a_1+d)+(a_1+2d)+...+(a_n–d)+a_n. \nonumber \]
Nous pouvons également inverser l'ordre des termes et écrire la somme comme
\[S_n=a_n+(a_n–d)+(a_n–2d)+...+(a_1+d)+a_1. \nonumber\]
Si nous ajoutons ces deux expressions pour la somme des premiers\(n\) termes d'une série arithmétique, nous pouvons obtenir une formule pour la somme des premiers\(n\) termes de n'importe quelle série arithmétique.
\[S_n=a_1+(a_1+d)+(a_1+2d)+...+(a_n–d)+a_n \nonumber\]
\[\underline{+S_n=a_n+(a_n–d)+(a_n–2d)+...+(a_1+d)+a_1} \nonumber\]
\[2S_n=(a_1+a_n)+(a_1+a_n)+...+(a_1+a_n) \nonumber\]
Comme il y a des\(n\) termes dans la série, nous pouvons simplifier cette somme en
\[2S_n=n(a_1+a_n). \nonumber \]
Nous divisons par\(2\) pour trouver la formule de la somme des premiers\(n\) termes d'une série arithmétique.
\[S_n=\dfrac{n(a_1+a_n)}{2} \nonumber \]
Une série arithmétique est la somme des termes d'une suite arithmétique. La formule pour la somme des premiers\(n\) termes d'une suite arithmétique est
\[S_n=\dfrac{n(a_1+a_n)}{2}\]
- Identifiez\(a_1\) et\(a_n\).
- Déterminez\(n\).
- Substituez des valeurs pour\(a_1\)\(a_n\), et\(n\) dans la formule\(S_n=\dfrac{n(a_1+a_n)}{2}\).
- Simplifiez pour trouver\(S_n\).
Détermine la somme de chaque série arithmétique.
- \(5 + 8 + 11 + 14 + 17 + 20 + 23 + 26 + 29 + 32\)
- \(20 + 15 + 10 +…+ −50\)
- \(\sum_{k=1}^{12}3k−8\)
Solution
- On nous donne\(a_1=5\) et\(a_n=32\).
Comptez le nombre de termes de la séquence à rechercher\(n=10\).
Remplacez les valeurs par\(a_1\)\(a_n\), et\(n\) dans la formule et simplifiez.
\[\begin{align*} S_n&=\dfrac{n(a_1+a_n)}{2}\\ S_{10}&=\dfrac{10(5+32)}{2}\\ &=185 \end{align*}\]
- On nous donne\(a_1=20\) et\(a_n=−50\).
Utilisez la formule du terme général d'une séquence arithmétique pour trouver\(n\).
\[\begin{align*} a_n&=a_1+(n-1)d\\ -50&=20+(n-1)(-5)\\ -70&=(n-1)(-5)\\ 14&=n-1\\ 15&=n \end{align*}\]
Remplacez les valeurs par\(a_1\)\(a_n\),\(n\) dans la formule et simplifiez.
\[\begin{align*} S_n&=\dfrac{n(a_1+a_n)}{2}\\ S_{15}&=\dfrac{15(20-50)}{2}\\ &=-225 \end{align*}\]
- Pour le trouver\(a_1\),\(k=1\) remplacez-le dans la formule explicite donnée.
\[\begin{align*} a_k&=3k-8\\ a_1&=3(1)-8\\ &=-5 \end{align*}\]
C'est ce que nous avons reçu\(n=12\). Pour le trouver\(a_12\),\(k=12\) remplacez-le dans la formule explicite donnée.
\[\begin{align*} a_k&=3k-8\\ a_{12}&=3(12)-8\\ &=28 \end{align*}\]
Remplacez les valeurs par\(a_1\)\(a_n\), et\(n\) dans la formule et simplifiez.
\[\begin{align*} S_n&=\dfrac{n(a_1+a_n)}{2}\\ S_{12}&=\dfrac{12(-5+28)}{2}\\ &=138 \end{align*}\]
Utilisez la formule pour trouver la somme de chaque série arithmétique.
\(1.4 + 1.6 + 1.8 + 2.0 + 2.2 + 2.4 + 2.6 + 2.8 + 3.0 + 3.2 + 3.4\)
- Réponse
-
\(26.4\)
\(13 + 21 + 29 + …+ 69\)
- Réponse
-
\(328\)
\(\sum_{k=1}{10}5−6k\)
- Réponse
-
\(−280\)
Le dimanche après une opération mineure, une femme peut marcher un demi-mile. Chaque dimanche, elle marche un quart de mile supplémentaire. Après des\(8\) semaines, quel sera le nombre total de kilomètres qu'elle aura parcourus ?
Solution
Ce problème peut être modélisé par une série arithmétique avec\(a_1=\dfrac{1}{2}\) et\(d=\dfrac{1}{4}\). Nous recherchons le nombre total de kilomètres parcourus après des\(8\) semaines, donc nous le savons et nous cherchons\(S_8\).\(n=8\) Pour le trouver\(a_8\), nous pouvons utiliser la formule explicite d'une séquence arithmétique.
\[\begin{align*} a_n&=a_1+d(n-1)\\ a_8&=\dfrac{1}{2}+\dfrac{1}{4}(8-1)\\ &=\dfrac{9}{4} \end{align*}\]
Nous pouvons maintenant utiliser la formule pour les séries arithmétiques.
\[\begin{align*} S_n&=\dfrac{n(a_1+a_n)}{2}\\ S_8&=\dfrac{8\left(\dfrac{1}{2}+\dfrac{9}{4}\right)}{2}\\ &=11 \end{align*}\]
Elle aura parcouru un total de\(11\) kilomètres.
Un homme gagne de l'\($100\)argent pendant la première semaine de juin. Chaque semaine, il gagne\($12.50\) plus que la semaine précédente. Au bout de\(12\) plusieurs semaines, combien a-t-il gagné ?
- Réponse
-
\($2,025\)
Utilisation de la formule pour les séries géométriques
Tout comme la somme des termes d'une séquence arithmétique est appelée série arithmétique, la somme des termes d'une séquence géométrique est appelée série géométrique. Rappelons qu'une séquence géométrique est une séquence dans laquelle le rapport de deux termes consécutifs est le ratio commun,\(r\). On peut écrire la somme des premiers\(n\) termes d'une série géométrique comme
\(S_n=a_1+ra_1+r^2a_1+...+r^{n–1}a_1\).
Tout comme pour les séries arithmétiques, nous pouvons effectuer des manipulations algébriques pour dériver une formule pour la somme des premiers\(n\) termes d'une série géométrique. Nous allons commencer par multiplier les deux côtés de l'équation par\(r\).
\(rS_n=ra_1+r^2a_1+r^3a_1+...+r^na_1\)
Ensuite, nous soustrayons cette équation de l'équation d'origine.
\[\begin{align*} S_n&=a_1+ra_1+r^2a_1+...+r^{n-1}a_1\\ \underline{-rS_n}&=\underline{-(ra_1+r^2a_1+r^3a_1+...+r^na_1)}\\ (1-r)S_n&=a_1-r^na_1 \end{align*}\]
Notez que lorsque nous soustrayons, tous les termes sauf le premier terme de l'équation supérieure et le dernier terme de l'équation inférieure s'annulent. Pour obtenir une formule pour\(S_n\), divisez les deux côtés par\((1−r)\).
\(S_n=\dfrac{a_1(1−r^n)}{1−r}\)\(r≠1\)
Une série géométrique est la somme des termes d'une séquence géométrique. La formule pour la somme des premiers\(n\) termes d'une séquence géométrique est représentée par
\(S_n=\dfrac{a_1(1−r^n)}{1−r}\)\(r≠1\)
- Identifiez\(a_1\)\(r\), et\(n\).
- Substituez des valeurs pour\(a_1\)\(r\), et\(n\) dans la formule\(S_n=\dfrac{a_1(1−r^n)}{1−r}\).
- Simplifiez pour trouver\(S_n\).
Utilisez la formule pour trouver la somme partielle indiquée de chaque série géométrique.
- \(S_{11}\)pour la série\(8 + -4 + 2 + …\)
- \(\sum_{ 6}^{k=1}3⋅2k\)
Solution
- \(a_1=8\), et c'est ce que nous avons reçu\(n=11\).
On peut le trouver\(r\) en divisant le deuxième terme de la série par le premier.
\(r=\dfrac{−4}{8}=−\dfrac{1}{2}\)
Remplacez les valeurs par\(a_1\)\(r\), et\(n\) dans la formule et simplifiez.
\[\begin{align*} S_n&=\dfrac{a_1(1-r^n)}{1-r}\\ S_{11}&=\dfrac{8\left(1-{\left(-\dfrac{1}{2}\right)}^{11}\right)}{1-\left(-\dfrac{1}{2}\right)}\\ &\approx 5.336 \end{align*}\]
- Recherchez\(a_1\) en le remplaçant\(k=1\) dans la formule explicite donnée.
\(a_1=3⋅2^1=6\)
Nous pouvons voir à partir de la formule explicite donnée que\(r=2\). La limite supérieure de la sommation est\(6\) donc\(n=6\).
Substituez des valeurs pour\(a_1\)\(r\), et\(n\) dans la formule, et simplifiez.
\[\begin{align*} S_n&=\dfrac{a_1(1-r^n)}{1-r}\\ S_6&=\dfrac{6(1-2^6)}{1-2}\\ &=378 \end{align*}\]
Utilisez la formule pour trouver la somme partielle indiquée de chaque série géométrique.
\(S_{20}\)pour la série\(1,000 + 500 + 250 + …\)
- Réponse
-
\(≈2,000.00\)
\(\sum_{k=1}^{8}3^k\)
- Réponse
-
\(9,840\)
À un nouvel emploi, le salaire de départ d'un employé est de\($26,750\). Il reçoit une augmentation\(1.6\%\) annuelle. Trouvez ses revenus totaux à la fin des\(5\) années.
Solution
Le problème peut être représenté par une série géométrique avec\(a_1=26,750\) ;\(n=5\) ; et\(r=1.016\). Remplacez des valeurs par\(a_1\)\(r\), et\(n\) dans la formule et simplifiez-la pour obtenir le montant total gagné à la fin des\(5\) années.
\[\begin{align*} S_n&=\dfrac{a_1(1-r^n)}{1-r}\\ S_5&=\dfrac{26,750(1-{1.016}^5)}{1-1.016}\\ &\approx 138,099.03 \end{align*}\]
Il aura gagné un total de d'\($138,099.03\)ici la fin des\(5\) années.
À un nouvel emploi, le salaire de départ d'un employé est de\($32,100\). Elle reçoit une augmentation\(2\%\) annuelle. Combien aura-t-elle gagné d'ici la fin des\(8\) années ?
- Réponse
-
\($275,513.31\)
Utilisation de la formule pour la somme d'une série géométrique infinie
Jusqu'à présent, nous n'avons examiné que les séries finies. Parfois, cependant, nous nous intéressons à la somme des termes d'une séquence infinie plutôt qu'à la somme des seuls premiers\(n\) termes. Une série infinie est la somme des termes d'une séquence infinie. Un exemple de série infinie est\(2+4+6+8+...\)
Cette série peut également être écrite en notation de sommation comme\(\sum_{k=1}^{\infty}2k\), où la limite supérieure de la sommation est l'infini. Comme les termes ne tendent pas vers zéro, la somme de la série augmente sans limite à mesure que nous ajoutons de nouveaux termes. La somme de cette série infinie n'est donc pas définie. Lorsque la somme n'est pas un nombre réel, on dit que la série diverge.
Déterminer si la somme d'une série géométrique infinie est définie
Si les termes d'une série géométrique infinie se\(0\) rapprochent, la somme d'une série géométrique infinie peut être définie. Les termes de cette série se présentent comme suit\(0\) :
\(1+0.2+0.04+0.008+0.0016+...\)
Le ratio commun\(r = 0.2\). Au fur et à mesure que cela\(n\) devient très grand, les valeurs de\(r^n\) deviennent très petites et se rapprochent\(0\). Chaque terme successif affecte la somme de manière inférieure à celle du terme précédent. À mesure que chaque terme suivant se rapproche\(0\), la somme des termes se rapproche d'une valeur finie. Les termes de toute série géométrique infinie avec\(−1<r<1\) approche\(0\) ; la somme d'une série géométrique est définie quand\(−1<r<1\).
La somme d'une série infinie est définie si la série est géométrique et\(−1<r<1\).
- Détermine le ratio entre le deuxième terme et le premier terme.
- Détermine le ratio entre le troisième terme et le deuxième terme.
- Continuez ce processus pour vous assurer que le rapport entre un terme et le terme précédent est constant tout au long du processus. Si tel est le cas, la série est géométrique.
- Si un ratio commun,\(r\), a été trouvé à l'étape 3, vérifiez-le\(−1<r<1\). Si tel est le cas, la somme est définie. Dans le cas contraire, la somme n'est pas définie.
Déterminez si la somme de chaque série infinie est définie.
- \(12 + 8 + 4 + …\)
- \(\dfrac{3}{4}+\dfrac{1}{2}+\dfrac{1}{3}+...\)
- \(\sum_{k=1}^{\infty}27⋅{(\dfrac{1}{3})}^k\)
- \(\sum_{k=1}^{\infty}5k\)
Solution
- Le rapport entre le deuxième terme et le premier est\(\dfrac{2}{3}\), qui n'est pas le même que le rapport entre le troisième terme et le second.\(\dfrac{1}{2}\) La série n'est pas géométrique.
- Le rapport entre le deuxième terme et le premier est le même que le rapport entre le troisième terme et le second. La série est géométrique avec un ratio commun de\(\dfrac{2}{3}\). La somme des séries infinies est définie.
- La formule donnée est exponentielle avec une base de\(\dfrac{1}{3}\) ; la série est géométrique avec un ratio commun de\(\dfrac{1}{3}\). La somme des séries infinies est définie.
- La formule donnée n'est pas exponentielle ; la série n'est pas géométrique car les termes augmentent et ne peuvent donc pas donner une somme finie.
Déterminez si la somme de la série infinie est définie.
\(\dfrac{1}{3}+\dfrac{1}{2}+\dfrac{3}{4}+\dfrac{9}{8}+...\)
- Réponse
-
La somme est définie. Elle est géométrique.
\(24+(−12)+6+(−3)+...\)
- Réponse
-
La somme des séries infinies est définie.
\(\sum_{k=1}^{\infty}15⋅{(–0.3)}^k\)
- Réponse
-
La somme des séries infinies est définie.
Trouver les sommes d'une série infinie
Lorsque la somme d'une série géométrique infinie existe, nous pouvons la calculer. La formule de la somme d'une série infinie est liée à la formule de la somme des premiers\(n\) termes d'une série géométrique.
\[S_n=\dfrac{a_1(1−r^n)}{1−r}\]
Nous examinerons une série infinie avec\(r=\dfrac{1}{2}\). Qu'arrive-t-il\(r^n\) aux\(n\) augmentations ?
\[\begin{align*} \left(\dfrac{1}{2}\right)^2&=\dfrac{1}{4}\\ \left(\dfrac{1}{2}\right)^3&=\dfrac{1}{8}\\ \left(\dfrac{1}{2}\right)^4&=\dfrac{1}{16} \end{align*}\]
La valeur de\(r^n\) diminue rapidement. Que se passe-t-il pour des valeurs supérieures de\(n\) ?
\[\begin{align*} {\left(\dfrac{1}{2}\right)}^{10} &= \dfrac{1}{1,024} \\ {\left(\dfrac{1}{2}\right)}^{20} &= \dfrac{1}{1,048,576} \\ {\left(\dfrac{1}{2}\right)}^{30} &= \dfrac{1}{1,073,741,824} \end{align*}\]
Comme\(n\) il devient très grand,\(r^n\) devient très petit. Nous disons que, lorsque les\(n\) augmentations ne sont pas limitées, elles se\(r^n\) rapprochent de 0. À mesure que\(r^n\) des approches\(0\)\(1\),\(−r^n\) des approches\(1\). Lorsque cela se produit, le numérateur approche\(a_1\). Cela nous donne une formule pour la somme d'une série géométrique infinie.
La formule pour la somme d'une série géométrique infinie avec\(−1<r<1\) est
\[S=\dfrac{a_1}{1−r}\]
- Identifiez\(a_1\) et\(r\).
- Confirmez cela\(–1<r<1\).
- Substituez des valeurs pour\(a_1\) et\(r\) dans la formule,\(S=\dfrac{a_1}{1−r}\).
- Simplifiez pour trouver\(S\).
Trouvez la somme, si elle existe, pour les éléments suivants :
- \(10+9+8+7+…\)
- \(248.6+99.44+39.776 + …\)
- \(\sum_{k=1}^{\infty}4,374⋅{(–\dfrac{1}{3})}^{k–1}\)
- \(\sum_{k=1}^{\infty}\dfrac{1}{9}⋅{(\dfrac{4}{3})}^k\)
Solution
- Il n'y a pas de ratio constant ; la série n'est pas géométrique.
- Le rapport est constant ; la série est géométrique. \(a_1=248.6\)et\(r=\dfrac{99.44}{248.6}=0.4\) donc la somme existe. Remplacez\(a_1=248.6\) et\(r=0.4\) dans la formule et simplifiez pour obtenir la somme :
\[ \begin{align*} S&=\dfrac{a_1}{1−r} \\[4pt] &=\dfrac{248.6}{1−0.4} \\[4pt] &=414.\overline{3} \end{align*}\]
- La formule est exponentielle, de sorte que la série est géométrique avec\(r=–\dfrac{1}{3}\). Trouvez\(a_1\) en remplaçant\(k=1\) dans la formule explicite donnée :
\(a_1=4,374⋅{(–\dfrac{1}{3})}^{1–1}=4,374\)
\(a_1=4,374\)Substituez et\(r=−\dfrac{1}{3}\) dans la formule, et simplifiez pour obtenir la somme :
\[ \begin{align*} S&=\dfrac{a_1}{1−r} \\[4pt] &= \dfrac{4,374}{1−\left(−\dfrac{1}{3}\right)} \\[4pt] &= 3,280.5 \end{align*}\]
- La formule est exponentielle, donc la série est géométrique, mais\(r>1\). La somme n'existe pas.
Trouvez une fraction équivalente pour la décimale répétée\(0.\overline{3}\)
Solution
Nous remarquons la décimale répétitive\(0.\overline{3}=0.333...\) afin de pouvoir la réécrire sous forme de somme de termes.
\(0.\overline{3}=0.3+0.03+0.003+...\)
À la recherche d'un modèle, nous réécrivons la somme, en remarquant que nous voyons le premier terme multiplié par au\(0.1\) deuxième terme et le second terme par\(0.1\) au troisième terme.

Remarquez le schéma ; nous multiplions chaque terme consécutif par un ratio commun\(0.1\) commençant par le premier terme de\(0.3\). Ainsi, en remplaçant dans notre formule une somme géométrique infinie, nous avons
\(S_n=\dfrac{a_1}{1−r}=\dfrac{0.3}{1−0.1}=\dfrac{0.3}{0.9}=\dfrac{1}{3}\).
Trouvez la somme, si elle existe.
\(2+23+29+...\)
- Réponse
-
\(3\)
\(\sum_{k=1}^{\infty}0.76k+1\)
- Réponse
-
La série n'est pas géométrique.
\(\sum_{k=1}^{\infty}{\left(−\dfrac{3}{8}\right)}^k\)
- Réponse
-
\(−\dfrac{3}{11}\)
Résoudre les problèmes de rente
Au début de la section, nous avons examiné un problème dans lequel un couple investissait un montant fixe chaque mois dans un fonds universitaire pendant six ans. Une rente est un investissement dans lequel l'acheteur effectue une série de paiements périodiques et égaux. Pour déterminer le montant d'une rente, il faut trouver la somme de tous les paiements et des intérêts perçus. Dans l'exemple, le couple investit\($50\) chaque mois. Il s'agit de la valeur du dépôt initial. Le compte payait des intérêts\(6\%\) annuels, composés mensuellement. Pour déterminer le taux d'intérêt par période de paiement, nous devons diviser le taux d'intérêt\(6\%\) annuel en pourcentage (TAEG) par\(12\). Donc, le taux d'intérêt mensuel est de\(0.5\%\). Nous pouvons multiplier le montant du compte chaque mois par\(100.5\%\) pour trouver la valeur du compte une fois les intérêts ajoutés.
Nous pouvons déterminer la valeur de la rente juste après le dernier dépôt en utilisant une série géométrique avec\(a_1=50\) et\(r=100.5%=1.005\). Après le premier dépôt, la valeur de la rente sera de\($50\). Voyons si nous pouvons déterminer le montant du fonds de l'université et les intérêts gagnés.
Nous pouvons déterminer la valeur de la rente après nn dépôts en utilisant la formule de la somme des nn premiers termes d'une série géométrique. En\(6\) années, il y a des\(72\) mois, donc\(n=72\). Nous pouvons remplacer\(a_1=50\)\(r=1.005\), et\(n=72\) dans la formule, et simplifier pour trouver la valeur de la rente après 6 ans.
\(S_{72}=\dfrac{50(1−{1.005}^{72})}{1−1.005}≈4,320.44\)
Après le dernier dépôt, le couple aura un total de sur\($4,320.44\) le compte. Remarquez, le couple a effectué des\(72\) paiements de\($50\) chacun pour un total de\(72(50) = $3,600\). Cela signifie qu'en raison de la rente, le couple a gagné des\($720.44\) intérêts dans le fonds de leur université.
- Déterminez\(a_1\) la valeur du dépôt initial.
- Déterminez\(n\) le nombre de dépôts.
- Déterminez\(r\).
- Divisez le taux d'intérêt annuel par le nombre de fois par an que l'intérêt est composé.
- Ajoutez 1 à ce montant pour le trouver\(r\).
- Substituez des valeurs pour\(a_1\)\(r\), et\(n\) dans la formule pour la somme des nn premiers termes d'une série géométrique,\(S_n=\dfrac{a_1(1–r^n)}{1–r}\).
- Simplifiez pour trouver\(S_n\), la valeur de la rente après\(n\) les dépôts.
Un dépôt de\($100\) est placé dans un fonds universitaire au début de chaque mois pendant des\(10\) années. Le fonds génère des intérêts\(9\%\) annuels, composés mensuellement et payés à la fin du mois. Quel est le montant sur le compte juste après le dernier dépôt ?
Solution
La valeur du dépôt initial est\($100\) donc\(a_1=100\). Un total de dépôts\(120\) mensuels sont effectués au\(10\) fil des ans, donc\(n=120\). Pour le trouver\(r\), divisez le taux d'intérêt annuel par\(12\) pour trouver le taux d'intérêt mensuel et ajoutez-le\(1\) pour représenter le nouveau dépôt mensuel.
\(r=1+\dfrac{0.09}{12}=1.0075\)
Remplacez\(a_1=100\)\(r=1.0075\), et\(n=120\) dans la formule par la somme des premiers\(n\) termes d'une série géométrique, et simplifiez pour trouver la valeur de la rente.
\(S_{120}=\dfrac{100(1−{1.0075}^{120})}{1−1.0075}≈19,351.43\)
Le compte a donc 19 351,43$ après le dernier dépôt.
Au début de chaque mois,\($200\) est déposé dans un fonds de retraite. Le fonds génère des intérêts\(6\%\) annuels, composés mensuellement et versés sur le compte à la fin du mois. Quel est le montant du compte si les dépôts sont effectués pendant des\(10\) années ?
- Réponse
-
\($92,408.18\)
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires avec les séries.
Équations clés
| somme des premiers\(n\) termes d'une série arithmétique | \(S_n=\dfrac{n(a_1+a_n)}{2}\) |
| somme des premiers\(n\) termes d'une série géométrique | \(S_n=\dfrac{a_1(1−r^n)}{1−r}\)⋅\(r≠1\) |
| somme d'une série géométrique infinie avec\(–1<r< 1\) | \(S_n=\dfrac{a_1}{1−r}\)⋅\(r≠1\) |
Concepts clés
- La somme des termes d'une séquence est appelée série.
- Une notation courante pour les séries est appelée notation de sommation, qui utilise la lettre grecque sigma pour représenter la somme. Voir l'exemple\(\PageIndex{1}\).
- La somme des termes d'une séquence arithmétique est appelée série arithmétique.
- La somme des premiers\(n\) termes d'une série arithmétique peut être trouvée à l'aide d'une formule. Voir Exemple\(\PageIndex{2}\) et Exemple\(\PageIndex{3}\).
- La somme des termes d'une séquence géométrique est appelée série géométrique.
- La somme des premiers\(n\) termes d'une série géométrique peut être trouvée à l'aide d'une formule. Voir Exemple\(\PageIndex{4}\) et Exemple\(\PageIndex{5}\).
- La somme d'une série infinie existe si la série est géométrique avec\(–1<r<1\).
- Si la somme d'une série infinie existe, elle peut être trouvée à l'aide d'une formule. Voir Exemple\(\PageIndex{6}\)\(\PageIndex{7}\), Exemple et Exemple\(\PageIndex{8}\).
- Une rente est un compte sur lequel l'investisseur effectue une série de versements réguliers. La valeur d'une rente peut être déterminée à l'aide de séries géométriques. Voir l'exemple\(\PageIndex{9}\).


