10.6 : Équations paramétriques
- Page ID
- 195541
- Paramétrez une courbe.
- Éliminez le paramètre.
- Trouvez une équation rectangulaire pour une courbe définie de manière paramétrique.
- Trouvez des équations paramétriques pour des courbes définies par des équations rectangulaires.
Considérez la trajectoire que suit une lune lorsqu'elle tourne autour d'une planète, qui tourne simultanément autour du soleil, comme le montre la figure\(\PageIndex{1}\). À tout moment, la lune se trouve à un endroit précis par rapport à la planète. Mais comment écrire et résoudre l'équation de la position de la lune lorsque la distance par rapport à la planète, la vitesse de l'orbite de la lune autour de la planète et la vitesse de rotation autour du soleil sont toutes inconnues ? Nous ne pouvons résoudre que pour une seule variable à la fois.
Dans cette section, nous examinerons des ensembles d'équations données par\(x(t)\) et\(y(t)\) où\(t\) est la variable indépendante du temps. Nous pouvons utiliser ces équations paramétriques dans un certain nombre d'applications lorsque nous recherchons non seulement une position particulière, mais également la direction du mouvement. Au fur et à mesure que nous traçons les valeurs successives de\(t\), l'orientation de la courbe devient claire. C'est l'un des principaux avantages de l'utilisation d'équations paramétriques : nous sommes capables de suivre le mouvement d'un objet le long d'une trajectoire en fonction du temps. Nous commençons cette section par un examen des composants de base des équations paramétriques et de ce que signifie paramétrer une courbe. Nous allons ensuite apprendre à éliminer le paramètre, à traduire les équations d'une courbe définie paramétriquement en équations rectangulaires et à trouver les équations paramétriques pour les courbes définies par des équations rectangulaires.
Paramétrer une courbe
Lorsqu'un objet se déplace le long d'une courbe (ou d'une trajectoire curviligne) dans une direction donnée et dans un laps de temps donné, la position de l'objet dans le plan est donnée par la coordonnée\(x\) - et la coordonnée\(y\) -. Cependant,\(x\) les deux\(y\) peuvent varier dans le temps, de même que les fonctions du temps. Pour cette raison, nous ajoutons une autre variable, le paramètre, dont les deux fonctions\(x\) et\(y\) sont dépendantes. Dans l'exemple de l'ouvreur de section, le paramètre est temps,\(t\). La\(x\) position de la lune à l'heure\(t\),, est représentée par la fonction\(x(t)\), et la\(y\) position de la lune à l'heure\(t\), est représentée par la fonction\(y(t)\). Ensemble,\(x(t)\) et\(y(t)\) sont appelées équations paramétriques, et génèrent une paire ordonnée\((x(t), y(t))\). Les équations paramétriques décrivent principalement le mouvement et la direction.
Lorsque nous paramétrons une courbe, nous traduisons une seule équation en deux variables, telles que\(x\) et\(y\), en une paire équivalente d'équations en trois variables\(x\),\(y\), et\(t\). L'une des raisons pour lesquelles nous paramétrons une courbe est que les équations paramétriques fournissent plus d'informations, notamment la direction du mouvement de l'objet dans le temps.
Lorsque nous dessinons des équations paramétriques, nous pouvons observer les comportements individuels de\(x\) et de\(y\). Un certain nombre de formes ne peuvent pas être représentées dans le formulaire\(y=f(x)\), ce qui signifie qu'il ne s'agit pas de fonctions. Par exemple, considérez le graphe d'un cercle, donné sous la forme\(r^2=x^2+y^2\). Résoudre pour\(y\) donner\(y=\pm \sqrt{r^2−x^2}\), ou deux équations :\(y_1=\sqrt{r^2−x^2}\) et\(y_2=−\sqrt{r^2−x^2}\). Si nous dessinons un graphique\(y_1\) et\(y_2\) ensemble, le graphique ne passera pas le test de la ligne verticale, comme le montre la figure\(\PageIndex{2}\). Ainsi, l'équation du graphe d'un cercle n'est pas une fonction.
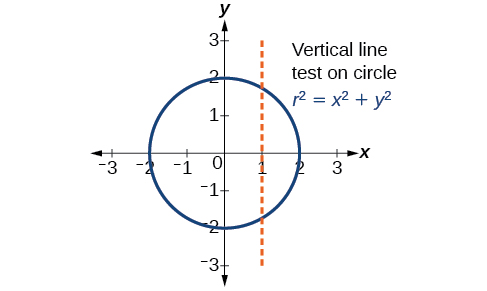
Toutefois, si nous devions représenter graphiquement chaque équation séparément, chacune passerait le test de la ligne verticale et représenterait donc une fonction. Dans certains cas, le concept de division de l'équation d'un cercle en deux fonctions est similaire au concept de création d'équations paramétriques, car nous utilisons deux fonctions pour produire une non-fonction. Cela deviendra plus clair à mesure que nous avancerons.
Supposons qu'\(t\)il s'agisse d'un nombre sur un intervalle,\(I\). L'ensemble de paires ordonnées\((x(t), y(t))\), où\(x=f(t)\) et\(y=g(t)\), forme une courbe plane en fonction du paramètre\(t\). Les équations\(x=f(t)\) et\(y=g(t)\) sont les équations paramétriques.
Paramétrez la courbe\(y=x^2−1\) en laissant\(x(t)=t\). Tracez les deux équations
Solution
Si\(x(t)=t\), alors pour trouver,\(y(t)\) nous remplaçons la variable\(x\) par l'expression donnée dans\(x(t)\). En d'autres termes,\(y(t)=t^2−1\) .Créez un tableau de valeurs similaire à Tableau\(\PageIndex{1}\) et esquissez le graphique.
| \(t\) | \(x(t)\) | \(y(t)\) |
|---|---|---|
| \ (t \) « >\(−4\) | \ (x (t) \) « >\(−4\) | \ (y (t) \) « >\(y(−4)={(−4)}^2−1=15\) |
| \ (t \) « >\(−3\) | \ (x (t) \) « >\(−3\) | \ (y (t) \) « >\(y(−3)={(−3)}^2−1=8\) |
| \ (t \) « >\(−2\) | \ (x (t) \) « >\(−2\) | \ (y (t) \) « >\(y(−2)={(−2)}^2−1=3\) |
| \ (t \) « >\(−1\) | \ (x (t) \) « >\(−1\) | \ (y (t) \) « >\(y(−1)={(−1)}^2−1=0\) |
| \ (t \) « >\(0\) | \ (x (t) \) « >\(0\) | \ (y (t) \) « >\(y(0)={(0)}^2−1=−1\) |
| \ (t \) « >\(1\) | \ (x (t) \) « >\(1\) | \ (y (t) \) « >\(y(1)={(1)}^2−1=0\) |
| \ (t \) « >\(2\) | \ (x (t) \) « >\(2\) | \ (y (t) \) « >\(y(2)={(2)}^2−1=3\) |
| \ (t \) « >\(3\) | \ (x (t) \) « >\(3\) | \ (y (t) \) « >\(y(3)={(3)}^2−1=8\) |
| \ (t \) « >\(4\) | \ (x (t) \) « >\(4\) | \ (y (t) \) « >\(y(4)={(4)}^2−1=15\) |
Voir les graphiques de la figure\(\PageIndex{3}\). Il peut être utile d'utiliser la fonction TRACE d'une calculatrice graphique pour voir comment les points sont générés à mesure que les points\(t\) augmentent.
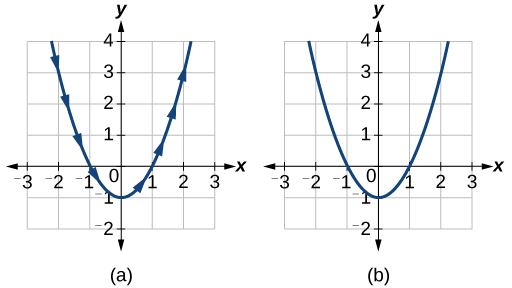
Analyse
Les flèches indiquent la direction dans laquelle la courbe est générée. Notez que la courbe est identique à la courbe de\(y=x^2−1\).
Construisez un tableau de valeurs et tracez les équations paramétriques :\(x(t)=t−3\),\(y(t)=2t+4\) ;\(−1≤t≤2\).
- Réponse
-
\(t\) \(x(t)\) \(y(t)\) \ (t \) « >\(-1\) \ (x (t) \) « >\(-4\) \ (y (t) \) « >\(2\) \ (t \) « >\(0\) \ (x (t) \) « >\(-3\) \ (y (t) \) « >\(4\) \ (t \) « >\(1\) \ (x (t) \) « >\(-2\) \ (y (t) \) « >\(6\) \ (t \) « >\(2\) \ (x (t) \) « >\(-1\) \ (y (t) \) « >\(8\) 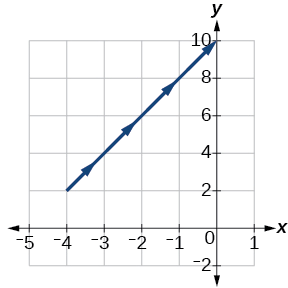
Figurine\(\PageIndex{4}\)
Trouvez une paire d'équations paramétriques qui modélisent le graphe de\(y=1−x^2\), à l'aide du paramètre\(x(t)=t\). Tracez quelques points et esquissez le graphique.
Solution
Si\(x(t)=t\) et nous le\(t\)\(x\) remplaçons dans l'\(y\)équation, alors\(y(t)=1−t^2\). Notre paire d'équations paramétriques est
\[\begin{align*} x(t) &=t \\ y(t) &= 1−t^2 \end{align*}\]
Pour représenter graphiquement les équations, nous construisons d'abord un tableau de valeurs comme celui de Tableau\(\PageIndex{2}\). Nous pouvons choisir des valeurs autour de\(t=0\), de\(t=−3\) à\(t=3\). Les valeurs de la\(x(t)\) colonne seront les mêmes que celles de la\(t\) colonne car\(x(t)=t\). Calculez les valeurs de la colonne\(y(t)\).
| \ (t) | \(x(t)=t\) | \(y(t)=1−t^2\) |
|---|---|---|
| \ (t) « > \ (−3 \) | \ (x (t) =t \) « >\(−3\) | \ (y (t) =1−t^2 \) « >\(y(−3)=1−{(−3)}^2=−8\) |
| \ (t) « > \ (−2 \) | \ (x (t) =t \) « >\(−2\) | \ (y (t) =1−t^2 \) « >\(y(−2)=1−{(−2)}^2=−3\) |
| \ (t) « > \ (−1 \) | \ (x (t) =t \) « >\(−1\) | \ (y (t) =1−t^2 \) « >\(y(−1)=1−{(−1)}^2=0\) |
| \ (t) « > \ (0 \) | \ (x (t) =t \) « >\(0\) | \ (y (t) =1−t^2 \) « >\(y(0)=1−0=1\) |
| \ (t) « > \ (1 \) | \ (x (t) =t \) « >\(1\) | \ (y (t) =1−t^2 \) « >\(y(1)=1−{(1)}^2=0\) |
| \ (t) « > \ (2 \) | \ (x (t) =t \) « >\(2\) | \ (y (t) =1−t^2 \) « >\(y(2)=1−{(2)}^2=−3\) |
| \ (t) « > \ (3 \) | \ (x (t) =t \) « >\(3\) | \ (y (t) =1−t^2 \) « >\(y(3)=1−{(3)}^2=−8\) |
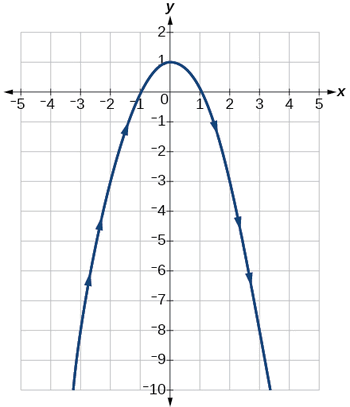
Le graphique de\(y=1−t^2\) est une parabole orientée vers le bas, comme le montre la figure\(\PageIndex{5}\). Nous avons cartographié la courbe sur l'intervalle\([−3, 3]\), représentée par une ligne continue avec des flèches indiquant l'orientation de la courbe en fonction de\(t\). L'orientation fait référence à la trajectoire tracée le long de la courbe en termes de valeurs croissantes de\(t\). Comme cette parabole est symétrique par rapport à la droite\(x=0\), les valeurs de\(x\) sont réfléchies sur l'axe y.
Paramétrez la courbe donnée par\(x=y^3−2y\).
- Réponse
-
\(x(t)=t^3−2t\)
\(y(t)=t\)
Un objet se déplace à une vitesse constante le long d'une trajectoire droite\((−5, 3)\) pour se retrouver\((3, −1)\) dans le même plan en quatre secondes. Les coordonnées sont mesurées en mètres. Trouvez des équations paramétriques pour la position de l'objet.
Solution
Les équations paramétriques sont de simples expressions linéaires, mais nous devons aborder ce problème étape par étape. La valeur x de l'objet commence en\(−5\) mètres et passe en\(3\) mètres. Cela signifie que la distance\(x\) a changé en\(8\) mètres en\(4\) secondes, soit un taux de\(\dfrac{8\space m}{4\space s}\), ou\(2\space m/s\). Nous pouvons écrire la coordonnée x sous forme de fonction linéaire par rapport au temps en tant que\(x(t)=2t−5\). Dans le modèle de fonction linéaire\(y=mx+b\),\(2t=mx\) et\(−5=b\).
De même, la\(y\) valeur -de l'objet commence à\(3\) et va à\(−1\), ce qui correspond à une modification\(y\) de la distance en\(−4\) mètres en\(4\) secondes, qui est un taux de\(\dfrac{−4\space m}{4\space s}\), ou\(−1\space m/s\). Nous pouvons également écrire la coordonnée y en tant que fonction linéaire\(y(t)=−t+3\). Ensemble, ce sont les équations paramétriques de la position de l'objet, où\(x\) et\(y\) sont exprimées en mètres et\(t\) représentent le temps :
\[\begin{align*} x(t) &= 2t−5 \\ y(t) &= −t+3 \end{align*}\]
À l'aide de ces équations, nous pouvons créer un tableau de valeurs pour\(t\)\(x\), et\(y\) (voir Tableau\(\PageIndex{3}\)). Dans cet exemple, nous avons limité les valeurs\(t\) à des nombres non négatifs. En général, n'importe quelle valeur de\(t\) peut être utilisée.
| \(t\) | \(x(t)=2t−5\) | \(y(t)=−t+3\) |
|---|---|---|
| \ (t \) « >\(0\) | \ (x (t) =2t−5 \) « >\(x=2(0)−5=−5\) | \ (y (t) =−t+3 \) « >\(y=−(0)+3=3\) |
| \ (t \) « >\(1\) | \ (x (t) =2t−5 \) « >\(x=2(1)−5=−3\) | \ (y (t) =−t+3 \) « >\(y=−(1)+3=2\) |
| \ (t \) « >\(2\) | \ (x (t) =2t−5 \) « >\(x=2(2)−5=−1\) | \ (y (t) =−t+3 \) « >\(y=−(2)+3=1\) |
| \ (t \) « >\(3\) | \ (x (t) =2t−5 \) « >\(x=2(3)−5=1\) | \ (y (t) =−t+3 \) « >\(y=−(3)+3=0\) |
| \ (t \) « >\(4\) | \ (x (t) =2t−5 \) « >\(x=2(4)−5=3\) | \ (y (t) =−t+3 \) « >\(y=−(4)+3=−1\) |
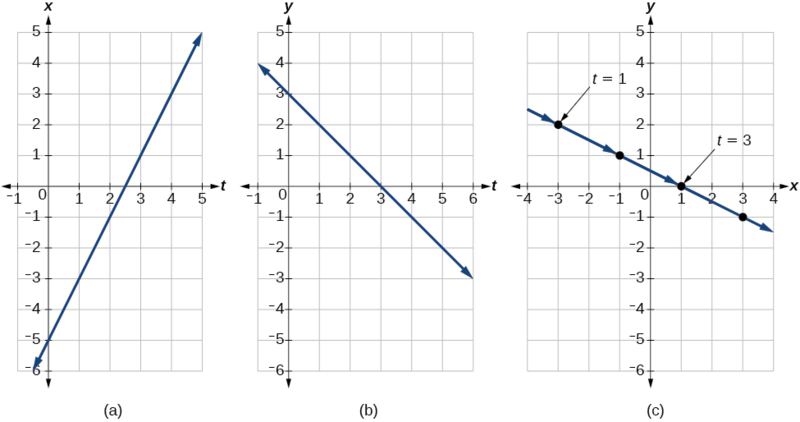
À partir de ce tableau, nous pouvons créer trois graphiques, comme le montre la figure\(\PageIndex{6}\).
Analyse
Encore une fois, nous voyons que, sur la Figure\(\PageIndex{6}\) (c), lorsque le paramètre représente le temps, nous pouvons indiquer le mouvement de l'objet le long de la trajectoire à l'aide de flèches.
Élimination du paramètre
Dans de nombreux cas, nous pouvons avoir une paire d'équations paramétriques, mais nous trouvons qu'il est plus simple de tracer une courbe si l'équation ne fait intervenir que deux variables, telles que\(x\) et\(y\). L'élimination du paramètre est une méthode qui peut faciliter la représentation graphique de certaines courbes. Cependant, s'il s'agit de cartographier l'équation en fonction du temps, il sera alors nécessaire d'indiquer également l'orientation de la courbe. Il existe différentes méthodes pour éliminer le paramètre\(t\) d'un ensemble d'équations paramétriques ; toutes ne fonctionnent pas pour tous les types d'équations. Nous allons passer en revue ici les méthodes utilisées pour les types d'équations les plus courants.
Élimination du paramètre dans les équations polynomiales, exponentielles et logarithmiques
Pour les équations polynomiales, exponentielles ou logarithmiques exprimées sous forme de deux équations paramétriques, nous choisissons l'équation la plus facile à manipuler et à résoudre\(t\). Nous remplaçons l'expression résultante par\(t\) dans la deuxième équation. Cela donne une équation entre\(x\) et\(y\).
\(x(t)=t^2+1\)Donne et\(y(t)=2+t\) élimine le paramètre et écris les équations paramétriques sous forme d'équation cartésienne.
Solution
Nous allons commencer par l'équation\(y\) car l'équation linéaire est plus facile à résoudre\(t\).
\[\begin{align*} y &= 2+t \\ y−2 &=t \end{align*}\]
Ensuite, remplacez\(y−2\)\(t\) in\(x(t)\).
\[\begin{align*} x &= t^2+1 \\ x &= {(y−2)}^2+1 \;\;\;\;\;\;\;\; \text{Substitute the expression for }t \text{ into }x. \\ x &= y^2−4y+4+1 \\ x &= y^2−4y+5 \\ x &= y^2−4y+5 \end{align*}\]
La forme cartésienne est\(x=y^2−4y+5\).
Analyse
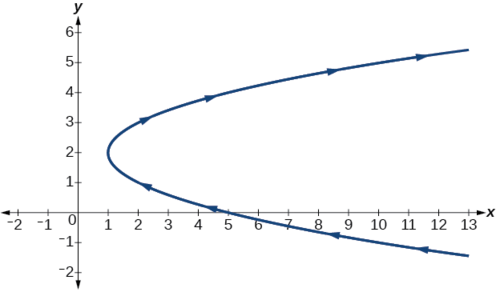
Il s'agit d'une équation pour une parabole dans laquelle, en termes rectangulaires,\(x\) dépend de\(y\). À partir du sommet de la courbe\((1,2)\) situé à, le graphique se déplace vers la droite. Voir la figure\(\PageIndex{7}\). Dans cette section, nous examinons des ensembles d'équations données par les fonctions\(x(t)\) et\(y(t)\), où\(t\) est la variable indépendante du temps. Remarquez que\(x\) les deux\(y\) sont des fonctions du temps ; donc en général, elles ne\(y\) sont pas fonction de\(x\).
Compte tenu des équations ci-dessous, éliminez le paramètre et écrivez comme une équation rectangulaire pour\(y\) en fonction de\(x\).
\[\begin{align*} x(t) &= 2t^2+6 \\ y(t) &= 5−t \end{align*}\]
- Réponse
-
\(y=5−\sqrt{\frac{1}{2}x−3}\)
Éliminez le paramètre et écrivez-le sous forme d'équation cartésienne :\(x(t)=e^{−t}\) et\(y(t)=3e^t\),\(t>0\).
Solution
Isoler\(e^t\).
\[\begin{align*} x &=e^{−t} \\ e^t &= \dfrac{1}{x} \end{align*}\]
Remplacez l'expression par\(y(t)\).
\[\begin{align*} y &= 3e^t \\ y &= 3 \left(\dfrac{1}{x}\right) \\ y &= \dfrac{3}{x} \end{align*}\]
La forme cartésienne est\(y=\dfrac{3}{x}\).
Analyse
Le graphique de l'équation paramétrique est illustré sur la figure\(\PageIndex{8a}\). Le domaine est limité à\(t>0\). L'équation cartésienne\(y=\dfrac{3}{x}\) est illustrée dans la figure\(\PageIndex{8b}\) et n'a qu'une seule restriction sur le domaine,\(x≠0\).
Éliminez le paramètre et écrivez-le sous forme d'équation cartésienne :\(x(t)=\sqrt{t}+2\) et\(y(t)=\log(t)\).
Solution
Résolvez la première équation pour\(t\).
\[\begin{align*} x &= \sqrt{t}+2 \\ x−2 &= \sqrt{t} \\ {(x−2)}^2 &= t \;\;\;\;\;\;\;\; \text{Square both sides.} \end{align*}\]
Ensuite, remplacez l'expression par\(t\) dans l'\(y\)équation.
\[\begin{align*} y &= \log(t) \\ y &= \log{(x−2)}^2 \end{align*}\]
La forme cartésienne est\(y=\log{(x−2)}^2\).
Analyse
Pour vous assurer que les équations paramétriques sont équivalentes à l'équation cartésienne, vérifiez les domaines. Les équations paramétriques limitent le domaine\(x=\sqrt{t}+2\) à\(t>0\) ; nous limitons le domaine\(x\) à\(x>2\). Le domaine de l'équation paramétrique\(y=\log(t)\) est limité à\(t>0\) ; nous le limitons\(y=\log{(x−2)}^2\) à\(x>2\).
Éliminez le paramètre et écrivez-le sous la forme d'une équation rectangulaire.
\[\begin{align*} x(t) &= t^2 \\ y(t) &= \ln t\text{, } t>0 \end{align*}\]
- Réponse
-
\(y=\ln \sqrt{x}\)
Élimination du paramètre des équations trigonométriques
L'élimination du paramètre des équations trigonométriques est une simple substitution. Nous pouvons utiliser quelques-unes des identités trigonométriques familières et le théorème de Pythagore.
Tout d'abord, nous utilisons les identités :
\[\begin{align*} x(t) &= a \cos t \\ y(t) &= b \sin t \end{align*}\]
Résoudre pour\(\cos t\) et\(\sin t\), nous avons
\[\begin{align*} \dfrac{x}{a} &= \cos t \\ \dfrac{y}{b} &= \sin t \end{align*}\]
Ensuite, utilisez le théorème de Pythagore :
\({\cos}^2 t+{\sin}^2 t=1\)
La substitution donne
\({\cos}^2 t+{\sin}^2 t={\left(\dfrac{x}{a}\right)}^2+{\left(\dfrac{y}{b}\right)}^2=1\)
Éliminez le paramètre de la paire d'équations trigonométriques donnée\(0≤t≤2\pi\) et esquissez le graphique.
\[\begin{align*} x(t) &=4 \cos t \\ y(t) &=3 \sin t \end{align*}\]
Solution
Résoudre pour\(\cos t\) et\(\sin t\), nous avons
\[\begin{align*} x &=4 \cos t \\ \dfrac{x}{4} &= \cos t \\ y &=3 \sin t \\ \dfrac{y}{3} &= \sin t \end{align*}\]
Ensuite, utilisez l'identité pythagoricienne et effectuez les substitutions.
\[\begin{align*} {\cos}^2 t+{\sin}^2 t &= 1 \\ {\left(\dfrac{x}{4}\right)}^2+{\left(\dfrac{y}{3}\right)}^2 &=1 \\ \dfrac{x^2}{16}+\dfrac{y^2}{9} &=1 \end{align*}\]
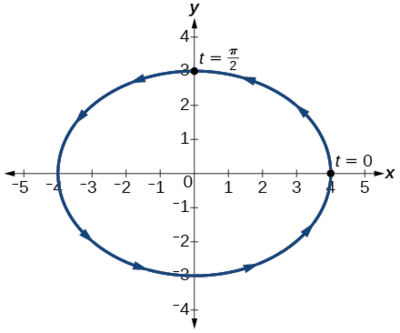
Le graphique de l'équation est illustré à la figure\(\PageIndex{9}\).
Analyse
En appliquant les équations générales pour les sections coniques (introduites dans la géométrie analytique), nous pouvons les identifier\(\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\) comme une ellipse centrée sur\((0,0)\). Remarquez que lorsque\(t=0\) les coordonnées sont\((4,0)\), et quand\(t=\dfrac{\pi}{2}\) les coordonnées le sont\((0,3)\). Cela montre l'orientation de la courbe avec des valeurs croissantes de\(t\).
Éliminez le paramètre de la paire d'équations paramétriques donnée et écrivez-le sous forme d'équation cartésienne :\(x(t)=2 \cos t\) et\(y(t)=3 \sin t\).
- Réponse
-
\(\dfrac{x^2}{4}+\dfrac{y^2}{9}=1\)
Trouver des équations cartésiennes à partir de courbes définies de manière paramétrique
Lorsque l'on nous donne un ensemble d'équations paramétriques et que nous devons trouver une équation cartésienne équivalente, nous « éliminons le paramètre ». Cependant, il existe différentes méthodes que nous pouvons utiliser pour réécrire un ensemble d'équations paramétriques sous la forme d'une équation cartésienne. La méthode la plus simple consiste à définir une équation égale au paramètre, telle que\(x(t)=t\). Dans ce cas, il\(y(t)\) peut s'agir de n'importe quelle expression. Par exemple, considérez la paire d'équations suivante.
\[\begin{align*} x(t) &=t \\ y(t) &= t^2−3 \end{align*}\]
La réécriture de cet ensemble d'équations paramétriques est une question de substitution\(x\) à\(t\). Ainsi, l'équation cartésienne est\(y=x^2−3\).
Utilisez deux méthodes différentes pour trouver l'équation cartésienne équivalente à l'ensemble d'équations paramétriques donné.
\[\begin{align*} x(t) &= 3t−2 \\ y(t) &= t+1 \end{align*}\]
Solution
Méthode 1. Tout d'abord, résolvons l'\(x\)équation pour\(t\). Ensuite, nous pouvons remplacer le résultat dans l'\(y\)équation.
\[\begin{align*} x &= 3t−2 \\ x+2 &= 3t \\ \dfrac{x+2}{3} &= t \end{align*}\]
Remplacez maintenant l'expression par\(t\) dans l'\(y\)équation.
\[\begin{align*} y &= t+1 \\ y & = \left(\dfrac{x+2}{3}\right)+1 \\ y &= \dfrac{x}{3}+\dfrac{2}{3}+1 \\ y &= \dfrac{1}{3}x+\dfrac{5}{3} \end{align*}\]
Méthode 2. Résolvez l'\(y\)équation\(t\) et remplacez-la dans l'\(x\)équation.
\[\begin{align*} y &= t+1 \\ y−1 &=t \end{align*}\]
Effectuez la substitution, puis résolvez pour\(y\).
\[\begin{align*} x &= 3(y−1)−2 \\ x &= 3y−3−2 \\ x &= 3y−5 \\ x+5 &= 3y \\ \dfrac{x+5}{3} &= y \\ y &= \dfrac{1}{3}x+\dfrac{5}{3} \end{align*}\]
Écrivez les équations paramétriques données sous forme d'équation cartésienne :\(x(t)=t^3\) et\(y(t)=t^6\).
- Réponse
-
\(y=x^2\)
Recherche d'équations paramétriques pour des courbes définies par des équations rectangulaires
Bien que nous venons de montrer qu'il n'existe qu'une seule façon d'interpréter un ensemble d'équations paramétriques comme une équation rectangulaire, il existe plusieurs manières d'interpréter une équation rectangulaire comme un ensemble d'équations paramétriques. Toute stratégie que nous pouvons utiliser pour trouver les équations paramétriques est valide si elle produit une équivalence. En d'autres termes, si nous choisissons une expression à représenter\(x\), puis que nous la substituons dans l'\(y\)équation, et qu'elle produit le même graphe sur le même domaine que l'équation rectangulaire, alors l'ensemble d'équations paramétriques est valide. Si le domaine devient restreint dans l'ensemble d'équations paramétriques et que la fonction n'autorise pas les mêmes valeurs\(x\) que le domaine de l'équation rectangulaire, les graphes seront alors différents.
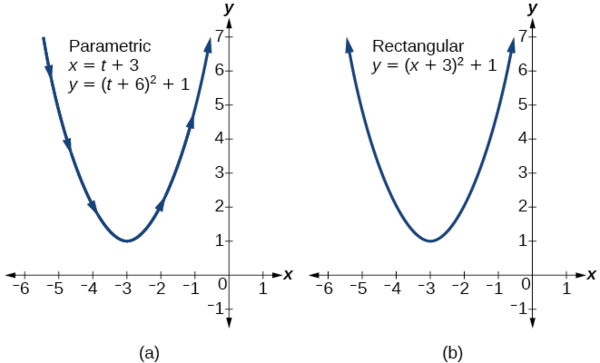
Trouvez un ensemble d'équations paramétriques équivalentes pour\(y={(x+3)}^2+1\).
Solution
Un choix évident serait de laisser\(x(t)=t\). Alors\(y(t)={(t+3)}^2+1\). Mais essayons quelque chose de plus intéressant. Et si on le laissait faire\(x=t+3\) ? Ensuite, nous avons
\[\begin{align*} y &= {(x+3)}^2+1 \\ y &= {((t+3)+3)}^2+1 \\ y &= {(t+6)}^2+1 \end{align*}\]
L'ensemble des équations paramétriques est
\[\begin{align*} x(t) &= t+3 \\ y(t) &= {(t+6)}^2+1 \end{align*}\]
Voir la figure\(\PageIndex{10}\).
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à utiliser des équations paramétriques.
- Introduction aux équations paramétriques
- Conversion d'équations paramétriques en forme rectangulaire
Concepts clés
- Le paramétrage d'une courbe implique la traduction d'une équation rectangulaire en deux variables\(y\),\(x\) et en deux équations en trois variables\(x\),\(y\), et\(t\). Souvent, plus d'informations sont obtenues à partir d'un ensemble d'équations paramétriques. Voir Exemple\(\PageIndex{1}\)\(\PageIndex{2}\), Exemple et Exemple\(\PageIndex{3}\).
- Les équations sont parfois plus simples à représenter graphiquement lorsqu'elles sont écrites sous forme rectangulaire. En éliminant\(t\), une équation entre\(x\) et\(y\) est le résultat.
- Pour éliminer\(t\), résolvez l'une des équations de\(t\) la deuxième équation et remplacez-la par l'expression. Voir Exemple\(\PageIndex{4}\), Exemple\(\PageIndex{5}\)\(\PageIndex{6}\), Exemple et Exemple\(\PageIndex{7}\).
- Trouver l'équation rectangulaire pour une courbe définie de manière paramétrique revient essentiellement à éliminer le paramètre. Résolvez pour\(t\) dans l'une des équations et remplacez l'expression dans la deuxième équation. Voir l'exemple\(\PageIndex{8}\).
- Il existe une infinité de manières de choisir un ensemble d'équations paramétriques pour une courbe définie comme une équation rectangulaire.
- Trouvez une expression pour\(x\) que le domaine de l'ensemble d'équations paramétriques reste le même que celui de l'équation rectangulaire d'origine. Voir l'exemple\(\PageIndex{9}\).


