10.3 : Coordonnées polaires

Objectifs d'apprentissage

• Tracez les points en utilisant des coordonnées polaires
• Convertissez les coordonnées polaires en coordonnées rectangulaires.
• Convertissez des coordonnées rectangulaires en coordonnées polaires.
• Transformez les équations entre formes polaires et rectangulaires.
• Identifiez et représentez graphiquement des équations polaires en les convertissant en équ

\(12\)À plus de kilomètres du port, un voilier fait face à des conditions météorologiques difficiles et est dévié de\(16\) sa trajectoire par un vent à nœud (voir Figure\(\PageIndex{1}\)). Comment le marin peut-il indiquer sa position à la Garde côtière ? Dans cette section, nous allons étudier une méthode de représentation de l'emplacement différente d'une grille de coordonnées standard.

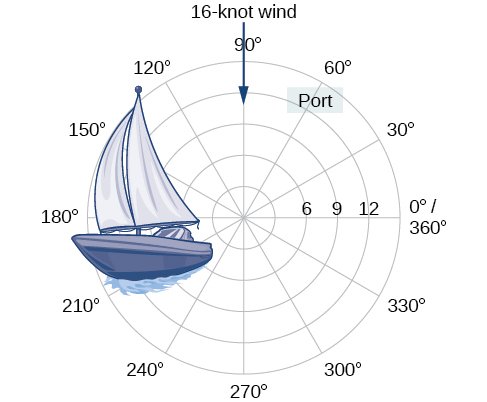
Figurine\(\PageIndex{1}\)

Tracer des points à l'aide de coordonnées polaires

Lorsque nous pensons à tracer des points dans le plan, nous pensons généralement à des coordonnées rectangulaires\((x,y)\) dans le plan de coordonnées cartésien. Cependant, il existe d'autres manières d'écrire une paire de coordonnées et d'autres types de systèmes de grille. Dans cette section, nous présentons les coordonnées polaires, qui sont des points étiquetés\((r,\theta)\) et tracés sur une grille polaire. La grille polaire est représentée par une série de cercles concentriques rayonnant à partir du pôle, ou de l'origine du plan de coordonnées.

La grille polaire est redimensionnée comme l'unité de cercle, l'axe positif\(x\) étant désormais considéré comme l'axe polaire et l'origine comme le pôle. La première coordonnée\(r\) est le rayon ou la longueur du segment de ligne dirigé à partir du pôle. L'angle\(\theta\), mesuré en radians, indique la direction de\(r\). Nous nous déplaçons dans le sens antihoraire par rapport à l'axe polaire d'un angle de\(\theta\) et mesurons un segment de ligne dirigée dont la longueur est\(r\) dans la direction de\(\theta\). Même si nous mesurons d'\(\theta\)abord et ensuite\(r\), le point polaire est écrit avec la\(r\) coordonnée en premier. Par exemple, pour tracer le point\(\left(2,\dfrac{\pi}{4}\right)\), nous déplacerons les\(\dfrac{\pi}{4}\) unités dans le sens antihoraire, puis sur une longueur égale à celle\(2\) du pôle. Ce point est tracé sur la grille de la figure\(\PageIndex{2}\).

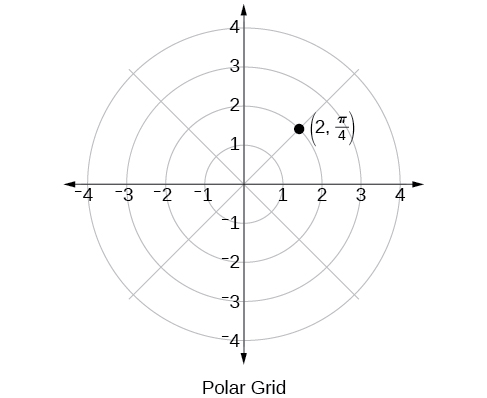
Figurine\(\PageIndex{2}\)

Exemple\(\PageIndex{1}\): Plotting a Point on the Polar Grid

Tracez le point\(\left(3,\dfrac{\pi}{2}\right)\) sur la grille polaire.

Solution

L'angle\(\dfrac{\pi}{2}\) est déterminé en balayant dans le sens antihoraire\(90°\) à partir de l'axe polaire. Le point est situé à une longueur d'\(3\)unités à partir du pôle dans la\(\dfrac{\pi}{2}\) direction, comme indiqué sur la figure\(\PageIndex{3}\).

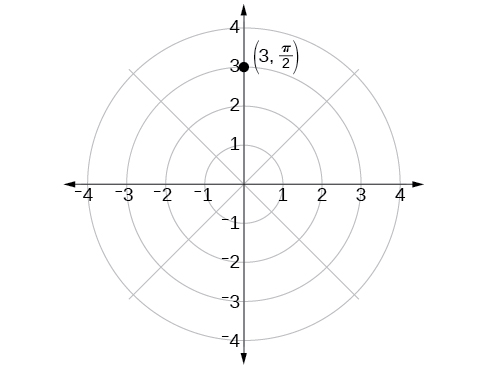
Figurine\(\PageIndex{3}\)

Exercice\(\PageIndex{1}\)

Tracez le point\(\left(2, \dfrac{\pi}{3}\right)\) dans la grille polaire.

Réponse

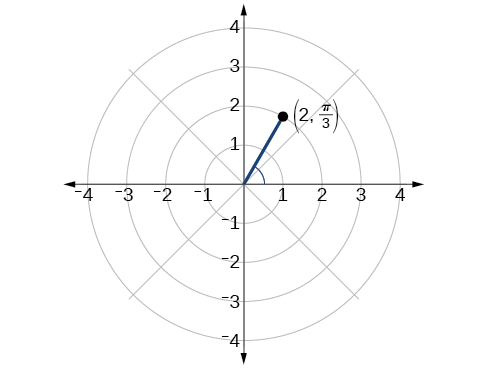
Figurine\(\PageIndex{4}\)

Exemple\(\PageIndex{2}\): Plotting a Point in the Polar Coordinate System with a Negative Component

Tracez le point\(\left(−2, \dfrac{\pi}{6}\right)\) sur la grille polaire.

Solution

Nous savons que cela se\(\dfrac{\pi}{6}\) trouve dans le premier quadrant. Toutefois,\(r=−2\). Nous pouvons aborder le tracé d'un point avec un négatif de deux\(r\) manières :

1. Tracez le point\(\dfrac{\pi}{6}\) en vous\(\left(2,\dfrac{\pi}{6}\right)\) déplaçant dans le sens antihoraire et en étendant les\(2\) unités d'un segment de ligne dirigée dans le premier quadrant. Retracez ensuite le segment de ligne dirigé à travers le pôle et continuez les\(2\) unités jusqu'au troisième quadrant ;
2. Déplacez-vous\(\dfrac{\pi}{6}\) dans le sens antihoraire et tracez le segment de ligne dirigé à partir des\(2\) unités polaires dans le sens négatif jusqu'au troisième quadrant.

Voir la figure\(\PageIndex{5a}\). Comparez cela au graphique des coordonnées polaires\((2,π6)\) illustré sur la figure\(\PageIndex{5b}\).

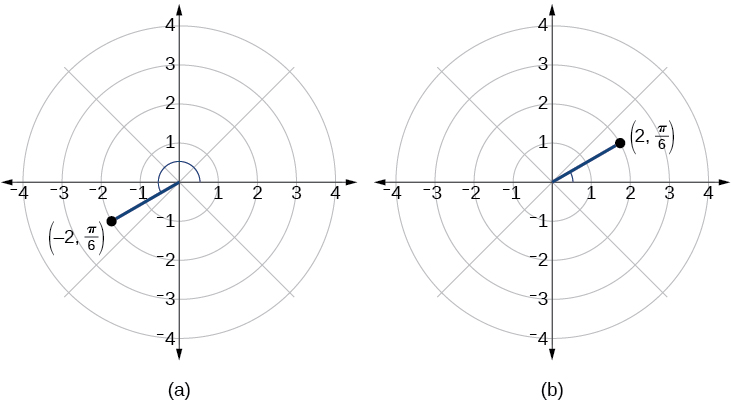
Figurine\(\PageIndex{5}\)

Exercice\(\PageIndex{2}\)

Tracez les points\(\left(3,−\dfrac{\pi}{6}\right)\) et\(\left(2,\dfrac{9\pi}{4}\right)\) sur la même grille polaire.

Réponse

Figurine\(\PageIndex{6}\)

Conversion de coordonnées polaires en coordonnées rectangulaires

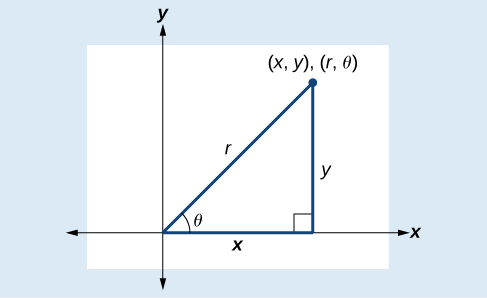
Lorsque l'on donne un ensemble de coordonnées polaires, il se peut que nous devions les convertir en coordonnées rectangulaires. Pour ce faire, nous pouvons rappeler les relations qui existent entre les variables\(x\)\(y\),\(r\), et\(\theta\).

\(\cos \theta=\dfrac{x}{r}\rightarrow x=r \cos \theta\)

\(\sin \theta=\dfrac{y}{r}\rightarrow y=r \sin \theta\)

Le fait de laisser tomber une perpendiculaire depuis le point du plan jusqu'à l'axe X forme un triangle droit, comme illustré à la figure\(\PageIndex{7}\). Un moyen facile de se souvenir des équations ci-dessus est de les considérer\(\cos \theta\) comme le côté adjacent au-dessus de l'hypoténuse et\(\sin \theta\) comme le côté opposé au-dessus de l'hypoténuse.

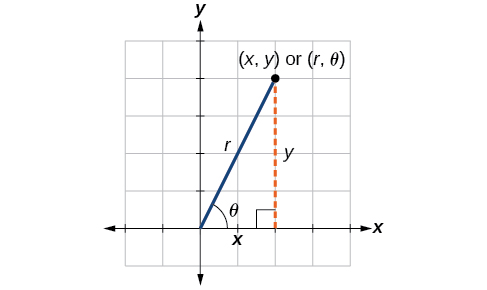
Figurine\(\PageIndex{7}\)

CONVERSION DE COORDONNÉES POLAIRES EN COORDONNÉES RECTANGULAIRES

Pour convertir les coordonnées polaires\((r, \theta)\) en coordonnées rectangulaires\((x, y)\), laissez

\[\cos \theta=\dfrac{x}{r}\rightarrow x=r \cos \theta\]

\[\sin \theta=\dfrac{y}{r}\rightarrow y=r \sin \theta\]

Procédure : à partir de coordonnées polaires, convertissez-les en coordonnées rectangulaires.

1. Étant donné la coordonnée polaire\((r,\theta)\), écrivez\(x=r \cos \theta\) et\(y=r \sin \theta\).
2. Évaluez\(\cos \theta\) et\(\sin \theta\).
3. Multipliez\(\cos \theta\) par\(r\) pour trouver la coordonnée\(x\) - de la forme rectangulaire.
4. Multipliez\(\sin \theta\) par\(r\) pour trouver la coordonnée\(y\) - de la forme rectangulaire.

Exemple\(\PageIndex{3A}\): Writing Polar Coordinates as Rectangular Coordinates

Écrivez les coordonnées polaires\(\left(3,\dfrac{\pi}{2}\right)\) sous forme de coordonnées rectangulaires.

Solution

Utilisez les relations équivalentes.

\[\begin{align*} x&= r \cos \theta\\ x&= 3 \cos \dfrac{\pi}{2}\\ &= 0\\ y&= r \sin \theta\\ y&= 3 \sin \dfrac{\pi}{2}\\ &= 3 \end{align*}\]

Les coordonnées rectangulaires sont\((0,3)\). Voir la figure\(\PageIndex{8}\).

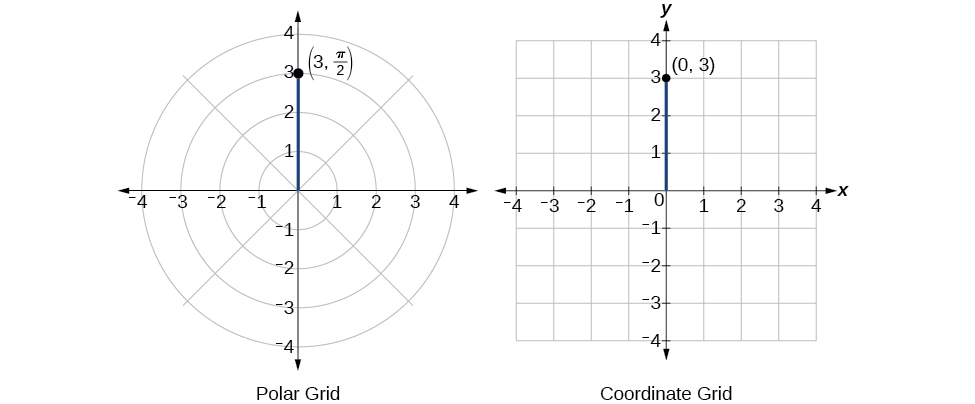
Figurine\(\PageIndex{8}\)

Exemple\(\PageIndex{3B}\): Writing Polar Coordinates as Rectangular Coordinates

Écrivez les coordonnées polaires\((−2,0)\) sous forme de coordonnées rectangulaires.

Solution

Voir la figure\(\PageIndex{9}\). En écrivant les coordonnées polaires sous forme rectangulaire, nous avons

\[\begin{align*} x&= r \cos \theta\\ x&= -2 \cos(0)\\ &= -2\\ y&= r \sin \theta\\ y&= -2 \sin(0)\\ &= 0 \end{align*}\]

Les coordonnées rectangulaires sont également\((−2,0)\).

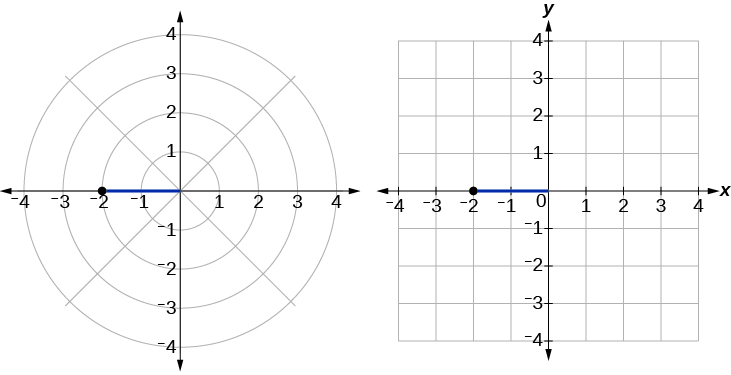
Figurine\(\PageIndex{9}\)

Exercice\(\PageIndex{3}\)

Écrivez les coordonnées polaires\(\left(−1,\dfrac{2\pi}{3}\right)\) sous forme de coordonnées rectangulaires.

Réponse

\((x,y)=\left(\dfrac{1}{2},−\dfrac{\sqrt{3}}{2}\right)\)

Conversion de coordonnées rectangulaires en coordonnées polaires

Pour convertir des coordonnées rectangulaires en coordonnées polaires, nous utiliserons deux autres relations familières. Avec cette conversion, nous devons toutefois être conscients qu'un ensemble de coordonnées rectangulaires produira plus d'un point polaire.

CONVERSION DE COORDONNÉES RECTANGULAIRES EN COORDONNÉES POLAIRES

La conversion de coordonnées rectangulaires en coordonnées polaires nécessite l'utilisation d'une ou de plusieurs des relations illustrées dans la figure\(\PageIndex{10}\).

\(\cos \theta=\dfrac{x}{r}\)ou\(x=r \cos \theta\)

\(\sin \theta=\dfrac{y}{r}\)ou\(y=r \sin \theta\)

\(r^2=x^2+y^2\)

\(\tan \theta=\dfrac{y}{x}\)

Figurine\(\PageIndex{10}\)

Exemple\(\PageIndex{4}\): Writing Rectangular Coordinates as Polar Coordinates

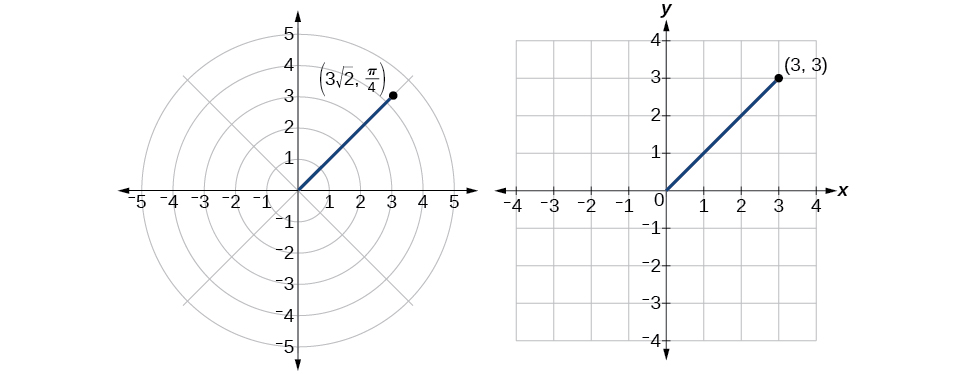
Convertissez les coordonnées rectangulaires\((3,3)\) en coordonnées polaires.

Solution

Nous voyons que le point d'origine\((3,3)\) se trouve dans le premier quadrant. Pour le trouver\(\theta\), utilisez la formule\(\tan \theta=\dfrac{y}{x}\). Cela donne

\[\begin{align*} \tan \theta&= \dfrac{3}{3}\\ \tan \theta&= 1\\ {\tan}^{-1}(1)&= \dfrac{\pi}{4} \end{align*}\]

Pour le trouver\(r\), nous substituons les valeurs pour\(x\) et\(y\) dans la formule\(r=\sqrt{x^2+y^2}\). Nous savons que cela\(r\) doit être positif, comme\(\dfrac{\pi}{4}\) c'est le cas dans le premier quadrant. Ainsi

\[\begin{align*} r&= \sqrt{3^2+3^2}\\ r&= \sqrt{9+9}\\ r&= \sqrt{18}\\ &= 3\sqrt{2} \end{align*}\]

Donc\(\theta=\dfrac{\pi}{4}\),\(r=3\sqrt{2}\) et en nous donnant le point polaire\((3\sqrt{2},\dfrac{\pi}{4})\). Voir la figure\(\PageIndex{11}\).

Figurine\(\PageIndex{11}\)

Analyse

Il existe d'autres ensembles de coordonnées polaires qui seront les mêmes que notre première solution. Par exemple, les points\(\left(−3\sqrt{2}, \dfrac{5\pi}{4}\right)\) et\(\left(3\sqrt{2},−\dfrac{7\pi}{4}\right)\) coïncideront avec la solution initiale de\(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). Le point\(\left(−3\sqrt{2}, \dfrac{5\pi}{4}\right)\) indique un mouvement plus loin dans le sens antihoraire\(\pi\), ce qui est directement opposé\(\dfrac{\pi}{4}\). Le rayon est exprimé sous la forme\(−3\sqrt{2}\). Cependant, l'angle\(\dfrac{5\pi}{4}\) est situé dans le troisième quadrant et, comme\(r\) il est négatif, nous étendons le segment de ligne dirigée dans la direction opposée, dans le premier quadrant. C'est le même point que\(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). Le point\(\left(3\sqrt{2}, −\dfrac{7\pi}{4}\right)\) est un mouvement plus loin dans le sens des aiguilles d'\(−\dfrac{7\pi}{4}\)une montre à partir de\(\dfrac{\pi}{4}\). Le rayon,\(3\sqrt{2}\), est le même.

Transformation d'équations entre formes polaires et rectangulaires

Nous pouvons maintenant convertir les coordonnées entre la forme polaire et la forme rectangulaire. La conversion d'équations peut s'avérer plus difficile, mais il peut être avantageux de pouvoir effectuer une conversion entre les deux formes. Comme il existe un certain nombre d'équations polaires qui ne peuvent pas être exprimées clairement sous forme cartésienne, et vice versa, nous pouvons utiliser les mêmes procédures que celles que nous avons utilisées pour convertir des points entre les systèmes de coordonnées. Nous pouvons ensuite utiliser une calculatrice graphique pour représenter graphiquement la forme rectangulaire ou la forme polaire de l'équation.

Comment : À partir d'une équation sous forme polaire, la représenter graphiquement à l'aide d'une calculatrice graphique

1. Changez le MODE en POL, représentant la forme polaire.
2. Appuyez sur la touche Y= pour faire apparaître un écran permettant la saisie de six équations :\(r_1\),\(r_2\),...,\(r_6\).
3. Entrez l'équation polaire, définie comme égale à\(r\).
4. Appuyez sur GRAPH.

Exemple\(\PageIndex{5A}\): Writing a Cartesian Equation in Polar Form

Écrivez l'équation\(x^2+y^2=9\) cartésienne sous forme polaire.

Solution

Le but est d'éliminer\(x\) et\(y\) de l'équation et d'introduire\(r\) et\(\theta\). Idéalement, nous écririons l'équation\(r\) en fonction de\(\theta\). Pour obtenir la forme polaire, nous utiliserons les relations entre\((x,y)\) et\((r,\theta)\). Depuis\(x=r \cos \theta\) et\(y=r \sin \theta\), nous pouvons remplacer et résoudre\(r\).

\(\begin{align*} {(r \cos \theta)}^2+{(r \sin \theta)}^2&= 9\\ r^2 {\cos}^2 \theta+r^2 {\sin}^2 \theta&= 9\\ r^2({\cos}^2 \theta+{\sin}^2 \theta)&= 9\\ r^2(1)&= 9\qquad \text {Substitute } {\cos}^2 \theta+{\sin}^2 \theta=1\\ r&= \pm 3\qquad \text {Use the square root property.} \end{align*}\)

Ainsi,\(x^2+y^2=9\)\(r=3\), et\(r=−3\) devrait générer le même graphe. Voir la figure\(\PageIndex{12}\).

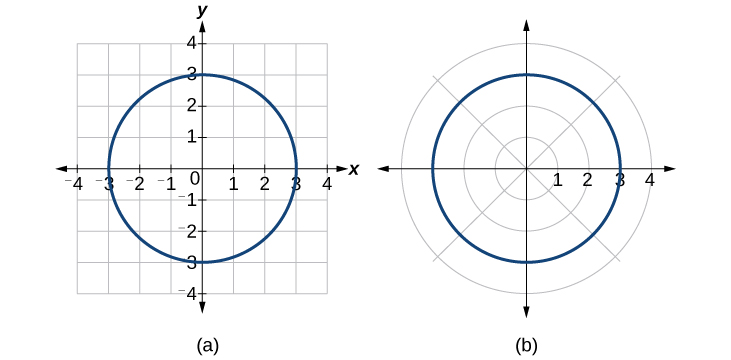
Figure\(\PageIndex{12}\) : (a) Forme cartésienne\(x^2+y^2=9\) (b) Forme polaire\(r=3\)

Pour tracer un cercle sous forme rectangulaire, nous devons d'abord résoudre\(y\).

\[\begin{align*} x^2+y^2&= 9\\ y^2&= 9-x^2\\ y&= \pm \sqrt{9-x^2} \end{align*}\]

Notez qu'il s'agit de deux fonctions distinctes, car un cercle échoue au test de la ligne verticale. Par conséquent, nous devons saisir les racines carrées positives et négatives séparément dans le calculateur, sous la forme de deux équations de la forme\(Y_1=\sqrt{9−x^2}\) et\(Y_2=−\sqrt{9−x^2}\). Appuyez sur GRAPH.

Exemple\(\PageIndex{5B}\): Rewriting a Cartesian Equation as a Polar Equation

Réécrivez l'équation cartésienne\(x^2+y^2=6y\) en tant qu'équation polaire.

Solution

Cette équation ressemble à l'exemple précédent, mais elle nécessite différentes étapes pour la convertir.

Nous pouvons toujours suivre les mêmes procédures que celles que nous avons déjà apprises et effectuer les substitutions suivantes :

\(\begin{array}{ll} r^2=6y & \text{Use }x^2+y^2=r^2. \\ r^2=6r \sin \theta & \text{Substitute }y=r \sin \theta. \\ r^2−6r \sin \theta=0 & \text{Set equal to }0. \\ r(r−6 \sin \theta)=0 & \text{Factor and solve.} \\ r=0 & \text{We reject }r=0 \text{, as it only represents one point, }(0,0). \\ \text{or }r=6 \sin \theta \end{array}\)

Par conséquent, les équations\(x^2+y^2=6y\) et\(r=6 \sin \theta\) devraient nous donner le même graphique. Voir la figure\(\PageIndex{13}\).

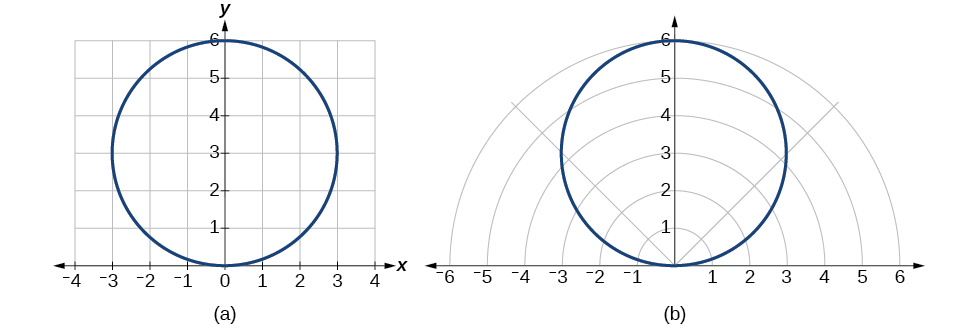
Figure\(\PageIndex{13}\) : (a) Forme cartésienne\(x^2+y^2=6y\) (b) Forme polaire\(r=6 \sin \theta\)

L'équation cartésienne ou rectangulaire est tracée sur la grille rectangulaire, et l'équation polaire est tracée sur la grille polaire. Il est clair que les graphiques sont identiques.

Exercice\(\PageIndex{4A}\):

Réécriture d'une équation cartésienne sous forme polaire

Réécrivez l'équation cartésienne\(y=3x+2\) en tant qu'équation polaire.

Réponse

Nous utiliserons les relations\(x=r \cos \theta\) et\(y=r \sin \theta\).

\(\begin{array}{cl} y=3x+2 \\ r \sin \theta=3r \cos \theta+2 \\ r \sin \theta−3r \cos \theta=2 \\ r(\sin \theta−3 \cos \theta)=2 & \text{Isolate }r. \\ r=2 \sin \theta−3\cos \theta & \text{Solve for }r. \end{array}\)

Exercice\(\PageIndex{4B}\):

Réécrivez l'équation\(y^2=3−x^2\) cartésienne sous forme polaire.

Réponse

\(r=\sqrt{3}\)

Identifier et représenter graphiquement des équations polaires par conversion en équations rectangulaires

Nous avons appris à convertir des coordonnées rectangulaires en coordonnées polaires, et nous avons vu que les points sont bien les mêmes. Nous avons également transformé des équations polaires en équations rectangulaires et vice versa. Nous allons maintenant démontrer que leurs graphiques, bien que dessinés sur des grilles différentes, sont identiques.

Exemple\(\PageIndex{6A}\): Graphing a Polar Equation by Converting to a Rectangular Equation

Convertissez l'équation polaire\(r=2 \sec \theta\) en équation rectangulaire et dessinez le graphique correspondant.

Solution

La conversion est

\[\begin{align*} r &=2 \sec \theta \\ r &= \dfrac{2}{\cos \theta} \\ r \cos \theta &=2 \\ x &=2 \end{align*}\]

Notez que l'équation\(r=2 \sec \theta\) tracée sur la grille polaire est clairement la même que la ligne verticale\(x=2\) tracée sur la grille rectangulaire (voir Figure\(\PageIndex{14}\)). Tout comme\(x=c\) la forme standard d'une ligne verticale de forme rectangulaire, la forme standard d'une ligne verticale de forme polaire l'\(r=c \sec \theta\)est également.

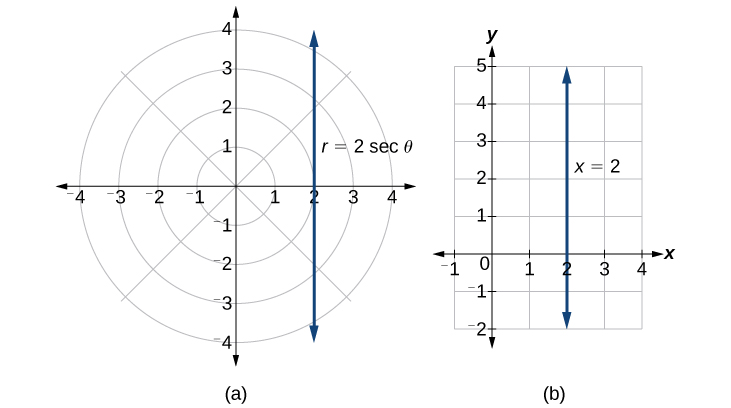
Figure\(\PageIndex{14}\) : (a) Grille polaire (b) Système de coordonnées rectangulaires

Une discussion similaire démontrerait que le graphique de la fonction\(r=2 \csc \theta\) sera la ligne horizontale\(y=2\). En fait,\(r=c \csc \theta\) c'est la forme standard d'une ligne horizontale en forme polaire, correspondant à la forme rectangulaire\(y=c\).

Exemple\(\PageIndex{6B}\): Rewriting a Polar Equation in Cartesian Form

Réécrivez l'équation polaire\(r=\dfrac{3}{1−2 \cos \theta}\) en tant qu'équation cartésienne.

Solution

L'objectif est d'éliminer\(\theta\) et\(r\), et d'introduire\(x\) et\(y\). Nous effaçons la fraction, puis utilisons la substitution. Pour remplacer\(r\) par\(x\) et\(y\), nous devons utiliser l'expression\(x^2+y^2=r^2\).

\(\begin{array} r =\dfrac{3}{1−2 \cos \theta} \\ r(1−2 \cos \theta)=3 \\ r\left(1−2\left(\dfrac{x}{r}\right)\right)=3 & \text{Use }\cos \theta=\dfrac{x}{r} \text{ to eliminate }\theta. \\ r−2x=3 \\ r=3+2x & \text{Isolate }r. \\ r^2={(3+2x)}^2 & \text{Square both sides.} \\ x^2+y^2={(3+2x)}^2 & \text{Use }x^2+y^2=r^2. \end{array}\)

L'équation cartésienne est\(x^2+y^2={(3+2x)}^2\). Cependant, pour le représenter graphiquement, en particulier à l'aide d'une calculatrice graphique ou d'un programme informatique, nous voulons isoler\(y\).

\[\begin{align*} x^2+y^2 &= {(3+2x)}^2 \\ y^2 &= {(3+2x)}^2-x^2 \\ y &= \pm {(3+2x)}^2-x^2 \end{align*}\]

Lorsque toute notre équation a été modifiée de\(r\) et\(\theta\) vers\(x\) et\(y\), nous pouvons arrêter, à moins qu'on ne nous demande de la résoudre\(y\) ou de la simplifier. Voir la figure\(\PageIndex{15}\).

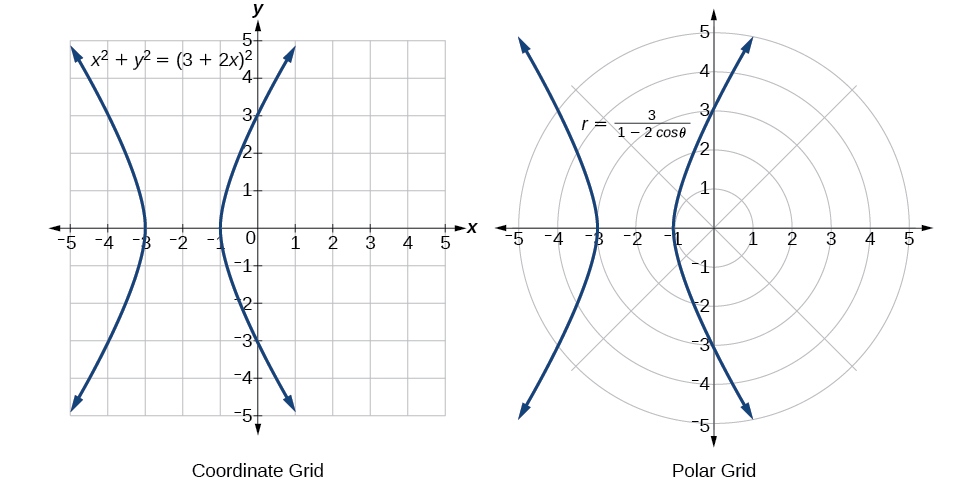
Figurine\(\PageIndex{15}\)

La forme en « sablier » du graphique est appelée hyperbole. Les hyperboles présentent de nombreuses caractéristiques et applications géométriques intéressantes, que nous étudierons plus en détail dans Géométrie analytique.

Analyse

Dans cet exemple, le côté droit de l'équation peut être développé et l'équation simplifiée davantage, comme indiqué ci-dessus. Cependant, l'équation ne peut pas être écrite comme une fonction unique sous forme cartésienne. Nous souhaiterons peut-être écrire l'équation rectangulaire sous la forme standard de l'hyperbole. Pour ce faire, nous pouvons commencer par l'équation initiale.

\(\begin{array}{ll} x^2+y^2={(3+2x)}^2 \\ x^2+y^2−{(3+2x)}^2=0 \\ x^2+y^2−(9+12x+4x^2)=0 \\ x^2+y^2−9−12x−4x^2=0 \\ −3x^2−12x+y^2=9 & \text{Multiply through by }−1. \\ 3x^2+12x−y^2=−9 \\ 3(x^2+4x)−y2=−9 & \text{Organize terms to complete the square for }x. \\ 3(x^2+4x+4)−y^2=−9+12 \\ 3{(x+2)}^2−y^2=3 \\ {(x+2)}^2−\dfrac{y^2}{3}=1\end{array}\)

Exercice\(\PageIndex{5}\)

Réécrivez l'équation\(r=2 \sin \theta\) polaire sous forme cartésienne.

Réponse

\(x^2+y^2=2y\)ou, dans la forme standard d'un cercle,\(x^2+{(y−1)}^2=1\)

Exemple\(\PageIndex{7}\): Rewriting a Polar Equation in Cartesian Form

Réécrivez l'équation\(r=\sin(2\theta)\) polaire sous forme cartésienne.

Solution

\(\begin{array}{cl} r=\sin(2\theta) & \text{Use the double angle identity for sine.} \\ r=2 \sin \theta \cos \theta & \text{Use }\cos \theta=\dfrac{x}{r} \text{ and } \sin \theta=\dfrac{y}{r}. \\ r=2 \dfrac{x}{r})(\dfrac{y}{r}) & \text{ Simplify.} \\ r=\dfrac{2xy}{r^2} & \text{Multiply both sides by }r^2. \\ r^3=2xy \\ {(x^2+y^2)}^3=2xy & \text{As }x^2+y^2=r^2, r=\sqrt{x^2+y^2}. \end{array}\)

Cette équation peut également être écrite sous la forme

\({(x^2+y^2)}^{\frac{3}{2}}=2xy \text{ or }x^2+y^2={(2xy)}^{\frac{2}{3}}\)

Médias

Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner avec les coordonnées polaires.

• Présentation des coordonnées polaires
• Comparaison des coordonnées polaires et rectangulaires

Équations clés

Des formules de conversion

\(\cos \theta=\dfrac{x}{r} \rightarrow x=r \cos\theta\) \(\sin \theta=\dfrac{y}{r} \rightarrow y=r \sin \theta\) \(r^2=x^2+y^2\) \(\tan \theta=\dfrac{y}{x}\)

Concepts clés

• La grille polaire est représentée par une série de cercles concentriques rayonnant à partir du pôle, ou de l'origine.
• Pour tracer un point dans le formulaire\((r,\theta)\)\(\theta>0\), déplacez-vous dans le sens antihoraire depuis l'axe polaire d'un angle de\(\theta\), puis étendez un segment de ligne dirigé à partir du pôle sur la longueur de\(r\) dans la direction de\(\theta\). Si la\(\theta\) valeur est négative, déplacez-vous dans le sens des aiguilles d'une montre et étendez un segment de ligne dirigé sur la longueur de\(r\) dans la direction de\(\theta\). Voir l'exemple\(\PageIndex{1}\).
• Si la\(r\) valeur est négative, étendez le segment de ligne dirigé dans la direction opposée à\(\theta\). Voir l'exemple\(\PageIndex{2}\).
• Pour convertir des coordonnées polaires en coordonnées rectangulaires, utilisez les formules\(x=r \cos \theta\) et\(y=r \sin \theta\). Voir Exemple\(\PageIndex{3}\) et Exemple\(\PageIndex{4}\).
• Pour convertir des coordonnées rectangulaires en coordonnées polaires, utilisez une ou plusieurs des formules suivantes :\(\cos \theta=\dfrac{x}{r}\)\(\sin \theta=\dfrac{y}{r}\),\(\tan \theta=\dfrac{y}{x}\), et\(r=\sqrt{x^2+y^2}\). Voir l'exemple\(\PageIndex{5}\).
• Transformer des équations entre des formes polaires et rectangulaires signifie effectuer les substitutions appropriées en fonction des formules disponibles, ainsi que des manipulations algébriques. Voir Exemple\(\PageIndex{6}\)\(\PageIndex{7}\), Exemple et Exemple\(\PageIndex{8}\).
• L'utilisation des substitutions appropriées permet de réécrire une équation polaire sous forme d'équation rectangulaire, puis de la représenter graphiquement dans le plan rectangulaire. Voir Exemple\(\PageIndex{9}\)\(\PageIndex{10}\), Exemple et Exemple\(\PageIndex{11}\).