10.2 : Triangles non droits - Loi des cosinus
- Page ID
- 195518
Dans cette section, vous allez :
- Utilisez la loi des cosinus pour résoudre des triangles obliques.
- Résolvez des problèmes appliqués en utilisant la loi des cosinus.
- Utilisez la formule de Heron pour déterminer l'aire d'un triangle.
Supposons qu'un bateau quitte le port, parcourt des\(10\) kilomètres, tourne en\(20\) degrés et parcourt encore 8 miles, comme indiqué sur la figure À\(\PageIndex{1}\) quelle distance du port se trouve le bateau ?
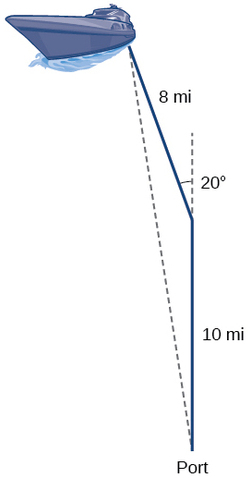
Figurine\(\PageIndex{1}\)
Malheureusement, bien que la loi des sinus nous permette de traiter de nombreux cas de triangle non droit, elle ne nous aide pas pour les triangles où l'angle connu se situe entre deux côtés connus, un triangle SAS (side-side-side side), ou lorsque les trois côtés sont connus, mais aucun angle n'est connu, un triangle SSS (side-side-side side). Dans cette section, nous allons étudier un autre outil permettant de résoudre les triangles obliques décrits dans ces deux derniers cas.
Utiliser la loi des cosinus pour résoudre des triangles obliques
L'outil dont nous avons besoin pour résoudre le problème de la distance entre le bateau et le port est la loi des cosinus, qui définit la relation entre les mesures d'angle et les longueurs des côtés dans les triangles obliques. Trois formules constituent la loi des cosinus. À première vue, les formules peuvent paraître compliquées car elles incluent de nombreuses variables. Cependant, une fois le schéma compris, la loi des cosinus est plus facile à utiliser que la plupart des formules à ce niveau mathématique.
Comprendre comment la loi des cosinus est dérivée sera utile pour utiliser les formules. La dérivation commence par le théorème généralisé de Pythagore, qui est une extension du théorème de Pythagore aux triangles non droits. Voici comment cela fonctionne : un triangle non droit arbitraire\(ABC\) est placé dans le plan de coordonnées avec un sommet\(A\) à l'origine, un côté\(c\) dessiné le long de l'axe x et un sommet\(C\) situé à un point\((x,y)\) donné du plan, comme illustré sur la figure\(\PageIndex{2}\). Généralement, les triangles existent n'importe où dans le plan, mais pour cette explication, nous allons placer le triangle comme indiqué.
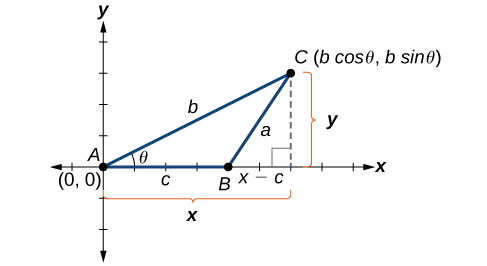
Figurine\(\PageIndex{2}\)
Nous pouvons faire tomber une perpendiculaire de\(C\) l'axe X (il s'agit de l'altitude ou de la hauteur). En rappelant les identités trigonométriques de base, nous savons que
\(\cos \theta=\dfrac{x(adjacent)}{b(hypotenuse)}\)et\(\sin \theta=\dfrac{y(opposite)}{b(hypotenuse)}\)
En termes de\(\theta\),\(x=b \cos \theta\) et\(y=b \sin \theta\). Le\((x,y)\) point situé à\(C\) possède des coordonnées\((b \cos \theta, b \sin \theta)\). En utilisant le côté\((x−c)\) comme jambe d'un triangle droit et\(y\) comme deuxième jambe, nous pouvons déterminer la longueur de l'hypoténuse à\(a\) l'aide du théorème de Pythagore. Ainsi,
\ (\ begin {array} {ll} a^2= {(x−c)} ^2+y^2 \ \ [4pt] \ ; \ ; \ ; \ ; = {(b \ cos \ theta−c)} ^2+ {(b \ sin \ theta)} ^2 & \ text {Substitut} (b \ cos \ theta) \ text {pour} x \ text {et} (b \ sin \ theta) \ text {pour} y \ \ [4pt] \ ; \ ; \ ; \ ; \ ; \ ; = (b^2 {\ cos} ^2 \ theta−2bc \ cos \ theta+c^2) +b^2 {\ sin} ^2 \ theta & \ text {Développez le carré.} \ \ [4pt] \ ; \ ; \ ; \ ; \ ; =b^2 {\ cos} ^2 \ theta+b^2 {\ sin} ^2 \ theta+c^2−2bc \ cos \ theta & \ text {Termes du groupe indiquant que} {\ cos} ^2 \ theta+ {\ sin} ^2 \ theta=1 \ \ [4pt] \ ; \ ; \ ; \ ; =b^2 ({\ cos} ^2 \ théta+ {\ sin} ^2 \ thêta) +c^2−2bc \ cos \ theta & \ text {Facteur de sortie} b^2 \ \ [4 points]
a^2=b^2+c^2−2bc \ cos \ thêta \ end {tableau} \)
La formule dérivée est l'une des trois équations de la loi des cosinus. Les autres équations se trouvent de la même manière.
N'oubliez pas qu'il est toujours utile d'esquisser le triangle lorsque vous déterminez des angles ou des côtés. Dans un scénario réel, essayez de dessiner un diagramme de la situation. Au fur et à mesure que de nouvelles informations apparaîtront, le diagramme devra peut-être être modifié. Apportez ces modifications au diagramme et, au final, le problème sera plus facile à résoudre.
La loi des cosinus indique que le carré de chaque côté d'un triangle est égal à la somme des carrés des deux autres côtés moins le double du produit des deux autres côtés et du cosinus de l'angle inclus.
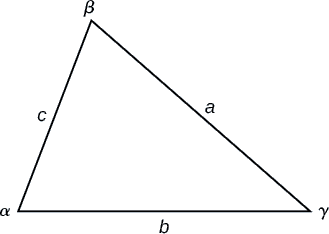
Figurine\(\PageIndex{3}\)
Pour les triangles étiquetés comme dans la figure\(\PageIndex{3}\), avec des angles\(\alpha\)\(\beta\) et\(\gamma\), et des côtés correspondants opposés\(a\)\(b\), et, respectivement\(c\), la loi des cosinus est donnée sous la forme de trois équations.
\[a^2=b^2+c^2−2bc \cos \alpha\]
\[b^2=a^2+c^2−2ac \cos \beta\]
\[c^2=a^2+b^2−2ab \cos \gamma\]
Pour résoudre une mesure latérale manquante, la mesure de l'angle opposé correspondante est nécessaire.
Lors de la résolution d'un angle, la mesure du côté opposé correspondante est nécessaire. Nous pouvons utiliser une autre version de la loi des cosinus pour déterminer un angle.
\[\cos \alpha=\dfrac{b^2+c^2−a^2}{2bc}\]
\[\cos \beta=\dfrac{a^2+c^2−b^2}{2ac}\]
\[\cos \gamma=\dfrac{a^2+b^2−c^2}{2ab}\]
- Esquissez le triangle. Identifiez les mesures des côtés et des angles connus. Utilisez des variables pour représenter les mesures des côtés et des angles inconnus.
- Appliquez la loi des cosinus pour déterminer la longueur du côté ou de l'angle inconnu.
- Appliquez la loi des sinus ou des cosinus pour déterminer la mesure d'un second angle.
- Calculez la mesure de l'angle restant.
Trouvez le côté et les angles inconnus du triangle dans la figure\(\PageIndex{4}\).
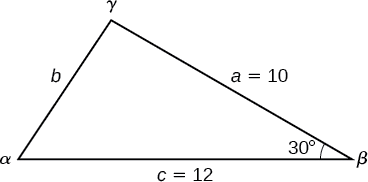
Figurine\(\PageIndex{4}\)
Solution
Tout d'abord, notez ce qui est donné : deux côtés et l'angle qui les sépare. Cet arrangement est classé SAS et fournit les données nécessaires à l'application de la loi des cosinus.
Chacune des trois lois des cosinus commence par le carré d'un côté inconnu opposé à un angle connu. Pour cet exemple, le premier côté à résoudre est le côté\(b\), car nous connaissons la mesure de l'angle opposé\(\beta\).
\(\begin{array}{ll} b^2=a^2+c^2−2ac \cos \beta \\[4pt] b^2={10}^2+{12}^2−2(10)(12)\cos(30°) & \text{Substitute the measurements for the known quantities.} \\[4pt] b^2=100+144−240 \left(\dfrac{\sqrt{3}}{2}\right) & \text{Evaluate the cosine and begin to simplify.} \\[4pt] b^2=244−120\sqrt{3} \\[4pt] b=\sqrt{244−120\sqrt{3}} & \text{Use the square root property.} \\[4pt] b≈6.013 \end{array}\)
Comme nous résolvons pour une longueur, nous utilisons uniquement la racine carrée positive. Maintenant que nous connaissons la longueur\(b\), nous pouvons utiliser la loi des sinus pour remplir les angles restants du triangle. En résolvant l'angle\(\alpha\), nous avons
\(\begin{array}{cc} \dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b} \\[4pt] \dfrac{\sin \alpha}{10}=\dfrac{\sin(30°)}{6.013} \\[4pt] \sin \alpha=\dfrac{10\sin(30°)}{6.013} & \text{Multiply both sides of the equation by }10. \\[4pt] \alpha={\sin}^{−1}\left(\dfrac{10\sin(30°)}{6.013}\right) & \text{Find the inverse sine of } \dfrac{10\sin(30°)}{6.013}. \\[4pt] \alpha≈56.3° \end{array}\)
L'autre possibilité\(\alpha\) serait\(\alpha=180°-56.3°≈123.7°\). Dans le schéma original,\(\alpha\) est adjacent au côté le plus long, il en\(\alpha\) va de même pour un angle aigu et, par conséquent,\(123.7°\) cela n'a aucun sens. Notez que si nous choisissons d'appliquer la loi des cosinus, nous arrivons à une réponse unique. Nous n'avons pas à considérer les autres possibilités, car le cosinus est unique pour les angles entre\(0°\) et\(180°\). En procédant\(\alpha≈56.3°\), nous pouvons ensuite trouver le troisième angle du triangle.
\[\begin{align*} \gamma&= 180^{\circ}-30^{\circ}-56.3^{\circ}\\ &\approx 93.7^{\circ} \end{align*}\]
L'ensemble complet des angles et des côtés est
\(\alpha≈56.3°\)\(a=10\)
\(\beta=30°\)\(b≈6.013\)
\(\gamma≈93.7°\)\(c=12\)
Trouvez le côté et les angles manquants du triangle donné :\(\alpha=30°\),\(b=12\),\(c=24\).
- Réponse
-
\(a≈14.9\),\(\beta≈23.8°\),\(\gamma≈126.2°\).
Trouvez l'angle\(\alpha\) du triangle donné s'il est côté\(a=20\)\(b=25\), côté et côté\(c=18\).
Solution
Pour cet exemple, nous n'avons aucun angle. Nous pouvons résoudre n'importe quel angle en utilisant la loi des cosinus. Pour résoudre l'angle\(\alpha\), nous avons
\(\begin{array}{ll} a^2=b^2+c^2−2bc \cos \alpha \\[4pt] {20}^2={25}^2+{18}^2−2(25)(18)\cos \alpha & \text{Substitute the appropriate measurements.} \\[4pt] 400=625+324−900 \cos \alpha & \text{ Simplify in each step.} \\[4pt] 400=949−900 \cos \alpha \\[4pt] −549=−900 \cos \alpha & \text{Isolate }\cos \alpha. \\[4pt] 0.61≈\cos \alpha & \text{Find the inverse cosine.} \\[4pt] \alpha≈52.4° \end{array}\)
Voir la figure\(\PageIndex{5}\).
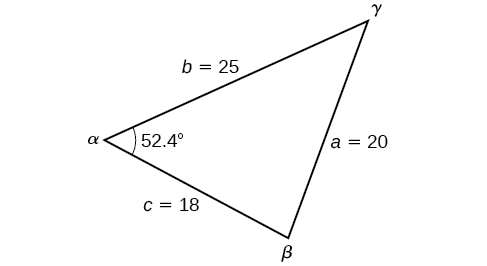
Figurine\(\PageIndex{5}\)
Analyse
Comme le cosinus inverse peut renvoyer n'importe quel angle entre\(0\) et\(180\) degrés, il n'y aura aucun cas ambigu en utilisant cette méthode.
Étant donné\(a=5\)\(b=7\), et\(c=10\), trouvez les angles manquants.
- Réponse
-
\(\alpha≈27.7°\),\(\beta≈40.5°\),\(\gamma≈111.8°\)
Résoudre des problèmes appliqués à l'aide de la loi des cosinus
Tout comme la loi des sinus a fourni les équations appropriées pour résoudre un certain nombre d'applications, la loi des cosinus est applicable aux situations dans lesquelles les données données correspondent aux modèles de cosinus. Nous pouvons les voir dans les domaines de la navigation, de l'arpentage, de l'astronomie et de la géométrie, pour n'en nommer que quelques-uns.
Sur de nombreux téléphones portables équipés d'un GPS, une position approximative peut être donnée avant la réception du signal GPS. Cela se fait grâce à un processus appelé triangulation, qui fonctionne en utilisant les distances à partir de deux points connus. Supposons qu'il y ait deux tours de téléphonie mobile à portée d'un téléphone portable. Les deux tours sont situées à quelques\(6000\) pieds l'une de l'autre le long d'une autoroute droite, d'est en ouest, et le téléphone portable se trouve au nord de l'autoroute. Sur la base du retard du signal, il peut être déterminé que le signal se trouve à\(5050\) quelques pieds de la première tour et à\(2420\) quelques pieds de la deuxième tour. Déterminez la position du téléphone cellulaire au nord et à l'est de la première tour et déterminez à quelle distance il se trouve de l'autoroute.
Solution
Pour plus de simplicité, nous commençons par dessiner un diagramme similaire à celui de la figure\(\PageIndex{6}\) et par étiqueter les informations que nous avons données
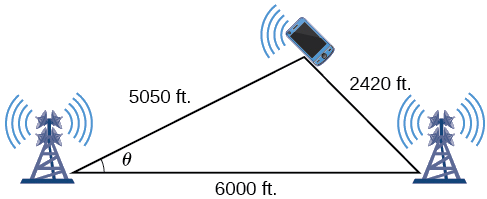
Figurine\(\PageIndex{6}\)
En utilisant la loi des cosinus, nous pouvons résoudre l'angle\(\theta\). Souvenez-vous que la loi des cosinus utilise le carré d'un côté pour trouver le cosinus de l'angle opposé. Pour cet exemple, laissez\(a=2420\)\(b=5050\), et\(c=6000\). \(\theta\)Correspond donc au côté opposé\(a=2420\).
\[\begin{align*} a^2 & =b^2+c^2−2bc \cos \theta \\[4pt] {(2420)}^2 &={(5050)}^2+{(6000)}^2−2(5050)(6000) \cos \theta \\[4pt] \cos \theta &≈ 0.9183 \\[4pt] \theta &≈ {\cos}^{−1}(0.9183) \\[4pt] \theta &≈ 23.3° \end{align*}\]
Pour répondre aux questions concernant la position du téléphone au nord et à l'est de la tour et la distance par rapport à l'autoroute, abaissez une perpendiculaire à la position du téléphone portable, comme sur la figure\(\PageIndex{7}\). Cela forme deux triangles droits, bien que nous n'ayons besoin que du triangle droit qui inclut la première tour pour ce problème.
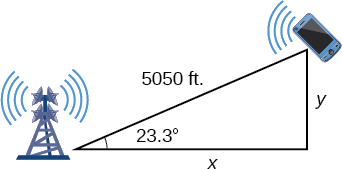
Figurine\(\PageIndex{7}\)
En utilisant l'angle\(\theta=23.3\)° et les identités trigonométriques de base, nous pouvons trouver les solutions. Ainsi
\[\begin{align*} \cos(23.3°) &= \dfrac{x}{5050} \\[4pt] x &= 5050\cos(23.3°) \\[4pt] x &≈ 4638.15\, feet\\[4pt] \sin(23.3°) &= \dfrac{y}{5050} \\[4pt] y &= 5050\sin(23.3°) \\[4pt] y &≈1997.5 \, feet \end{align*}\]
Le téléphone portable se trouve à environ\(4638\) pieds à l'est et\(1998\) pieds au nord de la première tour, et à\(1998\) quelques pas de l'autoroute.
Pour en revenir à notre problème au début de cette section, supposons qu'un bateau quitte le port, parcourt des\(10\) kilomètres, fait des\(20\) virages et parcourt des\(8\) kilomètres supplémentaires. À quelle distance du port se trouve le bateau ? Le schéma est reproduit ici sur la figure\(\PageIndex{8}\).
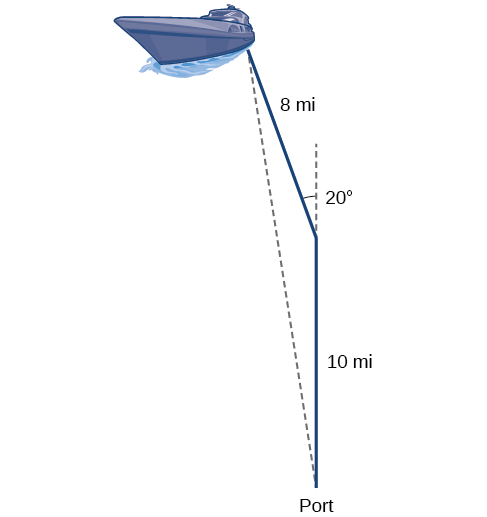
Figurine\(\PageIndex{8}\)
Solution
Le bateau a pivoté de 20 degrés, de sorte que l'angle obtus du triangle non droit est l'angle supplémentaire,\(180°−20°=160°\). Nous pouvons ainsi utiliser la loi des cosinus pour trouver le côté manquant du triangle obtus, c'est-à-dire la distance entre le bateau et le port.
\[\begin{align*} x^2 &= 8^2+{10}^2−2(8)(10)\cos(160°) \\[4pt] x^2 &= 314.35 \\[4pt] x &= \sqrt{314.35} \\[4pt] x&≈17.7\, miles \end{align*}\]
Le bateau se trouve\(17.7\) à environ miles du port.
Utilisation de la formule de Heron pour déterminer l'aire d'un triangle
Nous avons déjà appris à déterminer l'aire d'un triangle oblique lorsque nous connaissons deux côtés et un angle. Nous connaissons également la formule pour déterminer l'aire d'un triangle en utilisant la base et la hauteur. Cependant, lorsque nous connaissons les trois côtés, nous pouvons utiliser la formule de Heron au lieu de trouver la hauteur. Héron d'Alexandrie était un géomètre qui a vécu au premier siècle de notre ère. Il a découvert une formule permettant de déterminer l'aire des triangles obliques lorsque trois côtés sont connus.
La formule de Heron trouve l'aire des triangles obliques dans lesquels les côtés\(a\)\(b\), et\(c\) sont connus.
\[Area=\sqrt{s(s−a)(s−b)(s−c)}\]
où\(s=\dfrac{(a+b+c)}{2}\) est la moitié du périmètre du triangle, parfois appelé demi-périmètre.
Trouvez l'aire du triangle dans la figure en\(\PageIndex{9}\) utilisant la formule de Heron.
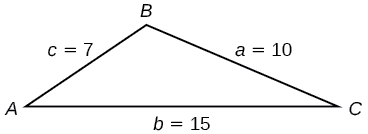
Figurine\(\PageIndex{9}\)
Solution
Tout d'abord, nous calculons\(s\).
\[\begin{align*} s&= \dfrac{(a+b+c)}{2}\\ s&= \dfrac{(10+15+7)}{2}\\ &= 16 \end{align*}\]
Ensuite, nous appliquons la formule.
\[\begin{align*} Area&= \sqrt{s(s-a)(s-b)(s-c)}\\ Area&= \sqrt{16(16-10)(16-15)(16-7)}\\ Area&\approx 29.4 \end{align*}\]
La superficie est d'environ des unités\(29.4\) carrées.
Utilisez la formule de Heron pour déterminer l'aire d'un triangle dont les côtés ont des longueurs\(a=29.7\)\(b=42.3\) ft, ft et\(c=38.4\) ft.
- Réponse
-
Surface = pieds\(552\) carrés
Un promoteur de la ville de Chicago souhaite construire un bâtiment composé de lofts d'artistes sur un terrain triangulaire bordé par Rush Street, Wabash Avenue et Pearson Street. La façade le long de Rush Street\(62.4\) mesure environ mètres, le long de l'avenue Wabash, elle est d'environ\(43.5\) mètres et le long de la rue Pearson, elle est d'environ\(34.1\) mètres. Combien de mètres carrés sont mis à la disposition du développeur ? Voir la figure\(\PageIndex{10}\) pour une vue de la propriété de la ville.
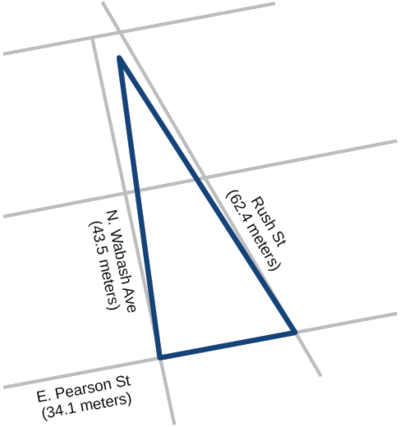
Figurine\(\PageIndex{10}\)
Solution
Trouvez la mesure pour\(s\), qui correspond à la moitié du périmètre.
\[\begin{align*} s&= \dfrac{(62.4+43.5+34.1)}{2}\\ s&= 70\; m\\ \text {Apply Heron's formula.}\\ Area&= \sqrt{70(70-62.4)(70-43.5)(70-34.1)}\\ Area&= \sqrt{506,118.2}\\ Area&\approx 711.4 \end{align*}\]
Le développeur dispose d'environ mètres\(711.4\) carrés.
Détermine l'aire d'un triangle donné en\(a=4.38\)\(b=3.79\) pieds, pieds et\(c=5.22\) pieds.
- Réponse
-
environ pieds\(8.15\) carrés
Accédez à ces ressources en ligne pour obtenir des instructions et des pratiques supplémentaires sur la Loi des cosinus.
Équations clés
| Loi des cosinus |
\(a^2=b^2+c^2−2bc \cos \alpha\) \(b^2=a^2+c^2−2ac \cos \beta\) \(c^2=a^2+b^2−2ab \cos \gamma\) |
| Formule de Heron |
\(Area=\sqrt{s(s−a)(s−b)(s−c)}\) où\(s=\dfrac{(a+b+c)}{2}\) |
Key Concepts
- The Law of Cosines defines the relationship among angle measurements and lengths of sides in oblique triangles.
- The Generalized Pythagorean Theorem is the Law of Cosines for two cases of oblique triangles: SAS and SSS. Dropping an imaginary perpendicular splits the oblique triangle into two right triangles or forms one right triangle, which allows sides to be related and measurements to be calculated. See Example \(\PageIndex{1}\) and Example \(\PageIndex{2}\).
- The Law of Cosines is useful for many types of applied problems. The first step in solving such problems is generally to draw a sketch of the problem presented. If the information given fits one of the three models (the three equations), then apply the Law of Cosines to find a solution. See Example \(\PageIndex{3}\) and Example \(\PageIndex{4}\).
- Heron’s formula allows the calculation of area in oblique triangles. All three sides must be known to apply Heron’s formula. See Example \(\PageIndex{5}\) and See Example \(\PageIndex{6}\).


