Skip to main content
Global

7.2 : Trigonométrie du triangle droit

  1. Last updated
  2. Save as PDF
  • Page ID
    195574

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    • Utilisez des triangles droits pour évaluer les fonctions trigonométriques.
    • Trouvez les valeurs des fonctions pour 30° (\(\dfrac{\pi}{6}\)), 45° (\(\dfrac{\pi}{4}\)) et 60° (\(\dfrac{\pi}{3}\)).
    • Utilisez des cofonctions égales d'angles complémentaires.
    • Utilisez les définitions des fonctions trigonométriques de n'importe quel angle.
    • Utilisez la trigonométrie du triangle droit pour résoudre les problèmes appliqués.

    Mont. L'Everest, qui chevauche la frontière entre la Chine et le Népal, est la plus haute montagne du monde. Mesurer sa hauteur n'est pas une tâche facile et, en fait, la mesure réelle est source de controverse depuis des centaines d'années. Le processus de mesure implique l'utilisation de triangles et d'une branche des mathématiques appelée trigonométrie. Dans cette section, nous allons définir un nouveau groupe de fonctions appelées fonctions trigonométriques et découvrir comment elles peuvent être utilisées pour mesurer des hauteurs, telles que celles des plus hautes montagnes.

    Nous avons précédemment défini le sinus et le cosinus d'un angle en termes de coordonnées d'un point sur le cercle unitaire intersecté par le côté terminal de l'angle :

    \[ \begin{align*} \cos t &= x \\ \sin t &=y \end{align*} \]

    Dans cette section, nous verrons une autre façon de définir les fonctions trigonométriques à l'aide des propriétés des triangles droits.

    Utilisation de triangles droits pour évaluer des fonctions trigonométriques

    Dans les sections précédentes, nous avons utilisé un cercle unitaire pour définir les fonctions trigonométriques. Dans cette section, nous allons étendre ces définitions afin de pouvoir les appliquer aux triangles droits. La valeur de la fonction sinus ou cosinus de\(t\) est sa valeur en\(t\) radians. Tout d'abord, nous devons créer notre triangle droit. La figure\(\PageIndex{1}\) montre un point sur un cercle unitaire de rayon 1. Si nous déposons un segment de ligne verticale du point\((x,y)\) vers l'axe x, nous obtenons un triangle droit dont le côté vertical a une longueur\(y\) et dont le côté horizontal a une longueur\(x\). Nous pouvons utiliser ce triangle droit pour redéfinir le sinus, le cosinus et les autres fonctions trigonométriques en tant que rapports des côtés d'un triangle droit.

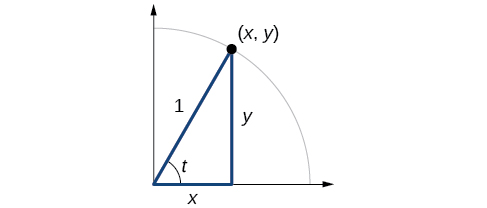
    Graphique d'un quart de cercle avec un rayon de 1. Triangle inscrit avec un angle de t. Le point de (x, y) se trouve à l'intersection du côté terminal de l'angle et du bord du cercle.
    Figurine\(\PageIndex{1}\)

    Nous savons

    \[ \cos t= \frac{x}{1}=x \]

    De même, nous savons

    \[ \sin t= \frac{y}{1}=y \]

    Ces ratios s'appliquent toujours aux côtés d'un triangle droit lorsqu'aucun cercle unitaire n'est impliqué et lorsque le triangle n'est pas dans une position standard et n'est pas représenté graphiquement à l'aide de\((x,y)\) coordonnées. Pour pouvoir utiliser librement ces ratios, nous allons donner aux côtés des noms plus généraux : au lieu de\(x\), nous appellerons le côté entre l'angle donné et l'angle droit le côté adjacent à l'angle\(t\). (Adjacent signifie « à côté ».) Au lieu de cela\(y\), nous appellerons le côté le plus éloigné de l'angle donné le côté opposé à l'angle\(t\). Et au lieu de cela\(1\), nous appellerons le côté d'un triangle droit opposé à l'angle droit l'hypoténuse. Ces côtés sont étiquetés sur la figure\(\PageIndex{2}\).

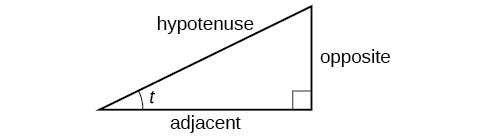
    Un triangle droit avec l'hypoténuse, les côtés opposés et adjacents étiquetés.
    Figure\(\PageIndex{2}\) : Les côtés d'un triangle droit par rapport à l'angle\(t\).

    Comprendre les relations du triangle droit

    Étant donné un triangle droit avec un angle aigu de\(t\),

    \[\begin{align} \sin (t) &= \dfrac{\text{opposite}}{\text{hypotenuse}} \label{sindef}\\ \cos (t) &= \dfrac{\text{adjacent}}{\text{hypotenuse}} \label{cosdef}\\ \tan (t) &= \dfrac{\text{opposite}}{\text{adjacent}} \label{tandef}\end{align}\]

    Un mnémotechnique courant pour se souvenir de ces relations est SohCahtoa, formé à partir des premières lettres de « S ine » est à l'opposé de l'hypotenuse, « C » l'osine est un adjacent à l'hypotenuse, « T angent » n'est pas opposé à un adjacent. »

    comment : étant donné la longueur des côtés d'un triangle droit et l'un des angles aigus, déterminer le sinus, le cosinus et la tangente de cet angle

    1. Déterminez le sinus comme le rapport entre le côté opposé et l'hypoténuse.
    2. Déterminez le cosinus comme le rapport entre le côté adjacent et l'hypoténuse.
    3. Trouver la tangente est le rapport entre le côté opposé et le côté adjacent.

    Exemple\(\PageIndex{1}\): Evaluating a Trigonometric Function of a Right Triangle

    À partir du triangle illustré sur la figure\(\PageIndex{3}\), trouvez la valeur de\(\cos α\).

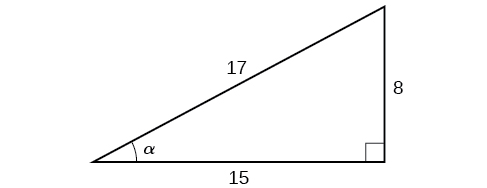
    Un triangle droit avec des longueurs de côté de 8, 15 et 17. Angle alpha également marqué qui est opposé au côté marqué 8.
    Figurine\(\PageIndex{3}\)

    Solution

    Le côté adjacent à l'angle est 15 et l'hypoténuse du triangle est 17, donc via l'équation \ ref {cosdef} :

    \[\begin{align*} \cos (α) &= \dfrac{\text{adjacent}}{\text{hypotenuse}} \\[4pt] &= \dfrac{15}{17} \end{align*}\]

    Exercice\(\PageIndex{1}\)

    À partir du triangle illustré sur la figure\(\PageIndex{4}\), trouvez la valeur de\(\sin t\).

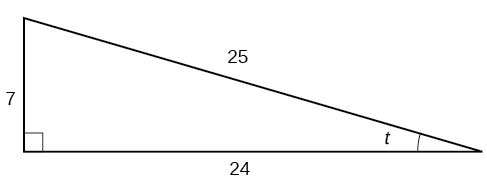
    Un triangle droit avec des côtés de 7, 24 et 25. L'angle t qui est opposé au côté marqué 7 est également étiqueté.
    Figurine\(\PageIndex{4}\)
    Réponse

    \(\frac{7}{25}\)

    Relier les angles et leurs fonctions

    Lorsque vous travaillez avec des triangles droits, les mêmes règles s'appliquent quelle que soit l'orientation du triangle. En fait, nous pouvons évaluer les six fonctions trigonométriques de l'un ou l'autre des deux angles aigus du triangle de la Figure\(\PageIndex{5}\). Le côté opposé à un angle aigu est le côté adjacent à l'autre angle aigu, et vice versa.

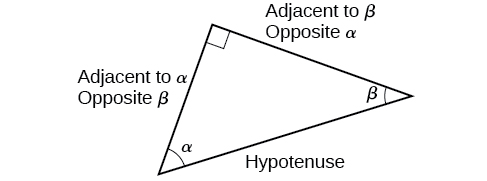
    Triangle droit avec angles alpha et bêta. Les côtés sont étiquetés hypoténuse, adjacents à alpha/opposés à bêta et adjacents à bêta/alpha opposé.
    Figure\(\PageIndex{5}\) : Le côté adjacent à un angle est opposé à l'autre.

    On nous demandera de trouver les six fonctions trigonométriques pour un angle donné dans un triangle. Notre stratégie consiste à trouver d'abord le sinus, le cosinus et la tangente des angles. Ensuite, nous pouvons facilement trouver les autres fonctions trigonométriques car nous savons que l'inverse du sinus est cosécante, l'inverse du cosinus est sécante et l'inverse de la tangente est cotangente.

    comment : Compte tenu de la longueur des côtés d'un triangle droit, évaluer les six fonctions trigonométriques de l'un des angles aigus

    1. Si nécessaire, dessinez le triangle droit et étiquetez l'angle fourni.
    2. Identifiez l'angle, le côté adjacent, le côté opposé à l'angle et l'hypoténuse du triangle droit.
    3. Trouvez la fonction requise :
      • sinus comme rapport entre le côté opposé et l'hypoténuse
      • cosinus comme rapport entre le côté adjacent et l'hypoténuse
      • tangente comme le rapport entre le côté opposé et le côté adjacent
      • sécante comme le rapport entre l'hypoténuse et le côté adjacent
      • cosécante comme le rapport entre l'hypoténuse et le côté opposé
      • cotangente comme le rapport entre le côté adjacent et le côté opposé

    Exemple\(\PageIndex{2}\): Evaluating Trigonometric Functions of Angles Not in Standard Position

    À l'aide du triangle illustré sur la figure\(\PageIndex{6}\), évaluez\( \sin α, \cos α, \tan α, \sec α, \csc α,\) et\( \cot α\).

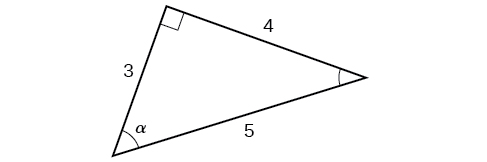
    Triangle droit avec les côtés 3, 4 et 5. L'angle alpha est également étiqueté, qui est opposé au côté marqué 4.
    Figurine\(\PageIndex{6}\)

    Solution

    \[ \begin{align*} \sin α &= \dfrac{\text{opposite } α}{\text{hypotenuse}} = \dfrac{4}{5} \\ \cos α &= \dfrac{\text{adjacent to }α}{\text{hypotenuse}}=\dfrac{3}{5} \\ \tan α &= \dfrac{\text{opposite }α}{\text{adjacent to }α}=\dfrac{4}{3} \\ \sec α &= \dfrac{\text{hypotenuse}}{\text{adjacent to }α}= \dfrac{5}{3} \\ \csc α &= \dfrac{\text{hypotenuse}}{\text{opposite }α}=\dfrac{5}{4} \\ \cot α &= \dfrac{\text{adjacent to }α}{\text{opposite }α}=\dfrac{3}{4} \end{align*}\]

    Exercice\(\PageIndex{2}\)

    À l'aide du triangle illustré sur la figure\(\PageIndex{7}\), évaluez\( \sin t, \cos t,\tan t, \sec t, \csc t,\) et\(\cot t\).

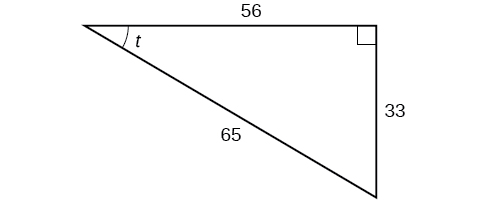
    Triangle droit avec côtés 33, 56 et 65. L'angle t est également marqué, qui est opposé au côté marqué 33.
    Figurine\(\PageIndex{7}\)
    Réponse

    \[\begin{align*} \sin t &= \frac{33}{65}, \cos t= \frac{56}{65},\tan t= \frac{33}{56}, \\ \\ \sec t &= \frac{65}{56},\csc t= \frac{65}{33},\cot t= \frac{56}{33} \end{align*}\]

    Détermination des fonctions trigonométriques d'angles spéciaux à l'aide de longueurs latérales

    Nous avons déjà discuté des fonctions trigonométriques en ce qui concerne les angles spéciaux sur le cercle unitaire. Maintenant, nous pouvons utiliser ces relations pour évaluer les triangles qui contiennent ces angles spéciaux. Nous procédons ainsi parce que lorsque nous évaluons les angles spéciaux dans les fonctions trigonométriques, celles-ci ont des valeurs relativement favorables, des valeurs qui ne contiennent aucune racine carrée ou une seule racine carrée dans le rapport. Ce sont donc les angles souvent utilisés dans les problèmes de mathématiques et de sciences. Nous utiliserons des multiples de\(30°, 60°,\) et\(45°\), cependant, rappelons que lorsqu'il s'agit de triangles droits, nous nous limitons aux angles entre les deux\(0° \text{ and } 90°\).

    Supposons que nous ayons un\(30°,60°,90°\) triangle, qui peut également être décrit comme un\(\frac{π}{6}, \frac{π}{3},\frac{π}{2}\) triangle. Les côtés ont des longueurs dans la relation\(s,\sqrt{3}s,2s.\) Les côtés d'un\(45°,45°,90° \) triangle, qui peut également être décrit comme un\(\frac{π}{4},\frac{π}{4},\frac{π}{2}\) triangle, ont des longueurs dans la relation.\(s,s,\sqrt{2}s.\) Ces relations sont illustrées sur la figure\(\PageIndex{8}\).

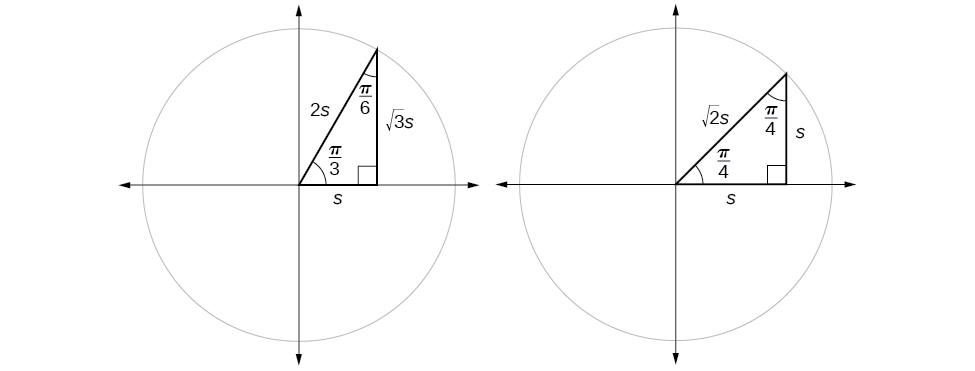
    Deux graphes côte à côte de cercles avec des angles inscrits. Le premier cercle a un angle pi/3 inscrit, un rayon de 2 s, une base de longueur s et une hauteur de longueur. Le deuxième cercle a un angle de pi/4 inscrit avec le rayon, la base de la longueur s et la hauteur de la longueur s.
    Figure\(\PageIndex{8}\) : Longueurs latérales des triangles spéciaux

    Nous pouvons ensuite utiliser les rapports des longueurs des côtés pour évaluer les fonctions trigonométriques d'angles spéciaux.

    Étant donné les fonctions trigonométriques d'un angle spécial, évaluez en utilisant les longueurs des côtés.

    1. Utilisez les longueurs de côté indiquées sur la figure\(\PageIndex{8}\) pour l'angle spécial que vous souhaitez évaluer.
    2. Utilisez le ratio des longueurs de côté approprié à la fonction que vous souhaitez évaluer.

    Exemple\(\PageIndex{3}\): Evaluating Trigonometric Functions of Special Angles Using Side Lengths

    Déterminez la valeur exacte des fonctions trigonométriques de\(\frac{π}{3}\), en utilisant les longueurs des côtés.

    Solution

    \[\begin{align*} \sin (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{hyp}}=\dfrac{\sqrt{3}s}{2s}=\dfrac{\sqrt{3}}{2} \\ \cos (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text{hyp}}=\dfrac{s}{2s}=\dfrac{1}{2} \\ \tan (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{adj}} =\dfrac{\sqrt{3}s}{s}=\sqrt{3} \\ \sec (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{adj}} = \dfrac{2s}{s}=2 \\ \csc (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{opp}} =\dfrac{2s}{\sqrt{3}s}=\dfrac{2}{\sqrt{3}}=\dfrac{2\sqrt{3}}{3} \\ \cot (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text{opp}}=\dfrac{s}{\sqrt{3}s}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3} \end{align*}\]

    Exercice\(\PageIndex{3}\)

    Déterminez la valeur exacte des fonctions trigonométriques\(\frac{π}{4}\) en utilisant les longueurs des côtés.

    Réponse

    \( \sin (\frac{π}{4})=\frac{\sqrt{2}}{2}, \cos (\frac{π}{4})=\frac{\sqrt{2}}{2}, \tan (\frac{π}{4})=1,\)

    \( \sec (\frac{π}{4})=\sqrt{2}, \csc (\frac{π}{4})=\sqrt{2}, \cot (\frac{π}{4}) =1 \)

    Utilisation de la cofonction égale des compléments

    Si nous examinons de plus près la relation entre le sinus et le cosinus des angles spéciaux par rapport au cercle unitaire, nous remarquerons un motif. Dans un triangle droit avec des angles de\(\frac{π}{6}\) et\(\frac{π}{3}\), nous voyons que le sinus de\(\frac{π}{3}\), à savoir\(\frac{\sqrt{3}}{2}\), est également le cosinus de\(\frac{π}{6}\), tandis que le sinus de\(\frac{π}{6}\), à savoir\(\frac{1}{2},\) est également le cosinus de\(\frac{π}{3}\) (Figure\(\PageIndex{9}\)).

    \[\begin{align*} \sin \frac{π}{3} &= \cos \frac{π}{6}=\frac{\sqrt{3}s}{2s}=\frac{\sqrt{3}}{2} \\ \sin \frac{π}{6} &= \cos \frac{π}{3}=\frac{s}{2s}=\frac{1}{2} \end{align*}\]

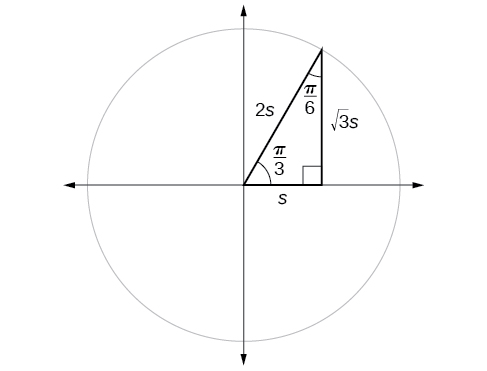
    Un graphe d'un cercle d'angle pi/3 inscrit avec un rayon de 2 s, une base de longueur s et une hauteur de.
    Figure\(\PageIndex{9}\) : Le sinus de\(\frac{π}{3}\) est égal au cosinus de\(\frac{π}{6}\) et vice versa.

    Ce résultat ne devrait pas être surprenant car, comme nous le voyons sur la figure\(\PageIndex{9}\), le côté opposé à l'angle de\(\frac{π}{3}\) est également le côté adjacent à\(\frac{π}{6}\), donc\(\sin (\frac{π}{3})\) et\(\cos (\frac{π}{6})\) sont exactement le même rapport entre les deux mêmes côtés,\(\sqrt{3} s\) et de\(2s.\) même,\( \cos (\frac{π}{3})\)\( \sin (\frac{π}{6})\) sont également le même ratio en utilisant les deux mêmes côtés,\(s\) et\(2s\).

    L'interrelation entre les sinus et les cosinus de\(\frac{π}{6}\) et vaut\(\frac{π}{3}\) également pour les deux angles aigus de tout triangle droit, puisque dans tous les cas, le rapport des deux mêmes côtés constituerait le sinus d'un angle et le cosinus de l'autre. Puisque les trois angles d'un triangle s'additionnent à π et que l'angle droit l'est\(\frac{π}{2}\), les deux angles restants doivent également s'additionner à\(\frac{π}{2}\). Cela signifie qu'un triangle droit peut être formé avec deux angles quelconques qui s'ajoutent\(\frac{π}{2}\) à, en d'autres termes, deux angles complémentaires. Nous pouvons donc énoncer une identité de cofonction : si deux angles sont complémentaires, le sinus de l'un est le cosinus de l'autre, et vice versa. Cette identité est illustrée sur la figure\(\PageIndex{10}\).

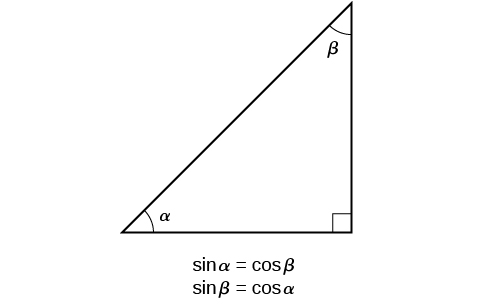
    Triangle droit avec angles alpha et bêta. Équivalence entre sin alpha et cos bêta. Équivalence entre sin bêta et cos alpha.
    Figure\(\PageIndex{10}\) : Identité de cofonction du sinus et du cosinus d'angles complémentaires

    En utilisant cette identité, nous pouvons affirmer sans calculer, par exemple, que le sinus de\(\frac{π}{12}\) est égal au cosinus de\(\frac{5π}{12}\), et que le sinus de\(\frac{5π}{12}\) est égal au cosinus de\(\frac{π}{12}\). Nous pouvons également affirmer que si, pour un certain angle\(t, \cos t= \frac{5}{13},\),\( \sin (\frac{π}{2}−t)=\frac{5}{13}\) alors aussi.

    IDENTITÉS DE COFONCTIONS

    Les identités de cofonctions en radians sont répertoriées dans le tableau\(\PageIndex{1}\).

    Tableau\(\PageIndex{1}\)
    \( \cos t= \sin (\frac{π}{2}−t)\) \( \sin t= \cos (\dfrac{π}{2}−t)\)
    \( \tan t= \cot (\dfrac{π}{2}−t) \) \( \cot t= \tan (\dfrac{π}{2}−t)\)
    \( \sec t= \csc (\dfrac{π}{2}−t) \) \( \csc t= \sec (\dfrac{π}{2}−t)\)

    comment faire : étant donné le sinus et le cosinus d'un angle, trouvez le sinus ou le cosinus de son complément.

    1. Pour déterminer le sinus de l'angle complémentaire, trouvez le cosinus de l'angle d'origine.
    2. Pour trouver le cosinus de l'angle complémentaire, trouvez le sinus de l'angle d'origine.

    Exemple\(\PageIndex{4}\): Using Cofunction Identities

    Si\( \sin t = \frac{5}{12},\) je trouve\(( \cos \frac{π}{2}−t)\).

    Solution

    Selon les identités de cofonctions pour le sinus et le cosinus,

    \[ \sin t= \cos (\dfrac{π}{2}−t). \nonumber\]

    Donc

    \[ \cos (\dfrac{π}{2}−t)= \dfrac{5}{12}. \nonumber\]

    Exercice\(\PageIndex{4}\)

    Si je\(\csc (\frac{π}{6})=2,\) trouve\( \sec (\frac{π}{3}).\)

    Solution

    2

    Utilisation de fonctions trigonométriques

    Dans les exemples précédents, nous avons évalué le sinus et le cosinus dans des triangles dont nous connaissions les trois côtés. Mais la véritable puissance de la trigonométrie du triangle droit apparaît lorsque nous examinons des triangles dont nous connaissons un angle mais dont nous ne connaissons pas tous les côtés.

    Comment : À partir d'un triangle droit, de la longueur d'un côté et de la mesure d'un angle aigu, trouvez les côtés restants

    1. Pour chaque côté, sélectionnez la fonction trigonométrique dont le côté inconnu est soit le numérateur, soit le dénominateur. Le côté connu sera à son tour le dénominateur ou le numérateur.
    2. Écrivez une équation définissant la valeur de fonction de l'angle connu égale au rapport des côtés correspondants.
    3. À l'aide de la valeur de la fonction trigonométrique et de la longueur de côté connue, déterminez la longueur de côté manquante.

    Exemple\(\PageIndex{5}\): Finding Missing Side Lengths Using Trigonometric Ratios

    Trouvez les côtés inconnus du triangle dans la figure\(\PageIndex{11}\).

    Un triangle droit avec les côtés a, c et 7. Un angle de 30 degrés est également marqué, qui est opposé au côté marqué 7.
    Figurine\(\PageIndex{11}\)

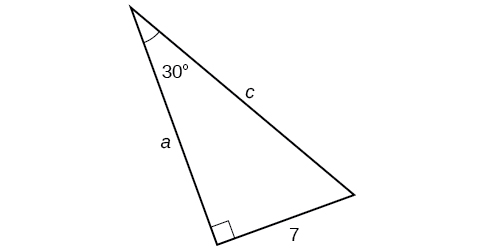
    Solution

    Nous connaissons l'angle et le côté opposé, nous pouvons donc utiliser la tangente pour trouver le côté adjacent.

    \[ \tan (30°)= \dfrac{7}{a} \nonumber\]

    Nous réorganisons pour résoudre\(a\).

    \[\begin{align} a &=\dfrac{7}{ \tan (30°)} \\ & =12.1 \end{align} \nonumber\]

    Nous pouvons utiliser le sinus pour trouver l'hypoténuse.

    \[ \sin (30°)= \dfrac{7}{c} \nonumber\]

    Encore une fois, nous réorganisons pour résoudre\(c\).

    \[\begin{align*} c &= \dfrac{7}{\sin (30°)} =14 \end{align*}\]

    Exercice\(\PageIndex{5}\):

    Un triangle droit a un angle\(\frac{π}{3}\) et une hypoténuse de 20. Trouvez les côtés et l'angle inconnus du triangle.

    Réponse

    \(\mathrm{adjacent=10; opposite=10 \sqrt{3}; }\)l'angle manquant est\(\frac{π}{6}\)

    Utilisation de la trigonométrie du triangle droit pour résoudre des problèmes appliqués

    La trigonométrie du triangle droit a de nombreuses applications pratiques. Par exemple, la possibilité de calculer la longueur des côtés d'un triangle permet de déterminer la hauteur d'un objet de grande taille sans grimper au sommet ou avoir à étendre un ruban à mesurer sur sa hauteur. Pour ce faire, nous mesurons la distance entre la base de l'objet et un point du sol situé à une certaine distance, où nous pouvons regarder le haut de l'objet en biais. L'angle d'élévation d'un objet au-dessus d'un observateur par rapport à l'observateur est l'angle entre l'horizontale et la ligne allant de l'objet à l'œil de l'observateur. Le triangle droit créé par cette position possède des côtés qui représentent la hauteur inconnue, la distance mesurée depuis la base et la ligne de visée inclinée entre le sol et le sommet de l'objet. Connaissant la distance mesurée par rapport à la base de l'objet et l'angle de la ligne de visée, nous pouvons utiliser des fonctions trigonométriques pour calculer la hauteur inconnue. De même, nous pouvons former un triangle à partir du haut d'un objet haut en regardant vers le bas. L'angle de dépression d'un objet situé sous un observateur par rapport à l'observateur est l'angle entre l'horizontale et la ligne allant de l'objet à l'œil de l'observateur. Voir la figure\(\PageIndex{12}\).

    Schéma d'une tour radio avec des segments de ligne s'étendant du sommet et de la base de la tour jusqu'à un point du sol situé à une certaine distance. Les deux lignes et la tour forment un triangle droit. L'angle près du sommet de la tour est l'angle de dépression. L'angle au sol à distance de la tour est l'angle d'élévation.
    Figurine\(\PageIndex{12}\)

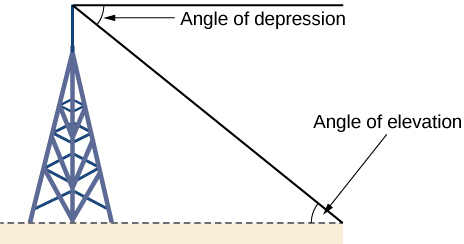
    Comment : Mesurez indirectement la hauteur d'un objet de grande taille

    1. Faites un croquis de la situation problématique pour suivre les informations connues et inconnues.
    2. Établissez une distance mesurée entre la base de l'objet et un point où le dessus de l'objet est clairement visible.
    3. À l'autre bout de la distance mesurée, regardez vers le haut de l'objet. Mesurez l'angle que fait la ligne de visée par rapport à l'horizontale.
    4. Écrivez une équation reliant la hauteur inconnue, la distance mesurée et la tangente de l'angle de la ligne de visée.
    5. Résolvez l'équation pour la hauteur inconnue.

    Exemple\(\PageIndex{6}\): Measuring a Distance Indirectly

    Pour trouver la hauteur d'un arbre, une personne marche jusqu'à un point situé à 30 pieds de la base de l'arbre. Elle mesure un angle de 57° 57° entre une ligne de visée au sommet de l'arbre et le sol, comme le montre la figure\(\PageIndex{13}\). Trouve la hauteur de l'arbre.

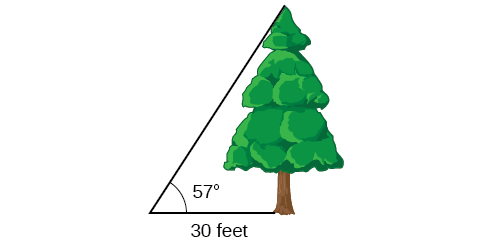
    Un arbre avec un angle de 57 degrés par rapport au point de vue. Le point de vue se trouve à 30 mètres de l'arbre.
    Figurine\(\PageIndex{13}\)

    Solution

    Nous savons que l'angle d'élévation est\(57°\) de 30 pieds de long sur le côté adjacent. Le côté opposé est la hauteur inconnue.

    La fonction trigonométrique reliant le côté opposé à un angle et le côté adjacent à l'angle est la tangente. Nous allons donc énoncer nos informations en termes de tangente de\(57°\), laissant\(h\) la hauteur inconnue.

    \[\begin{array}{cl} \tan θ = \dfrac{\text{opposite}}{\text{adjacent}} & \text{} \\ \tan (57°) = \dfrac{h}{30} & \text{Solve for }h. \\ h=30 \tan (57°) & \text{Multiply.} \\ h≈46.2 & \text{Use a calculator.} \end{array} \]

    L'arbre mesure environ 46 pieds de haut.

    Exercice\(\PageIndex{6}\):

    Quelle est la longueur d'une échelle pour atteindre un rebord de fenêtre situé à 50 pieds au-dessus du sol si l'échelle repose contre le bâtiment en formant un angle\(\frac{5π}{12}\) avec le sol ? Arrondir au pied le plus proche.

    Réponse

    Environ 52 pieds

    médias :

    Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à utiliser la trigonométrie du triangle droit.

    Visitez ce site Web pour des questions pratiques supplémentaires sur Learningpod.

    Équations clés

    Identités de cofonctions

    \[\begin{align*} \cos t &= \sin ( \frac{π}{2}−t) \\ \sin t &= \cos (\frac{π}{2}−t) \\ \tan t &= \cot (\frac{π}{2}−t) \\ \cot t &= \tan (\frac{π}{2}−t) \\ \sec t &= \csc (\frac{π}{2}−t) \\ \csc t &= \sec (\frac{π}{2}−t) \end{align*}\]

    Concepts clés

    • Nous pouvons définir les fonctions trigonométriques comme des rapports des longueurs des côtés d'un triangle droit. Voir l'exemple.
    • Les mêmes longueurs latérales peuvent être utilisées pour évaluer les fonctions trigonométriques de chaque angle aigu dans un triangle droit. Voir l'exemple.
    • Nous pouvons évaluer les fonctions trigonométriques des angles spéciaux, en connaissant les longueurs latérales des triangles dans lesquels ils apparaissent. Voir l'exemple.
    • Deux angles complémentaires quelconques peuvent être les deux angles aigus d'un triangle droit.
    • Si deux angles sont complémentaires, les identités de cofonctions indiquent que le sinus de l'un est égal au cosinus de l'autre et vice versa. Voir l'exemple.
    • Nous pouvons utiliser les fonctions trigonométriques d'un angle pour trouver des longueurs de côtés inconnues.
    • Sélectionnez la fonction trigonométrique représentant le rapport entre le côté inconnu et le côté connu. Voir l'exemple.
    • La trigonométrie en triangle droit permet de mesurer des hauteurs et des distances inaccessibles.
    • La hauteur ou la distance inconnue peut être trouvée en créant un triangle droit dans lequel la hauteur ou la distance inconnue est l'un des côtés et un autre côté et un autre angle sont connus. Voir l'exemple.

    Lexique

    côté adjacent
    dans un triangle droit, le côté compris entre un angle donné et l'angle droit
    angle de dépression
    l'angle entre l'horizontale et la ligne entre l'objet et l'œil de l'observateur, en supposant que l'objet est placé plus bas que l'observateur
    angle d'élévation
    l'angle entre l'horizontale et la ligne entre l'objet et l'œil de l'observateur, en supposant que l'objet est positionné plus haut que l'observateur
    côté opposé
    dans un triangle droit, le côté le plus éloigné d'un angle donné
    hypoténuse
    le côté d'un triangle droit opposé à l'angle droit