6.8 : Ajustement de modèles exponentiels aux données
- Page ID
- 195618
- Créez un modèle exponentiel à partir de données.
- Créez un modèle logarithmique à partir de données.
- Créez un modèle logistique à partir de données.
Dans les sections précédentes de ce chapitre, soit on nous a donné une fonction explicite à représenter graphiquement ou à évaluer, soit on nous a donné un ensemble de points dont la position sur la courbe était garantie. Ensuite, nous avons utilisé l'algèbre pour trouver l'équation qui correspond exactement aux points. Dans cette section, nous utilisons une technique de modélisation appelée analyse de régression pour trouver une courbe modélisant les données collectées à partir d'observations du monde réel. Avec l'analyse de régression, nous ne nous attendons pas à ce que tous les points se situent parfaitement sur la courbe. L'idée est de trouver le modèle le mieux adapté aux données. Ensuite, nous utilisons le modèle pour faire des prévisions sur les événements futurs.
Ne vous laissez pas confondre par le mot modèle. En mathématiques, nous utilisons souvent les termes fonction, équation et modèle de manière interchangeable, même s'ils ont chacun leur propre définition formelle. Le terme modèle est généralement utilisé pour indiquer que l'équation ou la fonction se rapproche d'une situation réelle.
Nous allons nous concentrer sur trois types de modèles de régression dans cette section : exponentiel, logarithmique et logistique. Le fait d'avoir déjà travaillé avec chacune de ces fonctions nous donne un avantage. Connaître leurs définitions formelles, le comportement de leurs graphes et certaines de leurs applications réelles nous donne l'occasion d'approfondir notre compréhension. Au fur et à mesure que chaque modèle de régression est présenté, les principales caractéristiques et définitions de sa fonction associée sont incluses à des fins d'examen. Prenez le temps de repenser chacune de ces fonctions, de réfléchir au travail que nous avons réalisé jusqu'à présent, puis d'explorer les façons dont la régression est utilisée pour modéliser des phénomènes du monde réel.
Création d'un modèle exponentiel à partir de données
Comme nous l'avons appris, il existe une multitude de situations qui peuvent être modélisées par des fonctions exponentielles, telles que la croissance des investissements, la désintégration radioactive, les changements de pression atmosphérique et les températures d'un objet en refroidissement. Qu'est-ce que ces phénomènes ont en commun ? D'une part, tous les modèles augmentent ou diminuent au fil du temps. Mais ce n'est pas tout. C'est la façon dont les données augmentent ou diminuent qui nous aide à déterminer s'il est préférable de les modéliser par une équation exponentielle. Connaître le comportement des fonctions exponentielles en général nous permet de savoir quand utiliser la régression exponentielle. Passons donc en revue la croissance et la décroissance exponentielles.
Rappelez-vous que les fonctions exponentielles ont la forme\(y=ab^x\) ou\(y=A_0e^{kx}\). Lors de l'analyse de régression, nous utilisons le formulaire le plus couramment utilisé sur les utilitaires de création de graphiques,\(y=ab^x\). Prenez un moment pour réfléchir aux caractéristiques que nous avons déjà apprises à propos de la fonction exponentielle\(y=ab^x\) (supposons\(a>0\)) :
- \(b\)doit être supérieur à zéro et non égal à un.
- La valeur initiale du modèle est\(y=a\).
- Si\(b>1\), la fonction modélise une croissance exponentielle. À mesure qu'ils\(x\) augmentent, les résultats du modèle augmentent lentement au début, puis augmentent de plus en plus rapidement, sans limites.
- Si\(0<b<1\), la fonction modélise la décroissance exponentielle. À mesure qu'ils\(x\) augmentent, les résultats du modèle diminuent rapidement au début, puis se stabilisent pour devenir asymptotiques par rapport à l'axe X. En d'autres termes, les sorties ne deviennent jamais égales ou inférieures à zéro.
Dans le cadre des résultats, votre calculatrice affichera un nombre appelé coefficient de corrélation, étiqueté par la variable\(r\), ou\(r^2\). (Vous devrez peut-être modifier les paramètres de la calculatrice pour qu'ils s'affichent.) Les valeurs indiquent la « qualité de l'ajustement » de l'équation de régression aux données. Nous utilisons plus souvent la valeur de\(r^2\) au lieu de\(r\), mais plus l'une ou l'autre des valeurs est proche\(1\), meilleure est l'équation de régression approximative des données.
La régression exponentielle est utilisée pour modéliser des situations dans lesquelles la croissance commence lentement puis s'accélère rapidement sans limite, ou dans lesquelles la décroissance commence rapidement puis ralentit pour se rapprocher de plus en plus de zéro. Nous utilisons la commande « ExPreg » sur un utilitaire graphique pour adapter une fonction exponentielle à un ensemble de points de données. Cela renvoie une équation de la forme,
\[y=ab^x\]
Notez que :
- \(b\)doit être non négatif.
- quand\(b>1\), nous avons un modèle de croissance exponentielle.
- quand\(0<b<1\), nous avons un modèle de décroissance exponentielle.
- Utilisez le menu STAT puis EDIT pour saisir des données données.
- Effacez toutes les données existantes des listes.
- Répertoriez les valeurs d'entrée dans la colonne L1.
- Répertoriez les valeurs de sortie dans la colonne L2.
- Tracez et observez un nuage de points des données à l'aide de la fonction STATPLOT.
- Utilisez ZOOM [9] pour ajuster les axes aux données.
- Vérifiez que les données suivent un schéma exponentiel.
- Trouvez l'équation qui modélise les données.
- Sélectionnez « ExPreg » dans le menu STAT puis CALC.
- Utilisez les valeurs renvoyées pour a et b pour enregistrer le modèle,\(y=ab^x\).
- Tracez le modèle dans la même fenêtre que le nuage de points pour vérifier qu'il correspond bien aux données.
Exemple\(\PageIndex{1}\): Using Exponential Regression to Fit a Model to Data
En 2007, une étude universitaire a été publiée sur le risque d'accident lié à la conduite avec facultés affaiblies par l'alcool. Les données relatives aux\(2,871\) accidents ont été utilisées pour mesurer l'association entre le taux d'alcoolémie (BAC) d'une personne et le risque d'accident. Le tableau\(\PageIndex{1}\) montre les résultats de l'étude. Le risque relatif est une mesure du nombre de fois plus élevé de risques pour une personne d'avoir un accident. Ainsi, par exemple, une personne dont le taux d'alcoolémie\(0.09\) est de\(3.54\) 5 fois plus susceptible de s'écraser qu'une personne qui n'a pas bu d'alcool.
| RETOUR | 0 | 0,01 | 0,03 | 0,05 | 0,07 | 0,09 |
|---|---|---|---|---|---|---|
| Risque relatif d'écrasement | 1 | 1,03 | 1,06 | 1,38 | 2.09 | 3,54 |
| RETOUR | 0,11 | 0,13 | 0,15 | 0,17 | 0,19 | 0,21 |
| Risque relatif d'écrasement | 6,41 | 12,6 | 22.1 | 39,05 | 65,32 | 99,78 |
- \(x\)Représentons le taux d'alcoolémie et\(y\) représentons le risque relatif correspondant. Utilisez la régression exponentielle pour adapter un modèle à ces données.
- Après avoir\(6\) bu, une personne pesant des\(160\) kilos aura un taux d'alcoolémie d'environ\(0.16\). Combien de fois plus de risques pour une personne de ce poids d'avoir un accident si elle conduit après avoir\(6\) bu un paquet de bière ? Arrondir au centième le plus proche.
Solution
- À l'aide du menu STAT puis EDIT d'un utilitaire graphique, répertoriez les valeurs du BAC en L1 et les valeurs de risque relatif en L2. Utilisez ensuite la fonction STATPLOT pour vérifier que le nuage de points suit le modèle exponentiel illustré à la figure\(\PageIndex{1}\) :
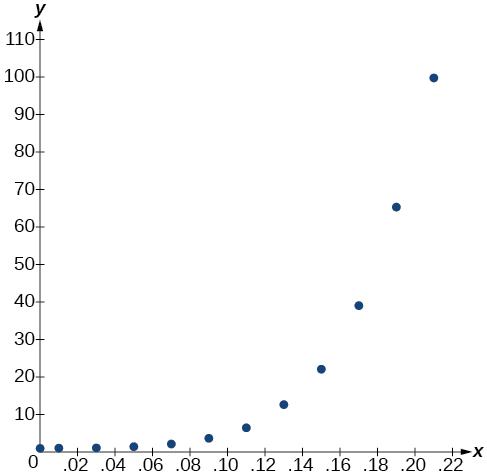
Figurine\(\PageIndex{1}\)
Utilisez la commande « ExPreg » du menu STAT puis CALC pour obtenir le modèle exponentiel,
\(y=0.58304829{(2.20720213E10)}^x\)
En convertissant à partir de la notation scientifique, nous avons :
\(y=0.58304829{(22,072,021,300)}^x\)
Notez\(r^2≈0.97\) ce qui indique que le modèle est bien ajusté aux données. Pour ce faire, tracez le modèle dans la même fenêtre que le nuage de points pour vérifier qu'il est bien ajusté, comme le montre la figure\(\PageIndex{2}\) :
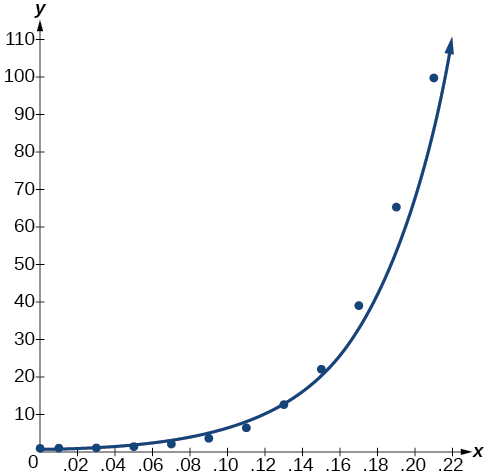
Figurine\(\PageIndex{2}\)
- Utilisez le modèle pour estimer le risque associé à un taux d'alcoolémie de\(0.16\). Remplacez par\(0.16\)\(x\) dans le modèle et résolvez par\(y\).
\[\begin{align*} y&= 0.58304829{(22,072,021,300)}^x \qquad \text{Use the regression model found in part } (a)\\ &= 0.58304829{(22,072,021,300)}^{0.16} \qquad \text{Substitute 0.16 for x}\\ &\approx 26.35 \qquad \text{Round to the nearest hundredth} \end{align*}\]
Si une personne\(160\) d'un kilo conduit après avoir\(6\) bu, elle est environ deux\(26.35\) fois plus susceptible de s'écraser que si elle conduit sobrement.
Le tableau\(\PageIndex{2}\) montre le solde de la carte de crédit d'un diplômé récent chaque mois après l'obtention de son diplôme
| Mois | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Dette ($) | 620,00 | 761,88 | 899,80 | 1039,93 | 1270,63 | 1589,04 | 1851,31 | 2154,92 |
- Utilisez la régression exponentielle pour adapter un modèle à ces données.
- Si les dépenses se poursuivent à ce rythme, quelle sera la dette de carte de crédit du diplômé un an après l'obtention de son diplôme ?
- Répondez à une
-
Le modèle de régression exponentielle qui correspond à ces données est\(y=522.88585984{(1.19645256)}^x\).
- Réponse b
-
Si les dépenses se poursuivent à ce rythme, la dette de carte de crédit du diplômé sera d'un an plus\($4,499.38\) tard.
Non. N'oubliez pas que les modèles sont formés à partir de données réelles collectées à des fins de régression. Il est généralement raisonnable de faire des estimations dans l'intervalle d'observation initiale (interpolation). Toutefois, lorsqu'un modèle est utilisé pour établir des prévisions, il est important de faire appel à des compétences de raisonnement pour déterminer si le modèle est pertinent pour les entrées bien au-delà de l'intervalle d'observation initial (extrapolation).
Création d'un modèle logarithmique à partir de données
Tout comme pour les fonctions exponentielles, les fonctions logarithmiques ont de nombreuses applications concrètes : intensité du son, pH des solutions, rendement des réactions chimiques, production de biens et croissance des nourrissons. Comme pour les modèles exponentiels, les données modélisées par des fonctions logarithmiques augmentent ou diminuent toujours à mesure que le temps avance. Encore une fois, c'est la façon dont ils augmentent ou diminuent qui nous aide à déterminer si un modèle logarithmique est le meilleur.
Souvenez-vous que les fonctions logarithmiques augmentent ou diminuent rapidement au début, mais qu'elles ralentissent ensuite progressivement au fil du temps. En réfléchissant aux caractéristiques que nous avons déjà apprises au sujet de cette fonction, nous pouvons mieux analyser les situations du monde réel qui reflètent ce type de croissance ou de déclin. Lors de l'analyse de régression logarithmique, nous utilisons la forme de la fonction logarithmique la plus couramment utilisée sur les utilitaires de création de graphiques,\(y=a+b\ln(x)\). Pour cette fonction
- Toutes les valeurs en entrée\(x\),, doivent être supérieures à zéro.
- Le point\((1,a)\) se trouve sur le graphique du modèle.
- Si\(b>0\), le modèle augmente. La croissance augmente rapidement au début, puis ralentit régulièrement au fil du temps.
- Si\(b<0\), le modèle est décroissant. La décomposition se produit rapidement au début, puis ralentit progressivement au fil du temps.
La régression logarithmique est utilisée pour modéliser des situations dans lesquelles la croissance ou la décroissance s'accélère rapidement au début, puis ralentit au fil du temps. Nous utilisons la commande « LNreg » sur un utilitaire graphique pour adapter une fonction logarithmique à un ensemble de points de données. Cela renvoie une équation de la forme,
\[y=a+b\ln(x)\]
Notez que
- toutes les valeurs d'entrée\(x\),, doivent être non négatives.
- quand\(b>0\), le modèle augmente.
- quand\(b<0\), le modèle est décroissant.
- Utilisez le menu STAT puis EDIT pour saisir des données données.
- Effacez toutes les données existantes des listes.
- Répertoriez les valeurs d'entrée dans la colonne L1.
- Répertoriez les valeurs de sortie dans la colonne L2.
- Tracez et observez un nuage de points des données à l'aide de la fonction STATPLOT.
- Utilisez ZOOM [9] pour ajuster les axes aux données.
- Vérifiez que les données suivent un schéma logarithmique.
- Trouvez l'équation qui modélise les données.
- Sélectionnez « LNreg » dans le menu STAT puis CALC.
- Utilisez les valeurs renvoyées pour a et b pour enregistrer le modèle,\(y=a+b\ln(x)\).
- Tracez le modèle dans la même fenêtre que le nuage de points pour vérifier qu'il correspond bien aux données.
En raison des progrès de la médecine et de l'amélioration du niveau de vie, l'espérance de vie augmente dans la plupart des pays développés depuis le début du XXe siècle. Le tableau\(\PageIndex{3}\) montre l'espérance de vie moyenne, en années, des Américains de 1900 à 2010.
| Année | 1900 | 1910 | 1920 | 1930 | 1940 | 1950 |
|---|---|---|---|---|---|---|
| Espérance de vie (années) | 47,3 | 50,0 | 54,1 | 59,7 | 62,9 | 68,2 |
| Année | 1960 | 1970 | 1980 | 1990 | 2000 | 2010 |
| Espérance de vie (années) | 69,7 | 70,8 | 73,7 | 75,4 | 76,8 | 78,7 |
- \(x\)Représentez le temps en décennies en commençant\(x=1\) par 1900,\(x=2\) pour 1910, et ainsi de suite. \(y\)Représentez l'espérance de vie correspondante. Utilisez la régression logarithmique pour ajuster un modèle à ces données.
- Utilisez le modèle pour prédire l'espérance de vie moyenne aux États-Unis pour 2030.
Solution
- À l'aide du menu STAT puis EDIT d'un utilitaire graphique, dressez la liste des années\(1–12\) à l'aide des valeurs de L1 et de l'espérance de vie correspondante en L2. Utilisez ensuite la fonction STATPLOT pour vérifier que le nuage de points suit un schéma logarithmique, comme illustré à la figure\(\PageIndex{3}\) :
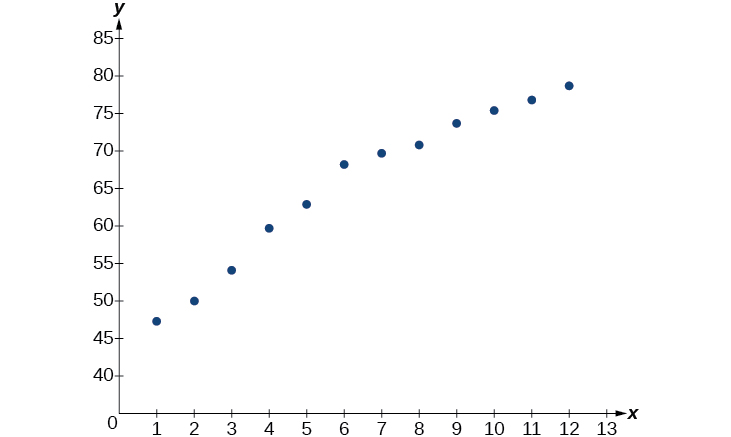
Figurine\(\PageIndex{3}\)
Utilisez la commande « LNreg » du menu STAT puis CALC pour obtenir le modèle logarithmique,
\(y=42.52722583+13.85752327\ln(x)\)
Ensuite, tracez le modèle dans la même fenêtre que le nuage de points pour vérifier qu'il est bien ajusté, comme indiqué dans la figure\(\PageIndex{4}\) :
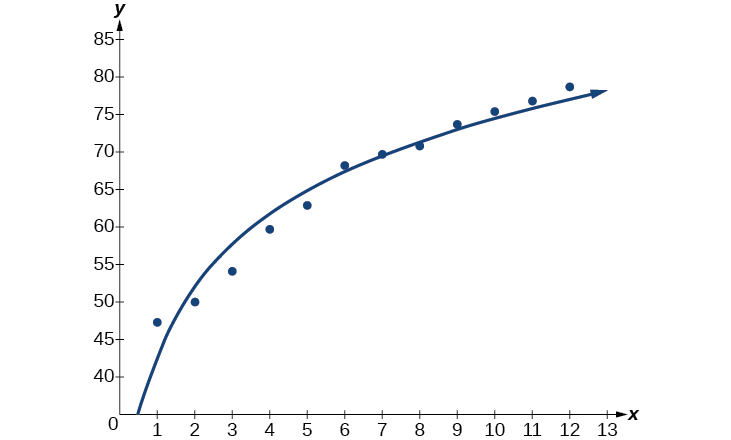
Figurine\(\PageIndex{4}\)
- Pour prédire l'espérance de vie d'un Américain dans l'année\(2030\), remplacez\(x=14\) le dans le modèle et résolvez\(y\) :
\[\begin{align*} y&= 42.52722583+13.85752327\ln(x) \qquad \text{Use the regression model found in part } (a)\\ &= 42.52722583+13.85752327\ln(14) \qquad \text{Substitute 14 for x}\\ &\approx 79.1 \qquad \text{Round to the nearest tenth} \end{align*}\]
Si l'espérance de vie continue d'augmenter à ce rythme, l'espérance de vie moyenne d'un Américain sera d'une année à\(79.1\) l'autre\(2030\).
Les ventes d'un jeu vidéo sorti en 2000 ont d'abord décollé, puis ont progressivement ralenti au fil du temps. Le tableau\(\PageIndex{4}\) montre le nombre de jeux vendus, en milliers, entre 2000 et 2010.
| Année | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
|---|---|---|---|---|---|---|
| Nombre vendu (en milliers) | 142 | 149 | 154 | 155 | 159 | 161 |
| Année | 2006 | 2007 | 2008 | 2009 | 2010 | - |
| Nombre vendu (en milliers) | 163 | 164 | 164 | 166 | 167 | - |
\(x\)Représentent le temps en années à partir\(x=1\) de l'an 2000. \(y\)Représentez le nombre de jeux vendus en milliers.
- Utilisez la régression logarithmique pour ajuster un modèle à ces données.
- Si les jeux continuent de se vendre à ce rythme, combien de jeux se vendront en 2015 ? Arrondir au millier le plus proche.
- Répondez à une
-
Le modèle de régression logarithmique qui s'adapte à ces données est\(y=141.91242949+10.45366573\ln(x)\)
- Réponse b
-
Si les ventes se poursuivent à ce rythme, environ\(171,000\) des jeux seront vendus au cours de l'année\(2015\).
Création d'un modèle logistique à partir de données
Tout comme la croissance exponentielle et logarithmique, la croissance logistique augmente au fil du temps. L'une des différences les plus notables avec les modèles de croissance logistique est qu'à un moment donné, la croissance ralentit régulièrement et que la fonction se rapproche d'une limite supérieure ou d'une valeur limite. De ce fait, la régression logistique est idéale pour modéliser des phénomènes où l'expansion a des limites, comme la disponibilité de l'espace de vie ou des nutriments.
Il convient de souligner que les fonctions logistiques modélisent en fait une croissance exponentielle limitée par des ressources. Il existe de nombreux exemples de ce type de croissance dans des situations réelles, notamment la croissance démographique et la propagation de maladies, les rumeurs et même les taches sur les tissus. Lors de l'analyse de régression logistique, nous utilisons le formulaire le plus couramment utilisé sur les utilitaires de création de graphiques :
\(y=\dfrac{c}{1+ae^{−bx}}\)
Rappelons que :
- \(\dfrac{c}{1+a}\)est la valeur initiale du modèle.
- lorsque\(b>0\), le modèle augmente rapidement dans un premier temps jusqu'à atteindre son point de taux de croissance maximal,\((\dfrac{\ln(a)}{b}, \dfrac{c}{2})\). À ce stade, la croissance ralentit régulièrement et la fonction devient asymptotique à la limite supérieure\(y=c\).
- \(c\)est la valeur limite, parfois appelée capacité de charge, du modèle.
La régression logistique est utilisée pour modéliser des situations dans lesquelles la croissance s'accélère rapidement dans un premier temps, puis ralentit régulièrement jusqu'à une limite supérieure. Nous utilisons la commande « Logistic » sur un utilitaire graphique pour adapter une fonction logistique à un ensemble de points de données. Cela renvoie une équation de la forme
\[y=\dfrac{c}{1+ae^{−bx}}\]
Notez que
- La valeur initiale du modèle est\(\dfrac{c}{1+a}\).
- Les valeurs de sortie du modèle s'approchent de plus en plus à\(y=c\) mesure que le temps passe.
- Utilisez le menu STAT puis EDIT pour saisir des données données.
- Effacez toutes les données existantes des listes.
- Répertoriez les valeurs d'entrée dans la colonne L1.
- Répertoriez les valeurs de sortie dans la colonne L2.
- Tracez et observez un nuage de points des données à l'aide de la fonction STATPLOT.
- Utilisez ZOOM [9] pour ajuster les axes aux données.
- Vérifiez que les données suivent un schéma logistique.
- Trouvez l'équation qui modélise les données.
- Sélectionnez « Logistique » dans le menu STAT puis CALC.
- Utilisez les valeurs renvoyées pour\(a\)\(b\), et\(c\) pour enregistrer le modèle,\(y=\dfrac{c}{1+ae^{−bx}}\).
- Tracez le modèle dans la même fenêtre que le nuage de points pour vérifier qu'il correspond bien aux données.
Le service de téléphonie mobile s'est développé rapidement en Amérique depuis le milieu des années 1990. Aujourd'hui, presque tous les résidents disposent d'un service cellulaire. Le tableau\(\PageIndex{5}\) montre le pourcentage d'Américains bénéficiant d'un service cellulaire entre 1995 et 2012.
| Année | Américains disposant d'un service cellulaire (%) | Année | Américains disposant d'un service cellulaire (%) |
|---|---|---|---|
| 1995 | 12,69 | 2004 | 62 852 |
| 1996 | 16,35 | 2005 | 68,63 |
| 1997 | 20,29 | 2006 | 76,64 |
| 1998 | 25,08 | 2007 | 82,47 |
| 1999 | 30,81 | 2008 | 85,68 |
| 2000 | 38,75 | 2009 | 89,14 |
| 2001 | 45,00 | 2010 | 91,86 |
| 2002 | 49,16 | 2011 | 95,28 |
| 2003 | 55,15 | 2012 | 98,17 |
- \(x\)Représentent le temps en années en commençant par\(x=0\) l'année 1995. \(y\)Représentez le pourcentage correspondant de résidents disposant d'un service cellulaire. Utilisez la régression logistique pour adapter un modèle à ces données.
- Utilisez le modèle pour calculer le pourcentage d'Américains bénéficiant d'un service cellulaire en 2013. Arrondir au dixième de pour cent le plus proche.
- Discutez de la valeur renvoyée pour la limite supérieure,\(c\). Qu'est-ce que cela vous apprend sur le modèle ? Quelle serait la valeur limite si le modèle était exact ?
Solution
- À l'aide du menu STAT puis EDIT d'un utilitaire graphique, répertoriez les années\(0–15\) à l'aide des valeurs de L1 et du pourcentage correspondant en L2. Utilisez ensuite la fonction STATPLOT pour vérifier que le nuage de points suit un schéma logistique, comme illustré à la figure\(\PageIndex{5}\) :
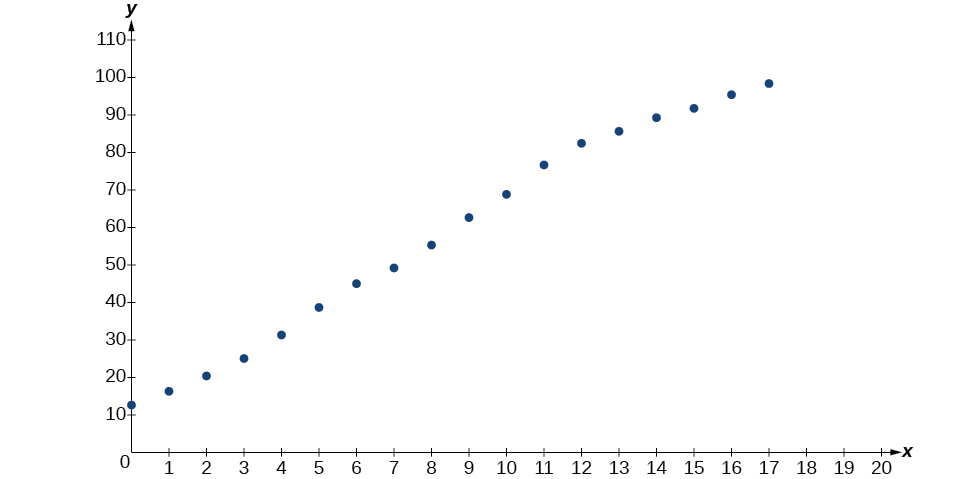
Figurine\(\PageIndex{5}\)
Utilisez la commande « Logistique » du menu STAT puis CALC pour obtenir le modèle logistique,
\[y=105.73795261+6.88328979e^{−0.2595440013x}\]
Ensuite, tracez le modèle dans la même fenêtre que celle illustrée sur\(\PageIndex{6}\) la figure du nuage de points pour vérifier qu'il est bien ajusté :
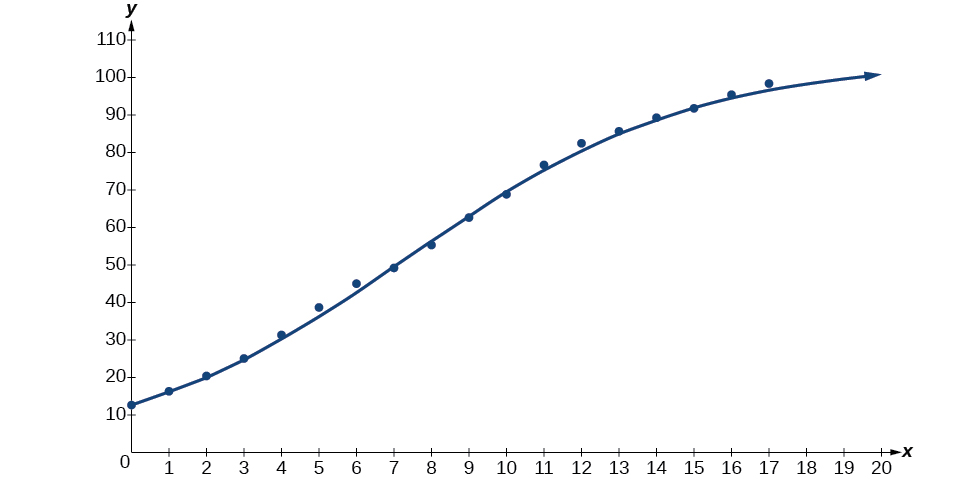
Figurine\(\PageIndex{6}\)
- Pour obtenir une estimation du pourcentage d'Américains bénéficiant d'un service cellulaire en 2013, remplacez\(x=18\) le dans le modèle et résolvez par\(y\) :
\[\begin{align*} y&= \dfrac{105.7379526}{1+6.88328979e^{-0.2595440013x}} \qquad \text{Use the regression model found in part } (a)\\ &= \dfrac{105.7379526}{1+6.88328979e^{-0.2595440013(18)}} \qquad \text{Substitute 18 for x}\\ &\approx 99.3 \qquad \text{Round to the nearest tenth} \end{align*}\]
Selon le modèle, environ 98,8 % des Américains bénéficiaient d'un service cellulaire en 2013.
- Le modèle donne une valeur limite d'environ\(105\). Cela signifie que le pourcentage maximum possible d'Américains disposant d'un service cellulaire serait\(105%\), ce qui est impossible. (Comment plus\(100%\) d'une population pourrait-elle avoir accès à un service cellulaire ?) Si le modèle était exact, la valeur limite serait\(c=100\) et les sorties du modèle s'en approcheraient très près, mais ne l'atteindraient jamais réellement\(100%\). Après tout, il y aura toujours quelqu'un qui n'a pas de service cellulaire !
Le tableau\(\PageIndex{6}\) montre la population, en milliers, de phoques communs dans la mer des Wadden entre 1997 et 2012.
| Année | Population de phoques (en milliers) | Année | Population de phoques (en milliers) |
|---|---|---|---|
| 1997 | 3 493 | 2005 | 19 590 |
| 1998 | 5.282 | 2006 | 21 955 |
| 1999 | 6.357 | 2007 | 22 862 |
| 2000 | 9.201 | 2008 | 23 869 |
| 2001 | 11 224 | 2009 | 24 243 |
| 2002 | 12 964 | 2010 | 24 344 |
| 2003 | 16,226 | 2011 | 24 919 |
| 2004 | 18.137 | 2012 | 25.108 |
\(x\)Représentent le temps en années\(x=0\) à partir de 1997. \(y\)Représentez le nombre de sceaux en milliers.
- Utilisez la régression logistique pour adapter un modèle à ces données.
- Utilisez le modèle pour prévoir la population de phoques pour l'année 2020.
- Au nombre entier le plus proche, quelle est la valeur limite de ce modèle ?
- Répondez à une
-
Le modèle de régression logistique qui correspond à ces données est\(y=\dfrac{25.65665979}{1+6.113686306e^{−0.3852149008x}}\).
- Réponse b
-
Si la population continue de croître à ce rythme, il y aura environ des\(25,634\) phoques en 2020.
- Réponse c
-
Au nombre entier le plus proche, la capacité de charge est de\(25,657\).
Accédez à cette ressource en ligne pour obtenir des instructions et des exercices supplémentaires sur les modèles de fonctions exponentiels.
Visitez ce site Web pour des questions pratiques supplémentaires sur Learningpod.
Key Concepts
- Exponential regression is used to model situations where growth begins slowly and then accelerates rapidly without bound, or where decay begins rapidly and then slows down to get closer and closer to zero.
- We use the command “ExpReg” on a graphing utility to fit function of the form \(y=ab^x\) to a set of data points. See Example \(\PageIndex{1}\).
- Logarithmic regression is used to model situations where growth or decay accelerates rapidly at first and then slows over time.
- We use the command “LnReg” on a graphing utility to fit a function of the form \(y=a+b\ln(x)\) to a set of data points. See Example \(\PageIndex{2}\).
- Logistic regression is used to model situations where growth accelerates rapidly at first and then steadily slows as the function approaches an upper limit.
- We use the command “Logistic” on a graphing utility to fit a function of the form \(y=\dfrac{c}{1+ae^{−bx}}\) to a set of data points. See Example \(\PageIndex{3}\).


