6.7 : Modèles exponentiels et logarithmiques
- Page ID
- 195641
- Modélisez la croissance et la décroissance exponentielles
- Utilisez la loi de refroidissement de Newton.
- Utilisez des modèles de croissance logistique.
- Choisissez un modèle approprié pour les données.
- Exprimez un modèle exponentiel en base\(e\).
Nous avons déjà exploré certaines applications de base des fonctions exponentielles et logarithmiques. Dans cette section, nous explorons plus en profondeur certaines applications importantes, notamment les isotopes radioactifs et la loi du refroidissement de Newton.

Modélisation de la croissance et de la dégradation
Dans les applications du monde réel, nous devons modéliser le comportement d'une fonction. En modélisation mathématique, nous choisissons une fonction générale familière dont les propriétés suggèrent qu'elle modélisera le phénomène réel que nous souhaitons analyser. Dans le cas d'une croissance rapide, on peut choisir la fonction de croissance exponentielle :
\[y=A_0e^{kt}\]
où\(A_0\) est égal à la valeur au temps zéro,\(e\) est la constante d'Euler et\(k\) est une constante positive qui détermine le taux (pourcentage) de croissance. Nous pouvons utiliser la fonction de croissance exponentielle dans des applications impliquant le doublement du temps, c'est-à-dire le temps nécessaire pour qu'une quantité double. Des phénomènes tels que les populations d'animaux sauvages, les investissements financiers, les échantillons biologiques et les ressources naturelles peuvent connaître une croissance basée sur un temps de doublement. Dans certaines applications, cependant, comme nous le verrons lorsque nous discuterons de l'équation logistique, le modèle logistique s'adapte parfois mieux aux données que le modèle exponentiel.
D'un autre côté, si une quantité baisse rapidement vers zéro, sans jamais atteindre zéro, alors nous devrions probablement choisir le modèle de décroissance exponentielle. Encore une fois, nous avons la forme\(y=A_0e^{kt}\) où\(A_0\) est la valeur de départ et\(e\) la constante d'Euler. \(k\)Il s'agit maintenant d'une constante négative qui détermine le taux de décroissance. Nous pouvons utiliser le modèle de décroissance exponentielle lorsque nous calculons la demi-vie, ou le temps qu'il faut à une substance pour se décomposer de façon exponentielle jusqu'à la moitié de sa quantité initiale. Nous utilisons la demi-vie dans les applications impliquant des isotopes radioactifs.
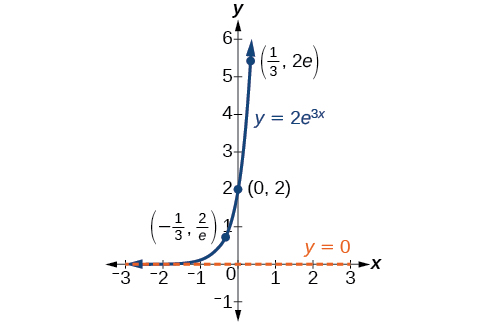
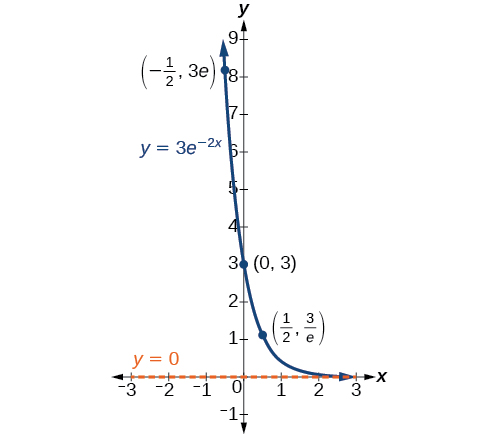
Lorsque nous choisissons une fonction qui servira de modèle mathématique, nous utilisons souvent des points de données collectés par des observations et des mesures minutieuses pour construire des points sur un graphique et espérons pouvoir reconnaître la forme du graphique. Les graphes de croissance et de décroissance exponentielles ont une forme distincte, comme nous pouvons le voir sur la figure\(\PageIndex{2}\) et la figure\(\PageIndex{3}\). Il est important de se rappeler que, bien que certaines parties de chacun des deux graphes semblent se trouver sur l'\(x\)axe des -, elles ne se trouvent en réalité qu'à une petite distance au-dessus de\(x\) l'axe.
La croissance et la décroissance exponentielles impliquent souvent des nombres très importants ou très petits. Pour décrire ces chiffres, nous utilisons souvent des ordres de grandeur. L'ordre de grandeur est la puissance de dix, lorsque le nombre est exprimé en notation scientifique, avec un chiffre à gauche de la décimale. Par exemple, la distance par rapport à l'étoile la plus proche, Proxima Centauri, mesurée en kilomètres, est en\(40,113,497,200,000\) kilomètres. Exprimé en notation scientifique, c'est\(4.01134972 × 1013\). Nous pourrions donc décrire ce nombre comme ayant un ordre de grandeur\(1013\).
Une fonction exponentielle avec la forme\(y=A_0e^{kt}\) présente les caractéristiques suivantes :
- fonction un à un
- asymptote horizontale :\(y=0\)
- domaine :\((–\infty, \infty)\)
- gamme :\((0,\infty)\)
- \(x\)interception : aucune
- \(y\)-intercepter :\((0,A_0)\)
- en augmentant si\(k>0\) (voir Figure\(\PageIndex{4}\))
- décroissant si\(k<0\) (voir Figure\(\PageIndex{4}\))
La population de bactéries double toutes les heures. Si la culture a débuté avec\(10\) des bactéries, représentez graphiquement la population en fonction du temps.
Solution
Lorsqu'une quantité augmente à un pourcentage fixe par unité de temps, la croissance est exponentielle. Pour trouver,\(A_0\) nous utilisons le fait que\(A_0\) c'est le montant au temps zéro, donc\(A_0=10\). Pour le trouver\(k\), utilisez le fait qu'au bout d'une heure,\((t=1)\) la population double de\(10\) à\(20\). La formule est dérivée comme suit
\[\begin{align*} 20&= 10e^{k\cdot 1}\\ 2&= e^k \qquad \text{Divide by 10}\\ \ln2&= k \qquad \text{Take the natural logarithm} \end{align*}\]
donc\(k=\ln(2)\). Ainsi, l'équation que nous voulons représenter graphiquement est\(y=10e^{(\ln2)t}=10{(e^{\ln2})}^t=10·2^t\). Le graphique est illustré dans la figure\(\PageIndex{5}\).
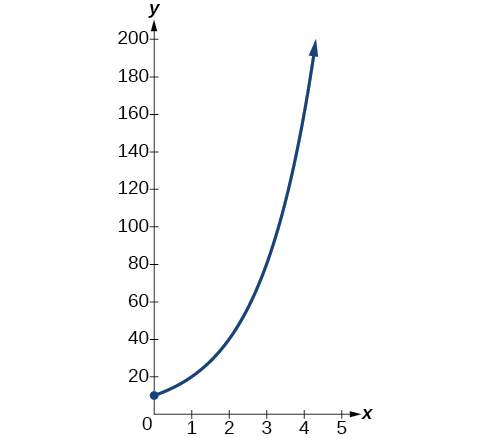
Analyse
La population de bactéries après dix heures est de\(10,240\). Nous pourrions décrire ce montant comme étant de l'ordre de grandeur\(10^4\). La population de bactéries après vingt heures est\(10,485,760\) de l'ordre de grandeur\(10^7\), on pourrait donc dire que la population a augmenté de trois ordres de grandeur en dix heures.
Demi-vie
Nous passons maintenant à la décroissance exponentielle. L'un des termes courants associés à la décroissance exponentielle, comme indiqué ci-dessus, est la demi-vie, c'est-à-dire le temps qu'il faut à une quantité en déclin exponentiel pour diminuer jusqu'à la moitié de sa quantité initiale. Chaque isotope radioactif a une demi-vie, et le processus décrivant la désintégration exponentielle d'un isotope est appelé désintégration radioactive.
Pour déterminer la demi-vie d'une fonction décrivant la décroissance exponentielle, résolvez l'équation suivante :
\(\dfrac{1}{2}A_0=A_0e^{kt}\)
Nous constatons que la demi-vie dépend uniquement de la constante\(k\) et non de la quantité de départ\(A_0\).
La formule est dérivée comme suit
\[\begin{align*} \dfrac{1}{2}A_0&= A_0e^{kt}\\ \dfrac{1}{2}&= e^{kt} \qquad \text{Divide by } A_0\\ \ln \left (\dfrac{1}{2} \right )&= ktv \qquad \text{Take the natural log}\\ -\ln(2)&= kt \qquad \text{Apply laws of logarithms}\\ -\ln(2)k&= t \qquad \text{Divide by k} \end{align*}\]
Puisque\(t\) le temps est positif,\(k\) il doit, comme prévu, être négatif. Cela nous donne la formule de demi-vie
\[t=−\dfrac{\ln(2)}{k}\]
- Écrivez\(A=A_0e^{kt}\).
- Remplacer\(A\) par\(\dfrac{1}{2}A_0\) et remplacer\(t\) par la demi-vie indiquée.
- Résolvez pour trouver\(k\). Exprimer\(k\) sous la forme d'une valeur exacte (ne pas arrondir).
Remarque : Il est également possible de trouver le taux de décroissance en utilisant\(k=−\ln(2)t\).
La demi-vie du carbone 14 est de\(5,730\) plusieurs années. Exprime la quantité de carbone 14 restante en fonction du temps,\(t\).
Solution
Cette formule est dérivée comme suit.
\[\begin{align*} A&= A_0e^{kt} \qquad \text{The continuous growth formula}\\ 0.5A_0&= A_0e^{k\cdot 5730} \qquad \text{Substitute the half-life for t and } 0.5A_0 \text{ for } f(t)\\ 0.5&= e^{5730k} \qquad \text{Divide by } A_0\\ \ln(0.5)&= 5730k \qquad \text{Take the natural log of both sides}\\ k&= \dfrac{\ln(0.5)}{5730} \qquad \text{Divide by the coefficient of k}\\ A&= A_0e^{ \left (\tfrac{\ln(0.5)}{5730} \right ) t} \qquad \text{Substitute for r in the continuous growth formula} \end{align*}\]
La fonction qui décrit cette décroissance continue est\(f(t)=A_0e^{\left (\tfrac{\ln(0.5)}{5730} \right )t}\). Nous observons que le coefficient de\(t\),\(\dfrac{\ln(0.5)}{5730}≈−1.2097×10^{−4}\) est négatif, comme prévu dans le cas d'une décroissance exponentielle.
La demi-vie du plutonium 244 est de\(80,000,000\) plusieurs années. La fonction Find donne la quantité de carbone 14 restante en fonction du temps, mesurée en années.
- Réponse
-
\(f(t)=A_0e^{−0.0000000087t}\)
Datation au radiocarbone
La formule de la désintégration radioactive est importante dans la datation au radiocarbone, qui est utilisée pour calculer la date approximative de la mort d'une plante ou d'un animal. La datation au radiocarbone a été découverte en 1949 par Willard Libby, qui a remporté un prix Nobel pour sa découverte. Il compare la différence entre le rapport de deux isotopes de carbone dans un artefact organique ou un fossile au rapport de ces deux isotopes dans l'air. On pense qu'il est exact à peu près à peu\(1\%\) près pour les plantes ou les animaux morts au cours des dernières\(60,000\) années.
Le carbone 14 est un isotope radioactif du carbone qui a une demi-vie de\(5,730\) plusieurs années. Il se trouve en petites quantités dans le dioxyde de carbone de l'air que nous respirons. La majeure partie du carbone de la Terre est du carbone 12, qui a un poids atomique\(12\) et n'est pas radioactif. Les scientifiques ont déterminé le rapport entre le carbone 14 et le carbone 12 dans l'air ces dernières\(60,000\) années à l'aide de cernes d'arbres et d'autres échantillons organiques de dates connues, bien que le rapport ait légèrement changé au fil des siècles.
Tant qu'une plante ou un animal est vivant, le rapport des deux isotopes du carbone dans son corps est proche de celui de l'atmosphère. Lorsqu'il meurt, le carbone 14 de son corps se désintègre et n'est pas remplacé. En comparant le rapport entre le carbone 14 et le carbone 12 dans un échantillon en décomposition au rapport connu dans l'atmosphère, la date de mort de la plante ou de l'animal peut être approximée.
Puisque la demi-vie du carbone 14 est de\(5,730\) plusieurs années, la formule pour la quantité de carbone 14 restante après des\(t\) années est
\(A≈A_0e^{\left (\tfrac{\ln(0.5)}{5730} \right )t}\)
où
- \(A\)est la quantité de carbone 14 restante
- \(A_0\)est la quantité de carbone 14 lorsque la plante ou l'animal a commencé à se décomposer.
Cette formule est dérivée comme suit :
\[\begin{align*} A&= A_0e^{kt} \qquad \text{The continuous growth formula}\\ 0.5A_0&= A_0e^{k\cdot 5730} \qquad \text{Substitute the half-life for t and } 0.5A_0 \text{ for f(t)}\\ 0.5&= e^{5730k} \qquad \text{Divide by } A_0\\ \ln(0.5)&= 5730k \qquad \text{Take the natural log of both sides}\\ k&= \dfrac{\ln(0.5)}{5730} \qquad \text{Divide by the coefficient of k}\\ A&= A_0e^{\left (\tfrac{\ln(0.5)}{5730} \right )t} \qquad \text{Substitute for r in the continuous growth formula}\\ \end{align*}\]
Pour déterminer l'âge d'un objet, nous résolvons cette équation pour\(t\) :
\(t=\dfrac{\ln \left (\dfrac{A}{A_0} \right )}{−0.000121}\)
Par nécessité, nous négligeons ici les nombreux détails qu'un scientifique prend en compte lors de la datation au carbone 14, et nous ne regardons que la formule de base. Le rapport entre le carbone 14 et le carbone 12 dans l'atmosphère est d'environ\(0.0000000001%\). \(r\)Soit le rapport entre le carbone 14 et le carbone 12 dans l'artefact organique ou le fossile à dater, déterminé par une méthode appelée scintillation liquide. À partir de l'équation,\(A≈A_0e^{−0.000121t}\) nous savons que le rapport entre le pourcentage de carbone 14 dans l'objet que nous datons et le pourcentage de carbone 14 dans l'atmosphère est\(r=\dfrac{A}{A_0}≈e^{−0.000121t}\). Nous résolvons cette équation pour\(t\), pour obtenir
\(t=\dfrac{\ln(r)}{−0.000121}\)
- Exprime le pourcentage donné de carbone 14 sous la forme d'une décimale équivalente,\(k\).
- Remplacez\(k\) dans l'équation\(t=\dfrac{\ln(r)}{−0.000121}\) et résolvez par l'âge,\(t\).
On trouve un fragment d'os qui contient\(20\%\) de son carbone 14 d'origine. Quel âge a l'os jusqu'à l'année la plus proche ?
Solution
Nous\(20\%=0.20\) substituons\(k\) dans l'équation et résolvons\(t\) :
\[\begin{align*} t&= \dfrac{\ln(r)}{-0.000121} \qquad \text{Use the general form of the equation}\\ &= \dfrac{\ln(0.20)}{-0.000121} \qquad \text{Substitute for r}\\ &\approx 13301 \qquad \text{Round to the nearest year} \end{align*}\]
Le fragment d'os a environ des\(13,301\) années.
Analyse
Les instruments qui mesurent le pourcentage de carbone 14 sont extrêmement sensibles et, comme nous l'avons mentionné plus haut, un scientifique devra faire beaucoup plus de travail que nous pour être satisfait. Toutefois, la datation au carbone n'est précise que sur environ\(1\%\), donc cet âge doit être donné en\(13,301\) années\(\pm 1\%\) ou en\(13,301\)\(\pm 133\) années.
Le césium-137 a une demi-vie d'environ\(30\) plusieurs années. Si nous commençons par\(200\) mg de césium-137, faudra-t-il plus ou moins de plusieurs\(230\) années avant qu'il ne reste plus qu'un\(1\) milligramme ?
- Réponse
-
moins de\(230\) 5 ans,\(229.3157\) pour être exact
Calcul du temps de doublement
Pour les quantités en décomposition, nous avons déterminé le temps qu'il fallait pour que la moitié d'une substance se décompose. Pour les quantités croissantes, nous pouvons vouloir savoir combien de temps il faut pour qu'une quantité double. Comme nous l'avons mentionné ci-dessus, le temps nécessaire pour qu'une quantité double est appelé temps de doublement.
Compte tenu de l'équation de croissance exponentielle de base\(A=A_0e^{kt}\), le temps de doublement peut être déterminé en déterminant le moment où la quantité initiale a doublé, c'est-à-dire en résolvant\(2A_0=A_0e^{kt}\).
La formule est dérivée comme suit :
\[\begin{align*} 2A_0&= A_0e^{kt}\\ 2&= e^{kt} \qquad \text{Divide by } A_0\\ \ln2&= kt \qquad \text{Take the natural logarithm}\\ t& =\dfrac{\ln2}{k} \qquad \text{Divide by the coefficient of t} \end{align*}\]
Ainsi, le temps de doublement est
\[t=\dfrac{\ln2}{k}\]
Selon la loi de Moore, le temps de doublement du nombre de transistors pouvant être placés sur une puce informatique est d'environ deux ans. Donnez une fonction qui décrit ce comportement.
Solution
La formule est dérivée comme suit :
\[\begin{align*} t&= \dfrac{\ln2}{k} \qquad \text{The doubling time formula}\\ 2&= \dfrac{\ln2}{k} \qquad \text{Use a doubling time of two years}\\ k&= \dfrac{\ln2}{2} \qquad \text{Multiply by k and divide by 2}\\ A&= A_0e^{\tfrac{\ln2}{2}t} \qquad \text{Substitute k into the continuous growth formula} \end{align*}\]
La fonction est\(A=A_0e^{\dfrac{\ln2}{2}t}\).
Des données récentes suggèrent qu'en 2013, le taux de croissance prévu par la loi de Moore n'est plus valable. La croissance a ralenti et a doublé environ trois ans. Trouvez la nouvelle fonction qui prend en compte ce temps de doublement plus long.
- Réponse
-
\(f(t)=A_0e^{\tfrac{\ln2}{3}t}\)
Utilisation de la loi de refroidissement de Newton
La décroissance exponentielle peut également être appliquée à la température. Lorsqu'un objet chaud est laissé dans l'air ambiant à une température plus basse, la température de l'objet diminue de façon exponentielle et se stabilise à mesure qu'elle approche de la température de l'air ambiant. Sur un graphique de la fonction de température, la stabilisation correspondra à une asymptote horizontale à la température de l'air ambiant. À moins que la température ambiante ne soit nulle, cela correspondra à un décalage vertical de la fonction de décroissance exponentielle générique. Cette traduction conduit à la loi du refroidissement de Newton, la formule scientifique de la température en fonction du temps lorsque la température d'un objet est égalisée avec la température ambiante
\(T(t)=ae^{kt}+T_s\)
Cette formule est dérivée comme suit :
\[\begin{align*} T(t)&= Ab^{ct}+T_s\\ T(t)&= Ae^{\ln(b^{ct})}+T_s \qquad \text{Laws of logarithms}\\ T(t)&= Ae^{ct\ln b}+T_s \qquad \text{Laws of logarithms}\\ T(t)&= Ae^{kt}+T_s \qquad \text{Rename the constant c } ln b \text{, calling it } k\\ \end{align*}\]
La température d'un objet\(T\), dans l'air ambiant avec la température, se\(T_s\) comportera selon la formule
\[T(t)=Ae^{kt}+T_s\]
où- \(t\)c'est le temps
- \(A\)est la différence entre la température initiale de l'objet et l'environnement
- \(k\)est une constante, la vitesse continue de refroidissement de l'objet
- \(T_s\)Défini égal à la\(y\) coordonnée de l'asymptote horizontale (généralement la température ambiante).
- Substituez les valeurs données dans la formule de croissance continue\(T(t)=Ae^{kt}+T_s\) pour trouver les paramètres\(A\) et\(k\).
- Remplacez-la au moment souhaité pour trouver la température ou à la température souhaitée pour trouver l'heure.
Un gâteau au fromage est sorti du four avec une température interne idéale de\(165°F\) et placé dans un\(35°F\) réfrigérateur. Après\(10\) quelques minutes, le cheesecake est refroidi à\(150°F\). Si nous devons attendre que le gâteau au fromage soit refroidi\(70°F\) avant de le manger, combien de temps devrons-nous attendre ?
Solution
Comme la température de l'air ambiant dans le réfrigérateur est de\(35\) degrés, la température du gâteau au fromage diminuera de façon exponentielle vers\(35\), selon l'équation
\(T(t)=Ae^{kt}+35\)
Nous savons que la température initiale était\(165\) donc\(T(0)=165\).
\[\begin{align*} 165&= Ae^{k0}+35 \qquad \text{Substitute } (0,165)\\ A&= 130 \qquad \text{Solve for A} \end{align*}\]
On nous a donné un autre point de données\(T(10)=150\), que nous pouvons utiliser pour résoudre\(k\).
\[\begin{align*} 150&= 130e^{k10}+35 \qquad \text{Substitute } (10, 150)\\ 115&= 130e^{k10} \qquad \text{Subtract 35}\\ \dfrac{115}{130}&= e^{10k} \qquad \text{Divide by 130}\\ \ln\left (\dfrac{115}{130} \right )&= 10k \qquad \text{Take the natural log of both sides}\\ k&= \dfrac{\ln \left (\dfrac{115}{130} \right )}{10}\\ &= -0.0123 \qquad \text{Divide by the coefficient of k} \end{align*}\]
Cela nous donne l'équation du refroidissement du cheesecake :\(T(t)=130e^{–0.0123t}+35\).
Nous pouvons maintenant déterminer le temps qu'il faudra pour que la température refroidisse en\(70\) degrés.
\[\begin{align*} 70&= 130e^{-0.0123t}+35 \qquad \text{Substitute in 70 for } T(t)\\ 35&= 130e^{-0.0123t} \qquad \text{Subtract 35}\\ \dfrac{35}{130}&= e^{-0.0123t} \qquad \text{Divide by 130}\\ \ln \left (\dfrac{35}{130} \right )&= -0.0123t \qquad \text{Take the natural log of both sides}\\ t&= \dfrac{\ln \left (\dfrac{35}{130} \right )}{-0.0123}\\ &\approx 106.68 \qquad \text{Divide by the coefficient of t} \end{align*}\]
Il faudra environ\(107\) quelques minutes, ou une heure et\(47\) quelques minutes, pour que le gâteau au fromage refroidisse\(70°F\).
Un pichet d'eau à\(40\) degrés Fahrenheit est placé dans une salle de\(70\) diplôme. Une heure plus tard, la température a atteint des\(45\) degrés. Combien de temps faudra-t-il pour que la température atteigne les\(60\) degrés ?
- Réponse
-
\(6.026\)heures
Utilisation de modèles de croissance logistique
La croissance exponentielle ne peut pas durer éternellement. Les modèles exponentiels, s'ils peuvent être utiles à court terme, ont tendance à s'effondrer au fur et à mesure qu'ils se poursuivent. Prenons l'exemple d'une écrivaine en herbe qui écrit une seule ligne le premier jour et qui prévoit de doubler le nombre de lignes qu'elle écrit chaque jour pendant un mois. À la fin du mois, elle doit écrire plus d'un\(17\) milliard de lignes, soit un demi-milliard de pages. Il n'est pas pratique, voire impossible, pour quiconque d'écrire autant en si peu de temps. Finalement, un modèle exponentiel doit commencer à se rapprocher d'une valeur limite, puis la croissance est obligée de ralentir. Pour cette raison, il est souvent préférable d'utiliser un modèle avec une limite supérieure plutôt qu'un modèle de croissance exponentielle, bien que le modèle de croissance exponentielle soit toujours utile à court terme, avant de s'approcher de la valeur limite.
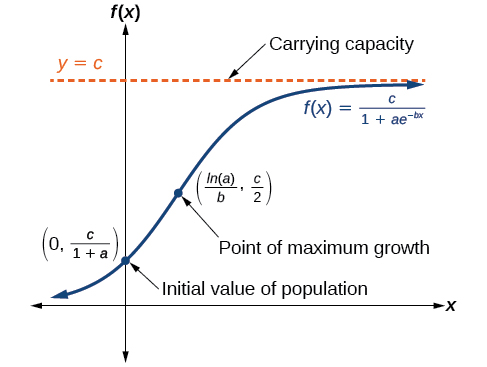
Le modèle de croissance logistique est approximativement exponentiel au début, mais son taux de croissance est réduit lorsque la production se rapproche de la limite supérieure du modèle, appelée capacité de charge. Pour les constantes\(a\)\(b\), et\(c\), la croissance logistique d'une population au fil du temps\(x\) est représentée par le modèle
\(f(x)=\dfrac{c}{1+ae^{−bx}}\)
Le graphique de la figure\(\PageIndex{6}\) montre l'évolution du taux de croissance au fil du temps. Le graphique augmente de gauche à droite, mais le taux de croissance n'augmente que jusqu'à ce qu'il atteigne son point de taux de croissance maximal, point auquel le taux d'augmentation diminue.
Le modèle de croissance logistique est
\[f(x)=\dfrac{c}{1+ae^{−bx}}\]
où
- \(\dfrac{c}{1+a}\)est la valeur initiale
- \(c\)est la capacité de charge, ou valeur limite
- \(b\)est une constante déterminée par le taux de croissance.
Une épidémie de grippe se propage rapidement au sein de la population, à un rythme qui dépend de deux facteurs : plus il y a de personnes atteintes de la grippe, plus elle se propage rapidement, et plus il y a de personnes non infectées, plus elle se propage rapidement. Ces deux facteurs font du modèle logistique un bon modèle pour étudier la propagation des maladies transmissibles. Et, de toute évidence, il existe une valeur maximale pour le nombre de personnes infectées : l'ensemble de la population.
Par exemple,\(t=0\) il arrive qu'une personne d'une communauté soit atteinte de\(1,000\) la grippe. Donc, dans cette communauté, la plupart des\(1,000\) gens peuvent avoir la grippe. Les chercheurs découvrent que pour cette souche particulière de grippe, la constante de croissance logistique est\(b=0.6030\). Estimez le nombre de personnes dans cette communauté qui auront contracté cette grippe au bout de dix jours. Prédisez combien de personnes dans cette communauté auront contracté cette grippe après une longue période.
Solution
Nous substituons les données fournies dans le modèle de croissance logistique
\(f(x)=\dfrac{c}{1+ae^{−bx}}\)
Comme la plupart des\(1,000\) gens, c'est-à-dire l'ensemble de la population de la communauté, peuvent contracter la grippe, nous savons que la valeur limite est\(c=1000\). Pour le trouver\(a\), nous utilisons la formule selon laquelle\(t=0\) est le nombre de cas à la fois\(\dfrac{c}{1+a}=1\), d'où il\(a=999\) découle que. Ce modèle prédit qu'après dix jours, le nombre de personnes ayant eu la grippe est de\(f(x)=\dfrac{1000}{1+999e^{−0.6030x}}≈293.8\). Parce que le nombre réel doit être un nombre entier (une personne a eu la grippe ou non), nous arrivons à\(294\). À long terme, le nombre de personnes qui contracteront la grippe est la valeur limite\(c=1000\).
Analyse
N'oubliez pas qu'étant donné que nous avons affaire à un virus, nous ne pouvons pas prédire avec certitude le nombre de personnes infectées. Le modèle ne donne qu'une approximation du nombre de personnes infectées et ne nous donnera pas de valeurs exactes ou réelles.
Le graphique de la figure\(\PageIndex{7}\) donne une bonne idée de la manière dont ce modèle s'ajuste aux données.
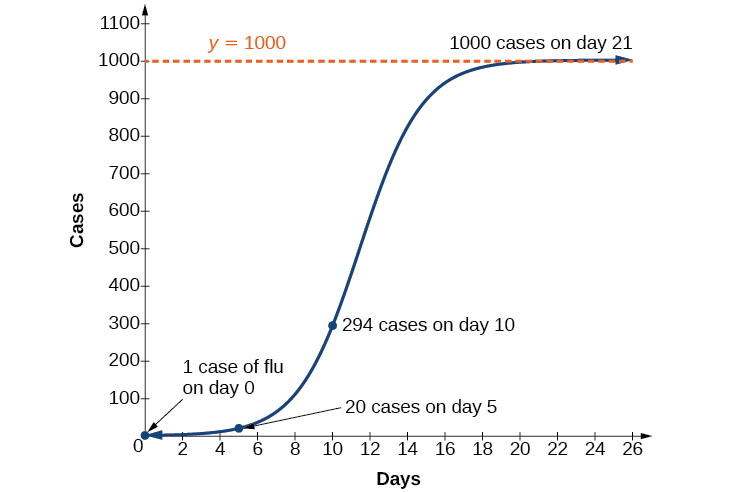
À l'aide du modèle de l'exemple ci-dessus, estimez le nombre de cas de grippe par jour\(15\).
- Réponse
-
\(895\)cas par jour\(15\)
Choisir un modèle approprié pour les données
Maintenant que nous avons discuté de divers modèles mathématiques, nous devons apprendre à choisir le modèle approprié pour les données brutes dont nous disposons. De nombreux facteurs influencent le choix d'un modèle mathématique, parmi lesquels l'expérience, les lois scientifiques et les modèles des données elles-mêmes. Toutes les données ne peuvent pas être décrites par des fonctions élémentaires. Parfois, on choisit une fonction qui rapproche les données sur un intervalle donné. Supposons, par exemple, que des données aient été recueillies sur le nombre de maisons achetées aux États-Unis entre 1960 et 2013. Après avoir tracé ces données dans un nuage de points, nous remarquons que la forme des données des années 2000 à 2013 suit une courbe logarithmique. Nous pourrions restreindre l'intervalle de 2000 à 2010, appliquer une analyse de régression à l'aide d'un modèle logarithmique et l'utiliser pour prédire le nombre d'acheteurs de maisons pour l'année 2015.
Trois types de fonctions souvent utiles dans les modèles mathématiques sont les fonctions linéaires, les fonctions exponentielles et les fonctions logarithmiques. Si les données se situent sur une ligne droite, ou semblent se trouver approximativement le long d'une ligne droite, un modèle linéaire peut être préférable. Si les données ne sont pas linéaires, nous envisageons souvent un modèle exponentiel ou logarithmique, bien que d'autres modèles, tels que des modèles quadratiques, puissent également être pris en compte.
Pour choisir entre un modèle exponentiel et un modèle logarithmique, nous examinons la façon dont les données se courbent. C'est ce qu'on appelle la concavité. Si nous tracons une ligne entre deux points de données et que toutes (ou la plupart) des données entre ces deux points se situent au-dessus de cette ligne, nous disons que la courbe est concave vers le bas. On peut le voir comme un bol qui se plie vers le bas et qui ne peut donc pas retenir l'eau. Si toutes (ou la plupart) des données entre ces deux points se situent en dessous de la ligne, nous disons que la courbe est concave vers le haut. Dans ce cas, on peut penser à un bol qui se penche vers le haut et qui peut donc contenir de l'eau. Une courbe exponentielle, qu'elle soit ascendante ou descendante, qu'elle représente la croissance ou la décroissance, est toujours concave vers le haut par rapport à son asymptote horizontale. Une courbe logarithmique est toujours concave par rapport à son asymptote verticale. Dans le cas de données positives, qui est le cas le plus courant, une courbe exponentielle est toujours concave vers le haut et une courbe logarithmique toujours concave vers le bas.
Une courbe logistique change de concavité. Il commence par être concave vers le haut, puis devient concave vers le bas au-delà d'un certain point, appelé point d'inflexion.
Après avoir utilisé le graphique pour nous aider à choisir le type de fonction à utiliser comme modèle, nous substituons des points et résolvons pour trouver les paramètres. Nous réduisons les erreurs d'arrondi en choisissant des points aussi éloignés que possible.
Un modèle linéaire, exponentiel, logarithmique ou logistique correspond-il le mieux aux valeurs répertoriées dans le tableau\(\PageIndex{1}\) ? Trouvez le modèle et utilisez un graphique pour vérifier votre choix.
| \(x\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| \(y\) | 0 | 1,386 | 2.197 | 2 773 | 3.219 | 3 584 | 3.892 | 4.159 | 4 394 |
Solution
Tout d'abord, tracez les données sur un graphique comme dans la figure\(\PageIndex{8}\). À des fins de représentation graphique, arrondissez les données à deux chiffres significatifs.
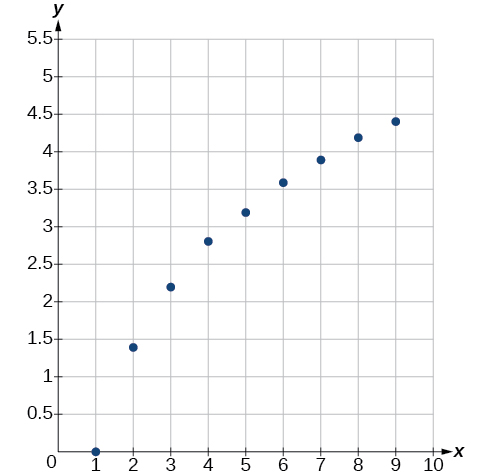
Il est clair que les points ne se situent pas sur une ligne droite, c'est pourquoi nous rejetons un modèle linéaire. Si nous tracons une ligne entre deux points, la plupart ou la totalité des points situés entre ces deux points se situent au-dessus de la ligne, de sorte que le graphique est concave vers le bas, ce qui suggère un modèle logarithmique. On peut essayer\(y=a\ln(bx)\). Brancher le premier point\((1,0)\), donne\(0=a\ln b\). Nous rejetons l'hypothèse selon laquelle\(a=0\) (si c'était le cas, toutes les sorties le seraient\(0\)), donc nous le savons\(\ln(b)=0\). Ainsi\(b=1\) et\(y=a\ln(x)\). Ensuite, nous pouvons utiliser le point\((9,4.394)\) pour résoudre\(a\) :
\[\begin{align*} y&= a\ln(x)\\ 4.394&= a\ln(9)\\ a&= \dfrac{4.394}{\ln(9)} \end{align*}\]
Parce que\(a=\dfrac{4.394}{\ln(9)}≈2\), un modèle approprié pour les données est\(y=2\ln(x)\).
Pour vérifier la précision du modèle, nous tracons la fonction avec les points donnés, comme sur la figure\(\PageIndex{9}\).
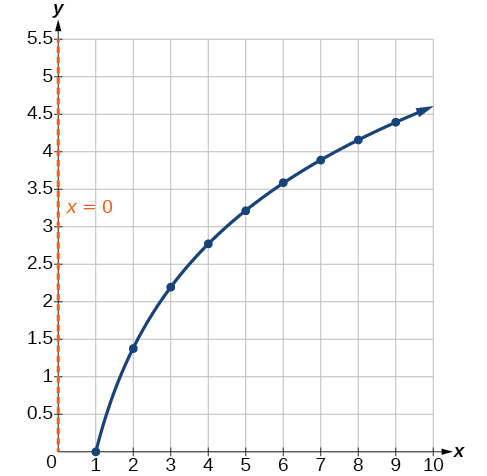
Nous pouvons conclure que le modèle est bien adapté aux données.
Comparez la figure\(\PageIndex{9}\) au graphique de la\(y=\ln(x^2)\) figure\(\PageIndex{10}\).
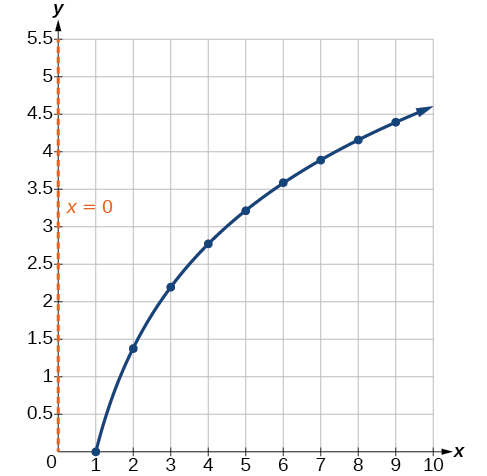
Les graphiques semblent identiques lorsque\(x>0\). Une vérification rapide confirme cette conclusion :\(y=\ln(x^2)=2\ln(x)\) pour\(x>0\).
Cependant, si\(x<0\), le graphique\(y=\ln(x^2)\) inclut une branche « supplémentaire », comme le montre la figure\(\PageIndex{11}\). Cela se produit parce que, bien qu'elle\(y=2\ln(x)\) ne puisse pas avoir de valeurs négatives dans le domaine (car de telles valeurs obligeraient l'argument à être négatif), la fonction\(y=\ln(x^2)\) peut avoir des valeurs de domaine négatives.
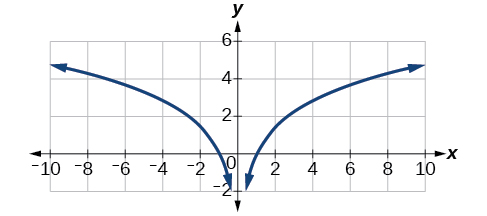
Un modèle linéaire, exponentiel ou logarithmique est-il le mieux adapté aux données du tableau\(\PageIndex{2}\) ? Trouvez le modèle.
| \(x\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| \(y\) | 3.297 | 5 437 | 8 963 | 14 778 | 24 365 | 40,172 | 66 231 | 109.196 | 180,034 |
- Réponse
-
Exponentiel\(y=2e^{0.5x}\).
Expression d'un modèle exponentiel en base\(e\)
Alors que les puissances et les logarithmes de n'importe quelle base peuvent être utilisés dans la modélisation, les deux bases les plus courantes sont\(10\) et\(e\). En sciences et en mathématiques, la base\(e\) est souvent préférée. Nous pouvons utiliser les lois des exposants et les lois des logarithmes pour changer n'importe quelle base en base\(e\).
- Réécrivez\(y=ab^x\) en tant que\(y=ae^{\ln(b^x)}\).
- Utilisez la règle de puissance des logarithmes pour réécrire\(y\) en tant que\(y=ae^{x\ln(b)}=ae^{\ln{(b)}^x}\).
- Notez cela\(a=A_0\) et\(k=\ln(b)\) dans l'équation\(y=A_0e^{kx}\).
Modifiez la fonction\(y=2.5{(3.1)}^x\) pour que cette même fonction soit écrite dans le formulaire\(y=A_0e^{kx}\).
Solution
La formule est dérivée comme suit
\[\begin{align*} y&= 2.5{(3.1)}^x\\ &= 2.5e^{\ln({3.1}^x)} \qquad \text{Insert exponential and its inverse}\\ &= 2.5e^{x\ln3.1} \qquad \text{Laws of logs}\\ &= 2.5e^{(\ln3.1)x} \qquad \text{Commutative law of multiplication} \end{align*}\]
Remplacez la fonction\(y=3{(0.5)}^x\) par une fonction ayant\(e\) comme base.
- Réponse
-
\(y=3e^{(\ln0.5)x}\)
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur les modèles exponentiels et logarithmiques.
- Application du logarithme — pH
- Modèle exponentiel — Âge utilisant la demi-vie
- Loi du refroidissement de Newton
- Croissance exponentielle avec un temps de doublement
- Croissance exponentielle — Trouvez le montant initial en doublant le temps
Équations clés
| Formule à demi-vie | Si\(A=A_0e^{kt}\)\(k<0\), la demi-vie est\(t=−\dfrac{\ln(2)}{k}\). |
| Datation au carbone 14 | \(t=\dfrac{\ln(\dfrac{A}{A_0})}{−0.000121}\). \(A_0\)\(A\)est la quantité de carbone 14 lorsque la plante ou l'animal \(t\) est mort est la quantité de carbone 14 restante aujourd'hui est l'âge du fossile en années |
| Formule de doublement du temps | Si\(A=A_0e^{kt}\)\(k>0\), le temps de doublement est\(t=\dfrac{\ln2}{k}\) |
| Loi du refroidissement de Newton | \(T(t)=Ae^{kt}+T_s\), où\(T_s\) est la température ambiante\(A=T(0)−T_s\), et\(k\) est la vitesse continue de refroidissement. |
Concepts clés
- La fonction exponentielle de base est\(f(x)=ab^x\). Si\(b>1\), nous avons une croissance exponentielle ; si\(0<b<1\), nous avons une décroissance exponentielle.
- Nous pouvons également écrire cette formule en termes de croissance continue comme\(A=A_0e^{kx}\), où\(A_0\) est la valeur de départ. Si\(A_0\) c'est positif, alors nous avons une croissance exponentielle quand\(k>0\) et une décroissance exponentielle quand\(k<0\). Voir l'exemple\(\PageIndex{1}\).
- En général, nous résolvons les problèmes impliquant une croissance ou une décroissance exponentielle en deux étapes. Tout d'abord, nous configurons un modèle et l'utilisons pour trouver les paramètres. Nous utilisons ensuite la formule avec ces paramètres pour prédire la croissance et la décroissance. Voir l'exemple\(\PageIndex{2}\).
- Nous pouvons déterminer l'âge d'un artefact organique en mesurant la quantité de carbone 14 restant dans l'artefact et en utilisant la formule\(t=\dfrac{\ln(k)}{−0.000121}\) pour le résoudre\(t\).\(t\)\(k\) Voir l'exemple\(\PageIndex{3}\).
- Étant donné le temps de doublement ou la mi-temps d'une substance, nous pouvons trouver une fonction qui représente sa croissance ou sa décroissance exponentielle. Voir l'exemple\(\PageIndex{4}\).
- Nous pouvons utiliser la loi de refroidissement de Newton pour déterminer le temps qu'il faudra à un objet en refroidissement pour atteindre la température souhaitée, ou pour déterminer la température à laquelle se situera un objet après un certain temps. Voir l'exemple\(\PageIndex{5}\).
- Nous pouvons utiliser des fonctions de croissance logistique pour modéliser des situations réelles dans lesquelles le taux de croissance change au fil du temps, telles que la croissance démographique, la propagation de maladies et la propagation de rumeurs. Voir l'exemple\(\PageIndex{6}\).
- Nous pouvons utiliser les données du monde réel recueillies au fil du temps pour observer les tendances. La connaissance des graphes linéaires, exponentiels, logarithmiques et logistiques nous aide à développer des modèles qui s'adaptent le mieux à nos données. Voir l'exemple\(\PageIndex{7}\).
- Toute fonction exponentielle avec le formulaire\(y=abx\) peut être réécrite en tant que fonction exponentielle équivalente avec le formulaire\(y=A_0e^{kx}\) où\(k=\ln b\). Voir l'exemple\(\PageIndex{8}\).


