6.6 : Équations exponentielles et logarithmiques
- Page ID
- 195632
- Utilisez des bases similaires pour résoudre des équations exponentielles.
- Utilisez des logarithmes pour résoudre des équations exponentielles.
- Utilisez la définition d'un logarithme pour résoudre des équations logarithmiques.
- Utilisez la propriété biunivoque des logarithmes pour résoudre des équations logarithmiques.
- Résolvez des problèmes appliqués impliquant des équations exponentielles et logarithmiques.
En 1859, un propriétaire foncier australien du nom de Thomas Austin a relâché des\(24\) lapins dans la nature pour la chasse. Comme l'Australie comptait peu de prédateurs et suffisamment de nourriture, la population de lapins a explosé. En moins de dix ans, la population de lapins s'est chiffrée à des millions.

La croissance incontrôlée de la population, comme chez les lapins sauvages en Australie, peut être modélisée à l'aide de fonctions exponentielles. Les équations résultant de ces fonctions exponentielles peuvent être résolues pour analyser et faire des prédictions concernant la croissance exponentielle. Dans cette section, nous allons apprendre des techniques pour résoudre des fonctions exponentielles.
Utilisation de bases similaires pour résoudre des équations exponentielles
La première technique implique deux fonctions ayant des bases similaires. Rappelez-vous que la propriété biunivoque des fonctions exponentielles nous indique que, pour tous les nombres réels\(b\)\(S\), et\(T\), où\(b>0\)\(b≠1\),\(b^S=b^T\) si et seulement si\(S=T\).
En d'autres termes, lorsqu'une équation exponentielle a la même base de chaque côté, les exposants doivent être égaux. Cela s'applique également lorsque les exposants sont des expressions algébriques. Par conséquent, nous pouvons résoudre de nombreuses équations exponentielles en utilisant les règles des exposants pour réécrire chaque côté sous forme de puissance ayant la même base. Ensuite, nous utilisons le fait que les fonctions exponentielles sont un-à-une pour définir les exposants égaux les uns aux autres et résoudre l'inconnu.
Prenons l'exemple de l'équation\(3^{4x−7}=\dfrac{3^{2x}}{3}\). Pour résoudre ce problème\(x\), nous utilisons la propriété de division des exposants pour réécrire le côté droit afin que les deux côtés aient la base commune,\(3\). Ensuite, nous appliquons la propriété individuelle des exposants en définissant les exposants égaux les uns aux autres et en résolvant les problèmes\(x\) suivants :
\[\begin{align*} 3^{4x-7}&= \dfrac{3^{2x}}{3}\\ 3^{4x-7}&= \dfrac{3^{2x}}{3^1} \qquad &&\text{Rewrite 3 as } 3^1\\ 3^{4x-7}&= 3^{2x-1} \qquad &&\text{Use the division property of exponents}\\ 4x-7&= 2x-1 \qquad &&\text{Apply the one-to-one property of exponents}\\ 2x&= 6 \qquad &&\text{Subtract 2x and add 7 to both sides}\\ x&= 3 \qquad &&\text{Divide by 3} \end{align*}\]
Pour toutes les expressions algébriques\(S\) et\(T\) pour tout nombre réel positif\(b≠1\),
\[\begin{align} b^S=b^T\text{ if and only if } S=T \end{align}\]
- Utilisez les règles des exposants pour simplifier, si nécessaire, afin que l'équation résultante ait la forme\(b^S=b^T\).
- Utilisez la propriété un-à-un pour définir des exposants égaux.
- Résolvez l'équation résultante\(S=T\),, pour l'inconnu.
Résoudre\(2^{x−1}=2^{2x−4}\).
Solution
\[\begin{align*} 2^{x-1}&= 2^{2x-4} \qquad &&\text{The common base is 2}\\ x-1&= 2x-4 \qquad &&\text{By the one-to-one property the exponents must be equal}\\ x&= 3 \qquad &&\text{Solve for x} \end{align*}\]
Résoudre\(5^{2x}=5^{3x+2}\).
- Réponse
-
\(x=−2\)
Réécrivez les équations pour que toutes les puissances aient la même base
Parfois, la base commune d'une équation exponentielle n'est pas explicitement indiquée. Dans ces cas, il suffit de réécrire les termes de l'équation sous forme de puissances ayant une base commune et de les résoudre en utilisant la propriété un-à-un.
Prenons l'exemple de l'équation\(256=4^{x−5}\). Nous pouvons réécrire les deux côtés de cette équation comme une puissance de\(2\). Nous appliquons ensuite les règles des exposants, ainsi que la propriété biunivoque, pour résoudre les problèmes\(x\) suivants :
\[\begin{align*} 256&= 4^{x-5}\\ 2^8&= {(2^2)}^{x-5} \qquad &&\text{Rewrite each side as a power with base 2}\\ 2^8&= 2^{2x-10} \qquad &&\text{Use the one-to-one property of exponents}\\ 8&= 2x-10 \qquad &&\text{Apply the one-to-one property of exponents}\\ 18&= 2x \qquad &&\text{Add 10 to both sides}\\ x&= 9 \qquad &&\text{Divide by 2} \end{align*}\]
- Réécrivez chaque côté de l'équation sous la forme d'une puissance ayant une base commune.
- Utilisez les règles des exposants pour simplifier, si nécessaire, afin que l'équation résultante ait la forme\(b^S=b^T\).
- Utilisez la propriété un-à-un pour définir des exposants égaux.
- Résolvez l'équation résultante\(S=T\),, pour l'inconnu.
Résoudre\(8^{x+2}={16}^{x+1}\).
Solution
\[\begin{align*} 8^{x+2}&= {16}^{x+1}\\ {(2^3)}^{x+2}&= {(2^4)}^{x+1} \qquad &&\text{Write 8 and 16 as powers of 2}\\ 2^{3x+6}&= 2^{4x+4} \qquad &&\text{To take a power of a power, multiply exponents}\\ 3x+6&= 4x+4 \qquad &&\text{Use the one-to-one property to set the exponents equal}\\ x&= 2 \qquad &&\text{Solve for x} \end{align*}\]
Résoudre\(5^{2x}={25}^{3x+2}\).
- Réponse
-
\(x=−1\)
Résoudre\(2^{5x}=\sqrt{2}\).
Solution
\[\begin{align*} 2^{5x}&= 2^{\frac{1}{2}} \qquad &&\text{Write the square root of 2 as a power of 2}\\ 5x&= \dfrac{1}{2} \qquad &&\text{Use the one-to-one property}\\ x&= \dfrac{1}{10} \qquad &&\text{Solve for x} \end{align*}\]
Résoudre\(5^x=\sqrt{5}\).
- Réponse
-
\(x=\dfrac{1}{2}\)
Non. Rappelez-vous que la plage d'une fonction exponentielle est toujours positive. Lors de la résolution de l'équation, nous pouvons obtenir une expression non définie.
Résoudre\(3^{x+1}=−2\).
Solution
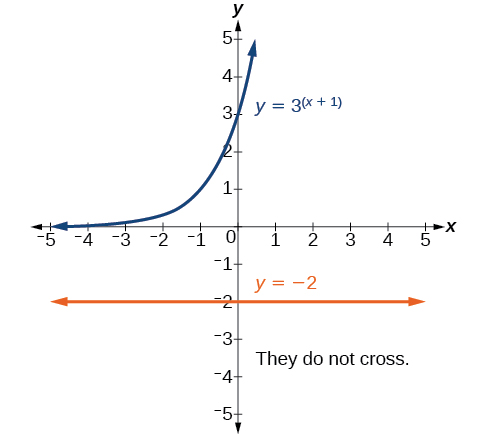
Cette équation n'a pas de solution. Il n'y a aucune valeur réelle\(x\) qui fera de l'équation une affirmation vraie, car toute puissance d'un nombre positif est positive.
Analyse
La figure\(\PageIndex{2}\) montre que les deux graphiques ne se croisent pas, de sorte que le côté gauche n'est jamais égal au côté droit. L'équation n'a donc pas de solution.
Résoudre\(2^x=−100\).
- Réponse
-
L'équation n'a pas de solution.
Résolution d'équations exponentielles à l'aide de logarithmes
Parfois, les termes d'une équation exponentielle ne peuvent pas être réécrits avec une base commune. Dans ces cas, nous résolvons en prenant le logarithme de chaque côté. Rappelons que puisque\(\log(a)=\log(b)\) c'est équivalent à\(a=b\), nous pouvons appliquer des logarithmes avec la même base des deux côtés d'une équation exponentielle.
- Appliquez le logarithme des deux côtés de l'équation.
- Si l'un des termes de l'équation a la base 10, utilisez le logarithme commun.
- Si aucun des termes de l'équation n'a la base 10, utilisez le logarithme naturel.
- Utilisez les règles des logarithmes pour résoudre l'inconnu.
Résoudre\(5^{x+2}=4^x\).
Solution
\ [\ begin {align*}
5^ {x+2} &= 4^x \ qquad && \ text {Il n'y a pas de moyen facile d'obtenir les pouvoirs pour avoir la même base} \ \ \ ln5^ {x+2} &=
\ ln4^x \ qquad && \ text {Prenez ln des deux côtés} \ \ (x+2) \ ln5&= x \ ln4 \ qquad && \ text {Prends ln des deux côtés} \ \
(x+2) \ ln5&= x \ ln4 \ qquad && \ text {Lois d'utilisation de journaux} \ \
x \ ln5+2 \ ln5&= x \ ln4 \ qquad && \ text {Utilisez la loi distributive} \ \
x \ ln5-x \ ln4&= -2 \ ln5 \ qquad && \ text {Obtenez des termes contenant x d'un côté, des termes sans x de l'autre} \ \
x (\ ln5- \ ln4) &= -2 \ ln5 \ qquad && \ text {Sur le côté gauche, efface un x} \ \
x \ ln \ left (\ dfrac {5} {4} \ right) &= \ ln \ left (\ dfrac {1} {25} \ right) \ qquad && \ text {Utilisez les lois des journaux} \ \
x&= \ dfrac {\ ln \ left (\ dfrac {1} {25} \ right)} {\ ln \ left (\ dfrac {1} {25} \ right)} {\ ln \ left (\ dfrac {5}} {4} \ right)} \ qquad && \ text {Diviser par le coefficient de x}
\ end { aligner*} \]
Résoudre\(2^x=3^{x+1}\).
- Réponse
-
\(x=\dfrac{\ln3}{\ln \left (\dfrac{2}{3} \right )}\)
Oui. La solution est\(0\).
Équations contenant\(e\)
Les équations à base constituent un type courant d'équations exponentielles\(e\). Cette constante se produit encore et encore dans la nature, en mathématiques, en sciences, en ingénierie et en finance. Lorsque nous avons une équation avec une base de chaque\(e\) côté, nous pouvons utiliser le logarithme naturel pour la résoudre.
- Divisez les deux côtés de l'équation par\(A\).
- Appliquez le logarithme naturel des deux côtés de l'équation.
- Divisez les deux côtés de l'équation par\(k\).
Résoudre\(100=20e^{2t}\).
Solution
\[\begin{align*} 100&= 20e^{2t}\\ 5&= e^{2t} \qquad &&\text{Divide by the coefficient of the power}\\ \ln5&= 2t \qquad &&\text{Take ln of both sides. Use the fact that } ln(x) \text{ and } e^x \text{ are inverse functions}\\ t&= \dfrac{\ln5}{2} \qquad &&\text{Divide by the coefficient of t} \end{align*}\]
Analyse
En utilisant les lois des journaux, nous pouvons également écrire cette réponse dans le formulaire\(t=\ln\sqrt{5}\). Si nous voulons une approximation décimale de la réponse, nous utilisons une calculatrice.
Résoudre\(3e^{0.5t}=11\).
- Réponse
-
\(t=2\ln \left (\dfrac{11}{3} \right )\)ou\(\ln{ \left (\dfrac{11}{3} \right )}^2\)
Non. Il existe une solution quand\(k≠0\) et quand\(y\) et\(A\) sont tous les deux 0 ou aucun 0, et ils ont le même signe. Voici un exemple d'équation de cette forme qui n'a pas de solution\(2=−3e^t\).
Résoudre\(4e^{2x}+5=12\).
Solution
\[\begin{align*} 4e^{2x}+5&= 12\\ 4e^{2x}&= 7 \qquad &&\text{Combine like terms}\\ e^{2x}&= \dfrac{7}{4} \qquad &&\text{Divide by the coefficient of the power}\\ 2x&= \ln \left (\dfrac{7}{4} \right ) \qquad &&\text{Take ln of both sides}\\ x&= \dfrac{1}{2}\ln \left (\dfrac{7}{4} \right ) \qquad &&\text{Solve for x} \end{align*}\]
Résoudre\(3+e^{2t}=7e^{2t}\).
- Réponse
-
\(t=\ln \left (\dfrac{1}{\sqrt{2}} \right )=−\dfrac{1}{2}\ln(2)\)
Solutions externes
Parfois, les méthodes utilisées pour résoudre une équation introduisent une solution externe, c'est-à-dire une solution qui est correcte sur le plan algébrique mais qui ne satisfait pas aux conditions de l'équation d'origine. L'une de ces situations se présente lors de la résolution lorsque le logarithme est pris des deux côtés de l'équation. Dans de tels cas, n'oubliez pas que l'argument du logarithme doit être positif. Si le nombre que nous évaluons dans une fonction logarithmique est négatif, il n'y a pas de sortie.
Résoudre\(e^{2x}−e^x=56\).
Solution
\[\begin{align*} e^{2x}-e^x&= 56\\ e^{2x}-e^x-56&= 0 \qquad &&\text{Get one side of the equation equal to zero}\\ (e^x+7)(e^x-8)&= 0 \qquad &&\text{Factor by the FOIL method}\\ e^x+7&= 0 \qquad &&\text{or} \\ e^x-8&= 0 \qquad &&\text{If a product is zero, then one factor must be zero}\\ e^x&= -7 \qquad &&\text{or} \\ e^x&= 8 \qquad &&\text{Isolate the exponentials}\\ e^x&= 8 \qquad &&\text{Reject the equation in which the power equals a negative number}\\ x&= \ln8 \qquad &&\text{Solve the equation in which the power equals a positive number} \end{align*}\]
Analyse
Lorsque nous prévoyons d'utiliser l'affacturage pour résoudre un problème, nous obtenons toujours zéro sur un côté de l'équation, car zéro possède la propriété unique que lorsqu'un produit est égal à zéro, l'un des facteurs ou les deux doivent être nuls. Nous rejetons l'équation\(e^x=−7\) car un nombre positif n'est jamais égal à un nombre négatif. La solution n'\(\ln(−7)\)est pas un nombre réel et, dans le système de nombres réels, cette solution est rejetée en tant que solution superflue.
Résoudre\(e^{2x}=e^x+2\).
- Réponse
-
\(x=\ln2\)
Non. Gardez à l'esprit que nous ne pouvons appliquer le logarithme qu'à un nombre positif. Vérifiez toujours la présence de solutions superflues.
Utiliser la définition d'un logarithme pour résoudre des équations logarithmiques
Nous avons déjà vu que chaque équation logarithmique\({\log}_b(x)=y\) est équivalente à l'équation exponentielle\(b^y=x\). Nous pouvons utiliser ce fait, ainsi que les règles des logarithmes, pour résoudre des équations logarithmiques où l'argument est une expression algébrique.
Par exemple, considérez l'équation\({\log}_2(2)+{\log}_2(3x−5)=3\). Pour résoudre cette équation, nous pouvons utiliser des règles de logarithmes pour réécrire le côté gauche sous forme compacte, puis appliquer la définition des logs à résoudre pour\(x\) :
\[\begin{align*} {\log}_2(2)+{\log}_2(3x-5)&= 3\\ {\log}_2(2(3x-5))&= 3 \qquad \text{Apply the product rule of logarithms}\\ {\log}_2(6x-10)&= 3 \qquad \text{Distribute}\\ 2^3&= 6x-10 \qquad \text{Apply the definition of a logarithm}\\ 8&= 6x-10 \qquad \text{Calculate } 2^3\\ 18&= 6x \qquad \text{Add 10 to both sides}\\ x&= 3 \qquad \text{Divide by 6} \end{align*}\]
Pour toutes les expressions algébriques\(S\) et les nombres réels\(b\) et\(c\)\(b>0\), où\(b≠1\),
\[\begin{align} {\log}_b(S)=c \text{ if and only if } b^c=S \end{align}\]
Résoudre\(2\ln x+3=7\).
Solution
\[\begin{align*} 2\ln x+3&= 7\\ 2\ln x&= 4 \qquad \text{Subtract 3}\\ \ln x&= 2 \qquad \text{Divide by 2}\\ x&= e^2 \qquad \text{Rewrite in exponential form} \end{align*}\]
Résoudre\(6+\ln x=10\).
- Réponse
-
\(x=e^4\)
Résoudre\(2\ln(6x)=7\).
Solution
\[\begin{align*} 2\ln(6x)&= 7\\ \ln(6x)&= \dfrac{7}{2} \qquad \text{Divide by 2}\\ 6x&= e^{\left (\dfrac{7}{2} \right )} \qquad \text{Use the definition of }\ln \\ x&= \dfrac{1}{6}e^{\left (\dfrac{7}{2} \right )} \qquad \text{Divide by 6} \end{align*}\]
Résoudre\(2\ln(x+1)=10\).
- Réponse
-
\(x=e^5−1\)
Résoudre\(\ln x=3\).
Solution
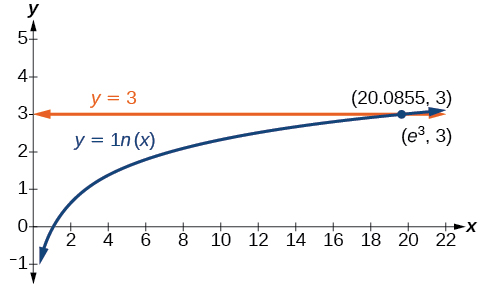
\[\begin{align*} \ln x&= 3\\ x&= e^3 \qquad \text{Use the definition of the natural logarithm} \end{align*}\]
La figure\(\PageIndex{3}\) représente le graphique de l'équation. Sur le graphique, la coordonnée x du point d'intersection des deux graphes est proche de\(20\). En d'autres termes\(e^3≈20\). Un calculateur donne une meilleure approximation :\(e^3≈20.0855\).
Utilisez une calculatrice graphique pour estimer la solution approximative de l'équation logarithmique avec\(2^x=1000\) des\(2\) décimales.
- Réponse
-
\(x≈9.97\)
Utilisation de la propriété biunivoque des logarithmes pour résoudre des équations logarithmiques
Comme pour les équations exponentielles, nous pouvons utiliser la propriété biunivoque pour résoudre des équations logarithmiques. La propriété biunivoque des fonctions logarithmiques nous indique que, pour tous les nombres réels\(x>0\)\(S>0\),\(T>0\) et pour tout nombre réel positif\(b\), où\(b≠1\),
\({\log}_bS={\log}_bT\)si et seulement si\(S=T\).
Par exemple,
Si\({\log}_2(x−1)={\log}_2(8)\), alors\(x−1=8\).
Donc, si\(x−1=8\), alors nous pouvons résoudre\(x\), et nous obtenons\(x=9\). Pour vérifier, on peut remplacer l'\(x=9\)équation d'origine :\({\log}_2(9−1)={\log}_2(8)=3\). En d'autres termes, lorsqu'une équation logarithmique a la même base de chaque côté, les arguments doivent être égaux. Cela s'applique également lorsque les arguments sont des expressions algébriques. Par conséquent, lorsqu'on donne une équation avec des logarithmes de la même base de chaque côté, nous pouvons utiliser des règles de logarithmes pour réécrire chaque côté en un logarithme unique. Ensuite, nous utilisons le fait que les fonctions logarithmiques sont un-à-une pour définir les arguments égaux les uns aux autres et résoudre l'inconnu.
Par exemple, considérez l'équation\(\log(3x−2)−\log(2)=\log(x+4)\). Pour résoudre cette équation, nous pouvons utiliser les règles des logarithmes pour réécrire le côté gauche sous la forme d'un logarithme unique, puis appliquer la propriété biunivoque pour résoudre\(x\) :
\[\begin{align*} \log(3x-2)-\log(2)&= \log(x+4)\\ \log \left (\dfrac{3x-2}{2} \right )&= \log(x+4) \qquad \text{Apply the quotient rule of logarithms}\\ \dfrac{3x-2}{2}&= x+4 \qquad \text{Apply the one to one property of a logarithm}\\ 3x-2&= 2x+8 \qquad \text{Multiply both sides of the equation by 2}\\ x&= 10 \qquad \text{Subtract 2x and add 2} \end{align*}\]
Pour vérifier le résultat, remplacez\(x=10\) par\(\log(3x−2)−\log(2)=\log(x+4)\).
\[\begin{align*} \log(3(10)-2)-\log(2)&= \log((10)+4) \\ \log(28)-\log(2)&= \log(14)\\ \log \left (\dfrac{28}{2} \right )&= \log(14) \qquad \text{The solution checks} \end{align*}\]
Pour toutes les expressions algébriques\(S\)\(T\) et tout nombre réel positif\(b\), où\(b≠1\),
\[\begin{align} b^S=b^T\text{ if and only if } S=T \end{align}\]
Notez que lorsque vous résolvez une équation impliquant des logarithmes, vérifiez toujours si la réponse est correcte ou s'il s'agit d'une solution superflue.
- Utilisez les règles des logarithmes pour combiner des termes similaires, si nécessaire, afin que l'équation résultante ait la forme\({\log}_bS={\log}_bT\).
- Utilisez la propriété un-à-un pour définir les arguments de manière égale.
- Résolvez l'équation résultante\(S=T\),, pour l'inconnu.
Résoudre\(\ln(x^2)=\ln(2x+3)\).
Solution
\[\begin{align*} \ln(x^2)&= \ln(2x+3)\\ x^2&= 2x+3 \qquad \text{Use the one-to-one property of the logarithm}\\ x^2-2x-3&= 0 \qquad \text{Get zero on one side before factoring}\\ (x-3)(x+1)&= 0 \qquad \text{Factor using FOIL}\\ x-3&= 0 \qquad \text{or } x+1=0 \text{ If a product is zero, one of the factors must be zero}\\ x=3 \qquad \text{or} \\ x&= -11 \qquad \text{Solve for x} \end{align*}\]
Analyse
Il existe deux solutions :\(3\) ou\(−1\). La solution\(−1\) est négative, mais elle vérifie si elle est remplacée dans l'équation d'origine, car l'argument des fonctions logarithmiques est toujours positif.
Résoudre\(\ln(x^2)=\ln1\).
- Réponse
-
\(x=1\)ou\(x=−1\)
Résolution de problèmes appliqués à l'aide d'équations exponentielles et logarithmiques
Dans les sections précédentes, nous avons appris les propriétés et les règles des fonctions exponentielles et logarithmiques. Nous avons vu que toute fonction exponentielle peut être écrite comme une fonction logarithmique et vice versa. Nous avons utilisé des exposants pour résoudre des équations logarithmiques et des logarithmes pour résoudre des équations exponentielles. Nous sommes maintenant prêts à combiner nos compétences pour résoudre des équations qui modélisent des situations du monde réel, que l'inconnu se trouve dans un exposant ou dans l'argument d'un logarithme.
L'une de ces applications est la science, qui consiste à calculer le temps nécessaire à la désintégration de la moitié de la matière instable contenue dans un échantillon d'une substance radioactive, appelé demi-vie. Le tableau\(\PageIndex{1}\) indique la demi-vie de plusieurs des substances radioactives les plus courantes.
| Substance | Utiliser | Demi-vie |
|---|---|---|
| gallium 67 | médecine nucléaire | 80 heures |
| cobalt-60 | fabrication | 5,3 ans |
| technétium 99 m | médecine nucléaire | 6 heures |
| américium-241 | construction | 432 années |
| carbone 14 | datation archéologique | 5 715 ans |
| uranium 235 | énergie atomique | 703 800 000 ans |
Nous pouvons voir dans quelle mesure les demi-vies de ces substances varient. Connaître la demi-vie d'une substance nous permet de calculer la quantité restante après un certain temps. Nous pouvons utiliser la formule de désintégration radioactive :
\[\begin{align} A(t)&= A_0e^{\tfrac{\ln(0.5)}{T}t}\\ A(t)&= A_0e^{\tfrac{\ln(0.5)t}{T}}\\ A(t)&= A_0{(e^{\ln(0.5)})}^{\tfrac{t}{T}}\\ A(t)&= A_0{\left (\dfrac{1}{2}\right )}^{\tfrac{t}{T}}\\ \end{align}\]
où
- \(A_0\)est le montant initialement présent
- \(T\)est la demi-vie de la substance
- \(t\)est la période pendant laquelle la substance est étudiée
- \(y\)est la quantité de substance présente après le temps\(t\)
Combien de temps faudra-t-il pour que dix pour cent\(1000\) d'un échantillon d'uranium 235 se désintègre ?
Solution
\[\begin{align*} y&= 1000e^{\tfrac{\ln(0.5)}{703,800,000}t}\\ 900&= 1000e^{\tfrac{\ln(0.5)}{703,800,000}t} \qquad \text{After } 10\% \text{ decays, 900 grams are left}\\ 0.9&= e^{\tfrac{\ln(0.5)}{703,800,000}t} \qquad \text{Divide by 1000}\\ \ln(0.9)&= \ln \left (e^{\tfrac{\ln(0.5)}{703,800,000}t} \right ) \qquad \text{Take ln of both sides}\\ \ln(0.9)&= \dfrac{\ln(0.5)}{703,800,000}t \qquad \ln(e^M)=M\\ t&= 703,800,000\times \dfrac{\ln(0.9)}{\ln(0.5)} \qquad \text{years Solve for t}\\ t&\approx 106,979,777 \qquad \text{years} \end {align*} \]
Analyse
Dix pour cent des\(1000\) grammes sont des\(100\) grammes. Si les\(100\) grammes se désintègrent, la quantité d'uranium 235 restante est de\(900\) grammes.
Combien de temps faudra-t-il avant que 20 % de notre échantillon de 1 000 grammes d'uranium 235 se décompose ?
- Réponse
-
\(t=703,800,000×\dfrac{\ln(0.8)}{\ln(0.5)}\)ans ≈ 226 572 993 ans.
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur les équations exponentielles et logarithmiques.
- Résolution d'équations logarithmiques
- Résolution d'équations exponentielles à l'aide de logarithmes
Équations clés
| Propriété univoque pour les fonctions exponentielles | Pour toutes les expressions algébriques\(S\)\(T\) et tout nombre réel positif\(b\), où\(b^S=b^T\) si et seulement si\(S=T\). |
| Définition d'un logarithme | Pour toute expression algébrique S et nombres réels positifs\(b\) et\(c\), où\(b≠1\),\({\log}_b(S)=c\) si et seulement si\(b^c=S\). |
| Propriété univoque pour les fonctions logarithmiques | Pour toutes les expressions algébriques\(S\)\(T\) et tout nombre réel positif\(b\), où\(b≠1\), \({\log}_bS={\log}_bT\) si et seulement si\(S=T\). |
Concepts clés
- Nous pouvons résoudre de nombreuses équations exponentielles en utilisant les règles des exposants pour réécrire chaque côté sous forme de puissance ayant la même base. Ensuite, nous utilisons le fait que les fonctions exponentielles sont un-à-une pour définir les exposants égaux les uns aux autres et résoudre l'inconnu.
- Lorsque l'on nous donne une équation exponentielle dans laquelle les bases sont explicitement indiquées comme étant égales, définissez les exposants égaux les uns aux autres et résolvez pour l'inconnu. Voir l'exemple\(\PageIndex{1}\).
- Lorsque l'on nous donne une équation exponentielle où les bases ne sont pas explicitement indiquées comme étant égales, réécrivez chaque côté de l'équation en tant que puissances de la même base, puis définissez les exposants égaux les uns aux autres et résolvez pour l'inconnu. Voir Exemple\(\PageIndex{2}\)\(\PageIndex{3}\), Exemple et Exemple\(\PageIndex{4}\).
- Lorsqu'une équation exponentielle ne peut pas être réécrite avec une base commune, résolvez-la en prenant le logarithme de chaque côté. Voir l'exemple\(\PageIndex{5}\).
- Nous pouvons résoudre des équations exponentielles avec la base\(e\), en appliquant le logarithme naturel des deux côtés, car les fonctions exponentielle et logarithmique sont inverses l'une de l'autre. Voir Exemple\(\PageIndex{6}\) et Exemple\(\PageIndex{7}\).
- Après avoir résolu une équation exponentielle, vérifiez chaque solution de l'équation d'origine pour trouver et éliminer toutes les solutions superflues. Voir l'exemple\(\PageIndex{8}\).
- Lorsque l'on donne une équation de la forme\({\log}_b(S)=c\), où\(S\) est une expression algébrique, nous pouvons utiliser la définition d'un logarithme pour réécrire l'équation en tant qu'équation\(b^c=S\) exponentielle équivalente et résoudre l'inconnu. Voir Exemple\(\PageIndex{9}\) et Exemple\(\PageIndex{10}\).
- Nous pouvons également utiliser la représentation graphique pour résoudre des équations avec le formulaire\({\log}_b(S)=c\). Nous dessinons les deux équations\(y={\log}_b(S)\)\(y=c\) sur le même plan de coordonnées et identifions la solution comme étant la valeur x du point d'intersection. Voir l'exemple\(\PageIndex{11}\).
- Lorsque l'on donne une équation de la forme\({\log}_bS={\log}_bT\), où\(S\) et\(T\) sont des expressions algébriques, nous pouvons utiliser la propriété individuelle des logarithmes\(S=T\) pour résoudre l'équation de l'inconnu. Voir l'exemple\(\PageIndex{12}\).
- En combinant les compétences acquises dans cette section et dans les sections précédentes, nous pouvons résoudre des équations qui modélisent des situations du monde réel, que l'inconnu se trouve dans un exposant ou dans l'argument d'un logarithme. Voir l'exemple\(\PageIndex{13}\).


