6.1 : Fonctions exponentielles
- Page ID
- 195669
- Évaluez les fonctions exponentielles.
- Trouvez l'équation d'une fonction exponentielle.
- Utilisez des formules d'intérêts composés.
- Évaluez les fonctions exponentielles avec base\(e\).
L'Inde est le deuxième pays le plus peuplé du monde avec une population d'environ un\(1.25\) milliard d'habitants en 2013. La population augmente à un rythme d'environ\(.2\%\) chaque année. Si ce taux se maintient, la population de l'Inde dépassera celle de la Chine d'ici 2031. Lorsque la population croît rapidement, nous disons souvent que la croissance est « exponentielle », ce qui signifie que quelque chose croît très rapidement. Pour un mathématicien, toutefois, le terme croissance exponentielle a une signification très spécifique. Dans cette section, nous examinerons les fonctions exponentielles qui modélisent ce type de croissance rapide.
Lors de l'exploration de la croissance linéaire, nous avons observé un taux de variation constant, c'est-à-dire un nombre constant d'augmentation de la production pour chaque augmentation unitaire des intrants. Par exemple, dans l'équation\(f(x)=3x+4\), la pente nous indique que la sortie augmente à\(3\) chaque fois que l'entrée augmente de\(1\). Le scénario de l'exemple de la population indienne est différent car nous avons une variation en pourcentage par unité de temps (plutôt qu'une variation constante) du nombre de personnes.
Définition d'une fonction exponentielle
Une étude a révélé que le pourcentage de la population végétalienne aux États-Unis a doublé entre 2009 et 2011. En 2011,\(2.5\%\) de la population était végétalienne et suivait un régime alimentaire qui ne comprenait aucun produit d'origine animale, sans viande, volaille, poisson, produits laitiers ou œufs. Si ce taux se maintient, les végétaliens constitueront\(10\%\) la population américaine en 2015,\(40\%\) en 2019 et\(80\%\) en 2050.
Que signifie exactement une croissance exponentielle ? Qu'est-ce que le mot double a en commun avec le pourcentage d'augmentation ? Les gens lancent ces mots de façon errante. Ces mots sont-ils utilisés correctement ? Les mots apparaissent certainement fréquemment dans les médias.
- La variation en pourcentage fait référence à une modification basée sur un pourcentage du montant initial.
- La croissance exponentielle fait référence à une augmentation basée sur un taux de variation multiplicatif constant sur des intervalles de temps égaux, c'est-à-dire une augmentation en pourcentage du montant initial au fil du temps.
- La décroissance exponentielle fait référence à une diminution basée sur un taux de variation multiplicatif constant sur des intervalles de temps égaux, c'est-à-dire une diminution en pourcentage de la quantité initiale au fil du temps.
Pour mieux comprendre la croissance exponentielle, comparons la croissance exponentielle à la croissance linéaire. Nous allons créer deux fonctions. La première fonction est exponentielle. Nous allons commencer par une entrée de\(0\), puis augmenter chaque entrée de\(1\). Nous allons doubler les sorties consécutives correspondantes. La deuxième fonction est linéaire. Nous allons commencer par une entrée de\(0\), puis augmenter chaque entrée de\(1\). Nous ajouterons\(2\) aux sorties consécutives correspondantes (Tableau\(\PageIndex{1}\)).
À partir du tableau,\(\PageIndex{1}\) nous pouvons déduire que pour ces deux fonctions, la croissance exponentielle surpasse la croissance linéaire.
- La croissance exponentielle fait référence à la valeur initiale de la plage qui augmente du même pourcentage sur des incréments égaux trouvés dans le domaine.
- La croissance linéaire fait référence à la valeur initiale de la plage qui augmente de la même quantité sur des incréments égaux trouvés dans le domaine.
| \(x\) | \(f(x)=2^x\) | \(g(x)=2x\) |
|---|---|---|
| \ (x \) » style="vertical-align:middle ; « >0 | \ (f (x) =2^x \) » style="vertical-align:middle ; « >1 | \ (g (x) =2x \) » style="vertical-align:middle ; « >0 |
| \ (x \) » style="vertical-align:middle ; « >1 | \ (f (x) =2^x \) » style="vertical-align:middle ; « >2 | \ (g (x) =2x \) » style="vertical-align:middle ; « >2 |
| \ (x \) » style="vertical-align:middle ; ">2 | \ (f (x) =2^x \) » style="vertical-align:middle ; « >4 | \ (g (x) =2x \) » style="vertical-align:middle ; « >4 |
| \ (x \) » style="vertical-align:middle ; « >3 | \ (f (x) =2^x \) » style="vertical-align:middle ; « >8 | \ (g (x) =2x \) » style="vertical-align:middle ; « >6 |
| \ (x \) » style="vertical-align:middle ; « >4 | \ (f (x) =2^x \) » style="vertical-align:middle ; « >16 | \ (g (x) =2x \) » style="vertical-align:middle ; « >8 |
| \ (x \) » style="vertical-align:middle ; « >5 | \ (f (x) =2^x \) » style="vertical-align:middle ; « >32 | \ (g (x) =2x \) » style="vertical-align:middle ; « >10 |
| \ (x \) » style="vertical-align:middle ; « >6 | \ (f (x) =2^x \) » style="vertical-align:middle ; « >64 | \ (g (x) =2x \) » style="vertical-align:middle ; « >12 |
Apparemment, la différence entre « le même pourcentage » et « le même montant » est assez significative. Pour une croissance exponentielle, par incréments égaux, le taux de variation multiplicatif constant a entraîné le doublement de la production chaque fois que l'entrée augmentait d'un. Pour la croissance linéaire, le taux de variation additif constant sur des incréments égaux a entraîné une addition\(2\) à la sortie chaque fois que l'entrée était augmentée d'une unité.
La forme générale de la fonction exponentielle est\(f(x)=ab^x\), où\(a\) est un nombre différent de zéro,\(b\) est un nombre réel positif non égal à\(1\).
- Si\(b>1\), la fonction croît à un rythme proportionnel à sa taille.
- Si\(0<b<1\), la fonction décroît à un rythme proportionnel à sa taille.
Regardons la fonction\(f(x)=2^x\) de notre exemple. Nous allons créer une table (Table\(\PageIndex{2}\)) pour déterminer les sorties correspondantes sur un intervalle dans le domaine de\(−3\) à\(3\).
| \(x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|---|---|---|
| \(f(x)=2^x\) | \(2^{−3}=\dfrac{1}{8}\) | \(2^{−2}=\dfrac{1}{4}\) | \(2^{−1}=\dfrac{1}{2}\) | \(2^0=1\) | \(2^1=2\) | \(2^2=4\) | \(2^3=8\) |
Examinons le graphique de\(f\) en traçant les paires ordonnées à partir du tableau,\(\PageIndex{2}\) puis faisons quelques observations\(\PageIndex{1}\).
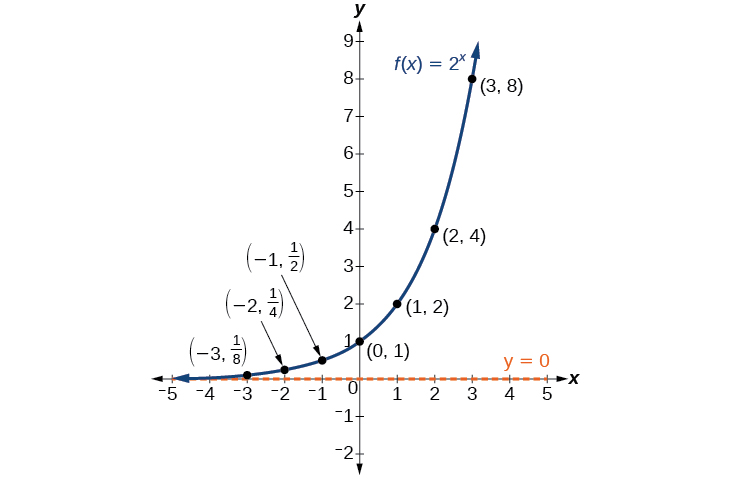
Définissons le comportement du graphe de la fonction exponentielle\(f(x)=2^x\) et soulignons certaines de ses principales caractéristiques.
- le domaine est\((−\infty,\infty)\),
- la gamme est\((0,\infty)\),
- en tant que\(x\rightarrow \infty\)\(f(x)\rightarrow \infty\),
- en tant que\(x\rightarrow −\infty\)\(f(x)\rightarrow 0\),
- \(f(x)\)est en constante augmentation,
- le graphe de ne\(f(x)\) touchera jamais l'axe x car la base deux élevée à un exposant n'a jamais pour résultat zéro.
- \(y=0\)est l'asymptote horizontale.
- l'intersection y est\(1\).
Pour tout nombre réel\(x\), une fonction exponentielle est une fonction de la forme
\[f(x)=ab^x\]
où
- \(a\)est un nombre réel différent de zéro appelé valeur initiale et
- \(b\)est un nombre réel positif tel que\(b≠1\).
- Le domaine de\(f\) ce sont tous des nombres réels.
- La plage de\(f\) est constituée de nombres réels positifs si\(a>0\).
- La plage de\(f\) est composée de tous les nombres réels négatifs si\(a<0\).
- L'intersection y est et\((0,a)\) l'asymptote horizontale est\(y=0\).
Parmi les équations suivantes, lesquelles ne sont pas des fonctions exponentielles ?
- \(f(x)=4^{3(x−2)}\)
- \(g(x)=x^3\)
- \(h(x)=\left(\dfrac{1}{3}\right)^x\)
- \(j(x)=(−2)^x\)
Solution
Par définition, une fonction exponentielle a une constante comme base et une variable indépendante comme exposant. Ainsi,\(g(x)=x^3\) ne représente pas une fonction exponentielle car la base est une variable indépendante. En fait,\(g(x)=x^3\) c'est une fonction de puissance.
Rappelez-vous que la base\(b\) d'une fonction exponentielle est toujours une constante positive, et\(b≠1\). Ainsi,\(j(x)={(−2)}^x\) ne représente pas une fonction exponentielle car la base,\(−2\), est inférieure à\(0\).
Laquelle des équations suivantes représente des fonctions exponentielles ?
- \(f(x)=2x^2−3x+1\)
- \(g(x)={0.875}^x\)
- \(h(x)=1.75x+2\)
- \(j(x)={1095.6}^{−2x}\)
- Réponse
-
\(g(x)={0.875}^x\)et\(j(x)={1095.6}^{−2x}\) représentent des fonctions exponentielles.
Évaluation des fonctions exponentielles
Rappelez-vous que la base d'une fonction exponentielle doit être un nombre réel positif autre que\(1\) .Pourquoi limitons-nous la base bb à des valeurs positives ? Pour s'assurer que les résultats seront des nombres réels. Observez ce qui se passe si la base n'est pas positive :
- Laissez\(b=−9\) et\(x=\dfrac{1}{2}\). Alors\(f(x)=f\left(\dfrac{1}{2}\right)={(−9)}^{\dfrac{1}{2}}=\sqrt{−9}\), ce n'est pas un vrai nombre.
Pourquoi limitons-nous la base à des valeurs positives autres que\(1\) ? Parce que\(1\) la base aboutit à la fonction constante. Observez ce qui se passe si la base est\(1\) :
- Laissez\(b=1\). Ensuite,\(f(x)=1^x=1\) pour n'importe quelle valeur de\(x\).
Pour évaluer une fonction exponentielle avec la forme\(f(x)=b^x\), il suffit de la remplacer\(x\) par la valeur donnée et de calculer la puissance résultante. Par exemple :
Laissez\(f(x)=2^x\). Qu'est-ce que\(f(3)\) ?
\[\begin{align*} f(x)&= 2^x\\ f(3)&= 2^3 \qquad \text{Substitute } x=3\\ &= 8 \qquad \text{Evaluate the power} \end{align*}\]
Pour évaluer une fonction exponentielle avec une forme autre que la forme de base, il est important de suivre l'ordre des opérations. Par exemple :
Laissez\(f(x)=30{(2)}^x\). Qu'est-ce que\(f(3)\) ?
\[\begin{align*} f(x)&= 30{(2)}^x\\ f(3)&= 30{(2)}^3 \qquad \text{Substitute } x=3\\ &= 30(8) \qquad \text{Simplify the power first}\\ &= 240 \qquad \text{Multiply} \end{align*}\]
Notez que si l'ordre des opérations n'était pas respecté, le résultat serait incorrect :
\[f(3)=30{(2)}^3≠{60}^3=216,000 \nonumber\]
Laissez\(f(x)=5{(3)}^{x+1}\). Évaluez\(f(2)\) sans utiliser de calculatrice.
Solution
Suivez l'ordre des opérations. Veillez à faire attention aux parenthèses.
\[\begin{align*} f(x)&= 5{(3)}^{x+1}\\ f(2)&= 5{(3)}^{2+1} \qquad \text{Substitute } x=2\\ &= 5{(3)}^3 \qquad \text{Add the exponents}\\ &= 5(27) \qquad \text{Simplify the power}\\ &= 135 \qquad \text{Multiply} \end{align*}\]
Laissez\(f(x)=8{(1.2)}^{x−5}\). Évaluez\(f(3)\) en utilisant une calculatrice. Arrondir à quatre décimales.
- Réponse
-
\(5.5556\)
Définition de la croissance exponentielle
Comme le résultat des fonctions exponentielles augmente très rapidement, le terme « croissance exponentielle » est souvent utilisé dans le langage courant pour décrire tout ce qui croît ou augmente rapidement. Cependant, la croissance exponentielle peut être définie plus précisément d'un point de vue mathématique. Si le taux de croissance est proportionnel à la quantité présente, la fonction modélise une croissance exponentielle.
Une fonction qui modélise la croissance exponentielle croît à un taux proportionnel à la quantité présente. Pour tout nombre réel\(x\) et tout nombre réel positif\(a\) et\(b\) tel que\(b≠1\), une fonction de croissance exponentielle a la forme
\[f(x)=ab^x\]
où
- \(a\)est la valeur initiale ou de départ de la fonction.
- \(b\)est le facteur de croissance ou le multiplicateur de croissance par unité\(x\).
De manière plus générale, nous avons une fonction exponentielle, dans laquelle une base constante est élevée à un exposant variable. Pour différencier les fonctions linéaires des fonctions exponentielles, considérons deux entreprises, A et B. La société A possède des\(100\) magasins et s'agrandit en ouvrant de\(50\) nouveaux magasins par an, de sorte que sa croissance puisse être représentée par la fonction\(A(x)=100+50x\). L'entreprise B possède\(100\) des magasins et s'agrandit en augmentant le nombre de magasins\(50\%\) chaque année, de sorte que sa croissance peut être représentée par la fonction\(B(x)=100{(1+0.5)}^x\).
Quelques années de croissance pour ces entreprises sont illustrées dans le tableau\(\PageIndex{3}\).
| Année,\(x\) | Boutiques, Entreprise A | Boutiques, Entreprise B |
|---|---|---|
| \ (x \) « >\(0\) | \(100+50(0)=100\) | \(100{(1+0.5)}^0=100\) |
| \ (x \) « >\(1\) | \(100+50(1)=150\) | \(100{(1+0.5)}^1=150\) |
| \ (x \) « >\(2\) | \(100+50(2)=200\) | \(100{(1+0.5)}^2=225\) |
| \ (x \) « >\(3\) | \(100+50(3)=250\) | \(100{(1+0.5)}^3=337.5\) |
| \ (x \) « >\(x\) | \(A(x)=100+50x\) | \(B(x)=100{(1+0.5)}^x\) |
Les graphiques comparant le nombre de magasins pour chaque entreprise sur une période de cinq ans sont présentés dans la figure\(\PageIndex{2}\). On constate qu'avec une croissance exponentielle, le nombre de magasins augmente beaucoup plus rapidement qu'avec une croissance linéaire.
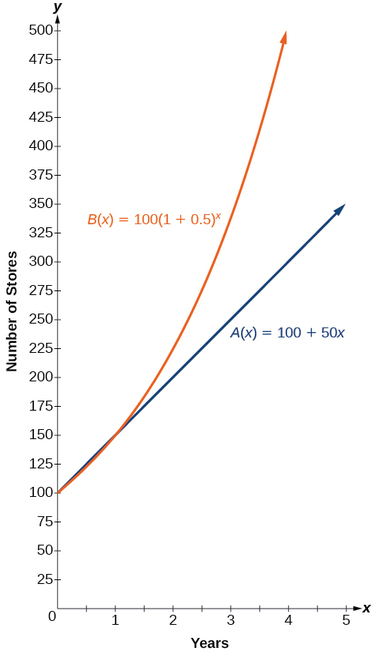
Notez que le domaine des deux fonctions est\([0,\infty)\) et que la plage des deux fonctions est\([100,\infty)\). Après la première année, l'entreprise B compte toujours plus de magasins que la société A.
Nous allons maintenant porter notre attention sur la fonction représentant le nombre de magasins pour Company\(B\),\(B(x)=100{(1+0.5)}^x\). Dans cette fonction exponentielle,\(100\) représente le nombre initial de magasins,\(0.50\) représente le taux de croissance et\(1+0.5=1.5\) représente le facteur de croissance. En généralisant davantage, nous pouvons écrire cette fonction comme\(B(x)=100{(1.5)}^x\) suit : où\(100\)\(1.5\) est la valeur initiale, est appelée base et\(x\) est appelée exposant.
Au début de cette section, nous avons appris que la population de l'Inde était d'environ un\(1.25\) milliard d'habitants en 2013, avec un taux de croissance annuel d'environ\(1.2\%\). Cette situation est représentée par la fonction de croissance\(P(t)=1.25{(1.012)}^t\), où\(t\) est le nombre d'années écoulées depuis 2013. Au millième près, quelle sera la population de l'Inde en 2031 ?
Solution
Pour estimer la population en 2031, nous évaluons les modèles pour\(t=18\), car 2031 se situe des\(18\) années après 2013. En arrondissant au millième le plus proche,
\[P(18)=1.25{(1.012)}^{18}≈1.549 \nonumber\]
Il y aura environ un\(1.549\) milliard de personnes en Inde en 2031.
La population de la Chine était\(1.39\) d'environ un milliard en 2013, avec un taux de croissance annuel d'environ\(0.6\%\). Cette situation est représentée par la fonction de croissance\(P(t)=1.39{(1.006)}^t\), où\(t\) est le nombre d'années écoulées depuis 2013. Au millième près, quelle sera la population de la Chine en 2031 ? Comment cela se compare-t-il à la prévision démographique que nous avons faite pour l'Inde dans Example\(\PageIndex{3}\) ?
- Réponse
-
Environ un\(1.548\) milliard de personnes ; d'ici 2031, la population de l'Inde dépassera celle de la Chine d'environ un\(0.001\) milliard, voire un\(1\) million de personnes.
Trouver des équations de fonctions exponentielles
Dans les exemples précédents, on nous a donné une fonction exponentielle, que nous avons ensuite évaluée pour une entrée donnée. Parfois, on nous donne des informations sur une fonction exponentielle sans la connaître explicitement. Nous devons utiliser les informations pour d'abord écrire la forme de la fonction, puis déterminer les constantes\(a, a\) et\(b, b\) évaluer la fonction.
- Si l'un des points de données possède la forme\((0,a)\), il\(a\) s'agit de la valeur initiale. En utilisant\(a\), remplacez le deuxième point dans l'équation\(f(x)=a{(b)}^x\) et résolvez pour\(b\).
- Si aucun des points de données n'a la forme\((0,a)\), remplacez les deux points en deux équations à l'aide de la forme\(f(x)=a{(b)}^x\). Résolvez le système résultant de deux équations dans deux inconnues pour trouver\(a\) et\(b\).
- En utilisant le\(a\) et\(b\) trouvé dans les étapes ci-dessus, écrivez la fonction exponentielle dans le formulaire\(f(x)=a{(b)}^x\).
En 2006, des\(80\) cerfs ont été introduits dans un refuge faunique. En 2012, la population était devenue des\(180\) cerfs. La population augmentait de façon exponentielle. Écrivez une fonction algébrique\(N(t)\) représentant la population\((N)\) de cerfs au fil du temps\(t\).
Solution
Nous avons laissé notre variable indépendante\(t\) être le nombre d'années après 2006. Ainsi, les informations données dans le problème peuvent être écrites sous forme de paires d'entrées-sorties : (0, 80) et (6, 180). Notez qu'en choisissant notre variable d'entrée à mesurer les années après 2006, nous nous sommes donné la valeur initiale de la fonction,\(a=80\). Nous pouvons maintenant remplacer le deuxième point de l'équation\(N(t)=80b^t\) pour trouver\(b\) :
\[\begin{align*} N(t)&= 80b^t\\ 180&= 80b^6 \qquad \text{Substitute using point } (6, 180)\\ \dfrac{9}{4}&= b^6 \qquad \text{Divide and write in lowest terms}\\ b&= {\left (\dfrac{9}{4} \right )}^{\tfrac{1}{6}} \qquad \text{Isolate b using properties of exponents}\\ b&\approx 1.1447 \qquad \text{Round to 4 decimal places} \end{align*}\]
Sauf indication contraire, n'arrondissez aucun calcul intermédiaire. Ensuite, arrondissez la réponse finale à quatre places pour le reste de cette section.
Le modèle exponentiel de la population de cerfs est\(N(t)=80{(1.1447)}^t\). (Notez que cette fonction exponentielle modélise la croissance à court terme. À mesure que les entrées deviennent volumineuses, la sortie augmente de plus en plus, à tel point que le modèle peut ne pas être utile à long terme.)
Nous pouvons représenter graphiquement notre modèle pour observer la croissance de la population de cerfs dans le refuge au fil du temps. Notez que le graphique de la figure\(\PageIndex{3}\) passe par les points initiaux indiqués dans le problème,\((0, 80)\) et\((6, 180)\). Nous pouvons également voir que le domaine de la fonction est\([0,\infty)\) et que la plage de la fonction est\([80,\infty)\).
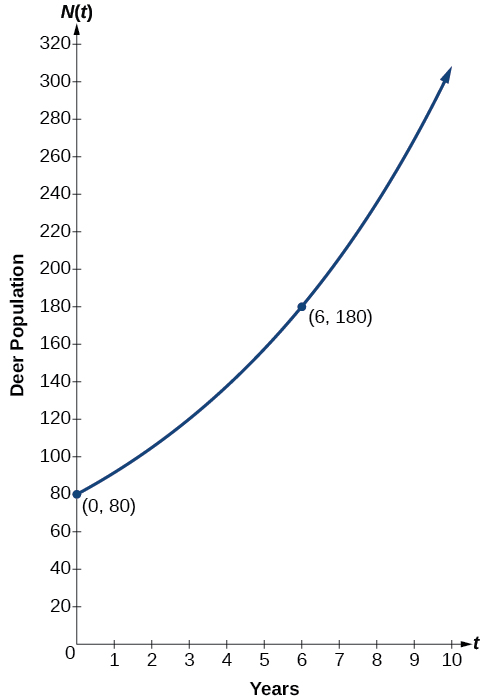
La population de loups croît de façon exponentielle. En 2011, les\(129\) loups ont été recensés. En 2013, la population avait atteint\(236\) les loups. Quels sont les deux points qui peuvent être utilisés pour dériver une équation exponentielle modélisant cette situation ? Écrivez l'équation représentant la population\(N\) de loups au fil du temps\(t\).
- Réponse
-
\((0,129)\)et\((2,236)\) ;\(N(t)=129{(1.3526)}^t\)
Trouvez une fonction exponentielle qui passe par les points\((−2,6)\) et\((2,1)\).
Solution
Comme nous n'avons pas la valeur initiale, nous substituons les deux points dans une équation de la forme\(f(x)=ab^x\), puis nous résolvons le système pour\(a\) et\(b\).
- La substitution\((−2,6)\) donne\(6=ab^{−2}\)
- La substitution\((2,1)\) donne\(1=ab^2\)
Utilisez la première équation à résoudre\(a\) en termes de\(b\) :
\[\begin{align*} 6&= ab^{-2}\\ \dfrac{6}{b^{-2}}&= a \qquad \text{Divide}\\ a&= 6b^2 \qquad \text{Use properties of exponents to rewrite the denominator} \end{align*}\]
Substituez a dans la deuxième équation et résolvez pour\(b\) :
\[\begin{align*} 1&= ab^{2}\\ 1&= 6b^2 b^2\\ &= 6b^4 \qquad \text{Substitute a}\\ b&= \left (\dfrac{1}{6} \right )^{\tfrac{1}{4}} \qquad \text{Round 4 decimal places rewrite the denominator}\\ b&\approx 0.6389 \end{align*}\]
Utilisez la valeur de\(b\) dans la première équation pour obtenir la valeur de\(a\) :
\[\begin{align*} a&= 6b^{2}\\ &\approx 6(0.6389)^2 \\ &\approx 2.4492 \end{align*}\]
Ainsi, l'équation est\(f(x)=2.4492{(0.6389)}^x\).
Nous pouvons représenter graphiquement notre modèle pour vérifier notre travail. Notez que le graphique de la figure\(\PageIndex{4}\) passe par les points initiaux indiqués dans le problème,\((−2, 6)\) et\((2, 1)\). Le graphique est un exemple de fonction de décroissance exponentielle.
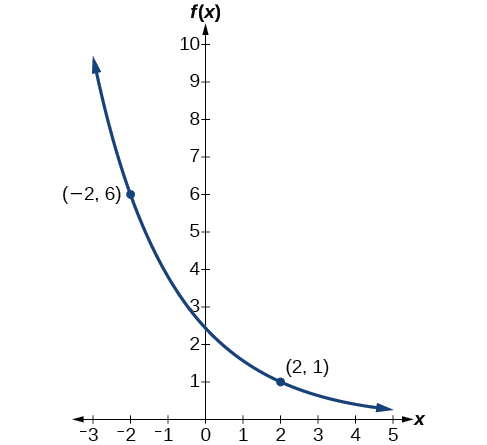
Étant donné les deux points\((1,3)\) et\((2,4.5)\), trouvez l'équation de la fonction exponentielle qui passe par ces deux points.
- Réponse
-
\(f(x)=2{(1.5)}^x\)
Oui, à condition que les deux points se trouvent soit au-dessus de l'axe X, soit en dessous de l'axe X et qu'ils aient des coordonnées X différentes. Mais gardez à l'esprit que nous devons également savoir que le graphique est en fait une fonction exponentielle. Tous les graphes qui semblent exponentiels ne le sont pas vraiment. Nous devons savoir que le graphique est basé sur un modèle qui montre le même pourcentage de croissance pour chaque unité d'augmentation\(x\), ce qui, dans de nombreux cas réels, implique du temps.
- Tout d'abord, identifiez deux points sur le graphique. Choisissez le\(y\) -intercept comme l'un des deux points autant que possible. Essayez de choisir des points aussi éloignés que possible afin de réduire les erreurs d'arrondi.
- Si l'un des points de données est le\(y\) -intercept\((0,a)\), il\(a\) s'agit de la valeur initiale. En utilisant\(a\), remplacez le deuxième point dans l'équation\(f(x)=a{(b)}^x\) et résolvez pour\(b\)
- Si aucun des points de données n'a la forme\((0,a)\), remplacez les deux points en deux équations à l'aide de la forme\(f(x)=a{(b)}^x\). Résolvez le système résultant de deux équations dans deux inconnues pour trouver\(a\) et\(b\).
- Écrivez la fonction exponentielle,\(f(x)=a{(b)}^x\).
Trouvez une équation pour la fonction exponentielle illustrée dans la figure\(\PageIndex{5}\).
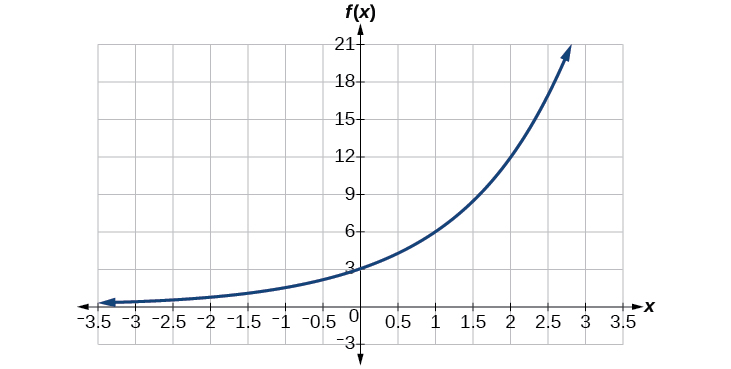
Solution
Nous pouvons choisir l'\(y\)intersection du graphe,\((0,3)\), comme premier point. Cela nous donne la valeur initiale,\(a=3\). Ensuite, choisissez un point de la courbe situé à une certaine distance et\((0,3)\) qui possède des coordonnées entières. L'un de ces points est\((2,12)\).
\[\begin{align*} y&= ab^x \qquad \text{Write the general form of an exponential equation}\\ y&= 3b^x \qquad \text{Substitute the initial value } 3 \text{ for } a\\ 12&= 3b^2 \qquad \text{Substitute in 12 for } y \text{ and } 2 \text{ for } x\\ 4&= b^2 \qquad \text{Divide by }3\\ b&= \pm 2 \qquad \text{Take the square root} \end{align*}\]
Parce que nous nous limitons à des valeurs positives de\(b\), nous utiliserons\(b=2\). Remplacez\(a\) et\(b\) dans le formulaire standard pour obtenir l'équation\(f(x)=3{(2)}^x\).
Trouvez une équation pour la fonction exponentielle illustrée dans la figure\(\PageIndex{6}\).
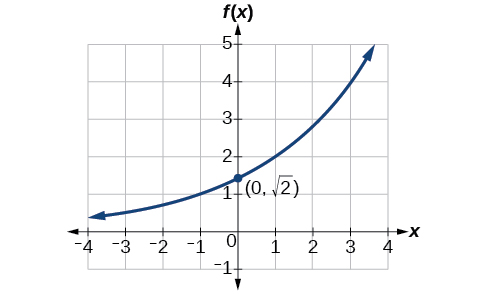
- Réponse
-
\(f(x)=\sqrt{2}{(\sqrt{2})}^x\). Les réponses peuvent varier en raison d'une erreur d'arrondi. La réponse devrait être très proche de\(1.4142{(1.4142)}^x\).
- Appuyez sur [STAT].
- Effacez toutes les entrées existantes dans les colonnes L1 ou L2.
- Dans L1, entrez les coordonnées x données.
- Dans L2, entrez les coordonnées y correspondantes.
- Appuyez de nouveau sur [STAT]. Passez le curseur vers la droite sur CALC, faites défiler l'écran vers le bas jusqu'à ExPreg (régression exponentielle) et appuyez sur [ENTER].
- L'écran affiche les valeurs de a et b dans l'équation exponentielle\(y=a⋅b^x\).
Utilisez une calculatrice graphique pour trouver l'équation exponentielle qui inclut les points\((2,24.8)\) et\((5,198.4)\).
Solution
Suivez les directives ci-dessus. Appuyez d'abord sur [STAT], [EDIT], [1 : Modifier...] et effacez les listes L1 et L2. Ensuite, dans la colonne L1, entrez les\(x\) coordonnées\(2\) et\(5\). Faites de même dans la colonne L2 pour les\(y\) coordonnées,\(24.8\) et\(198.4\).
Appuyez maintenant sur [STAT], [CALC], [0 : ExPreg] et appuyez sur [ENTER]. Les valeurs\(a=6.2\) et\(b=2\) seront affichées. L'équation exponentielle est\(y=6.2⋅2^x\).
Utilisez une calculatrice graphique pour trouver l'équation exponentielle qui inclut les points\((3, 75.98)\) et\((6, 481.07)\).
- Réponse
-
\(y≈12⋅{1.85}^x\)
Application de la formule des intérêts composés
Les instruments d'épargne dans lesquels les bénéfices sont continuellement réinvestis, tels que les fonds communs de placement et les comptes de retraite, utilisent des intérêts composés. Le terme composition fait référence aux intérêts perçus non seulement sur la valeur initiale, mais aussi sur la valeur cumulée du compte.
Le taux annuel en pourcentage (TAEG) d'un compte, également appelé taux nominal, est le taux d'intérêt annuel gagné par un compte de placement. Le terme nominal est utilisé lorsque la composition a lieu un certain nombre de fois, sauf une fois par an. En fait, lorsque l'intérêt est composé plus d'une fois par an, le taux d'intérêt effectif finit par être supérieur au taux nominal ! Il s'agit d'un outil puissant pour investir.
Nous pouvons calculer l'intérêt composé à l'aide de la formule des intérêts composés, qui est une fonction exponentielle des variables temps\(t\)\(P\)\(APR\)\(r\), principal et nombre de périodes composées au cours d'une année\(n\) :
\[A(t)=P{\left (1+\dfrac{r}{n} \right )}^{nt} \nonumber\]
Par exemple, observez le tableau\(\PageIndex{4}\), qui montre le résultat d'un investissement\($1,000\)\(10\%\) pendant un an. Remarquez comment la valeur du compte augmente à mesure que la fréquence de composition augmente.
| Fréquence | Valeur après\(1\) année |
|---|---|
| Annuellement | \ (1 \) an">\($1100\) |
| Semestriellement | \ (1 \) an">\($1102.50\) |
| trimestriel | \ (1 \) an">\($1103.81\) |
| mensuel | \ (1 \) an">\($1104.71\) |
| Au quotidien | \ (1 \) an">\($1105.16\) |
L'intérêt composé peut être calculé à l'aide de la formule
\[A(t)=P{\left (1+\dfrac{r}{n} \right )}^{nt}\]
où
- \(A(t)\)est la valeur du compte,
- \(t\)est mesuré en années,
- \(P\)est le montant de départ du compte, souvent appelé principal, ou plus généralement la valeur actuelle,
- \(r\)est le taux annuel en pourcentage (TAEG) exprimé sous forme décimale, et
- \(n\)est le nombre de périodes de composition au cours d'une année.
Si nous investissons\($3,000\) dans un compte de placement payant des\(3\%\) intérêts composés tous les trimestres, quelle sera la valeur du compte en\(10\) années ?
Solution
Parce que nous commençons par\($3,000\),\(P=3000\). Notre taux d'intérêt est\(3\%\) donc\(r = 0.03\). Comme nous composons tous les trimestres, nous calculons des\(4\) fois par an, donc\(n=4\). Nous voulons connaître la valeur du compte en\(10\) années, c'est pourquoi nous cherchons\(A(10)\) la valeur à quel moment\(t = 10\).
\[\begin{align*} A(t)&= P{\left (1+\dfrac{r}{n} \right )}^{nt} \qquad \text{Use the compound interest formula}\\ A(10)&= 3000{\left (1+\dfrac{0.03}{4} \right )}^{(4)\cdot (10)} \qquad \text{Substitute using given values}\\ &\approx \$4045.05 \qquad \text{Round to two decimal places} \end{align*}\]
Le compte vaudra environ\($4,045.05\) dans des\(10\) années.
Un investissement initial\($100,000\) à\(12\%\) intérêt est composé chaque semaine (utilisez des\(52\) semaines par an). Quelle sera la valeur de l'investissement dans les\(30\) années à venir ?
- Réponse
-
à propos\($3,644,675.88\)
Un plan 529 est un plan d'épargne universitaire qui permet aux proches d'investir de l'argent pour payer les futurs frais de scolarité universitaires d'un enfant ; le compte augmente en franchise d'impôt. Lily souhaite créer un compte 529 pour sa nouvelle petite-fille et souhaite que le compte s'étende au\($40,000\) fil des\(18\) années. Elle croit que le compte rapportera des revenus\(6\%\) composés semestriellement (deux fois par an). Au dollar le plus proche, combien Lily devra-t-elle investir sur le compte maintenant ?
Solution
Le taux d'intérêt nominal est\(6\%\) donc\(r=0.06\). Les intérêts sont composés deux fois par an, donc\(k=2\).
Nous voulons trouver l'investissement initial nécessaire pour que la valeur du compte soit valable\($40,000\) en\(18\) années.\(P\) Substituez les valeurs données dans la formule des intérêts composés et résolvez pour\(P\).
\[\begin{align*} A(t)&= P{\left (1+\dfrac{r}{n} \right )}^{nt} \qquad \text{Use the compound interest formula}\\ 40,000&= P{\left (1+\dfrac{0.06}{2} \right )}^{2(18)} \qquad \text{Substitute using given values } A, r, n, t\\ 40,000&= P{(1.03)}^{36} \qquad \text{Simplify}\\ \dfrac{40,000}{ {(1.03)}^{36} }&= P \qquad \text{Isolate } P\\ P&\approx \$13,801 \qquad \text{Divide and round to the nearest dollar} \end{align*}\]
Lily devra investir pour\($13,801\) l'avoir\(18\) depuis\($40,000\) des années.
Reportez-vous à l'exemple\(\PageIndex{9}\). Au dollar le plus proche, combien Lily devrait-elle investir si le compte est composé tous les trimestres ?
- Réponse
-
\($13,693\)
Évaluation des fonctions avec Base\(e\)
Comme nous l'avons vu précédemment, le montant gagné sur un compte augmente à mesure que la fréquence de composition augmente. Le tableau\(\PageIndex{5}\) montre que l'augmentation de la composition annuelle à la composition semestrielle est plus importante que l'augmentation de la composition mensuelle à la composition quotidienne. Cela peut nous amener à nous demander si cette tendance va se poursuivre.
Examinez la valeur de l'\($1\)investissement avec\(100\%\) intérêt pour\(1\) l'année, composée à différentes fréquences, répertoriées dans le tableau\(\PageIndex{5}\).
| Fréquence | \(A(t)={\left (1+\dfrac{1}{n} \right )}^n\) | Valeur |
|---|---|---|
| Annuellement | \ (A (t) = {\ left (1+ \ dfrac {1} {n} \ right)} ^n \) » style="vertical-align:middle ; « >\({\left (1+\dfrac{1}{1} \right )}^1\) | \($2\) |
| Semestriellement | \ (A (t) = {\ left (1+ \ dfrac {1} {n} \ right)} ^n \) » style="vertical-align:middle ; « >\({\left (1+\dfrac{1}{2} \right )}^2\) | \($2.25\) |
| trimestriel | \ (A (t) = {\ left (1+ \ dfrac {1} {n} \ right)} ^n \) » style="vertical-align:middle ; « >\({\left (1+\dfrac{1}{4} \right )}^4\) | \($2.441406\) |
| mensuel | \ (A (t) = {\ left (1+ \ dfrac {1} {n} \ right)} ^n \) » style="vertical-align:middle ; « >\({\left (1+\dfrac{1}{12} \right )}^{12}\) | \($2.613035\) |
| Au quotidien | \ (A (t) = {\ left (1+ \ dfrac {1} {n} \ right)} ^n \) » style="vertical-align:middle ; « >\({\left (1+\dfrac{1}{365} \right )}^{365}\) | \($2.714567\) |
| Horaire | \ (A (t) = {\ left (1+ \ dfrac {1} {n} \ right)} ^n \) » style="vertical-align:middle ; « >\({\left (1+\dfrac{1}{8760} \right )}^{8760}\) | \($2.718127\) |
| Une fois par minute | \ (A (t) = {\ left (1+ \ dfrac {1} {n} \ right)} ^n \) » style="vertical-align:middle ; « >\({\left (1+\dfrac{1}{525600} \right )}^{525600}\) | \($2.718279\) |
| Une fois par seconde | \ (A (t) = {\ left (1+ \ dfrac {1} {n} \ right)} ^n \) » style="vertical-align:middle ; « >\({\left (1+\dfrac{1}{31536000} \right )}^{31536000}\) | \($2.718282\) |
Ces valeurs semblent s'approcher d'une limite à mesure qu'elles\(n\) augmentent sans limite. En fait, au\(n\) fur et à mesure qu'elle grandit, l'expression se\({\left (1+\dfrac{1}{n} \right )}^n\) rapproche d'un nombre si fréquemment utilisé en mathématiques qu'elle porte son propre nom : la lettre\(e\). Cette valeur est un nombre irrationnel, ce qui signifie que son expansion décimale se poursuit indéfiniment sans se répéter. Son approximation à six décimales est indiquée ci-dessous.
La lettre\(e\) représente le nombre irrationnel
\[{\left (1+\dfrac{1}{n} \right )}^n\]
sous forme\(n\) d'augmentations sans limite
La lettre\(e\) est utilisée comme base pour de nombreux modèles exponentiels du monde réel. Pour travailler avec la base\(e\), nous utilisons l'approximation,\(e≈2.718282\). La constante a été nommée par le mathématicien suisse Leonhard Euler (1707—1783) qui a d'abord étudié et découvert bon nombre de ses propriétés.
Calculez\(e^{3.14}\). Arrondir à cinq décimales.
Solution
Sur une calculatrice, appuyez sur le bouton étiqueté\([e^x]\). La fenêtre s'affiche\([e {}^( ]\). Tapez\(3.14\) puis fermez les parenthèses,\([)]\). Appuyez sur [ENTER]. En arrondissant à la\(5\) décimale,\(e^{3.14}≈23.10387\). Attention : De nombreuses calculatrices scientifiques possèdent un bouton « Exp », qui permet de saisir des nombres en notation scientifique. Il n'est pas utilisé pour trouver des pouvoirs de\(e\).
Utilisez une calculatrice pour trouver\(e^{−0.5}\). Arrondir à cinq décimales.
- Réponse
-
\(e^{−0.5}≈0.60653\)
Étudier la croissance continue
Jusqu'à présent, nous avons travaillé avec des bases rationnelles pour les fonctions exponentielles. Pour la plupart des phénomènes du monde réel,\(e\) il est toutefois utilisé comme base pour les fonctions exponentielles. Les modèles exponentiels utilisés\(e\) comme base sont appelés modèles de croissance continue ou de décroissance. Nous voyons ces modèles dans les domaines de la finance, de l'informatique et de la plupart des sciences, telles que la physique, la toxicologie et la dynamique des fluides.
Pour tous les nombres\(t\) réels et tous les nombres positifs\(a\) et\(r\), la croissance ou la décroissance continue est représentée par la formule
\[A(t)=ae^{rt}\]
où
- \(a\)est la valeur initiale,
- \(r\)est le taux de croissance continu par unité de temps,
- \(t\)est le temps écoulé.
Si\(r>0\), alors la formule représente une croissance continue. Si\(r<0\), alors la formule représente une décroissance continue.
Pour les applications commerciales, la formule de croissance continue est appelée formule de composition continue et prend la forme
\[A(t)=Pe^{rt}\]
où
- \(P\)est le capital ou le capital initial investi,
- \(r\)est la croissance ou le taux d'intérêt par unité de temps,
- \(t\)est la période ou la durée de l'investissement.
- Utilisez les informations du problème pour déterminer\(a\) la valeur initiale de la fonction.
- Utilisez les informations du problème pour déterminer le taux de croissance\(r\).
- Si le problème fait référence à une croissance continue, alors\(r>0\).
- Si le problème fait référence à une décroissance continue, alors\(r<0\).
- Utilisez les informations du problème pour déterminer l'heure\(t\).
- Remplacez les informations fournies dans la formule de croissance continue et résolvez pour\(A(t)\).
Une personne qui a investi\($1,000\) dans un compte gagnant un montant nominal\(10\%\) par an composé de façon continue. Quel était le montant du compte à la fin d'un an ?
Solution
Comme la valeur du compte augmente, il s'agit d'un problème continu qui s'ajoute au taux de croissance\(r=0.10\). L'investissement initial l'était\($1,000\), donc\(P=1000\). Nous utilisons la formule de composition continue pour déterminer la valeur après\(t=1\) année :
\[\begin{align*} A(t)&= Pe^{rt} \qquad \text{Use the continuous compounding formula}\\ &= 1000{(e)}^{0.1} \qquad \text{Substitute known values for } P, r, t\\ &\approx 1105.17 \qquad \text{Use a calculator to approximate} \end{align*}\]
Le compte vaut au\($1,105.17\) bout d'un an.
Une personne investit\($100,000\) à un taux d'\(12\%\)intérêt nominal par an composé de façon continue. Quelle sera la valeur de l'investissement dans les\(30\) années à venir ?
- Réponse
-
\($3,659,823.44\)
\(Radon-222\)se décompose à un rythme continu de\(17.3\%\) par jour. À quel point se\(100 mg\)\(Radon-222\) décomposera en\(3\) quelques jours ?
Solution
Comme la substance se décompose, le taux est négatif.\(17.3\%\) Donc,\(r = −0.173\). La quantité initiale de\(Radon-222\) était de\(100\) mg, donc\(a=100\). Nous utilisons la formule de décroissance continue pour trouver la valeur après\(t=3\) quelques jours :
\[\begin{align*} A(t)&= ae^{rt} \qquad \text{Use the continuous growth formula}\\ &= 100e6{-0.173(3)} \qquad \text{Substitute known values for } a, r, t\\ &\approx 59.5115 \qquad \text{Use a calculator to approximate} \end{align*}\]
Il\(59.5115\) en\(Radon-222\) restera donc beaucoup.
En utilisant les données de l'exemple\(\PageIndex{12}\), combien\(Radon-222\) restera-t-il après un an ?
- Réponse
-
\(3.77E-26\)(Il s'agit d'une notation calculatrice pour le nombre écrit comme\(3.77×10^{−26}\) en notation scientifique. Bien que la sortie d'une fonction exponentielle ne soit jamais nulle, ce nombre est si proche de zéro que, pour toutes raisons pratiques, nous pouvons accepter zéro comme réponse.)
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires grâce à des fonctions exponentielles.
- Fonction de croissance exponentielle
- Intérêt composé
Équations clés
| définition de la fonction exponentielle | \(f(x)=b^x\), où\(b>0\),\(b≠1\) |
| définition de la croissance exponentielle | \(f(x)=ab^x\), où\(a>0\)\(b>0\),\(b≠1\) |
| formule d'intérêt composé |
\(A(t)=P{(1+\dfrac{r}{n})}^{nt}\), où\(A(t)\) est la valeur du compte au moment\(t\) \(t\)est le nombre d'années \(P\)est l'investissement initial, souvent appelé capital \(r\)est le taux annuel en pourcentage (TAEG), ou taux nominal \(n\)est le nombre de périodes de composition au cours d'une année |
| formule de croissance continue | \(A(t)=ae^{rt}\), où\(t\) est le nombre de périodes unitaires de croissance\(a\) est la quantité de départ (dans la formule de composition continue\(P\), a est remplacé par le principal)\(e\) est la constante mathématique,\(e≈2.718282\) |
Concepts clés
- Une fonction exponentielle est définie comme une fonction dont la constante positive n'est pas\(1\) élevée à un exposant variable. Voir l'exemple.
- Une fonction est évaluée en la résolvant à une valeur spécifique. Voir Exemple et Exemple.
- Un modèle exponentiel peut être trouvé lorsque le taux de croissance et la valeur initiale sont connus. Voir l'exemple.
- Un modèle exponentiel peut être trouvé lorsque les deux points de données du modèle sont connus. Voir l'exemple.
- Un modèle exponentiel peut être trouvé à l'aide de deux points de données du graphique du modèle. Voir l'exemple.
- Un modèle exponentiel peut être trouvé à l'aide de deux points de données du graphique et d'une calculatrice. Voir l'exemple.
- La valeur d'un compte\(t\) peut être calculée à tout moment à l'aide de la formule d'intérêt composé lorsque le principal, le taux d'intérêt annuel et les périodes de composition sont connus. Voir l'exemple.
- L'investissement initial d'un compte peut être déterminé à l'aide de la formule d'intérêt composé lorsque la valeur du compte, le taux d'intérêt annuel, les périodes composées et la durée de vie du compte sont connus. Voir l'exemple.
- Le nombre\(e\) est une constante mathématique souvent utilisée comme base des modèles de croissance et de décroissance exponentiels du monde réel. Son approximation décimale est\(e≈2.718282\).
- Les calculatrices scientifiques et graphiques ont la clé\([ex]\) ou\([exp(x)]\) pour calculer des puissances de\(e\). Voir l'exemple.
- Les modèles de croissance ou de décroissance continue sont des modèles exponentiels qui\(e\) servent de base. Des modèles de croissance et de décroissance continues peuvent être trouvés lorsque la valeur initiale et le taux de croissance ou de décroissance sont connus. Voir Exemple et Exemple.


