5.1 : Fonctions quadratiques

Last updated
Save as PDF

Page ID: 195550

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Reconnaître les caractéristiques des paraboles.
Comprenez comment le graphe d'une parabole est lié à sa fonction quadratique.
Déterminez la valeur minimale ou maximale d'une fonction quadratique.
Résolvez les problèmes liés à la valeur minimale ou maximale d'une fonction quadratique.

Les antennes incurvées, telles que celles illustrées sur la figure$\PageIndex{1}$, sont couramment utilisées pour focaliser les micro-ondes et les ondes radio afin de transmettre des signaux de télévision et téléphoniques, ainsi que des communications par satellite et par satellite. La section transversale de l'antenne a la forme d'une parabole, qui peut être décrite par une fonction quadratique.

$Antennes paraboliques$

Figure$\PageIndex{1}$ : Un ensemble d'antennes paraboliques. (crédit : Matthew Colvin de Valle, Flickr)

Dans cette section, nous étudierons les fonctions quadratiques, qui modélisent fréquemment des problèmes impliquant la zone et le mouvement du projectile. Travailler avec des fonctions quadratiques peut être moins complexe que travailler avec des fonctions de degré supérieur. Elles constituent donc une bonne opportunité pour une étude détaillée du comportement des fonctions.

Reconnaître les caractéristiques des paraboles

Le graphe d'une fonction quadratique est une courbe en U appelée parabole. Une caractéristique importante du graphe est qu'il possède un point extrême, appelé sommet. Si la parabole s'ouvre, le sommet représente le point le plus bas du graphique, ou la valeur minimale de la fonction quadratique. Si la parabole s'ouvre vers le bas, le sommet représente le point le plus élevé du graphique, ou la valeur maximale. Dans les deux cas, le sommet est un point tournant sur le graphique. Le graphique est également symétrique par rapport à une ligne verticale tracée à travers le sommet, appelée axe de symétrie. Ces fonctionnalités sont illustrées dans la figure$\PageIndex{2}$.

alt — Figure$\PageIndex{2}$ : Graphique d'une parabole montrant où se trouvent les$y$ points d'intersection$x$ et, le sommet et l'axe de symétrie.

L'intersection y est le point où la parabole traverse l'$y$axe. Les points d'intersection X sont les points auxquels la parabole traverse l'$x$axe. S'ils existent, les intercepts X représentent les zéros, ou racines, de la fonction quadratique, dont les valeurs sont$y=0$.$x$

Exemple$\PageIndex{1}$: Identifying the Characteristics of a Parabola

Déterminez le sommet, l'axe de symétrie, les zéros et l'intersection y de la parabole illustrée à la figure$\PageIndex{3}$.

Graphique d'une parabole avec un sommet à (3, 1) et une intersection y à (0, 7). — Chiffre$\PageIndex{3}$.

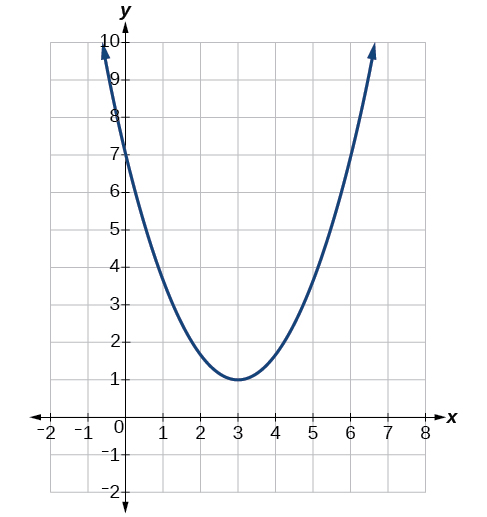
Solution

Le sommet est le point tournant du graphe. Nous pouvons voir que le sommet est à$(3,1)$. Comme cette parabole s'ouvre vers le haut, l'axe de symétrie est la ligne verticale qui coupe la parabole au sommet. Donc, l'axe de symétrie est$x=3$. Cette parabole ne traverse pas l'axe X, elle ne comporte donc pas de zéros. Il traverse l'$y$axe -en$(0,7)$, donc c'est l'intersection Y.

Comprendre comment les graphes des paraboles sont liés à leurs fonctions quadratiques

La forme générale d'une fonction quadratique présente la fonction sous la forme

\[f(x)=ax^2+bx+c\]

où$a$$b$, et$c$ sont des nombres réels et$a{\neq}0$. Si$a>0$, la parabole s'ouvre vers le haut. Si$a<0$, la parabole s'ouvre vers le bas. Nous pouvons utiliser la forme générale d'une parabole pour trouver l'équation de l'axe de symétrie.

L'axe de symétrie est défini par$x=−\frac{b}{2a}$. Si nous utilisons la formule quadratique$x=\frac{−b{\pm}\sqrt{b^2−4ac}}{2a}$,$ax^2+bx+c=0$ pour résoudre les points d'intersection X, ou zéros, nous trouvons que la valeur de la$x$ moitié entre eux est toujours$x=−\frac{b}{2a}$, l'équation de l'axe de symétrie.

La figure$\PageIndex{4}$ représente le graphe de la fonction quadratique écrite sous forme générale sous la forme$y=x^2+4x+3$. Sous cette forme$a=1$,$b=4$, et$c=3$. Parce que$a>0$ la parabole s'ouvre vers le haut. L'axe de symétrie est$x=−\frac{4}{2(1)}=−2$. Cela a également du sens car nous pouvons voir sur le graphique que la ligne verticale$x=−2$ divise le graphique en deux. Le sommet se trouve toujours le long de l'axe de symétrie. Pour une parabole qui s'ouvre vers le haut, le sommet se trouve au point le plus bas du graphique, dans ce cas,$(−2,−1)$. Les points d'intersection X, c'est-à-dire les points où la parabole croise l'axe des abscisses, se situent à$(−3,0)$ et$(−1,0)$.

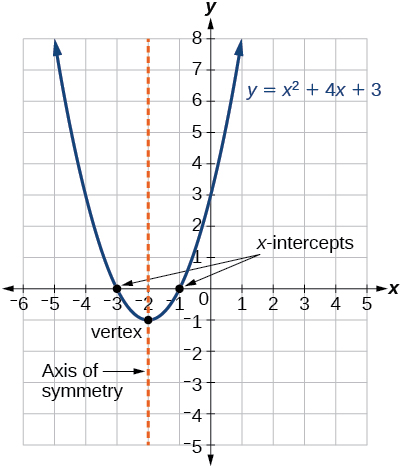
Graphique d'une parabole montrant où se situent les intersections x et y, le sommet et l'axe de symétrie pour la fonction y=x^2+4x+3. — Figure$\PageIndex{4}$ : Graphique d'une parabole montrant où se situent les$y$ points d'intersection$x$ et, le sommet et l'axe de symétrie de la fonction$y=x^2+4x+3$.

La forme standard d'une fonction quadratique présente la fonction sous la forme

\[f(x)=a(x−h)^2+k\]

où$(h, k)$ se trouve le sommet. Comme le sommet apparaît sous la forme standard de la fonction quadratique, cette forme est également connue sous le nom de forme de sommet d'une fonction quadratique.

Comme pour la forme générale, si$a>0$, la parabole s'ouvre vers le haut et le sommet est minimal. Si$a<0$, la parabole s'ouvre vers le bas et le sommet est maximal. La figure$\PageIndex{5}$ représente le graphe de la fonction quadratique écrite sous forme standard sous la forme$y=−3(x+2)^2+4$. Puisque$x–h=x+2$ dans cet exemple,$h=–2$. Sous cette forme$a=−3$,$h=−2$, et$k=4$. Parce que$a<0$ la parabole s'ouvre vers le bas. Le sommet se trouve à$(−2, 4)$.

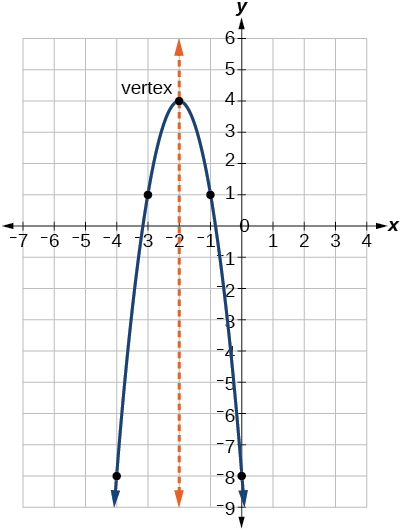
Graphique d'une parabole montrant où se situent les intersections x et y, le sommet et l'axe de symétrie pour la fonction y=-3 (x+2) ^2+4. — Figure$\PageIndex{5}$ : Graphique d'une parabole montrant où se situent les$y$ points d'intersection$x$ et, le sommet et l'axe de symétrie de la fonction$y=-3(x+2)^2+4$.

Le formulaire standard est utile pour déterminer comment le graphe est transformé à partir du graphe de$y=x^2$. La figure$\PageIndex{6}$ est le graphique de cette fonction de base.

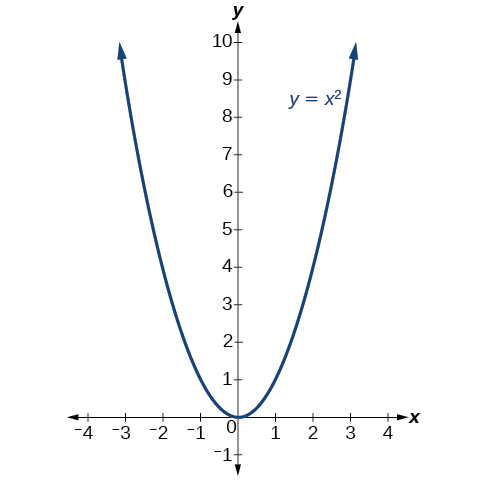
Si$k>0$, le graphique se déplace vers le haut, alors que si$k<0$, le graphique se déplace vers le bas. Dans la figure$\PageIndex{5}$$k>0$, le graphique est donc décalé de 4 unités vers le haut. Si$h>0$, le graphique se déplace vers la droite et si$h<0$, le graphique se déplace vers la gauche. Dans la figure$\PageIndex{5}$$h<0$, le graphique est donc décalé de 2 unités vers la gauche. La magnitude de$a$ indique l'étirement du graphique. Si$|a|>1$ le point associé à une valeur x particulière s'éloigne de l'axe X, le graphe semble se rétrécir et il y a un étirement vertical. Mais si$|a|<1$ le point associé à une valeur x particulière se rapproche de l'axe X, le graphe semble s'élargir, alors qu'il y a compression verticale. Dans la figure$\PageIndex{5}$$|a|>1$, le graphique devient plus étroit.

La forme standard et la forme générale sont des méthodes équivalentes pour décrire la même fonction. Nous pouvons le constater en développant le formulaire général et en le mettant sur un pied d'égalité avec le formulaire standard.

\[\begin{align*} a(x−h)^2+k &= ax^2+bx+c \\[4pt] ax^2−2ahx+(ah^2+k)&=ax^2+bx+c \end{align*} \]

Pour que les termes linéaires soient égaux, les coefficients doivent être égaux.

\[–2ah=b \text{, so } h=−\dfrac{b}{2a}. \nonumber\]

Il s'agit de l'axe de symétrie que nous avons défini précédemment. Régler les termes constants comme étant égaux :

\[\begin{align*} ah^2+k&=c \\ k&=c−ah^2 \\ &=c−a\cdot\Big(-\dfrac{b}{2a}\Big)^2 \\ &=c−\dfrac{b^2}{4a} \end{align*}\]

En pratique, cependant, il est généralement plus facile de se souvenir qu'il$k$ s'agit de la valeur de sortie de la fonction lorsque l'entrée est$h$, donc$f(h)=k$.

Définitions : Formes de fonctions quadratiques

Une fonction quadratique est une fonction du degré deux. Le graphe d'une fonction quadratique est une parabole.

La forme générale d'une fonction quadratique est$f(x)=ax^2+bx+c$ où$a$$b$, et$c$ sont des nombres réels et$a{\neq}0$.
La forme standard d'une fonction quadratique est$f(x)=a(x−h)^2+k$.
Le sommet$(h,k)$ est situé à\[h=–\dfrac{b}{2a},\;k=f(h)=f(\dfrac{−b}{2a}).\]

HOWTO : Ecrire une fonction quadratique sous une forme générale

À partir du graphe d'une fonction quadratique, écrivez l'équation de la fonction sous forme générale.

Identifiez le décalage horizontal de la parabole ; cette valeur est$h$. Identifiez le décalage vertical de la parabole ; cette valeur est$k$.
Remplacez les valeurs du décalage horizontal et vertical par$h$ et$k$. dans la fonction$f(x)=a(x–h)^2+k$.
Remplacez les valeurs de n'importe quel point, autre que le sommet, sur le graphique de la parabole par$x$ et$f(x)$.
Résolvez le facteur d'étirement,$|a|$.
Si la parabole s'ouvre,$a>0$. Si la parabole s'ouvre vers le bas,$a<0$ car cela signifie que le graphe a été réfléchi autour de l'axe X.
Développez et simplifiez pour écrire sous une forme générale.

Exemple$\PageIndex{2}$: Writing the Equation of a Quadratic Function from the Graph

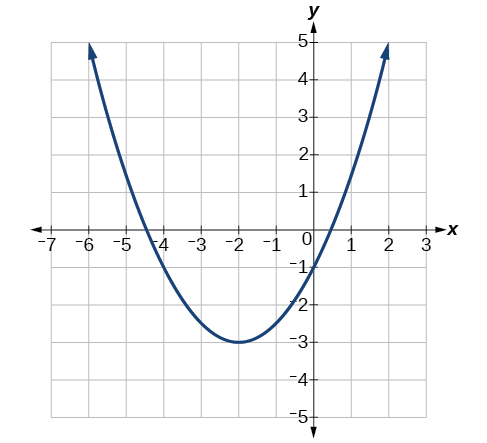
Écrivez une équation pour la fonction quadratique$g$ dans la figure$\PageIndex{7}$ sous forme de transformation de$f(x)=x^2$, puis développez la formule et simplifiez les termes pour écrire l'équation sous une forme générale.

alt — Figure$\PageIndex{7}$ : Graphique d'une parabole dont le sommet est à$(-2, -3)$.

Solution

Nous pouvons voir que le graphique de$g$ est le graphique du$f(x)=x^2$ décalage vers la gauche de 2 et vers le bas de 3, donnant une formule dans le formulaire$g(x)=a(x+2)^2–3$.

En substituant les coordonnées d'un point de la courbe$(0,−1)$, nous pouvons par exemple résoudre le facteur d'étirement.

\[\begin{align} −1&=a(0+2)^2−3 \\ 2&=4a \\ a&=\dfrac{1}{2} \end{align}\]

Dans sa forme standard, le modèle algébrique de ce graphe est$g(x)=\dfrac{1}{2}(x+2)^2–3$.

Pour l'écrire sous forme polynomiale générale, nous pouvons étendre la formule et simplifier les termes.

\[\begin{align} g(x)&=\dfrac{1}{2}(x+2)^2−3 \\ &=\dfrac{1}{2}(x+2)(x+2)−3 \\ &=\dfrac{1}{2}(x^2+4x+4)−3 \\ &=\dfrac{1}{2}x^2+2x+2−3 \\ &=\dfrac{1}{2}x^2+2x−1 \end{align}\]

Notez que les décalages horizontaux et verticaux du graphe de base de la fonction quadratique déterminent l'emplacement du sommet de la parabole ; le sommet n'est pas affecté par les étirements et les compressions.

Analyse

Nous pouvons vérifier notre travail à l'aide de la fonction de tableau d'un utilitaire graphique. Entrez d'abord$\mathrm{Y1=\dfrac{1}{2}(x+2)^2−3}$. Ensuite, sélectionnez$\mathrm{TBLSET}$, puis utilisez$\mathrm{TblStart=–6}$ et$\mathrm{ΔTbl = 2}$, et sélectionnez$\mathrm{TABLE}$. Voir le tableau$\PageIndex{1}$

Tableau$\PageIndex{1}$
$x$	-6	-4	-2	0	2
$y$	-5	-1	-3	-1	5

Les paires ordonnées dans le tableau correspondent aux points du graphique.

Exercice$\PageIndex{2}$

Une grille de coordonnées a été superposée sur la trajectoire quadratique d'un ballon de basket dans la Figure$\PageIndex{8}$. Trouvez une équation pour la trajectoire de la balle. Est-ce que c'est le tireur qui fabrique le panier ?

$alt$

Figure$\PageIndex{8}$ : Photo d'un garçon lançant un ballon de basket dans un cerceau pour montrer la courbe parabolique que cela fait.
(crédit : modification de l'œuvre de Dan Meyer)

Réponse: Le chemin passe par l'origine et a un sommet à$(−4, 7)$, donc$h(x)=–\frac{7}{16}(x+4)^2+7$. Pour réussir le tir, il$h(−7.5)$ faudrait avoir environ 4 mais$h(–7.5){\approx}1.64$ il n'y arrive pas.

$alt$ À partir d'une fonction quadratique sous une forme générale, trouvez le sommet de la parabole.

Identifiez$a$$b$, et$c$.
Trouvez$h$, la coordonnée X du sommet, en la remplaçant par$a$ et$b$ dans$h=–\frac{b}{2a}$.
Trouvez$k$ la coordonnée y du sommet en évaluant$k=f(h)=f\Big(−\frac{b}{2a}\Big)$.

Exemple$\PageIndex{3}$: Finding the Vertex of a Quadratic Function

Détermine le sommet de la fonction quadratique$f(x)=2x^2–6x+7$. Réécrivez le quadratique sous forme standard (forme de sommet).

Solution

La coordonnée horizontale du sommet sera à

\[\begin{align} h&=–\dfrac{b}{2a} \\ &=-\dfrac{-6}{2(2)} \\ &=\dfrac{6}{4} \\ &=\dfrac{3}{2}\end{align}\]

La coordonnée verticale du sommet sera à

\[\begin{align} k&=f(h) \\ &=f\Big(\dfrac{3}{2}\Big) \\ &=2\Big(\dfrac{3}{2}\Big)^2−6\Big(\dfrac{3}{2}\Big)+7 \\ &=\dfrac{5}{2} \end{align}\]

En réécrivant sous une forme standard, le facteur d'étirement sera le même que$a$ dans le quadratique d'origine.

\[f(x)=ax^2+bx+c \\ f(x)=2x^2−6x+7\]

Utiliser le sommet pour déterminer les décalages,

\[f(x)=2\Big(x–\dfrac{3}{2}\Big)^2+\dfrac{5}{2}\]

Analyse

L'une des raisons pour lesquelles nous pouvons vouloir identifier le sommet de la parabole est que ce point nous indiquera quelle est la valeur maximale ou minimale de la fonction et où elle se trouve$(h)$.$(k)$

Exercice$\PageIndex{3}$

Compte tenu de l'équation$g(x)=13+x^2−6x$, écrivez l'équation sous forme générale puis sous forme standard.

Réponse: $g(x)=x^2−6x+13$sous forme générale ;$g(x)=(x−3)^2+4$ sous forme standard.

Déterminer le domaine et la plage d'une fonction quadratique

N'importe quel nombre peut être la valeur d'entrée d'une fonction quadratique. Par conséquent, le domaine de toute fonction quadratique est constitué de nombres réels. Comme les paraboles ont un point maximum ou un point minimum, la plage est limitée. Comme le sommet d'une parabole sera un maximum ou un minimum, la plage sera composée de toutes les valeurs y supérieures ou égales à la coordonnée y au point de retournement ou inférieures ou égales à la coordonnée y au point de retournement, selon que la parabole s'ouvre vers le haut ou vers le bas.

Définition : Domaine et plage d'une fonction quadratique

Le domaine de toute fonction quadratique est constitué de nombres réels.

La plage d'une fonction quadratique écrite sous forme générale$f(x)=ax^2+bx+c$ avec une$a$ valeur positive est$f(x){\geq}f ( −\frac{b}{2a}\Big)$, ou$[ f(−\frac{b}{2a}),∞ ) $ ; la plage d'une fonction quadratique écrite sous forme générale avec une valeur négative est$f(x) \leq f(−\frac{b}{2a})$, ou$(−∞,f(−\frac{b}{2a})]$.

La plage d'une fonction quadratique écrite sous forme standard$f(x)=a(x−h)^2+k$ avec une$a$ valeur positive est$f(x) \geq k;$ la plage d'une fonction quadratique écrite sous forme standard avec une$a$ valeur négative is$f(x) \leq k$.

$alt$ À partir d'une fonction quadratique, trouvez le domaine et la plage.

Identifiez le domaine de n'importe quelle fonction quadratique sous la forme de tous les nombres réels.
Déterminez si$a$ c'est positif ou négatif. Si elle$a$ est positive, la parabole a un minimum. Si elle$a$ est négative, la parabole a un maximum.
Déterminez la valeur maximale ou minimale de la parabole,$k$.
Si la parabole a un minimum, la plage est donnée par$f(x){\geq}k$, ou$\left[k,\infty\right)$. Si la parabole a un maximum, la plage est donnée par$f(x){\leq}k$, ou$\left(−\infty,k\right]$.

Exemple$\PageIndex{4}$: Finding the Domain and Range of a Quadratic Function

Trouvez le domaine et la gamme de$f(x)=−5x^2+9x−1$.

Solution

Comme pour toute fonction quadratique, le domaine est composé uniquement de nombres réels.

Parce que$a$ c'est négatif, la parabole s'ouvre vers le bas et a une valeur maximale. Nous devons déterminer la valeur maximale. Nous pouvons commencer par déterminer la valeur x du sommet.

\[\begin{align} h&=−\dfrac{b}{2a} \\ &=−\dfrac{9}{2(-5)} \\ &=\dfrac{9}{10} \end{align}\]

La valeur maximale est donnée par$f(h)$.

\[\begin{align} f(\dfrac{9}{10})&=5(\dfrac{9}{10})^2+9(\dfrac{9}{10})-1 \\&= \dfrac{61}{20}\end{align}\]

La gamme est de$f(x){\leq}\frac{61}{20}$, ou$\left(−\infty,\frac{61}{20}\right]$.

Exercice$\PageIndex{4}$

Trouvez le domaine et la gamme de$f(x)=2\Big(x−\frac{4}{7}\Big)^2+\frac{8}{11}$.

Réponse: Le domaine est composé uniquement de vrais nombres. La gamme est de$f(x){\geq}\frac{8}{11}$, ou$\left[\frac{8}{11},\infty\right)$.

Détermination des valeurs maximale et minimale des fonctions quadratiques

La sortie de la fonction quadratique au sommet est la valeur maximale ou minimale de la fonction, en fonction de l'orientation de la parabole. Nous pouvons voir les valeurs maximales et minimales dans la figure$\PageIndex{9}$.

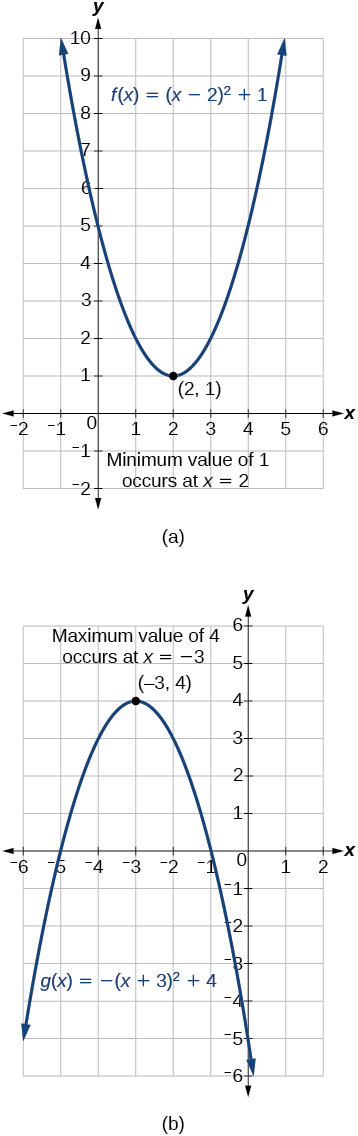
Deux graphiques où le premier graphique montre la valeur maximale pour f (x) = (x-2) ^2+1 qui se trouve à (2, 1) et le second graphique montre la valeur minimale pour g (x) =- (x+3) ^2+4 qui se trouve à (-3, 4). — Figure$\PageIndex{9}$ : Minimum et maximum de deux fonctions quadratiques.

Il existe de nombreux scénarios réels qui impliquent de déterminer la valeur maximale ou minimale d'une fonction quadratique, tels que des applications impliquant une zone et des revenus.

Exemple$\PageIndex{5}$: Finding the Maximum Value of a Quadratic Function

Une agricultrice veut délimiter un espace rectangulaire pour un nouveau jardin dans sa cour clôturée. Elle a acheté une clôture métallique de 80 pieds pour fermer trois côtés, et elle utilisera une section de la clôture de la cour arrière comme quatrième côté.

Trouvez une formule pour la zone délimitée par la clôture si les côtés de la clôture perpendiculaires à la clôture existante ont une longueur$L$.
Quelles dimensions devrait-elle aménager son jardin pour maximiser l'espace clos ?

Solution

Utilisons un diagramme tel que Figure$\PageIndex{10}$ pour enregistrer les informations données. Il est également utile d'introduire une variable temporaire$W$, pour représenter la largeur du jardin et la longueur de la section de clôture parallèle à la clôture de la cour arrière.

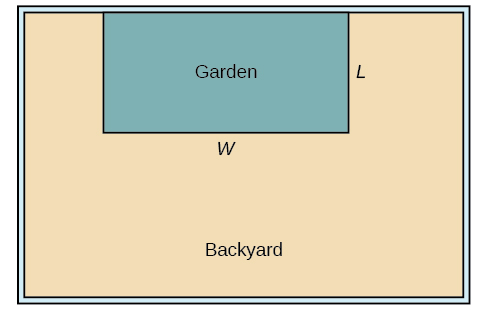
Figure$\PageIndex{10}$ : Schéma du jardin et de l'arrière-cour.

a. Nous savons que nous n'avons que 80 pieds de clôture disponibles$L+W+L=80$, et, plus simplement,$2L+W=80$. Cela nous permet de représenter la largeur$W$, en termes de$L$.

\[W=80−2L\]

Nous sommes maintenant prêts à écrire une équation pour la zone que la clôture entoure. Nous savons que l'aire d'un rectangle est la longueur multipliée par la largeur, donc

\[\begin{align} A&=LW=L(80−2L) \\ A(L)&=80L−2L^2 \end{align}\]

Cette formule représente la surface de la clôture en termes de longueur variable$L$. La fonction, écrite sous forme générale, est

\[A(L)=−2L^2+80L\].

Le quadratique a un coefficient d'attaque négatif, de sorte que le graphique s'ouvrira vers le bas et que le sommet sera la valeur maximale de la zone. Pour trouver le sommet, il faut faire attention car l'équation n'est pas écrite sous forme polynomiale standard avec des puissances décroissantes. C'est pourquoi nous avons réécrit la fonction dans sa forme générale ci-dessus. Puisque$a$ est le coefficient du terme carré,$a=−2$,$b=80$, et$c=0$.

Pour trouver le sommet :

\[\begin{align} h& =−\dfrac{80}{2(−2)} &k&=A(20) \\ &=20 & \text{and} \;\;\;\; &=80(20)−2(20)^2 \\ &&&=800 \end{align}\]

La valeur maximale de la fonction est une surface de 800 pieds carrés, qui se produit en$L=20$ pieds. Lorsque les côtés les plus courts mesurent 20 pieds, il reste 40 pieds de clôture pour le côté le plus long. Pour maximiser la surface, elle doit clôturer le jardin de manière à ce que les deux côtés les plus courts aient une longueur de 20 pieds et que le côté le plus long parallèle à la clôture existante ait une longueur de 40 pieds.

Analyse

Ce problème pourrait également être résolu en traçant graphiquement la fonction quadratique. Nous pouvons voir où se situe la surface maximale sur un graphique de la fonction quadratique de la figure$\PageIndex{11}$.

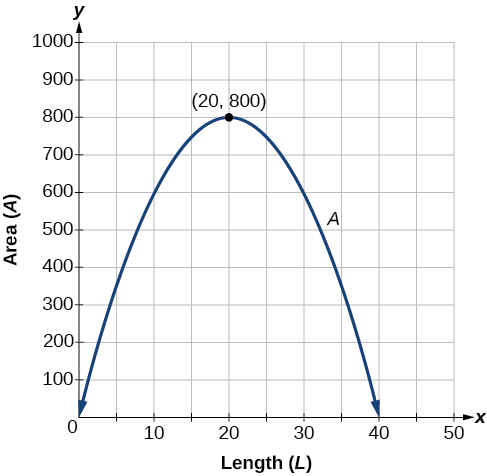
Graphique de la fonction parabolique A (L) =-2L^2+80L, dont l'axe x est étiqueté Longueur (L) et l'axe y est étiqueté Surface (A). Le sommet se trouve à (20 800). — Figure$\PageIndex{11}$ : Graphique de la fonction parabolique$A(L)=-2L^2+80L$

$alt$ Dans le cas d'une application impliquant des recettes, utilisez une équation quadratique pour déterminer le maximum.

Écrivez une équation quadratique pour les recettes.
Détermine le sommet de l'équation quadratique.
Déterminez la valeur y du sommet.

Exemple$\PageIndex{6}$: Finding Maximum Revenue

Le prix unitaire d'un article influe sur son offre et sa demande. En d'autres termes, si le prix unitaire augmente, la demande pour l'article diminuera généralement. Par exemple, un journal local compte actuellement 84 000 abonnés pour un coût trimestriel de 30 dollars. Une étude de marché suggère que si les propriétaires augmentaient le prix à 32 dollars, ils perdraient 5 000 abonnés. En supposant que les abonnements sont liés de manière linéaire au prix, quel prix le journal doit-il facturer pour un abonnement trimestriel afin de maximiser ses revenus ?

Solution

Le chiffre d'affaires est le montant d'argent qu'une entreprise rapporte. Dans ce cas, le chiffre d'affaires peut être trouvé en multipliant le prix par abonnement par le nombre d'abonnés ou la quantité. Nous pouvons introduire des variables,$p$ pour le prix par abonnement et$Q$ pour la quantité, pour nous donner l'équation$\text{Revenue}=pQ$.

Comme le nombre d'abonnés varie en fonction du prix, nous devons trouver une relation entre les variables. Nous le savons actuellement$p=30$ et$Q=84,000$. Nous savons également que si le prix atteignait 32 dollars, le journal perdrait 5 000 abonnés, ce qui donne une deuxième paire de valeurs,$p=32$ et$Q=79,000$. À partir de là, nous pouvons trouver une équation linéaire reliant les deux quantités. La pente sera

\[\begin{align} m&=\dfrac{79,000−84,000}{32−30} \\ &=−\dfrac{5,000}{2} \\ &=−2,500 \end{align}\]

Cela nous indique que le journal perdra 2 500 abonnés pour chaque dollar augmenté. Nous pouvons ensuite résoudre l'intersection Y.

\[\begin{align} Q&=−2500p+b &\text{Substitute in the point $Q=84,000$ and $p=30$} \\ 84,000&=−2500(30)+b &\text{Solve for $b$} \\ b&=159,000 \end{align}\]

Cela nous donne l'équation$Q=−2,500p+159,000$ linéaire reliant le coût et le nombre d'abonnés. Nous revenons maintenant à notre équation des recettes.

\[\begin{align} \text{Revenue}&=pQ \\ \text{Revenue}&=p(−2,500p+159,000) \\ \text{Revenue}&=−2,500p^2+159,000p \end{align}\]

Nous avons désormais une fonction quadratique des recettes en fonction des frais d'abonnement. Pour trouver le prix qui maximisera les revenus du journal, nous pouvons trouver le sommet.

\[\begin{align} h&=−\dfrac{159,000}{2(−2,500)} \\ &=31.8 \end{align}\]

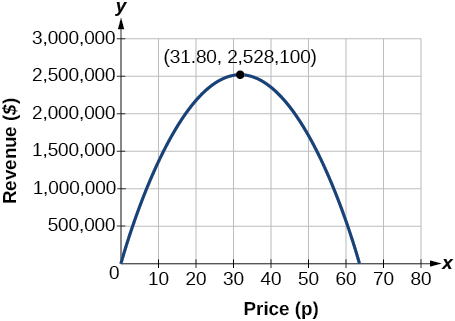
Le modèle nous indique que les recettes maximales seront atteintes si le journal facture 31,80$ pour un abonnement. Pour déterminer quel est le revenu maximum, nous évaluons la fonction des recettes.

\[\begin{align} \text{maximum revenue}&=−2,500(31.8)^2+159,000(31.8) \\ &=2,528,100 \end{align}\]

Analyse

Cela pourrait également être résolu en traçant le quadratique comme dans la figure$\PageIndex{12}$. Nous pouvons voir le revenu maximum sur un graphique de la fonction quadratique.

Graphique de la fonction parabolique dont l'axe X est étiqueté Price (p) et l'axe y est étiqueté Revenue ($). Le sommet est à (31,80, 258100). — Figure$\PageIndex{12}$ : Graphique de la fonction parabolique

Trouver les points d'intersection X et Y d'une fonction quadratique

Tout comme nous l'avons fait pour les problèmes d'application ci-dessus, nous devons également trouver des interceptions d'équations quadratiques pour représenter graphiquement des paraboles. Rappelons que nous trouvons l'intersection y d'une quadratique en évaluant la fonction à une entrée de zéro, et que nous trouvons les interceptions X aux emplacements où la sortie est nulle. Remarquez sur la figure$\PageIndex{13}$ que le nombre d'interceptions en X peut varier en fonction de l'emplacement du graphique.

" src="https://math.libretexts.org/@api/dek..._03_02_013.jpg">

Figure$\PageIndex{13}$ : Nombre d'interceptions en X d'une parabole.

$alt$ À partir d'une fonction quadratique$f(x)$, trouvez les interceptions y et x.

Évaluez$f(0)$ pour trouver l'intersection Y.
Résolvez l'équation quadratique$f(x)=0$ pour trouver les interceptions X.

Exemple$\PageIndex{7}$: Finding the y- and x-Intercepts of a Parabola

Trouvez les points d'intersection y et x du quadratique$f(x)=3x^2+5x−2$.

Solution

Nous trouvons l'intersection Y en évaluant$f(0)$.

\[\begin{align} f(0)&=3(0)^2+5(0)−2 \\ &=−2 \end{align}\]

L'intersection Y est donc à$(0,−2)$.

Pour les x-intercepts, nous trouvons toutes les solutions de$f(x)=0$.

\[0=3x^2+5x−2\]

Dans ce cas, le quadratique peut être facilement factorisé, fournissant ainsi la méthode de solution la plus simple.

\[0=(3x−1)(x+2)\]

\[\begin{align} 0&=3x−1 & 0&=x+2 \\ x&= \frac{1}{3} &\text{or} \;\;\;\;\;\;\;\; x&=−2 \end{align}\]

Les x-intercepts sont donc à$(\frac{1}{3},0)$ et$(−2,0)$.

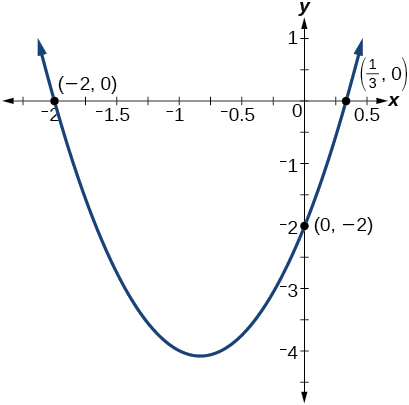
Analyse

En représentant graphiquement la fonction, nous pouvons confirmer que le graphique croise l'$y$axe -en$(0,−2)$. Nous pouvons également confirmer que le graphique croise l'axe des abscisses à$\Big(\frac{1}{3},0\Big)$ et$(−2,0)$. Voir la figure$\PageIndex{14}$.

Graphique d'une parabole qui possède les interceptions suivantes (-2, 0), (1/3, 0) et (0, -2). — Figure$\PageIndex{14}$ : Graphique d'une parabole.

Réécriture des quadratiques sous forme standard

Dans l'exemple$\PageIndex{7}$, le quadratique a été facilement résolu par factorisation. Cependant, de nombreux quadratiques ne peuvent pas être pris en compte. Nous pouvons résoudre ces quadratiques en les réécrivant d'abord sous une forme standard.

$alt$ À partir d'une fonction quadratique, trouvez les x-intercepts en les réécrivant sous forme standard.

Remplacez a et$b$ par$h=−\frac{b}{2a}$.
$x=h$Remplacez par la forme générale de la fonction quadratique pour trouver$k$.
Réécrivez le quadratique sous forme standard en utilisant$h$ et$k$.
Déterminez quand la sortie de la fonction sera nulle pour trouver les interceptions X.

Exemple$\PageIndex{8}$: Finding the x-Intercepts of a Parabola

Trouvez les points d'intersection X de la fonction quadratique$f(x)=2x^2+4x−4$.

Solution

Nous commençons par déterminer quand la sortie sera nulle.

\[0=2x^2+4x−4 \nonumber\]

Comme le quadratique n'est pas facilement factorisable dans ce cas, nous résolvons les interceptions en réécrivant d'abord le quadratique sous une forme standard.

\[f(x)=a(x−h)^2+k\nonumber\]

Nous le savons$a=2$. Ensuite, nous résolvons pour$h$ et$k$.

\[\begin{align*} h&=−\dfrac{b}{2a} & k&=f(−1) \\ &=−\dfrac{4}{2(2)} & &=2(−1)^2+4(−1)−4 \\ &=−1 & &=−6 \end{align*}\]

Nous pouvons donc maintenant réécrire sous forme standard.

\[f(x)=2(x+1)^2−6\nonumber\]

Nous pouvons maintenant déterminer quand la sortie sera nulle.

\[\begin{align*} 0&=2(x+1)^2−6 \\ 6&=2(x+1)^2 \\ 3&=(x+1)^2 \\ x+1&={\pm}\sqrt{3} \\ x&=−1{\pm}\sqrt{3} \end{align*}\]

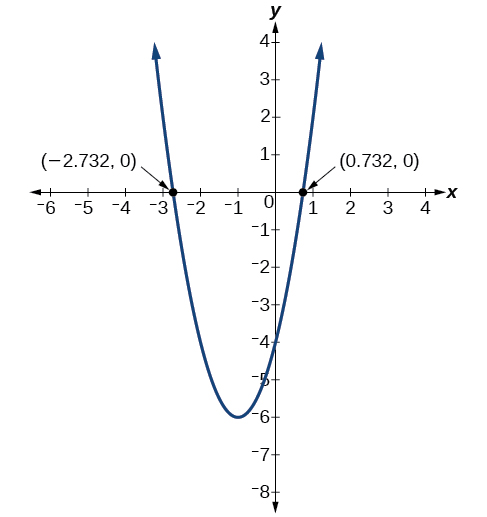
Le graphique a des interceptions X à$(−1−\sqrt{3},0)$ et$(−1+\sqrt{3},0)$.

Analyse

Nous pouvons vérifier notre travail en représentant graphiquement la fonction donnée sur un utilitaire de création graphique et en observant les intersections X. Voir la figure$\PageIndex{15}$.

Graphique d'une parabole qui possède les interceptions X suivantes (-2,732, 0) et (0,732, 0). — Figure$\PageIndex{15}$ : Graphique d'une parabole qui possède les interceptions X suivantes :$(-2.732, 0)$ et$(0.732, 0)$.

Exercice$\PageIndex{1}$

Dans Try It$\PageIndex{1}$, nous avons trouvé la forme standard et générale de la fonction$g(x)=13+x^2−6x$. Trouvez maintenant les interceptions y et x (le cas échéant).

Réponse: y-intercept at$(0, 13)$, pas de x-intercepts

Exemple$\PageIndex{9}$: Solving a Quadratic Equation with the Quadratic Formula

Résoudre$x^2+x+2=0$.

Solution

Commençons par écrire la formule quadratique :$x=\frac{−b{\pm}\sqrt{b^2−4ac}}{2a}$.

Lors de l'application de la formule quadratique, nous identifions les coefficients$a$,$b$ et$c$. Pour l'équation$x^2+x+2=0$, nous avons$a=1$$b=1$, et$c=2$. En remplaçant ces valeurs dans la formule, nous avons :

\[\begin{align*} x&=\dfrac{−b{\pm}\sqrt{b^2−4ac}}{2a} \\ &=\dfrac{−1{\pm}\sqrt{1^2−4⋅1⋅(2)}}{2⋅1} \\ &=\dfrac{−1{\pm}\sqrt{1−8}}{2} \\ &=\dfrac{−1{\pm}\sqrt{−7}}{2} \\ &=\dfrac{−1{\pm}i\sqrt{7}}{2} \end{align*}\]

Les solutions à l'équation sont$x=\frac{−1+i\sqrt{7}}{2}$$x=−\frac{1}{2}+\frac{i\sqrt{7}}{2}$ et$x=\frac{−1-i\sqrt{7}}{2}$ ou$x=\frac{-1}{2}−\frac{i\sqrt{7}}{2}$.

Exemple$\PageIndex{10}$: Applying the Vertex and x-Intercepts of a Parabola

Une balle est lancée vers le haut depuis le haut d'un bâtiment de 40 pieds de haut à une vitesse de 80 pieds par seconde. La hauteur de la balle au-dessus du sol peut être modélisée par l'équation$H(t)=−16t^2+80t+40$.

Quand la balle atteint-elle la hauteur maximale ?
Quelle est la hauteur maximale de la balle ?
Quand est-ce que la balle touche le sol ?

La balle atteint la hauteur maximale au sommet de la parabole.
\[\begin{align} h &= −\dfrac{80}{2(−16)} \\ &=\dfrac{80}{32} \\ &=\dfrac{5}{2} \\ & =2.5 \end{align}\]

La balle atteint sa hauteur maximale après 2,5 secondes.

Pour déterminer la hauteur maximale, trouvez la coordonnée y du sommet de la parabole.
\[\begin{align} k &=H(−\dfrac{b}{2a}) \\ &=H(2.5) \\ &=−16(2.5)^2+80(2.5)+40 \\ &=140 \end{align}\]

Le ballon atteint une hauteur maximale de 140 pieds.

Pour savoir quand la balle touche le sol, nous devons déterminer quand la hauteur est nulle,$H(t)=0$.

Nous utilisons la formule quadratique.

\[\begin{align} t & =\dfrac{−80±\sqrt{80^2−4(−16)(40)}}{2(−16)} \\ & = \dfrac{−80±\sqrt{8960}}{−32} \end{align} \]

Comme la racine carrée ne se simplifie pas bien, nous pouvons utiliser une calculatrice pour approximer les valeurs des solutions.

\[t=\dfrac{−80-\sqrt{8960}}{−32} ≈5.458 \text{ or }t=\dfrac{−80+\sqrt{8960}}{−32} ≈−0.458 \]

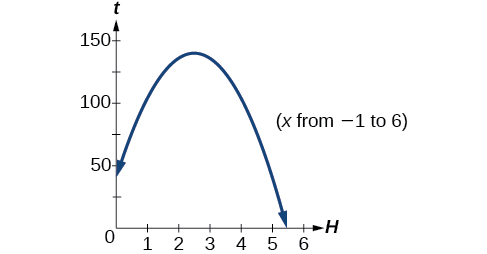
La deuxième réponse se situe en dehors du domaine raisonnable de notre modèle. Nous concluons donc que la balle touchera le sol après environ 5,458 secondes. Voir la figure$\PageIndex{16}$.

$alt$ $\PageIndex{5}$: Un rocher est projeté vers le haut depuis le sommet d'une falaise de 112 pieds de haut surplombant l'océan à une vitesse de 96 pieds par seconde. La hauteur de la roche au-dessus de l'océan peut être modélisée par l'équation$H(t)=−16t^2+96t+112$.

Quand est-ce que le rocher atteint sa hauteur maximale ?
Quelle est la hauteur maximale du rocher ?
Quand est-ce que le rocher entre en contact avec l'océan ?

Solution

a. 3 secondes b. 256 pieds c. 7 secondes

Équations clés

forme générale d'une fonction quadratique :$f(x)=ax^2+bx+c$
la formule quadratique :$x=\dfrac{−b{\pm}\sqrt{b^2−4ac}}{2a}$
forme standard d'une fonction quadratique :$f(x)=a(x−h)^2+k$

Concepts clés

Une fonction polynomiale de degré deux est appelée fonction quadratique.
Le graphe d'une fonction quadratique est une parabole. Une parabole est une courbe en forme de U qui peut s'ouvrir vers le haut ou vers le bas.
L'axe de symétrie est la ligne verticale passant par le sommet. Les zéros, ou points d'intersection X, sont les points auxquels la parabole traverse l'axe des abscisses. L'intersection y est le point où la parabole traverse l'$y$axe.
Les fonctions quadratiques sont souvent écrites sous une forme générale. La forme standard ou de sommet est utile pour identifier facilement le sommet d'une parabole. Les deux formes peuvent être écrites à partir d'un graphique.
Le sommet peut être trouvé à partir d'une équation représentant une fonction quadratique.
Le domaine d'une fonction quadratique est constitué de tous les nombres réels. La plage varie en fonction de la fonction.
La valeur minimale ou maximale d'une fonction quadratique est donnée par la valeur y du sommet.
La valeur minimale ou maximale d'une fonction quadratique peut être utilisée pour déterminer l'étendue de la fonction et pour résoudre de nombreux types de problèmes du monde réel, y compris des problèmes liés à la superficie et aux recettes.
Certaines équations quadratiques doivent être résolues à l'aide de la formule quadratique.
Le sommet et les points d'intersection peuvent être identifiés et interprétés pour résoudre des problèmes du monde réel.

Lexique

axe de symétrie
: ligne verticale passant par le sommet d'une parabole autour de laquelle la parabole est symétrique ; elle est définie par$x=−\frac{b}{2a}$.

forme générale d'une fonction quadratique
la fonction qui décrit une parabole, écrite sous la forme$f(x)=ax^2+bx+c$, où$a,b,$ et$c$ sont des nombres réels et a≥0.

forme standard d'une fonction quadratique
la fonction qui décrit une parabole, écrite sous la forme$f(x)=a(x−h)^2+k$, où se$(h, k)$ trouve le sommet.

sommet
le point auquel une parabole change de direction, correspondant à la valeur minimale ou maximale de la fonction quadratique

forme vertex d'une fonction quadratique,
autre nom pour la forme standard d'une fonction quadratique

zéros
dans une fonction donnée, dont les$x$ valeurs sont$y=0$, également appelées racines

Tableau\(\PageIndex{1}\)
\(x\)	-6	-4	-2	0	2
\(y\)	-5	-1	-3	-1	5