4.1 : Fonctions linéaires
- Page ID
- 194935
- Représentez une fonction linéaire.
- Déterminez si une fonction linéaire est croissante, décroissante ou constante.
- Interprétez la pente comme un taux de variation.
- Écrivez et interprétez une équation pour une fonction linéaire.
- Tracez les fonctions linéaires.
- Déterminez si les lignes sont parallèles ou perpendiculaires.
- Ecrivez l'équation d'une droite parallèle ou perpendiculaire à une droite donnée.
Tout comme pour la croissance d'un bambou, de nombreuses situations impliquent des changements constants au fil du temps. Prenons, par exemple, le premier train maglev commercial au monde, le train MagLev de Shanghai (train maglev) au monde, le train MagLev de Shanghai (Figure\(\PageIndex{1}\)). Il transporte confortablement les passagers pendant un trajet de 30 kilomètres de l'aéroport à la station de métro en seulement huit minutes.
Supposons qu'un train maglev parcourt une longue distance et qu'il maintienne une vitesse constante de 83 mètres par seconde pendant un certain temps une fois qu'il se trouve à 250 mètres de la gare. Comment analyser la distance entre le train et la gare en fonction du temps ? Dans cette section, nous étudierons un type de fonction utile à cette fin et l'utiliserons pour étudier des situations réelles, telles que la distance entre le train et la gare à un moment donné. Les trains maglev devaient parcourir une longue distance et maintenir une vitesse constante de 83 mètres par seconde pendant un certain temps une fois qu'il se trouve à 250 mètres de la gare. Comment analyser la distance entre le train et la gare en fonction du temps ? Dans cette section, nous étudierons un type de fonction utile à cette fin et nous l'utiliserons pour étudier des situations réelles, telles que la distance entre le train et la gare à un moment donné.
Représentation de fonctions linéaires
La fonction décrivant le mouvement du train est une fonction linéaire, définie comme une fonction dont le taux de variation est constant, c'est-à-dire un polynôme de degré 1. Il existe plusieurs manières de représenter une fonction linéaire, notamment sous forme de mot, de notation de fonction, de forme tabulaire et de forme graphique. Nous allons décrire le mouvement du train en tant que fonction en utilisant chaque méthode.
Représentation d'une fonction linéaire sous forme de texte
Commençons par décrire la fonction linéaire avec des mots. Pour le problème du train que nous venons d'examiner, la phrase verbale suivante peut être utilisée pour décrire la relation entre les fonctions.
- La distance entre le train et la gare est fonction du temps pendant lequel le train se déplace à vitesse constante et de sa distance initiale par rapport à la gare lorsqu'il a commencé à rouler à vitesse constante.
La vitesse est le taux de variation. Rappelez-vous qu'un taux de variation est une mesure de la rapidité avec laquelle la variable dépendante change par rapport à la variable indépendante. Le taux de variation de cet exemple est constant, ce qui signifie qu'il est identique pour chaque valeur d'entrée. Lorsque le temps (entrée) augmente d'une seconde, la distance correspondante (sortie) augmente de 83 mètres. Le train a commencé à rouler à cette vitesse constante à une distance de 250 mètres de la gare.
Représentation d'une fonction linéaire dans la notation des fonctions
Une autre approche pour représenter les fonctions linéaires consiste à utiliser la notation des fonctions. Un exemple de notation de fonction est une équation écrite sous la forme connue sous le nom de forme d'intersection de pente d'une ligne, où x est la valeur d'entrée,\(m\) le taux de variation et\(b\) la valeur initiale de la variable dépendante.
\[\begin{align*} &\text{Equation form } &y=mx+b \\[4pt] &\text{Equation notation } &f(x)=mx+b \end{align*}\]
Dans l'exemple du train, nous pouvons utiliser la notation\(D(t)\) dans laquelle la distance totale\(D\) est fonction du temps\(t\). Le taux est\(m\) de 83 mètres par seconde. La valeur initiale de la variable dépendante\(b\) est la distance initiale par rapport à la station, soit 250 mètres. Nous pouvons écrire une équation généralisée pour représenter le mouvement du train.
\[D(t)=83t+250\]
Représentation d'une fonction linéaire sous forme tabulaire
Une troisième méthode de représentation d'une fonction linéaire consiste à utiliser un tableau. La relation entre la distance de la station et le temps est représentée sur la figure\(\PageIndex{2}\). Sur le tableau, nous pouvons voir que la distance change de 83 mètres pour chaque seconde d'augmentation du temps.
Non. L'entrée représente le temps, donc si des nombres rationnels et irrationnels non négatifs sont possibles, des nombres réels négatifs ne sont pas possibles pour cet exemple. L'entrée est composée de nombres réels non négatifs.
Représentation d'une fonction linéaire sous forme graphique
Une autre façon de représenter les fonctions linéaires est de les représenter visuellement à l'aide d'un graphique. Nous pouvons utiliser la relation de fonction ci-dessus\(D(t)=83t+250\), pour dessiner un graphique, représenté sur la figure\(\PageIndex{3}\). Remarquez que le graphique est une ligne. Lorsque nous tracons une fonction linéaire, le graphique est toujours une ligne.
Le taux de variation, qui est constant, détermine l'inclinaison ou la pente de la ligne. Le point auquel la valeur d'entrée est nulle est l'intersection verticale, ou intersection y, de la ligne. Nous pouvons voir sur le graphique de la figure\(\PageIndex{3}\) que l'intersection y dans l'exemple de train que nous venons de voir est\((0,250)\) et représente la distance entre le train et la gare lorsqu'il a commencé à se déplacer à vitesse constante.
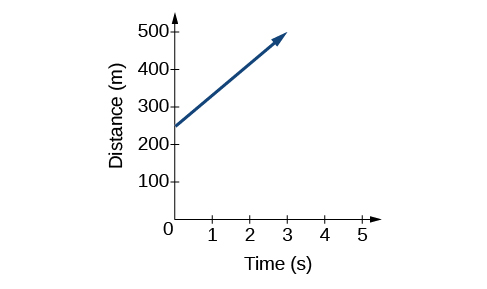
Notez que le graphique de l'exemple de train est restreint, mais ce n'est pas toujours le cas. Considérez le graphique de la ligne\(f(x)=2x+1\). Demandez-vous quels nombres peuvent être saisis dans la fonction, c'est-à-dire quel est le domaine de la fonction. Le domaine est composé de tous les nombres réels, car n'importe quel nombre peut être doublé, puis ajouté au produit.
Une fonction linéaire est une fonction dont le graphe est une ligne. Les fonctions linéaires peuvent être écrites sous la forme d'une ligne à l'intersection de la pente
\[f(x)=mx+b\]
où\(b\) est la valeur initiale ou de départ de la fonction (lors de l'entrée\(x=0\)) et\(m\) est le taux de variation constant, ou la pente de la fonction. L'intersection Y est à\((0,b)\).
La pression\(P\), en livres par pouce carré (PSI), sur la plongeuse de la figure\(\PageIndex{4}\) dépend de sa profondeur sous la surface de l'eau\(d\), en pieds. Cette relation peut être modélisée par l'équation,\(P(d)=0.434d+14.696\). Reformulez cette fonction avec des mots.
Pour reformuler la fonction avec des mots, nous devons décrire chaque partie de l'équation. La pression en fonction de la profondeur est égale à quatre cent trente-quatre millièmes de fois la profondeur plus quatorze et six cent quatre-vingt-seize millièmes.
Analyse
La valeur initiale, 14,696, est la pression en lb/po² sur le plongeur à une profondeur de 0 pied, soit la surface de l'eau. Le taux de variation, ou pente, est de 0,434 lb/po² par pied. Cela nous indique que la pression sur le plongeur augmente de 0,434 psi pour chaque pied de profondeur.
Déterminer si une fonction linéaire est croissante, décroissante ou constante
Les fonctions linéaires que nous avons utilisées dans les deux exemples précédents ont augmenté au fil du temps, mais ce n'est pas le cas de toutes les fonctions linéaires. Une fonction linéaire peut être croissante, décroissante ou constante. Pour une fonction croissante, comme dans l'exemple du train, les valeurs de sortie augmentent à mesure que les valeurs d'entrée augmentent. Le graphique d'une fonction croissante présente une pente positive. Une ligne avec une pente positive est inclinée vers le haut de gauche à droite, comme dans la Figure\(\PageIndex{5}\) (a). Pour une fonction décroissante, la pente est négative. Les valeurs de sortie diminuent à mesure que les valeurs d'entrée augmentent. Une ligne avec une pente négative est inclinée vers le bas de gauche à droite, comme dans la Figure\(\PageIndex{5}\) (b). Si la fonction est constante, les valeurs de sortie sont les mêmes pour toutes les valeurs d'entrée, de sorte que la pente est nulle. Une ligne avec une pente nulle est horizontale comme dans la Figure\(\PageIndex{5}\) (c).
![Trois graphiques représentant une fonction croissante, une fonction décroissante et une fonction constante.] Fonctions croissantes et décroissantes](https://math.libretexts.org/@api/deki/files/1061/CNX_Precalc_Figure_02_01_004abc.jpg)
Fonctions croissantes et décroissantes
Fonctions croissantes et décroissantes
La pente détermine si la fonction est une fonction linéaire croissante, une fonction linéaire décroissante ou une fonction constante.
- \(f(x)=mx+b\)est une fonction croissante si\(m>0\).
- \(f(x)=mx+b\)est une fonction décroissante si\(m<0\).
- \(f(x)=mx+b\)est une fonction constante si\(m=0\).
Certaines études récentes suggèrent qu'un adolescent envoie en moyenne 60 textos par jour. Pour chacun des scénarios suivants, trouvez la fonction linéaire qui décrit la relation entre la valeur d'entrée et la valeur de sortie. Déterminez ensuite si le graphique de la fonction est croissant, décroissant ou constant.
- Le nombre total de textos qu'un adolescent envoie est considéré comme une fonction du temps en jours. L'entrée est le nombre de jours et la sortie est le nombre total de textes envoyés.
- Un adolescent a une limite de 500 textos par mois dans son forfait de données. L'entrée est le nombre de jours et la sortie est le nombre total de textes restants pour le mois.
- Un adolescent a un nombre illimité de textos dans son forfait de données pour un coût de 50$ par mois. L'entrée est le nombre de jours et la sortie est le coût total de l'envoi de SMS chaque mois.
Solution
Analysez chaque fonction.
- La fonction peut être représentée\(f(x)=60x\) par\(x\) le nombre de jours. La pente, 60, est positive, donc la fonction augmente. Cela est logique car le nombre total de textes augmente chaque jour.
- La fonction peut être représentée\(f(x)=500−60x\) par\(x\) le nombre de jours. Dans ce cas, la pente est négative, donc la fonction est décroissante. Cela est logique car le nombre de textes restants diminue chaque jour et cette fonction représente le nombre de textes restant dans le plan de données après des\(x\) jours.
- La fonction de coût peut être représentée comme\(f(x)=50\) suit : le nombre de jours n'affecte pas le coût total. La pente étant de 0, la fonction est constante.
Calcul et interprétation de la pente
Dans les exemples que nous avons vus jusqu'à présent, la pente nous a été fournie. Cependant, nous avons souvent besoin de calculer la pente en fonction des valeurs d'entrée et de sortie. Étant donné deux valeurs pour l'entrée\(x_2\),\(x_1\) et deux valeurs correspondantes pour la sortie,\(y_1\) et\(y_2\) —qui peuvent être représentées par un ensemble de points,\((x_1,y_1)\) et\((x_2,y_2)\) —nous pouvons calculer la pente\(m\), comme suit
\[\begin{align*} m &= \dfrac{\text{change in output (rise)}}{ \text{change in input (run)}} \\[4pt] &= \dfrac{{\Delta}y}{ {\Delta}x} = \dfrac{y_2−y_1}{x_2−x_1} \end{align*}\]
où\({\Delta}y\) est le déplacement vertical et\({\Delta}x\) est le déplacement horizontal. Notez dans la notation des fonctions deux valeurs correspondantes pour la sortie\(y_1\) et\(y_2\) pour la fonction\(f\),\(y_1=f(x_1)\) et\(y_2=f(x_2)\), afin que nous puissions écrire de manière équivalente
\[m=\dfrac{f(x_2)-f(x_1)}{x_2-x_1} \nonumber\]
La figure\(\PageIndex{6}\) indique comment la pente de la ligne entre les points\((x_1,y_1)\) et\((x_2,y_2)\) est calculée. Rappelons que la pente mesure la pente. Plus la valeur absolue de la pente est élevée, plus la ligne est raide.
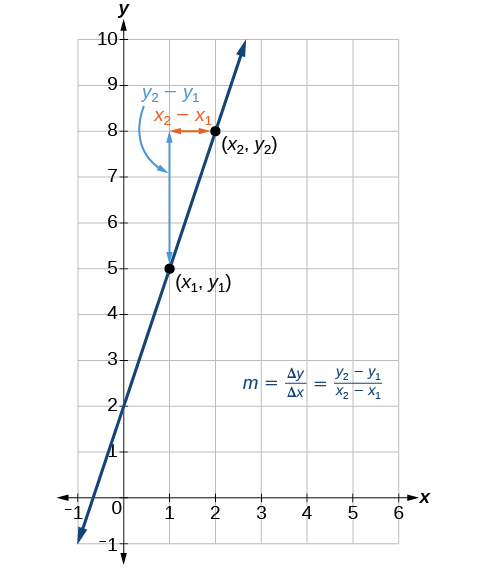
Les unités de pente\(\frac{\text{units for the output}}{ \text{units for the input}}\) sont-elles toujours utilisées ?
Oui. Considérez les unités comme la variation de la valeur de sortie pour chaque unité de variation de la valeur d'entrée. Un exemple de pente peut être des miles par heure ou des dollars par jour. Notez que les unités apparaissent sous la forme d'un ratio d'unités pour la sortie par unités pour l'entrée.
La pente, ou le taux de variation, d'une fonction\(m\) peut être calculé comme suit :
\[m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{{\Delta}y}{{\Delta}x}=\dfrac{y_2-y_1}{x_2-x_1}\]
où\(x_1\) et\(x_2\) sont des valeurs d'entrée\(y_1\) et\(y_2\) des valeurs de sortie.
À partir de deux points d'une fonction linéaire, calculez et interprétez la pente.
- Déterminez les unités pour les valeurs de sortie et d'entrée.
- Calculez la variation des valeurs de sortie et la modification des valeurs d'entrée.
- Interprétez la pente comme la variation des valeurs de sortie par unité de la valeur d'entrée.
S'il s'\(f(x)\)agit d'une fonction linéaire\((3,−2)\) et\((8,1)\) que sont des points sur la ligne, trouvez la pente. Cette fonction augmente-t-elle ou diminue-t-elle ?
Solution
Les paires de coordonnées sont\((3,−2)\) et\((8,1)\). Pour déterminer le taux de variation, nous divisons la variation de la production par la variation des entrées.
\[m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{1-(-2)}{8-3}=\dfrac{3}{5}\]
Nous pourrions également écrire la pente comme\(m=0.6\). La fonction augmente parce que\(m>0\).
Analyse
Comme indiqué précédemment, l'ordre dans lequel nous écrivons les points n'a pas d'importance lorsque nous calculons la pente de la droite tant que la première valeur de sortie, ou coordonnée y, utilisée correspond à la première valeur d'entrée, ou coordonnée x, utilisée.
S'il s'\(f(x)\)agit d'une fonction linéaire\((2, 3)\) et\((0,4)\) que sont des points sur la ligne, trouvez la pente. Cette fonction augmente-t-elle ou diminue-t-elle ?
- Réponse
-
\(m=\frac{4−3}{0−2} =\frac{1}{-2}=-\frac{1}{2}\); décroissant parce que\(m<0\).
La population d'une ville est passée de 23 400 à 27 800 habitants entre 2008 et 2012. Déterminez la variation de la population par an si nous supposons que la variation a été constante entre 2008 et 2012.
Le taux de variation met en relation l'évolution de la population avec l'évolution dans le temps. La population a augmenté de\(27,800−23,400=4400\) personnes au cours de l'intervalle de quatre ans. Pour déterminer le taux de variation, divisez la variation du nombre de personnes par le nombre d'années.
\[\dfrac{4,400 \text{ people}}{4 \text{ years}} =1,100 \dfrac{\text{people}}{\text{year}}\]
La population a donc augmenté de 1 100 personnes par an.
Analyse
Comme on nous dit que la population a augmenté, on peut s'attendre à ce que la pente soit positive. Cette pente positive que nous avons calculée est donc raisonnable.
La population d'une petite ville est passée de 1 442 à 1 868 habitants entre 2009 et 2012. Déterminez la variation de la population par an si nous supposons que la variation a été constante de 2009 à 2012.
- Réponse
-
\(m=\frac{1,868−1,442}{2,012−2,009} = \frac{426}{3} =\text{ 142 people per year}\)
Écrire la forme de pente ponctuelle d'une équation linéaire
Jusqu'à présent, nous avons utilisé la forme d'intersection de pente d'une équation linéaire pour décrire des fonctions linéaires. Ici, nous allons apprendre une autre façon d'écrire une fonction linéaire, la forme à pente ponctuelle.
\[y-y_1=m(x-x_1)\]
La forme de pente ponctuelle est dérivée de la formule de pente.
\[ \begin{align*} &m=\dfrac{y-y_1}{x-x_1} &\text{assuming }x{\neq}x_1 \\ &m(x-x_1)=\dfrac{y-y_1}{x-x_1}(x-x_1) &\text{Multiply both sides by }(x-x_1). \\ &m(x-x_1)=y-y_1 &\text{Simplify} \\ &y-y_1=m(x-x_1) &\text{Rearrange} \end{align*}\]
N'oubliez pas que la forme d'intersection de pente et la forme de pente ponctuelle peuvent être utilisées pour décrire la même fonction. Nous pouvons passer d'une forme à une autre en utilisant l'algèbre de base. Par exemple, supposons qu'on nous donne une équation sous forme de pente ponctuelle,\(y−4=− \frac{1}{2}(x−6)\). Nous pouvons le convertir en forme d'interception de pente comme indiqué.
\[\begin{align*} y-4&=-\dfrac{1}{2}(x-6) \\ y-4&=-\dfrac{1}{2}x+3 &\text{Distribute the }-\dfrac{1}{2}. \\ y&=-\dfrac{1}{2}x+7 &\text{Add 4 to each side.}\end{align*}\]
Par conséquent, la même ligne peut être décrite sous forme d'intersection de pente que\(y=\dfrac{1}{2}x+7\).
La forme de pente ponctuelle d'une équation linéaire prend la forme
\[y-y_1=m(x−x_1)\]
où\(m\) est la pente\(x_1\) et\(y_1\) les\(y\) coordonnées\(x\) et d'un point spécifique par lequel passe la ligne.
Écrire l'équation d'une droite à l'aide d'un point et de la pente
La forme de pente ponctuelle est particulièrement utile si nous connaissons un point et la pente d'une droite. Supposons, par exemple, qu'on nous dise qu'une ligne a une pente de 2 et passe par le point\((4,1)\). Nous savons cela\(m=2\) et cela\(x_1=4\) et\(y_1=1\). Nous pouvons remplacer ces valeurs dans l'équation générale de pente ponctuelle.
\[\begin{align*} y−y_1&=m(x−x_1) \\ y−1&=2(x−4) \end{align*}\]
Si nous voulions ensuite réécrire l'équation sous forme d'intersection de pente, nous appliquons des techniques algébriques.
\[\begin{align*} y−1&=2(x−4) \\ y−1&=2x−8 &\text{Distribute the 2.} \\ y&=2x−7 &\text{Add 1 to each side.} \end{align*}\]
Les deux équations\(y=2x–7\),\(y−1=2(x−4)\) et, décrivent la même droite. Voir la figure\(\PageIndex{7}\).
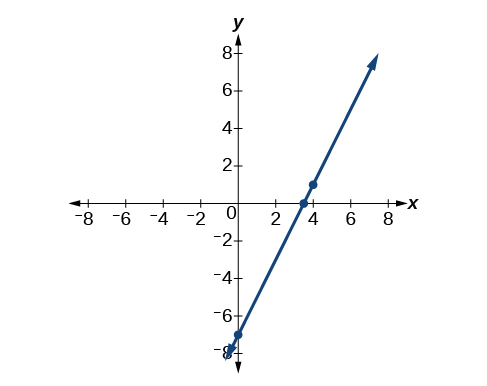
Écrivez la forme en pente ponctuelle de l'équation d'une droite de pente 3 qui passe par le point\((6,–1)\). Réécrivez-le ensuite sous la forme Slope-Intercept.
Solution
Découvrons ce que nous savons à partir des informations données. La pente est donc de 3\(m=3\). Nous connaissons également un point, donc nous savons\(x_1=6\) et\(y_1 =−1\). Nous pouvons maintenant remplacer ces valeurs dans l'équation générale de pente ponctuelle.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y−(−1)&=3(x−6) &\text{Substitute known values.} \\ y+1&=3(x−6) &\text{Distribute −1 to find point-slope form.} \end{align*}\]
Ensuite, nous utilisons l'algèbre pour trouver la forme d'intersection de pente.
\[\begin{align*} y+1&=3(x−6) \\ y+1&=3x−18 &\text{Distribute 3.} \\ y&=3x−19 &\text{Simplify to slope-intercept form.} \end{align*}\]
Écrivez la forme en pente ponctuelle de l'équation d'une droite avec une pente de —2 qui passe par le point\((–2, 2)\). Réécrivez-le ensuite sous la forme Slope-Intercept.
- Réponse
-
\(y−2=−2(x+2)\);\(y=−2x−2\)
Écrire l'équation d'une droite à l'aide de deux points
La forme en pente ponctuelle d'une équation est également utile si nous connaissons deux points par lesquels passe une droite. Supposons, par exemple, que nous sachions qu'une ligne passe par les points\((0, 1)\) et\((3, 2)\). Nous pouvons utiliser les coordonnées des deux points pour trouver la pente.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{2-1}{3-0} \\ &=\dfrac{1}{3} \end{align*}\]
Nous pouvons maintenant utiliser la pente que nous avons trouvée et les coordonnées de l'un des points pour trouver l'équation de la droite. Utilisons-le\((0,1)\) pour notre point de vue.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-1&=\dfrac{1}{3}(x-0) \end{align*}\]
Comme précédemment, nous pouvons utiliser l'algèbre pour réécrire l'équation sous forme d'intersection de pente.
\[\begin{align*} y-1&=\dfrac{1}{3}(x-0) \\ y-1&=\dfrac{1}{3}x &\text{Distribute the }\dfrac{1}{3}. \\ y&=\dfrac{1}{3}x+1 &\text{Add 1 to each side.} \end{align*}\]
Les deux équations décrivent la ligne illustrée à la figure\(\PageIndex{8}\).
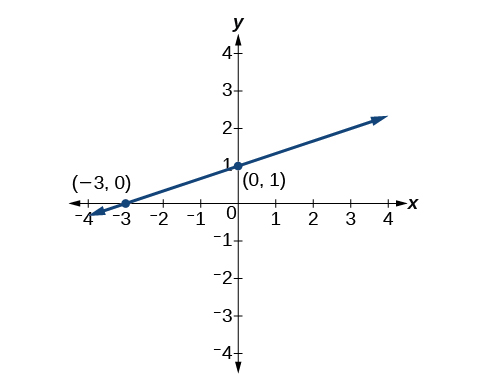
Écrivez la forme en pente ponctuelle d'une équation d'une droite passant par les points\((5,1)\) et\((8, 7)\). Réécrivez-le ensuite sous la forme Slope-Intercept.
Commençons par trouver la pente.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{7-1}{8-5} \\ &=\dfrac{6}{3} \\ &= 2 \end{align*}\]
Donc\(m=2\). Ensuite, nous substituons la pente et les coordonnées de l'un des points dans l'équation générale de la pente ponctuelle. Nous pouvons choisir l'un ou l'autre point, mais nous utiliserons\((5,1)\).
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-1&=2(x-5) \end{align*}\]
L'équation de pente ponctuelle de la droite est\(y_2–1=2(x_2–5)\). Pour réécrire l'équation sous forme d'intersection de pente, nous utilisons l'algèbre.
\[\begin{align*} y-1&=2(x-5) \\ y-1&=2x-10 \\ y&=2x-9 \end{align*}\]
L'équation pente-intersection de la droite est\(y=2x–9\).
\(\PageIndex{4}\): Ecrivez la forme en pente ponctuelle de l'équation d'une droite passant par les points\((–1,3)\) et\((0,0)\). Réécrivez-le ensuite sous la forme Slope-Intercept.
Solution
\(y−0=−3(x−0)\);\(y=−3x\)
Écrire et interpréter une équation pour une fonction linéaire
Maintenant que nous avons écrit des équations pour les fonctions linéaires sous forme de pente d'intersection et de pente ponctuelle, nous pouvons choisir la méthode à utiliser en fonction des informations qui nous sont fournies. Ces informations peuvent être fournies sous la forme d'un graphique, d'un point et d'une pente, de deux points, etc. Regardez le graphique de la fonction\(f\) dans la figure\(\PageIndex{9}\).
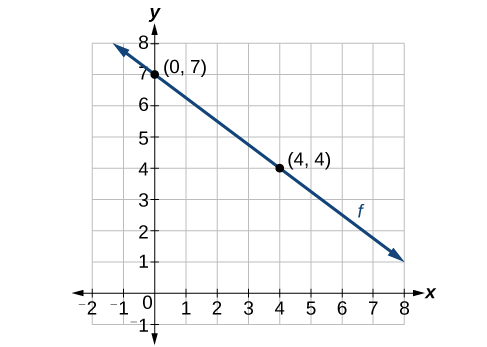
On ne nous donne pas la pente de la ligne, mais nous pouvons choisir deux points de la ligne pour trouver la pente. Choisissons\((0,7)\) et\((4, 4)\). Nous pouvons utiliser ces points pour calculer la pente.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{4-7}{4-0} \\&=-\dfrac{3}{4}\end{align*}\]
Nous pouvons maintenant remplacer la pente et les coordonnées de l'un des points dans la forme de pente ponctuelle.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-4&=-\dfrac{3}{4}(x-4) \end{align*}\]
Si nous voulons réécrire l'équation sous la forme de l'intersection de la pente, nous trouverions
\[\begin{align*} y-4&=-\dfrac{3}{4}(x-4) \\ y-4 &=-\dfrac{3}{4}x+3 \\ y&=-\dfrac{3}{4}x+7\end{align*}\]
Si nous voulions trouver la forme d'intersection de pente sans d'abord écrire la forme de pente ponctuelle, nous aurions pu reconnaître que la ligne traverse l'axe y lorsque la valeur de sortie est de 7. Par conséquent,\(b=7\). Nous avons maintenant la valeur initiale\(b\) et la pente,\(m\) ce qui nous permet de remplacer\(m\) et de\(b\) prendre la forme d'intersection de pente d'une ligne.
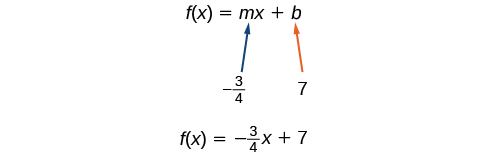
La fonction est donc\(f(x)=−\frac{3}{4}x+7\), et l'équation linéaire le serait\(y=−\frac{3}{4}x+7\).
À partir du graphe d'une fonction linéaire, écrivez une équation pour représenter la fonction.
- Identifiez deux points sur la ligne.
- Utilisez les deux points pour calculer la pente.
- Déterminez où la ligne croise l'axe Y pour identifier l'intersection des Y par inspection visuelle.
- Remplacez la pente et l'intersection y par la forme d'intersection de pente d'une équation linéaire.
Écrivez une équation pour une fonction linéaire à l'aide d'un graphique\(f\) illustré à la figure\(\PageIndex{11}\).
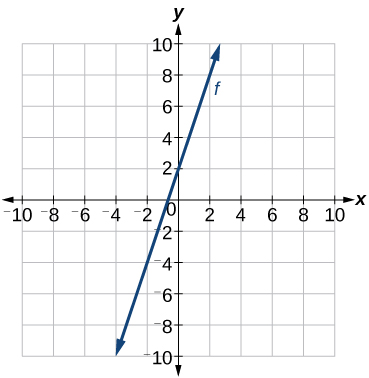
Solution
Identifiez deux points sur la ligne, tels que\((0, 2)\) et\((−2,−4)\). Utilisez les points pour calculer la pente.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{4-2}{-2-0} \\ &=\dfrac{-6}{-2} \\ &=3 \end{align*}\]
Substituez la pente et les coordonnées de l'un des points dans le formulaire de pente ponctuelle.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-(-4)&=3(x-(-2)) \\ y+4 &= 3(x+2)\end{align*}\]
Nous pouvons utiliser l'algèbre pour réécrire l'équation sous forme d'intersection de pente.
\[\begin{align*} y+4&= 3(x+2) \\ y+4&= 3x+6 \\ y & = 3x + 2 \end{align*}\]
Analyse
Cela est logique car nous pouvons voir sur la figure\(\PageIndex{12}\) que la ligne traverse l'axe y au point\((0, 2)\), qui est l'intersection y, donc\(b=2\).
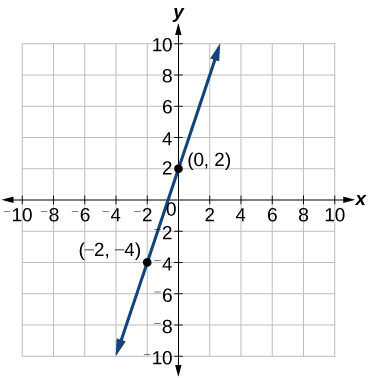
Supposons que Ben crée une entreprise dans laquelle il assume un coût fixe de 1 250 dollars par mois pour les frais généraux, y compris le loyer de son bureau. Ses coûts de production sont de 37,50$ par article. Écrivez une fonction linéaire\(C\) où\(C(x)\) est le coût des\(x\) articles produits au cours d'un mois donné.
Solution
Le coût fixe est présent chaque mois, soit 1 250$. Les coûts qui peuvent varier incluent le coût de production de chaque article, qui est de 37,50$ pour Ben. Le coût variable, appelé coût marginal, est représenté par 37,5. Le coût encouru par Ben est la somme de ces deux coûts, représentée par\(C(x)=1250+37.5x\).
Analyse
Si Ben produit 100 articles par mois, son coût mensuel est représenté par
\[\begin{align*} C(100)&=1250+37.5(100) \\ &=5000 \end{align*}\]
Son coût mensuel serait donc de 5 000$.
C'\(f\)est une fonction linéaire, avec et\(f(3)=−2\)\(f(8)=1\), trouvez une équation pour la fonction sous forme d'intersection de pente.
Solution
Nous pouvons écrire les points donnés en utilisant des coordonnées.
\[\begin{align*} f(3)&= -2{\rightarrow}(3,2) \\ f(8)&=1{\rightarrow}(8,1) \end{align*}\]
Nous pouvons ensuite utiliser les points pour calculer la pente.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{1-(-2)}{8-3} \\ &=\dfrac{3}{5} \end{align*}\]
Substituez la pente et les coordonnées de l'un des points dans le formulaire de pente ponctuelle.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-(-2)&=\dfrac{3}{5}(x-3) \end{align*}\]
Nous pouvons utiliser l'algèbre pour réécrire l'équation sous forme d'intersection de pente.
\[\begin{align*} y+2&=\dfrac{3}{5}(x-3) \\ y+2&=\dfrac{3}{5}x-\dfrac{9}{5} \\ y&=\dfrac{3}{5}x-\dfrac{19}{5} \end{align*}\]
C'\(f(x)\)est une fonction linéaire, avec et\(f(2)=–11\)\(f(4)=−25\), trouvez une équation pour la fonction sous forme d'intersection de pente.
- Réponse
-
\(y=−7x+3\)
Modélisation de problèmes réels avec des fonctions linéaires
Dans le monde réel, les problèmes ne sont pas toujours énoncés explicitement en termes de fonction ou représentés par un graphique. Heureusement, nous pouvons analyser le problème en le représentant d'abord comme une fonction linéaire, puis en interprétant les composantes de la fonction. Tant que nous connaissons ou pouvons déterminer la valeur initiale et le taux de variation d'une fonction linéaire, nous pouvons résoudre de nombreux types de problèmes du monde réel.
À partir d'une fonction linéaire\(f\) et de la valeur initiale et du taux de variation, évaluez\(f(c)\).
- Déterminez la valeur initiale et le taux de variation (pente).
- Remplacez les valeurs par\(f(x)=mx+b\).
- Évaluez la fonction à\(x=c\).
Marcus a actuellement 200 chansons dans sa collection de musique. Chaque mois, il ajoute 15 nouvelles chansons. Écrivez une formule pour le nombre de chansons\(N\), dans sa collection en fonction du temps\(t\), du nombre de mois. Combien de chansons possèdera-t-il en un an ?
Solution
La valeur initiale de cette fonction est 200 car il possède actuellement 200 chansons, donc\(N(0)=200\), ce qui signifie que\(b=200\).
Le nombre de chansons augmente de 15 chansons par mois, de sorte que le taux de variation est de 15 chansons par mois. Nous le savons donc\(m=15\). Nous pouvons substituer la valeur initiale et le taux de variation à la forme d'intersection de pente d'une ligne.
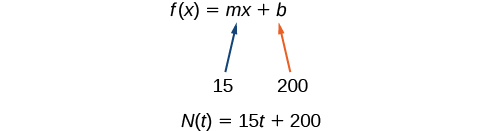
Nous pouvons écrire la formule\(N(t)=15t+200\).
Avec cette formule, nous pouvons ensuite prédire combien de chansons Marcus aura en 1 an (12 mois). En d'autres termes, nous pouvons évaluer la fonction à\(t=12\).
\[\begin{align*} N(12)&=15(12)+200 \\ &=180+200 \\ &= 380 \end{align*}\]
Marcus aura 380 chansons en 12 mois.
Analyse
Notez qu'il\(N\) s'agit d'une fonction linéaire croissante. À mesure que l'entrée (le nombre de mois) augmente, la sortie (nombre de chansons) augmente également.
En tant que vendeur d'assurance, Ilya gagne un salaire de base plus une commission sur chaque nouvelle police. Par conséquent, le revenu hebdomadaire d'Ilya, moi, dépend du nombre de nouvelles polices\(n\), il vend pendant la semaine. La semaine dernière, il a vendu 3 nouvelles polices et a gagné 760$ pour la semaine. La semaine précédente, il avait vendu 5 nouvelles polices et gagné 920$. Trouvez une équation pour\(I(n)\) et interprétez la signification des composantes de l'équation.
Solution
L'information donnée nous donne deux paires d'entrées-sorties :\((3,760)\) et\((5,920)\). Nous commençons par déterminer le taux de variation.
\[\begin{align*} m&=\dfrac{920-760}{5-3} \\ &=\dfrac{$160}{2 \text{ policies}} \\ &=$80 \text{ per policy} \end{align*}\]
Le suivi des unités peut nous aider à interpréter cette quantité. Le revenu a augmenté de 160$ lorsque le nombre de polices a augmenté de 2, de sorte que le taux de variation est de 80$ par police. Par conséquent, Ilya gagne une commission de 80$ pour chaque police vendue au cours de la semaine.
Nous pouvons ensuite résoudre la valeur initiale.
\[\begin{align*} I(n)&=80n+b \\ 760&=80(3)+b \text{ when } n=3, I(3)=760 \\ 760-80(3)&=b \\ 520 & =b \end{align*}\]
La valeur de\(b\) est la valeur de départ de la fonction et représente les revenus d'Ilya lorsque\(n=0\) ou lorsqu'aucune nouvelle police n'est vendue. Nous pouvons interpréter cela comme le salaire de base d'Ilya pour la semaine, qui ne dépend pas du nombre de polices vendues.
Nous pouvons maintenant écrire l'équation finale.
\[I(n)=80n+520 \nonumber\]
Notre interprétation finale est que le salaire de base d'Ilya est de 520 dollars par semaine et qu'il gagne une commission supplémentaire de 80 dollars pour chaque police vendue.
équation pour une fonction linéaire
Le\(\PageIndex{1}\) tableau indique le nombre de rats d'une population en fonction du temps, en semaines. Utilisez le tableau pour écrire une équation linéaire.
| w, nombre de semaines | 0 | 2 | 4 | 6 |
|---|---|---|---|---|
| P (w), nombre de rats | 1000 | 1080 | 1160 | 1240 |
Solution
Nous pouvons voir dans le tableau que la valeur initiale du nombre de rats est de 1000, donc\(b=1000\).
Plutôt que de nous contenter d'une solution\(m\), nous pouvons constater en regardant le tableau que la population augmente de 80 pour toutes les deux semaines qui s'écoulent. Cela signifie que le taux de variation est de 80 rats par 2 semaines, ce qui peut être simplifié à 40 rats par semaine.
\[P(w)=40w+1000 \nonumber\]
Si nous ne remarquions pas le taux de variation indiqué dans le tableau, nous pourrions tout de même calculer la pente en utilisant deux points quelconques du tableau. Par exemple, en utilisant\((2,1080)\) et\((6,1240)\)
\[\begin{align*} m&=\dfrac{1240-1080}{6-2} \\ &=\dfrac{160}{4} \\ &= 40\end{align*}\]
La valeur initiale est-elle toujours fournie dans une table de valeurs telle que Table\(\PageIndex{1}\) ?
Non. Parfois, la valeur initiale est fournie dans un tableau de valeurs, mais parfois elle ne l'est pas. Si vous voyez une entrée de 0, la valeur initiale serait la sortie correspondante. Si la valeur initiale n'est pas fournie car aucune valeur en entrée de la table n'est égale à 0, trouvez la pente, remplacez une paire de coordonnées et la pente par\(f(x)=mx+b\), et résolvez pour\(b\).
\(\PageIndex{5}\): Un nouvel engrais a été introduit dans un jeune arbre afin de tester son effet sur la hauteur de l'arbre. Le tableau\(\PageIndex{2}\) indique la hauteur de l'arbre, en pieds,\(x\) mois depuis le début des mesures. Écrivez une fonction linéaire\(H(x)\), où\(x\) est le nombre de mois écoulés depuis le début de l'expérience.
| \(x\) | 0 | 2 | 4 | 8 | 12 |
|---|---|---|---|---|---|
| \(H(x)\) | 12,5 | 13,5 | 14,5 | 16,5 | 18,5 |
Solution
\(H(x)=0.5x+12.5\)
Équations clés
- forme d'interception en pente d'une ligne :\(f(x)=mx+b\)
- pente :\(m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{{\Delta}y}{{\Delta}x}=\dfrac{y_2-y_1}{x_2-x_1}\)
- forme d'une ligne en pente ponctuelle :\(y−y_1 =m(x-x_1)\)
Concepts clés
- Les paires ordonnées données par une fonction linéaire représentent des points sur une ligne.
- Les fonctions linéaires peuvent être représentées sous forme de mots, de notation fonctionnelle, sous forme tabulaire et sous forme graphique.
- Le taux de variation d'une fonction linéaire est également appelé pente.
- Une équation sous forme d'intersection de pente d'une droite inclut la pente et la valeur initiale de la fonction.
- La valeur initiale, ou intersection y, est la valeur de sortie lorsque l'entrée d'une fonction linéaire est nulle. Il s'agit de la valeur y du point où la ligne croise l'axe Y.
- Une fonction linéaire croissante produit un graphique incliné vers le haut de gauche à droite et présentant une pente positive.
- Une fonction linéaire décroissante produit un graphique incliné vers le bas de gauche à droite et présentant une pente négative.
- Une fonction linéaire constante produit un graphique qui est une ligne horizontale.
- L'analyse de la pente dans le contexte d'un problème indique si une fonction linéaire est croissante, décroissante ou constante.
- La pente d'une fonction linéaire peut être calculée en divisant la différence entre les valeurs y par la différence entre les valeurs x correspondantes de deux points quelconques de la ligne.
- La pente et la valeur initiale peuvent être déterminées à l'aide d'un graphique ou de deux points quelconques sur la ligne.
- L'un des types de notation des fonctions est la forme d'intersection de pente d'une équation.
- La forme de pente ponctuelle est utile pour trouver une équation linéaire lorsqu'on lui donne la pente d'une droite et un point.
- La forme à pente ponctuelle est également pratique pour trouver une équation linéaire lorsque l'on indique deux points par lesquels passe une droite.
- L'équation d'une fonction linéaire peut être écrite si la pente\(m\) et la valeur initiale\(b\) sont connues.
- Une fonction linéaire peut être utilisée pour résoudre des problèmes du monde réel.
- Une fonction linéaire peut être écrite sous forme de tableau.
Notes
1 www.chinahighlights.com/shang... glev-train.htm
2 www.cbsnews.com/8301-501465_1... ay-study-says/
Lexique
fonction linéaire décroissante
une fonction avec une pente négative : Si\(f(x)=mx+b\), alors\(m<0\).
fonction linéaire croissante
une fonction avec une pente positive : Si\(f(x)=mx+b\), alors\(m>0\).
fonction linéaire
fonction à taux de variation constant qui est un polynôme de degré 1 et dont le graphe est une ligne droite
forme à pente ponctuelle
l'équation d'une droite qui représente une fonction linéaire de la forme \ (y−y_1=m (x−x_1)
pente
le rapport entre la variation des valeurs de sortie et la variation des valeurs d'entrée ; une mesure de la pente d'une ligne
formulaire d'interception de pente
l'équation d'une droite qui représente une fonction linéaire dans le formulaire\(f(x)=mx+b\)
Interception Y
la valeur d'une fonction lorsque la valeur d'entrée est nulle ; également appelée valeur initiale