2.2 : Équations linéaires dans une variable
- Page ID
- 195138
- Résolvez algébriquement les équations d'une variable.
- Résolvez une équation rationnelle.
- Trouvez une équation linéaire.
- À partir des équations de deux droites, déterminez si leurs graphes sont parallèles ou perpendiculaires.
- Ecrivez l'équation d'une droite parallèle ou perpendiculaire à une droite donnée.
Caroline est une étudiante à temps plein qui planifie des vacances de printemps. Pour gagner suffisamment d'argent pour le voyage, elle a accepté un emploi à temps partiel à la banque locale qui paie\($15.00/hr\) et elle a ouvert un compte d'épargne avec un dépôt initial du 15\($400\) janvier. Elle a pris des dispositions pour le dépôt direct de ses chèques de paie. Si les vacances de printemps commencent le 20 mars et que le voyage coûtera environ\($2,500\), combien d'heures devra-t-elle travailler pour gagner suffisamment pour payer ses vacances ? Si elle ne peut travailler que des\(4\) heures par jour, combien de jours par semaine devra-t-elle travailler ? Combien de semaines cela prendra-t-il ? Dans cette section, nous étudierons des problèmes de ce type et d'autres, qui génèrent des graphiques tels que la ligne de la figure\(\PageIndex{1}\).
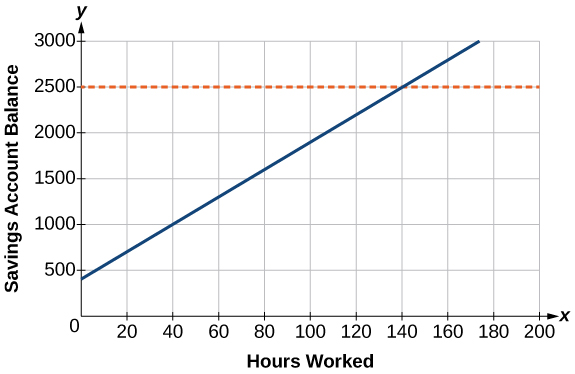
Résolution d'équations linéaires dans une variable
Une équation linéaire est une équation d'une ligne droite, écrite dans une variable. La seule puissance de la variable est\(1\). Les équations linéaires d'une variable peuvent prendre la forme\(ax +b=0\) et être résolues à l'aide d'opérations algébriques de base. Nous commençons par classer les équations linéaires d'une variable en trois types : identitaires, conditionnelles ou incohérentes.
- Une équation d'identité est vraie pour toutes les valeurs de la variable. Voici un exemple d'équation d'identité :\[3x=2x+x \nonumber \] L'ensemble de solutions comprend toutes les valeurs qui rendent l'équation vraie. Pour cette équation, l'ensemble de solutions est composé uniquement de nombres réels, car tout nombre réel substitué à cela\(x\) rendra l'équation vraie.
- Une équation conditionnelle n'est vraie que pour certaines valeurs de la variable. Par exemple, si nous voulons résoudre l'équation\(5x+2=3x−6\), nous avons ce qui suit :\[\begin{align*} 5x+2&=3x-6 \\ 2x &=-8 \\ x&=-4 \end{align*} \] Le jeu de solutions se compose d'un nombre :\({−4}\). C'est la seule solution et nous avons donc résolu une équation conditionnelle.
- Une équation incohérente donne lieu à une fausse déclaration. Par exemple, si nous voulons résoudre\(5x−15=5(x−4)\), nous avons ce qui suit :\[\begin{align*} 5x−15 &=5x−20 \\ 5x−15-5x &= 5x−20-5x \\ −15 &\neq −20 \end{align*}\] En effet,\(−15≠−20\). Il n'y a pas de solution car il s'agit d'une équation incohérente.
La résolution d'équations linéaires dans une variable implique les propriétés fondamentales de l'égalité et les opérations algébriques de base. Un bref aperçu de ces opérations suit.
Une équation linéaire dans une variable peut être écrite sous la forme
\[ax+b=0\]
où a et b sont des nombres réels,\(a≠0\).
Les étapes suivantes permettent de manipuler une équation et d'isoler la variable inconnue, de sorte que la dernière ligne indique\(x=\) _________, si\(x\) c'est l'inconnu. Il n'y a pas d'ordre défini, car les étapes utilisées dépendent de ce qui est donné :
- Nous pouvons ajouter, soustraire, multiplier ou diviser une équation par un nombre ou une expression tant que nous faisons la même chose des deux côtés du signe égal. Notez que nous ne pouvons pas diviser par zéro.
- Appliquez la propriété distributive selon les besoins :\(a(b+c)=ab+ac\).
- Isolez la variable d'un côté de l'équation.
- Lorsque la variable est multipliée par un coefficient au stade final, multipliez les deux côtés de l'équation par l'inverse du coefficient.
Résolvez l'équation suivante :\(2x+7=19\).
Solution
Cette équation peut être écrite sous la forme\(ax +b=0\) en soustrayant 19 des deux côtés. Cependant, nous pouvons procéder à la résolution de l'équation dans sa forme originale en effectuant des opérations algébriques.
\[\begin{align*} 2x+7&=19\\ 2x&=12\qquad \text{Subtract 7 from both sides}\\ x&=6\qquad \text{Multiply both sides by } \dfrac{1}{2} \text{ or divide by } 2 \end{align*}\]
La solution est\(6\).
Résolvez l'équation linéaire en une variable :\(2x+1=−9\).
- Réponse
-
\(x=−5\)
Résolvez l'équation suivante :\(4(x−3)+12=15−5(x+6)\).
Solution
Appliquez les propriétés algébriques standard.
\[\begin{align*} 4(x-3)+12&=15-5(x+6)\\ 4x-12+12&=15-5x-30\qquad \text{Apply the distributive property}\\ 4x&=-15-5x\qquad \text{Combine like terms}\\ 9x&=-15\qquad \text{Place x terms on one side and simplify}\\ x&=-\dfrac{15}{9}\qquad \text{Multiply both sides by } \dfrac{1}{9} \text { , the reciprocal of } 9\\ x&=-\dfrac{5}{3} \end{align*}\]
Analyse
Ce problème nécessite que la propriété distributive soit appliquée deux fois, puis que les propriétés de l'algèbre soient utilisées pour atteindre la ligne finale\(x=-\dfrac{5}{3}\).
Résolvez l'équation en une variable :\(−2(3x−1)+x=14−x\).
- Réponse
-
\(x=-3\)
Résoudre une équation rationnelle
Dans cette section, nous examinons des équations rationnelles qui, après quelques manipulations, aboutissent à une équation linéaire. Si une équation contient au moins une expression rationnelle, elle est considérée comme une équation rationnelle. Rappelez-vous qu'un nombre rationnel est le rapport entre deux nombres, tels que\(\dfrac{2}{3}\) ou\(\dfrac{7}{2}\). Une expression rationnelle est le rapport, ou quotient, de deux polynômes. Voici trois exemples.
\[\dfrac{x+1}{x^2-4} \nonumber \]
\[\dfrac{1}{x-3} \nonumber \]
ou
\[\dfrac{4}{x^2+x-2} \nonumber \]
Les équations rationnelles ont une variable dans le dénominateur d'au moins un des termes. Notre objectif est d'effectuer des opérations algébriques afin que les variables apparaissent dans le numérateur. En fait, nous allons éliminer tous les dénominateurs en multipliant les deux côtés de l'équation par le plus petit dénominateur commun (LCD). Trouver l'écran LCD consiste à identifier une expression qui contient la puissance la plus élevée de tous les facteurs de tous les dénominateurs. Nous faisons cela parce que lorsque l'équation est multipliée par l'écran LCD, les facteurs communs à l'écran LCD et à chaque dénominateur seront égaux à un et s'annuleront.
Résolvez l'équation rationnelle :
\[\dfrac{7}{2x}-\dfrac{5}{3x}=\dfrac{22}{3} \nonumber \]
Solution
Nous avons trois dénominateurs ;\(2x\)\(3x\), et\(3\). L'écran LCD doit contenir\(2x\)\(3x\), et\(3\). Un écran LCD de\(6x\) contient les trois dénominateurs. En d'autres termes, chaque dénominateur peut être réparti uniformément sur l'écran LCD. Ensuite, multipliez les deux côtés de l'équation par l'écran LCD\(6x\).
\ [\ begin {align*}
(6x) \ left [\ dfrac {7} {2x} - \ dfrac {5} {3x} \ right] &= \ left [\ dfrac {22} {3} \ right] (6x) \ \ (6x) \ left (\ dfrac {7} {2x} \ right) -
(6x) \ left (\ dfrac {7} {2x} \ right) - (6x) \ left (\ dfrac {7} {2x} \ right) - (6x) \ left (\ dfrac {7} ac {5} {3x} \ right) &= \ left (\ dfrac {22} {3} \ right) (6x) \ qquad \ text {Utilisez la propriété distributive. Annulez les facteurs communs} \ \
3 (7) -2 (5) &=22 (2x) \ qquad \ text {Multipliez les facteurs restants par chaque numérateur.} \ \
21-10&=44x \ \
11&=44x \ \
\ dfrac {11} {44} &=x \ \
\ dfrac {1} {4} &=x
\ end {align*} \]
Une erreur courante commise lors de la résolution d'équations rationnelles consiste à trouver l'écran LCD lorsque l'un des dénominateurs est un binôme (deux termes ajoutés ou soustraits), tel que\((x+1)\). Considérez toujours un binôme comme un facteur individuel ; les termes ne peuvent pas être séparés. Supposons, par exemple, qu'un problème comporte trois termes et que les dénominateurs soient\(x\)\(x−1\), et\(3x−3\). Tout d'abord, factorisez tous les dénominateurs. Nous avons donc\(x\)\((x−1)\), et\(3(x−1)\) comme dénominateurs. (Notez les parenthèses placées autour du deuxième dénominateur.) Seuls les deux derniers dénominateurs ont un facteur commun de\((x−1)\). Le x dans le premier dénominateur est séparé du\(x\) dans les\((x−1)\) dénominateurs. Un moyen efficace de s'en souvenir est d'écrire les dénominateurs factoriels et binomiaux entre parenthèses et de considérer chaque parenthèse comme une unité ou un facteur distinct. Dans ce cas, l'écran LCD est obtenu en multipliant le\(x\), un facteur de\((x−1)\), et le 3. Ainsi, l'écran LCD est le suivant :
\(x(x−1)3=3x(x−1)\)
Ainsi, les deux côtés de l'équation seraient multipliés par\(3x(x−1)\). Laissez l'écran LCD sous forme pondérée, car cela permet de voir plus facilement comment chaque dénominateur du problème s'annule.
Un autre exemple est un problème avec deux dénominateurs, tels que\(x\) et\(x^2+2x\). Une fois que le deuxième dénominateur est pris en compte comme\(x^2+2x=x(x+2)\), il existe un facteur commun entre\(x\) les deux dénominateurs et l'écran LCD l'est\(x(x+2)\).
Parfois, nous avons une équation rationnelle sous forme de proportion, c'est-à-dire lorsqu'une fraction est égale à une autre fraction et qu'il n'y a aucun autre terme dans l'équation.
\[\dfrac{a}{b}=\dfrac{c}{d}\]
Nous pouvons utiliser une autre méthode pour résoudre l'équation sans trouver l'écran LCD : la multiplication croisée. Nous multiplions les termes en croisant le signe égal.
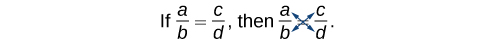
Multipliez a (d) et b (c), ce qui donne\(ad=bc\).
Toute solution qui fait en sorte qu'un dénominateur dans l'expression d'origine soit égal à zéro doit être exclue des possibilités.
Une équation rationnelle contient au moins une expression rationnelle dans laquelle la variable apparaît dans au moins l'un des dénominateurs.
- Facturez tous les dénominateurs de l'équation.
- Trouvez et excluez les valeurs qui attribuent à chaque dénominateur la valeur zéro.
- Trouvez l'écran LCD.
- Multipliez l'équation complète par l'écran LCD. Si l'écran LCD est correct, il ne restera aucun dénominateur.
- Résolvez l'équation restante.
- Assurez-vous de vérifier les solutions dans les équations d'origine pour éviter qu'une solution ne produise zéro dans un dénominateur
Résolvez l'équation rationnelle suivante :
\(\dfrac{2}{x}-\dfrac{3}{2}=\dfrac{7}{2x}\)
SolutionNous avons trois dénominateurs :\(x\),\(2\), et\(2x\). Aucun affacturage n'est requis. Le produit des deux premiers dénominateurs est égal au troisième dénominateur, donc l'écran LCD l'est\(2x\). Une seule valeur est exclue d'un ensemble de solutions,\(0\). Ensuite, multipliez l'ensemble de l'équation (des deux côtés du signe égal) par\(2x\).
\[\begin{align*} 2x\left[\dfrac{2}{x}-\dfrac{3}{2}\right]&=\left[\dfrac{7}{2x}\right](2x)\\ 2x\left(\dfrac{2}{x}\right)-2x\left(\dfrac{3}{2}\right)&=\left(\dfrac{7}{2x}\right)(2x)\qquad \text{Distribute } 2x\\ 2(2)-3x&=7\qquad \text{Denominators cancel out.}\\ 4-3x&=7\\ -3x&=3\\ x&=-1 \text { or } \{-1\} \end{align*}\]
La solution proposée est\(−1\), qui n'est pas une valeur exclue, de sorte que l'ensemble de solutions contient un chiffre ou est\(\{−1\}\) écrit en notation d'ensemble.\(x=−1\)
Résolvez l'équation rationnelle :
\(\dfrac{2}{3x}=\dfrac{1}{4}-\dfrac{1}{6x}\)
- Réponse
-
\(x=\dfrac{10}{3}\)
Résolvez l'équation rationnelle suivante :
\(\dfrac{1}{x}=\dfrac{1}{10}-\dfrac{3}{4x}\)
Solution
Trouvez d'abord le dénominateur commun. Les trois dénominateurs sous forme pondérée sont\(x,10=2⋅5\), et\(4x=2⋅2⋅x\). La plus petite expression divisible par chacun des dénominateurs est\(20x\). Seule\(x=0\) est une valeur exclue. Multipliez l'ensemble de l'équation par\(20x\).
\[\begin{align*} 20x\left(\dfrac{1}{x}\right)&= \left(\dfrac{1}{10}-\dfrac{3}{4x}\right)20x\\ 20&= 2x-15\\ 35&= 2x\\ \dfrac{35}{2}&= x \end{align*}\]
La solution est\(\dfrac{35}{2}\).
Résolvez l'équation rationnelle :
\[-\dfrac{5}{2x}+\dfrac{3}{4x}=-\dfrac{7}{4} \nonumber \]
- Réponse
-
\(x=1\)
Résolvez les équations rationnelles suivantes et indiquez les valeurs exclues :
- \(\dfrac{3}{x-6}=\dfrac{5}{x}\)
- \(\dfrac{x}{x-3}=\dfrac{5}{x-3}-\dfrac{1}{2}\)
- \(\dfrac{x}{x-2}=\dfrac{5}{x-2}-\dfrac{1}{2}\)
Solution
un.
Les dénominateurs\(x\) et les dénominateurs n'\(x−6\)ont rien en commun. Par conséquent, l'écran LCD est le produit\(x(x−6)\). Cependant, pour ce problème, nous pouvons effectuer une multiplication croisée.
\[\begin{align*} \dfrac{3}{x-6}&=\dfrac{5}{x}\\ 3x&=5(x-6)\qquad \text{Distribute.}\\ 3x&=5x-30\\ -2x&=-30\\ x&=15 \end{align*}\]
La solution est\(15\). Les valeurs exclues sont\(6\) et\(0\).
b.
L'écran LCD est\(2(x−3)\). Multipliez les deux côtés de l'équation par\(2(x−3)\).
\[\begin{align*} 2(x-3)\left [\dfrac{x}{x-3} \right ]&= \left [\dfrac{5}{x-3}-\dfrac{1}{2} \right ]2(x-3)\\ \dfrac{2(x-3)x}{x-3}&= \dfrac{2(x-3)5}{x-3}-\dfrac{2(x-3)}{2}\\ 2x&= 10-(x-3)\\ 2x&= 13-x\\ 3x&= 13\\ x&= \dfrac{13}{3} \end{align*}\]
La solution est\(\dfrac{13}{3}\). La valeur exclue est\(3\).
c.
Le plus petit dénominateur commun est\(2(x−2)\). Multipliez les deux côtés de l'équation par\(x(x−2)\).
\[\begin{align*} 2(x-2)\left [\dfrac{x}{x-2} \right ]&= \left [\dfrac{5}{x-2}-\dfrac{1}{2} \right ]2(x-2)\\ 2x&= 10-(x-2)\\ 2x&= 12-x\\ 3x&= 12\\ x&= 4 \end{align*}\]
La solution est\(4\). La valeur exclue est\(2\).
Résoudre\(\dfrac{-3}{2x+1}=\dfrac{4}{3x+1}\). Indiquez les valeurs exclues.
- Réponse
-
\(x=-\dfrac{7}{17}\). Les valeurs exclues sont\(x=−12\) et\(x=−13\).
Résolvez l'équation rationnelle après avoir factorisé les dénominateurs :\(\dfrac{2}{x+1}-\dfrac{1}{x-1}=\dfrac{2x}{x^2-1}\). Indiquez les valeurs exclues.
Solution
Nous devons prendre en compte le dénominateur\(x^2−1\). Nous reconnaissons cela comme la différence de carrés et la factorisons comme\((x−1)(x+1)\). Ainsi, l'écran LCD qui contient chaque dénominateur est\((x−1)(x+1)\). Multipliez l'équation complète par l'écran LCD, annulez les dénominateurs et résolvez l'équation restante.
\[\begin{align*} (x+1)(x-1)\left [\dfrac{2}{x+1}-\dfrac{1}{x-1} \right ]&= \left [\dfrac{2x}{x^2-1} \right ](x+1)(x-1)\\ 2(x-1)-(x+1)&= 2x\\ 2x-2-x-1&= 2x \text{ Distribute the negative sign}\\ -3-x&= 0\\ x&= -3 \end{align*}\]
La solution est\(−3\). Les valeurs exclues sont\(1\) et\(−1\).
Résolvez l'équation rationnelle :
\(\dfrac{2}{x-2}+\dfrac{1}{x+1}=\dfrac{1}{x^2-x-2}\)
- Réponse
-
\(x=\dfrac{1}{3}\)
Trouver une équation linéaire
La forme la plus familière d'une équation linéaire est peut-être la forme d'intersection de pente, écrite comme «\[y=mx+b\] où »\(m=\text{slope}\) et\(b=\text{y−intercept.}\) « Commençons par la pente ».
La pente d'une ligne fait référence au rapport entre la variation\(y\) verticale et la variation horizontale\(x\) entre deux points quelconques d'une ligne. Il indique la direction dans laquelle une ligne s'incline ainsi que sa pente. La pente est parfois décrite comme une montée au-dessus d'une course.
Si la pente est positive, la ligne est inclinée vers la droite. Si la pente est négative, la ligne est inclinée vers la gauche. À mesure que la pente augmente, la ligne devient plus raide. Quelques exemples sont présentés dans la figure\(\PageIndex{2}\). Les lignes indiquent les pentes suivantes :\(m=−3\),\(m=2\), et\(m=\dfrac{1}{3}\).
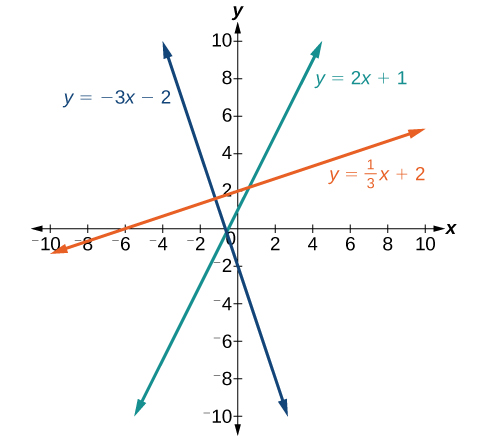
La pente d'une droite,\(m\), représente la variation\(y\) par rapport à la variation de\(x\). Étant donné deux points,\((x_1,y_1)\) et\((x_2,y_2)\), la formule suivante détermine la pente d'une ligne contenant ces points :
\[m=\dfrac{y_2-y_1}{x_2-x_1}\]
Détermine la pente d'une ligne passant par les points\((2,−1)\) et\((−5,3)\).
Solution
Nous remplaçons les\(y\) valeurs -et les\(x\) valeurs -dans la formule.
\[\begin{align*} m&= \dfrac{3-(-1)}{-5-2}\\ &= \dfrac{4}{-7}\\ &= -\dfrac{4}{7} \end{align*}\]
La pente est\(-\dfrac{4}{7}\)
Analyse
Peu importe quel point est appelé\((x_1,y_1)\) ou\((x_2,y_2)\). Tant que nous respectons l'ordre des\(y\) termes et l'ordre des\(x\) termes au numérateur et au dénominateur, le calcul donnera le même résultat.
Déterminez la pente de la ligne qui passe par les points\((−2,6)\) et\((1,4)\).
- Réponse
-
\(m=-\dfrac{2}{3}\)
Identifiez la pente et l'\(y\)intersection, en fonction de l'équation\(y=-\dfrac{3}{4}x-4\).
Solution
Comme la ligne est en\(y=mx+b\) forme, la ligne donnée a une pente de\(m=-\dfrac{3}{4}\). Le\(y\) -intercept est\(b=−4\).
Analyse
L'\(y\)-intercept est le point auquel la ligne croise l'\(y\)axe. Sur l'\(y\)axe -,\(x=0\). Nous pouvons toujours identifier le\(y\) -intercept lorsque la ligne est sous forme d'intersection inclinée, car elle sera toujours égale\(b\). Ou, remplacez-la\(x=0\) et résolvez simplement\(y\).
La formule Point-Slope
Étant donné la pente et un point sur une droite, nous pouvons trouver l'équation de la droite à l'aide de la formule de pente ponctuelle.
\[y−y_1=m(x−x_1)\]
Il s'agit d'une formule importante, car elle sera utilisée dans d'autres domaines de l'algèbre universitaire et souvent en calcul pour trouver l'équation d'une tangente. Nous n'avons besoin que d'un point et de la pente de la droite pour utiliser la formule. Après avoir substitué la pente et les coordonnées d'un point dans la formule, nous la simplifions et l'écrivons sous forme d'intersection de pente.
À partir d'un point et de la pente, la formule de pente ponctuelle aboutira à l'équation d'une droite :
\[y−y_1=m(x−x_1)\]
Écrivez l'équation de la droite avec pente\(m=−3\) et passant par le point\((4,8)\). Écrivez l'équation finale sous forme d'intersection de pente.
Solution
À l'aide de la formule de pente ponctuelle, remplacez\(−3\) m et le point\((4,8)\) par\((x_1,y_1)\).
\[\begin{align*} y-y_1&= m(x-x_1)\\ y-8&= -3(x-4)\\ y-8&= -3x+12\\ y&= -3x+20 \end{align*}\]
Analyse
Notez que n'importe quel point de la ligne peut être utilisé pour trouver l'équation. Si cela est fait correctement, la même équation finale sera obtenue.
Étant donné\(m=4\), trouvez l'équation de la droite sous forme d'intersection de pente passant par le point\((2,5)\).
- Réponse
-
\(y=4x−3\)
Trouvez l'équation de la droite passant par les points\((3,4)\) et\((0,−3)\). Écrivez l'équation finale sous forme d'intersection de pente.
Solution
Nous calculons d'abord la pente à l'aide de la formule de pente et de deux points.
\[\begin{align*} m&= \dfrac{-3-4}{0-3}\\ m&= \dfrac{-7}{-3}\\ m&= \dfrac{7}{3}\\ \end{align*}\]
Ensuite, nous utilisons la formule de pente ponctuelle avec la pente de\(\dfrac{7}{3}\), et l'un ou l'autre point. Choisissons le point\((3,4)\) pour\((x_1,y_1)\).
\[\begin{align*} y-4&= \dfrac{7}{3}(x-3)\\ y-4&= \dfrac{7}{3}x-7\\ y&= \dfrac{7}{3}x-3\\ \end{align*}\]
Sous forme d'intersection de pente, l'équation s'écrit comme suit :\(y=\dfrac{7}{3}x-3\)
Analyse
Pour prouver que l'un ou l'autre point peut être utilisé, utilisons le deuxième point\((0,−3)\) et voyons si nous obtenons la même équation.
\[\begin{align*} y-(-3)&= \dfrac{7}{3}(x-0)\\ y+3&= \dfrac{7}{3}x\\ y&= \dfrac{7}{3}x-3\\ \end{align*}\]
Nous voyons que la même ligne sera obtenue en utilisant l'un ou l'autre point. Cela est logique car nous avons utilisé les deux points pour calculer la pente.
Forme standard d'une ligne
Une autre façon de représenter l'équation d'une droite est la forme standard. Le formulaire standard est donné sous la forme
\[Ax+By=C\]
où\(A\)\(B\), et\(C\) sont des nombres entiers. Les\(y\) termes\(x\) - et - se trouvent d'un côté du signe égal et le terme constant se trouve de l'autre côté.
Trouvez l'équation de la droite avec\(m=−6\) et passant par le point\(\left(\dfrac{1}{4},−2\right)\). Écrivez l'équation sous forme standard.
Solution
Nous commençons par utiliser la formule de pente ponctuelle.
\[\begin{align*} y-(-2)&= -6\left(x-\dfrac{1}{4}\right)\\ y+2&= -6x+\dfrac{3}{2}\\ \end{align*}\]
À partir de là, nous multiplions par\(2\), car aucune fraction n'est autorisée dans la forme standard, puis nous déplaçons les deux variables vers la gauche du signe égal et déplaçons les constantes vers la droite.
\[\begin{align*} 2(y+2)&= \left(-6x+\dfrac{3}{2}\right)2\\ 2y+4&= -12x+3\\ 12x+2y&= -1 \end{align*}\]
Cette équation est maintenant écrite sous forme standard.
Trouvez l'équation de la droite sous forme standard avec pente\(m=−\dfrac{1}{3}\) et passant par le point\((1,13)\).
- Réponse
-
\(x+3y=2\)
Lignes verticales et horizontales
Les équations des lignes verticales et horizontales ne nécessitent aucune des formules précédentes, bien que nous puissions utiliser les formules pour prouver que les équations sont correctes. L'équation d'une droite verticale est donnée sous la forme
où\(c\) est une constante. La pente d'une ligne verticale n'est pas définie et, quelle que soit la\(y\) valeur -de n'importe quel point de la ligne, la\(x\) coordonnée du point sera\(c\).
Supposons que nous souhaitions trouver l'équation d'une droite contenant les points suivants :\((−3,−5)\)\((−3,1)\),\((−3,3)\), et\((−3,5)\). Nous allons d'abord trouver la pente.
Zéro dans le dénominateur signifie que la pente n'est pas définie et que, par conséquent, nous ne pouvons pas utiliser la formule de pente ponctuelle. Cependant, nous pouvons tracer les points. Notez que toutes les\(x\) coordonnées sont identiques et que nous trouvons une ligne verticale\(x=−3\). Voir la figure\(\PageIndex{3}\).
L'équation d'une droite horizontale est donnée sous la forme
\[y=c\]
où\(c\) est une constante. La pente d'une ligne horizontale est nulle, et pour toute\(x\) valeur -d' un point de la ligne, la\(y\) coordonnée sera\(c\).
Supposons que nous souhaitions trouver l'équation d'une droite contenant l'ensemble de points suivant :\((−2,−2)\)\((0,−2)\),\((3,−2)\), et\((5,−2)\). Nous pouvons utiliser la formule de pente ponctuelle. Tout d'abord, nous trouvons la pente en utilisant deux points quelconques sur la ligne.
\[\begin{align*} m&= \dfrac{-2-(-2)}{0-(-2)}\\ &= \dfrac{0}{2}\\ &= 0 \end{align*}\]
Utilisez n'importe quel point de la formule ou utilisez l'intersection Y.\((x_1,y_1)\)
\[\begin{align*} y-(-2)&= 0(x-3)\\ y+2&= 0\\ y&= -2 \end{align*}\]
Le graphique est une ligne horizontale traversante\(y=−2\). Notez que toutes les coordonnées y sont identiques. Voir la figure\(\PageIndex{3}\).
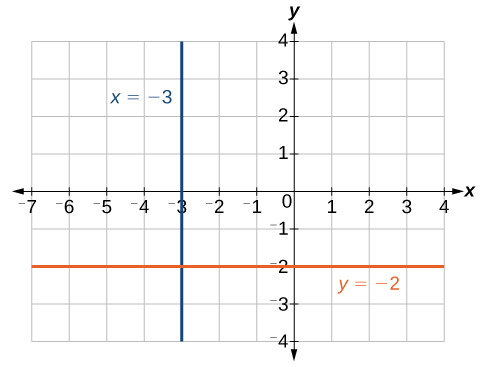
Trouvez l'équation de la droite passant par les points donnés :\((1,−3)\) et\((1,4)\).
Solution
La\(x\) coordonnée des deux points est\(1\). Par conséquent, nous avons une ligne verticale,\(x=1\).
Trouvez l'équation de la droite passant par\((−5,2)\) et\((2,2)\).
- Réponse
-
Ligne horizontale :\(y=2\)
Déterminer si les graphes de lignes sont parallèles ou perpendiculaires
Les lignes parallèles ont la même pente et des intersections Y différentes. Les lignes parallèles ne se croisent jamais. Par exemple, la figure\(\PageIndex{4}\) montre les graphes de différentes lignes ayant la même pente,\(m=2\).
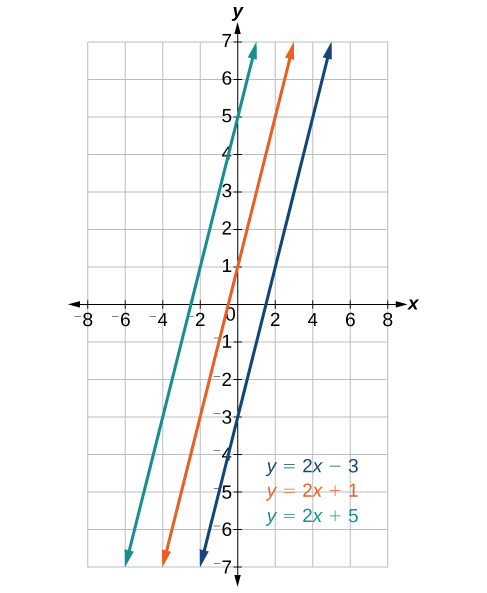
Toutes les lignes affichées sur le graphique sont parallèles car elles ont la même pente et des intersections Y différentes.
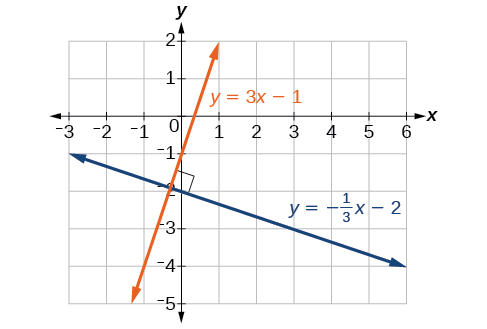
Les lignes perpendiculaires se croisent pour former un\(90^{\circ}\) angle. La pente d'une droite est l'inverse négatif de l'autre. Nous pouvons montrer que deux droites sont perpendiculaires si le produit des deux pentes est\(−1:m_1⋅m_2=−1\). Par exemple, la figure\(\PageIndex{5}\) montre le graphique de deux lignes perpendiculaires. Une ligne a une pente de\(3\) ; l'autre ligne a une pente de\(-\dfrac{1}{3}\).
\[\begin{align*} m_1\cdot m_2&= -1\\ 3\cdot \left (-\dfrac{1}{3} \right )&= -1\\ \end{align*}\]
Représentez graphiquement les équations des droites données et indiquez si elles sont parallèles, perpendiculaires ou aucune des deux :\(3y=−4x+3\) et\(3x−4y=8\).
Solution
La première chose que nous voulons faire est de réécrire les équations de manière à ce que les deux équations soient sous forme d'intersection de pente.
Première équation :
\[\begin{align*} 3y&= -4x+3\\ y&= -\dfrac{4}{3}x+1\\ \end{align*}\]
Deuxième équation :
\[\begin{align*} 3x-4y&= 8\\ -4y&= -3x+8\\ y&= \dfrac{3}{4}x-2 \end{align*}\]
Voir le graphique des deux lignes dans la figure\(\PageIndex{6}\).
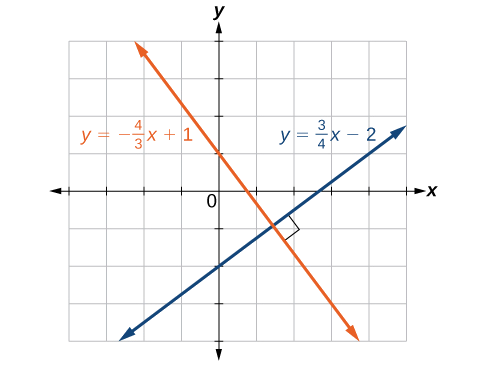
Sur le graphique, nous pouvons voir que les lignes apparaissent perpendiculaires, mais nous devons comparer les pentes.
\[\begin{align*} m_1&=-\dfrac{4}{3}\\ m_2&=\dfrac{3}{4}\\ m_1\cdot m_2&=\left(-\dfrac{4}{3}\right)\left(\dfrac{3}{4}\right)\\ &=-1 \end{align*}\]
Les pentes sont réciproques négatives, ce qui confirme que les lignes sont perpendiculaires.
Tracez les deux lignes et déterminez si elles sont parallèles, perpendiculaires ou aucune des deux :\(2y−x=10\) et\(2y=x+4\).
- Réponse
-
Lignes parallèles : les équations sont écrites sous forme d'intersection de pente.
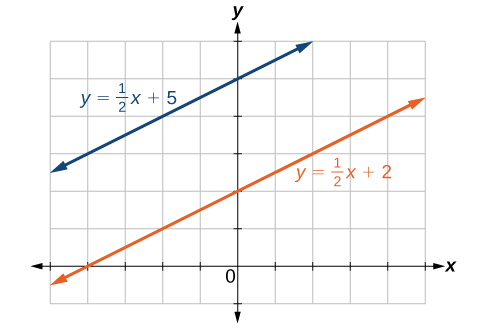
Figurine\(\PageIndex{7}\)
Écrire les équations de droites parallèles ou perpendiculaires à une droite donnée
Comme nous l'avons appris, déterminer si deux droites sont parallèles ou perpendiculaires consiste à déterminer les pentes. Pour écrire l'équation d'une droite parallèle ou perpendiculaire à une autre droite, nous suivons les mêmes principes que pour trouver l'équation de n'importe quelle droite. Après avoir trouvé la pente, utilisez la formule de pente ponctuelle pour écrire l'équation de la nouvelle droite.
À
- Détermine la pente de la ligne donnée. Le moyen le plus simple de le faire est d'écrire l'équation sous forme d'intersection de pente.
- Utilisez la pente et le point donné avec la formule de pente ponctuelle.
- Simplifiez la forme de la ligne à l'intersection de la pente et comparez l'équation à la droite donnée.
Ecrivez l'équation de la droite parallèle à a\(5x+3y=1\) et passant par le point\((3,5)\).
Solution
Nous allons d'abord écrire l'équation sous forme d'intersection de pente pour trouver la pente.
\[\begin{align*} 5x+3y&= 1\\ 3y&= -5x+1\\ y&= -\dfrac{5}{3}x+\dfrac{1}{3} \end{align*}\]
La pente est\(m=−\dfrac{5}{3}\). L'intersection y l'est\(13\), mais cela ne rentre pas vraiment dans notre problème, car la seule chose dont nous avons besoin pour que deux lignes soient parallèles est la même pente. La seule exception est que si les\(y\) -intercepts sont identiques, alors les deux lignes sont identiques. L'étape suivante consiste à utiliser cette pente et le point donné avec la formule de pente ponctuelle.
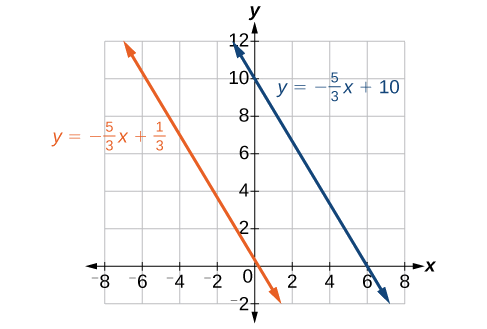
\[\begin{align*} y-5&= -\dfrac{5}{3}(x-3)\\ y-5&= -\dfrac{5}{3}x+5\\ y&= -\dfrac{5}{3}x+10 \end{align*}\]
L'équation de la droite est\(y=−\dfrac{5}{3}x+10\). Voir la figure\(\PageIndex{8}\).
Trouvez l'équation de la droite parallèle au point\(5x=7+y\) et passant par celui-ci\((−1,−2)\).
- Réponse
-
\(y=5x+3\)
Détermine l'équation de la droite perpendiculaire à\(5x−3y+4=0\space(−4,1)\).
Solution
La première étape consiste à écrire l'équation sous forme d'intersection de pente.
\[\begin{align*} 5x-3y+4&= 0\\ -3y&= -5x-4\\ y&= \dfrac{5}{3}x+\dfrac{4}{3} \end{align*}\]
Nous voyons que la pente est\(m=\dfrac{5}{3}\). Cela signifie que la pente de la droite perpendiculaire à la droite donnée est l'inverse négatif, ou\(-\dfrac{3}{5}\). Ensuite, nous utilisons la formule de pente ponctuelle avec cette nouvelle pente et le point donné.
\[\begin{align*} y-1&= -\dfrac{3}{5}(x-(-4))\\ y-1&= -\dfrac{3}{5}x-\dfrac{12}{5}\\ y&= -\dfrac{3}{5}x-\dfrac{12}{5}+\dfrac{5}{5}\\ y&= -\dfrac{3}{5}x-\dfrac{7}{5} \end{align*}\]
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur les équations linéaires.
- Résoudre des équations
- Équation d'une droite à deux points
- Trouver l'équation d'une droite perpendiculaire à une autre droite passant par un point donné
- Trouver l'équation d'une droite parallèle à une autre droite passant par un point donné
Key Concepts
- We can solve linear equations in one variable in the form \(ax +b=0\) using standard algebraic properties. See Example and Example.
- A rational expression is a quotient of two polynomials. We use the LCD to clear the fractions from an equation. See Example and Example.
- All solutions to a rational equation should be verified within the original equation to avoid an undefined term, or zero in the denominator. See Example and Example.
- Given two points, we can find the slope of a line using the slope formula. See Example.
- We can identify the slope and \(y\)-intercept of an equation in slope-intercept form. See Example.
- We can find the equation of a line given the slope and a point. See Example.
- We can also find the equation of a line given two points. Find the slope and use the point-slope formula. See Example.
- The standard form of a line has no fractions. See Example.
- Horizontal lines have a slope of zero and are defined as \(y=c\), where \(c\) is a constant.
- Vertical lines have an undefined slope (zero in the denominator), and are defined as \(x=c\), where \(c\) is a constant. See Example.
- Parallel lines have the same slope and different \(y\)-intercepts. See Example.
- Perpendicular lines have slopes that are negative reciprocals of each other unless one is horizontal and the other is vertical. See Example.


