Chapitre 10 Exercices de révision
- Page ID
- 194608
Chapitre 10 Exercices de révision
10.1 Résoudre des équations quadratiques en utilisant la propriété de racine carrée
Dans les exercices suivants, résolvez à l'aide de la propriété Square Root.
\(x^2=100\)
- Réponse
-
\(x=\pm10\)
\(y^2=144\)
\(m^2−40=0\)
- Réponse
-
\(m=\pm2\sqrt{10}\)
\(n^2−80=0\)
\(4a^2=100\)
- Réponse
-
\(a=\pm5\)
\(2b^2=72\)
\(r^2+32=0\)
- Réponse
-
aucune solution
\(t^2+18=0\)
\(\frac{4}{3}v^2+4=28\)
- Réponse
-
\(v=\pm3\sqrt{2}\)
\(\frac{2}{3}w^2−20=30\)
\(5c^2+3=19\)
- Réponse
-
\(c=\pm\frac{4\sqrt{5}}{5}\)
\(3d^2−6=43\)
Dans les exercices suivants, résolvez à l'aide de la propriété Square Root.
\((p−5)^2+3=19\)
- Réponse
-
p=1, 9
\((q+4)^2=9\)
\((u+1)^2=45\)
- Réponse
-
\(u=−1\pm3\sqrt{5}\)
\((z−5)^2=50\)
\((x−\frac{1}{4})^2=\frac{3}{16}\)
- Réponse
-
\(x=\frac{1}{4}\pm\frac{\sqrt{3}}{4}\)
\((y−\frac{2}{3})^2=\frac{2}{9}\)
\((m−7)^2+6=30\)
- Réponse
-
\(m=7\pm2\sqrt{6}\)
\((n−4)^2−50=150\)
\((5c+3)^2=−20\)
- Réponse
-
aucune solution
\((4c−1)^2=−18\)
\(m^2−6m+9=48\)
- Réponse
-
\(m=3\pm4\sqrt{3}\)
\(n^2+10n+25=12\)
\(64a^2+48a+9=81\)
- Réponse
-
a=−32, 34
\(4b^2−28b+49=25\)
10.2 Résoudre des équations quadratiques en complétant le carré
Dans les exercices suivants, complétez le carré pour obtenir un trinôme carré parfait. Écrivez ensuite le résultat sous la forme d'un carré binomial.
\(x^2+22x\)
- Réponse
-
\((x+11)^2\)
\(y^2+6y\)
\(m^2−8m\)
- Réponse
-
\((m−4)^2\)
\(n^2−10n\)
\(a^2−3a\)
- Réponse
-
\((a−\frac{3}{2})^2\)
\(b^2+13b\)
\(p^2+\frac{4}{5}p\)
- Réponse
-
\((p+\frac{2}{5})^2\)
\(q^2−13q\)
Dans les exercices suivants, résolvez en complétant le carré.
\(c^2+20c=21\)
- Réponse
-
c=1, −21
\(d^2+14d=−13\)
\(x^2−4x=32\)
- Réponse
-
x=−4, 8
\(y^2−16y=36\)
\(r^2+6r=−100\)
- Réponse
-
aucune solution
\(t^2−12t=−40\)
\(v^2−14v=−31\)
- Réponse
-
\(v=7\pm3\sqrt{2}\)
\(w^2−20w=100\)
\(m^2+10m−4=−13\)
- Réponse
-
\(m=−9,−1\)
\(n^2−6n+11=34\)
\(a^2=3a+8\)
- Réponse
-
\(a=\frac{3}{2}\pm\frac{\sqrt{41}}{2}\)
\(b^2=11b−5\)
\((u+8)(u+4)=14\)
- Réponse
-
\(u=−6\pm2\sqrt{2}\)
\((z−10)(z+2)=28\)
\(3p^2−18p+15=15\)
- Réponse
-
p=0, 6
\(5q^2+70q+20=0\)
\(4y^2−6y=4\)
- Réponse
-
\(y=−\frac{1}{2}, 2\)
\(2x^2+2x=4\)
\(3c^2+2c=9\)
- Réponse
-
\(c=−\frac{1}{3}\pm\frac{2\sqrt{7}}{3}\)
\(4d^2−2d=8\)
10.3 Résoudre des équations quadratiques à l'aide de la formule quadratique
Dans les exercices suivants, résolvez en utilisant la formule quadratique.
\(4x^2−5x+1=0\)
- Réponse
-
\(x=14, 1\)
\(7y^2+4y−3=0\)
\(r^2−r−42=0\)
- Réponse
-
\(r=−6, 7\)
\(t^2+13t+22=0\)
\(4v^2+v−5=0\)
- Réponse
-
\(v=−\frac{5}{4}, 1\)
\(2w^2+9w+2=0\)
\(3m^2+8m+2=0\)
- Réponse
-
\(m=\frac{−4\pm\sqrt{10}}{3}\)
\(5n^2+2n−1=0\)
\(6a^2−5a+2=0\)
- Réponse
-
pas de véritable solution
\(4b^2−b+8=0\)
\(u(u−10)+3=0\)
- Réponse
-
\(u=5\pm2\sqrt{2}\)
\(5z(z−2)=3\)
\(\frac{1}{8}p^2−\frac{1}{5}p=−\frac{1}{20}\)
- Réponse
-
\(p=\frac{4\pm\sqrt{6}}{5}\)
\(\frac{2}{5}q^2+\frac{3}{10}q=\frac{1}{10}\)
\(4c^2+4c+1=0\)
- Réponse
-
\(c=−\frac{1}{2}\)
\(9d^2−12d=−4\)
Dans les exercices suivants, déterminez le nombre de solutions pour chaque équation quadratique.
- \(9x^2−6x+1=0\)
- \(3y^2−8y+1=0\)
- \(7m^2+12m+4=0\)
- \(5n^2−n+1=0\)
- Réponse
-
- 1
- 2
- 2
- aucune
- \(5x^2−7x−8=0\)
- \(7x^2−10x+5=0\)
- \(25x^2−90x+81=0\)
- \(15x^2−8x+4=0\)
Dans les exercices suivants, identifiez la méthode la plus appropriée (affacturage, racine carrée ou formule quadratique) à utiliser pour résoudre chaque équation quadratique.
- \(16r^2−8r+1=0\)
- \(5t^2−8t+3=9\)\(3(c+2)^2=15\)
- Réponse
-
- facteur
- Formule quadratique
- racine carrée
- \(4d^2+10d−5=21\)
- \(25x^2−60x+36=0\)
- \(6(5v−7)^2=150\)
10.4 Résoudre des applications modélisées par des équations quadratiques
Dans les exercices suivants, résolvez en utilisant des méthodes de factorisation, le principe de la racine carrée ou la formule quadratique.
Trouve deux nombres impairs consécutifs dont le produit est 323.
- Réponse
-
Deux nombres impairs consécutifs dont le produit est 323 sont 17 et 19, et −17 et −19.
Trouvez deux nombres pairs consécutifs dont le produit est 624.
Une bannière triangulaire a une superficie de 351 centimètres carrés. La longueur de la base est supérieure de deux centimètres à quatre fois la hauteur. Détermine la hauteur et la longueur de la base.
- Réponse
-
La hauteur de la bannière est de 13 cm et la longueur du côté est de 54 cm.
Julius a construit une vitrine triangulaire pour sa collection de pièces. La hauteur de la vitrine est inférieure de six pouces à deux fois la largeur de la base. La surface du dos du boîtier est de 70 pouces carrés. Trouvez la hauteur et la largeur du boîtier.
Une mosaïque de carreaux en forme de triangle droit est utilisée comme angle d'un chemin rectangulaire. L'hypoténuse de la mosaïque est de 5 pieds. Un côté de la mosaïque est deux fois plus long que l'autre. Quelle est la longueur des côtés ? Arrondir au dixième le plus proche.

- Réponse
-
Les longueurs des côtés de la mosaïque sont de 2,2 et 4,4 pieds.
Un morceau rectangulaire de contreplaqué a une diagonale qui mesure deux pieds de plus que la largeur. La longueur du contreplaqué est le double de la largeur. Quelle est la longueur de la diagonale du contreplaqué ? Arrondir au dixième le plus proche.
La promenade qui mène de la rue à la maison de Pam a une superficie de 250 pieds carrés. Sa longueur est de deux fois moins que quatre fois sa largeur. Déterminez la longueur et la largeur du trottoir. Arrondir au dixième le plus proche.
- Réponse
-
La largeur du trottoir avant est de 8,1 pieds et sa longueur de 30,8 pieds.
Pour la fête de fin d'études de Sophia, plusieurs tables de même largeur seront disposées bout à bout pour donner une table de service d'une superficie totale de 75 pieds carrés. La longueur totale des tables sera deux fois plus que trois fois la largeur. Trouvez la longueur et la largeur de la table de service afin que Sophia puisse acheter la bonne taille de nappe. La réponse est arrondie au dixième le plus proche.
Une balle est lancée verticalement en l'air à une vitesse de 160 pieds/sec. Utilisez la formule\(h=−16t^2+v_{0}t\) pour déterminer quand la balle se trouvera à 384 pieds du sol. Arrondir au dixième le plus proche.
- Réponse
-
Le ballon atteindra 384 pieds en montant en 4 secondes et en descendant en 6 secondes.
Une balle est tirée directement du sol à une vitesse de 320 pieds/sec. Utilisez la formule\(h=−16t^2+v_{0}t\) pour déterminer quand la balle atteindra 800 pieds. Arrondir au dixième le plus proche.
10.5 Représentation graphique d'équations quadratiques à deux variables
Dans les exercices suivants, tracez un graphique par point.
Graphe\(y=x^2−2\)
- Réponse
-
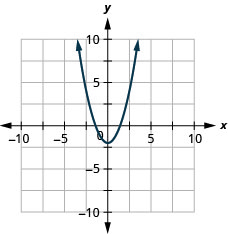
Graphe\(y=−x^2+3\)
Dans les exercices suivants, déterminez si les paraboles suivantes s'ouvrent vers le haut ou vers le bas.
\(y=−3x^2+3x−1\)
- Réponse
-
en bas
\(y=5x^2+6x+3\)
\(y=x^2+8x−1\)
- Réponse
-
en haut
UN\(y=−4x^2−7x+1\)
Dans les exercices suivants, trouvez
- l'axe de symétrie et,
- le sommet.
\(y=−x^2+6x+8\)
- Réponse
-
- x=3
- (3, 17)
\(y=2x^2−8x+1\)
Dans les exercices suivants, trouvez les points d'intersection x et y.
\(y=x^2−4x+5\)
- Réponse
-
y : (0,5) ; x : (5,0), (−1,0)
\(y=x^2−8x+15\)
\(y=x^2−4x+10\)
- Réponse
-
y : (0,10) ; x : aucun
\(y=−5x^2−30x−46\)
\(y=16x^2−8x+1\)
- Réponse
-
y : (0,1) ; x : (14,0)
\(y=x^2+16x+64\)
Dans les exercices suivants, tracez un graphique à l'aide des points d'intersection, du sommet et de l'axe de symétrie.
\(y=x^2+8x+15\)
- Réponse
-
y : (0,15) ; x : (−3,0), (−5,0) ;
axe : x=−4 ; sommet :( −4, −1)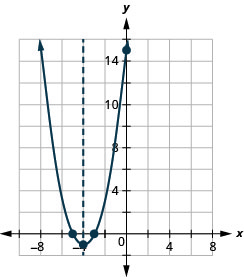
\(y=x^2−2x−3\)
\(y=−x^2+8x−16\)
- Réponse
-
y : (0, −16) ; x : (4,0) ;
axe : x=4 ; sommet :( 4,0)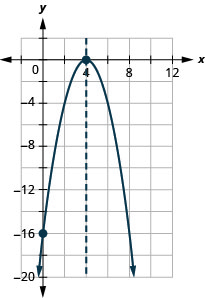
\(y=4x^2−4x+1\)
\(y=x^2+6x+13\)
- Réponse
-
y : (0,13) ; x : aucun ;
axe : x=−3 ; sommet :( −3,4)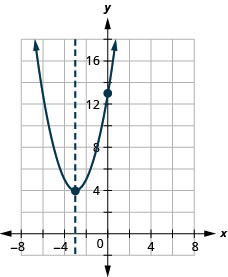
\(y=−2x^2−8x−12\)
\(y=−4x^2+16x−11\)
- Réponse
-
y : (0, −11) ; x : (3,1,0), (0,9,0) ;
axe : x=2 ; sommet :( 2,5)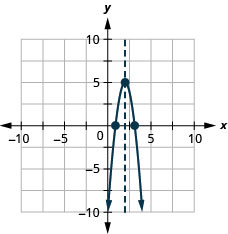
\(y=x^2+8x+10\)
Dans les exercices suivants, déterminez la valeur minimale ou maximale.
\(y=7x^2+14x+6\)
- Réponse
-
La valeur minimale est −1 lorsque\(x=−1\).
\(y=−3x^2+12x−10\)
Dans les exercices suivants, résolvez. En arrondissant les réponses au dixième le plus proche.
Une balle est lancée vers le haut depuis le sol à une vitesse initiale de 112 pieds/sec. Utilisez l'équation quadratique\(h=−16t^2+112t\) pour déterminer le temps qu'il faudra à la balle pour atteindre la hauteur maximale, puis déterminez la hauteur maximale.
- Réponse
-
En 3,5 secondes, le ballon atteint sa hauteur maximale de 196 pieds.
Une garderie délimite un espace rectangulaire le long du bâtiment pour que les enfants puissent jouer à l'extérieur. Ils doivent maximiser la surface en utilisant une clôture de 180 pieds sur trois côtés de la cour. L'équation quadratique\(A=−2x^2+180x\) donne la superficie, A, de la cour pour la longueur, x, du bâtiment qui bordera la cour. Déterminez la longueur du bâtiment qui doit border la cour pour maximiser la surface, puis trouvez la surface maximale.
Test d'entraînement
Utilisez la propriété Square Root pour résoudre l'équation quadratique :\(3(w+5)^2=27\).
- Réponse
-
w=−2, −8
Utilisez Compléter le carré pour résoudre l'équation quadratique :\(a^2−8a+7=23\)
Utilisez la formule quadratique pour résoudre l'équation quadratique :\(2m^2−5m+3=0\).
- Réponse
-
m=1, 32
Résolvez les équations quadratiques suivantes. Utilisez n'importe quelle méthode.
\(8v^2+3=35\)
\(3n^2+8n+3=0\)
- Réponse
-
\(n=\frac{−4\pm\sqrt{7}}{3}\)
\(2b^2+6b−8=0\)
\(x(x+3)+12=0\)
- Réponse
-
pas de véritable solution
\(\frac{4}{3}y^2−4y+3=0\)
Utilisez le discriminant pour déterminer le nombre de solutions de chaque équation quadratique.
\(6p^2−13p+7=0\)
- Réponse
-
2
\(3q^2−10q+12=0\)
Résolvez en utilisant la factorisation, la propriété de la racine carrée ou la formule quadratique.
Trouvez deux nombres pairs consécutifs dont le produit est 360.
- Réponse
-
Deux nombres pairs consécutifs sont −20 et −18 et 18 et 20.
La longueur de la diagonale d'un rectangle est trois de plus que la largeur. La longueur du rectangle est trois fois la largeur. Détermine la longueur de la diagonale. (Arrondir au dixième le plus proche.)
Pour chaque parabole, trouvez
- de quelle manière il s'ouvre,
- l'axe de symétrie,
- le sommet,
- les interceptions x et y, et
- la valeur maximale ou minimale.
\(y=3x^2+6x+8\)
- Réponse
-
- en haut
- \(x=−1\)
- (−1,5)
- y : (0,8) ; x : aucun ; y : (0,8)
- valeur minimale de 5 lorsque\(x=−1\).
\(y=x^2−4\)
\(y=x^2+10x+24\)
- Réponse
-
- en haut
- \(x=−5\)
- (−5, −1)
- y : (0,24) ; x : (−6,0), (−4,0)
- valeur minimale de −5 lorsque\(x=−1\)
\(y=−3x^2+12x−8\)
\(y=−x^2−8x+16\)
- Réponse
-
- vers le bas
- \(x=−4\)
- (−4,32)
- y ; (0,16) ; x : (−9,7,0), (1,7, 0)
- valeur maximale de 32 lorsque\(x=−4\)
Tracez les paraboles suivantes en utilisant les points d'intersection, le sommet et l'axe de symétrie.
\(y=2x^2+6x+2\)
\(y=16x^2+24x+9\)
- Réponse
-
y : (0,9) ; x : (−34,0)
axe :\( x=−\frac{3}{4}\) ; sommet :\((−\frac{3}{4},0)\)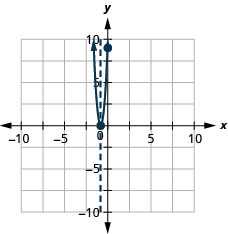
Résoudre.
Un ballon d'eau est lancé vers le haut à une vitesse de 86 pieds par seconde. À l'aide de la formule h=−16t^2+86t, déterminez le temps qu'il faudra au ballon pour atteindre la hauteur maximale, puis déterminez la hauteur maximale. Arrondir au dixième le plus proche.