9.4 : Multiplier les racines carrées
- Page ID
- 194487
À la fin de cette section, vous serez en mesure de :
- Multipliez les racines
- Utilisez la multiplication polynomiale pour multiplier les racines carrées
Avant de commencer, répondez à ce questionnaire de préparation.
- Simplifiez : (3u) (8v).
Si vous avez oublié ce problème, consultez l'exemple 6.2.31. - Simplifier : 6 (12−7n).
Si vous avez oublié ce problème, consultez l'exemple 6.3.1. - Simplifier : (2+a) (4−a).
Si vous avez oublié ce problème, consultez l'exemple 6.3.34.
Multipliez les racines
Nous avons utilisé la propriété de produit des racines carrées pour simplifier les racines carrées en supprimant les facteurs carrés parfaits. La propriété du produit de Square Roots dit
\[\sqrt{ab}=\sqrt{a}·\sqrt{b} \nonumber\]
Nous pouvons utiliser la propriété de produit des racines carrées « à l'envers » pour multiplier les racines carrées.
\[\sqrt{a}·\sqrt{b}=\sqrt{ab} \nonumber\]
N'oubliez pas que nous supposons que toutes les variables sont supérieures ou égales à zéro.
Nous allons réécrire la propriété du produit de Square Roots afin de voir les deux côtés.
Si a, b sont des nombres réels non négatifs, alors
\(\sqrt{ab}=\sqrt{a}·\sqrt{b}\)et\(\sqrt{a}·\sqrt{b}=\sqrt{ab}\).
Nous pouvons donc multiplier\(\sqrt{3}·\sqrt{5}\) in this way:
\[\begin{array}{l} {\sqrt{3}·\sqrt{5}}\\ {\sqrt{3·5}}\\ {\sqrt{15}}\\ \nonumber \end{array}\]
Parfois, le produit nous donne un carré parfait :
\[\begin{array}{l} {\sqrt{2}·\sqrt{8}}\\ {\sqrt{2·8}}\\ {\sqrt{16}}\\ {4}\\ \nonumber \end{array}\]
Même lorsque le produit n'est pas un carré parfait, nous devons rechercher des facteurs de carré parfait et simplifier le radical autant que possible.
Multiplier des radicaux par des coefficients est un peu comme multiplier des variables par des coefficients. Pour multiplier 4x·3y, nous multiplions les coefficients ensemble, puis les variables. Le résultat est 12xy. Gardez cela à l'esprit lorsque vous créez ces exemples.
Simplifiez :
- \(\sqrt{2}·\sqrt{6}\)
- \((4\sqrt{3})(2\sqrt{12})\).
- Réponse
-
1. \(\sqrt{2}·\sqrt{6}\) Multipliez en utilisant la propriété du produit. \(\sqrt{12}\) Simplifiez le radical. \(\sqrt{4}·\sqrt{3}\) Simplifiez. \(2\sqrt{3}\) 2. \((4\sqrt{3})(2\sqrt{12})\) Multipliez en utilisant la propriété du produit. \(8\sqrt{36}\) Simplifiez le radical. \(8·6\) Simplifiez. \(48\)
Simplifiez :
- \(\sqrt{3}·\sqrt{6}\)
- \((2\sqrt{6})(3\sqrt{12})\).
- Réponse
-
- \(3\sqrt{2}\)
- \(36\sqrt{2}\)
Simplifiez :
- \(\sqrt{5}·\sqrt{10}\)
- \((6\sqrt{3})(5\sqrt{6})\)
- Réponse
-
- \(5\sqrt{2}\)
- \(90\sqrt{2}\)
Simplifiez :\((6\sqrt{2})(3\sqrt{10})\)
- Réponse
-
\((6\sqrt{2})(3\sqrt{10})\) Multipliez en utilisant la propriété du produit. \(18\sqrt{20}\) Simplifiez le radical. \(18\sqrt{4}·\sqrt{5}\) Simplifiez. \(18·2·\sqrt{5}\) \(36\sqrt{5}\)
Simplifiez :\((3\sqrt{2})(2\sqrt{30})\)
- Réponse
-
\(12\sqrt{15}\)
Simplifiez :\((3\sqrt{3})(3\sqrt{6})\).
- Réponse
-
\(27\sqrt{2}\)
Lorsque nous devons multiplier les racines carrées, nous trouvons d'abord le produit, puis nous supprimons tous les facteurs carrés parfaits.
Simplifiez :
- \((\sqrt{8x^3})(\sqrt{3x})\)
- \((\sqrt{20y^2})(\sqrt{5y^3})\)
- Réponse
-
1. \((\sqrt{8x^3})(\sqrt{3x})\) Multipliez en utilisant la propriété du produit. \(\sqrt{24x^4}\) Simplifiez le radical. \(\sqrt{4x^4}·\sqrt{6}\) Simplifiez. \(2x^2\sqrt{6}\) 2. \((\sqrt{20y^2})(\sqrt{5y^3})\) Multipliez en utilisant la propriété du produit. \(\sqrt{100y^5}\) Simplifiez le radical. \(10y^2\sqrt{y}\)
Simplifiez :
- \((\sqrt{6x^3})(\sqrt{3x})\)
- \((\sqrt{2y^3})(\sqrt{50y^2})\).
- Réponse
-
- \(3x^2\sqrt{2}\)
- \(10y^2\sqrt{y}\)
Simplifiez :
- \((\sqrt{6x^5})(\sqrt{2x})\)
- \((\sqrt{12y^2})(\sqrt{3y^5})\)
- Réponse
-
- \(2x^3\sqrt{3}\)
- \(6y^2\sqrt{y}\)
Simplifiez :\((10\sqrt{6p^3})(3\sqrt{18p})\)
- Réponse
-
\((10\sqrt{6p^3})(3\sqrt{18p})\) Multipliez. \(30\sqrt{108p^4}\) Simplifiez le radical. \(30\sqrt{36p^4}·\sqrt{3}\) \(30·6p^2·\sqrt{3}\) \(180p^2\sqrt{3}\)
Simplifiez :\((\sqrt{62x^2})(8\sqrt{45x^4})\)
- Réponse
-
\(144x^3\sqrt{10}\)
Simplifiez :\((2\sqrt{6y^4})(12\sqrt{30y})\).
- Réponse
-
\(144y^2\sqrt{5y}\)
Simplifiez :
- \((\sqrt{2})^2\)
- \((−\sqrt{11})^2\).
- Réponse
-
1. \((\sqrt{2})^2\) Réécrivez en tant que produit. \((\sqrt{2})(\sqrt{2})\) Multipliez. \(\sqrt{4}\) Simplifiez. 2 2. \((−\sqrt{11})^2\) Réécrivez en tant que produit. \((−\sqrt{11})(−\sqrt{11})\) Multipliez. \(\sqrt{121}\) Simplifiez. 11
Simplifiez :
- \((\sqrt{12})^2\)
- \((−\sqrt{15})^2\).
- Réponse
-
- 12
- 15
Simplifiez :
- \((\sqrt{16})^2\)
- \((−\sqrt{20})^2\).
- Réponse
-
- 16
- 20
Les résultats de l'exemple précédent nous amènent à cette propriété.
Si a est un nombre réel non négatif, alors
\((\sqrt{a})^2=a\)
En réalisant que la mise au carré et la prise d'une racine carrée sont des opérations « opposées », nous pouvons simplifier\((\sqrt{2})^2\) et obtenir 2 immédiatement. Lorsque nous multiplions les deux racines carrées similaires dans la partie (a) de l'exemple suivant, cela équivaut à la mise au carré.
Simplifiez :
- \((2\sqrt{3})(8\sqrt{3})\)
- \((3\sqrt{6})^2\).
- Réponse
-
1. \((2\sqrt{3})(8\sqrt{3})\) Multipliez. N'oubliez pas,\((\sqrt{3}^2)\) 16·3 Simplifiez. 48 2. \((3\sqrt{6})^2\) Multipliez. 9·6 Simplifiez. 54
Simplifiez :
- \((6\sqrt{11})(5\sqrt{11})\)
- \((5\sqrt{8})^2\).
- Réponse
-
- 330
- 200
Simplifiez :
- \((3\sqrt{7})(10\sqrt{7})\)
- \((−4\sqrt{6})^2\).
- Réponse
-
- 210
- 96
Utiliser la multiplication polynomiale pour multiplier les racines carrées
Dans les exemples suivants, nous utiliserons la propriété distributive pour multiplier des expressions avec des racines carrées.
Nous allons d'abord distribuer puis simplifier les racines carrées lorsque cela est possible.
Simplifiez :
- \(3(5−\sqrt{2})\)
- \(\sqrt{2}(4−\sqrt{10})\).
- Réponse
-
1. \(3(5−\sqrt{2})\) Distribuez. \(15−3\sqrt{2})\) 2. \(\sqrt{2}(4−\sqrt{10})\) Distribuez. \(4\sqrt{2}−\sqrt{20}\) Simplifiez. \(4\sqrt{2}−2\sqrt{5}\)
Simplifiez :
- \(2(3−\sqrt{5})\)
- \(\sqrt{3}(2−\sqrt{18})\).
- Réponse
-
- \(6−2\sqrt{5}\)
- \(2\sqrt{3}−3\sqrt{6}\)
Simplifiez :
- \(6(2+\sqrt{6})\)
- \(\sqrt{7}(1+\sqrt{14})\).
- Réponse
-
- \(12+\sqrt{6}\)
- \(\sqrt{7}+7\sqrt{2}\)
Simplifiez :
- \(\sqrt{5}(7+2\sqrt{5})\)
- \(\sqrt{6}(\sqrt{2}+\sqrt{18})\).
- Réponse
-
1. \(\sqrt{5}(7+2\sqrt{5})\) Distribuez. \(7\sqrt{5}+2·5\) Simplifiez. \(7\sqrt{5}+10\) \(10+7\sqrt{5}\) 2. \(\sqrt{6}(\sqrt{2}+\sqrt{18})\) Multipliez. \(\sqrt{12}+\sqrt{108}\) Simplifiez. \((\sqrt{4}·\sqrt{3}+\sqrt{36}·\sqrt{3})\) \(2\sqrt{3}+6\sqrt{3}\) Combinez comme des radicaux. \(8\sqrt{3}\)
Simplifiez :
- \(\sqrt{6}(1+3\sqrt{6})\)
- \(\sqrt{12}(\sqrt{3}+\sqrt{24})\)
- Réponse
-
- \(18+\sqrt{6}\)
- \(6+12\sqrt{2}\)
Simplifiez :
- \(\sqrt{8}(2−5\sqrt{8})\)
- \(\sqrt{14}(\sqrt{2}+\sqrt{42})\)
- Réponse
-
- \(−40+4\sqrt{2}\)
- \(2\sqrt{7}+14\sqrt{3}\)
Lorsque nous travaillions avec des polynômes, nous multipliions les binômes par les binômes. N'oubliez pas que cela nous a donné quatre produits avant de combiner des termes similaires. Pour être sûrs d'obtenir les quatre produits, nous avons organisé notre travail, généralement selon la méthode FOIL.
Simplifiez :\((2+\sqrt{3})(4−\sqrt{3})\)
- Réponse
-
\((2+\sqrt{3})(4−\sqrt{3})\) Multipliez. \(8−2\sqrt{3}+4\sqrt{3}−3\) Combinez les mêmes termes. \(5+2\sqrt{3}\)
Simplifiez :\((1+\sqrt{6})(3−\sqrt{6})\).
- Réponse
-
\(−3+2\sqrt{6}\)
Simplifiez :\((4−\sqrt{10})(2+\sqrt{10})\).
- Réponse
-
\(−2+2\sqrt{10}\)
Simplifiez :\((3−2\sqrt{7})(4−2\sqrt{7})\).
- Réponse
-
\((3−2\sqrt{7})(4−2\sqrt{7})\) Multipliez. \(12−6\sqrt{7}−8\sqrt{7}+4·7\) Simplifiez. \(12−6\sqrt{7}−8\sqrt{7}+28\) Combinez les mêmes termes. \(40−14\sqrt{7}\)
Simplifiez :\((6−3\sqrt{7})(3+4\sqrt{7})\).
- Réponse
-
\(−66+15\sqrt{7}\)
Simplifiez :\((2−3\sqrt{11})(4−\sqrt{11})\)
- Réponse
-
\(41+14\sqrt{11}\)
Simplifiez :\((3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})\).
- Réponse
-
\(3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})\) Multipliez. \(3·2+12\sqrt{10}−\sqrt{10}−4·5\) Simplifiez. \(6+12\sqrt{10}−\sqrt{10}−20\) Combinez les mêmes termes. \(−14+11\sqrt{10}\)
Simplifiez :\((5\sqrt{3}−\sqrt{7})(\sqrt{3}+2\sqrt{7})\)
- Réponse
-
\(1+9\sqrt{21}\)
Simplifiez :\((\sqrt{6}−3\sqrt{8})(2\sqrt{6}+\sqrt{8})\)
- Réponse
-
\(−12−20\sqrt{3}\)
Simplifiez :\((4−2\sqrt{x})(1+3\sqrt{x})\).
- Réponse
-
\((4−2\sqrt{x})(1+3\sqrt{x})\). Multipliez. \(4+12\sqrt{x}−2\sqrt{x}−6x\) Combinez les mêmes termes. \(4+10\sqrt{x}−6x\)
Simplifiez :\((6−5\sqrt{m})(2+3\sqrt{m})\).
- Réponse
-
\(12+8\sqrt{m}−15m\)
Simplifiez :\((10+3\sqrt{n})(1−5\sqrt{n})\)
- Réponse
-
\(10−47\sqrt{n}−15n\)
Notez que certains produits spéciaux nous ont facilité le travail lorsque nous avons multiplié les binômes plus tôt. Cela est également vrai lorsque nous multiplions les racines carrées. Les formules de produits spéciales que nous avons utilisées sont présentées ci-dessous.
\[\begin{array}{ll} {\textbf{Binomial Squares}}&{\textbf{Product of Conjugates}}\\ {(a+b)^2=a^2+2ab+b^2}&{(a−b)(a+b)=a^2−b^2}\\ {(a−b)^2=a^2−2ab+b^2}&{}\\ \nonumber \end{array}\]
Nous utiliserons les formules spéciales des produits dans les prochains exemples. Nous allons commencer par la formule des carrés binomiaux.
Simplifiez :
- \((2+\sqrt{3})^2\)
- \((4−2\sqrt{5})^2\).
- Réponse
-
Assurez-vous d'inclure le terme 2ab lors de la mise au carré d'un binôme.
1.
2.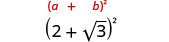
Multipliez en utilisant le motif carré binomial. 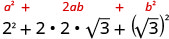
Simplifiez. 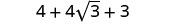
Combinez les mêmes termes. 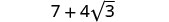
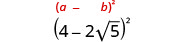
Multipliez en utilisant le motif carré binomial. 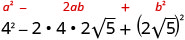
Simplifiez. 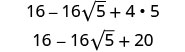
Combinez les mêmes termes. 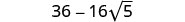
Simplifiez :
- \((10+\sqrt{2})^2\)
- \((1+3\sqrt{6})^2\).
- Réponse
-
- \(102+20\sqrt{2}\)
- \(55+6\sqrt{6}\)
Simplifiez :
- \((6-\sqrt{5})^2\)
- \((9-2\sqrt{10})^2\).
- Réponse
-
- \(41-12\sqrt{5}\)
- \(121-36\sqrt{10}\)
Simplifiez :\((1+3\sqrt{x})^2\).
- Réponse
-
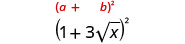
Multipliez en utilisant le motif carré binomial. 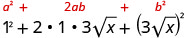
Simplifiez. 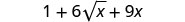
Simplifiez :\((2+5\sqrt{m})^2\).
- Réponse
-
\(4+20\sqrt{m}+25m\)
Simplifiez :\((3−4\sqrt{n})^2\).
- Réponse
-
\(9−24\sqrt{n}+16n\)
Dans les deux exemples suivants, nous trouverons le produit de conjugués.
Simplifiez :\((4−\sqrt{2})(4+\sqrt{2})\).
- Réponse
-
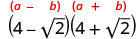
Multipliez en utilisant le motif carré binomial. 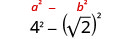
Simplifiez. 
Simplifiez :\((2−\sqrt{3})(2+\sqrt{3})\)
- Réponse
-
1
Simplifiez :\((1+\sqrt{5})(1−\sqrt{5})\)
- Réponse
-
−4
Simplifiez :\((5−2\sqrt{3})(5+2\sqrt{3})\)
- Réponse
-
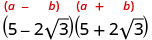
Multipliez en utilisant le motif carré binomial. 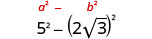
Simplifiez. 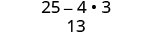
Simplifiez :\((3−2\sqrt{5})(3+2\sqrt{5})\).
- Réponse
-
−11
Simplifiez :\((4+5\sqrt{7})(4−5\sqrt{7})\).
- Réponse
-
−159
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à multiplier les racines carrées.
- Propriété du produit
- Multipliez les binômes avec des racines carrées
Concepts clés
- Propriété de produit des racines carrées Si a, b sont des nombres réels non négatifs, alors
\(\sqrt{ab}=\sqrt{a·b}\)et\(\sqrt{a}·\sqrt{b}=\sqrt{ab}\)
- Formules spéciales pour multiplier les binômes et les conjugués :
\[\begin{array}{ll} {(a+b)^2=a^2+2ab+b^2}&{(a−b)(a+b)=a^2−b^2}\\ {(a−b)^2=a^2−2ab+b^2 }&{}\\ \nonumber \end{array}\]
- La méthode FOIL peut être utilisée pour multiplier des binômes contenant des radicaux.


