9.1 : Simplifier et utiliser des racines carrées
- Page ID
- 194549
À la fin de cette section, vous serez en mesure de :
- Simplifiez les expressions avec des racines
- Estimer les racines car
- Racines carrés approximatives
- Simplifier les expressions variables avec des racines car
Avant de commencer, répondez à ce questionnaire de préparation.
- Simplifier : ⓐ\(9^2\) ⓑ\((−9)^2\) ⓒ\(−9^2\).
Si vous avez oublié ce problème, consultez [lien]. - Arrondissez 3,846 au centième le plus proche.
Si vous avez oublié ce problème, consultez [lien]. - Pour chaque numéro, déterminez s'il s'agit d'un nombre réel ou non :
ⓐ\(−\sqrt{100}\) ⓑ\(\sqrt{−100}\).
Si vous avez oublié ce problème, consultez [lien].
Simplifiez les expressions avec des racines
N'oubliez pas que lorsqu'un nombre n est multiplié par lui-même, nous l'écrivons\(n^2\) et le lisons « n au carré ». Par exemple,\(15^2\) se lit comme « 15 au carré », et 225 est appelé le carré de 15, depuis\(15^2=225\).
Si\(n^2=m\), alors m est le carré de n.
Parfois, nous devrons examiner la relation entre les nombres et leurs carrés à l'envers. Comme 225 est le carré de 15, on peut aussi dire que 15 est une racine carrée de 225. Un nombre dont le carré est m est appelé racine carrée de m.
Si\(n^2=m\), alors n est la racine carrée de m.
Avis\((−15)^2=225\) also, so −15 is also a square root of 225. Therefore, both 15 and −15 are square roots of 225.
Ainsi, chaque nombre positif a deux racines carrées : une positive et une négative. Et si nous ne voulions que la racine carrée positive d'un nombre positif ? Le signe radical,\(\sqrt{m}\), indique la racine carrée positive. La racine carrée positive est également appelée racine carrée principale.
Nous utilisons également le signe radical pour la racine carrée de zéro. Parce que\(0^2=0\),\(\sqrt{0}=0\). Notez que zéro n'a qu'une seule racine carrée.
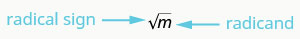
\(\sqrt{m}\)se lit comme « la racine carrée de m ».
Si\(m=n^2\), alors\(\sqrt{m}=n\), pour\(n \ge 0\).
La racine carrée de m,\(\sqrt{m}\), est le nombre positif dont le carré est m.
Puisque 15 est la racine carrée positive de 225, nous écrivons\(\sqrt{225}=15\). Fill in Figure pour créer un tableau de racines carrées auquel vous pouvez vous référer lorsque vous travaillez dans ce chapitre.

Nous savons que chaque nombre positif a deux racines carrées et que le signe radical indique la racine positive. Nous écrivons\(\sqrt{225}=15\). Si nous voulons trouver la racine carrée négative d'un nombre, nous plaçons un négatif devant le signe radical. Par exemple,\(−\sqrt{225}=−15\).
Simplifiez :
- \(\sqrt{36}\)
- \(\sqrt{196}\)
- \(−\sqrt{81}\)
- \(−\sqrt{289}\).
- Réponse
-
1.
\[\begin{array}{ll} {}&{\sqrt{36}}\\ {\text{Since} 6^2=36}&{6}\\ \end{array}\]
2.
\[\begin{array}{ll} {}&{\sqrt{196}}\\ {\text{Since} 14^2=196}&{14}\\ \end{array}\]
3.
\[\begin{array}{ll} {}&{−\sqrt{81}}\\ {\text{The negative is in front of the radical sign}}&{−9}\\ \end{array}\]
4.
\[\begin{array}{ll} {}&{−\sqrt{289}}\\ {\text{The negative is in front of the radical sign}}&{−17}\\ \end{array}\]
Simplifiez :
- \(−\sqrt{49}\)
- \(\sqrt{225}\).
- Réponse
-
- −7
- 15
Simplifier :
- \(\sqrt{64}\)
- \(−\sqrt{121}\).
- Réponse
-
- 8
- −11
Simplifiez :
- \(\sqrt{−169}\)
- \( −\sqrt{64}\)
- Réponse
-
1.
\[\begin{array}{ll} {}&{\sqrt{−169}}\\ {\text{There is no real number whose square is} s−169}&{\sqrt{−169} \text{is not a real number.}}\\ \end{array}\]
2.\[\begin{array}{ll} {}&{−\sqrt{64}}\\ {\text{The negative is in front of the radical sign}}&{−8}\\ \end{array}\]
Simplifiez :
- \(\sqrt{−196}\)
- \(−\sqrt{81}\).
- Réponse
-
- ce n'est pas un vrai chiffre
- −9
Simplifiez :
- \(−\sqrt{49}\)
- \(\sqrt{ −121}\).
- Réponse
-
- −7
- ce n'est pas un vrai chiffre
Lorsque vous utilisez l'ordre des opérations pour simplifier une expression ayant des racines carrées, nous traitons le radical comme un symbole de regroupement.
Simplifiez :
- \(\sqrt{25} +\sqrt{144}\)
- \(\sqrt{25+144}\).
- Réponse
-
1.
\[\begin{array}{ll} {}&{\sqrt{25} +\sqrt{144}}\\ {\text{Use the order of operations}}&{5+12}\\ {\text{Simplify.}}&{17}\\ \end{array}\]
2.\[\begin{array}{ll} {}&{\sqrt{25+144}}\\ {\text{Simplify under the radical sign.}}&{\sqrt{169}}\\ {\text{Simplify.}}&{13}\\ \end{array}\]
Remarquez les différentes réponses dans les parties 1 et 2 !
Simplifiez :
- \(\sqrt{9}+\sqrt{16}\)
- \(\sqrt{9+16}\).
- Réponse
-
- 7
- 5
Simplifiez :
- \(\sqrt{64+225}\)
- \(\sqrt{64}+\sqrt{225}\).
- Réponse
-
- 17
- 23
Estimez Square Roots
Jusqu'à présent, nous n'avons considéré que les racines carrées des nombres carrés parfaits. Les racines carrées des autres nombres ne sont pas des nombres entiers. Regardez le tableau ci-dessous.
| Numéro | Racine carrée |
|---|---|
| 4 | \(\sqrt{4}=2\) |
| 5 | \(\sqrt{5}\) |
| 6 | \(\sqrt{6}\) |
| 7 | \(\sqrt{7}\) |
| 8 | \(\sqrt{8}\) |
| 9 | \(\sqrt{9}=3\) |
Les racines carrées des nombres compris entre 4 et 9 doivent se trouver entre les deux nombres entiers consécutifs 2 et 3, et ce ne sont pas des nombres entiers. Sur la base du schéma du tableau ci-dessus, on pourrait dire que cela\(\sqrt{5}\) doit être compris entre 2 et 3. En utilisant des symboles d'inégalité, nous écrivons :
\(2<\sqrt{5}<3\)
Estimation\(\sqrt{60}\) entre deux nombres entiers consécutifs.
- Réponse
-
Pensez aux nombres carrés parfaits les plus proches de 60. Faites un petit tableau avec ces carrés parfaits et leurs racines carrées.
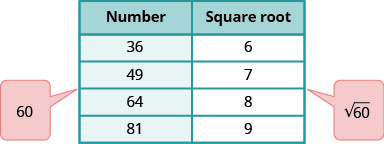
Localisez 60 entre deux carrés parfaits consécutifs. 
\(\sqrt{60}\)se trouve entre leurs racines carrées. 
Estimez la racine carrée\(\sqrt{38}\) entre deux nombres entiers consécutifs.
- Réponse
-
\(6<\sqrt{38}<7\)
Estimez la racine carrée\(\sqrt{84}\) entre deux nombres entiers consécutifs.
- Réponse
-
\(9<\sqrt{84}<10\)
Racines carrés approximatives
Il existe des méthodes mathématiques pour approximer les racines carrées, mais de nos jours, la plupart des gens utilisent une calculatrice pour les trouver. Trouvez la\(\sqrt{x}\) clé sur votre calculatrice. Vous utiliserez cette clé pour approximer les racines carrées.
Lorsque vous utilisez votre calculatrice pour trouver la racine carrée d'un nombre qui n'est pas un carré parfait, la réponse que vous voyez n'est pas la racine carrée exacte. Il s'agit d'une approximation précise du nombre de chiffres affichés sur l'écran de votre calculatrice. Le symbole d'une approximation est\(\approx\) et se lit « approximativement ».
Supposons que votre calculatrice dispose d'un affichage à 10 chiffres. Tu verrais que
\(\sqrt{5} \approx 2.236067978\)
Si nous voulions arrondir\(\sqrt{5}\) à deux décimales, nous dirions
\(\sqrt{5} \approx 2.24\)
Comment savons-nous que ces valeurs sont des approximations et non des valeurs exactes ? Regardez ce qui se passe lorsque nous les mettons au point :
\[\begin{array}{c} {(2.236067978)^2=5.000000002}\\ {(2.24)^2=5.0176}\\ \end{array}\]
Leurs carrés sont proches de 5, mais ne sont pas exactement égaux à 5.
En utilisant la racine carrée d'une calculatrice, puis en arrondissant à deux décimales, nous pouvons trouver :
\[\begin{array}{c} {\sqrt{4}=2}\\ {\sqrt{5} \approx 2.24}\\ {\sqrt{6} \approx 2.45}\\ {\sqrt{7} \approx 2.65}\\ {\sqrt{8} \approx 2.83}\\ {\sqrt{9}=3}\\ \end{array}\]
Arrondir\(\sqrt{17}\) à deux décimales.
- Réponse
-
\[\begin{array}{ll} {}&{\sqrt{17}}\\ {\text{Use the calculator square root key.}}&{4.123105626...}\\ {\text{Round to two decimal places.}}&{4.12}\\ {}&{\sqrt{17} \approx 4.12} \end{array}\]
Arrondir\(\sqrt{11}\) à deux décimales.
- Réponse
-
\(\approx 3.32\)
Arrondir\(\sqrt{13}\) à deux décimales.
- Réponse
-
\(\approx 3.61\)
Simplifier les expressions variables avec des racines car
Et si nous devions trouver la racine carrée d'une expression avec une variable ? Considérez\(\sqrt{9x^2}\). Pouvez-vous imaginer une expression dont le carré est\(9x^2\) ?
\[\begin{array}{cc} {(?)^2=9x^2}&{}\\ {(3x)^2=9x^2}&{\text{so} \sqrt{9x^2}=3x}\\ \end{array}\]
Lorsque nous utilisons le signe radical pour prendre la racine carrée d'une expression variable, nous devons spécifier que x≥0x≥0 pour nous assurer d'obtenir la racine carrée principale.
Cependant, dans ce chapitre, nous supposerons que chaque variable d'une expression à racine carrée représente un nombre non négatif et que nous n'écrirons donc pas à\(x \ge 0\) côté de chaque radical.
Qu'en est-il des racines carrées des puissances supérieures des variables ? Réfléchissez à la propriété de puissance des exposants que nous avons utilisée au chapitre 6.
\((a^m)^n=a^{m·n}\)
Si nous mettons au carré\(a^m\), l'exposant deviendra 2 m.
\((a^m)^2=a^{2m}\)
Comment cela nous aide-t-il à prendre des racines carrées ? Regardons-en quelques-unes :
\[\begin{array}{cc} {\sqrt{25u^8}=5u^4}&{\text{Because} (5u^4)^2=25u^8}\\ {\sqrt{16r^{20}}=4r^{10}}&{\text{Because} (4r^{10})^2=16r^{20}}\\ {\sqrt{196q^{36}}=14q^{18}}&{\text{Because} (14r^{18})^2=196q^{36}}\\ \end{array}\]
Simplifiez :
- \(\sqrt{x^6}\)
- \(\sqrt{y^{16}}\)
- Réponse
-
1.
\[\begin{array}{ll} {}&{\sqrt{x^6}}\\ {\text{Since} (x^3)^2=x^6}&{x^3}\\ \end{array}\]
2.\[\begin{array}{ll} {}&{\sqrt{y^{16}}}\\ {\text{Since} (y^8)^2=y^{16}}&{y^8}\\ \end{array}\]
Simplifiez :
- \(\sqrt{y^8}\)
- \(\sqrt{z^{12}}\).
- Réponse
-
- \(y^4\)
- \(z^6\)
Simplifiez :
- \(\sqrt{m^4}\)
- \(\sqrt{b^{10}}\).
- Réponse
-
- \(m^2\)
- \(b^5\)
Simplifiez :\(\sqrt{16n^2}\)
- Réponse
-
\[\begin{array}{ll} {}&{\sqrt{16n^2}}\\ {\text{Since} (4n)^2=16n^2}&{4n}\\ \end{array}\]
Simplifiez :\(\sqrt{64x^2}\).
- Réponse
-
\(8x\)
Simplifiez :\(\sqrt{169y^2}\).
- Réponse
-
\(13y\)
Simplifiez :\(−\sqrt{81c^2}\).
- Réponse
-
\[\begin{array}{ll} {}&{−\sqrt{81c^2}}\\ {\text{Since} (9c)^2=81c^2}&{−9c}\\ \end{array}\]
Simplifiez :\(−\sqrt{121y^2}\).
- Réponse
-
\(−11y\)
Simplifiez :\(−\sqrt{100p^2}\).
- Réponse
-
\(−10p\)
Simplifiez :\(\sqrt{36x^{2}y^{2}}\).
- Réponse
-
\[\begin{array}{ll} {}&{\sqrt{36x^{2}y^{2}}}\\ {\text{Since} (6xy)^2=\sqrt{36x^{2}y^{2}}}&{6xy}\\ \end{array}\]
Simplifiez :\(\sqrt{100a^{2}b^{2}}\).
- Réponse
-
10 ab
Simplifiez :\(\sqrt{225m^{2}n^{2}}\).
- Réponse
-
15 mn
Simplifiez :\(\sqrt{64p^{64}}\).
- Réponse
-
\[\begin{array}{ll} {}&{\sqrt{64p^{64}}}\\ {\text{Since} (8p^8)^2=\sqrt{64p^{64}}}&{8p^8}\\ \end{array}\]
Simplifiez :\(\sqrt{49x^{30}}\).
- Réponse
-
\(7x^{15}\)
Simplifiez :\(\sqrt{81w^{36}}\)
- Réponse
-
\(9w^{18}\)
Simplifiez :\(\sqrt{121a^{6}b^{8}}\)
- Réponse
-
\[\begin{array}{ll} {}&{\sqrt{121a^{6}b^{8}}}\\ {\text{Since} (11a^{3}b^{4})^2=\sqrt{121a^{6}b^{8}}}&{11a^{3}b^{4}}\\ \end{array}\]
Simplifiez :\(\sqrt{169x^{10}y^{14}}\)
- Réponse
-
\(13x^{5}y^{7}\)
Simplifiez :\(\sqrt{144p^{12}q^{20}}\)
- Réponse
-
\(\sqrt{12p^{6}q^{10}}\)
Accédez à cette ressource en ligne pour obtenir des instructions supplémentaires et vous entraîner avec les racines carrées.
- Racines carrées
Concepts clés
- Notez que la racine carrée d'un nombre négatif n'est pas un nombre réel.
- Chaque nombre positif a deux racines carrées, une positive et une négative. La racine carrée positive d'un nombre positif est la racine carrée principale.
- Nous pouvons estimer les racines carrées en utilisant les carrés parfaits situés à proximité.
- Nous pouvons estimer les racines carrées à l'aide d'une calculatrice
- Lorsque nous utilisons le signe radical pour prendre la racine carrée d'une expression variable, nous devons le spécifier\(x \ge 0\) pour nous assurer d'obtenir la racine carrée principale.
Lexique
- carré d'un nombre
-
- Si\(n^2=m\), alors m est le carré de n
- racine carrée d'un nombre
-
- Si\(n^2=m\), alors n est la racine carrée de m
- notation à racine carrée
-
- Si\(m=n^2\), alors\(\sqrt{m}=n\). Nous\(\sqrt{m}\) lisons « la racine carrée de m ».


