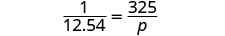Skip to main content
Global

8.7 : Résoudre les applications de proportions et de figures similaires

  1. Last updated
  2. Save as PDF
  • Page ID
    194797

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Résoudre les proportions
    • Résolvez des applications avec des
    Remarque

    Avant de commencer, répondez à ce questionnaire de préparation.

    Si vous manquez un problème, revenez à la section répertoriée et passez en revue les informations.

    1. Résoudre\(\dfrac{n}{3}=30\).
      Si vous avez oublié ce problème, passez en revue l'exercice 2.2.25.
    2. Le périmètre d'une fenêtre triangulaire est de 23 pieds. La longueur des deux côtés est de dix pieds et six pieds. Quelle est la longueur du troisième côté ?
      Si vous avez oublié ce problème, consultez l'exemple 3.4.2

    Résoudre les proportions

    Lorsque deux expressions rationnelles sont égales, l'équation qui les relie est appelée proportion.

    Définition : PROPORTION

    Une proportion est une équation de la forme\(\dfrac{a}{b}=\dfrac{c}{d}\), où\(b \ne 0\),\(d \ne 0\).

    La proportion se lit comme suit : « a est à b, comme c est à d »

    L'équation\(\dfrac{1}{2}=\dfrac{4}{8}\) is a proportion because the two fractions are equal.

    La proportion\(\dfrac{1}{2}=\dfrac{4}{8}\) se lit comme suit : « 1 vaut pour 2 et 4 pour 8 ».

    Les proportions sont utilisées dans de nombreuses applications pour « augmenter » les quantités. Nous allons commencer par un exemple très simple afin que vous puissiez voir comment fonctionnent les proportions. Même si vous pouvez trouver la réponse à l'exemple immédiatement, assurez-vous également d'apprendre à le résoudre en utilisant des proportions.

    Supposons qu'un directeur d'école souhaite avoir un enseignant pour 20 élèves. Elle pourrait utiliser les proportions pour déterminer le nombre d'enseignants pour 60 élèves. Nous utilisons x le nombre d'enseignants pour 60 élèves, puis nous établissons la proportion :

    \[\dfrac{1\,\text{teacher}}{20\,\text{students}}=\dfrac{x\,\text{teachers}}{60\,\text{students}}\nonumber\]

    Nous prenons soin de faire correspondre les unités des numérateurs et les unités des dénominateurs : enseignants dans les numérateurs, étudiants dans les dénominateurs.

    Comme une proportion est une équation avec des expressions rationnelles, nous allons résoudre les proportions de la même manière que nous avons résolu des équations dans Solve Rational Equations. Nous allons multiplier les deux côtés de l'équation par l'écran LCD pour effacer les fractions, puis résoudre l'équation résultante.

      .
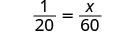    Multipliez les deux côtés par l'écran LCD, 60. .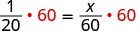
    Simplifiez. .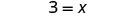
      Le directeur a besoin de 3 professeurs pour 60 élèves.

    Nous allons maintenant faire quelques exemples de résolution de proportions numériques sans aucune unité. Ensuite, nous allons résoudre les applications en utilisant des proportions.

    Exemple\(\PageIndex{1}\)

    \(\dfrac{x}{63}=\dfrac{4}{7}\).

        .
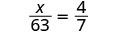    Pour isoler x, multipliez les deux côtés par l'écran LCD, 63.   .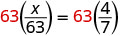
    Simplifiez.   .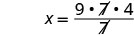
    Divisez les facteurs communs.   .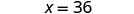
    Vérifiez. Pour vérifier notre réponse, nous la remplaçons dans la proportion d'origine.    
      .  
    . .  
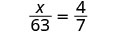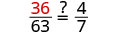    Afficher les facteurs communs. .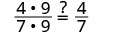  
    Simplifiez. .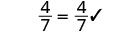  
    Essayez-le\(\PageIndex{1}\)

    \(\dfrac{n}{84}=\dfrac{11}{12}\).

    Réponse

    77

    Essayez-le\(\PageIndex{2}\)

    \(\dfrac{y}{96}=\dfrac{13}{12}\).

    Réponse

    104

    Exemple\(\PageIndex{2}\)

    \(\dfrac{144}{a}=\dfrac{9}{4}\).

        .
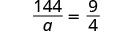    Multipliez les deux côtés par l'écran LCD.   .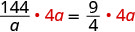
    Supprimez les facteurs communs de chaque côté.   .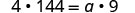
    Simplifiez.   .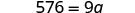
    Divisez les deux côtés par 9.   .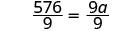
    Simplifiez.   .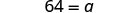
    Vérifiez.    
      .  
    . .  
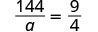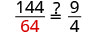    Afficher les facteurs communs. .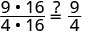  
    Simplifiez. .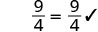  
    Essayez-le\(\PageIndex{3}\)

    \(\dfrac{91}{b}=\dfrac{7}{5}\).

    Réponse

    65

    Essayez-le\(\PageIndex{4}\)

    \(\dfrac{39}{c}=\dfrac{13}{8}\).

    Réponse

    24

    Exemple\(\PageIndex{3}\)

    \(\dfrac{n}{n+14}=\dfrac{5}{7}.\)

        .
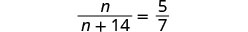    Multipliez les deux côtés par l'écran LCD.   .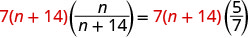
    Supprimez les facteurs communs de chaque côté.   .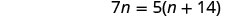
    Simplifiez.   .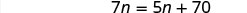
    Résolvez pour n.   .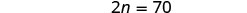
        .
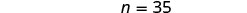    Vérifiez.    
      .  
    . .  
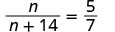    Simplifiez. .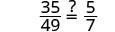  
    Afficher les facteurs communs. .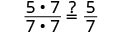  
    Simplifiez. .  
    Essayez-le\(\PageIndex{5}\)

    \(\dfrac{y}{y+55}=\dfrac{3}{8}\).

    Réponse

    33

    Essayez-le\(\PageIndex{6}\)

    \(\dfrac{z}{z−84}=−\dfrac{1}{5}\).

    Réponse

    14

    Exemple\(\PageIndex{4}\)

    \(\dfrac{p+12}{9}=\dfrac{p−12}{6}\).

        .
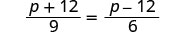    Multipliez les deux côtés par l'écran LCD, 18.   .
    Simplifiez.   .
    Distribuez.   .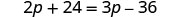
    Résolvez pour p.   .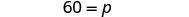
    Vérifiez.    
      .  
    . .  
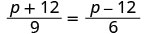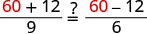    Simplifiez. .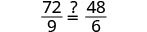  
    Diviser. .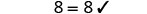  
    Essayez-le\(\PageIndex{7}\)

    \(\dfrac{v+30}{8}=\dfrac{v+66}{12}\).

    Réponse

    42

    Essayez-le\(\PageIndex{8}\)

    \(\dfrac{2x+15}{9}=\dfrac{7x+3}{15}\).

    Réponse

    6

    Pour résoudre les applications avec des proportions, nous suivrons notre stratégie habituelle de résolution des applications. Mais lorsque nous établissons la proportion, nous devons nous assurer que les unités sont correctes : les unités des numérateurs doivent correspondre et les unités des dénominateurs doivent correspondre.

    Exemple\(\PageIndex{5}\)

    Lorsque les pédiatres prescrivent de l'acétaminophène à des enfants, ils prescrivent 5 millilitres (ml) d'acétaminophène pour chaque tranche de 25 livres de poids de l'enfant. Si Zoé pèse 80 livres, combien de millilitres d'acétaminophène son médecin prescrira-t-il ?

    Identifiez ce que l'on nous demande de trouver et choisissez une variable pour le représenter. Combien de ml d'acétaminophène le médecin vous prescrira-t-il ?
      Soit a = ml d'acétaminophène.
    Écrivez une phrase qui donne les informations nécessaires pour le trouver. Si 5 ml sont prescrits pour 25 livres, quelle quantité sera prescrite pour 80 livres ?
    Traduisez en proportion, faites attention aux unités.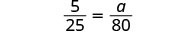

    .
    Multipliez les deux côtés par l'écran LCD, 400. .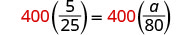
    Supprimez les facteurs communs de chaque côté. .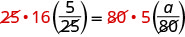
    Simplifiez, mais ne multipliez pas sur la gauche. Remarquez quelle sera la prochaine étape. .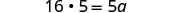
    Résolvez pour un. .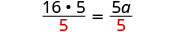
    Vérifiez. .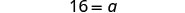
    La réponse est-elle raisonnable ?  
    Oui, puisque 80 correspond à environ 3 fois 25, le médicament doit être environ 3 fois 5. Donc, 16 ml ont du sens.  
    .  
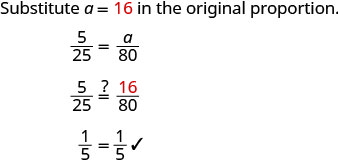    Écrivez une phrase complète. Le pédiatre prescrirait 16 ml d'acétaminophène à Zoé.
    Essayez-le\(\PageIndex{9}\)

    Les pédiatres prescrivent 5 millilitres (ml) d'acétaminophène pour chaque tranche de 25 livres de poids d'un enfant. Combien de millilitres d'acétaminophène le médecin prescrira-t-il à Emilia, qui pèse 60 livres ?

    Réponse

    12 ml

    Essayez-le\(\PageIndex{10}\)

    Pour chaque kilogramme (kg) de poids d'un enfant, les pédiatres prescrivent 15 milligrammes (mg) d'un antifièvre. Si Isabella pèse 12 kg, combien de milligrammes de réducteur de fièvre le pédiatre prescrira-t-il ?

    Réponse

    180 ml

    Exemple\(\PageIndex{6}\)

    Un macchiato au caramel glacé de 16 onces contient 230 calories. Combien de calories contient un macchiato au caramel glacé de 24 onces ?

    Identifiez ce que l'on nous demande de trouver et choisissez une variable pour le représenter. Combien de calories contient un macchiato au caramel glacé de 24 onces ?
      Soit c = calories en 24 onces.
    Écrivez une phrase qui donne les informations nécessaires pour le trouver. S'il y a 230 calories dans 16 onces, alors combien de calories y a-t-il dans 24 onces ?
    Traduisez en proportion, faites attention aux unités.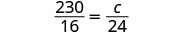

    .
    Multipliez les deux côtés par l'écran LCD, 48. .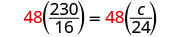
    Supprimez les facteurs communs de chaque côté. .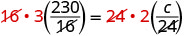
    Simplifiez. .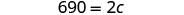
    Résolvez pour c. .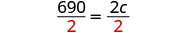
      .
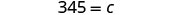    Vérifiez.  
    La réponse est-elle raisonnable ?  
    Oui, 345 calories pour 24 onces, c'est plus de 290 calories pour 16 onces, mais pas trop.  
    .  
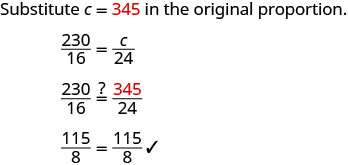    Écrivez une phrase complète. Il y a 345 calories dans un macchiato au caramel glacé de 24 onces.
    Essayez-le\(\PageIndex{11}\)

    Dans un restaurant de restauration rapide, un shake au chocolat de 22 onces contient 850 calories. Combien de calories se trouvent dans leur boisson chocolatée de 12 onces ? Arrondissez votre réponse au nombre entier le plus proche.

    Réponse

    464 calories

    Essayez-le\(\PageIndex{12}\)

    Yaneli adore les bonbons Starburst, mais veut garder ses collations à 100 calories. Si les bonbons contiennent 160 calories pour 8 morceaux, combien de morceaux peut-elle avoir dans sa collation ?

    Réponse

    5 pièces

    Exemple\(\PageIndex{7}\)

    Josiah est allé au Mexique pour les vacances de printemps et a changé 325 dollars en pesos mexicains. À cette époque, le taux de change était de 1 dollar américain, soit 12,54 pesos mexicains. Combien de pesos mexicains a-t-il reçu pour son voyage ?

    Qu'est-ce qu'on vous demande de trouver ? Combien de pesos mexicains Josiah a-t-il reçu ?
    Assignez une variable. Soit p = le nombre de pesos mexicains.
    Écrivez une phrase qui donne les informations nécessaires pour le trouver. Si 1 dollar américain équivaut à 12,54 pesos mexicains, 325 dollars, c'est combien de pesos ?

    Traduisez en proportion, faites attention aux unités.

    .
    Multipliez les deux côtés par l'écran LCD, 12,54 p. .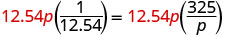
    Supprimez les facteurs communs de chaque côté. .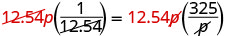
    Simplifiez. .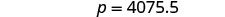
    Vérifiez.  
    La réponse est-elle raisonnable ?  
    Oui, 100 dollars équivaudraient à 1 254 pesos. 325 dollars, c'est un peu plus de 3 fois ce montant, donc notre réponse de 4075,5 pesos est logique.  
    .  
    Écrivez une phrase complète. Josiah a reçu 4075,5 pesos pour son voyage de relâche.
    Essayez-le\(\PageIndex{13}\)

    Yurianna part en Europe et veut changer 800 dollars en euros. Au taux de change actuel, 1 dollar américain équivaut à 0,738 euro. Combien d'euros disposera-t-elle pour son voyage ?

    Réponse

    590,4 euros

    Essayez-le\(\PageIndex{14}\)

    Corey et Nicole voyagent au Japon et doivent échanger 600 dollars contre des yens japonais. Si chaque dollar vaut 94,1 yens, combien de yens obtiendront-ils ?

    Réponse

    56 460 yens

    Dans l'exemple ci-dessus, nous avons lié le nombre de pesos au nombre de dollars en utilisant une proportion. On pourrait dire que le nombre de pesos est proportionnel au nombre de dollars. Si deux quantités sont liées par une proportion, on dit qu'elles sont proportionnelles.

    Résoudre des applications de figures similaires

    Lorsque vous réduisez ou agrandissez une photo sur un téléphone ou une tablette, que vous déterminez une distance sur une carte, que vous utilisez un motif pour construire une bibliothèque ou coudre une robe, vous travaillez avec des figures similaires. Si deux figures ont exactement la même forme, mais des tailles différentes, on dit qu'elles sont similaires. L'un est une maquette de l'autre. Tous leurs angles correspondants ont les mêmes mesures et leurs côtés correspondants sont dans le même rapport.

    Définition : FIGURES SIMILAIRES

    Deux figures sont similaires si les mesures de leurs angles correspondants sont égales et que leurs côtés correspondants sont dans le même rapport.

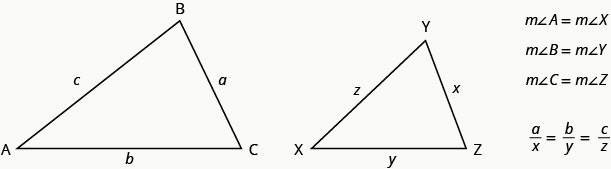
    Par exemple, les deux triangles de la figure sont similaires. Chaque côté de ΔABC est 4 fois la longueur du côté correspondant de ΔXYZ.

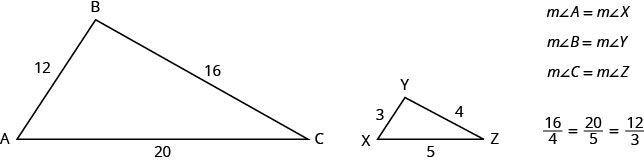
    L'image ci-dessus montre les étapes pour résoudre la proportion 1 divisée par 12,54 égale 325 divisée par p. Que demandez-vous ? Combien de pesos mexicains a-t-il reçu ? Assignez une variable. Soit p le nombre de pesos. Écrivez une phrase qui donne les informations nécessaires pour le trouver. Si un dollar américain est égal à 12,54 pesos, alors 325 dollars est le nombre de pesos. Traduisez en proportion, faites attention aux unités. Les dollars divisés en pesos sont égaux aux dollars divisés par les pesos pour obtenir 1 divisé par 12,54 équivaut à 325 divisé par p. Multipliez les deux côtés par l'écran LCD, 12,54 p pour obtenir 1 divisé par 12,54 p fois 1 divisé par 12,54 équivaut à 12,54 p fois 325 divisé par p. Supprimez les facteurs communs des deux côtés. Barrez 12,54 du côté gauche de l'équation. Barrez p du côté droit de l'équation. Simplifiez pour obtenir p égal à 4075,5 dans la proportion d'origine. Vérifiez. La réponse est-elle raisonnable ? Oui, 100 dollars seraient 1254 pesos. 325 dollars, c'est un peu plus de 3 fois ce montant, donc notre réponse de 4075,5 pesos est logique. Le substitut p est égal à 4075,5 dans la proportion initiale. Utilisez une calculatrice. Nous avons maintenant 1 divisé par 12,54 égal 325 divisé par p. Ensuite, 1 divisé par 12,54 équivaut à 325 divisé par 4075,5 pour obtenir 0,07874 égal à 0,07874. La réponse est vérifiée.

    Ceci est résumé dans la propriété des triangles similaires.

    Définition : PROPRIÉTÉ DE TRIANGLES SIMILAIRES

    Si ΔABC est similaire à ΔXYZ

    La figure ci-dessus montre deux triangles similaires. Le plus grand triangle étiqueté A B C. La longueur de A à B est c, La longueur de B à C est a. La longueur de C à A est b. Le plus grand triangle est étiqueté X Y Z. La longueur de X à Y est z. La longueur de Y à Z est x. La longueur de X à Z est y. À droite des triangles, il est indiqué que la mesure de l'angle correspondant A est égale à la mesure de l'angle correspondant X, la mesure de l'angle correspondant B est égale à la mesure de l'angle correspondant Y, et la mesure de l'angle correspondant C est égale à la mesure de l'angle Z correspondant. Par conséquent, a divisé par x est égal à b divisé par y est égal à c divisé par z.

    Pour résoudre des applications avec des chiffres similaires, nous suivrons la stratégie de résolution de problèmes pour les applications de géométrie que nous avons utilisée précédemment.

    Définition : RÉSOUDRE DES APPLICATIONS DE GÉOMÉTRIE.
    1. Lisez le problème et faites comprendre tous les mots et toutes les idées. Dessinez la figure et étiquetez-la avec les informations données.
    2. Identifiez ce que nous recherchons.
    3. Nommez ce que vous recherchez en choisissant une variable pour le représenter.
    4. Traduisez en équation en écrivant la formule ou le modèle approprié à la situation. Remplacer dans les informations données.
    5. Résolvez l'équation en utilisant de bonnes techniques d'algèbre.
    6. Vérifiez la réponse au problème et assurez-vous qu'elle est logique.
    7. Répondez à la question par une phrase complète.
    Exemple\(\PageIndex{8}\)

    ΔABC est similaire à ΔXYZ

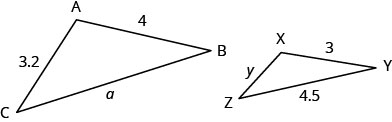
    L'image ci-dessus montre deux triangles similaires. Deux côtés sont indiqués pour chaque triangle. Le plus grand triangle est étiqueté A B C. La longueur de A à B est de 4. La longueur de B à C est a. La longueur de C à A est de 3,2. Le plus petit triangle est étiqueté X Y Z. La longueur de X à Y est de 3. La longueur de Y à Z est de 4,5. La longueur de Z à X est y.

    Étape 1. Lisez le problème. Dessinez la figure et étiquetez-la avec les informations données. Le chiffre est donné.
    Étape 2. Identifiez ce que nous recherchons. la longueur des côtés de triangles similaires.
    Étape 3. Nommez les variables.

    Soit a = longueur du troisième côté de ΔABC.

    y = longueur du troisième côté de ΔXYZ.
    Étape 4. Traduisez. Les triangles étant similaires, les côtés correspondants sont proportionnels.
    Nous devons écrire une équation qui compare le côté que nous recherchons à un ratio connu. Puisque le côté AB = 4 correspond au côté XY = 3, nous le savons\(\dfrac{AB}{XY}=\dfrac{4}{3}\). Nous écrivons donc des équations avec\(\dfrac{AB}{XY}\) pour trouver les côtés que nous recherchons. Veillez à faire correspondre correctement les côtés correspondants. \(\dfrac{AB}{XY}=\dfrac{BC}{YZ}=\dfrac{AC}{XZ}\).
    .
    Substitut. ..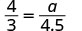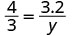
    Étape 5. Résolvez l'équation.
    .
    Figure_08_07_030f_img_new.jpg « />
      ..
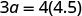
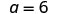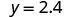    Étape 6. Vérifiez.
    Étape 7. Réponds à la question. Le troisième côté de ΔABC est 6 et le troisième côté de ΔXYZ est 2,4.
    Essayez-le\(\PageIndex{15}\)

    ΔABC est similaire à ΔXYZ. Les longueurs des deux côtés de chaque triangle sont indiquées sur la figure.

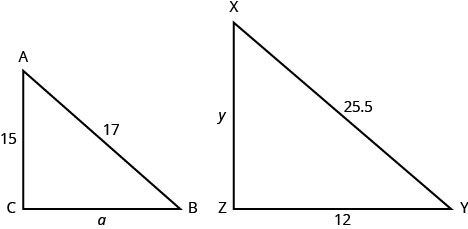
    L'image ci-dessus montre deux triangles similaires. Le plus petit triangle est marqué A B C. La longueur des deux côtés est donnée pour le petit triangle A B C. La longueur de A à B est de 17. La longueur de B à C est a. La longueur de C à D est de 15. Le plus grand triangle est étiqueté X Y Z. La longueur est donnée pour deux côtés. La longueur de X à Y est de 25,5. La longueur de Y à Z est de 12. La longueur de Z à X est y.

    Détermine la longueur du côté a

    Réponse

    8

    Essayez-le\(\PageIndex{16}\)

    ΔABC est similaire à ΔXYZ. Les longueurs des deux côtés de chaque triangle sont indiquées sur la figure.

    Réponse

    22,5

    L'exemple suivant montre comment des triangles similaires sont utilisés avec des cartes.

    Exemple\(\PageIndex{9}\)

    Sur une carte, San Francisco, Las Vegas et Los Angeles forment un triangle dont les côtés sont illustrés dans la figure ci-dessous. Si la distance réelle entre Los Angeles et Las Vegas est de 270 miles, trouvez la distance entre Los Angeles et San Francisco.

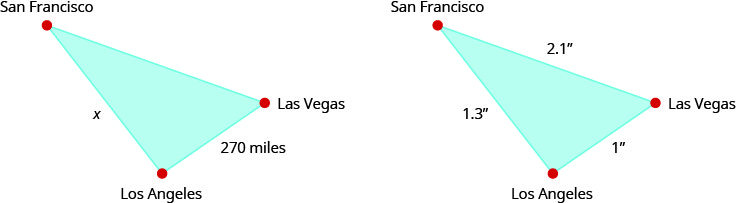
    L'image ci-dessus montre deux triangles similaires et la façon dont ils sont utilisés avec les cartes. Le petit triangle sur la gauche montre San Francisco, Las Vegas et Los Angeles sur les trois points. San Francisco à Los Angeles est de 1,3 pouce. De Los Angeles à Las Vegas, c'est 1 pouce. De Las Vegas à San Francisco, c'est 2,1 pouces. Le deuxième plus grand triangle montre les mêmes points. La distance entre San Francisco et Los Angeles est x. La distance entre Los Angeles et Las Vegas est 270 miles. La distance entre Las Vegas et San Francisco n'est pas notée.

    Lisez le problème. Dessinez les figures et étiquetez avec les informations données. Les chiffres sont présentés ci-dessus.
    Identifiez ce que nous recherchons. La distance réelle entre Los Angeles et San Francisco.
    Nommez les variables. Soit x = distance entre Los Angeles et San Francisco.
    Traduisez en une équation. Les triangles
    étant similaires, les côtés correspondants sont
    proportionnels. Nous allons faire les numérateurs
    « miles » et les dénominateurs « pouces ».    		 .
      .
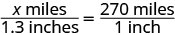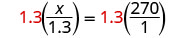    Résolvez l'équation. .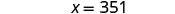
    Vérifiez.  
    Sur la carte, la distance entre Los Angeles et
    San Francisco est supérieure à la distance entre
    Los Angeles et Las Vegas. Puisque 351 est
    plus que 270, la réponse est logique.    		  
    .  
    Réponds à la question. La distance entre Los Angeles et San Francisco est de 351 miles.
    ESSAYEZ-LE\(\PageIndex{17}\)

    Sur la carte, Seattle, Portland et Boise forment un triangle dont les côtés sont illustrés dans la figure ci-dessous. Si la distance réelle entre Seattle et Boise est de 400 miles, trouvez la distance entre Seattle et Portland.

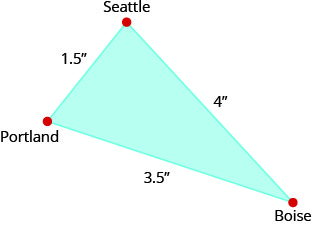
    L'image ci-dessus est un triangle dont un côté est étiqueté « Seattle, 4,5 pouces ». L'autre face est étiquetée « Portland 3,5 pouces ». La troisième face est étiquetée 1,5 pouces. Le sommet est étiqueté « Boise ».

    Réponse

    150 milles

    Essayez-le\(\PageIndex{18}\)

    À l'aide de la carte ci-dessus, trouvez la distance entre Portland et Boise.

    Réponse

    350 milles

    Nous pouvons utiliser des chiffres similaires pour trouver des hauteurs que nous ne pouvons pas mesurer directement.

    Exemple\(\PageIndex{10}\)

    Tyler mesure 6 pieds. En fin d'après-midi, son ombre mesurait 8 pieds de long. Au même moment, l'ombre d'un arbre mesurait 24 pieds de long. Trouve la hauteur de l'arbre.

    Lisez le problème et dessinez une figure. .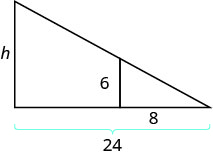
    Nous cherchons h, la hauteur de l'arbre.  
    Nous utiliserons des triangles similaires pour écrire une équation.  
    Le petit triangle est similaire au grand triangle. .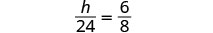
    Résolvez la proportion. .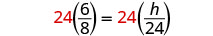
    Simplifiez. .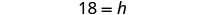
    Vérifiez.  

    La hauteur de Tyler est inférieure à la longueur de son ombre, il est donc logique que la hauteur de l'arbre soit inférieure à la longueur de son ombre.

    		  
    .  
    Essayez-le\(\PageIndex{19}\)

    Un poteau téléphonique projette une ombre de 50 pieds de long. À proximité, un panneau de signalisation de 8 pieds de haut projette une ombre de 10 pieds de long. Quelle est la hauteur du poteau téléphonique ?

    Réponse

    40 pieds

    Essayez-le\(\PageIndex{20}\)

    Un pin projette une ombre de 80 pieds à côté d'un bâtiment de 30 pieds de haut qui projette une ombre de 40 pieds. Quelle est la hauteur du pin ?

    Réponse

    60 pieds

    Concepts clés

    • Propriété de triangles similaires
      • Si ΔABC est similaire à ΔXYZ
    • Stratégie de résolution de problèmes pour les applications de géométrie
      1. Lisez le problème et assurez-vous que tous les mots et toutes les idées sont compris. Dessinez la figure et étiquetez-la avec les informations données.
      2. Identifiez ce que nous recherchons.
      3. Nommez ce que vous recherchez en choisissant une variable pour le représenter.
      4. Traduisez en équation en écrivant la formule ou le modèle approprié à la situation. Remplacer dans les informations données.
      5. Résolvez l'équation en utilisant de bonnes techniques d'algèbre.
      6. Vérifiez la réponse au problème et assurez-vous qu'elle est logique.
      7. Répondez à la question par une phrase complète.

    Lexique

    proportion
    Une proportion est une équation de la forme\(\dfrac{a}{b}=\dfrac{c}{d}, where \(b \ne 0\),\(d \ne 0\). La proportion se lit comme suit : « a est à b, c est à d. ».
    figures similaires
    Deux figures sont similaires si les mesures de leurs angles correspondants sont égales et que leurs côtés correspondants sont dans le même rapport.