Chapitre 4 Exercices de révision

Chapitre 4 Exercices de révision

Système de coordonnées rectangulaires

Tracer des points dans un système de coordonnées rectangulaires

Dans les exercices suivants, tracez chaque point dans un système de coordonnées rectangulaires.

Exercice$\PageIndex{1}$

1. (−1, −5)
2. (−3,4)
3. (2, −3)
4. $\left(1, \frac{5}{2}\right)$

Exercice$\PageIndex{2}$

1. (4,3)
2. (−4,3)
3. (−4, −3)
4. (4, −3)

Réponse

Exercice$\PageIndex{3}$

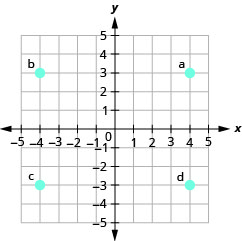
1. (−2,0)
2. (0, −4)
3. (0,5)
4. (3,0)

Exercice$\PageIndex{4}$

1. $\left(2, \frac{3}{2}\right)$
2. $\left(3, \frac{4}{3}\right)$
3. $\left(\frac{1}{3},-4\right)$
4. $\left(\frac{1}{2},-5\right)$

Réponse

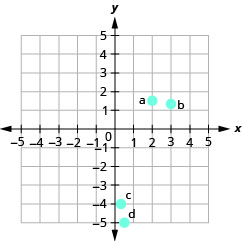
Identifier des points sur un graphique

Dans les exercices suivants, nommez la paire ordonnée de chaque point indiqué dans le système de coordonnées rectangulaires.

Exercice$\PageIndex{5}$

Exercice$\PageIndex{6}$

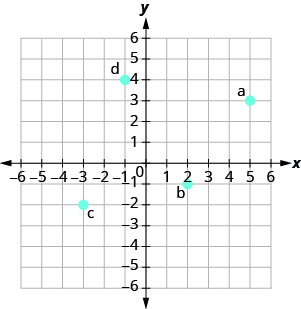
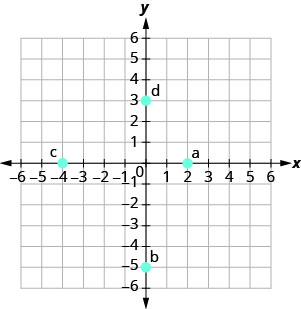
Réponse

une (2,0)

b (0, −5)

c (−4,0)

d (0,3)

Vérifier les solutions à une équation à deux variables

Dans les exercices suivants, quelles paires ordonnées sont des solutions aux équations données ?

Exercice$\PageIndex{7}$

$5x+y=10$

1. (5,1)
2. (2,0)
3. (4, −10)

Exercice$\PageIndex{8}$

$y=6x−2$

1. (1,4)
2. $\left(\frac{1}{3}, 0\right)$
3. (6, −2)

Réponse

1, 2

Compléter un tableau des solutions à une équation linéaire à deux variables

Dans les exercices suivants, complétez le tableau pour trouver des solutions à chaque équation linéaire.

Exercice$\PageIndex{9}$

$y=4 x-1$

x	y	(x, y)
0
1
-2

Exercice$\PageIndex{10}$

$y=-\frac{1}{2} x+3$

x	y	(x, y)
0
4
-2

Réponse

x	y	(x, y)
0	3	(0,3)
4	1	(4, 1)
−2	4	(−2,4)

Exercice$\PageIndex{11}$

$x+2 y=5$

x	y	(x, y)
	0
1
-1

Exercice$\PageIndex{12}$

$3x+2y=6$

x	y	(x, y)
0
	0
-2

Réponse

x	y	(x, y)
0	−3	(0, −3)
2	0	(2,0)
−2	−6	(−2, −6)

Trouver des solutions à une équation linéaire à deux variables

Dans les exercices suivants, trouvez trois solutions pour chaque équation linéaire.

Exercice$\PageIndex{13}$

$x+y=3$

Exercice$\PageIndex{14}$

$x+y=-4$

Réponse

Les réponses peuvent varier.

Exercice$\PageIndex{15}$

$y=3 x+1$

Exercice$\PageIndex{16}$

$y=-x-1$

Réponse

Les réponses peuvent varier.

Représentation graphique d'équations linéaires

Reconnaître la relation entre les solutions d'une équation et son graphe

Dans les exercices suivants, déterminez pour chaque paire ordonnée :

1. La paire ordonnée est-elle une solution à l'équation ?
2. Est-ce que le but est en jeu ?

Exercice$\PageIndex{17}$

$y=−x+4$

(0,4) (−1,3)

(2,2) (−2,6)

Exercice$\PageIndex{18}$

$y=\frac{2}{3} x-1$
$(0,-1) (3,1)$
$(-3,-3) (6,4)$

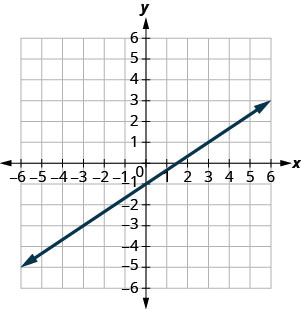
Réponse

1. Oui ; Oui
2. Oui ; Non

Tracez une équation linéaire en traçant des points

Dans les exercices suivants, tracez un graphique en traçant des points.

Exercice$\PageIndex{19}$

$y=4x-3$

Exercice$\PageIndex{20}$

$y=-3x$

Réponse

Exercice$\PageIndex{21}$

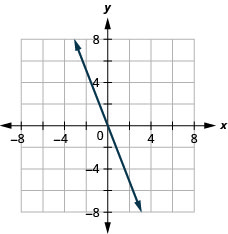
$y=\frac{1}{2} x+3$

Exercice$\PageIndex{22}$

$x-y=6$

Réponse

Exercice$\PageIndex{23}$

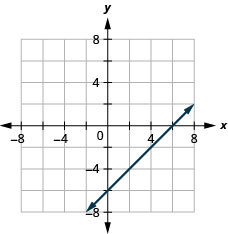
$2x+y=7$

Exercice$\PageIndex{24}$

$3x-2y=6$

Réponse

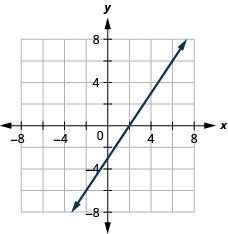
Tracez des lignes verticales et horizontales

Dans les exercices suivants, tracez chaque équation.

Exercice$\PageIndex{25}$

$y=-2$

Exercice$\PageIndex{26}$

$x=3$

Réponse

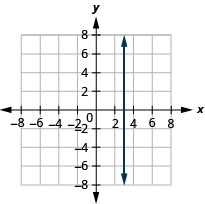
Dans les exercices suivants, tracez chaque paire d'équations dans le même système de coordonnées rectangulaires.

Exercice$\PageIndex{27}$

$y=-2 x$et$y=-2$

Exercice$\PageIndex{28}$

$y=\frac{4}{3} x$et$y=\frac{4}{3}$

Réponse

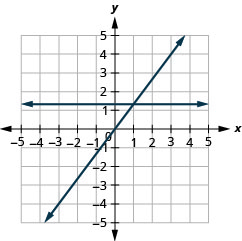
Création de graphiques avec Intercepts

Identifier les$x$ - et$y$ - Intercepts sur un graphique

Dans les exercices suivants, trouvez les$x$ - et$y$ -intercepts.

Exercice$\PageIndex{29}$

Exercice$\PageIndex{30}$

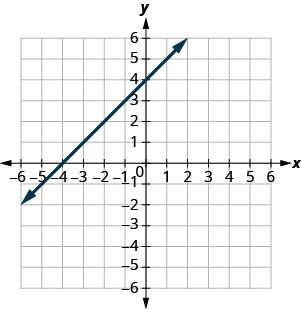
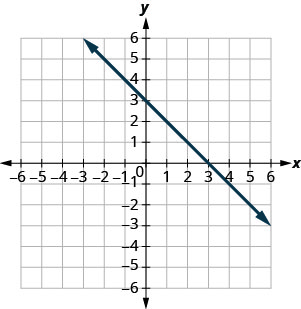
Réponse

$(3,0)$et$(0,3)$

Trouvez les valeurs$x$ - et$y$ -interceptes à partir de l'équation d'une droite

Dans les exercices suivants, trouvez les points d'intersection de chaque équation.

Exercice$\PageIndex{31}$

$x+y=5$

Exercice$\PageIndex{32}$

$x-y=-1$

Réponse

$(-1,0),(0,1)$

Exercice$\PageIndex{33}$

$x+2y=6$

Exercice$\PageIndex{34}$

$2x+3y=12$

Réponse

$(6,0),(0,4)$

Exercice$\PageIndex{35}$

$y=\frac{3}{4} x-12$

Exercice$\PageIndex{36}$

$y=3x$

Réponse

$(0,0)$

Tracez une ligne à l'aide des interceptions

Dans les exercices suivants, tracez un graphique à l'aide des interceptions.

Exercice$\PageIndex{37}$

$-x+3y=3$

Exercice$\PageIndex{38}$

$x+y=-2$

Réponse

Exercice$\PageIndex{39}$

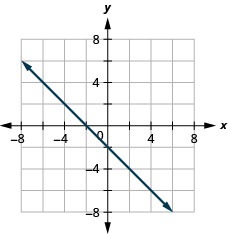
$x-y=4$

Exercice$\PageIndex{40}$

$2x-y=5$

Réponse

Exercice$\PageIndex{41}$

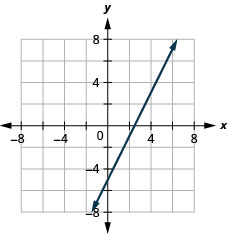
$2x-4y=8$

Exercice$\PageIndex{42}$

$y=2x$

Réponse

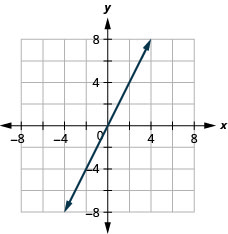
Pente d'une ligne

Utiliser des géoboards pour modéliser la pente

Dans les exercices suivants, trouvez la pente modélisée sur chaque géoboard.

Exercice$\PageIndex{43}$

Exercice$\PageIndex{44}$

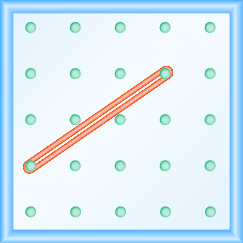
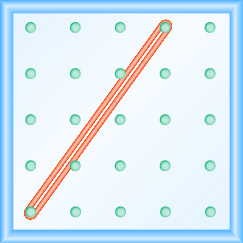
Réponse

$\frac{4}{3}$

Exercice$\PageIndex{45}$

Exercice$\PageIndex{46}$

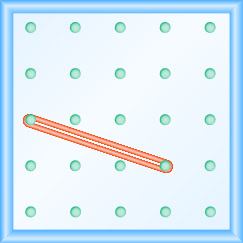
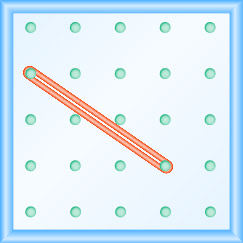
Réponse

$-\frac{2}{3}$

Exercice$\PageIndex{47}$

$\frac{1}{3}$

Exercice$\PageIndex{48}$

$\frac{3}{2}$

Réponse

Exercice$\PageIndex{49}$

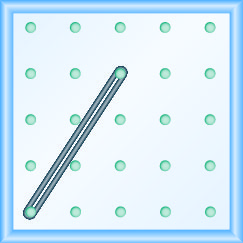
$-\frac{2}{3}$

Exercice$\PageIndex{50}$

$-\frac{1}{2}$

Réponse

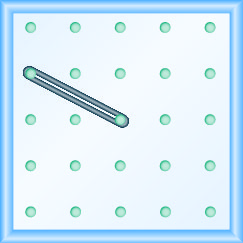
$m=\frac{\text { rise }}{\text { run }}$Sert à déterminer la pente d'une droite à partir de son graphe

Dans les exercices suivants, déterminez la pente de chaque ligne affichée.

Exercice$\PageIndex{51}$

Exercice$\PageIndex{52}$

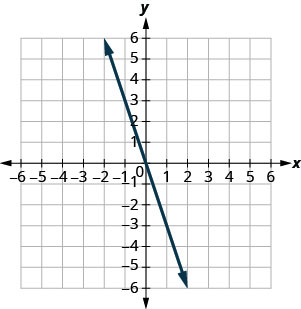
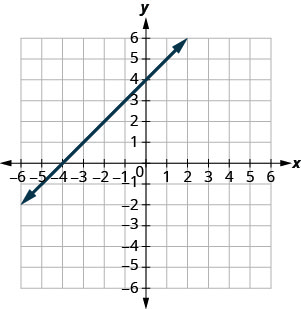
Réponse

1

Exercice$\PageIndex{53}$

Exercice$\PageIndex{54}$

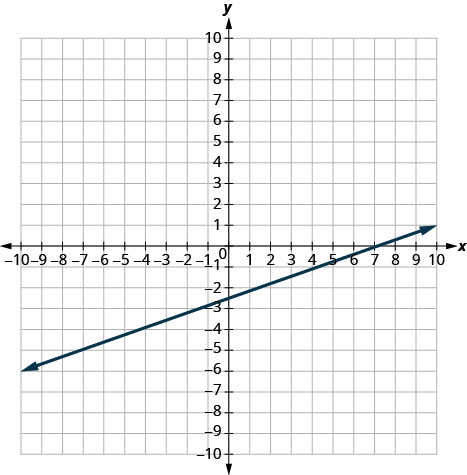
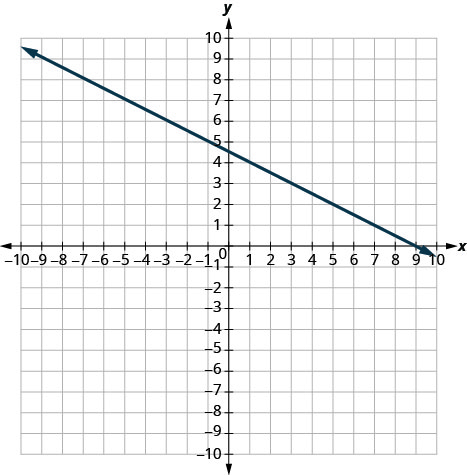
Réponse

$-\frac{1}{2}$

Déterminer la pente des lignes horizontales et verticales

Dans les exercices suivants, déterminez la pente de chaque ligne.

Exercice$\PageIndex{55}$

$y=2$

Exercice$\PageIndex{56}$

$x=5$

Réponse

indéfini

Exercice$\PageIndex{57}$

$x=-3$

Exercice$\PageIndex{58}$

$y=-1$

Réponse

0

Utilisez la formule de pente pour déterminer la pente d'une droite entre deux points

Dans les exercices suivants, utilisez la formule de pente pour déterminer la pente de la ligne entre chaque paire de points.

Exercice$\PageIndex{59}$

$(-1,-1),(0,5)$

Exercice$\PageIndex{60}$

$(3,5),(4,-1)$

Réponse

−6

Exercice$\PageIndex{61}$

$(-5,-2),(3,2)$

Exercice$\PageIndex{62}$

$(2,1),(4,6)$

Réponse

$\frac{5}{2}$

Tracez une droite en fonction d'un point et de la pente

Dans les exercices suivants, tracez chaque ligne avec le point et la pente donnés.

Exercice$\PageIndex{63}$

$(2,-2) ; \quad m=\frac{5}{2}$

Exercice$\PageIndex{64}$

$(-3,4) ; \quad m=-\frac{1}{3}$

Réponse

Exercice$\PageIndex{65}$

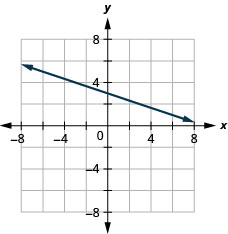
$x$-intercepter$-4 ; \quad m=3$

Exercice$\PageIndex{66}$

$y$-intercepter$1 ; \quad m=-\frac{3}{4}$

Réponse

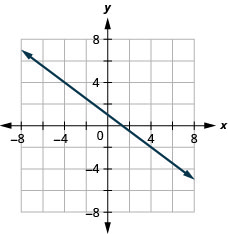
Résolvez les applications

Dans les exercices suivants, résolvez ces applications de pente.

Exercice$\PageIndex{67}$

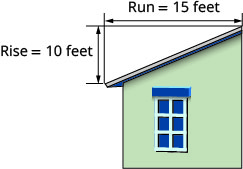
Le toit illustré ci-dessous présente une élévation et une course de$15$ pieds.$10$ Quelle est sa pente ?

Exercice$\PageIndex{68}$

Une route de montagne s'élève$50$ pour une course$500$ d'un pied. Quelle est sa pente ?

Réponse

$\frac{1}{10}$

Forme d'interception d'une équation d'une droite

Reconnaître la relation entre le graphe et la forme pente-intersection d'une équation d'une droite

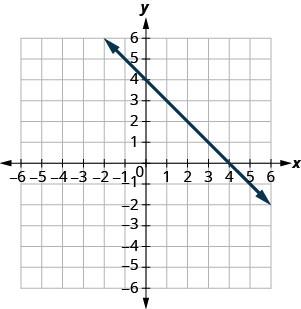
Dans les exercices suivants, utilisez le graphique pour déterminer la pente et l'intersection y de chaque droite. Comparez les valeurs à l'équation$y=mx+b$.

Exercice$\PageIndex{69}$

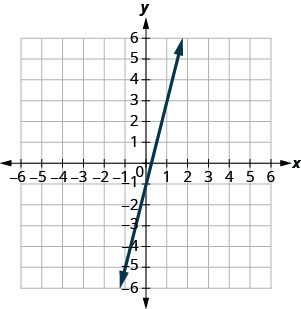
$y=4x−1$

Exercice$\PageIndex{70}$

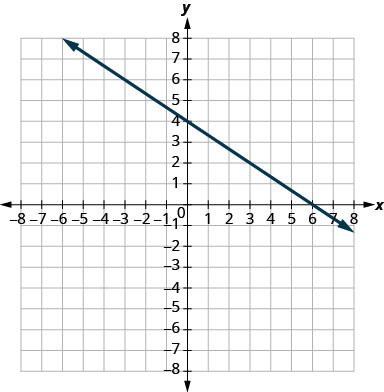
$y=-\frac{2}{3} x+4$

Réponse

pente$m=-\frac{2}{3}$ et$y$ intersection$(0,4)$

Identifier la pente et l'intersection Y à partir de l'équation d'une droite

Dans les exercices suivants, identifiez la pente et l'$y$intersection de chaque ligne.

Exercice$\PageIndex{71}$

$y=-4 x+9$

Exercice$\PageIndex{72}$

$y=\frac{5}{3} x-6$

Réponse

$\frac{5}{3} ;(0,-6)$

Exercice$\PageIndex{73}$

$5x+y=10$

Exercice$\PageIndex{74}$

$4x-5y=8$

Réponse

$\frac{4}{5} ;\quad \left(0,-\frac{8}{5}\right)$

Tracez une ligne en utilisant sa pente et son intersection

Dans les exercices suivants, tracez la droite de chaque équation en utilisant sa pente et son$y$ point d'intersection.

Exercice$\PageIndex{75}$

$y=2x+3$

Exercice$\PageIndex{76}$

$y=-x-1$

Réponse

Exercice$\PageIndex{77}$

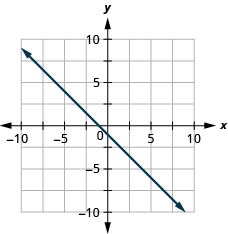
$y=-\frac{2}{5} x+3$

Exercice$\PageIndex{78}$

$4x-3y=12$

Réponse

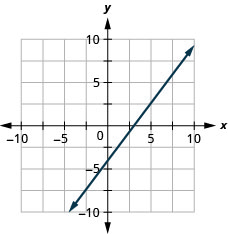
Dans les exercices suivants, déterminez la méthode la plus pratique pour représenter graphiquement chaque ligne.

Exercice$\PageIndex{79}$

$x=5$

Exercice$\PageIndex{80}$

$y=-3$

Réponse

ligne horizontale

Exercice$\PageIndex{81}$

$2x+y=5$

Exercice$\PageIndex{82}$

$x-y=2$

Réponse

intercepte

Exercice$\PageIndex{83}$

$y=x+2$

Exercice$\PageIndex{84}$

$y=\frac{3}{4} x-1$

Réponse

points de traçage

Graphisme et interprétation des applications de Slope—Intercept

Exercice$\PageIndex{85}$

Katherine est chef privée. L'équation$C=6.5m+42$ modélise la relation entre son coût hebdomadaire$C$, en dollars,$m$ et le nombre de repas qu'elle sert.

1. Trouvez le coût d'une semaine pour Katherine lorsqu'elle ne sert aucun repas.
2. Trouvez le coût d'une semaine lorsqu'elle sert des$14$ repas.
3. Interprétez la pente et l'$C$intersection de l'équation.
4. Tracez l'équation.

Exercice$\PageIndex{86}$

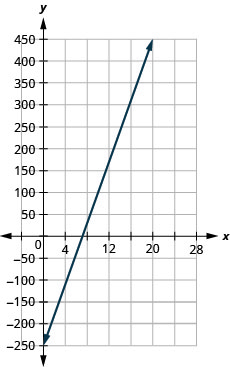
Marjorie enseigne le piano. L'équation$P=35h−250$ modélise la relation entre son bénéfice hebdomadaire$P$, en dollars,$s$ et le nombre de leçons qu'elle enseigne aux étudiants.

1. Trouvez le profit de Marjorie pendant une semaine lorsqu'elle ne donne aucun cours aux élèves.
2. Trouvez le profit pendant une semaine où elle donne des cours aux$20$ étudiants.
3. Interprétez la pente et l'$P$intersection de l'équation.
4. Tracez l'équation.

Réponse

1. $−$250$
2. $$450$
3. La pente signifie que le bénéfice hebdomadaire de Marjorie augmente$$35$ pour chaque leçon supplémentaire qu'elle donne à un élève.$35$$P$ Le$P$ -intercept signifie que lorsque le nombre de leçons est atteint$0$, Marjorie perd$$250$.

Utiliser les pentes pour identifier les lignes parallèles

Dans les exercices suivants, utilisez les pentes et$y$ les interceptions pour déterminer si les lignes sont parallèles.

Exercice$\PageIndex{87}$

$4x-3y=-1 ; \quad y=\frac{4}{3} x-3$

Exercice$\PageIndex{88}$

$2 x-y=8 ; \quad x-2 y=4$

Réponse

pas parallèle

Utiliser les pentes pour identifier les lignes perpendiculaires

Dans les exercices suivants, utilisez les pentes et les intersections y pour déterminer si les lignes sont perpendiculaires.

Exercice$\PageIndex{89}$

$y=5x-1 ; \quad 10x+2y=0$

Exercice$\PageIndex{90}$

$3x-2y=5 ; \quad 2x+3y=6$

Réponse

perpendiculaire

Trouvez l'équation d'une droite

Trouvez une équation de la droite en fonction de la pente et de l'intersection y

Dans les exercices suivants, trouvez l'équation d'une droite avec une pente et une$y$ intersection données. Écrivez l'équation sous forme de pente et d'intersection.

Exercice$\PageIndex{91}$

pente$\frac{1}{3}$ et$y$ intersection$(0,-6)$

Exercice$\PageIndex{92}$

pente$-5$ et$y$ intersection$(0,-3)$

Réponse

$y=-5x-3$

Exercice$\PageIndex{93}$

pente$0$ et$y$ intersection$(0,4)$

Exercice$\PageIndex{94}$

pente$-2$ et$y$ intersection$(0,0)$

Réponse

$y=-2x$

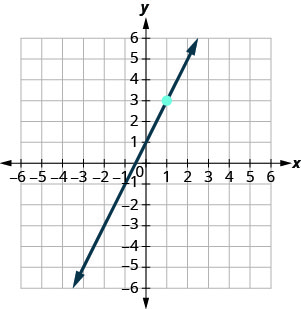
Dans les exercices suivants, trouvez l'équation de la droite affichée sur chaque graphique. Écrivez l'équation sous forme de pente et d'intersection.

Exercice$\PageIndex{95}$

Exercice$\PageIndex{96}$

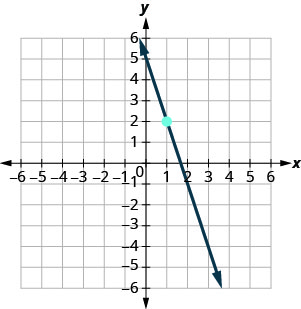
Réponse

$y=-3x+5$

Exercice$\PageIndex{97}$

Exercice$\PageIndex{98}$

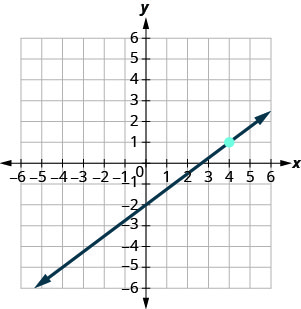
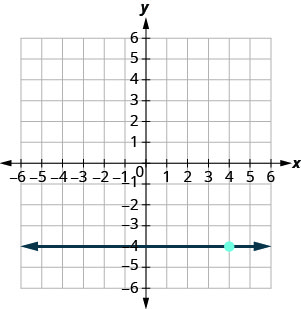
Réponse

$y=-4$

Trouvez une équation de la droite en fonction de la pente et d'un point

Dans les exercices suivants, trouvez l'équation d'une droite avec une pente donnée et contenant le point donné. Écrivez l'équation sous forme de pente et d'intersection.

Exercice$\PageIndex{99}$

$m=-\frac{1}{4},$point$(-8,3)$

Exercice$\PageIndex{100}$

$m=\frac{3}{5},$point$(10,6)$

Réponse

$y=\frac{3}{5} x$

Exercice$\PageIndex{101}$

Ligne horizontale contenant$(-2,7)$

Exercice$\PageIndex{102}$

$m=-2,$point$(-1,-3)$

Réponse

$y=-2x-5$

Trouvez une équation de la droite à partir de deux points

Dans les exercices suivants, trouvez l'équation d'une droite contenant les points donnés. Écrivez l'équation sous forme de pente et d'intersection.

Exercice$\PageIndex{103}$

$(2,10)$et$(-2,-2)$

Exercice$\PageIndex{104}$

$(7,1)$et$(5,0)$

Réponse

$y=\frac{1}{2} x-\frac{5}{2}$

Exercice$\PageIndex{105}$

$(3,8)$et$(3,-4)$

Exercice$\PageIndex{106}$

$(5,2)$et$(-1,2)$

Réponse

$y=2$

Trouver l'équation d'une droite parallèle à une droite donnée

Dans les exercices suivants, trouvez l'équation d'une droite parallèle à la droite donnée et contenant le point donné. Écrivez l'équation sous forme de pente et d'intersection.

Exercice$\PageIndex{107}$

$y=-3x+6,$point de ligne$(1,-5)$

Exercice$\PageIndex{108}$

$2x+5y=-10,$point de ligne$(10,4)$

Réponse

$y=-\frac{2}{5} x+8$

Exercice$\PageIndex{109}$

$x=4,$point de ligne$(-2,-1)$

Exercice$\PageIndex{110}$

$y=-5,$point de ligne$(-4,3)$

Réponse

$y=3$

Trouver l'équation d'une droite perpendiculaire à une droite donnée

Dans les exercices suivants, trouvez l'équation d'une droite perpendiculaire à la droite donnée et contenant le point donné. Écrivez l'équation sous forme de pente et d'intersection.

Exercice$\PageIndex{111}$

$y=-\frac{4}{5} x+2,$point de ligne$(8,9)$

Exercice$\PageIndex{112}$

$2x-3y=9,$point de ligne$(-4,0)$

Réponse

$y=-\frac{3}{2} x-6$

Exercice$\PageIndex{113}$

$y=3,$point de ligne$(-1,-3)$

Exercice$\PageIndex{114}$

$x=-5$point de ligne$(2,1)$

Réponse

$y=1$

Graphique des inégalités linéaires

Vérifier les solutions à une inégalité entre deux variables

Dans les exercices suivants, déterminez si chaque paire ordonnée est une solution à l'inégalité donnée.

Exercice$\PageIndex{115}$

Déterminez si chaque paire ordonnée est une solution à l'inégalité$y<x−3$ :

1. $(0,1)$
2. $(−2,−4)$
3. $(5,2)$
4. $(3,−1)$
5. $(−1,−5)$

Exercice$\PageIndex{116}$

Déterminez si chaque paire ordonnée est une solution à l'inégalité$x+y>4$ :

1. $(6,1)$
2. $(−3,6)$
3. $(3,2)$
4. $(−5,10)$
5. $(0,0)$

Réponse

1. oui
2. non
3. oui
4. oui
5. non

Reconnaître la relation entre les solutions d'une inégalité et son graphe

Dans les exercices suivants, écrivez l'inégalité indiquée par la région ombrée.

Exercice$\PageIndex{117}$

Écrivez l'inégalité indiquée par le graphique avec la ligne de démarcation$y=−x+2$.

Exercice$\PageIndex{118}$

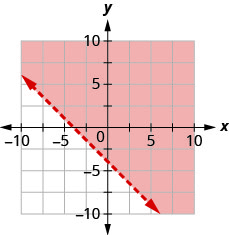
Écrivez l'inégalité indiquée par le graphique avec la ligne de démarcation$y=\frac{2}{3} x-3$

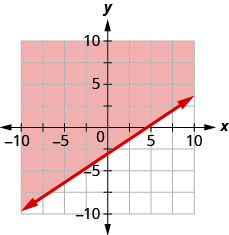
Réponse

$y>\frac{2}{3} x-3$

Exercice$\PageIndex{119}$

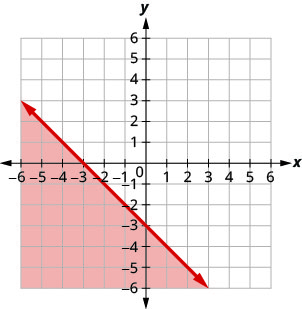
Écrivez l'inégalité indiquée par la région ombrée dans le graphique avec la ligne de démarcation$x+y=−4$.

Exercice$\PageIndex{120}$

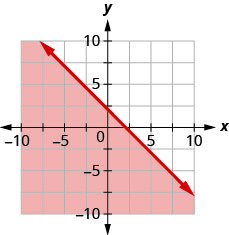
Écrivez l'inégalité indiquée par la région ombrée dans le graphique avec la ligne de démarcation$x−2y=6$.

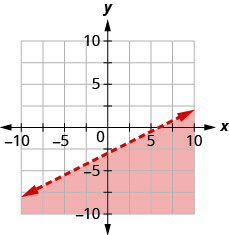
Réponse

$x-2 y \geq 6$

Diagramme des inégalités

Dans les exercices suivants, représentez graphiquement chaque inégalité linéaire.

Exercice$\PageIndex{121}$

Représenter graphiquement l'inégalité linéaire$y>\frac{2}{5} x-4$

Exercice$\PageIndex{122}$

Représenter graphiquement l'inégalité linéaire$y \leq-\frac{1}{4} x+3$

Réponse

Exercice$\PageIndex{123}$

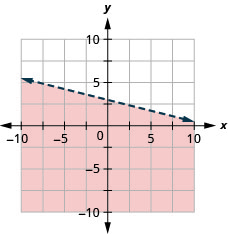
Représenter graphiquement l'inégalité linéaire$x-y \leq 5$

Exercice$\PageIndex{124}$

Représenter graphiquement l'inégalité linéaire$3 x+2 y>10$

Réponse

Exercice$\PageIndex{125}$

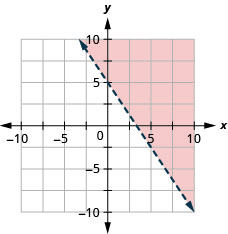
Représenter graphiquement l'inégalité linéaire$y \leq-3 x$

Exercice$\PageIndex{126}$

Représenter graphiquement l'inégalité linéaire$y<6$

Réponse

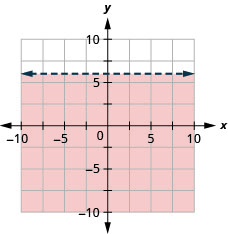
Test d'entraînement

Exercice$\PageIndex{1}$

Tracez chaque point dans un système de coordonnées rectangulaires.

1. $(2,5)$
2. $(−1,−3)$
3. $(0,2)$
4. $\left(-4, \frac{3}{2}\right)$
5. $(5,0)$

Exercice$\PageIndex{2}$

Parmi les paires ordonnées données, lesquelles sont des solutions à l'équation$3x−y=6$ ?

1. $(3,3)$
2. $(2,0)$
3. $(4,−6)$

Réponse

1. oui
2. oui
3. non

Exercice$\PageIndex{3}$

Trouvez trois solutions à l'équation linéaire$y=-2x-4$

Exercice$\PageIndex{4}$

Trouvez les$y$ points d'intersection$x$ - et - de l'équation$4x-3y=12$

Réponse

$(3,0),(0,-4)$

Déterminez la pente de chaque ligne affichée.

Exercice$\PageIndex{5}$

Exercice$\PageIndex{6}$

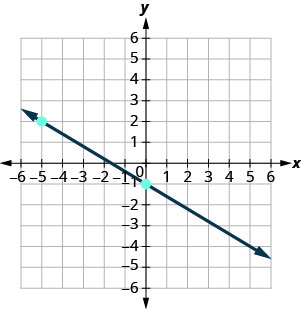
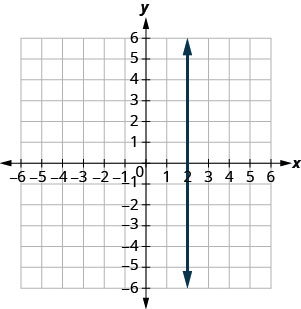
Réponse

indéfini

Exercice$\PageIndex{7}$

Exercice$\PageIndex{8}$

Détermine la pente de la ligne entre les points$(5,2)$ et$(-1,-4)$

Réponse

1

Exercice$\PageIndex{9}$

Tracez la ligne avec la pente$\frac{1}{2}$ contenant le point$(-3,-4)$

Tracez la droite pour chacune des équations suivantes.

Exercice$\PageIndex{10}$

$y=\frac{5}{3} x-1$

Réponse

Exercice$\PageIndex{11}$

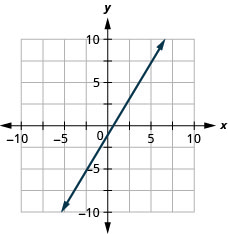
$y=-x$

Exercice$\PageIndex{12}$

$x-y=2$

Réponse

Exercice$\PageIndex{13}$

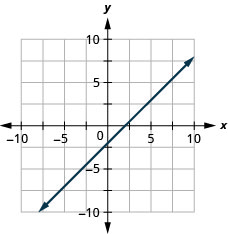
$4x+2y=-8$

Exercice$\PageIndex{14}$

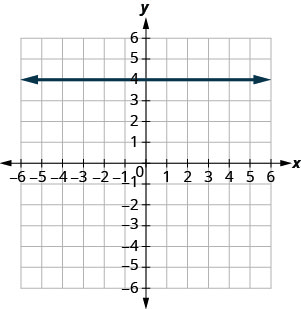
$y=2$

Réponse

Exercice$\PageIndex{15}$

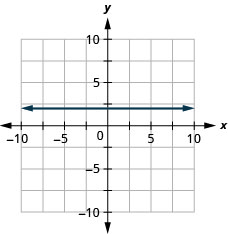
$x=-3$

Trouvez l'équation de chaque droite. Écrivez l'équation sous forme de pente et d'intersection.

Exercice$\PageIndex{16}$

pente$-\frac{3}{4}$ et$y$ intersection$(0,-2)$

Réponse

$y=-\frac{3}{4} x-2$

Exercice$\PageIndex{17}$

$m=2,$point$(-3,-1)$

Exercice$\PageIndex{18}$

contenant$(10,1)$ et$(6,-1)$

Réponse

$y=\frac{1}{2} x-4$

Exercice$\PageIndex{19}$

parallèle à la ligne$y=-\frac{2}{3} x-1,$ contenant le point$(-3,8)$

Exercice$\PageIndex{20}$

perpendiculaire à la ligne$y=\frac{5}{4} x+2,$ contenant le point$(-10,3)$

Réponse

$y=-\frac{4}{5} x-5$

Exercice$\PageIndex{21}$

Écrivez l'inégalité indiquée par le graphique avec la ligne de démarcation$y=−x−3$.

Tracez chaque inégalité linéaire.

Exercice$\PageIndex{22}$

$y>\frac{3}{2} x+5$

Réponse

Exercice$\PageIndex{23}$

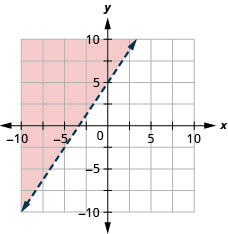
$x-y \geq-4$

Exercice$\PageIndex{24}$

$y \leq-5 x$

Réponse

Exercice$\PageIndex{1}$

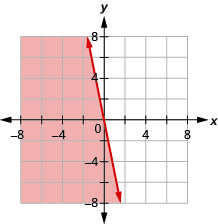
$y<3$