4.7 : Graphiques des inégalités linéaires

Last updated
Save as PDF

Page ID: 194740

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

Vérifier les solutions à une inégalité entre deux variables
Reconnaître la relation entre les solutions d'une inégalité et son graphe
Représenter les inégalités linéaires

Remarque

Avant de commencer, répondez à ce questionnaire de préparation.

Solution :$4x+3>23.$
Si vous avez oublié ce problème, passez en revue l'exercice 2.7.22.
Traduisez de l'algèbre vers l'anglais :$x<5.$
si vous avez oublié ce problème, passez en revue l'exercice 1.3.1.
Évaluez à$x=1, \, y=−2.$
quel$3x−2y$ moment si vous avez oublié ce problème, passez en revue l'exercice 1.5.28.

Vérifier les solutions à une inégalité entre deux variables

Nous avons appris à résoudre les inégalités dans une seule variable. Nous allons maintenant examiner les inégalités entre deux variables. Les inégalités entre deux variables ont de nombreuses applications. Si vous dirigiez une entreprise, par exemple, vous souhaiteriez que vos revenus soient supérieurs à vos coûts, afin que votre entreprise puisse réaliser des bénéfices.

INÉGALITÉ LINÉAIRE

Une inégalité linéaire est une inégalité qui peut être écrite sous l'une des formes suivantes :

\[A x+B y>C \quad A x+B y \geq C \quad A x+B y<C \quad A x+B y \leq C \nonumber\]

où$A$ et ne$B$ sont pas tous les deux nuls.

Vous souvenez-vous qu'une inégalité avec une seule variable avait de nombreuses solutions ? La solution à l'inégalité$x>3$ est un nombre supérieur à$3$. Nous l'avons montré sur la ligne numérique en ombrant la ligne numérique à droite de$3$ et en plaçant une parenthèse ouverte à$3$. Voir la figure$\PageIndex{1}$.

La figure montre une ligne numérique allant de moins 5 à 5. Une parenthèse est indiquée au point 3 positif et une flèche s'étend du positif 3 à l'infini positif. — Figurine$\PageIndex{1}$

De même, les inégalités entre deux variables ont de nombreuses solutions. Toute paire ordonnée$ (x, y)$ qui rend l'inégalité vraie lorsque nous la substituons dans les valeurs est une solution de l'inégalité.

Solution d'une inégalité linéaire

Une paire ordonnée$ (x, y)$ est une solution d'une inégalité linéaire si l'inégalité est vraie lorsque nous substituons les valeurs de$x$ et$y$.

Exercice$\PageIndex{1}$

Déterminez si chaque paire ordonnée est une solution à l'inégalité$y>x+4$ :

$(0,0)$
$(1,6)$
$(2,6)$
$(−5,−15)$
$(−8,12)$

Réponse

$(0,0)$		$.$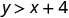
$.$		$.$
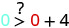
Simplifiez.	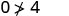	$.$ Donc, n'$(0,0)$est pas une solution à$y>x+4$.

$(1,6)$		$.$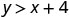
$.$		$.$
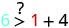
Simplifiez.	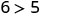	$.$ Donc,$(1,6)$ est une solution pour$y>x+4$.

$(2,6)$		$.$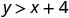
$.$		$.$
Simplifiez.	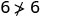	$.$ Donc, n'$(2,6)$est pas une solution à$y>x+4$.

$(−5,−15)$		$.$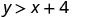
$.$		$.$
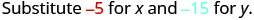
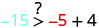
Simplifiez.	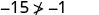	$.$ Donc, n'$(−5,−15)$est pas une solution à$y>x+4$.

(−8,12)		$.$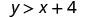
$.$		$.$
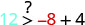
Simplifiez.	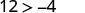	$.$ Donc,$(−8,12)$ est une solution pour$y>x+4$.

Exercice$\PageIndex{2}$

Déterminez si chaque paire ordonnée est une solution à l'inégalité$y>x−3$ :

$(0,0)$
$(4,9)$
$(−2,1)$
$(−5,−3)$
$(5,1)$

Réponse

Exercice$\PageIndex{3}$

Déterminez si chaque paire ordonnée est une solution à l'inégalité$y<x+1$ :

$(0,0)$
$(8,6)$
$(−2,−1)$
$(3,4)$
$(−1,−4)$

Réponse

Reconnaître la relation entre les solutions d'une inégalité et son graphe

Nous allons maintenant voir comment les solutions d'une inégalité sont liées à son graphe.

Repensons à la ligne numérique de la$\PageIndex{1}$ Figure. Le point$x=3$ séparait cette ligne numérique en deux parties. D'un côté se$3$ trouvent tous les nombres inférieurs à$3$. De l'autre côté de$3$ tous les nombres sont supérieurs à$3$. Voir la figure$\PageIndex{2}$.

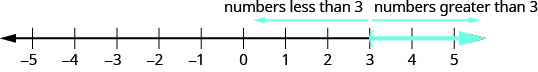
La solution$x>3$ est la partie ombrée de la ligne numérique à droite de$x=3$.

De même, la ligne$y=x+4$ sépare le plan en deux régions. D'un côté de la ligne se trouvent des points avec$y<x+4$. De l'autre côté de la ligne se trouvent les points avec$y>x+4$. Nous appelons cette ligne$y=x+4$ une ligne de démarcation.

LIGNE DE DÉMARCATION

La ligne avec équation$Ax+By=C$ est la ligne de démarcation qui sépare la région où$Ax+By>C$ de la région où$Ax+By<C$.

Pour une inégalité dans une variable, le point de terminaison est indiqué entre parenthèses ou crochets selon que aa est inclus ou non dans la solution :

$La figure montre deux lignes numériques. La ligne numérique sur la gauche est étiquetée x est inférieur à a. La ligne numérique montre une parenthèse en a et une flèche pointant vers la gauche. La ligne numérique sur la droite est étiquetée x est inférieur ou égal à a. La ligne numérique montre un crochet au niveau de a et une flèche pointant vers la gauche.$

De même, pour une inégalité entre deux variables, la ligne de démarcation est représentée par une ligne continue ou pointillée pour indiquer si elle est incluse ou non dans la solution. Ceci est résumé dans le tableau$\PageIndex{1}$.

Tableau$\PageIndex{1}$
$Ax+By<C$	$Ax+By\leq C$
$Ax+By>C$	$Ax+By\geq C$
La ligne de démarcation n'est pas incluse dans la solution.	La ligne de démarcation est incluse dans la solution.
La ligne de démarcation est pointillée.	La ligne de démarcation est pleine.

Maintenant, regardons ce que nous avons découvert dans Exercice$\PageIndex{1}$. Nous allons commencer par tracer la ligne$y=x+4$, puis nous allons tracer les cinq points que nous avons testés. Voir la figure$\PageIndex{3}$.

Le graphique montre le plan de coordonnées x y. Les axes x et y vont chacun de moins 10 à 10. La ligne y est égale à x plus 4 et est tracée sous la forme d'une flèche s'étendant du coin inférieur gauche vers le coin supérieur droit. Les points suivants sont tracés et étiquetés (négatif 8, 12), (1, 6), (2, 6), (0, 0) et (négatif 5, négatif 15). — Figurine$\PageIndex{3}$

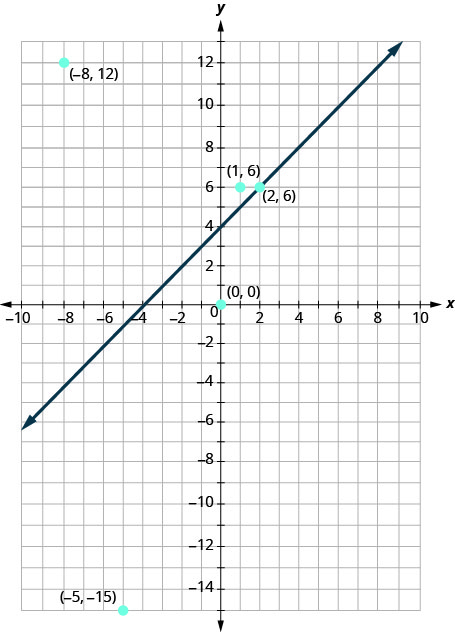
Au cours de l'exercice,$\PageIndex{1}$ nous avons constaté que certains points étaient des solutions à l'inégalité$y>x+4$ et d'autres non.

Parmi les points que nous avons tracés, lesquels constituent des solutions à l'inégalité$y>x+4$ ? Les points$(1,6)$ et$(−8,12)$ sont des solutions à l'inégalité$y>x+4$. Notez qu'ils se trouvent tous les deux du même côté de la ligne de démarcation$y=x+4$.

Les deux points$(0,0)$$(−5,−15)$ se situent de l'autre côté de la ligne$y=x+4$ de démarcation et ne constituent pas des solutions à l'inégalité$y>x+4$. Pour ces deux points,$y<x+4$.

Qu'en est-il de ce point$(2,6)$ ? Parce$6=2+4$ que le point est une solution à l'équation$y=x+4$. Le point$(2,6)$ se trouve donc sur la ligne de démarcation.

Prenons un autre point sur le côté gauche de la ligne de démarcation et testons s'il s'agit ou non d'une solution à l'inégalité$y>x+4$. Le point semble$(0,10)$ clairement se trouver à gauche de la ligne de démarcation, n'est-ce pas ? Est-ce une solution à l'inégalité ?

\[\begin{array}{l}{y>x+4} \\ {10\stackrel{?}{>}0+4} \\ {10>4} &{\text{So, }(0,10)\text{ is a solution to }y>x+4.}\end{array}\]

Tout point que vous choisissez sur le côté gauche de la ligne de démarcation constitue une solution à l'inégalité$y>x+4$. Tous les points sur la gauche sont des solutions.

De même, tous les points situés du côté droit de la ligne de démarcation, du côté avec$(0,0)$ et$(−5,−15)$, ne constituent pas des solutions$y>x+4$. Voir la figure$\PageIndex{4}$.

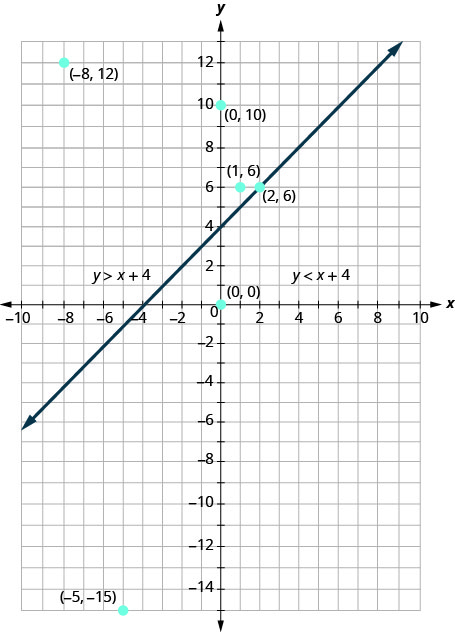
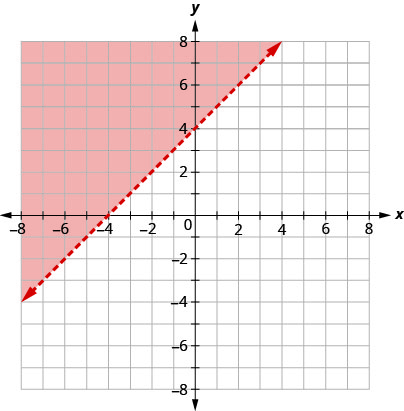
Le graphique de l'inégalité$y>x+4$ est illustré dans la figure$\PageIndex{5}$ ci-dessous. La ligne$y=x+4$ divise le plan en deux régions. La partie ombrée montre les solutions à l'inégalité$y>x+4$.

Les points de la ligne de démarcation, ceux où$y=x+4$, ne sont pas des solutions à l'inégalité$y>x+4$, de sorte que la ligne elle-même ne fait pas partie de la solution. Nous le montrons en faisant en sorte que la ligne soit pointillée et non pleine.

Exercice$\PageIndex{4}$

La ligne de démarcation indiquée est$y=2x−1$. Écrivez l'inégalité indiquée par le graphique.

Réponse

La ligne$y=2x−1$ est la ligne de démarcation. D'un côté de la ligne se trouvent les points avec$y>2x−1$ et de l'autre côté de la ligne se trouvent les points avec$y<2x−1$.

Testons le point$(0,0)$ et voyons quelle inégalité décrit son côté de la ligne de démarcation.

À$(0,0)$, quelle inégalité est vraie :

\[\begin{array}{ll}{y>2 x-1} & {\text { or }} & {y<2 x-1 ?} \\ {y>2 x-1} && {y<2 x-1} \\ {0>2 \cdot 0-1} && {0<2 \cdot 0-1} \\ {0>-1 \text { True }} && {0<-1 \text { False }}\end{array}\]

Comme$y>2x−1$ c'est vrai, le côté de la ligne avec$(0,0)$, est la solution. La zone ombrée montre la solution de l'inégalité$y>2x−1$.

Comme la ligne de démarcation est représentée par une ligne continue, l'inégalité inclut le signe égal.

Le graphique montre l'inégalité$y\geq 2x−1$.

Nous pouvons utiliser n'importe quel point comme point de test, à condition qu'il ne soit pas sur la ligne. Pourquoi avons-nous choisi$(0,0)$ ? Parce que c'est le plus facile à évaluer. Vous pouvez choisir un point de l'autre côté de la ligne de démarcation et le vérifier$y<2x−1$.

Exercice$\PageIndex{5}$

Écrivez l'inégalité indiquée par le graphique avec la ligne de démarcation$y=−2x+3$.

Réponse: $y\geq −2x+3$

Exercice$\PageIndex{6}$

Écrivez l'inégalité indiquée par le graphique avec la ligne de démarcation$y=\frac{1}{2}x−4$.

Réponse: $y \leq \frac{1}{2}x - 4$

Exercice$\PageIndex{7}$

La ligne de démarcation indiquée est$2x+3y=6$. Écrivez l'inégalité indiquée par le graphique.

Réponse

La ligne$2x+3y=6$ est la ligne de démarcation. D'un côté de la ligne se trouvent les points avec$2x+3y>6$ et de l'autre côté de la ligne se trouvent les points avec$2x+3y<6$.

Testons le point$(0,0)$ et voyons quelle inégalité décrit son côté de la ligne de démarcation.

À$(0,0)$, quelle inégalité est vraie :

\[\begin{array}{rr}{2 x+3 y>6} && {\text { or } \quad 2 x+3 y<6 ?} \\ {2 x+3 y>6} && {2 x+3 y<6} \\ {2(0)+3(0)>6} & & {2(0)+3(0)<6} \\ {0} >6 & {\text { False }} & {0<6}&{ \text { True }}\end{array}\]

Donc, le côté avec$(0,0)$ est le côté où$2x+3y<6$.

(Vous pouvez choisir un point de l'autre côté de la ligne de démarcation et le vérifier$2x+3y>6$.)

Comme la ligne de démarcation est représentée sous la forme d'une ligne pointillée, l'inégalité n'inclut pas de signe égal.

Le graphique montre la solution à l'inégalité$2x+3y<6$.

Exercice$\PageIndex{8}$

Écrivez l'inégalité indiquée par la région ombrée dans le graphique avec la ligne de démarcation$x−4y=8$.

Réponse: $x-4 y \leq 8$

Exercice$\PageIndex{9}$

Écrivez l'inégalité indiquée par la région ombrée dans le graphique avec la ligne de démarcation$3x−y=6$.

Réponse: $3 x-y \leq 6$

Diagramme des inégalités

Maintenant, nous sommes prêts à rassembler tout cela pour représenter graphiquement les inégalités linéaires.

Exercice$\PageIndex{10}$: How to Graph Linear Inequalities

Tracez l'inégalité linéaire$y \geq \frac{3}{4} x-2$.

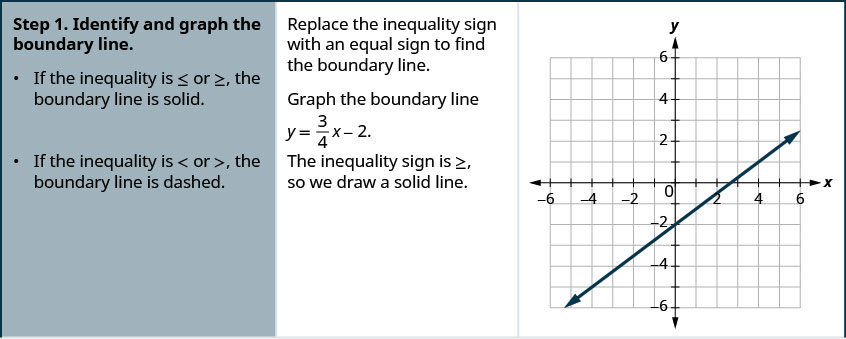
Réponse: $Cette figure est un tableau composé de trois colonnes et de trois lignes. La première colonne est une colonne d'en-tête qui contient les noms et les numéros de chaque étape. La deuxième colonne contient d'autres instructions écrites. La troisième colonne contient des données mathématiques. Dans la rangée supérieure du tableau, la première cellule de gauche se lit comme suit : « Étape 1. Identifiez et tracez la ligne de démarcation. Si l'inégalité est inférieure ou égale à, supérieure ou égale à, la ligne de démarcation est pleine. Si l'inégalité est inférieure ou supérieure à, la ligne de démarcation est pointillée. Le texte de la deuxième cellule se lit comme suit : « Remplacez le signe d'inégalité par un signe égal pour trouver la limite. Sur un graphique, la ligne de démarcation y est égale aux trois quarts x moins 2. Le signe d'inégalité est supérieur ou égal à, nous dessinons donc une ligne continue. La troisième cellule contient le graphique de la droite des trois quarts x moins 2 sur un plan de coordonnées.$ $Dans la deuxième rangée du tableau, la première cellule indique : « Étape 2. Testez un point qui ne se trouve pas sur la ligne de démarcation. Est-ce une solution à l'inégalité ? Dans la deuxième cellule, les instructions indiquent : « Nous allons tester (0, 0). Est-ce une solution à l'inégalité ? » La troisième cellule demande : At (0, 0), y est-il supérieur ou égal aux trois quarts x moins 2 ? En dessous, l'inégalité 0 est supérieure ou égale aux trois quarts de 0 moins 2, avec un point d'interrogation au-dessus du symbole d'inégalité. En dessous, l'inégalité 0 est supérieure ou égale à moins 2. 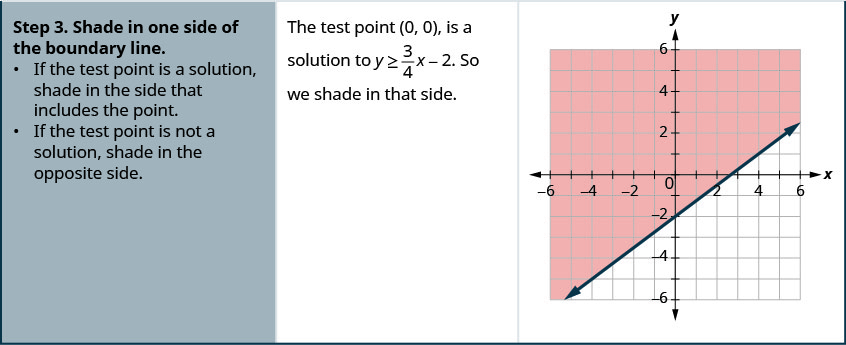En dessous se trouve : « Donc (0, 0) se trouve une solution.$ $Dans la troisième rangée du tableau, la première cellule indique : « Étape 3. De l'ombre sur un côté de la ligne de démarcation. Si le point d'essai est une solution, ombrez le côté qui inclut le point. Si le point d'essai n'est pas une solution, ombrez le côté opposé. Dans la deuxième cellule, les instructions indiquent : Le point de test (0, 0) est une solution pour y est supérieur ou égal aux trois quarts x moins 2. Nous faisons donc de l'ombre sur ce côté. » Dans la troisième cellule se trouve le graphique de la droite des trois quarts x moins 2 sur un plan de coordonnées, la région au-dessus de la ligne étant ombrée.$

Exercice$\PageIndex{11}$

Tracez l'inégalité linéaire$y \geq \frac{5}{2} x-4$.

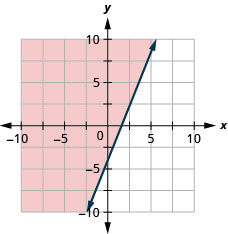
Réponse: $Le graphique montre le plan de coordonnées x y. Les axes x et y vont chacun de moins 10 à 10. La ligne y est égale à cinq moitiés x moins 4 et est tracée sous la forme d'une flèche continue s'étendant du coin inférieur gauche vers le haut à droite. La région au-dessus de la ligne est ombrée.$

Exercice$\PageIndex{12}$

Tracez l'inégalité linéaire$y<\frac{2}{3} x-5$.

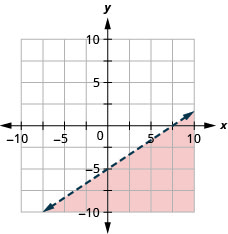
Réponse: $Le graphique montre le plan de coordonnées x y. Les axes x et y vont chacun de moins 10 à 10. La ligne y est égale aux deux tiers x moins 5 et est tracée sous la forme d'une flèche pointillée s'étendant du coin inférieur gauche vers le haut à droite. La zone située en dessous de la ligne est ombrée.$

Les étapes que nous prenons pour représenter graphiquement une inégalité linéaire sont résumées ici.

REPRÉSENTEZ UNE INÉGALITÉ LINÉAIRE.

Identifiez et tracez la ligne de démarcation.
- Si l'inégalité est$≤$ ou$≥$, la ligne de démarcation est pleine.
- Si l'inégalité est$<$ ou$>$, la ligne de démarcation est pointillée.
Testez un point qui ne se trouve pas sur la ligne de démarcation. Est-ce une solution à l'inégalité ?
De l'ombre sur un côté de la ligne de démarcation.
- Si le point d'essai est une solution, ombrez le côté qui inclut le point.
- Si le point d'essai n'est pas une solution, ombrez le côté opposé.

Exercice$\PageIndex{13}$

Tracez l'inégalité linéaire$x−2y<5$.

Réponse

Nous allons d'abord tracer la ligne de démarcation$x−2y=5$. L'inégalité, c'est$<$ que nous tracons une ligne pointillée.

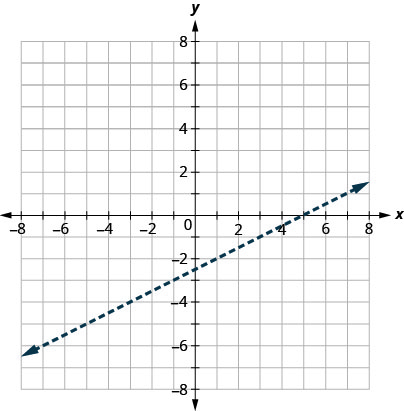
$Le graphique montre le plan de coordonnées x y. Les axes x et y vont chacun de moins 10 à 10. La ligne x moins 2 y égale 5 est tracée sous la forme d'une flèche pointillée s'étendant du coin inférieur gauche vers le haut à droite.$

Ensuite, nous testons un point. Nous l'utiliserons$(0,0)$ à nouveau parce qu'il est facile à évaluer et qu'il ne se trouve pas sur la ligne de démarcation.

Est-ce$(0,0)$ qu'une solution de$x−2y<5$ ?

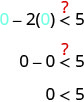
$La figure montre que l'inégalité 0 moins 2 fois 0 entre parenthèses est inférieur à 5, avec un point d'interrogation au-dessus du symbole d'inégalité. La ligne suivante indique que 0 moins 0 est inférieur à 5, avec un point d'interrogation au-dessus du symbole d'inégalité. La troisième ligne indique que 0 est inférieur à 5.$

Le point$(0,0)$ est une solution de$x−2y<5$, donc nous ombrageons de ce côté de la ligne de démarcation.

Exercice$\PageIndex{14}$

Tracez l'inégalité linéaire$2x−3y\leq 6$.

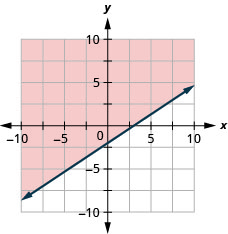
Réponse: $Le graphique montre le plan de coordonnées x y. Les axes x et y vont chacun de moins 10 à 10. La ligne 2 x moins 3 y égale 6 est tracée sous la forme d'une flèche continue s'étendant du coin inférieur gauche vers le haut à droite. La région au-dessus de la ligne est ombrée.$

Exercice$\PageIndex{15}$

Tracez l'inégalité linéaire$2x−y>3$.

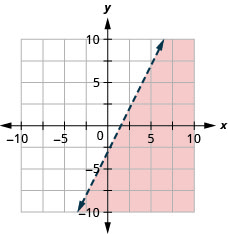
Réponse: $Le graphique montre le plan de coordonnées x y. Les axes x et y vont chacun de moins 10 à 10. La ligne 2 x moins y est égale à 3 est tracée sous la forme d'une flèche pointillée s'étendant du coin inférieur gauche vers le haut à droite. La zone située en dessous de la ligne est ombrée.$

Et si la ligne de démarcation passe par l'origine ? Dans ce cas, nous ne pourrons pas l'utiliser$(0,0)$ comme point de test. Pas de problème, nous allons simplement choisir un autre point qui ne se trouve pas sur la ligne de démarcation.

Exercice$\PageIndex{16}$

Tracez l'inégalité linéaire$y\leq −4x$.

Réponse

Nous allons d'abord tracer la ligne de démarcation$y=−4x$. Il se présente sous forme de pente et d'interception, avec$m=−4$ et$b=0$. L'inégalité, c'est$≤$ ainsi que nous tracons une ligne continue.

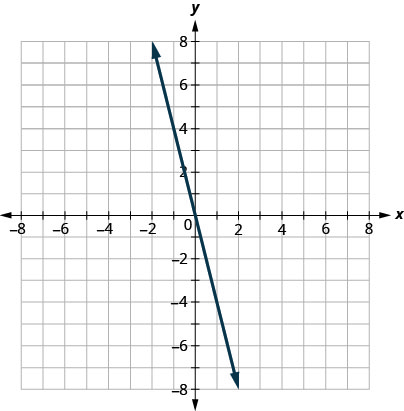
$Le graphique montre le plan de coordonnées x y. Les axes x et y vont chacun de moins 10 à 10. La ligne s y est égale à moins 4 x est tracée sous la forme d'une flèche continue s'étendant du haut à gauche vers le bas à droite.$

Maintenant, nous avons besoin d'un point de test. Nous pouvons voir que le point ne$(1,0)$ se trouve pas sur la ligne de démarcation.

Est-ce$(1,0)$ qu'une solution de$y≤−4x$ ?

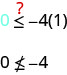
$La figure montre que 0 est inférieur ou égal à moins 4 fois 1 entre parenthèses, avec un point d'interrogation au-dessus du symbole d'inégalité. La ligne suivante indique que 0 n'est pas inférieur ou égal à moins 4.$

Le point n'$(1,0)$étant pas une solution$y≤−4x$, nous faisons de l'ombre sur le côté opposé de la ligne de démarcation. Voir la figure$\PageIndex{6}$.

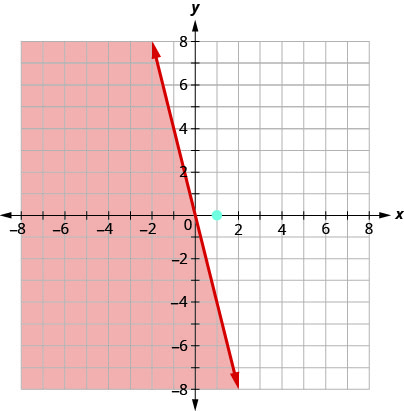
Le graphique montre le plan de coordonnées x y. Les axes x et y vont chacun de moins 10 à 10. La ligne y est égale à moins 4 x est tracée sous la forme d'une flèche continue s'étendant du haut à gauche vers le bas à droite. Le point (1, 0) est tracé, mais pas étiqueté. La région située à gauche de la ligne est ombrée. — Figurine$\PageIndex{6}$

Exercice$\PageIndex{17}$

Tracez l'inégalité linéaire$y>−3x$.

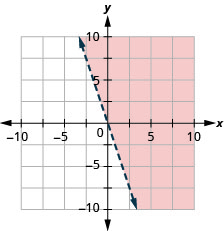
Réponse: $Le graphique montre le plan de coordonnées x y. Les axes x et y vont chacun de moins 10 à 10. La ligne y est égale à moins 3 x est tracée sous la forme d'une flèche pointillée s'étendant du coin supérieur gauche vers le bas à droite. La région située à droite de la ligne est ombrée.$

Exercice$\PageIndex{18}$

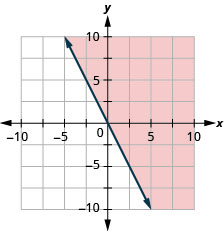
Tracez l'inégalité linéaire$y\geq −2x$.

Réponse: $Le graphique montre le plan de coordonnées x y. Les axes x et y vont chacun de moins 10 à 10. La ligne y est égale à moins 2 x est tracée sous la forme d'une flèche continue s'étendant du haut à gauche vers le bas à droite. La région située à droite de la ligne est ombrée.$

Certaines inégalités linéaires ne comportent qu'une seule variable. Ils peuvent avoir un$x$ mais non$y$, ou un$y$ mais non$x$. Dans ces cas, la ligne de démarcation sera verticale ou horizontale. Tu t'en souviens ?

$\begin{array}{ll}{x=a} & {\text { vertical line }} \\ {y=b} & {\text { horizontal line }}\end{array}$

Exercice$\PageIndex{19}$

Tracez l'inégalité linéaire$y>3$.

Réponse

Nous allons d'abord tracer la ligne de démarcation$y=3$. Il s'agit d'une ligne horizontale. L'inégalité, c'est$>$ que nous tracons une ligne pointillée.

Nous testons ce point$(0,0)$.

\[y>3 \\ 0\not>3\]

$(0,0)$n'est pas une solution à$y>3$.

Nous ombrons donc le côté qui n'inclut pas$(0,0)$.

Exercice$\PageIndex{20}$

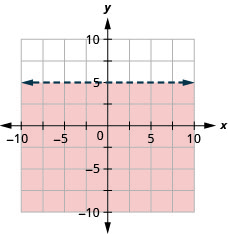
Tracez l'inégalité linéaire$y<5$.

Réponse: $Le graphique montre le plan de coordonnées x y. Les axes x et y vont chacun de moins 10 à 10. La ligne y égale 5 est tracée sous la forme d'une flèche pointillée horizontalement à travers le plan. La région au-dessus de la ligne est ombrée.$

Exercice$\PageIndex{21}$

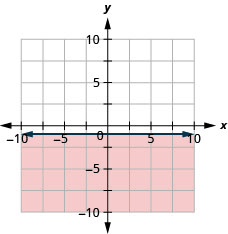
Tracez l'inégalité linéaire$y \leq-1$.

Réponse: $Le graphique montre le plan de coordonnées x y. Les axes x et y vont chacun de moins 10 à 10. La ligne y égale moins 1 est tracée sous la forme d'une flèche pointillée horizontalement à travers le plan. La zone située en dessous de la ligne est ombrée.$

Concepts clés

Pour représenter graphiquement une inégalité linéaire
1. Identifiez et tracez la ligne de démarcation.
  Si l'inégalité est$≤$ ou$≥$, la ligne de démarcation est pleine.
  Si l'inégalité est$<$ ou$>$, la ligne de démarcation est pointillée.
2. Testez un point qui ne se trouve pas sur la ligne de démarcation. Est-ce une solution à l'inégalité ?
3. De l'ombre sur un côté de la ligne de démarcation.
  Si le point d'essai est une solution, ombrez le côté qui inclut le point.
  Si le point d'essai n'est pas une solution, ombrez le côté opposé.

Lexique

ligne de démarcation: La ligne avec l'équation$A x+B y=C$ qui sépare la région où$A x+B y>C$ de la région où$A x+B y<C$.

inégalité linéaire: Une inégalité qui peut s'écrire sous l'une des formes suivantes :
\[A x+B y>C \quad A x+B y \geq C \quad A x+B y<C \quad A x+B y \leq C\]
où$A$ et ne$B$ sont pas tous les deux nuls.

solution d'une inégalité linéaire: Une paire ordonnée$(x,\,y)$ est une solution à une inégalité linéaire. L'inégalité est vraie lorsque nous substituons les valeurs de$x$ et$y$.

INÉGALITÉ LINÉAIRE

Solution d'une inégalité linéaire

Exercice\(\PageIndex{1}\)

Exercice\(\PageIndex{2}\)

Exercice\(\PageIndex{3}\)

LIGNE DE DÉMARCATION

Exercice\(\PageIndex{4}\)

Exercice\(\PageIndex{5}\)

Exercice\(\PageIndex{6}\)

Exercice\(\PageIndex{7}\)

Exercice\(\PageIndex{8}\)

Exercice\(\PageIndex{9}\)

Exercice\(\PageIndex{10}\): How to Graph Linear Inequalities

Exercice\(\PageIndex{11}\)

Exercice\(\PageIndex{12}\)

REPRÉSENTEZ UNE INÉGALITÉ LINÉAIRE.

Exercice\(\PageIndex{13}\)

Exercice\(\PageIndex{14}\)

Exercice\(\PageIndex{15}\)

Exercice\(\PageIndex{16}\)

Exercice\(\PageIndex{17}\)

Exercice\(\PageIndex{18}\)

Exercice\(\PageIndex{19}\)

Exercice\(\PageIndex{20}\)

Exercice\(\PageIndex{21}\)

\((0,0)\)		$.$
$.$		$.$
Simplifiez.		$.$ Donc, n'\((0,0)\)est pas une solution à\(y>x+4\).

\((1,6)\)		$.$
$.$		$.$
Simplifiez.		$.$ Donc,\((1,6)\) est une solution pour\(y>x+4\).

\((2,6)\)		$.$
$.$		$.$
Simplifiez.		$.$ Donc, n'\((2,6)\)est pas une solution à\(y>x+4\).

\((−5,−15)\)		$.$
$.$		$.$
Simplifiez.		$.$ Donc, n'\((−5,−15)\)est pas une solution à\(y>x+4\).

(−8,12)		$.$
$.$		$.$
Simplifiez.		$.$ Donc,\((−8,12)\) est une solution pour\(y>x+4\).

\(Ax+By<C\)	\(Ax+By\leq C\)
\(Ax+By>C\)	\(Ax+By\geq C\)
La ligne de démarcation n'est pas incluse dans la solution.	La ligne de démarcation est incluse dans la solution.
La ligne de démarcation est pointillée.	La ligne de démarcation est pleine.