4.6 : Trouver l'équation d'une droite
- Page ID
- 194695
À la fin de cette section, vous serez en mesure de :
- Trouvez une équation de la droite en fonction de la pente et de l'intersection Y
- Trouvez une équation de la droite en fonction de la pente et d'un point
- Trouvez une équation de la droite à partir de deux points
- Trouve l'équation d'une droite parallèle à une droite donnée
- Trouve l'équation d'une droite perpendiculaire à une droite donnée
Avant de commencer, répondez à ce questionnaire de préparation.
- Résoudre :\(\frac{2}{3} = \frac{x}{5}\).
Si vous avez oublié ce problème, passez en revue l'exercice 2.2.4. - Simplifiez :\(−\frac{2}{5}(x−15)\).
Si vous avez oublié ce problème, passez en revue l'exercice 1.10.34.
Comment les détaillants en ligne savent-ils que « vous pouvez également aimer » un article en particulier en fonction de ce que vous venez de commander ? Comment les économistes peuvent-ils savoir comment une hausse du salaire minimum affectera le taux de chômage ? Comment les chercheurs en médecine créent-ils des médicaments pour cibler les cellules cancéreuses ? Comment les ingénieurs de la circulation peuvent-ils prévoir l'effet sur votre temps de trajet d'une hausse ou d'une baisse du prix de l'essence ? Ce ne sont que des mathématiques.
Vous êtes à une étape passionnante de votre parcours mathématique, car les mathématiques que vous étudiez ont des applications intéressantes dans le monde réel.
Les sciences physiques, les sciences sociales et le monde des affaires regorgent de situations qui peuvent être modélisées à l'aide d'équations linéaires reliant deux variables. Les données sont collectées et représentées graphiquement. Si les points de données semblent former une ligne droite, une équation de cette droite peut être utilisée pour prédire la valeur d'une variable en fonction de la valeur de l'autre variable.
Pour créer un modèle mathématique d'une relation linéaire entre deux variables, nous devons être en mesure de trouver l'équation de la droite. Dans cette section, nous allons examiner plusieurs manières d'écrire l'équation d'une droite. La méthode spécifique que nous utilisons sera déterminée par les informations qui nous seront fournies.
Trouvez une équation de la droite en fonction de la pente et de l'intersection y
Nous pouvons facilement déterminer la pente et l'intersection d'une droite si l'équation a été écrite sous la forme pente-intersection, y=mx+b. Maintenant, nous allons faire l'inverse : nous allons commencer par la pente et l'intersection y et les utiliser pour trouver l'équation de la droite.
Trouvez l'équation d'une droite avec une pente −7 et une intersection y (0, −1).
- Réponse
-
Comme on nous donne la pente et l'intersection y de la droite, nous pouvons substituer les valeurs nécessaires dans la forme pente-intersection, y=mx+b.
Donnez un nom à la pente. 
Nommez l'intercept y. 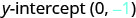
Remplacez les valeurs par y=mx+b. 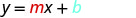
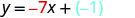
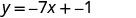
Trouvez l'équation d'une droite avec pente\(\frac{2}{5}\) et y -intercept (0,4).
- Réponse
-
\(y = \frac{2}{5}x + 4\)
Trouvez l'équation d'une droite avec une pente −1 et une intersection y (0, −3).
- Réponse
-
\(y=−x−3\)
Parfois, la pente et l'intersection doivent être déterminées à partir du graphique.
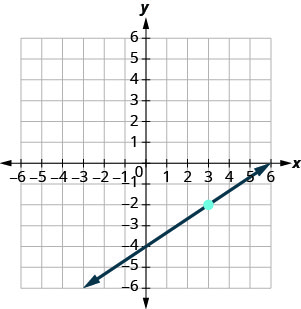
Trouvez l'équation de la droite affichée.
- Réponse
-
Nous devons trouver la pente et l'intersection y de la droite à partir du graphique afin de pouvoir substituer les valeurs nécessaires dans la forme pente-intersection, y=mx+by=mx+b.
Pour trouver la pente, nous choisissons deux points sur le graphique.
L'intersection y est (0, −4) et le graphe passe par (3, −2).
Déterminez la pente en comptant la montée et la course. 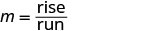

Trouvez l'intersection y. 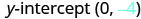
Remplacez les valeurs par y=mx+b. 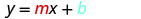
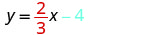
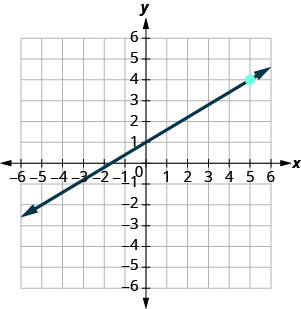
Trouvez l'équation de la droite indiquée sur le graphique.
- Réponse
-
\(y=\frac{3}{5}x+1\)
Trouvez l'équation de la droite indiquée sur le graphique.
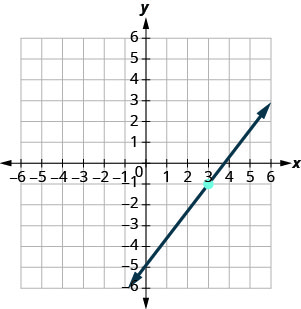
- Réponse
-
\(y=\frac{4}{3}x−5\)
Trouvez une équation de la droite en fonction de la pente et d'un point
La recherche de l'équation d'une droite à l'aide de la forme pente-intersection de l'équation fonctionne bien lorsque l'on vous donne la pente et l'intersection y ou lorsque vous les lisez sur un graphique. Mais que se passe-t-il lorsque vous avez un autre point au lieu de l'intersection y ?
Nous allons utiliser la formule de pente pour dériver une autre forme d'équation de la droite. Supposons que nous ayons une droite qui a une pente mm et qui contient un point spécifique\((x_{1}, y_{1})\) et un autre point, que nous appellerons simplement (x, y). Nous pouvons écrire la pente de cette ligne, puis la changer sous une forme différente.
\(\begin{array} {lrll}&m &=\frac{y-y_{1}}{x-x_{1}} \\ \text{Multiply both sides of the equation by }x−x_{1}.&m\left(x-x_{1}\right) &=\left(\frac{y-y_{1}}{x-x_{1}}\right)\left(x-x_{1}\right) \\ \text{Simplify.}&m\left(x-x_{1}\right) &=y-y_{1} \\ \text{Rewrite the equation with the y terms on the left.} &y-y_{1} &=m\left(x-x_{1}\right) \end{array}\)
Ce format est appelé forme point—pente d'une équation d'une droite.
La forme point—pente de l'équation d'une droite de pente mm et contenant le point\((x_{1}, y_{1})\) est
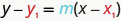
Nous pouvons utiliser la forme point—pente d'une équation pour trouver l'équation d'une droite lorsque l'on nous donne la pente et un point. Nous allons ensuite réécrire l'équation sous forme pente-intersection. La plupart des applications d'équations linéaires utilisent la forme pente-intersection.
Trouvez l'équation d'une droite avec une pente\(m=\frac{2}{5}\) qui contient le point (10,3). Écrivez l'équation sous forme de pente et d'intersection.
- Réponse
-




Trouvez l'équation d'une droite avec pente\(m=\frac{5}{6}\) et contenant le point (6,3).
- Réponse
-
\(y=\frac{5}{6}x−2\)
Trouvez l'équation d'une droite avec pente\(m=\frac{2}{3}\) et contenant le point (9,2).
- Réponse
-
\(y=\frac{2}{3}x−4\)
- Identifiez la pente.
- Identifiez le point.
- Substituez les valeurs dans la forme à pente ponctuelle,\(y−y_{1}=m(x−x_{1})\).
- Écrivez l'équation sous forme de pente et d'intersection.
Trouvez l'équation d'une droite avec pente\(m=−\frac{1}{3}\) qui contient le point (6, −4). Écrivez l'équation sous forme de pente et d'intersection.
- Réponse
-
Comme on nous donne un point et la pente de la droite, nous pouvons substituer les valeurs nécessaires dans la forme point—pente,\(y−y_{1}=m(x−x_{1})\).
Identifiez la pente. 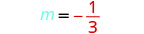
Identifiez le point. 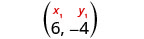
Remplacez les valeurs par\(y−y_{1}=m(x−x_{1})\). 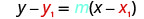
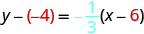
Simplifiez. 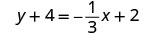
Écrivez sous forme de pente et d'interception. 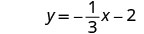
Trouve l'équation d'une droite avec pente\(m=−\frac{2}{5}\) et contenant le point (10, −5).
- Réponse
-
\(y=−\frac{2}{5}x−1\)
Trouve l'équation d'une droite avec pente\(m=−\frac{3}{4}\) et contenant le point (4, −7).
- Réponse
-
\(y=−\frac{3}{4}x−4\)
Trouvez l'équation d'une ligne horizontale contenant le point (−1,2). Écrivez l'équation sous forme de pente et d'intersection.
- Réponse
-
Chaque ligne horizontale a une pente 0. Nous pouvons remplacer la pente et les points par la forme point—pente,\(y−y_{1}=m(x−x_{1})\).
Avons-nous fini par avoir la forme d'une ligne horizontale, y=a ?Identifiez la pente. 
Identifiez le point. 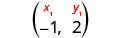
Remplacez les valeurs par\(y−y_{1}=m(x−x_{1})\). 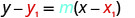
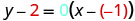
Simplifiez. 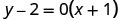
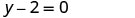
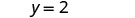
Écrivez sous forme de pente et d'interception. Il est au format y, mais peut être écrit y=0x+2.
Trouvez l'équation d'une ligne horizontale contenant le point (−3,8).
- Réponse
-
y = 8
Trouvez l'équation d'une ligne horizontale contenant le point (−1,4).
- Réponse
-
y = 4
Trouvez une équation de la droite à partir de deux points
Lorsque des données du monde réel sont collectées, un modèle linéaire peut être créé à partir de deux points de données. Dans l'exemple suivant, nous verrons comment trouver l'équation d'une droite lorsque seulement deux points sont donnés.
Jusqu'à présent, deux options s'offrent à nous pour trouver l'équation d'une droite : pente-intersection ou point—pente. Comme nous connaîtrons deux points, il sera plus judicieux d'utiliser la forme point—pente.
Mais ensuite, nous avons besoin de la pente. Pouvons-nous trouver la pente avec seulement deux points ? Oui. Ensuite, une fois que nous avons la pente, nous pouvons l'utiliser avec l'un des points donnés pour trouver l'équation.
Trouvez l'équation d'une droite contenant les points (5,4) et (3,6). Écrivez l'équation sous forme de pente et d'intersection.
- Réponse
-




Utilisez le point (3,6) et veillez à obtenir la même équation.
Trouvez l'équation d'une droite contenant les points (3,1) et (5,6).
- Réponse
-
\(y=\frac{5}{2}x−\frac{13}{2}\)
Trouvez l'équation d'une droite contenant les points (1,4) et (6,2).
- Réponse
-
\(y=−\frac{2}{5}x+\frac{22}{5}\)
- Trouvez la pente en utilisant les points donnés.
- Choisissez un point.
- Substituez les valeurs dans la forme à pente ponctuelle,\(y−y_{1}=m(x−x_{1})\).
- Écrivez l'équation sous forme de pente et d'intersection.
Trouvez l'équation d'une droite contenant les points (−3, −1) et (2, −2). Écrivez l'équation sous forme de pente et d'intersection.
- Réponse
-
Comme nous avons deux points, nous trouverons une équation de la droite en utilisant la forme point—pente. La première étape sera de trouver la pente.
Détermine la pente de la droite passant par (−3, −1) et (2, −2). 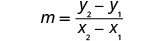
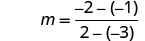
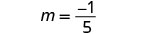
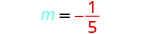
Choisissez l'un ou l'autre point 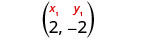
Remplacez les valeurs par\(y−y_{1}=m(x−x_{1})\). 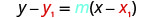
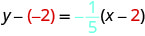
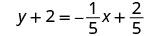
Écrivez sous forme de pente et d'interception. 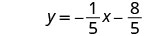
Trouvez l'équation d'une droite contenant les points (−2, −4) et (1, −3).
- Réponse
-
\(y=\frac{1}{3}x−\frac{10}{3}\)
Trouvez l'équation d'une droite contenant les points (−4, −3) et (1, −5).
- Réponse
-
\(y=−\frac{2}{5}x−\frac{23}{5}\)
Trouvez l'équation d'une droite contenant les points (−2,4) et (−2, −3). Écrivez l'équation sous forme de pente et d'intersection.
- Réponse
-
Encore une fois, la première étape sera de trouver la pente.
\(\begin{array}{lrl} \text { Find the slope of the line through }(-2,4) \text { and }(-2,-3) & & &\\ &m &=&\frac{y_{2}-x_{1}}{x_{2}-x_{1}} \\ &m &=&\frac{-3-4}{-2-(-2)} \\ &m &= &\frac{-7}{0} \\ \\ \text { The slope is undefined. } & & &\end{array}\)
Cela nous indique qu'il s'agit d'une ligne verticale. Nos deux points ont une coordonnée x de −2. Notre équation de la droite est donc x=−2. Comme il n'y a pas de yy, nous ne pouvons pas l'écrire sous forme pente-interception.
Vous pouvez dessiner un graphique en utilisant les deux points donnés. Le graphique est-il en accord avec notre conclusion selon laquelle il s'agit d'une ligne verticale ?
Trouve l'équation d'une droite contenant les points (5,1) et (5, −4).
- Réponse
-
x = 5
Trouvez l'équation d'une droite contenant les points (−4,4) et (−4,3).
- Réponse
-
x=−4
Nous avons vu que nous pouvons utiliser soit la forme pente-intersection, soit la forme point—pente pour trouver l'équation d'une droite. Le formulaire que nous utilisons dépend des informations qui nous sont fournies. Ceci est résumé dans le tableau\(\PageIndex{1}\).
| Pour écrire l'équation d'une droite | ||
| En cas d'administration : | Utilisation : | Formulaire : |
| Pente et intersection en Y | pente — interception | y=mx+b |
| Pente et point | point—pente | \(y−y_{1}=m(x−x_{1})\) |
| Deux points | point—pente | \(y−y_{1}=m(x−x_{1})\) |
Trouver l'équation d'une droite parallèle à une droite donnée
Supposons que nous devions trouver l'équation d'une droite passant par un point spécifique et parallèle à une droite donnée. Nous pouvons utiliser le fait que les lignes parallèles ont la même pente. Nous aurons donc un point et la pente, exactement ce dont nous avons besoin pour utiliser l'équation point—pente.
Regardons d'abord cela graphiquement.
Le graphique montre le graphe de y=2x−3. Nous voulons tracer une ligne parallèle à cette droite et passant par le point (−2,1).
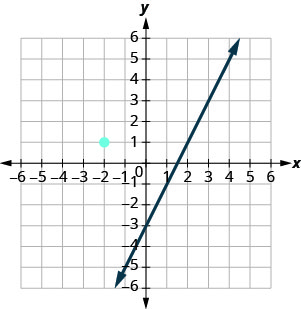
Nous savons que les lignes parallèles ont la même pente. La deuxième ligne aura donc la même pente que y=2x−3. Cette pente l'est\(m_{\|} = 2\). Nous utiliserons la notation\(m_{\|}\) pour représenter la pente d'une droite parallèle à une droite de pente m. (Remarquez que l'indice ressemble à deux lignes parallèles.)
La deuxième ligne passera par (-2,1) et aura m=2. Pour tracer la courbe, nous partons de (−2,1) et comptons la hausse et la course. Avec m=2 (ou\(m=\frac{2}{1}\)), on compte la hausse 2 et la course 1. Nous tracons la ligne.
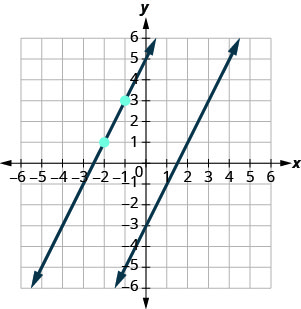
Les lignes apparaissent-elles parallèles ? Est-ce que la deuxième ligne passe par (−2,1) ?
Voyons maintenant comment procéder algébriquement.
Nous pouvons utiliser la forme pente-intersection ou la forme point—pente pour trouver l'équation d'une droite. Ici, nous connaissons un point et pouvons trouver la pente. Nous allons donc utiliser la forme point—pente.
Trouvez l'équation d'une droite parallèle à y=2x−3 qui contient le point (−2,1). Écrivez l'équation sous forme de pente et d'intersection.
- Réponse
-
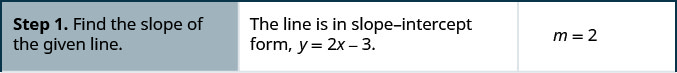




Cette équation a-t-elle du sens ? Qu'est-ce que l'intersection y de la ligne ? Quelle est la pente ?
Trouvez l'équation d'une droite parallèle à la droite y=3x+1 qui contient le point (4,2). Écrivez l'équation sous forme de pente et d'intersection.
- Réponse
-
y=3 x − 10
Trouvez l'équation d'une droite parallèle à la droite\(y=\frac{1}{2}x−3\) contenant le point (6,4).
- Réponse
-
\(y=\frac{1}{2}x+1\)
- Détermine la pente de la ligne donnée.
- Détermine la pente de la ligne parallèle.
- Identifiez le point.
- Substituez les valeurs sous la forme d'une pente ponctuelle,\(y−y_{1}=m(x−x_{1})\).
- Écrivez l'équation sous forme de pente et d'intersection.
Trouver l'équation d'une droite perpendiculaire à une droite donnée
Maintenant, considérons les lignes perpendiculaires. Supposons que nous ayons besoin de trouver une ligne passant par un point spécifique et qui soit perpendiculaire à une ligne donnée. Nous pouvons utiliser le fait que les lignes perpendiculaires ont des pentes réciproques négatives. Nous utiliserons à nouveau l'équation point—pente, comme nous l'avons fait pour les droites parallèles.
Le graphique montre le graphe de y=2x−3. Nous voulons maintenant tracer une droite perpendiculaire à cette droite et la traversant (−2,1).

Nous savons que les lignes perpendiculaires ont des pentes réciproques négatives. Nous utiliserons la notation\(m_{\perp}\) pour représenter la pente d'une droite perpendiculaire à une droite de pente m. (Notez que l'indice\(_{\perp}\) ressemble aux angles droits formés par deux lignes perpendiculaires.)
\[\begin{array}{cl}{y=2 x-3} & {\text { perpendicular line }} \\ {m=2} & {m_{\perp}=-\frac{1}{2}}\end{array}\]
Nous savons maintenant que la droite perpendiculaire passera par (−2,1) avec\(m_{\perp}=−\frac{1}{2}\).
Pour tracer la courbe, nous allons commencer à (−2,1) et compter la hausse −1 et la course 2. Ensuite, nous tracons la ligne.
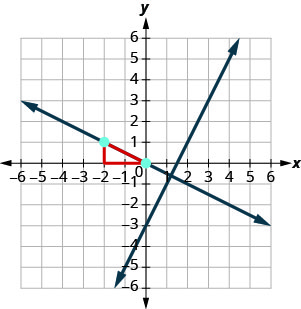
Les lignes paraissent-elles perpendiculaires ? Est-ce que la deuxième ligne passe par (−2,1) ?
Voyons maintenant comment procéder algébriquement. Nous pouvons utiliser la forme pente-intersection ou la forme point—pente pour trouver l'équation d'une droite. Dans cet exemple, nous connaissons un point et pouvons trouver la pente. Nous allons donc utiliser la forme point—pente.
Trouvez l'équation d'une droite perpendiculaire à y=2x−3 qui contient le point (−2,1). Écrivez l'équation sous forme de pente et d'intersection.
- Réponse
-





Trouvez l'équation d'une droite perpendiculaire à la droite y=3x+1 qui contient le point (4,2). Écrivez l'équation sous forme de pente et d'intersection.
- Réponse
-
\(y=−\frac{1}{3}x+\frac{10}{3}\)
Trouvez l'équation d'une droite perpendiculaire à la droite\(y=\frac{1}{2}x−3\) contenant le point (6,4).
- Réponse
-
y=−2x+16
- Détermine la pente de la ligne donnée.
- Détermine la pente de la ligne perpendiculaire.
- Identifiez le point.
- Substituez les valeurs sous la forme d'une pente ponctuelle,\(y−y_{1}=m(x−x_{1})\).
- Écrivez l'équation sous forme de pente et d'intersection.
Trouvez l'équation d'une droite perpendiculaire à x=5 qui contient le point (3, −2). Écrivez l'équation sous forme de pente et d'intersection.
- Réponse
-
Encore une fois, puisque nous connaissons un point, l'option point—pente semble plus prometteuse que l'option pente-interception. Nous avons besoin de la pente pour utiliser cette forme, et nous savons que la nouvelle ligne sera perpendiculaire à x=5. Cette ligne est verticale, donc sa perpendiculaire sera horizontale. Cela nous indique le\(m_{\perp}=0\).
\(\begin{array}{lrll}{\text { Identify the point. }} &{(3}&{,}&{-2)}\\ {\text { Identify the slope of the perpendicular line. }} & {m_{\perp}}&{=}&{0} \\ {\text { Substitute the values into } y-y_{1}=m\left(x-x_{1}\right) .} & {y-y_{1}}&{=}&{m\left(x-x_{1}\right)} \\{} &{y−(−2)}&{=}&{0(x−3)} \\{\text { Simplify. }} & {y+2}&{=}&{0} \\ &{y}&{=}&{-2}\end{array}\)
Esquissez le graphique des deux lignes. Sont-elles perpendiculaires ?
Trouvez l'équation d'une droite perpendiculaire à la droite x=4 qui contient le point (4, −5). Écrivez l'équation sous forme de pente et d'intersection.
- Réponse
-
y=−5
Trouvez l'équation d'une droite perpendiculaire à la droite x=2 qui contient le point (2, -1). Écrivez l'équation sous forme de pente et d'intersection.
- Réponse
-
y=−1
Dans l'exercice\(\PageIndex{31}\), nous avons utilisé la forme point—pente pour trouver l'équation. Nous aurions pu envisager la question d'une autre manière.
Nous voulons trouver une droite perpendiculaire à x=5 qui contient le point (3, −2). Le graphique nous montre la droite x=5 et le point (3, -2).
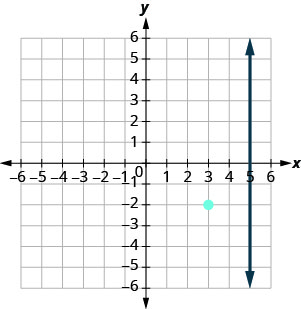
Nous savons que chaque ligne perpendiculaire à une ligne verticale est horizontale, nous allons donc esquisser la ligne horizontale passant par (3, −2).
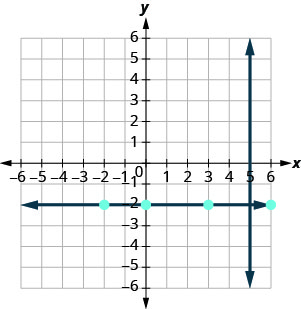
Les lignes paraissent-elles perpendiculaires ?
Si nous examinons quelques points sur cette ligne horizontale, nous remarquons qu'ils ont tous des coordonnées y de −2. Ainsi, l'équation de la droite perpendiculaire à la droite verticale x=5 est y=-2.
Trouvez l'équation d'une droite perpendiculaire à y=−4 qui contient le point (−4,2). Écrivez l'équation sous forme de pente et d'intersection.
- Réponse
-
La ligne y=-4 est une ligne horizontale. Toute ligne perpendiculaire à celle-ci doit être verticale, sous la forme x=a. Comme la ligne perpendiculaire est verticale et passe par (−4,2), chaque point de cette ligne possède une coordonnée x de −4. L'équation de la droite perpendiculaire est x=−4. Vous pouvez dessiner les lignes. Sont-elles perpendiculaires ?
Trouvez l'équation d'une droite perpendiculaire à la droite y=1 qui contient le point (−5,1). Écrivez l'équation sous forme de pente et d'intersection.
- Réponse
-
x=−5
Trouvez l'équation d'une droite perpendiculaire à la droite y=−5 qui contient le point (−4, −5).
- Réponse
-
x=−4
Accédez à cette ressource en ligne pour obtenir des instructions supplémentaires et vous entraîner à trouver l'équation d'une droite.
Concepts clés
- Pour trouver l'équation d'une droite en fonction de la pente et d'un point
- Identifiez la pente.
- Identifiez le point.
- Substituez les valeurs dans la forme à pente ponctuelle,\(y−y_{1}=m(x−x_{1})\).
- Écrivez l'équation sous forme d'intersection de pente.
- Pour trouver l'équation d'une droite à deux points
- Trouvez la pente en utilisant les points donnés.
- Choisissez un point.
- Substituez les valeurs dans la forme à pente ponctuelle,\(y−y_{1}=m(x−x_{1})\).
- Écrivez l'équation sous forme d'intersection de pente.
- Pour écrire l'équation d'une droite
- Si les options slope et\(y\) -intercept sont données, utilisez la forme slope—intercept\(y=mx+b\).
- Si vous avez une pente et un point, utilisez la forme point—pente\(y−y_{1}=m(x−x_{1})\).
- Si vous avez deux points, utilisez la forme point—pente\(y−y_{1}=m(x−x_{1})\).
- Pour trouver l'équation d'une droite parallèle à une droite donnée
- Détermine la pente de la ligne donnée.
- Détermine la pente de la ligne parallèle.
- Identifiez le point.
- Substituez les valeurs dans la forme à pente ponctuelle,\(y−y_{1}=m(x−x_{1})\).
- Écrivez l'équation sous forme d'intersection de pente.
- Pour trouver l'équation d'une droite perpendiculaire à une droite donnée
- Détermine la pente de la ligne donnée.
- Détermine la pente de la ligne perpendiculaire.
- Identifiez le point.
- Substituez les valeurs dans la forme à pente ponctuelle,\(y−y_{1}=m(x−x_{1})\).
- Écrivez l'équation sous forme d'intersection de pente.
Lexique
- forme point—pente
- La forme point—pente de l'équation d'une droite avec une pente mm et contenant le point\(\left(x_{1}, y_{1}\right)\) est\(y-y_{1}=m\left(x-x_{1}\right)\).


