4.5 : Utiliser la forme pente-intersection d'une équation d'une droite
- Page ID
- 194712
À la fin de cette section, vous serez en mesure de :
- Reconnaître la relation entre le graphe et la forme pente-intersection d'une équation d'une droite
- Identifier la pente et la forme d'intersection Y d'une équation d'une droite
- Tracez une ligne en utilisant sa pente et son intersection
- Choisissez la méthode la plus pratique pour tracer une ligne
- Représenter graphiquement et interpréter les applications de la pente et de l'interception
- Utiliser les pentes pour identifier les lignes parallèles
- Utiliser les pentes pour identifier les lignes perpendiculaires
Avant de commencer, répondez à ce questionnaire de préparation.
- Ajoutez :\(\frac{x}{4} + \frac{1}{4}\).
Si vous avez oublié ce problème, passez en revue l'exercice 1.7.1. - Trouvez la réciproque de\(\frac{3}{7}\).
Si vous avez oublié ce problème, passez en revue l'exercice 1.6.19. - Résolvez\(2x−3y=12\) pour\(y\).
Si vous avez oublié ce problème, passez en revue l'exercice 2.6.16.
Reconnaître la relation entre le graphe et la forme pente-intersection d'une équation d'une droite
Nous avons représenté graphiquement des équations linéaires en traçant des points, en utilisant des points d'intersection, en reconnaissant les lignes horizontales et verticales et en utilisant la méthode point—pente. Une fois que nous aurons vu comment une équation sous forme pente-intersection et son graphe sont liés, nous aurons une autre méthode que nous pourrons utiliser pour tracer des lignes.
Dans Graph Linear Equations in Two Variables, nous avons représenté graphiquement la ligne de l'équation\(y=12x+3\) en traçant des points. Voir la figure\(\PageIndex{1}\). Trouvons la pente de cette ligne.
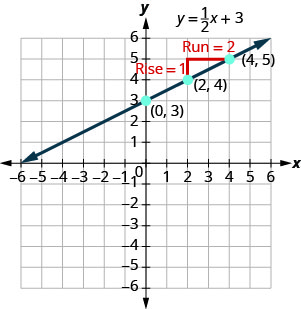
Les lignes rouges nous indiquent la hausse\(1\) et la course\(2\). Substituer dans la formule de pente :
\[\begin{aligned} m &=\frac{\text { rise }}{\text { rise }} \\ m &=\frac{1}{2} \end{aligned}\]
Qu'est-ce que l'\(y\)-intercept de la ligne ? Le\(y\) -intercept est l'endroit où la ligne croise l'\(y\)axe -, donc\(y\) -intercept est\((0,3)\). L'équation de cette droite est la suivante :
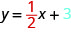
Remarquez que la ligne contient :

Lorsqu'une équation linéaire est résolue pour\(y\), le coefficient du\(x\) terme -est la pente et le terme constant est la\(y\) coordonnée de l'\(y\)intersection. Nous disons que l'équation\(y=\frac{1}{2}x+3\) est sous forme de pente et d'intersection.
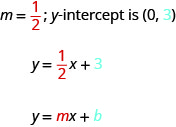
La forme pente-intersection d'une équation d'une droite avec pente mm et\(y\) -intersection\((0,b)\) est,
\[y=mx+b\]
Parfois, la forme pente-intersection est appelée « forme y ».
Utilisez le graphique pour déterminer la pente et l'\(y\)intersection de la droite,\(y=2x+1\).
Comparez ces valeurs à l'équation\(y=mx+b\).
- Réponse
-
Pour trouver la pente de la ligne, nous devons choisir deux points sur la ligne. Nous utiliserons les points\((0,1)\) et\((1,3)\).
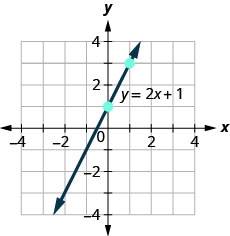
Trouvez la montée et la course. 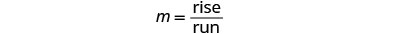
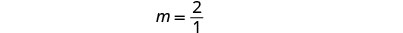
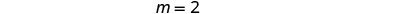
Trouvez le\(y\) -intercept de la ligne. Le\(y\) -intercept est le point\((0, 1)\). 
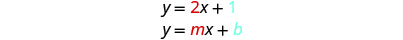
La pente est identique au coefficient de\(x\) et la\(y\) coordonnée\(y\) -de l'intersection est identique au terme constant.
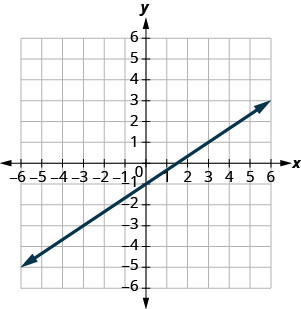
Utilisez le graphique pour déterminer la pente et l'\(y\)intersection de la droite\(y=\frac{2}{3}x−1\). Comparez ces valeurs à l'équation\(y=mx+b\).
- Réponse
-
pente\(m = \frac{2}{3}\) et\(y\) intersection\((0,−1)\)
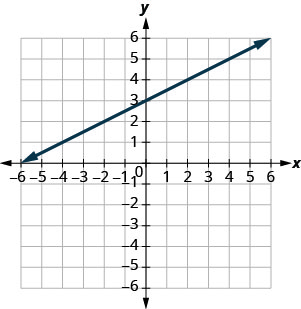
Utilisez le graphique pour déterminer la pente et l'\(y\)intersection de la droite\(y=\frac{1}{2}x+3\). Comparez ces valeurs à l'équation\(y=mx+b\).
- Réponse
-
pente\(m = \frac{1}{2}\) et\(y\) intersection\((0,3)\)
Identifier la pente et l'\(y\)intersection à partir de l'équation d'une droite
Dans Comprendre la[1] pente d'une ligne, nous avons tracé une ligne à l'aide de la pente et d'un point. Lorsque l'on nous donne une équation sous forme pente-intersection, nous pouvons utiliser\(y\) -intercept comme point, puis compter la pente à partir de là. Entraînons-nous à trouver les valeurs de la pente et de l'\(y\)intersection à partir de l'équation d'une droite.
Identifiez la pente et l'\(y\)intersection de la droite à l'aide d'une équation\(y=−3x+5\).
- Réponse
-
Nous comparons notre équation à la forme pente-intersection de l'équation.
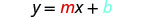
Écrivez l'équation de la droite. 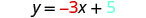
Identifiez la pente. 
Identifiez le\(y\) -intercept. 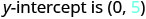
Identifiez la pente et\(y\) l'intersection de la ligne\(y=\frac{2}{5}x−1\).
- Réponse
-
\(\frac{2}{5}\); (0, -1)
Identifiez la pente et\(y\) l'intersection de la ligne\(y=−\frac{4}{3}x+1\).
- Réponse
-
\(-\frac{4}{3}\); (0,1)
Lorsqu'une équation d'une droite n'est pas donnée sous forme pente-intersection, notre première étape consiste à résoudre l'équation pour\(y\).
Identifiez la pente et l'\(y\)intersection de la droite à l'aide d'une équation\(x+2y=6\).
- Réponse
-
Cette équation n'est pas sous forme de pente et d'intersection. Afin de la comparer à la forme pente-intersection, nous devons d'abord résoudre l'équation pour\(y\).
Résolvez pour\(y\). \(x+2y=6\) Soustrayez x de chaque côté. 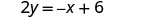
Divisez les deux côtés par\(2\). 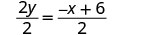
Simplifiez. 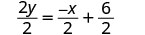
(N'oubliez pas :\(\frac{a+b}{c} = \frac{a}{c} + \frac{b}{c}\)) Simplifiez. 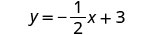
Écrivez la forme pente-intersection de l'équation de la droite. 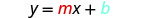
Écrivez l'équation de la droite. 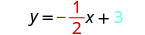
Identifiez la pente. 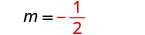
Identifiez le\(y\) -intercept. 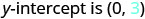
Identifiez la pente et\(y\) l'intersection de la ligne\(x+4y=8\).
- Réponse
-
\(-\frac{1}{4}\);( 0,2)
Identifiez la pente et\(y\) l'intersection de la ligne\(3x+2y=12\).
- Réponse
-
\(-\frac{2}{3}\);( 0,6)
Tracez une ligne en utilisant sa pente et son intersection
Maintenant que nous savons comment déterminer la pente et l'\(y\)intersection d'une droite à partir de son équation, nous pouvons tracer la droite en traçant l'\(y\)intersection et en utilisant la pente pour trouver un autre point.
Tracez la droite de l'équation\(y=4x−2\) en utilisant sa pente et son\(y\) point d'intersection.
- Réponse
-


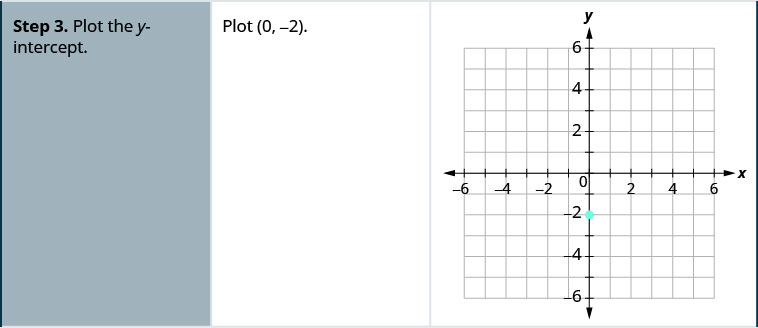

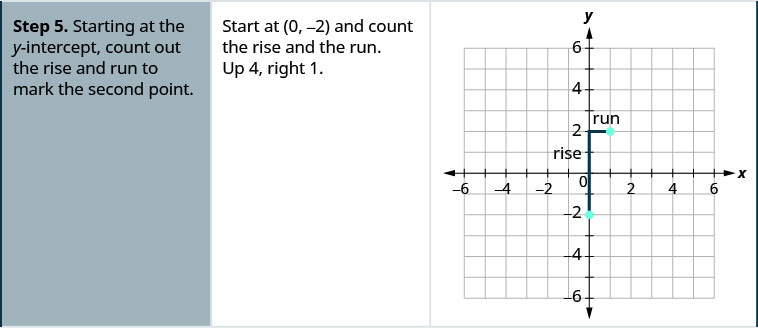
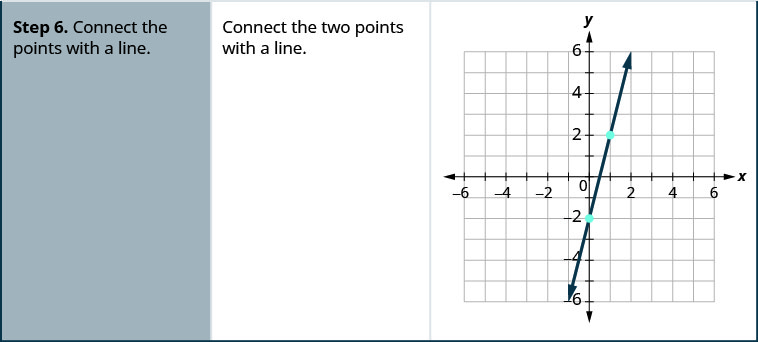
Tracez la droite de l'équation\(y=4x+1\) en utilisant sa pente et son\(y\) point d'intersection.
- Réponse
-
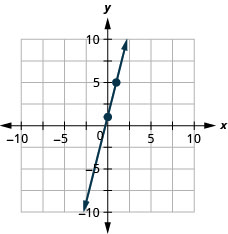
Tracez la droite de l'équation\(y=2x−3\) en utilisant sa pente et son\(y\) point d'intersection.
- Réponse
-
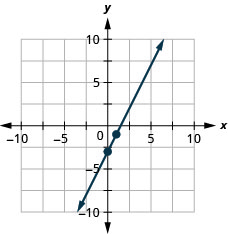
- Détermine la forme d'intersection de pente de l'équation de la droite.
- Identifiez la pente et\(y\) l'intersection.
- Tracez l'\(y\)erreur -intercepter.
- Utilisez la formule\(\frac{\text{rise}}{\text{run}}\) de pente pour identifier la montée et la course.
- À partir de l'\(y\)intersection -cept, comptez la montée et la course pour marquer le deuxième point.
- Reliez les points par une ligne.
Tracez la droite de l'équation\(y=−x+4\) en utilisant sa pente et son\(y\) point d'intersection.
- Réponse
-
vérifier.\(y=mx+b\) L'équation se présente sous la forme pente-intersection. \(y=−x+4\) Identifiez la pente et\(y\) l'intersection. \(m=−1\) \(y\)-intercepter c'est\((0, 4)\) Tracez l'\(y\)erreur -intercepter. Voir le graphique ci-dessous. Identifiez la hausse et la course. \(m = \frac{-1}{1}\) Comptez la montée et la course pour marquer le deuxième point. lever\(−1\), courir\(1\) Tracez la ligne. 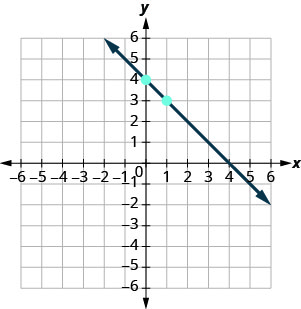
Pour vérifier votre travail, vous pouvez trouver un autre point sur la ligne et vous assurer qu'il s'agit d'une solution de l'équation. Sur le graphique, nous voyons la ligne passer\((4, 0)\). - \(\begin{array}{l}{y=-x+4} \\ {0\stackrel{?}{=}-4+4} \\ {0=0\checkmark}\end{array}\)
Tracez la droite de l'équation\(y=−x−3\) en utilisant sa pente et son\(y\) point d'intersection.
- Réponse
-
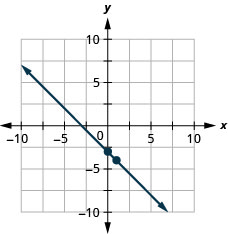
Tracez la droite de l'équation\(y=−x−1\) en utilisant sa pente et son\(y\) point d'intersection.
- Réponse
-
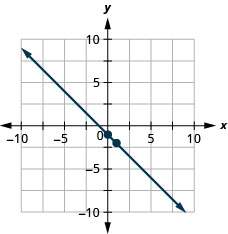
Tracez la droite de l'équation\(y=−\frac{2}{3}x−3\) en utilisant sa pente et son\(y\) point d'intersection.
- Réponse
-
\(y=mx+b\) L'équation se présente sous la forme pente-intersection. \(y=−\frac{2}{3}x−3\) Identifiez la pente et\(y\) l'intersection. \(m = -\frac{2}{3}\);\(y\) -intercepter est\((0, −3)\) Tracez l'\(y\)erreur -intercepter. Voir le graphique ci-dessous. Identifiez la hausse et la course. Comptez la montée et la course pour marquer le deuxième point. Tracez la ligne. 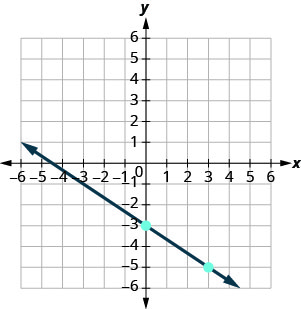
Tracez la droite de l'équation\(y=−\frac{5}{2}x+1\) en utilisant sa pente et son\(y\) point d'intersection.
- Réponse
-
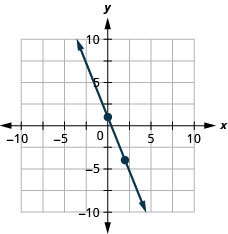
Tracez la droite de l'équation\(y=−\frac{3}{4}x−2\) en utilisant sa pente et son\(y\) point d'intersection.
- Réponse
-
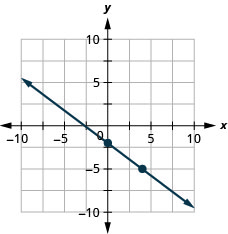
Tracez la droite de l'équation\(4x−3y=12\) en utilisant sa pente et son\(y\) point d'intersection.
- Réponse
-
\(4x−3y=12\) Déterminez la forme pente-intersection de l'équation. \(−3y=−4x+12\) \(−\frac{3y}{3}=\frac{−4x+12}{−3}\) L'équation se présente maintenant sous la forme pente-intersection. \(y=\frac{4}{3}x−4\) Identifiez la pente et\(y\) l'intersection. \(m=\frac{4}{3}\) \(y\)-Intercept est\((0, −4)\) Tracez l'\(y\)argument -intercepter. Voir le graphique ci-dessous. Identifiez la montée et la course ; comptez la montée et la course pour marquer le deuxième point. Tracez la ligne. 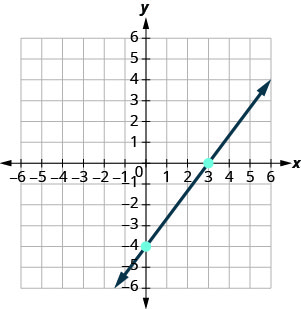
Tracez la droite de l'équation\(2x−y=6\) en utilisant sa pente et son\(y\) point d'intersection.
- Réponse
-
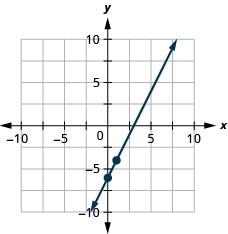
Tracez la droite de l'équation\(3x−2y=8\) en utilisant sa pente et son\(y\) point d'intersection.
- Réponse
-
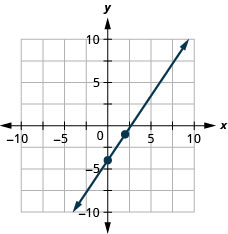
Nous avons utilisé une grille avec\(x\) et\(y\) les deux allant d'environ\(−10\) à\(10\) pour toutes les équations que nous avons représentées jusqu'à présent. Toutes les équations linéaires ne peuvent pas être représentées graphiquement sur cette petite grille. Souvent, en particulier dans les applications contenant des données du monde réel, nous devrons étendre les axes à des nombres positifs plus importants ou à des nombres négatifs plus petits.
Tracez la droite de l'équation\(y=0.2x+45\) en utilisant sa pente et son\(y\) point d'intersection.
- Réponse
-
Nous utiliserons une grille dont les axes vont d'environ\(−80\) à\(80\).
\(y=mx+b\) L'équation se présente sous la forme pente-intersection. \(y=0.2x+45\) Identifiez la pente et\(y\) l'intersection. \(m=0.2\) Le\(y\) -intercept est\((0, 45)\) Tracez l'\(y\)argument -intercepter. Voir le graphique ci-dessous. Comptez la montée et la course pour marquer le deuxième point. La pente est\(m=0.2\) ; sous forme de fraction, cela signifie\(m=\frac{2}{10}\). Compte tenu de l'échelle de notre graphique, il serait plus facile d'utiliser la fraction équivalente\(m=\frac{10}{50}\). Tracez la ligne. 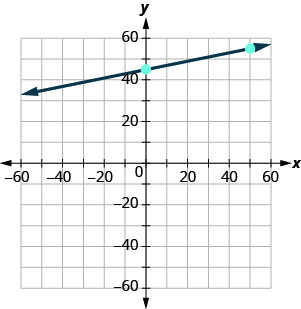
Tracez la droite de l'équation\(y=0.5x+25\) en utilisant sa pente et son\(y\) point d'intersection.
- Réponse
-
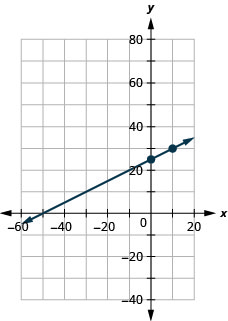
Tracez la droite de l'équation\(y=0.1x−30\) en utilisant sa pente et son\(y\) point d'intersection.
- Réponse
-
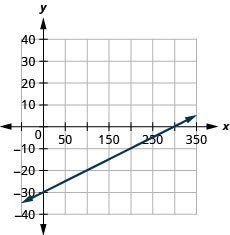
Maintenant que nous avons tracé des lignes à l'aide de la pente et de l'\(y\)intersection, résumons toutes les méthodes que nous avons utilisées pour tracer des lignes. Voir la figure\(\PageIndex{2}\).

Choisissez la méthode la plus pratique pour tracer une ligne
Maintenant que nous avons vu plusieurs méthodes que nous pouvons utiliser pour tracer des lignes, comment savoir quelle méthode utiliser pour une équation donnée ?
Bien que nous puissions tracer des points, utiliser la forme pente-intersection ou trouver les points d'intersection pour n'importe quelle équation, si nous trouvons le moyen le plus pratique de représenter graphiquement un certain type d'équation, notre travail sera plus facile. En général, tracer des points n'est pas la méthode la plus efficace pour tracer une ligne. Nous avons vu de meilleures méthodes dans les sections 4.3, 4.4 et plus tôt dans cette section. Examinons quelques modèles qui vous aideront à déterminer la méthode la plus pratique pour tracer une ligne.
Voici six équations que nous avons tracées dans ce chapitre, ainsi que la méthode que nous avons utilisée pour représenter graphiquement chacune d'elles.
\[\begin{array}{lll}{\text{#1}}&{\text {Equation }} & {\text { Method }} \\ {\text{#2}}&{x=2} & {\text { Vertical line }} \\ {\text{#3}}&{y=4} & {\text { Hortical line }} \\ {\text{#4}}&{-x+2 y=6} & {\text { Intercepts }} \\ {\text{#5}}&{4 x-3 y=12} & {\text { Intercepts }} \\ {\text{#6}}&{y=4 x-2} & {\text { Slope-intercept }} \\{\text{#7}}& {y=-x+4} & {\text { Slope-intercept }}\end{array}\]
Les équations #1 et #2 n'ont chacune qu'une seule variable. Rappelez-vous que dans les équations de cette forme, la valeur de cette variable est constante ; elle ne dépend pas de la valeur de l'autre variable. Les équations de cette forme comportent des graphes qui sont des lignes verticales ou horizontales.
Dans les équations #3 et #4, les deux\(x\) et\(y\) sont du même côté de l'équation. Ces deux équations sont de la forme\(Ax+By=C\). Nous l'avons remplacé\(y=0\) pour trouver le\(x\) -intercept et\(x=0\) pour trouver le\(y\) -intercept, puis nous avons trouvé un troisième point en choisissant une autre valeur pour\(x\) ou\(y\).
Les équations #5 et #6 sont écrites sous forme pente-intersection. Après avoir identifié la pente et l'\(y\)intersection à partir de l'équation, nous les avons utilisées pour tracer la ligne.
Cela conduit à la stratégie suivante.
Réfléchissez à la forme de l'équation.
- S'il ne comporte qu'une seule variable, il s'agit d'une ligne verticale ou horizontale.
- \(x=a\)est une ligne verticale passant par l'\(x\)axe -en\(a\).
- \(y=b\)est une ligne horizontale passant par l'\(y\)axe -en\(b\).
- Il\(y\) est isolé d'un côté de l'équation, sous la forme\(y=mx+b\), graphique en utilisant la pente et l'\(y\)intersection.
- Identifiez la pente et l'\(y\)intersection, puis tracez un graphique.
- Si l'équation est de la forme\(Ax+By=C\), trouvez les points d'intersection.
- Trouvez les\(y\) interceptions\(x\) - et -, un troisième point, puis tracez un graphique.
Déterminez la méthode la plus pratique pour représenter graphiquement chaque ligne.
- \(y=−6\)
- \(5x−3y=15\)
- \(x=7\)
- \(y=\frac{2}{5}x−1\).
- Réponse
-
1. \(y=−6\)
Cette équation ne comporte qu'une seule variable,\(y\). Son graphique est une ligne horizontale traversant l'\(y\)axe -en\(−6\).2. \(5x−3y=15\)
Cette équation est de la forme\(Ax+By=C\). Le moyen le plus simple de le représenter graphiquement sera de trouver les interceptions et un point de plus.3. \(x=7\)
Il n'y a qu'une seule variable,\(x\). Le graphique est une ligne verticale croisant l'\(x\)axe -en\(7\).4. \(y=\frac{2}{5}x−1\)
Comme cette équation est sous\(y=mx+b\) forme, il sera plus facile de tracer cette droite en utilisant la pente et l'\(y\)intersection.
Déterminez la méthode la plus pratique pour représenter graphiquement chaque ligne :
- \(3x+2y=12\)
- \(y=4\)
- \(y=\frac{1}{5}x−4\)
- \(x=−7\)
- Réponse
-
- intercepte
- ligne horizontale
- pente — interception
- ligne verticale
Déterminez la méthode la plus pratique pour représenter graphiquement chaque ligne :
- \(x=6\)
- \(y=−\frac{3}{4}x+1\)
- \(y=−8\)
- \(4x−3y=−1\)
- Réponse
-
- ligne verticale
- pente — interception
- ligne horizontale
- intercepte
Graphisme et interprétation des applications de Slope—Intercept
De nombreuses applications du monde réel sont modélisées par des équations linéaires. Nous allons examiner quelques applications ici afin que vous puissiez voir comment les équations écrites sous forme pente-intersection se rapportent à des situations réelles.
Généralement, lorsqu'une équation linéaire modélise une situation réelle, différentes lettres sont utilisées pour les variables, au lieu de\(x\) et\(y\). Les noms des variables nous rappellent les quantités mesurées.
L'équation\(F=\frac{9}{5}C+32\) est utilisée pour convertir les températures\(C\), sur l'échelle Celsius, en températures\(F\), sur l'échelle Fahrenheit.
- Trouvez la température Fahrenheit pour une température Celsius de\(0\).
- Trouvez la température Fahrenheit pour une température Celsius de\(20\).
- Interprétez la pente et l'\(F\)intersection de l'équation.
- Tracez l'équation.
- Réponse
-
1. \(\begin{array}{ll}{\text { Find the Fahrenheit temperature for a Celsius temperature of } 0 .} & {F=\frac{9}{5} C+32} \\ {\text { Find } F \text { when } C=0 .} & {F=\frac{9}{5}(0)+32} \\ {\text { Simplify. }} & {F=32}\end{array}\)
2. \ begin {array} {ll} {\ text {Trouvez la température Fahrenheit pour une température Celsius de} 20.} & {F= \ frac {9} {5} C+32} \ \ {\ text {Trouver} F \ text {quand} C=20.} & {F= \ frac {9} {5} (20) +32} \ \ {\ text {Simplifier.}} & {F=36+32} \ \ {\ text {Simplifier.}} & {F=68} \ end {tableau}
3. Interprétez la pente et l'\(F\)intersection de l'équation.
Même si cette équation utilise\(F\) et\(C\), elle est toujours sous forme pente-interception.
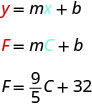
La pente,\(\frac{9}{5}\), signifie que la température Fahrenheit (\(F\)) augmente en\(9\) degrés lorsque la température Celsius (\(C\)) augmente en\(5\) degrés.
Le\(F\) -intercept signifie que lorsque la température est\(0°\) sur l'échelle Celsius, elle est\(32°\) sur l'échelle Fahrenheit.
4. Tracez l'équation.
Nous devrons utiliser une échelle plus grande que d'habitude. Commencez par\(F\) -intercept\((0,32)\), puis comptez la montée\(9\) et la course de\(5\) pour obtenir un deuxième point. Voir la figure\(\PageIndex{3}\).
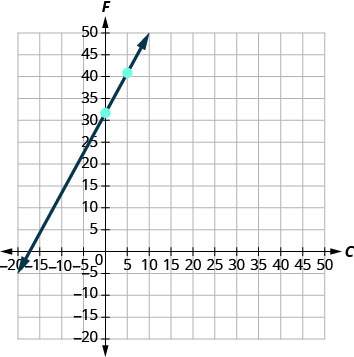
Figurine\(\PageIndex{3}\)
L'équation\(h=2s+50\) est utilisée pour estimer la taille d'une femme en pouces\(h\), en fonction de sa pointure\(s\).
- Estimez la taille d'un enfant qui porte une pointure pour femme\(0\).
- Estimez la taille d'une femme avec la pointure\(8\).
- Interprétez la pente et l'\(h\)intersection de l'équation.
- Tracez l'équation.
- Réponse
-
- \(50\)pouces
- \(66\)pouces
- La pente,\(2\), signifie que la hauteur augmente de\(2\) pouces lorsque la pointure de la chaussure augmente de\(1\).\(h\)\(s\) Le\(h\) -intercept signifie que lorsque la taille de la chaussure est\(0\), la hauteur est\(50\) en pouces.
L'équation\(T=\frac{1}{4}n+40\) est utilisée pour estimer la température en degrés Fahrenheit\(T\), sur la base du nombre de gazouillis de grillon\(n\), en une minute.
- Estimez la température lorsqu'il n'y a pas de gazouillis.
- Estimez la température lorsque le nombre de gazouillis en une minute est égal à\(100\).
- Interprétez la pente et l'\(T\)intersection de l'équation.
- Tracez l'équation.
- Réponse
-
- \(40\)degrés
- \(65\)degrés
- La pente,\(\frac{1}{4}\), signifie que la température Fahrenheit (\(F\)) augmente de\(1\) degré lorsque le nombre de gazouillis augmente de\(4\).\(n\) Le\(T\) -intercept signifie que lorsque le nombre de chirps est égal à\(0\), la température est\(40°\).
Le coût de fonctionnement de certains types d'entreprises comporte deux éléments : un coût fixe et un coût variable. Le coût fixe est toujours le même quel que soit le nombre d'unités produites. Il s'agit du coût du loyer, de l'assurance, de l'équipement, de la publicité et des autres éléments qui doivent être payés régulièrement. Le coût variable dépend du nombre d'unités produites. C'est pour le matériel et la main-d'œuvre nécessaires à la production de chaque article.
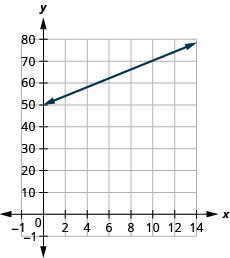
Stella possède une entreprise à domicile qui vend des pizzas gastronomiques. L'équation\(C=4p+25\) modélise la relation entre son coût hebdomadaire\(C\), en dollars,\(p\) et le nombre de pizzas qu'elle vend.
- Trouvez le prix de Stella pour une semaine lorsqu'elle ne vend pas de pizzas.
- Trouvez le coût d'une semaine lorsqu'elle vend des\(15\) pizzas.
- Interprétez la pente et l'\(C\)intersection de l'équation.
- Tracez l'équation.
- Réponse
-
1. Trouvez le prix de Stella pour une semaine lorsqu'elle ne vend pas de pizzas. 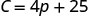
\(C\)Trouve quand\(p=0\). 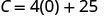
Simplifiez. 
Le coût fixe de Stella, c'est\($25\) lorsqu'elle ne vend pas de pizzas. 2. Trouvez le coût d'une semaine lorsqu'elle vend des\(15\) pizzas. 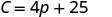
\(C\)Trouve quand\(p=15\). 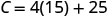
Simplifiez. 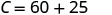

Stella paie\($85\) quand elle vend des\(15\) pizzas. 3. Interprétez la pente et l'\(C\)intersection de l'équation. 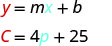
La pente signifie que le coût augmente\($4\) pour chaque pizza vendue par Stella.\(4\) Le\(C\) -intercepter signifie que même lorsque Stella ne vend pas de pizzas, ses frais pour la semaine sont de\($25\). 4. Tracez l'équation. Nous devrons utiliser une échelle plus grande que d'habitude. Commencez par\(C\) -intercept\((0, 25)\), puis comptez la montée\(4\) et la course de\(1\) pour obtenir un deuxième point. 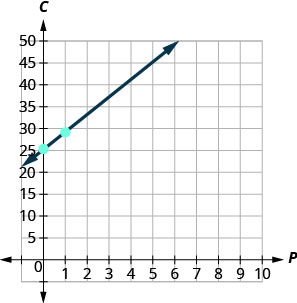
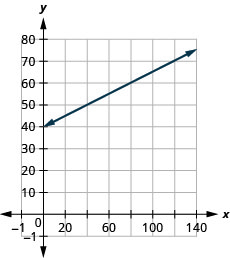
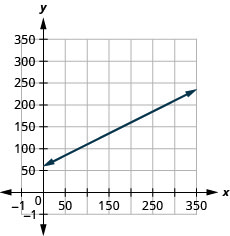
Sam conduit un fourgon de livraison. L'équation\(C=0.5m+60\) modélise la relation entre son coût hebdomadaire\(C\), en dollars,\(m\) et le nombre de miles qu'il parcourt.
- Trouvez le coût d'une semaine pour Sam quand il parcourt des\(0\) kilomètres.
- Trouvez le coût d'une semaine lorsqu'il parcourt des\(250\) kilomètres.
- Interprétez la pente et l'\(C\)intersection de l'équation.
- Tracez l'équation.
- Réponse
-
- \($60\)
- \($185\)
- La pente signifie que le coût hebdomadaire augmente\($0.50\) lorsque le nombre de kilomètres parcourus augmente de\(1\).\(0.5\)\(C\)\(n\) Le\(C\) -intercept signifie que lorsque le nombre de miles parcourus est égal à\(0\), le coût hebdomadaire est de\($60\).
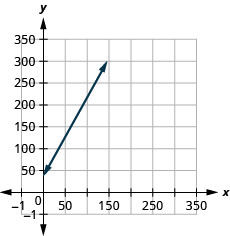
Loreen a une entreprise de calligraphie. L'équation\(C=1.8n+35\) modélise la relation entre son coût hebdomadaire\(C\), en dollars, et le nombre d'invitations de mariage\(n\), qu'elle écrit.
- Trouvez le prix de Loreen pour une semaine alors qu'elle n'écrit aucune invitation.
- Trouvez le coût d'une semaine lorsqu'elle écrit\(75\) des invitations.
- Interprétez la pente et l'\(C\)intersection de l'équation.
- Tracez l'équation.
- Réponse
-
- \($35\)
- \($170\)
- La pente\(1.8\),, signifie que le coût hebdomadaire augmente\($1.80\) lorsque le nombre d'invitations augmente de\(1.80\).\(C\)\(n\) Le\(C\) -intercept signifie que lorsque le nombre d'invitations est égal à\(0\), le coût hebdomadaire est de\($35\).
Utiliser les pentes pour identifier les lignes parallèles
La pente d'une ligne indique la pente de la ligne et indique si elle monte ou descend lorsque nous la lisons de gauche à droite. Deux lignes qui ont la même pente sont appelées lignes parallèles. Les lignes parallèles ne se croisent jamais.

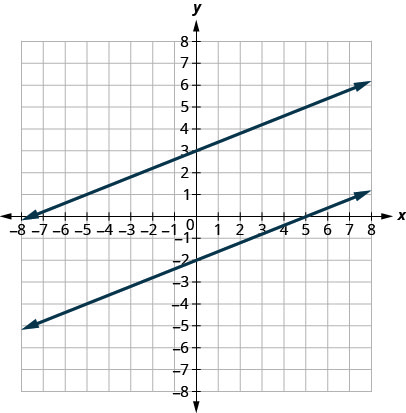
Qu'en est-il des lignes verticales ? La pente d'une ligne verticale n'étant pas définie, les lignes verticales ne correspondent pas à la définition ci-dessus. Nous disons que les lignes verticales qui ont des\(x\) interceptions différentes sont parallèles. Voir la figure\(\PageIndex{5}\).
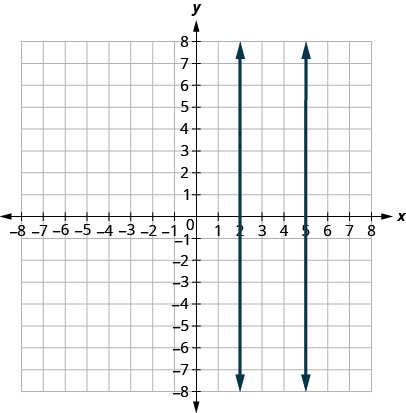
Les lignes parallèles sont des lignes situées dans le même plan qui ne se croisent pas.
- Les lignes parallèles ont la même pente et des\(y\) intersections différentes.
- Si\(m_{1}\) et\(m_{2}\) sont les pentes de deux lignes parallèles alors\(m_{1} = m_{2}\).
- Les lignes verticales parallèles ont des\(x\) -intercepts différents.
Tracons les\(y=−2x+3\) équations\(2x+y=−1\) sur la même grille. La première équation est déjà sous forme pente-intersection :\(y=−2x+3\). Nous résolvons la deuxième équation pour\(y\) :
\[\begin{aligned} 2x+y &=-1 \\ y &=-2x-1 \end{aligned}\]
Tracez les lignes.
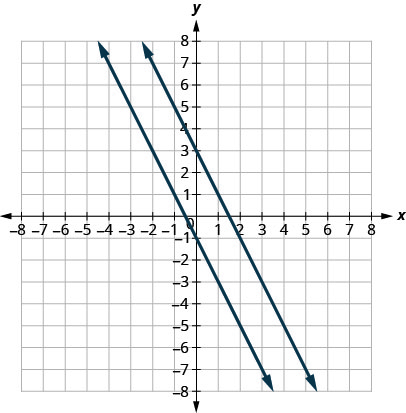
Remarquez que les lignes semblent parallèles. Quelle est la pente de chaque ligne ? Qu'est-ce que l'\(y\)-intercept de chaque ligne ?
\[\begin{array}{lll} {y} & {=m x+b} & {y=m x+b} \\ {y} & {=-2 x+3} & {y=-2 x-1} \\ {m} & {=-2} & {m=-2}\\ {b} & {=3,(0,3)} & {b=-1,(0,-1)}\end{array}\]
Les pentes des lignes sont les mêmes et l'\(y\)intersection de chaque ligne est différente. Nous savons donc que ces lignes sont parallèles.
Comme les droites parallèles ont la même pente et des\(y\) interceptions différentes, il suffit maintenant de regarder la forme pente-intersection des équations des droites et de décider si les droites sont parallèles.
Utilisez les pentes et les\(y\) -intercepts pour déterminer si les lignes\(3x−2y=6\) et B\(y = \frac{3}{2}x + 1\) sont parallèles.
- Réponse
-
\(\begin{array} {lrll} {\text { Solve the first equation for } y .} &{ 3 x-2 y} &{=} &{6}\\{} & {\frac{-2 y}{-2}} &{ =}&{-3 x+6 }\\ {} &{\frac{-2 y}{-2}}&{ =}&{\frac{-3 x+6}{-2}} \\ {} & {y }&{=}&{\frac{3}{2} x-3} \end{array}\)
L'équation se présente maintenant sous la forme pente-intersection.
L'équation de la deuxième droite est déjà sous forme pente-intersection.
Identifiez la pente et\(y\) l'intersection des deux lignes.
\(\begin{array}{lll}{y=\frac{3}{2} x+1} & {} & {y=\frac{3}{2} x-3} \\ {y=m x+b} & {} & {y=m x+b}\\ {m=\frac{3}{2}} & {} & {m=\frac{3}{2}} \\ {y\text{-intercept is }(0, 1)} & {} & {y\text{-intercept is }(0, −3)} \end{array}\)
Les lignes ont la même pente et des\(y\) intersections différentes, elles sont donc parallèles. Vous pouvez représenter graphiquement les lignes pour vérifier si elles sont parallèles.
Utilisez les pentes et les\(y\) -intercepts pour déterminer si les lignes\(2x+5y=5\) et B\(y=−\frac{2}{5}x−4\) sont parallèles.
- Réponse
-
parallèle
Utilisez les pentes et les\(y\) -intercepts pour déterminer si les lignes\(4x−3y=6\) et B\(y=\frac{4}{3}x−1\) sont parallèles.
- Réponse
-
parallèle
Utilisez les pentes et les\(y\) -intercepts pour déterminer si les lignes\(y=−4\) et B\(y=3\) sont parallèles.
- Réponse
-
\(\begin{array}{llll}{\text{Write each equation in slope-intercept form.}} &{y=-4} & {\text { and }} &{ y=3} \\ {\text{Since there is no }x\text{ term we write }0x.} &{y=0 x-4} & {} &{y=0 x+3} \\ {\text{Identify the slope and }y\text{-intercept of both lines.}} &{y=m x+b} &{} & {y=m x+b} \\ {} &{m=0} &{} & {m=0} \\{} & {y\text {-intercept is }(0,4)} &{} & {y \text {-intercept is }(0,3)}\end{array}\)
Les lignes ont la même pente et des\(y\) intersections différentes, elles sont donc parallèles.
Il existe un autre moyen de regarder cet exemple. Si vous reconnaissez immédiatement à partir des équations qu'il s'agit de lignes horizontales, vous savez que leurs pentes sont les deux\(0\). Puisque les lignes horizontales croisent l'\(y\)axe -at\(y=−4\) et at\(y=3\), nous savons que les\(y\) -intercepts sont\((0,−4)\) et\((0,3)\). Les lignes ont la même pente et des\(y\) intersections différentes, elles sont donc parallèles.
Utilisez les pentes et les\(y\) -intercepts pour déterminer si les lignes\(y=8\) et B\(y=−6\) sont parallèles.
- Réponse
-
parallèle
Utilisez les pentes et les\(y\) -intercepts pour déterminer si les lignes\(y=1\) et B\(y=−5\) sont parallèles.
- Réponse
-
parallèle
Utilisez les pentes et les\(y\) -intercepts pour déterminer si les lignes\(x=−2\) et B\(x=−5\) sont parallèles.
- Réponse
-
\[x=-2 \text { and } x=-5\]
Comme il n'y en a pas\(y\), les équations ne peuvent pas être présentées sous forme pente-intersection. Mais nous les reconnaissons comme des équations de lignes verticales. Leurs\(x\) -intercepts sont\(−2\) et\(−5\). Comme leurs\(x\) -intercepts sont différents, les lignes verticales sont parallèles.
Utilisez les pentes et les\(y\) -intercepts pour déterminer si les lignes\(x=1\) et B\(x=−5\) sont parallèles.
- Réponse
-
parallèle
Utilisez les pentes et les\(y\) -intercepts pour déterminer si les lignes\(x=8\) et B\(x=−6\) sont parallèles.
- Réponse
-
parallèle
Utilisez les pentes et les\(y\) -intercepts pour déterminer si les lignes\(y=2x−3\) et B\(−6x+3y=−9\) sont parallèles. Vous pouvez également créer un graphique de ces lignes pour voir à quoi elles ressemblent.
- Réponse
-
\(\begin{array} {llll} {\text { The first equation is already in slope-intercept form. }} & {y=2x-3}&{}&{} \\ \\ {\text { Solve the second equation for } y} & {-6x+3y} &{=}&{-9} \\{} & {3y}&{=}&{6x-9} \\ {}&{\frac{3y}{3} }&{=}&{\frac{6x-9}{3}} \\{} & {y}&{=}&{2x-3}\end{array}\)
La deuxième équation est maintenant sous forme de pente et d'intersection également.
Identifiez la pente et\(y\) l'intersection des deux lignes.
\[\begin{array}{lll}{y=2x-3} &{} & {y=2x-3} \\ {y=mx+b} &{} & {y=mx+b} \\ {m=2} &{} & {m=2} \\ {\text{The }y\text{-intercept is }(0 ,−3)} &{} & {\text{The }y\text{-intercept is }(0 ,−3)} \end{array} \nonumber\]
Les lignes ont la même pente, mais elles ont également les mêmes\(y\) -intercepts. Leurs équations représentent la même droite. Ils ne sont pas parallèles ; ils forment la même ligne.
Utilisez les pentes et les\(y\) -intercepts pour déterminer si les lignes\(y=−\frac{1}{2}x−1\) et B\(x+2y=2\) sont parallèles.
- Réponse
-
pas parallèle ; même ligne
Utilisez les pentes et les\(y\) -intercepts pour déterminer si les lignes\(y=\frac{3}{4}x−3\) et B\(3x−4y=12\) sont parallèles.
- Réponse
-
pas parallèle ; même ligne
Utiliser les pentes pour identifier les lignes perpendiculaires
Regardons les lignes dont les équations sont\(y=\frac{1}{4}x−1\) et\(y=−4x+2\), illustrées sur la figure\(\PageIndex{5}\).
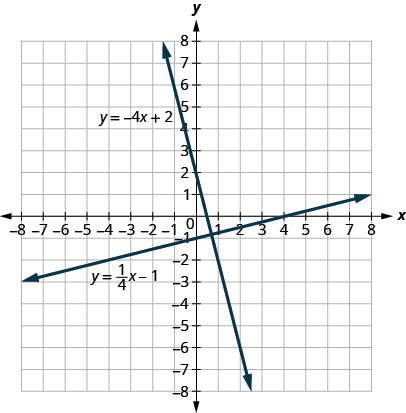
Ces lignes se situent dans le même plan et se croisent à angle droit. Nous appelons ces lignes perpendiculaires.
Que remarquez-vous sur les pentes de ces deux lignes ? Comme nous le lisons de gauche à droite, la ligne\(y=14x−1\) s'élève, donc sa pente est positive. La ligne\(y=−4x+2\) descend de gauche à droite, elle a donc une pente négative. Est-il logique pour vous que les pentes de deux lignes perpendiculaires aient des signes opposés ?
Si nous examinons la pente de la première ligne et la pente de la deuxième ligne\(m_{2}=−4\), nous pouvons voir que ce sont des réciproques négatifs l'un de l'autre.\(m_{1}=14\) Si on les multiplie, leur produit l'est\(−1\).
\[\begin{array}{c}{m_{1} \cdot m_{2}} \\ {\frac{1}{4}(-4)} \\ {-1}\end{array}\]
Cela est toujours vrai pour les lignes perpendiculaires et nous amène à cette définition.
Les lignes perpendiculaires sont des lignes situées dans le même plan et qui forment un angle droit.
Si m1 et m2 sont les pentes de deux droites perpendiculaires, alors :
\[m_{1} \cdot m_{2}=-1 \text { and } m_{1}=\frac{-1}{m_{2}}\]
Les lignes verticales et les lignes horizontales sont toujours perpendiculaires entre elles.
Nous avons pu examiner la forme pente-intersection des équations linéaires et déterminer si les droites étaient parallèles ou non. Nous pouvons faire de même pour les lignes perpendiculaires.
Nous trouvons la forme pente-intersection de l'équation, puis nous voyons si les pentes sont des réciproques négatives. Si le produit des pentes est égal à\(−1\), les lignes sont perpendiculaires. Les lignes perpendiculaires peuvent avoir les mêmes\(y\) -intercepts.
Utilisez les pentes pour déterminer si les lignes,\(y=−5x−4\) et\(x−5y=5\) sont perpendiculaires.
- Réponse
-
La première équation est déjà sous forme pente-intersection :\(\quad y=−5x−4\)
\(\begin{array} {llll} {\text{Solve the second equation for }y.} &{x-5y} &{=} &{5} \\{} &{-5 y} &{=} &{-x+5} \\ {} & {\frac{-5 y}{-5}} &{=} &{\frac{-x+5}{-5}} \\ {} &{y} &{=} &{\frac{1}{5} x-1} \end{array}\)La deuxième équation est désormais également sous forme d'intersection de pente.
\(\begin{array} {lrllllll} {\text{Identify the slope of each line.}} &{y} &{=} &{-5 x-4} & {} &{y} &{=} &{\frac{1}{5} x-1} \\ {} &{y} &{=} &{m x+b} & {} &{y} &{=} &{m x+b}\\ {} &{m_{1}} &{=}&{-5} & {} &{m_{2}} &{=}&{\frac{1}{5}}\end{array}\)
Les pentes sont réciproques négatives les unes des autres, de sorte que les lignes sont perpendiculaires. On vérifie en multipliant les pentes,
\[\begin{array}{l}{m_{1} \cdot m_{2}} \\ {-5\left(\frac{1}{5}\right)} \\ {-1\checkmark}\end{array}\]
Utilisez les pentes pour déterminer si les lignes 1\(y=−3x+2\) et 3\(x−3y=4\) sont perpendiculaires.
- Réponse
-
perpendiculaire
Utilisez les pentes pour déterminer si les lignes 1\(y=2x−5\) et 3\(x+2y=−6\) sont perpendiculaires.
- Réponse
-
perpendiculaire
Utilisez les pentes pour déterminer si les lignes,\(7x+2y=3\) et\(2x+7y=5\) sont perpendiculaires.
- Réponse
-
\(\begin{array}{lrlrl}{\text{Solve the equations for y.}} &{7 x+2 y} & {=3} & {2 x+7 y}&{=}&{5} \\{} & {2 y} & {=-7 x+3} & {7 y}&{=}&{-2 x+5} \\ {} &{\frac{2 y}{2}} & {=\frac{-7 x+3}{2} \quad} & {\frac{7 y}{7}}&{=}&{\frac{-2 x+5}{7}} \\ {} &{y} & {=-\frac{7}{2} x+\frac{3}{2}} &{y}&{=}&{\frac{-2}{7}x + \frac{5}{7}}\\ \\{\text{Identify the slope of each line.}} & {y}&{=m x+b} &{y}&{=}&{m x+b} \\{} & {m_{1}} & {=-\frac{7}{2} }&{ m_{2}}&{=}&{-\frac{2}{7}}\end{array}\)
Les pentes sont réciproques, mais elles ont le même signe. Comme ce ne sont pas des réciproques négatifs, les lignes ne sont pas perpendiculaires.
Utilisez les pentes pour déterminer si les lignes 1\(5x+4y=1\) et 3\(4x+5y=3\) sont perpendiculaires.
- Réponse
-
non perpendiculaire
Utilisez les pentes pour déterminer si les lignes 1\(2x−9y=3\) et 3\(9x−2y=1\) sont perpendiculaires.
- Réponse
-
non perpendiculaire
Accédez à cette ressource en ligne pour obtenir des instructions supplémentaires et vous entraîner à utiliser des graphiques.
Concepts clés
- La forme pente-intersection d'une équation d'une droite avec pente mm et\(y\) -intersection\((0,b)\) est,\(y=mx+b\).
- Tracez une ligne à l'aide de sa pente et de son\(y\) intersection
- Détermine la forme d'intersection de pente de l'équation de la droite.
- Identifiez la pente et\(y\) l'intersection.
- Tracez l'\(y\)argument -intercepter.
- Utilisez la formule\(m = \dfrac{\text{rise}}{\text{run}}\) de pente pour identifier la montée et la course.
- À partir de l'\(y\)intersection -cept, comptez la montée et la course pour marquer le deuxième point.
- Reliez les points par une ligne.
- Stratégie pour choisir la méthode la plus pratique pour tracer une courbe : considérez la forme de l'équation.
- S'il ne comporte qu'une seule variable, il s'agit d'une ligne verticale ou horizontale.
\(x = a\)est une ligne verticale passant par l'\(x\)axe -en a.
\(y = b\) est une ligne horizontale passant par l'\(y\)axe -en\(b\). - Il\(y\) est isolé d'un côté de l'équation, sous la forme\(y=mx+b\), graphique en utilisant la pente et l'\(y\)intersection.
Identifiez la pente et l'\(y\)intersection, puis tracez un graphique. - Si l'équation est de la forme\(Ax+By=C\), trouvez les points d'intersection.
Trouvez les\(y\) interceptions\(x\) - et -, un troisième point, puis tracez un graphique.
- S'il ne comporte qu'une seule variable, il s'agit d'une ligne verticale ou horizontale.
- Les lignes parallèles sont des lignes situées dans le même plan qui ne se croisent pas.
- Les lignes parallèles ont la même pente et des\(y\) intersections différentes.
- Si\(m_1\) et\(m_2\) sont les pentes de deux lignes parallèles alors\(m_1 = m_2\).
- Les lignes verticales parallèles ont des\(x\) -intercepts différents.
- Les lignes perpendiculaires sont des lignes dans le même plan qui forment un angle droit.
- Si\(m_1\) et\(m_2\) sont les pentes de deux droites perpendiculaires, alors\(m_1\cdot m_2=−1\) et\(m_1=\frac{−1}{m_2}\).
- Les lignes verticales et les lignes horizontales sont toujours perpendiculaires entre elles.
Lexique
- lignes parallèles
- Lignes dans le même plan qui ne se croisent pas.
- lignes perpendiculaires
- Lignes situées dans le même plan et formant un angle droit.
- forme d'intersection de pente d'une équation d'une droite
- La forme pente-intersection d'une équation d'une droite avec pente mm et\(y\) -intersection\((0,b)\) est,\(y=mx+b\).


