Skip to main content
Global

1.8 : Décimales

  1. Last updated
  2. Save as PDF
  • Page ID
    195355

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Nommez et écrivez des décimales
    • Décimales rondes
    • Ajouter et soustraire des décimales
    • Multipliez et divisez les décimales
    • Convertir des décimales, des fractions et des pourcentages
    Remarque

    Une introduction plus complète aux sujets abordés dans cette section se trouve dans le chapitre sur la préalgèbre, Décimaux.

    Nommez et écrivez des décimales

    Les décimales sont une autre façon d'écrire des fractions s dont les dénominateurs sont des puissances de 10.

    \[\begin{array} {ll} {0.1 = \frac { 1 } { 10 }} &{0.1 \text { is "one tenth" }} \\ {0.01 = \frac { 1 } { 100 }} &{0.01 \text { is "one hundredth }} \\ {0.001 = \frac { 1 } { 1,000 }} &{0.001 \text { is "one thousandth }} \\ {0.0001 = \frac { 1 } { 10,000 }} &{0.0001 \text { is "one ten-thousandth" }} \end{array}\]

    Notez que « dix mille » est un nombre supérieur à un, mais « un dix mille » est un nombre inférieur à un. Le « th » à la fin du nom indique que le nombre est inférieur à un.

    Lorsque nous nommons un nombre entier, le nom correspond à la valeur de position basée sur la puissance de dix. Nous lisons 10 000 comme « dix mille » et 10 000 000 comme « dix millions ». De même, les noms des décimales correspondent à leurs valeurs de fraction. La figure\(\PageIndex{1}\) montre les noms des valeurs de position à gauche et à droite de la virgule décimale.

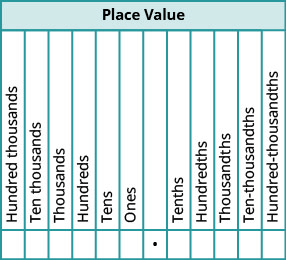
    Un tableau est affiché avec le titre Place Value. De gauche à droite, la rangée indique « Cent milliers », « Dix milliers », « Des milliers », « Des centaines », « Des dizaines » et « Un ». Ensuite, il y a une cellule vide et en dessous se trouve un point décimal. À droite, les cellules indiquent « Dixièmes », « Centièmes », « Millièmes », « Dix millièmes » et « Cent millièmes ».
    Figure\(\PageIndex{1}\) : La valeur nominale des nombres décimaux est indiquée à gauche et à droite de la virgule décimale.
    Exercice\(\PageIndex{1}\)

    Nommez la décimale\(4.3\).

    Réponse

    Un tableau comportant quatre étapes est présenté. De plus, le chiffre 4,3 est donné. La première étape se lit comme suit : « Étape 1. Nommez le nombre situé à gauche de la virgule décimale. » À droite, il est noté que « 4 est à gauche de la virgule décimale ». À droite, on peut lire « quatre », suivi d'un grand espace vide.La deuxième étape se lit comme suit : « Étape 2. Écrivez « et » pour la virgule décimale. » À droite, on peut lire « quatre et », suivi d'un espace.La troisième étape se lit comme suit : « Étape 3. Nommez la partie « numérique » à droite de la virgule décimale comme s'il s'agissait d'un nombre entier. » À droite, on peut lire « 3 est à droite de la virgule décimale ». À droite, on peut lire « quatre et trois », suivi d'un blanc.Enfin, la dernière étape se lit comme suit : « Étape 4. Nommez la décimale. » À droite, on peut lire « quatre et trois dixièmes ».

    Exercice\(\PageIndex{2}\)

    Nommez la décimale\(6.7\).

    Réponse

    six et sept dixièmes

    Exercice\(\PageIndex{3}\)

    Nommez la décimale\(5.8\).

    Réponse

    cinq et huit dixièmes

    Nous résumons les étapes nécessaires pour nommer une décimale ci-dessous.

    NOMMEZ UNE DÉCIMALE.
    1. Nommez le nombre situé à gauche de la virgule décimale.
    2. Écrivez « et » pour la virgule décimale.
    3. Nommez la partie « numérique » à droite de la virgule décimale comme s'il s'agissait d'un nombre entier.
    4. Nommez la décimale du dernier chiffre.
    Exercice\(\PageIndex{4}\)

    Nommez la décimale :\(−15.571\).

    Réponse
      \(−15.571\)
    Nommez le nombre situé à gauche de la virgule décimale. moins quinze __________________________________
    Écrivez « et » pour la virgule décimale. moins quinze et ______________________________
    Nommez le nombre situé à droite de la virgule décimale. moins quinze et cinq cent soixante et onze __________
    \(1\)Il est à la millième place. moins quinze et cinq cent soixante et onze millièmes
    Exercice\(\PageIndex{5}\)

    Nommez la décimale :\(−13.461\).

    Réponse

    moins treize et quatre cent soixante et un millièmes

    Exercice\(\PageIndex{6}\)

    Nommez la décimale :\(−2.053\).

    Réponse

    moins deux mille trois millièmes

    Lorsque nous écrivons un chèque, nous inscrivons à la fois les chiffres et le nom du numéro. Voyons comment écrire la décimale à partir du nom.

    Exercice\(\PageIndex{7}\): How to Write decimals

    Écrivez « quatorze et vingt-quatre millièmes » sous forme décimale.

    Réponse

    Un tableau comportant quatre étapes est présenté. La première étape se lit comme suit : « Étape 1. Recherchez l'œuvre « et » : elle permet de localiser la virgule décimale. Placez un point décimal sous le mot « et ». Traduisez les mots avant « et » en un nombre entier et placez-le à gauche de la virgule décimale. » À droite, nous avons les mots « quatorze et vingt-quatre millièmes ». En dessous de ce mot, il y a « quatorze et vingt-quatre millièmes » avec le mot « et » souligné. En dessous de ce mot, nous avons un petit espace vide séparé d'un espace vide plus grand par un point décimal. En dessous, nous avons 14 dans le petit espace vide suivi de la virgule décimale et de l'espace vide le plus grand.La deuxième étape se lit comme suit : « Étape 2. Marquez le nombre de décimales nécessaires à droite de la virgule décimale en notant la valeur de position indiquée par le dernier mot. » À droite, on peut lire « Le dernier mot, c'est les millièmes ». À droite, il y a le chiffre 14 suivi d'un point décimal et de trois petits espaces vides. Sous les espaces vides, les mots « dixièmes », « centièmes » et « millièmes » sont écrits.La troisième étape se lit comme suit : « Étape 3. Traduisez les mots après « et » dans le nombre situé à droite de la virgule décimale. Inscrivez le numéro dans les espaces, en mettant le dernier chiffre à la dernière place. » À droite, nous avons 14 suivi d'une décimale suivie d'un espace vide suivi de 2 et 4 sur les deux autres espaces précédemment vides.Enfin, la dernière étape se lit comme suit : « Étape 4. Remplissez des zéros pour les espaces vides selon les besoins. » À droite, on peut lire « Des zéros sont nécessaires à la dixième place ». À droite, nous avons 14 suivis d'un point décimal suivi de 0, 2 et 4, respectivement, sur les espaces vides. En dessous, nous avons « quatorze millièmes et vingt-quatre millièmes s'écrivent 14.024 ».

    Exercice\(\PageIndex{8}\)

    Ecrivez sous forme décimale : treize et quatre-vingt huit millièmes.

    Réponse

    13 068

    Exercice\(\PageIndex{9}\)

    Ecrivez sous forme décimale : cinq et quatre millièmes.

    Réponse

    5 094

    Nous résumons les étapes pour écrire une décimale.

    ECRIVEZ UNE DÉCIMALE.
    1. Recherchez le mot « et » : il indique la virgule décimale.
      • Placez un point décimal sous le mot « et ». Traduisez les mots avant « et » en un nombre entier et placez-le à gauche de la virgule décimale.
      • S'il n'y a pas de « et », écrivez un « 0 » avec un point décimal à sa droite.
    2. Marquez le nombre de décimales nécessaires à droite de la virgule décimale en notant la valeur de position indiquée par le dernier mot.
    3. Traduisez les mots après « et » dans le chiffre situé à droite de la virgule décimale. Écrivez le numéro dans les espaces, en plaçant le dernier chiffre à la dernière place.
    4. Remplissez des zéros pour les espaces réservés si nécessaire.

    Décimales rondes

    L'arrondissement des décimales est un peu comme arrondir des nombres entiers. Nous arrondirons les décimales avec une méthode basée sur celle que nous avons utilisée pour arrondir les nombres entiers.

    Exercice\(\PageIndex{10}\)

    Arrondissez 18,379 au centième le plus proche.

    Réponse

    Un tableau comportant quatre étapes est présenté. La première étape se lit comme suit : « Étape 1 : Localisez la valeur de position donnée et marquez-la avec une flèche ». À droite, nous avons le chiffre 18.379 ; au-dessus, se trouvent les mots des centaines de places, avec une flèche pointant vers le 7.La deuxième étape se lit comme suit : « Étape 2. Soulignez le chiffre situé à droite de la valeur de position donnée. » À droite, nous avons 18.379 avec le 9 souligné.La troisième étape se lit comme suit : « Étape 3. Ce chiffre est-il supérieur ou égal à 5 ? En dessous, on peut lire : « Oui : ajoutez 1 au chiffre dans la valeur de position donnée ». En dessous, on peut lire : « Non : ne modifiez pas le chiffre de la valeur de position donnée ». À droite, il est écrit « Parce que 9 est supérieur ou égal à ». À droite, nous avons le numéro 18.379 avec le 9 marqué « supprimer » et le 7 marqué « ajouter 1 ».Enfin, la dernière étape se lit comme suit : « Étape 4. Réécrivez le chiffre en supprimant tous les chiffres situés à droite du chiffre arrondi. » À droite, nous avons 18,38 suivi de « 18,38 est 18,379 arrondis au centième le plus proche ».

    Exercice\(\PageIndex{11}\)

    Arrondir au centième le plus proche : 1,047.

    Réponse

    1,05

    Exercice\(\PageIndex{12}\)

    Arrondir au centième le plus proche : 9,173.

    Réponse

    9,17

    Nous résumons ici les étapes pour arrondir une décimale.

    DÉCIMALES RONDES.
    1. Localisez la valeur de position donnée et marquez-la avec une flèche.
    2. Soulignez le chiffre situé à droite de la valeur de la position.
    3. Ce chiffre est-il supérieur ou égal à 5 ?
      • Oui : ajoutez 1 au chiffre dans la valeur de position donnée.
      • Non : ne modifiez pas le chiffre dans la valeur de position spécifiée.
    4. Réécrivez le nombre en supprimant tous les chiffres situés à droite du chiffre arrondi.
    Exercice\(\PageIndex{13}\)

    Tournez le 18.379 jusqu'au plus proche

    1. dixième
    2. nombre entier.
    Réponse

    Tour 18.379

    1. au dixième le plus proche

    Localisez la dixième place à l'aide d'une flèche. .
    Soulignez le chiffre situé à droite de la valeur de position donnée. .
    Comme 7 est supérieur ou égal à 5, ajoutez 1 au 3. .
    Réécrivez le nombre en supprimant tous les chiffres situés à droite du chiffre arrondi. .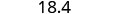
    Notez que les chiffres supprimés n'ont PAS été remplacés par des zéros. Ainsi, 18,379 arrondi au dixième le plus proche est 18,4.


    2. au nombre entier le plus proche
    Localisez leur emplacement à l'aide d'une flèche. .
    Soulignez le chiffre situé à droite de la valeur de position donnée. .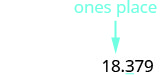
    Puisque 3 n'est pas supérieur ou égal à 5, n'ajoutez pas 1 au 8. .
    Réécrivez le nombre en supprimant tous les chiffres situés à droite du chiffre arrondi. .
      Ainsi, 18,379 arrondi au nombre entier le plus proche est 18.
    Exercice\(\PageIndex{14}\)

    Arrondir le 6.582 au plus proche

    1. centième
    2. dixième
    3. nombre entier.
    Réponse
    1. 6,58
    2. 6.6
    3. 7
    Exercice\(\PageIndex{15}\)

    Tournez le 15.2175 jusqu'au plus proche

    1. millième
    2. centième
    3. dixième.
    Réponse
    1. 15.218
    2. 15,22
    3. 15,2

    Ajouter et soustraire des décimales

    Pour ajouter ou soustraire des décimales, nous alignons les décimales. En alignant les décimales de cette façon, nous pouvons ajouter ou soustraire les valeurs de position correspondantes. Nous ajoutons ou soustrayons ensuite les nombres comme s'il s'agissait de nombres entiers, puis nous plaçons le point décimal dans la somme.

    AJOUTEZ OU SOUSTRAYEZ DES DÉCIMALES.
    1. Écrivez les nombres de manière à ce que les décimales soient alignées verticalement.
    2. Utilisez des zéros comme emplacements, selon les besoins.
    3. Ajoutez ou soustrayez les nombres comme s'il s'agissait de nombres entiers. Placez ensuite le point décimal dans la réponse sous les décimales des nombres donnés.
    Exercice\(\PageIndex{16}\)

    Ajoutez :\(23.5+41.38\).

    Réponse

    \[\text{Write the numbers so that the decimal points line up vertically.} \quad \begin{array} {r} { 23.50 } \\ { + 41.38 } \\ \hline \end{array}\]
    \[\text{Put 0 as a placeholder after the 5 in 23.5. Remember, } \frac{5}{10} = \frac{50}{100}, \text{ so } 0.5 = 0.50 \quad \begin{array} {r} { 23.50 } \\ { + 41.38 } \\ \hline \end{array}\]
    \[\text{Add the numbers as if they were whole numbers . Then place the decimal point in the sum.} \quad \begin{array} {r} { 23.50 } \\ { + 41.38 } \\ \hline 64.88 \end{array}\]

    Exercice\(\PageIndex{17}\)

    Ajoutez :\(4.8+11.69\).

    Réponse

    \(16.49\)

    Exercice\(\PageIndex{18}\)

    Ajoutez :\(5.123+18.47\).

    Réponse

    \(23.593\)

    Exercice\(\PageIndex{19}\)

    Soustraire :\(20−14.65\).

    Réponse

    \[\begin{array} {ll} {\text{Write the numbers so that the decimal points line up vertically.}} &{ \begin{align} {20 - 14.65} \\ {20.} \\ {-14.65} \\ \hline \end{align}} \\ {\text{Remember, 20 is a whole number, so place the decimal point after the 0.}} &{} \end{array}\]
    \[\begin{array} {ll} {\text{Put zeros to the right as placeholders.}} &{ \begin{align} {20.00} \\ {-14.65} \\ \hline \end{align}} \end{array}\]
    \[\begin{array} {ll} {\text{Write the numbers so that the decimal points line up vertically.}} &{ \begin{align} {\tiny{9} \quad \tiny{9}\qquad} \\ {\small{1} \not{\small{10}} \not{\small10}\not{\small10}}\\ {\not{2}\not{0.}\not{0}\not{0}} \\ {-14.65} \\ \hline \\{5.35} \end{align}} \end{array}\]

    Exercice\(\PageIndex{20}\)

    Soustraire :\(10−9.58\).

    Réponse

    0,42

    Exercice\(\PageIndex{21}\)

    Soustraire :\(50−37.42\).

    Réponse

    12,58

    Multipliez et divisez les décimales

    Multiplier des décimales est un peu comme multiplier des nombres entiers : il suffit de déterminer où placer le point décimal. La procédure de multiplication des décimales aura du sens si nous les convertissons d'abord en fractions, puis que nous les multiplions.

    Voyons donc ce que nous obtiendrions en tant que produit des décimales en les convertissant d'abord en fractions. Nous allons faire deux exemples côte à côte. Cherchez un motif !

      .

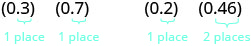    Convertir en fractions.    		 .
    Multipliez. .
    Convertir en décimales. .
    Tableau\(\PageIndex{1}\)

    Notez que dans le premier exemple, nous avons multiplié deux nombres comportant chacun un chiffre après la virgule décimale et le produit avait deux décimales. Dans le deuxième exemple, nous avons multiplié un nombre avec une décimale par un nombre avec deux décimales et le produit avait trois décimales.

    Nous multiplions les nombres comme nous le faisons pour les nombres entiers, en ignorant temporairement la virgule décimale. Nous comptons ensuite le nombre de décimales dans les facteurs et cette somme nous indique le nombre de décimales du produit.

    Les règles de multiplication des nombres positifs et négatifs s'appliquent également aux décimales, bien entendu !

    Lorsque vous multipliez deux nombres,

    • si leurs signes sont les mêmes, le produit est positif.
    • si leurs signes sont différents, le produit est négatif.

    Lorsque nous multiplions des décimales signées, nous déterminons d'abord le signe du produit, puis nous multiplions comme si les nombres étaient tous deux positifs. Enfin, nous écrivons le produit avec le signe approprié.

    MULTIPLIEZ LES DÉCIMALES.
    1. Déterminez le signe du produit.
    2. Écrivez au format vertical en alignant les chiffres sur la droite. Multipliez les nombres comme s'ils étaient des nombres entiers, en ignorant temporairement les décimales.
    3. Placez le point décimal. Le nombre de décimales dans le produit est la somme du nombre de décimales des facteurs.
    4. Écrivez le produit avec le signe approprié.
    Exercice\(\PageIndex{22}\)

    Multipliez :\((−3.9)(4.075)\).

    Réponse
      \((−3.9)(4.075)\)
    Les signes sont différents. Le produit sera négatif.  
    Écrivez au format vertical en alignant les chiffres sur la droite. .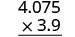
    Multipliez. .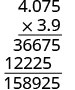
    Ajoutez le nombre de décimales dans les facteurs\((1 + 3)\).

    .
    Placez la virgule décimale à 4 places en partant de la droite.    		 .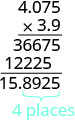
    Les signes sont différents, donc le produit est négatif. \((−3.9)(4.075) = −15.8925\)
    Exercice\(\PageIndex{23}\)

    Multipliez :\(−4.5(6.107)\).

    Réponse

    \(−27.4815\)

    Exercice\(\PageIndex{24}\)

    Multipliez : −10,79 (8,12).

    Réponse

    \(−87.6148\)

    Dans la plupart de vos autres classes, en particulier dans les sciences, vous multiplierez les décimales par des puissances de 10 (10, 100, 1000, etc.). Si vous multipliez quelques produits sur du papier, vous remarquerez peut-être un schéma reliant le nombre de zéros de la puissance de 10 au nombre de décimales : nous déplaçons la virgule décimale vers la droite pour obtenir le produit.

    MULTIPLIEZ UNE DÉCIMALE PAR UNE PUISSANCE DE DIX.
    1. Déplacez la virgule décimale vers la droite autant de places que le nombre de zéros de la puissance 10.
    2. Ajoutez des zéros à la fin du numéro si nécessaire.
    Exercice\(\PageIndex{25}\)

    Multipliez 5,63

    1. par 10
    2. par 100
    3. par 1 000.
    Réponse

    En regardant le nombre de zéros dans le multiple de dix, nous voyons le nombre de décimales dont nous avons besoin pour déplacer la décimale vers la droite.

    ⓐ

      \(5.63(10)\)
    Il y a 1 zéro sur 10, donc déplacez la virgule décimale d'une place vers la droite. .

    ⓑ

      \(5.63(100)\)
    Il y a 2 zéros sur 100, déplacez donc la virgule décimale de 2 places vers la droite. .

    ⓒ

       
    Comme il y a 3 zéros sur 1 000, déplacez la virgule décimale de 3 places vers la droite. .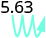
    Un zéro doit être ajouté à la fin. .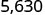
    Exercice\(\PageIndex{26}\)

    Multipliez 2,58

    1. par 10
    2. par 100
    3. par 1 000.
    Réponse
    1. 25,8
    2. 258
    3. 2 580
    Exercice\(\PageIndex{27}\)

    Multipliez 14,2

    1. par 10
    2. par 100
    3. par 1 000.
    Réponse
    1. 142
    2. 1 420
    3. 14 200

    Tout comme pour la multiplication, la division des décimales ressemble beaucoup à la division de nombres entiers. Nous devons juste déterminer où le point décimal doit être placé.

    Pour diviser des nombres décimaux, déterminez la puissance de 10 par laquelle vous devez multiplier le dénominateur pour obtenir un nombre entier. Multipliez ensuite le numérateur par la même puissance de 10. En raison de la propriété des fractions équivalentes, nous n'avons pas modifié la valeur de la fraction ! Cela a pour effet de déplacer les décimales du numérateur et du dénominateur du même nombre de décimales vers la droite. Par exemple :

    \[\begin{array} { c } { \frac { 0.8 } { 0.4 } } \\ { \frac { 0.8 ( 10 ) } { 0.4 ( 10 ) } } \\ { \frac { 8 } { 4 } } \end{array}\]

    Nous utilisons également les règles pour diviser les nombres positifs et négatifs par des décimales. Lorsque vous divisez des nombres décimaux signés, déterminez d'abord le signe du quotient, puis divisez comme si les deux nombres étaient positifs. Enfin, écrivez le quotient avec le signe approprié.

    Nous passons en revue la notation et le vocabulaire de la division :

    \[\begin{array} {ll} {} &{\underset{\text{quotient}}{c}} \\ {\underset{\text{dividend}}{a} \div \underset{\text{divisor}}{b} = \underset{\text{quotient}}{c}} & {\underset{\text{divisor}}{b})\overline{\underset{\text{dividend}}{a}}} \end{array}\]

    Nous allons écrire les étapes à suivre pour diviser des décimales, pour faciliter la consultation.

    DIVISEZ LES DÉCIMALES.
    1. Déterminez le signe du quotient.
    2. Faites du diviseur un nombre entier en « déplaçant » la virgule complètement vers la droite. « Déplacez » la virgule décimale du dividende du même nombre de positions, en ajoutant des zéros si nécessaire.
    3. Diviser. Placez la virgule décimale dans le quotient au-dessus de la virgule décimale du dividende.
    4. Écrivez le quotient avec le signe approprié.
    Exercice\(\PageIndex{28}\)

    Diviser :\(−25.65\div (−0.06)\).

    Réponse

    N'oubliez pas que vous pouvez « déplacer » les décimales du diviseur et du dividende grâce à la propriété Fractions équivalentes.

      \(−25.65\div (−0.06)\)
    Les signes sont les mêmes. Le quotient est positif.
    Faites du diviseur un nombre entier en « déplaçant » la virgule complètement vers la droite.  
    « Déplacez » la virgule décimale du dividende du même nombre de places. .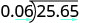
    Diviser.
    Placez la virgule décimale dans le quotient au-dessus de la virgule décimale du dividende.    		 .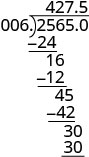
    Écrivez le quotient avec le signe approprié. \(−25.65\div (−0.06) = 427.5\)
    Exercice\(\PageIndex{29}\)

    Diviser :\(−23.492\div (−0.04)\).

    Réponse

    687,3

    Exercice\(\PageIndex{30}\)

    Diviser :\(−4.11\div(−0.12)\).

    Réponse

    34,25

    La division de nombres entiers en décimales est une application courante lorsque nous voulons trouver le prix d'un article vendu dans le cadre d'un emballage multiple. Supposons, par exemple, qu'une caisse de 24 bouteilles d'eau coûte cher\($3.99\). Pour trouver le prix d'une bouteille d'eau, nous diviserions\($3.99\) par 24. Nous montrons cette division dans Exercice\(\PageIndex{31}\). Dans les calculs avec de l'argent, nous arrondirons la réponse au centième le plus proche.

    Exercice\(\PageIndex{31}\)

    Diviser :\($3.99\div 24\).

    Réponse
    On obtient 0,99 divisé par 24. Un problème de division longue est créé avec 24 divisant 3,99. Un tableau est présenté avec les instructions à gauche et les étapes mathématiques à droite. La première étape se lit comme suit : « Placez la virgule décimale dans le quotient au-dessus de la virgule décimale du dividende. Divisez comme d'habitude. Quand est-ce qu'on s'arrête ? Comme cette division implique de l'argent, nous l'arrondissons au centième le plus proche. Pour ce faire, nous devons porter la division à la millième place. » À droite de cela, nous avons un problème de division longue configuré avec 24 divisant 3,990. Le quotient est donné à 0,166. Pour montrer l'œuvre, en dessous de 3.990, on peut lire 24, ligne horizontale continue, 159, 144, ligne horizontale continue, 150, 144, ligne horizontale continue, et enfin 6. La cinquième étape se lit comme suit : « Arrondir au cent le plus proche ». À droite de cela, nous avons 0,166$ soit approximativement égal à 0,17$ et donc > 0,99 divisé par 24 soit 0,17$. » >
      \($3.99\div 24\)
    Placez la virgule décimale dans le quotient au-dessus de la virgule décimale du dividende.  
    Divisez comme d'habitude.
    Quand est-ce qu'on s'arrête ? Comme cette division implique de l'argent, nous l'arrondissons au centième le plus proche. Pour ce faire, il faut porter la division à la millième place.    		 .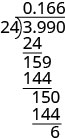
    Arrondir au centime le plus proche. \($0.166\approx $0.17\)
    \($3.99\div 2\approx $0.17\)
    Exercice\(\PageIndex{32}\)

    Diviser :\($6.99\div 36\).

    Réponse

    \($0.19\)

    Exercice\(\PageIndex{33}\)

    Diviser :\($4.99\div 12\).

    Réponse

    \($0.42\)

    Convertir des décimales, des fractions et des pourcentages

    Nous convertissons les décimales en fractions en identifiant la valeur de position du dernier chiffre (le plus à droite). Dans la décimale 0,03, le 3 est au centième, donc 100 est le dénominateur de la fraction équivalente à 0,03.

    \[00.03 = \frac { 3 } { 100 }\]

    Remarquez que lorsque le nombre à gauche de la décimale est zéro, nous obtenons une fraction dont le numérateur est inférieur à son dénominateur. De telles fractions sont appelées fractions propres.

    Les étapes à suivre pour convertir une décimale en fraction sont résumées dans l'encadré de procédure.

    CONVERTISSEZ UNE DÉCIMALE EN FRACTION APPROPRIÉE.
    1. Déterminez la valeur de position du dernier chiffre.
    2. Écrivez la fraction.
      • numérateur : les « nombres » à droite de la virgule décimale
      • dénominateur : valeur de position correspondant au dernier chiffre
    Exercice\(\PageIndex{34}\)

    Ecrivez 0,374 sous forme de fraction.

    Réponse
      0,374
    Déterminez la valeur de position du dernier chiffre. .

    Écrivez la fraction pour 0,374 :

    • Le numérateur est 374.
    • Le dénominateur est 1 000.
    		 \(\dfrac{374}{1000}\)
    Simplifiez la fraction. \(\dfrac{2\cdot 187}{2\cdot 500}\)
    Répartissez les facteurs communs. \(\dfrac{187}{500}\)
    donc,\(0.374=\dfrac{187}{500}\)

    Avez-vous remarqué que le nombre de zéros dans le dénominateur de\(\dfrac{374}{1000}\) est identique au nombre de décimales de 0,374 ?

    Exercice\(\PageIndex{35}\)

    Ecrivez 0,234 sous forme de fraction.

    Réponse

    \(\dfrac{117}{500}\)

    Exercice\(\PageIndex{36}\)

    Ecrivez 0,024 sous forme de fraction.

    Réponse

    \(\dfrac{3}{125}\)

    Nous avons appris à convertir les décimales en fractions. Nous allons maintenant faire l'inverse : convertir les fractions en décimales. N'oubliez pas que la barre de fraction signifie division. Ainsi\(\dfrac{4}{5}\) peut être écrit\(4\div 5\) ou\(5)\overline{4}\). Cela conduit à la méthode suivante pour convertir une fraction en décimal.

    CONVERTISSEZ UNE FRACTION EN DÉCIMAL.

    Pour convertir une fraction en décimal, divisez le numérateur de la fraction par le dénominateur de la fraction.

    Exercice\(\PageIndex{37}\)

    Ecrivez\(-\dfrac{5}{8}\) sous forme décimale.

    Réponse

    Comme une barre de fraction signifie division, nous commençons par écrire\(\dfrac{5}{8}\) comme\(8)\overline{5}\). Maintenant, divisez.

    Il s'agit d'un problème de division longue, 8 divisant 5 000 et 0,625 comme quotient. En dessous de 5 000, nous en avons 48, une ligne horizontale continue, 20, 16, une ligne horizontale continue, 40, 40 et une ligne horizontale finale. Donc, cinq huitièmes sont égaux à 0,625.

    Exercice\(\PageIndex{38}\)

    Ecrivez\(-\dfrac{7}{8}\) sous forme décimale.

    Réponse

    −0,875

    Exercice\(\PageIndex{39}\)

    Ecrivez\(-\dfrac{3}{8}\) sous forme décimale.

    Réponse

    −0,375

    Lorsque nous divisons, nous n'obtenons pas toujours un reste nul. Parfois, le quotient se termine par une décimale qui se répète. Une décimale répétée est une décimale dans laquelle le dernier chiffre ou groupe de chiffres se répète à l'infini. Une barre est placée au-dessus du bloc de chiffres répétitif pour indiquer qu'il se répète.

    DÉCIMAL RÉPÉTÉ

    Une décimale répétée est une décimale dans laquelle le dernier chiffre ou groupe de chiffres se répète à l'infini.

    Une barre est placée au-dessus du bloc de chiffres répétitif pour indiquer qu'il se répète.

    Exercice\(\PageIndex{40}\)

    Ecrivez\(\dfrac{43}{22}\) sous forme décimale.

    Réponse

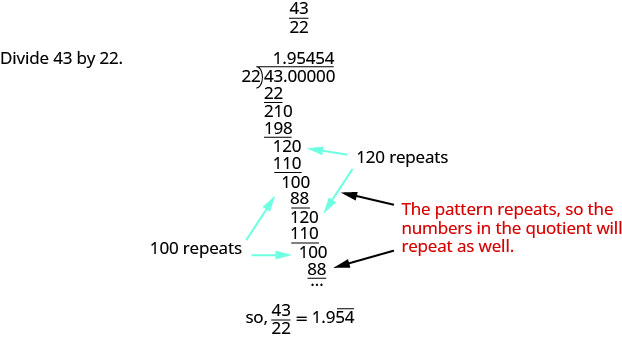
    Le numéro 43/22 est donné. La directive est donnée de « Diviser 43 par 22 ». Un problème de division longue est donné, 22 divisant 43,00000 par 1,95454 comme quotient. En dessous de 43 000, nous avons 22, une ligne horizontale pleine, 210, 198, une ligne horizontale pleine, 120, 110, une ligne horizontale, 100, 88, une ligne horizontale pleine, 120, 110, une ligne horizontale continue, 100, 88, une ligne horizontale continue, puis trois points. On note que les 120 répétitions et que les 100 répétitions. Cela est expliqué plus en détail comme suit : « Le schéma se répète, de sorte que les nombres du quotient se répètent également. À la fin, on nous indique que 43/22 équivaut à 1,954 avec une petite ligne horizontale au-dessus du 54.

    Exercice\(\PageIndex{41}\)

    Ecrivez\(\dfrac{27}{11}\) sous forme décimale.

    Réponse

    \(2.\overline{45}\)

    Exercice\(\PageIndex{42}\)

    Ecrivez\(\dfrac{51}{22}\) sous forme décimale.

    Réponse

    \(2.3\overline{18}\)

    Il se peut que nous devions parfois simplifier des expressions en combinant des fractions et des décimales.

    Exercice\(\PageIndex{43}\)

    Simplifiez :\(\dfrac{7}{8}+6.4\).

    Réponse

    Nous devons d'abord changer un numéro pour que les deux numéros soient sous la même forme. Nous pouvons changer la fraction en décimale, ou changer la décimale en fraction. Il est généralement plus facile de changer la fraction en décimale.

        \(\dfrac{7}{8}+6.4\)
    Passez\(\dfrac{7}{8}\) à une décimale. .  
    Ajoutez.   \(0.875+6.4\)
        \(7.275\)
        Donc,\(\dfrac{7}{8}+6.4 = 7.275\)
    Exercice\(\PageIndex{44}\)

    Simplifiez :\(\dfrac{3}{8}+4.9\).

    Réponse

    \(5.275\)

    Exercice\(\PageIndex{45}\)

    Simplifiez :\(5.7 + \dfrac{13}{20}\).

    Réponse

    \(6.35\)

    Un pourcentage est un ratio dont le dénominateur est 100. Le pourcentage signifie par cent. Nous utilisons le symbole du pourcentage, %, pour afficher le pourcentage.

    POURCENTAGE

    Un pourcentage est un ratio dont le dénominateur est 100.

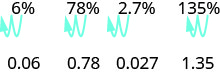
    Comme un pourcentage est un ratio, il peut facilement être exprimé sous forme de fraction. Le pourcentage signifie pour 100, donc le dénominateur de la fraction est 100. Nous changeons ensuite la fraction en décimale en divisant le numérateur par le dénominateur.

    \[\begin{array} {llll} {} &{\text{6%}} &{\text{78%}} &{\text{135%}} \\ {\text { Write as a ratio with denominator } 100. } &{\dfrac{6}{100}} &{\dfrac{78}{100}} &{\dfrac{135}{100}} \\ { \text { Change the fraction to a decimal by dividing}} &{0.06} &{0.78} &{1.35}\\ {\text{the numerator by the denominator.}} &{} &{} &{} \end{array}\]

    Voyez-vous le schéma ? Pour convertir un pourcentage en nombre décimal, nous déplaçons la virgule décimale de deux places vers la gauche.

    La première partie de cette figure montre 6 % avec une flèche tracée entre le signe 6 et le signe du pourcentage vers l'espace situé à gauche de 6, puis vers l'espace le plus à gauche de cet espace. En dessous, le nombre 0,06 est donné. La deuxième partie de cette figure montre 78 % avec une flèche tracée entre le signe 8 et le signe du pourcentage vers l'espace entre le 7 et le 8, puis vers l'espace situé à gauche du 7. En dessous, le nombre 0,78 est donné. La troisième partie de cette figure montre 2,7 % avec une flèche tracée depuis la virgule décimale vers l'espace situé à gauche du 2, puis vers l'espace le plus à gauche de cet espace. En dessous, le nombre 0,027 est donné. La quatrième partie de cette figure montre 135 % avec une flèche tracée entre le signe 5 et le signe du pourcentage vers l'espace entre 3 et 5, puis vers l'espace entre 1 et 3. En dessous, le chiffre 1,35 est donné.
    Figurine\(\PageIndex{2}\)
    Exercice\(\PageIndex{46}\)

    Convertissez chaque pourcentage en décimal :

    1. 62 %
    2. 135 %
    3. 35,7 %.
    Réponse
    1.  
      .
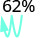
    Déplace la virgule décimale de deux places vers la gauche. 0,62
    2.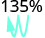  
      .
    Déplace la virgule décimale de deux places vers la gauche. 1,35
    3.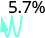  
      .
    Déplace la virgule décimale de deux places vers la gauche. 0,057
    Exercice\(\PageIndex{47}\)

    Convertissez chaque pourcentage en décimal :

    1. 9 %
    2. 87 %
    3. 3,9 %.
    Réponse
    1. 0,09
    2. 0,87
    3. 0,039
    Exercice\(\PageIndex{48}\)

    Convertissez chaque pourcentage en décimal :

    1. 3 %
    2. 91 %
    3. 8,3 %.
    Réponse
    1. 0,03
    2. 0,91
    3. 0,083

    La conversion d'une décimale en pourcentage est logique si nous nous souvenons de la définition du pourcentage et si nous gardons la valeur de place à l'esprit.

    Pour convertir une décimale en pourcentage, n'oubliez pas que le pourcentage signifie pour cent. Si nous changeons la décimale en une fraction dont le dénominateur est 100, il est facile de changer cette fraction en pourcentage.

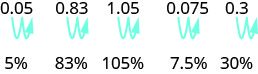
    \[\begin{array} {llll} {} &{0.83} &{1.05} &{0.075} \\ {\text {Write as a fraction }} &{\frac{83}{100}} &{\small{1}\frac{5}{100}} &{\frac{75}{1000}} \\ { \text {The denominator is 100.}} &{} &{\frac{105}{100}} &{\frac{7.5}{100}}\\ {\text{Write the ratio as a percent.}} &{\text{83%}} &{\text{105%}} &{\text{7.5%}} \end{array}\]

    Vous reconnaissez le schéma ? Pour convertir une décimale en pourcentage, nous déplaçons la virgule décimale de deux places vers la droite, puis nous ajoutons le signe du pourcentage.

    La première partie de cette figure indique 0,05 avec une flèche tracée depuis la virgule décimale jusqu'à l'espace compris entre 0 et 5, puis vers l'espace après 5. En dessous, le chiffre 5 % est donné. La deuxième partie de cette figure montre 0,83 avec une flèche tracée depuis la virgule décimale jusqu'à l'espace compris entre 8 et 3, puis vers l'espace après 3. En dessous, le chiffre 83 % est donné. La troisième partie de cette figure montre 1,05 avec une flèche tracée depuis la virgule décimale jusqu'à l'espace compris entre 0 et 5, puis jusqu'à l'espace après 5. En dessous, le chiffre 105 % est donné. La quatrième partie de cette figure indique 0,075 avec une flèche tracée depuis la virgule décimale jusqu'à l'espace compris entre 0 et 7, puis vers l'espace entre 7 et 5. En dessous, le chiffre de 7,5 % est donné. La cinquième partie de cette figure indique 0,3 avec une flèche tracée depuis la virgule décimale jusqu'à l'espace après 3, puis vers l'espace situé plus à droite de ce 3. En dessous, le chiffre 30 % est donné.
    Figurine\(\PageIndex{3}\)
    Exercice\(\PageIndex{49}\)

    Convertissez chaque décimale en pourcentage :

    1. 0,51
    2. 1,25
    3. 0,093.
    Réponse
    1.  
      .
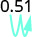
    Déplacez la virgule décimale de deux places vers la droite. \(51%\)
    2.  
      .
    Déplacez la virgule décimale de deux places vers la droite. \(125%\)
    3.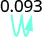  
      .
    Déplacez la virgule décimale de deux places vers la droite. \(9.3%\)
    Exercice\(\PageIndex{50}\)

    Convertissez chaque décimale en pourcentage :

    1. 0,17
    2. 1,75
    3. 0,0825
    Réponse
    1. 17 %
    2. 175 %
    3. 8,25 %
    Exercice\(\PageIndex{51}\)

    Convertissez chaque décimale en pourcentage :

    1. 0,41
    2. 2,25
    3. 0,0925.
    Réponse
    1. 41 %
    2. 225 %
    3. 9,25 %

    Concepts clés

    • Nommez une décimale
      1. Nommez le nombre situé à gauche de la virgule décimale.
      2. Écrivez « et » pour la virgule décimale.
      3. Nommez la partie « numérique » à droite de la virgule décimale comme s'il s'agissait d'un nombre entier.
      4. Nommez la décimale du dernier chiffre.
    • Écrire une décimale
      1. Recherchez le mot « et » : il indique la virgule décimale. Placez un point décimal sous le mot « et ». Traduisez les mots avant « et » en un nombre entier et placez-le à gauche de la virgule décimale. S'il n'y a pas de « et », écrivez un « 0 » avec un point décimal à sa droite.
      2. Marquez le nombre de décimales nécessaires à droite de la virgule décimale en notant la valeur de position indiquée par le dernier mot.
      3. Traduisez les mots après « et » dans le nombre situé à droite de la virgule décimale. Écrivez le numéro dans les espaces, en plaçant le dernier chiffre à la dernière place.
      4. Remplissez des zéros pour les espaces réservés si nécessaire.
    • Arrondir une décimale
      1. Localisez la valeur de position donnée et marquez-la avec une flèche.
      2. Soulignez le chiffre situé à droite de la valeur de la position.
      3. Ce chiffre est-il supérieur ou égal à 5 ? Oui : ajoutez 1 au chiffre dans la valeur de position donnée. Non : ne modifiez pas le chiffre dans la valeur de position spécifiée.
      4. Réécrivez le nombre en supprimant tous les chiffres situés à droite du chiffre arrondi.
    • Ajouter ou soustraire des décimales
      1. Écrivez les nombres de manière à ce que les décimales soient alignées verticalement.
      2. Utilisez des zéros comme emplacements, selon les besoins.
      3. Ajoutez ou soustrayez les nombres comme s'il s'agissait de nombres entiers. Placez ensuite la décimale dans la réponse sous les décimales des nombres donnés.
    • Multipliez les décimales
      1. Déterminez le signe du produit.
      2. Écrivez au format vertical en alignant les chiffres sur la droite. Multipliez les nombres comme s'ils étaient des nombres entiers, en ignorant temporairement les décimales.
      3. Placez le point décimal. Le nombre de décimales du produit est la somme des décimales des facteurs.
      4. Écrivez le produit avec le signe approprié.
    • Multipliez une décimale par une puissance de dix
      1. Déplacez la virgule décimale vers la droite autant de places que le nombre de zéros de la puissance 10.
      2. Ajoutez des zéros à la fin du numéro si nécessaire.
    • Diviser les décimales
      1. Déterminez le signe du quotient.
      2. Faites du diviseur un nombre entier en « déplaçant » la virgule complètement vers la droite. « Déplacez » la virgule décimale du dividende du même nombre de places, en ajoutant des zéros si nécessaire.
      3. Diviser. Placez la virgule décimale dans le quotient au-dessus de la virgule décimale du dividende.
      4. Écrivez le quotient avec le signe approprié.
    • Convertir une décimale en fraction appropriée
      1. Déterminez la valeur de position du dernier chiffre.
      2. Écrivez la fraction : numérateur, les « nombres » à droite de la virgule décimale ; dénominateur, valeur de position correspondant au dernier chiffre.
    • Convertir une fraction en décimal Divisez le numérateur de la fraction par le dénominateur.