1.4 : Ajouter et soustraire des entiers

Objectifs d'apprentissage

• Utilisez des négatifs et des contraires
• Simplifier : expressions à valeur absolue
• Ajouter des nombres entiers
• Soustraire des entiers

Vous trouverez une introduction plus complète aux sujets abordés dans cette section dans le chapitre Préalgèbre, Entiers.

Utilisez des négatifs et des contraires

Jusqu'à présent, notre travail n'a porté que sur les nombres de comptage et les nombres entiers. Mais si vous avez déjà constaté une température inférieure à zéro ou si vous avez accidentellement débité votre compte courant, vous connaissez déjà les chiffres négatifs. Les nombres négatifs sont des nombres inférieurs à$0$. Les nombres négatifs se situent à gauche de zéro sur la ligne numérique. Voir la figure$\PageIndex{1}$.

Chiffre$\PageIndex{1}$. La ligne numérique indique l'emplacement des nombres positifs et négatifs.

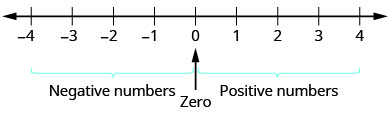
Les flèches aux extrémités de la ligne numérique indiquent que les chiffres continuent indéfiniment. Il n'y a pas de plus grand nombre positif et il n'y a pas de plus petit nombre négatif.

Le zéro est-il un nombre positif ou négatif ? Les nombres supérieurs à zéro sont positifs et les nombres inférieurs à zéro sont négatifs. Le zéro n'est ni positif ni négatif.

Réfléchissez à la façon dont les nombres sont classés sur la ligne numérique. En allant de gauche à droite, les chiffres prennent de la valeur. En allant de droite à gauche, les chiffres diminuent en valeur. Voir la figure$\PageIndex{2}$.

Chiffre$\PageIndex{2}$. Les nombres sur une ligne numérique augmentent en valeur en allant de gauche à droite et diminuent en valeur en allant de droite à gauche.

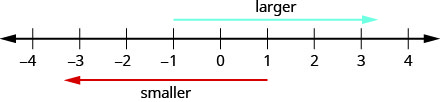
L'activité Mathématiques manipulatrices « Number Line-part 2 » vous aidera à mieux comprendre les nombres entiers.

N'oubliez pas que nous utilisons la notation :

$a \lt b$(lire «$a$ est inférieur à$b$ ») lorsque$a$ se trouve à gauche de$b$ sur la ligne numérique.

$a \gt b$(lire «$a$ est supérieur à$b$ ») lorsque$a$ se trouve à droite de$b$ sur la ligne numérique.

Maintenant, nous devons étendre la ligne numérique qui affichait les nombres entiers pour inclure également les nombres négatifs. Les nombres marqués par des points sur la figure$\PageIndex{3}$. sont appelés entiers. Les entiers sont des nombres$...−3, −2, −1, 0, 1, 2, 3…$

Chiffre$\PageIndex{3}$. Tous les nombres marqués sont appelés entiers.

Exemple$\PageIndex{1}$

Classez chacune des paires de nombres suivantes, en utilisant$<$ ou$>$ :

1. $14 \; \_\_\_\; 6$
2. $-1\; \_\_\_ \;9$
3. $-1\; \_\_\_ -4$
4. $\;\; 2 \;\_\_\_ -20$

Solution :

Il peut être utile de se référer à la ligne numérique affichée.

Figurine$\PageIndex{4}$

\ (\ begin {align*} 1. \ quad & 14 \ ; \ _ \ _ \ _ \ ; 6 \ \ [4 points]
& 14 > 6 && \ text {$14$se trouve à$6$ droite de la ligne numérique.} \ \ [8 points]
2. \ quad & -1 \ ; \ _ \ _ \ _ \ ; 9 \ \ [4 points]
& -1 < 9 && \ text {$-1$se trouve à$9$ gauche de la ligne numérique.} \ \ [8 points]
3. \ quad & -1 \ ; \ _ \ _ \ _-4 \ \ [4 points]
& -1 > -4 && \ text {$-1$se trouve à$-4$ droite de la ligne numérique.} \ \ [8 points]
4. \ quad & 2 \ ; \ _ \ _ \ _-20 \ \ [4pt]
& 2 > -20 && \ text {$2$se trouve à$-20$ droite de la ligne numérique.} \
 \ end {align*} \)

Essayez-le$\PageIndex{1}$

Organisez chacune des paires de nombres suivantes, en utilisant$<$ or $>$:

1. $15 \; \_\_\_\; 7$
2. $-2 \; \_\_\_\; 5$
3. $-3 \; \_\_\_\; -7$
4. $5 \; \_\_\_\; -17$

Answer

1. $<$
2. $>$
3. $<$
4. $>$

Try It $\PageIndex{2}$

Classez chacune des paires de nombres suivantes, en utilisant$<$ ou$>$ :

1. $8 \; \_\_\_\; 13$
2. $3 \; \_\_\_\; -4$
3. $-5 \; \_\_\_\; -2$
4. $9 \; \_\_\_\; -21$

Réponse

1. $<$
2. $>$
3. $<$
4. $>$

Vous avez peut-être remarqué que, sur la ligne numérique, les nombres négatifs sont une image miroir des nombres positifs, avec zéro au milieu. Comme les nombres$2$ et$−2$ sont à la même distance de zéro, ils sont appelés opposés s. Le contraire de l'$2$est$−2$ et le contraire de l'$−2$est$2$.

OPPOSÉ

L'opposé d'un nombre est le nombre qui se trouve à la même distance de zéro sur la ligne numérique mais du côté opposé à zéro.

La figure$\PageIndex{5}$ illustre la définition.

Figure$\PageIndex{5}$ : Le contraire de$3$ c'est$−3$.

Parfois, en algèbre, le même symbole a des significations différentes. Tout comme certains mots en anglais, la signification spécifique devient claire en regardant comment ils sont utilisés. Vous avez vu le symbole «$−$ » utilisé de trois manières différentes.

\ [\ begin {align*} &10 − 4 \ quad \ text {Entre deux nombres, cela indique l'opération de} \ textit {soustraction}. \ \ & \ qquad \ qquad \ text {On lit} 10 - 4 \, \ text {comme «} 10 \, \ text {minus}} \, 4. \ text {»} \ \ [5pt]
&-8 \ quad \ text {Devant un chiffre, cela indique un} \ textit {négatif} \ text {numéro.} \ \ & \ qquad \ qquad \ text {Nous lisons} -8 \ text {comme « huit négatif ».} \ \ [5pt]
&-x \ quad \ text {Devant une variable, cela indique le} \ textit {ci-contre.} \ \ & \ qquad \ qquad \ text {Nous lisons} -x \ text {comme « l'opposé de} x \ text {»} \ \ [5pt]
&- (-2) \ quad \ text {Ici, il y a deux signes « − ».} \ \
& \ qquad \ qquad \ text {Celui entre parenthèses nous indique que le nombre est négatif} 2. \ \
& \ qquad \ qquad \ text {Celui qui se trouve hors des parenthèses nous indique de prendre le} \ textit {opposite} \ text {of} −2. \ \
& \ qquad \ qquad \ text {Nous lisons} − (−2) \ text {comme « l'opposé de moins deux. »} \ end {align*} \]

NOTATION OPPOSÉE

$−a$signifie l'opposé du nombre$a$.

La notation$−a$ est lue comme « l'opposé de »$a$.

Exemple$\PageIndex{2}$

Trouvez :

1. le contraire de$7$
2. le contraire de$−10$
3. le contraire de$−(−6)$

Solution :

1. $\quad −7$est à la même distance$0$ que$7$, mais du côté opposé de$0$. Le contraire de l'$7$est$-7$.

2. $\quad 10$est à la même distance$0$ que$−10$, mais du côté opposé de$0$. Le contraire de l'$-10$est$10$.

3. $\quad$Le contraire de l'$-(-6)$est$-6$.

Essayez-le$\PageIndex{3}$

Trouvez :

1. le contraire de$4$
2. the opposite of $−3$
3. $−(−1)$

Answer

1. $-4$
2. $3$
3. $1$

Try It $\PageIndex{4}$

Trouvez :

1. le contraire de$8$
2. le contraire de$−5$
3. $−(−5)$

Réponse

1. $-8$
2. $5$
3. $5$

Notre travail avec les contraires nous permet de définir les nombres entiers. Les nombres entiers et leurs contraires sont appelés entiers. Les entiers sont des nombres$…−3,−2,−1,0,1,2,3…$

NOMBRES ENTIERS

Les nombres entiers et leurs contraires sont appelés entiers.

Les entiers sont des nombres

$$…−3,−2,−1,0,1,2,3… \nonumber$$

Lorsque nous évaluons le contraire d'une variable, nous devons être très prudents. Sans savoir si la variable représente un nombre positif ou négatif, nous ne savons pas si −x−x est positif ou négatif. Nous pouvons le voir dans l'exemple$\PageIndex{1}$.

Exemple$\PageIndex{3}$:

Évaluer

1. $-x$, quand$x = 8$
2. $-x$, quand$x = -8$

Solution :

1. 	-x
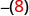
   Écrivez le contraire de 8.	-8

2. 	-x
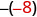
   Écrivez le contraire de -8.	8

Essayez-le$\PageIndex{5}$

Évaluer$-n$, when

1. $n = 4$
2. $n = -4$

Answer

1. $-4$
2. $4$

Try It $\PageIndex{6}$

Évaluer$-m$, quand

1. $m = 11$
2. $m = -11$

Réponse

1. $-11$
2. $11$

Simplifier : expressions avec valeur absolue

Nous avons vu que les nombres tels que$2$ et$−2$ sont opposés parce qu'ils se trouvent à la même distance$0$ sur la ligne numérique. Ils sont tous deux à deux unités de$0$. La distance entre$0$ et n'importe quel nombre sur la ligne numérique est appelée valeur absolue de ce nombre.

VALEUR ABSOLUE

La valeur absolue d'un nombre est sa distance par rapport$0$ à la ligne numérique.

La valeur absolue d'un nombre\(n\) s'écrit sous la forme$|n|$.

Par exemple,

• $−5$est éloigné$5$ des unités$0$, donc$|−5|=5$.
• $5$est éloigné$5$ des unités$0$, donc$|5|=5$.

La figure$\PageIndex{6}$ illustre cette idée.

Figure$\PageIndex{6}$ : Les nombres entiers$5$ et les$5$ unités sont éloignées de$0$.

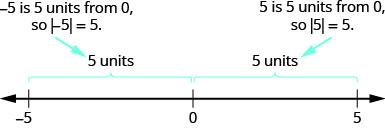
La valeur absolue d'un nombre n'est jamais négative (car la distance ne peut pas être négative). Le seul nombre dont la valeur absolue est égale à zéro est le nombre zéro lui-même, car la distance$0$ entre et$0$ sur la ligne numérique est de zéro unité.

PROPRIÉTÉ DE VALEUR ABSOLUE

$|n| \geq 0$pour tous les numéros

Les valeurs absolues sont toujours supérieures ou égales à zéro !

Les mathématiciens le disent plus précisément : « Les valeurs absolues ne sont toujours pas négatives ». Non négatif signifie supérieur ou égal à zéro.

Exemple$\PageIndex{4}$:

Simplifiez :

1. $|3|$
2. $|-44|$
3. $|0|$

Solution :

La valeur absolue d'un nombre est la distance entre le nombre et zéro. La distance n'est jamais négative, donc la valeur absolue n'est jamais négative.

1. $|3| = 3$
2. $|-44| = 44$
3. $|0| = 0$

Essayez-le$\PageIndex{7}$

Simplifiez :

1. $|4|$
2. $|-28|$
3. $|0|$

Answer

1. $4$
2. $28$
3. $0$

Try It $\PageIndex{8}$

Simplifiez :

1. $|-13|$
2. $|47|$

Réponse

1. $13$
2. $47$

Dans l'exemple suivant, nous allons classer les expressions avec des valeurs absolues. N'oubliez pas que les nombres positifs sont toujours supérieurs aux nombres négatifs !

Exemple$\PageIndex{5}$:

Renseignez chacune des paires de chiffres suivantes :$<, >, \text{or} =$

1. $|−5| \; {\underline{\hspace {2 em}}} \;−|−5|$
2. $8 \;{\underline{\hspace {2 em}}} \;−|−8|$
3. $-9 \;{\underline{\hspace {2 em}}} \;−|−9|$
4. $-(-16) \;{\underline{\hspace {2 em}}}\; −|−16|$

Solution :

1. 
   $\begin{array} {llll} {\text{Simplification}} &{|-5|} & {\underline{\hspace {2 em}}} &{-|-5|} \\ {\text{Order.}} &{5} &{\underline{\hspace {2 em}}} &{-5} \\ {} &{5} &{>} &{-5} \\ {} &{|-5|} &{>} &{-|-5|} \\ \end{array}$
2. 
   $\begin{array} {llll} {\text{Simplification}} &{8} & {\underline{\hspace {2 em}}} &{-|-8|} \\ {\text{Order.}} &{8} &{\underline{\hspace {2 em}}} &{-8} \\ {} &{8} &{>} &{-8} \\ \text{so }\\ {} & {|8|} &{>} &{-|-8|} \\ \end{array}$
3. 
   $\begin{array} {llll} {\text{Simplification}} &{-9} & {\underline{\hspace {2 em}}} &{-|-9|} \\ {\text{Order.}} &{-9} &{\underline{\hspace {2 em}}} &{-9} \\ {} &{-9} &{=} &{-9} \\ \text{so } \\ {} & {-9} &{=} &{-|-9|} \\ \end{array}$
4. 
   $\begin{array} {llll} {\text{Simplification}} &{-(-16)} & {\underline{\hspace {2 em}}} &{-|16|} \\ {\text{Order.}} &{16} &{\underline{\hspace {2 em}}} &{-16} \\ {} &{16} &{>} &{-16} \\ \text{so } \\ {} & {-(-16)} &{>} &{-|-16|} \\ \end{array}$

Essayez-le$\PageIndex{9}$

Remplir$<, >, \text{or} =$ for each of the following pairs of numbers:

1. $|−9| \;{\underline{\hspace {2 em}}} \; −|−9|$
2. $2 \;{\underline{\hspace {2 em}}} \; −|−2|$
3. $-8 \;{\underline{\hspace {2 em}}} \; −|−8|$
4. $-(-9) \;{\underline{\hspace {2 em}}} \; −|−9|$

Answer

1. $>$
2. $>$
3. $<$
4. $>$

Try It $\PageIndex{10}$

Renseignez chacune des paires de chiffres suivantes :$<, >, \text{or} =$

1. $7 \;{\underline{\hspace {2 em}}} \; −|−7|$
2. $-(-10) \;{\underline{\hspace {2 em}}} \; −|−10|$
3. $|-4| \;{\underline{\hspace {2 em}}} \; −|−4|$
4. $-1 \;{\underline{\hspace {2 em}}} \; |−1|$

Réponse

1. $>$
2. $>$
3. $>$
4. $<$

Nous ajoutons maintenant des barres de valeurs absolues à notre liste de symboles de regroupement. Lorsque nous utilisons l'ordre des opérations, nous simplifions d'abord autant que possible l'intérieur des barres de valeurs absolues, puis nous prenons la valeur absolue du nombre obtenu.

REGROUPEMENT DE SYMBOLES

$$\begin{array} {llll} {\text{Parentheses}} &{()} & {\text{Braces}} & {\{\}} \\ {\text{Brackets}} &{[\space]} &{\text{Absolute}} &{|\space|} \\ \end{array} \nonumber$$

Dans l'exemple suivant, nous simplifierons d'abord les expressions à l'intérieur des barres de valeurs absolues, comme nous le faisons avec les parenthèses.

Exemple$\PageIndex{6}$:

Simplifiez :$24 - |19 - 3(6 - 2)|$

Solution :

$$\begin{array} {ll} {} &{24 - |19 - 3(6 - 2)|} \\ {\text{Work inside parentheses first: subtract } 2\space \text{from } 6} &{24 - |19 - 3(4)|} \\ {\text{Multiply }3(4)} &{24 - |19 - 12|} \\ {\text{Subtract inside the absolute value bars. }} &{24 - |7|} \\ {\text{Take the absolute value.}} &{24 - 7} \\ {\text{Subtract.}} &{17} \end{array}\nonumber$$

Essayez-le$\PageIndex{11}$

Simplifiez :$19 - |11 - 4(3 - 1)|$

Answer

$16$

Try It $\PageIndex{12}$

Simplifiez :$9 - |8 - 4(7 - 5)|$

Réponse

$9$

Exemple$\PageIndex{7}$

Évaluez :

1. $|x|$quand$x = -35$
2. $|y|$quand$y = -20$
3. $-|u|$quand$u = 12$
4. $-|p|$quand$p = -14$

Solution :

1. $|x|$quand$x = -35$

$\begin{array} {ll} {} &{|x|} \\ {\text{Substitute } -35 \space \text{for }x} &{|-35|} \\ {\text{Take the absolute value.}} &{35} \end{array}$

2. $|y|$quand$y = -20$

$\begin{array} {ll} {} &{|-y|} \\ {\text{Substitute } -20 \space \text{for }y} &{|-(-20)|} \\ {\text{Simplify}} &{|20|} \\ {\text{Take the absolute value.}} &{20} \end{array}$

3. $-|u|$quand$u = 12$

$\begin{array} {ll} {} &{-|u|} \\ {\text{Substitute } 12 \space \text{for }u} &{|-12|} \\ {\text{Take the absolute value.}} &{-12} \end{array}$

4. $-|p|$quand$p = -14$

$\begin{array} {ll} {} &{-|p|} \\ {\text{Substitute } -14 \space \text{for }p} &{-|-14|} \\ {\text{Take the absolute value.}} &{-14} \end{array}$

Essayez-le$\PageIndex{13}$

Évaluez :

1. $|x|$ when $x = -17$
2. $|y|$ when $y = -39$
3. $-|m|$ when $m = 22$
4. $-|p|$ when $p = -11$

Answer

1. $17$
2. $39$
3. $-22$
4. $-11$

Try It $\PageIndex{14}$

Évaluez :

1. $|y|$quand$y = -23$
2. $|-y|$quand$y = -21$
3. $-|n|$quand$n = 37$
4. $-|q|$quand$q = -49$

Réponse

1. $23$
2. $21$
3. $-37$
4. $-49$

Ajouter des entiers

La plupart des étudiants sont à l'aise avec les faits d'addition et de soustraction pour les nombres positifs. Mais faire des additions ou des soustractions avec des nombres positifs et négatifs peut s'avérer plus difficile.

L'activité Mathématiques manipulatrices « Addition de nombres signés » vous aidera à mieux comprendre l'ajout d'entiers. »

Nous utiliserons deux compteurs de couleurs pour modéliser l'addition et la soustraction de négatifs afin que vous puissiez visualiser les procédures au lieu de mémoriser les règles.

Nous laissons une couleur (le bleu) représenter le positif. L'autre couleur (rouge) représentera les négatifs. Si nous avons un compteur positif et un compteur négatif, la valeur de la paire est nulle. Ils forment une paire neutre. La valeur de cette paire neutre est nulle.

Figurine$\PageIndex{7}$

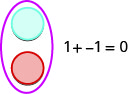
Nous utiliserons les compteurs pour montrer comment additionner les quatre faits supplémentaires à l'aide des chiffres$5, −5$ et$3,−3$.

$$\begin{array} {llll} {5 + 3} &{-5 + (-3)} &{-5 + 3} &{5 + (-3)} \end{array} \nonumber$$

De plus$5+3$, nous sommes conscients que$5+3$ cela signifie la somme de$5$ et$3$.

Nous commençons par des$5$ points positifs.
Ensuite, nous ajoutons des$3$ points positifs.
Nous avons maintenant des$8$ points positifs. La somme de$5$ et$3$ est$8$.

Maintenant, nous allons ajouter$−5 + (−3)$. Surveillez les similitudes avec le dernier exemple$5 + 3 = 8$.

De plus$−5 + (−3)$, nous sommes conscients que cela signifie la somme de$−5$ et$−3$.

Nous commençons par$5$ les négatifs.
Ensuite, nous ajoutons$3$ des négatifs.
Nous avons maintenant un$8$ résultat négatif. La somme de$-5$ et$-3$ est$-8$.

En quoi ces deux premiers exemples étaient-ils similaires ?

• Le premier exemple ajoute des$5$ éléments positifs et$3$ positifs, tous deux positifs.
• Le deuxième exemple ajoute$5$ des éléments$3$ négatifs et négatifs, tous deux négatifs.

Dans chaque cas, nous avons obtenu$8$ des$8$ points positifs ou$8$ négatifs.

Lorsque les panneaux étaient les mêmes, les compteurs étaient tous de la même couleur, nous les avons donc ajoutés.

Figurine$\PageIndex{7}$

Exemple$\PageIndex{8}$

Ajoutez :

1. $1 + 4$
2. $-1 + (-4)$

Solution :

1.

$1$positif plus$4$ positif est$5$ positif.

2.

$1$le$4$ négatif et le négatif sont$5$ des négatifs.

Essayez-le$\PageIndex{15}$

Ajoutez :

1. $2 + 4$
2. $-2 + (-4)$

Answer

1. $6$
2. $-6$

Try It $\PageIndex{16}$

Ajoutez :

1. $2 + 5$
2. $-2 + (-5)$

Réponse

1. $7$
2. $-7$

Alors, que se passe-t-il lorsque les signes sont différents ? Ajoutons$−5+3$. Nous sommes conscients que cela signifie la somme de$−5$ et$3$. Lorsque les compteurs étaient de la même couleur, nous les avons placés dans une rangée. Lorsque les compteurs sont d'une couleur différente, nous les alignons les uns sous les autres.

Tableau$\PageIndex{1}$

	$-5 + 3$signifie la somme de$-5$ et$3$.
Nous commençons par$5$ les négatifs.
Ensuite, nous ajoutons des$3$ points positifs.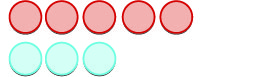
Nous supprimons toutes les paires neutres.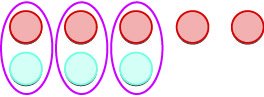
Il nous reste$2$ des points négatifs.
La somme de$-5$ et$3$ est$-2$.	$-5 + 3 = 2$

Remarquez qu'il y avait plus de négatifs que de positifs, donc le résultat était négatif.

Ajoutons maintenant la dernière combinaison,$5+(−3)$.

Tableau$\PageIndex{2}$

	$5 + (-3)$signifie la somme de$-5$ et$-3$.
Nous commençons par des$5$ points positifs.
Ensuite, nous ajoutons$3$ des négatifs.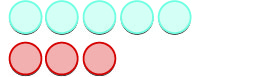
Nous supprimons toutes les paires neutres.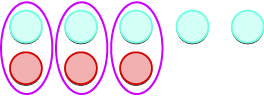
Il nous reste$2$ des points positifs.
La somme de$5$ et$-3$ est$2$.	$5 + (-3) = 2$

Lorsque nous utilisons des compteurs pour modéliser l'addition d'entiers positifs et négatifs, il est facile de voir s'il y a plus de compteurs positifs ou négatifs. Nous savons donc si la somme sera positive ou négative.

Figurine$\PageIndex{8}$

Exemple$\PageIndex{9}$

Ajoutez :

1. $-1 + 5$
2. $1 + (-5)$

Solution :

1. $-1 + 5$

Il y a plus de points positifs, donc la somme est positive.

Donc,$-1 + 5 = 4$.

2. $1 + (-5)$

Il y a plus de points négatifs, donc la somme est négative.

Donc,$1 + (-5) = -4$

Essayez-le$\PageIndex{17}$

Ajoutez :

1. $-2 + 4$
2. $2 + (-4)$

Answer

1. $2$
2. $-2$

Try It $\PageIndex{18}$

Ajoutez :

1. $-2 + 5$
2. $2 + (-5)$

Réponse

1. $3$
2. $-3$

Maintenant que nous avons ajouté de petits entiers positifs et négatifs à un modèle, nous pouvons visualiser le modèle dans notre esprit pour simplifier les problèmes liés à n'importe quel nombre.

Lorsque vous devez ajouter des nombres tels que$37+(−53)$, vous ne voulez vraiment pas avoir à compter les compteurs$37$ bleus et les compteurs$53$ rouges. Avec le modèle en tête, pouvez-vous visualiser ce que vous feriez pour résoudre le problème ?

Imaginez des compteurs$37$ bleus avec des compteurs$53$ rouges alignés en dessous. Comme il y aurait plus de compteurs rouges (négatifs) que de compteurs bleus (positifs), la somme serait négative. Combien de compteurs rouges y aurait-il encore ? Parce qu'$53−37=16$il y a$16$ plus de compteurs rouges.

Donc, la somme de$37+(−53)$ est$−16$.

$$37+(−53)=−16\nonumber$$

Essayons-en un autre. Nous allons ajouter$−74+(−27)$. Encore une fois, imaginez des compteurs$74$ rouges et$27$ plus de compteurs rouges, donc nous aurions des compteurs$101$ rouges. Cela signifie que la somme est$−101$.

$$−74+(−27)=−101\nonumber$$

Regardons les résultats de l'ajout des différentes combinaisons de$5,−5$ et$3, -3$.

ADDITION DE NOMBRES ENTIERS POSITIFS ET NÉGATIFS

$$\begin{array} {ll} {5 + 3=8} &{-5 + (-3)=-8} \\{\text{both positive, sum positive}} &{\text{both positive, sum positive}} \end{array}\nonumber$$

Lorsque les signes sont les mêmes, les compteurs seraient tous de la même couleur, alors ajoutez-les.

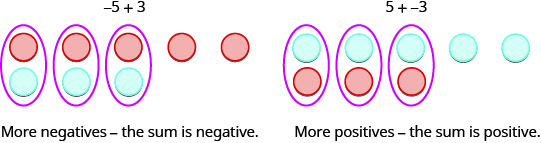
$$\begin{array} {ll} {5 + 3=-2} &{-5 + (-3)=2} \\{\text{different signs, more negatives, sum negative}} &{\text{different signs, more positives, sum positive}} \end{array}\nonumber$$

Lorsque les signes sont différents, certains compteurs forment des paires neutres, alors soustrayez pour voir combien il en reste.

Visualisez le modèle à mesure que vous simplifiez les expressions dans les exemples suivants.

Exemple$\PageIndex{10}$

Simplifiez :

1. $19 + (-47)$
2. $-14 + (-36)$

Solution :

1. Puisque les signes sont différents, on soustrait$19$ de$47$. La réponse sera négative car il y a plus de négatifs que de positifs.

$\text{Add.} \qquad 19 + (-47) = -28$

2. Puisque les signes sont les mêmes, nous ajoutons. La réponse sera négative car il y a plus de négatifs que de positifs.

$\text{Add.} \qquad-14 + (-36) = -50$

Essayez-le$\PageIndex{19}$

Simplifiez :

1. $-31 + (-19)$
2. $15 + (-32)$

Answer

1. $-50$
2. $-17$

Try It $\PageIndex{20}$

Simplifiez :

1. $-42 + (-28)$
2. $25 + (-61)$

Réponse

1. $-70$
2. $-36$

Les techniques utilisées jusqu'à présent s'étendent à des problèmes plus complexes, comme ceux que nous avons vus auparavant. N'oubliez pas de suivre l'ordre des opérations !

Exemple$\PageIndex{11}$

Simplifiez :

$-5 + 3(-2 + 7)$

Solution :

$$\begin{array} {ll} {} &{-5 + 3(-2 + 7)} \\ {\text{Simplify inside the parenthesis}} &{-5 + 3(5)} \\{\text{Multiply}} &{-5 + 15} \\{\text{add left to right}} &{10} \end{array}\nonumber$$

Essayez-le$\PageIndex{21}$

Simplifiez :

$-2 + 5(-4 + 7)$

Answer

$13$

Try It $\PageIndex{22}$

Simplifiez :

$-4 + 2(-3 + 5)$

Réponse

$0$

Soustraire des entiers

Remarque

L'activité de mathématiques manipulatrices « Soustraction de nombres signés » vous aidera à mieux comprendre la soustraction d'entiers.

Nous continuerons à utiliser des compteurs pour modéliser la soustraction. N'oubliez pas que les compteurs bleus représentent des nombres positifs et les compteurs rouges des nombres négatifs.

Peut-être que quand tu étais plus jeune, tu lisais «$5−3$ » comme « à$5$ emporter »$3$. Lorsque vous utilisez des compteurs, vous pouvez penser à la soustraction de la même manière !

Nous modéliserons les quatre faits de soustraction à l'aide des nombres$5$ et$3$.

$$\begin{array} {llll} {5 - 3} &{-5 - (-3))} &{-5 -3} &{5 - (-3)} \end{array}\nonumber$$

Pour soustraire$5−3$, nous reformulons le problème comme « à$5$ emporter »$3$.

Tableau$\PageIndex{3}$

Nous commençons par des$5$ points positifs.
Nous « retirons » les$3$ points positifs.
Il nous reste$2$ des points positifs.
La différence entre$5$ et$3$ est$2$.	$2$

Maintenant, nous allons soustraire$−5−(−3)$. Surveillez les similitudes avec le dernier exemple$5−3=2$.

Pour soustraire$−5−(−3)$, nous redisons cela comme « à$–5$ emporter$–3$ »

Tableau$\PageIndex{4}$

Nous commençons par$5$ les négatifs.
Nous « retirons »$3$ les négatifs.
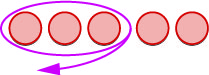Il nous reste$2$ des points négatifs.
La différence entre$-5$ et$-3$ est$-2$.	$-2$

Notez que ces deux exemples sont très similaires : dans le premier exemple, nous soustrayons 3 positifs de 5 positifs et nous nous retrouvons avec 2 positifs.

Dans le deuxième exemple, nous soustrayons 3 négatifs de 5 négatifs et nous obtenons 2 négatifs.

Chaque exemple utilisait des compteurs d'une seule couleur, et le modèle de soustraction « à emporter » était facile à appliquer.

Figurine$\PageIndex{9}$

Exemple$\PageIndex{12}$

Soustraire :

1. $7 - 5$
2. $-7 - (-5)$

Solution :

1. $$\begin{array} {ll} {7 - 5} \\ {2}&{\text{Take }5\space \text{positives from }7 \space \text{positives and get }2\space \text{positives}} & \end{array}\nonumber$$
2. $$\begin{array} {ll} {-7 - (-5)} \\ {-2} &{\text{Take }5\space \text{negatives from }7 \space \text{negatives and get }2\space \text{negatives}} \end{array}\nonumber$$

Essayez-le$\PageIndex{23}$

Soustraire :

1. $6 - 4$
2. $-6 - (-4)$

Answer

1. $2$
2. $-2$

Try It $\PageIndex{24}$

Soustraire :

1. $7 - 4$
2. $-7 - (-4)$

Réponse

1. $3$
2. $-3$

Que se passe-t-il lorsque nous devons soustraire un nombre positif et un nombre négatif ? Nous devrons utiliser à la fois des compteurs blancs et rouges ainsi que des paires neutres. L'ajout d'une paire neutre ne modifie pas la valeur. C'est comme remplacer les pièces par des pièces de cinq cents : la valeur est la même, mais elle a une apparence différente.

• Pour le soustraire$−5−3$, nous le reformulons comme à$−5$ emporter$3$.

Nous commençons par$5$ les négatifs. Nous devons retirer des$3$ points positifs, mais nous n'avons aucun point positif à retirer.

N'oubliez pas qu'une paire neutre a une valeur nulle. Si on ajoute$0$ à$5$ sa valeur, c'est encore$5$. Nous ajoutons des paires neutres aux points$5$ négatifs jusqu'à ce que nous obtenions des$3$ points positifs à retirer.

Tableau$\PageIndex{5}$

	$-5 -3$signifie à$-5$ emporter$3$
Nous commençons par$5$ les négatifs.
Nous ajoutons maintenant les neutres nécessaires pour obtenir des$3$ points positifs.
Nous supprimons les$3$ points positifs.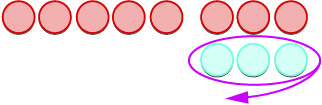
Il nous reste des$8$ points négatifs.
La différence entre$-5$ et$3$ est$-8$.	$-5 - 3 = -8$

Et maintenant, le quatrième cas,$5−(−3)$. Nous commençons par des$5$ points positifs. Nous devons éliminer$3$ les points négatifs, mais il n'y a aucun négatif à emporter. Nous ajoutons donc des paires neutres jusqu'à ce que nous ayons$3$ des négatifs à emporter.

Tableau$\PageIndex{6}$

	$5 -(-3)$signifie à$5$ emporter$-3$
Nous commençons par des$5$ points positifs.
Nous ajoutons maintenant les paires de neutres nécessaires.
Nous supprimons$3$ les négatifs.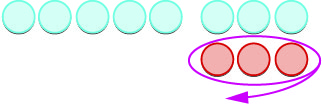
Il nous reste des$8$ points positifs.
La différence entre$5$ et$-3$ est$8$.	$5 - (-3) = 8$

Exemple$\PageIndex{13}$

Soustraire :

1. $-3 -1$
2. $3 - (-1)$

Solution :

1.

Prenez 1 résultat positif de la paire neutre ajoutée.

$\begin{array} {l} {-3 -1} \\ {-4} \end{array}$

2.

Prenez 1 négatif de la paire neutre ajoutée.

$\begin{array} {l} {3 - (-1)} \\ {4} \end{array}$

Essayez-le$\PageIndex{25}$

Soustraire :

1. $-6 -4$
2. $6 - (-4)$

Answer

1. $-10$
2. $10$

Try It $\PageIndex{26}$

Soustraire :

1. $-7-4$
2. $7 - (-4)$

Réponse

1. $-11$
2. $11$

Avez-vous remarqué qu'il est possible de soustraire des nombres signés en ajoutant le contraire ? Dans l'exercice$\PageIndex{33}$,$−3−1$ est identique à$−3+(−1)$ et$3−(−1)$ est identique à$3+1$. Vous verrez souvent cette idée, la propriété de soustraction, écrite comme suit :

PROPRIÉTÉ DE SOUSTRACTION

$$a−b=a+(−b) \nonumber$$

Soustraire un nombre revient à ajouter son opposé.

Regardez ces deux exemples.

Figure$\PageIndex{10}$ :$6−4$ donne la même réponse que$6+(−4)$.

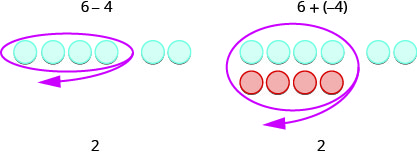
Bien sûr, lorsque vous avez un problème de soustraction qui ne contient que des nombres positifs, par exemple$6−4$, vous faites simplement la soustraction. Vous saviez déjà comment soustraire il y a$6−4$ longtemps. Mais savoir cela$6−4$ donne la même réponse que$6+(−4)$ cela aide lorsque vous soustrayez des nombres négatifs. Assurez-vous de comprendre comment$6−4$ et de$6+(−4)$ donner les mêmes résultats !

Exemple$\PageIndex{14}$

Simplifiez :

1. $13 - 8 \space \text{and } 13 + (-8)$
2. $-17 - 9 \space \text{and } -17 + (-9)$

Solution :

1. $\begin{array} {llll} {\text{Subtract.}} &{13 - 8} &{\text{and}} &{13 + (-8)} \\ {} &{5} &{} &{5} \end{array}$
2. $\begin{array} {llll} {\text{Subtract.}} &{-17 - 9} &{\text{and}} &{-17 + (-9)} \\ {} &{-26} &{} &{-26} \end{array}$

Essayez-le$\PageIndex{27}$

Simplifiez :

1. $21 - 13 \space \text{and } 21 + (-13)$
2. $-11 - 7 \space \text{and } -11 + (-7)$

Answer

1. $8$
2. $-18$

Try It $\PageIndex{28}$

Simplifiez :

1. $15 - 7 \space \text{and } 15 + (-7)$
2. $-14 - 8 \space \text{and } -14 + (-8)$

Réponse

1. $8$
2. $-22$

Regardez ce qui se passe lorsque nous soustrayons un négatif.

Figure$\PageIndex{11}$ :$8−(−5)$ donne la même réponse que$8+5$

Soustraire un nombre négatif, c'est comme ajouter un positif !

Vous verrez souvent cela écrit comme$a−(−b)=a+b$.

Est-ce que cela fonctionne aussi pour d'autres numéros ? Prenons l'exemple suivant et voyons.

Exemple$\PageIndex{15}$

Simplifiez :

1. $9 - (-15) \space \text{and } 9 + 15$
2. $-7 - (-4) \space \text{and } -7 + 4$

Solution :

1. $\begin{array} {lll} {} &{9 - (-15)} &{9 + 15} \\ {\text{Subtract}} &{24} &{24} \end{array}$
2. $\begin{array} {lll} {} &{-7 - (-4)} &{-7 + 4} \\ {\text{Subtract}} &{-3} &{-3} \end{array}$

Essayez-le$\PageIndex{29}$

Simplifiez :

1. $6 - (-13) \space \text{and } 6 + 13$
2. $-5 - (-1) \space \text{and } -5 + 1$

Answer

1. $19$
2. $-4$

Try It $\PageIndex{30}$

Simplifiez :

1. $4 - (-19) \space \text{and } 4 + 19$
2. $-4 - (-7) \space \text{and } -4 + 7$

Réponse

1. $23$
2. $3$

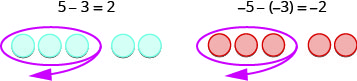
Regardons les résultats de la soustraction des différentes combinaisons de$5,−5$ et$3,−3$.

SOUSTRACTION DE NOMBRES ENTIERS

$$\begin{array} {l} {5 - 3} &{-5 - (-3)} \\ {2} &{-2} \\ {5\space\text{positives take away }3\space\text{positives}} &{5\space\text{negatives take away }3\space\text{negatives}} \\ {2\space\text{positives}} &{2\space\text{negatives}} \end{array}\nonumber$$

Quand il y a suffisamment de compteurs de la couleur à emporter, soustrayez.

$$\begin{array} {l} {-5 - 3} &{5 - (-3)} \\ {-8} &{8} \\ {5\space\text{negatives, want to take away }3\space\text{positives}} &{5\space\text{positives, want to take away }3\space\text{negatives}} \\ {\text{need neutral pairs}} &{\text{need neutral pairs}} \end{array}\nonumber$$

Lorsqu'il n'y a pas assez de compteurs de la couleur à emporter, ajoutez.

Que se passe-t-il lorsqu'il y a plus de trois entiers ? Nous utilisons simplement l'ordre des opérations comme d'habitude.

Exemple$\PageIndex{16}$

Simplifiez :

$7 - (-4 -3) - 9$

Solution :

$$\begin{array} {ll} {} &{7 - (-4 - 3) - 9} \\ {\text{Simplify inside the parenthesis first.}} &{7 - (-7) - 9} \\ {\text{Subtract left to right.}} &{14 - 9} \\ {\text{Subtract}} &{5} \end{array}\nonumber$$

Essayez-le$\PageIndex{31}$

Simplifiez :

$8−(−3−1)−9$

Answer

$3$

Try It $\PageIndex{32}$

Simplifiez :

$12−(−9−6)−14$

Réponse

$12$

Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à ajouter et à soustraire des nombres entiers. Vous devez activer Java dans votre navigateur Web pour utiliser les applications.

• Ajouter une puce colorée
• Soustraire une puce colorée

Concepts clés

• Addition d'entiers positifs et négatifs

$$\begin{array} {ll} {5 + 3} &{-5+(-3)} \\ {8} &{-8} \\ {\text{both positive,}} &{\text{both negative,}} \\ {\text{sum positive}} &{\text{sum negative}} \end{array}\nonumber$$

$$\begin{array} {ll} {-5 + 3} &{5+(-3)} \\ {-2} &{2} \\ {\text{different signs,}} &{\text{different signs,}} \\ {\text{more negatives}} &{\text{more positives}} \\ {\text{sum negative}} &{\text{sum positive}} \end{array}\nonumber$$

• Propriété de valeur absolue :

$|n| \geq 0$pour tous les numéros. Les valeurs absolues sont toujours supérieures ou égales à zéro !

• Soustraction de nombres entiers

$$\begin{array} {ll} {5 - 3} &{-5-(-3)} \\ {2} &{-2} \\ {5\space\text{positives}} &{5\space\text{negatives}} \\ {\text{take away 3 positives}} &{\text{take away 3 negatives}} \\ {\text{2 positives}} &{\text{2 negatives}} \end{array}\nonumber$$

$$\begin{array} {ll} {-5 - 3} &{5-(-3)} \\ {-8} &{8} \\ {\text{5 negatives, want to}} &{\text{5 positives, want to}} \\ {\text{subtract 3 positives}} &{\text{subtract 3 negatives}} \\ {\text{need neutral pairs}} &{\text{need neutral pairs}}\end{array}\nonumber$$

• Propriété de soustraction : Soustraire un nombre revient à ajouter son opposé.

Lexique

valeur absolue

La valeur absolue d'un nombre est sa distance par rapport à 0 sur la ligne numérique. La valeur absolue d'un nombre nn s'écrit |n|.

nombres entiers

Les nombres entiers et leurs contraires sont appelés entiers :$...−3, −2, −1, 0, 1, 2, 3...$

opposé

L'opposé d'un nombre est le nombre qui se trouve à la même distance de zéro sur la droite numérique mais du côté opposé à zéro : −$a$ signifie l'opposé du nombre. La notation −$a$ se lit « à l'opposé de »$a$.