1.3 : Utiliser le langage de l'algèbre
- Page ID
- 195264
À la fin de cette section, vous serez en mesure de :
- Utiliser des variables et des symboles algébriques
- Simplifier les expressions en utilisant l'ordre des opérations
- Evaluer une expression
- Identifier et combiner des termes similaires
- Traduisez une phrase anglaise en une expression algébrique
Utiliser des variables et des symboles algébriques
Supposons que cette année Greg ait des\(20\) années et Alex l'est\(23\). Tu sais qu'Alex a des\(3\) années de plus que Greg. Quand Greg l'était\(12\), Alex l'était\(15\). Quand Greg le sera\(35\), Alex le sera\(38\). Peu importe l'âge de Greg, Alex aura toujours 3 ans de plus, non ? Dans le langage de l'algèbre, nous disons que l'âge de Greg et l'âge d'Alex sont des variables et qu'\(3\)il s'agit d'une constante. Les âges changent (« varient ») mais les\(3\) années qui les séparent restent toujours les mêmes (« constantes »). Puisque l'âge de Greg et celui d'Alex seront toujours différents d'une\(3\) année à l'autre,\(3\) c'est la constante. En algèbre, nous utilisons des lettres de l'alphabet pour représenter des variables. Donc, si nous appelons l'âge de Greg\(g\), nous pourrions utiliser\(g + 3g + 3\) pour représenter l'âge d'Alex. Voir le tableau\(\PageIndex{1}\).
| L'âge de Greg | L'âge d'Alex |
|---|---|
| \(12\) | \(15\) |
| \(20\) | \(23\) |
| \(35\) | \(38\) |
| \(g\) | \(g+3\) |
Les lettres utilisées pour représenter ces âges changeants sont appelées variables. Les lettres les plus couramment utilisées pour les variables sont\(x, y, a, b,\) et\(c\).
Une variable est une lettre qui représente un nombre dont la valeur peut changer.
Une constante est un nombre dont la valeur reste toujours la même.
Pour écrire de manière algébrique, nous avons besoin de symboles d'opération ainsi que de nombres et de variables. Nous utiliserons plusieurs types de symboles.
Il existe quatre opérations arithmétiques de base : addition, soustraction, multiplication et division. Nous listerons les symboles utilisés pour indiquer ces opérations ci-dessous (Tableau\(\PageIndex{2}\)). Vous reconnaîtrez probablement certains d'entre eux. \(\require{enclose}\)
| Opération | Notation | Dis : | Le résultat est... |
|---|---|---|---|
| Ajout | \(a+b\) | \(a\)plus\(b\) | la somme de\(a\) et\(b\) |
| Soustraction | \(a−b\) | \(a\)moins\(b\) | la différence entre\(a\) et\(b\) |
| MULTIPLICATION | \(a·b,ab,(a)(b),(a)b,a(b)\) | \(a\)fois\(b\) | le produit de\(a\) et\(b\) |
| Division | \(a\div{b}, a/b,\dfrac{a}{b}, b \enclose{longdiv}{a}\) | \(a\)divisé par\(b\) | le quotient de\(a\) et\(b\), s'\(a\)appelle le dividende, et s'\(b\)appelle le diviseur |
Nous effectuons ces opérations sur deux numéros. Lorsque vous traduisez d'une forme symbolique vers l'anglais, ou de l'anglais vers une forme symbolique, faites attention aux mots « of » et « and ».
- La différence\(9\) et les\(2\) moyens soustraient\(9\) et\(2\), en d'autres termes,\(9\) moins\(2\), que nous écrivons symboliquement comme\(9−2\).
- Le produit de\(4\) et\(8\) signifie multiplier\(4\) et\(8\), en d'autres termes, le\(4\) temps\(8\), que nous écrivons symboliquement\(4\cdot 8\).
En algèbre, le symbole de la croix n'est pas utilisé pour montrer la multiplication car ce symbole peut prêter à confusion.\(\times\) \(3xy\)Cela signifie-t-il\(3\times y\) (« trois fois\(y\) ») ou\(3\cdot x \cdot y\) (trois\(x\) fois\(y\)) ? Pour clarifier les choses, utilisez\(\cdot\) des parenthèses pour la multiplication.
Lorsque deux quantités ont la même valeur, on dit qu'elles sont égales et on les relie par un signe égal.
\(a = b\)se lit comme suit : «\(a\) est égal à\(b\) »
Le symbole\(“=”\) s'appelle le signe égal.
Sur la ligne numérique, les chiffres s'agrandissent à mesure qu'ils vont de gauche à droite. La ligne numérique peut être utilisée pour expliquer les symboles\(“<”\) et\(“>"\).
\(a<b\)se lit comme suit : «\(a\) est inférieur à\(b\) »
\(a\)se trouve à gauche de\(b\) sur la ligne numérique
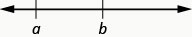
\(a>b\)se lit comme suit : «\(a\) est supérieur à\(b\) »
\(a\)se trouve à droite de\(b\) sur la ligne numérique
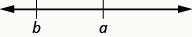
Les expressions\(a < b\) ou\(a > b\) peuvent être lues de gauche à droite ou de droite à gauche, bien qu'en anglais, nous lisons généralement de gauche à droite Table\(\PageIndex{3}\). En général,\(a < b\) est équivalent à\(b > a\). Par exemple,\(7 < 11\) est équivalent à\(11 > 7\). Et\(a > b\) est équivalent à\(b < a\). Par exemple,\(17 > 4\) est équivalent à\(4 < 17\).
| Les symboles d'inégalité | Paroles |
|---|---|
| \(a \neq b\) | \(a\)n'est pas égal à\(b\) |
| \(a < b\) | \(a\)est inférieur à\(b\) |
| \(a \leq b\) | \(a\)est inférieur ou égal à\(b\) |
| \(a > b\) | \(a\)est supérieur à\(b\) |
| \(a \geq b\) | \(a\)est supérieur ou non égal à\(b\) |
Traduisez de l'algèbre vers l'anglais :
- \(17 \leq 26\)
- \(8 \neq 17 - 3\)
- \(12 > 27 \div 3\)
- \(y + 7 < 19\)
- Réponse
-
- \(17 \leq 26\),\(17\) est inférieur ou égal à\(26\)
- \(8 \neq 17 - 3\), n'\(8\)est pas égal à\(17\) moins\(3\)
- \(12 > 27 \div 3\),\(12\) est plus grand que\(27\) divisé par\(3\)
- \(y + 7 < 19\),\(y\) plus\(7\) est inférieur à\(19\)
Traduisez de l'algèbre vers l'anglais :
- \(14 \leq 27\)
- \(19 - 2 \neq 8\)
- \(12 > 4 \div 2\)
- \(x - 7 < 1\)
- Réponse
-
- \(14\)est inférieur ou égal à\(27\)
- \(19\)moins n'\(2\)est pas égal à\(8\)
- \(12\)est supérieur à\(4\) divisé par\(2\)
- \(x\)moins\(7\) est inférieur à\(1\)
Traduisez de l'algèbre vers l'anglais :
- \(19 \leq 15\)
- \(7 = 12 - 5\)
- \(15 \div 3 < 8\)
- \(y + 3 < 6\)
- Réponse
-
- \(19\)est supérieur ou égal à\(15\)
- \(7\)est égal à\(12\) moins\(5\)
- \(15\)divisé par\(3\) est inférieur à\(8\)
- \(y\)plus\(3\) est supérieur à\(6\)
Les symboles de regroupement en algèbre ressemblent beaucoup aux virgules, aux deux-points et aux autres signes de ponctuation en anglais. Ils aident à préciser quelles expressions doivent être conservées ensemble et séparées des autres expressions. Nous allons maintenant introduire trois types.
\[\begin{align*} & \text{Parentheses} & & ( ) \\ & \text{Brackets} & & [ ] \\ & \text{Braces} & & \{ \} \end{align*}\]
Voici quelques exemples d'expressions qui incluent des symboles de regroupement. Nous simplifierons les expressions de ce type plus loin dans cette section.
\[8(14−8) \qquad 21−3[2 + 4(9−8)] \qquad 24\div \{ 13−2[1(6−5)+4] \nonumber\}\]
Quelle est la différence en anglais entre une phrase et une phrase ? Une phrase exprime une pensée unique qui est incomplète en elle-même, mais une phrase fait une déclaration complète. « Courir très vite » est une phrase, mais « Le joueur de football courait très vite » est une phrase. Une phrase a un sujet et un verbe. En algèbre, nous avons des expressions et des équations.
Une expression est un nombre, une variable ou une combinaison de nombres et de variables utilisant des symboles d'opération.
Une expression est comme une phrase anglaise. Voici quelques exemples d'expressions :
| Expression | Paroles | Phrase anglaise |
|---|---|---|
| \(3 + 5\) | \(3\)plus\(5\) | la somme de trois et cinq |
| \(n − 1\) | \(n\)moins un | la différence entre\(n\) et un |
| \(6\cdot 7\) | \(6\)fois\(7\) | le produit de six et sept |
| \(\dfrac{x}{y}\) | \(x\)divisé par\(y\) | le quotient de\(x\) et\(y\) |
Notez que les phrases anglaises ne forment pas une phrase complète car la phrase ne possède pas de verbe. Une équation est constituée de deux expressions liées par un signe égal. Lorsque vous lisez les mots que les symboles représentent dans une équation, vous obtenez une phrase complète en anglais. Le signe égal donne le verbe.
Une équation est constituée de deux expressions reliées par un signe égal.
Voici quelques exemples d'équations.
| équation | Phrase anglaise |
|---|---|
| \(3+5=8\) | la somme de trois et cinq est égale à huit |
| \(n−1=14\) | \(n\)moins un est égal à quatorze |
| \(6 \cdot 7=42\) | Le produit de six et sept est égal à quarante-deux |
| \(x=53\) | \(x\)est égal à cinquante-trois |
| \(y+9=2y−3\) | \(y\)plus neuf est égal à deux\(y\) moins trois |
Déterminez si chacune est une expression ou une équation :
- \(2(x + 3) = 10\)
- \(4(y - 1) + 1\)
- \(x \div 25\)
- \(y + 8 = 40\)
- Réponse
-
- \(2(x + 3) = 10\). Il s'agit d'une équation : deux expressions sont liées par un signe égal.
- \(4(y - 1) + 1\). C'est une expression, pas un signe égal.
- \(x \div 25\). C'est une expression, pas un signe égal.
- \(y + 8 = 40\). Il s'agit d'une équation : deux expressions sont liées par un signe égal.
Déterminez si chacune est une expression ou une équation :
- \(3(x - 7) = 27\)
- \(5(4y - 2) - 7\)
- Réponse
-
- équation
- expression
Déterminez si chacune est une expression ou une équation :
- \(y^{3} \div 14\)
- \(4x - 6 = 22\)
- Réponse
-
- expression
- équation
Supposons que nous devions multiplier neuf facteurs de\(2\). On pourrait écrire ça comme\(2\cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2\). C'est fastidieux et il peut être difficile de suivre tous ces 2, nous utilisons donc des exposants. Nous écrivons\(2\cdot 2 \cdot 2\) au fur\(2^{3}\) et à\(2\cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2\) mesure\(2^{9}\). Dans des expressions telles que\(2^{3}\), on\(2\)\(3\) appelle la base et l'exposant. L'exposant nous indique combien de fois nous devons multiplier la base.

Nous\(2^{3}\) entendons « deux à la troisième puissance » ou « deux cubes ».
Nous disons\(2^{3}\) est en notation exponentielle et\(2\cdot 2 \cdot 2\) est en notation étendue.
\(a^{n}\)désigne le produit des\(n\) facteurs de\(a\).
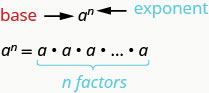
L'expression\(a^{n}\) est lue\(a\) à la\(n^{th}\) puissance.
Alors que nous\(a^{n}\) lisons «\(a\) au\(n^{th}\) pouvoir », nous lisons généralement :
- \(a^{2}\)« un carré »
- \(a^{3}\)« un cube »
Nous verrons plus tard pourquoi\(a^{2}\) et nous aurons\(a^{3}\) des noms spéciaux.
Le tableau\(\PageIndex{6}\) montre comment nous lisons certaines expressions avec des exposants.
| Expression | En mots |
|---|---|
| \(7^{2}\) | \(7\)à la deuxième puissance ou\(7\) au carré |
| \(5^{3}\) | \(5\)à la troisième puissance ou au\(5\) cube |
| \(9^{4}\) | \(9\)à la quatrième puissance |
| \(12^{5}\) | \(12\)jusqu'à la cinquième puissance |
Simplifiez :\(3^{4}\)
- Réponse
-
\[\quad 3^{4}\nonumber\]
\ [\ begin {align*} & Développez l'expression & & 3 \ cdot 3 \ cdot 3 \ cdot 3 \ \ [5pt]
& \ text {Multipliez de gauche à droite} & & 9 \ cdot 3 \ cdot 3 \ \ [5pt]
& \ text {Multipliez} & & & & 27 \ cdot 3 \ \ [5pt]
& \ text {Multipliez} & & & 81 \ end {align*} \]
Simplifiez :
- \(5^{3}\)
- \(1^{7}\)
- Réponse
-
- \(125\)
- \(1\)
- \(7^{2}\)
- \(0^{5}\)
- Réponse
-
- \(49\)
- \(0\)
Simplifier les expressions en utilisant l'ordre des opérations
Simplifier une expression signifie faire tous les calculs possibles. Par exemple, pour simplifier,\(4\cdot 2 + 1\) nous devons d'abord multiplier\(4\cdot 2\) pour obtenir,\(8\) puis ajouter le\(1\) pour obtenir\(9\). Une bonne habitude à prendre est de travailler en bas de la page, en écrivant chaque étape du processus en dessous de l'étape précédente. L'exemple qui vient d'être décrit ressemblerait à ceci :
\[4\cdot 2 + 1\nonumber\]
\[8 + 1\nonumber\]
\[9\nonumber\]
En n'utilisant pas le signe égal lorsque vous simplifiez une expression, vous pouvez éviter de confondre expressions et équations.
Pour simplifier une expression, effectuez toutes les opérations qu'elle contient.
Nous avons introduit la plupart des symboles et des notations utilisés en algèbre, mais nous devons maintenant clarifier l'ordre des opérations. Sinon, les expressions peuvent avoir des significations différentes et donner lieu à des valeurs différentes. Par exemple, considérez l'expression :
\[4 + 3\cdot 7\nonumber\]
Si vous simplifiez cette expression, qu'obtenez-vous ?
Certains étudiants disent :\(49\)
\[4 + 3\cdot 7\nonumber\]
Depuis\(4+3\) donne\(7\).
\[7 \cdot 7\nonumber\]
Et\(7\cdot 7\) c'est\(49\)\[49\nonumber\]
D'autres disent :\(25\)
\[4 + 3\cdot 7\nonumber\]
Depuis\(3\cdot 7\)\(21\).
\[4 + 21\nonumber\]
Et\(21 + 4\) fait\(25\).
\[25\nonumber\]
Imaginez la confusion qui régnerait dans notre système bancaire si chaque problème avait plusieurs réponses correctes !
La même expression doit donner le même résultat. Les mathématiciens ont donc très tôt établi des directives appelées l'Ordre des opérations.
- Parenthèses et autres symboles de regroupement
- Simplifiez toutes les expressions entre parenthèses ou autres symboles de regroupement, en commençant par les parenthèses les plus internes.
- Exposants
- Simplifiez toutes les expressions avec des exposants.
- Multiplication et division
- Effectuez toutes les multiplications et divisions dans l'ordre de gauche à droite. Ces opérations ont la même priorité.
- Addition et soustraction
- Effectuez toutes les additions et soustractions dans l'ordre, de gauche à droite. Ces opérations ont la même priorité.
L'activité de mathématiques manipulatrices « Game of 24 » vous permettra de vous entraîner à utiliser l'ordre des opérations.
Les élèves demandent souvent : « Comment me souviendrai-je de la commande ? » Voici une façon de vous aider à vous en souvenir : prenez la première lettre de chaque mot clé et remplacez-la par la phrase stupide : « Excusez ma chère tante Sally ».
\ [\ begin {align*} & \ textbf {P} \ text {parenthèses} & & & \ textbf {P} \ text {lease} \ \ [5pt]
& \ textbf {E} \ text {xponents} & & & \ textbf {E} \ text {xcuse} \ \ [5 points]
& \ textbf {M} \ text {ultiplication} \ space \ textbf {D} \ text {ivision} & & \ textbf {M} \ text {y} \ space \ textbf {D} \ text {ear} \ \ [5pt]
& \ textbf {A} \ text {ddition} \ space \ textbf {S} \ text {soustraction} & & & \ textbf {A} \ text {unt} \ space \ textbf {S} \ text {ally} \ end {align*} \]
C'est une bonne chose que «\(\textbf{M}\text{y}\space\textbf{D}\text{ear}\) » aille de pair, car cela nous rappelle que ma multiplication et ma division ont la même priorité. Nous ne faisons pas toujours la multiplication avant la division ou nous ne faisons pas toujours la division avant la multiplication. Nous les faisons dans l'ordre de gauche à droite.
De même, «\(\textbf{A}\text{unt}\space\textbf{S}\text{ally}\) » va de pair et nous rappelle qu'une addition et une soustraction ont également la même priorité et que nous les faisons dans l'ordre de gauche à droite.
Essayons un exemple.
Simplifiez :
- \(4 + 3\cdot 7\)
- \((4 + 3)\cdot 7\)
- Réponse
- 1.
\(4 + 3 \cdot 7\) Y a-t-il des parenthèses ? Non. Y a-t-il des opposants ? Non. Y a-t-il une multiplication ou une division de ma division ? Oui. Multipliez d'abord \(4 + {\color{red}{3 \cdot 7}}\) Ajoutez. \(4+21\) \(25\) 2.
\((4 + 3)\cdot 7\) Y a-t-il des parenthèses ? Oui. \({\color{red}{(4 + 3)}}\cdot 7\) Simplifiez entre parenthèses. \(({\color{red}{7}})7\) Y a-t-il des opposants ? Non. Y a-t-il une multiplication ou une division de ma division ? Oui. Multipliez. \(49\)
Simplifiez :
- \(12 - 5\cdot 2\)
- \((12 - 5)\cdot 2\)
- Réponse
-
- \(2\)
- \(14\)
Simplifiez :
- \(8 + 3\cdot 9\)
- \((8 + 3)\cdot 9\)
- Réponse
-
- \(35\)
- \(99\)
Simplifiez :\(18\div 6 + 4(5 - 2)\)
- Réponse
-
Des parenthèses ? Oui, soustrayez d'abord. \(18\div 6 + 4(5 - 2)\)
\(18\div 6 + 4(3)\)Des exposants ? Non. Multiplication ou division ? Oui. \({\color{red}{18\div 6}} + {\color{red}{4(3)}}\) Divisez d'abord car nous multiplions et divisons de gauche à droite. \(3+{\color{red}{4(3)}}\) Y a-t-il une autre multiplication ou division ? Oui. Multipliez. \(3 + 12\) Y a-t-il une autre multiplication ou division ? Non. Une addition ou une soustraction ? Oui. \(15\)
Simplifiez :\(30\div 5 + 10(3 - 2)\)
- Réponse
-
\(16\)
Simplifiez :\(70\div 10 + 4(6 - 2)\)
- Réponse
-
\(23\)
Lorsqu'il existe plusieurs symboles de regroupement, nous simplifions d'abord les parenthèses les plus internes et nous travaillons vers l'extérieur.
Simplifiez :\(5 + 2^{3} + 3[6 - 3(4 - 2)]\).
- Réponse
-
\(5 + 2^{3} + 3[6 - 3(4 - 2)]\) Y a-t-il des parenthèses (ou un autre symbole de regroupement) ? Oui. Concentrez-vous sur les parenthèses qui se trouvent à l'intérieur des crochets. \(5 + 2^{3} + 3[6 - 3{\color{red}{(4 - 2)}}]\) Soustraire. \(5 + 2^{3} + 3[6 - {\color{red}{3(2)}}]\) Continuez entre crochets et multipliez. \(5 + 2^{3} + 3[{\color{red}{6 - 6}}]\) Continuez entre crochets et soustrayez. \(5 + 2^{3} + 3[{\color{red}{0}}]\) L'expression entre crochets n'a pas besoin d'être simplifiée davantage. Y a-t-il des exposants ? Oui. \(5 + {\color{red}{2^{3}}}+ 3[0]\) Simplifiez les exposants. \(5 + 8 + {\color{red}{3[0]}}\) Y a-t-il une multiplication ou une division ? Oui. Multipliez. \({\color{red}{5 + 8}}+0\) Y a-t-il une addition ou une soustraction ? Oui. Ajoutez. \({\color{red}{13 + 0}}\) Ajoutez. \(13\)
Simplifiez :\(9 + 5^{3} - [4(9 + 3)]\).
- Réponse
-
\(86\)
Simplifiez :\(7^{2} - 2[4(5 + 1)]\).
- Réponse
-
\(1\)
Evaluer une expression
Dans les derniers exemples, nous avons simplifié les expressions en utilisant l'ordre des opérations. Nous allons maintenant évaluer certaines expressions, toujours en suivant l'ordre des opérations. Évaluer une expression signifie trouver la valeur de l'expression lorsque la variable est remplacée par un nombre donné.
Évaluer une expression signifie trouver la valeur de l'expression lorsque la variable est remplacée par un nombre donné.
Pour évaluer une expression, remplacez ce nombre par la variable de l'expression, puis simplifiez l'expression.
Évaluer\(7x - 4\), quand
- \(x = 5\)
- \(x = 1\)
- Réponse
-
1.
quand\(x = {\color{red}{5}}\) \(7x - 4\) \(7({\color{red}{5}}) - 4\) Multipliez. \(35 - 4\) Soustraire. \(31\) 2.
quand\(x = {\color{red}{1}}\) \(7x - 4\) \(7({\color{red}{1}}) - 4\) Multipliez. \(7 - 4\) Soustraire. \(3\)
Évaluer\(8x - 3\), quand
- \(x = 2\)
- \(x = 1\)
- Réponse
-
- \(13\)
- \(5\)
Évaluer\(4y - 4\), quand
- \(y = 3\)
- \(y = 5\)
- Réponse
-
- \(8\)
- \(16\)
Évaluer\(x = 4\), quand
- \(x^{2}\)
- \(3^{x}\)
- Réponse
-
1.
\(x^{2}\) Remplacez\(x\) par\({\color{red}{4}}\). \(({\color{red}{4}})^{2}\) Utilisez la définition de l'exposant. \(4\cdot 4\) Simplifiez. \(16\) 2.
\(3^{x}\) Remplacez\(x\) par\({\color{red}{4}}\). \(3^ (click for details)\)Callstack: at (Francais/Livre_:_Algèbre_élémentaire_(OpenStax)/01:_Fondations/1.03:_Utiliser_le_langage_de_l'algèbre), /content/body/div[4]/div[5]/div/dl/dd/table[2]/tbody/tr[2]/td[2]/span/span, line 1, column 1Utilisez la définition de l'exposant. \(3\cdot3\cdot3\cdot3\) Simplifiez. \(81\)
Évaluer\(x = 3\), quand
- \(x^{2}\)
- \(4^{x}\)
- Réponse
-
- \(9\)
- \(64\)
Évaluer\(x = 6\), quand
- \(x^{3}\)
- \(2^{x}\)
- Réponse
-
- \(216\)
- \(64\)
Évaluez\(2x^{2} + 3x + 8\) quand\(x = 4\).
- Réponse
-
\(2x^{2} + 3x + 8\) Substitut\(x = {\color{red}{4}}\). \(\small{2x^{2} + 3x + 8}\)
\(2({\color{red}{4}})^{2} + 3({\color{red}{4}}) + 8\)Suivez l'ordre des opérations. \(2(16)+3(4)+8\) \(32+12+8\) \(52\)
Évaluez\(3x^{2} + 4x + 1\) quand\(x = 3\).
- Réponse
-
\(40\)
Évaluez\(6x^{2} - 4x - 7\) quand\(x = 2\).
- Réponse
-
\(9\)
Identifier et combiner des termes similaires
Les expressions algébriques sont composées de termes. Un terme est une constante, ou le produit d'une constante et d'une ou plusieurs variables.
Un terme est une constante, ou le produit d'une constante et d'une ou plusieurs variables.
Des exemples de termes sont\(7, y, 5x^{2}, 9a\), et\(b^{5}\).
La constante qui multiplie la variable s'appelle le coefficient.
Le coefficient d'un terme est la constante qui multiplie la variable d'un terme.
Considérez le coefficient comme le nombre situé devant la variable. Le coefficient du terme\(3x\) est\(3\). Lorsque nous écrivons\(x\), le coefficient est\(1\), puisque\(x=1\cdot x\).
Identifiez le coefficient de chaque terme :
- \(14y\)
- \(15x^{2}\)
- \(a\)
- Réponse
-
- Le coefficient de\(14y\) est\(14\)
- Le coefficient de\(15x^{2}\) est\(15\)
- Le coefficient de\(a\) est\(1\) depuis\(a=1a\).
Identifiez le coefficient de chaque terme :
- \(17x\)
- \(41b^{2}\)
- \(z\)
- Réponse
-
- \(14\)
- \(41\)
- \(1\)
Identifiez le coefficient de chaque terme :
- \(9p\)
- \(13a^{2}\)
- \(y^{3}\)
- Réponse
-
- \(9\)
- \(13\)
- \(1\)
Certains termes ont des traits communs. Examinez les 6 termes suivants. Lesquels semblent avoir des traits communs ?
\[5x \qquad 7 \qquad n^{2} \qquad 4 \qquad 3x \qquad 9n^{2}\nonumber\]
Les\(7\) et les\(4\) sont tous deux des termes constants.
Les\(5x\) et les\(3x\) sont tous deux des termes avec\(x\).
Les\(n^{2}\) et les\(9n^{2}\) sont tous deux des termes avec\(n^{2}\).
Lorsque deux termes sont des constantes ou ont la même variable et le même exposant, nous disons que ce sont des termes similaires.
- \(7\)et\(4\) sont similaires à des termes.
- \(5x\)et\(3x\) sont similaires à des termes.
- \(x^{2}\)et\(9x^{2}\) sont similaires à des termes.
Les termes qui sont soit des constantes, soit des termes dont les mêmes variables sont augmentées aux mêmes puissances sont appelés termes similaires.
Identifiez les termes similaires :\(y^{3},7x^{2}, 14, 23, 4y^{3}, 9x, 5x^{2}\).
- Réponse
-
\(y^{3}\)et\(4y^{3}\) sont similaires à des termes parce que les deux ont\(y^{3}\) ; la variable et l'exposant correspondent.
\(7x^{2}\)et\(5x^{2}\) sont similaires à des termes parce que les deux ont\(x^{2}\) ; la variable et l'exposant correspondent.
\(14\)et\(23\) sont similaires à des termes parce que les deux sont des constantes.
Il n'y a pas d'autre terme comme\(9x\).
Identifiez les termes similaires :\(9, 2x^{3},y^{2}, 8x^{3}, 15, 9y, 11y^{2}\).
- Réponse
-
\(9\)et\(15\),\(y^{2}\) et\(11y^{2}\),\(2x^{3}\) et\(8x^{3}\)
Identifiez les termes similaires :\(4x^{3},8x^{2}, 19, 3x^{3}, 24, 6x^{3}\).
- Réponse
-
\(19\)et\(24\),\(8x^{2}\) et\(3x^{2}\),\(4x^{3}\) et\(6x^{3}\)
Identifiez les termes de chaque expression.
- \(9x^{2}+7x+12\)
- \(8x+3y\)
- Réponse
-
- Les termes de\(9x^{2}+7x+12\) sont\(9x^{2}, 7x\), et\(12\).
- Les termes de\(8x+3y\) sont\(8x\) et\(3y\).
Identifiez les termes de l'expression\(4x^{2}+5x+17\).
- Réponse
-
\(4x^{2}, 5x, 17\)
Identifiez les termes de l'expression\(5x+2y\).
- Réponse
-
\(5x, 2y\)
Si une expression contient des termes similaires, vous pouvez simplifier l'expression en combinant les termes similaires. À votre avis, qu'est-ce\(4x+7x+x\) qui simplifierait ? Si tu le pensais\(12x\), tu aurais raison !
\[\begin{array} { c } { 4 x + 7 x + x } \\ { x + x + x + x \quad + x + x + x + x + x + x + x \quad+ x } \\ { 12 x } \end{array}\]
Ajoutez les coefficients et conservez la même variable. Peu importe ce qu'est x : si vous avez 4 éléments de quelque chose et que vous en ajoutez 7 de plus, puis que vous en ajoutez 1 de plus, vous obtenez 12 d'entre eux. Par exemple, 4 oranges plus 7 oranges plus 1 orange font 12 oranges. Nous aborderons les propriétés mathématiques sous-jacentes à cela plus tard.
Simplifiez :\(4x+7x+x\)
Ajoutez les coefficients. \(12x\)
Simplifiez :\(2x^{2} + 3x + 7 + x^{2} + 4x + 5\)
- Réponse
-


Simplifiez :\(3x^{2} + 7x + 9 + 7x^{2} + 9x + 8\).
- Réponse
-
\(10x^{2}+16x+17\)
Simplifiez :\(4y^{2} + 5y + 2 + 8y^{2} + 4y + 5\).
- Réponse
-
\(12y^{2}+9y+7\)
- Identifiez les termes similaires.
- Réorganisez l'expression de manière à ce que les termes soient ensemble.
- Ajoutez ou soustrayez les coefficients et conservez la même variable pour chaque groupe de termes similaires.
Traduire une phrase anglaise en une expression algébrique
Dans la dernière section, nous avons répertorié de nombreux symboles d'opération utilisés en algèbre, puis nous avons traduit des expressions et des équations en phrases et expressions anglaises. Nous allons maintenant inverser le processus. Nous allons traduire des phrases anglaises en expressions algébriques. Les symboles et les variables dont nous avons parlé nous aideront à y parvenir. Le tableau les\(\PageIndex{7}\) résume.
| Opération | Expression | Expression |
|---|---|---|
| Ajout | \(a\)plus\(b\) la somme\(a\) et\(b\) \(a\) une augmentation de\(b\) \(b\) plus que\(a\) le total\(a\) des\(b\) \(b\)ajouté à\(a\) |
\[a+b\] |
| Soustraction | \(a\)moins\(b\) la différence de\(a\) et\(b\) \(a\) diminuée de\(b\) \(b\) moins que\(a\) \(b\) soustraite de\(a\) |
\[a−b\] |
| MULTIPLICATION | \(a\)fois\(b\) le produit de\(a\) et\(b\) deux fois\(a\) |
\[a\cdot b, ab, a(b), (a)(b)\] \[2a\] |
| Division | \(a\)divisé par\(b\) le quotient\(a\) et\(b\) le ratio de\(a\) et\(b\) \(b\) divisé en\(a\) |
\[a\div b, a/b, \frac{a}{b}, b \enclose{longdiv}{a}\] |
Examinez attentivement ces phrases à l'aide des quatre opérations suivantes :

Chaque phrase nous indique d'opérer sur deux nombres. Recherchez les mots de et et pour trouver les chiffres.
Traduisez chaque phrase anglaise en une expression algébrique :
- la différence entre\(17x\) et\(5\)
- le quotient de\(10x^{2}\) et\(7\).
- Réponse
-
- Le mot clé est différence, qui nous indique que l'opération est la soustraction. Recherchez les mots de et t pour trouver les nombres à soustraire.
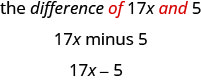
- Le mot clé est « quotient », qui nous indique que l'opération est la division.
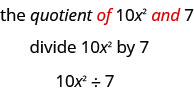
Cela peut également être écrit\(10x^{2}/7\) ou\(\dfrac{10x^{2}}{7}\).
- Le mot clé est différence, qui nous indique que l'opération est la soustraction. Recherchez les mots de et t pour trouver les nombres à soustraire.
Traduisez chaque phrase anglaise en une expression algébrique :
- la différence entre\(14x^{2}\) et\(13\)
- le quotient de\(12x\) et\(2\).
- Réponse
-
- \(14x^{2} - 13\)
- \(12x \div 2\)
Traduisez chaque phrase anglaise en une expression algébrique :
- la somme de\(17y^{2}\) et\(19\)
- le produit de\(7\) et\(y\).
- Réponse
-
- \(17y^{2} + 19\)
- \(7y\)
Quel âge auras-tu dans huit ans ? Quel âge fait huit ans de plus que votre âge actuel ? Avez-vous ajouté 8 à votre âge actuel ? Huit « plus que » signifie 8 ajoutés à votre âge actuel. Quel âge aviez-vous il y a sept ans ? C'est 7 ans de moins que ton âge maintenant. Vous soustrayez 7 de votre âge actuel. Sept « moins que » signifie 7 soustraits de votre âge actuel.
Traduisez la phrase anglaise en une expression algébrique :
- Dix-sept de plus\(y\)
- Neuf de moins que\(9x^{2}\).
- Réponse
-
- Les mots clés sont plus que. Ils nous disent que l'opération est un ajout. Plus que cela signifie « ajouté à ».
\(\begin{array} { c } { \text { Seventeen more than } y } \\ { \text { Seventeen added to } y } \\ { y + 17 } \end{array}\)
- Les mots clés sont inférieurs à. Ils nous disent de soustraire. Moins que signifie « soustrait de ».
\(\begin{array} { c } { \text { Nine less than } 9 x ^ { 2 } } \\ { \text { Nine subtracted from } 9 x ^ { 2 } } \\ { 9 x ^ { 2 } - 9 } \end{array}\)
- Les mots clés sont plus que. Ils nous disent que l'opération est un ajout. Plus que cela signifie « ajouté à ».
Traduisez la phrase anglaise en une expression algébrique :
- Onze de plus que x
- Quatorze de moins que\(11a\).
- Réponse
-
- \(x+11\)
- \(11a−14\)
Traduisez la phrase anglaise en une expression algébrique :
- \(13\)plus de\(z\)
- \(18\)inférieur à\(8x\).
- Réponse
-
1. \(z+13\)
2. \(8x−18\)
Traduisez la phrase anglaise en une expression algébrique :
- cinq fois la somme de\(m\) et\(n\)
- la somme de cinq fois\(m\) et\(n\).
- Réponse
-
Il y a deux mots d'opération : les temps nous indiquent de multiplier et la somme nous indique d'ajouter.
1. Comme nous\(5\) multiplions par la somme, nous avons besoin de parenthèses autour de la somme de\(m\) et\(n\),\((m+n)\). Cela nous oblige à déterminer d'abord la somme. (N'oubliez pas l'ordre des opérations.)\[\begin{array} { c } { \text { five times the sum of } m \text { and } n } \\ { 5 ( m + n ) } \end{array}\]
2. Pour faire la somme, nous cherchons les mots « de » et « et » pour voir ce qui est ajouté. Nous prenons ici la somme de cinq fois\(m\) et \ (n \.)\[\begin{array} { c } { \text { the sum of five times } m \text { and } n } \\ { 5 m + n } \end{array}\]
Traduisez la phrase anglaise en une expression algébrique :
- quatre fois la somme de\(p\) et\(q\)
- la somme de quatre fois\(p\) et\(q\).
- Réponse
-
- \(4(p+q)\)
- \(4p+q\)
Traduisez la phrase anglaise en une expression algébrique :
- la différence de deux fois x et\(8\),
- deux fois la différence entre x et\(8\).
- Réponse
-
- \(2x−8\)
- \(2(x−8)\)
Plus tard dans ce cours, nous appliquerons nos compétences en algèbre à la résolution d'applications. La première étape consistera à traduire une phrase anglaise en une expression algébrique. Nous verrons comment procéder dans les deux exemples suivants.
La longueur d'un rectangle est\(6\) inférieure à sa largeur. \(w\)Représentent la largeur du rectangle. Écrivez une expression pour la longueur du rectangle.
- Réponse
-
\[\begin{array} { l l } { \text { Write a phrase about the length of the rectangle. } } &{ 6 \text { less than the width } } \\ { \text { Substitute } w \text { for "the width." } } &{\text{6 less then w}} \\ { \text { Rewrite "less than" as "subtracted from." } } &{\text{6 subtracted from w}} \\ { \text { Translate the phrase into algebra. } } &{w - 6} \end{array}\]
La longueur d'un rectangle est\(7\) inférieure à sa largeur. \(w\)Représentent la largeur du rectangle. Écrivez une expression pour la longueur du rectangle.
- Réponse
-
\(w - 7\)
La largeur d'un rectangle est\(6\) inférieure à sa longueur. \(l\)Représentent la longueur du rectangle. Ecrivez une expression pour la largeur du rectangle.
- Réponse
-
\(l - 6\)
June a des pièces de dix cents dans son sac à main. Le nombre de pièces de dix cents est trois fois inférieur à quatre fois le nombre de trimestres. \(q\)Représentez le nombre de trimestres. Écrivez une expression pour le nombre de centimes.
- Réponse
-
\[\begin{array} { ll } { \text { Write the phrase about the number of dimes. } } &{\text{three less than four times the number of quarters}} \\ { \text { Substitute } q \text { for the number of quarters. } } &{\text{3 less than 4 times q}} \\ { \text { Translate "4 times } q \text { ." } } &{\text{3 less than 4q}} \\ { \text { Translate the phrase into algebra. } } &{\text{4q - 3}} \end{array}\]
Geoffrey a des pièces de dix cents en poche. Le nombre de pièces de dix cents est inférieur à quatre fois le nombre de trimestres. \(q\)Représentez le nombre de trimestres. Écrivez une expression pour le nombre de centimes.
- Réponse
-
\(4q - 8\)
Lauren a des pièces de dix cents dans son sac à main. Le nombre de dix cents est trois fois plus que sept fois supérieur à celui des pièces de cinq cents. \(n\)Représentent le nombre de nickels. Écrivez une expression pour le nombre de centimes.
- Réponse
-
\(7n + 3\)
Concepts clés
- Notation Le résultat est...
\(\begin{array} { l l } {\bullet \space a + b } &{ \text { the sum of } a \text { and } b } \\ { \bullet \space a - b } &{ \text { the difference of } a \text { and } b } \\ {\bullet\space a \cdot b , a b , ( a ) ( b ) ( a ) b , a ( b ) } &{ \text { the product of } a \text { and } b } \\ {\bullet\space a \div b , a / b , \frac { a } { b } , b ) \overline{a} } &{ \text { the quotient of } a \text { and } b } \end{array}\) - Inégalité
\(\begin{array} { l l } { \bullet \space a < b \text { is read "a is less than } b ^ { \prime \prime } } &{a \text { is to the left of } b \text { on the number line } } \\ { \bullet \space a > b \text { is read "a is greater than } b ^ { \prime \prime } } & { a \text { is to the right of } b \text { on the number line } } \end{array}\) - Mots, symboles d'inégalité
\(\begin{array} {ll} { \bullet a \neq b } &{ a \text { is not equal to } b } \\ { \bullet a < b } &{ a \text { is less than } b } \\ { \bullet a \leq b } &{ a \text { is less than or equal to } b } \\ { \bullet a > b } & { a \text { is greater than } b } \\ { \bullet a \geq b } & { a \text { is greater than or equal to } b } \end{array}\) - Regroupement de symboles
- Parenthèses ()
- Supports []
- Bretelles {}
- Notation exponentielle
- \(a^{n}\)désigne le produit des\(n\) facteurs de\(a\). L'expression\(a^{n}\) est lue\(a\) à la\(n^{th}\) puissance.
- Ordre des opérations : Lorsque vous simplifiez des expressions mathématiques, effectuez les opérations dans l'ordre suivant :
- Parenthèses et autres symboles de regroupement : simplifiez toutes les expressions entre parenthèses ou autres symboles de regroupement, en commençant par les parenthèses les plus internes.
- Exposants : simplifiez toutes les expressions à l'aide d'exposants.
- Multiplication et division : effectuez toutes les multiplications et divisions dans l'ordre, de gauche à droite. Ces opérations ont la même priorité.
- Addition et soustraction : effectuez toutes les additions et soustractions dans l'ordre, de gauche à droite. Ces opérations ont la même priorité.
- Combiner des termes similaires
- Identifiez les termes similaires.
- Réorganisez l'expression de manière à ce que les termes soient ensemble.
- Ajoutez ou soustrayez les coefficients et conservez la même variable pour chaque groupe de termes similaires.
Lexique
- coefficient
- Le coefficient d'un terme est la constante qui multiplie la variable d'un terme.
- constante
- Une constante est un nombre dont la valeur reste toujours la même.
- symbole de l'égalité
- Le symbole «\(=\) » est appelé signe égal. Nous\(a=b\) lisons «\(a\) est égal à »\(b\).
- équation
- Une équation est constituée de deux expressions reliées par un signe égal.
- évaluer une expression
- Évaluer une expression signifie trouver la valeur de l'expression lorsque la variable est remplacée par un nombre donné.
- expression
- Une expression est un nombre, une variable ou une combinaison de nombres et de variables utilisant des symboles d'opération.
- termes similaires
- Les termes qui sont soit des constantes, soit des termes dont les mêmes variables sont augmentées aux mêmes puissances sont appelés termes similaires.
- simplifier une expression
- Pour simplifier une expression, effectuez toutes les opérations qu'elle contient.
- terme
- Un terme est une constante ou le produit d'une constante et d'une ou plusieurs variables.
- variable
- Une variable est une lettre qui représente un nombre dont la valeur peut changer.


