Skip to main content
Global

1.2 : Introduction aux nombres entiers

  1. Last updated
  2. Save as PDF
  • Page ID
    195222

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage
    • À la fin de cette section, vous serez en mesure de :
    • Utiliser la valeur nominale avec des nombres entiers
    • Identifiez les multiples et appliquez des tests de divisibilité
    • Trouvez les factorisations principales et les multiples les moins courants

    Alors que nous commençons notre étude de l'algèbre élémentaire, nous devons rafraîchir certaines de nos compétences et de notre vocabulaire. Ce chapitre se concentrera sur les nombres entiers, les entiers, les fractions, les décimales et les nombres réels. Nous commencerons également à utiliser la notation et le vocabulaire algébriques.

    Utiliser la valeur de position avec des nombres entiers

    Les nombres les plus élémentaires utilisés en algèbre sont les nombres que nous utilisons pour compter les objets de notre monde :\(1, 2, 3, 4\), et ainsi de suite. C'est ce qu'on appelle le nombre de comptage s. Les nombres de comptage sont également appelés nombres naturels. Si nous ajoutons zéro aux nombres de comptage, nous obtenons l'ensemble des nombres entiers s.

    • Comptage des nombres :\(1, 2, 3, …\)
    • Nombres entiers :\(0, 1, 2, 3, …\)

    La notation «\(…\) » est appelée ellipse et signifie « et ainsi de suite », ou que le motif se poursuit à l'infini.

    Nous pouvons visualiser le comptage des nombres et des nombres entiers sur une ligne numérique (voir Figure\(\PageIndex{1}\)).

    Une ligne numérique horizontale avec des flèches à chaque extrémité et des valeurs comprises entre zéro et six s'étend au bas du diagramme. Une deuxième ligne horizontale avec une flèche orientée vers la gauche se trouve au-dessus de la première et s'étend de zéro à trois. Cette ligne est étiquetée « plus petite ». Une troisième ligne horizontale avec une flèche orientée vers la droite se trouve au-dessus des deux premières, mais va de trois à six et est étiquetée « plus grande ».
    Figure\(\PageIndex{1}\) : Les chiffres sur la ligne numérique grossissent lorsqu'ils vont de gauche à droite et diminuent lorsqu'ils vont de droite à gauche. Bien que cette ligne numérique ne montre que les\(0\) nombres entiers\(6\), les nombres continuent sans fin.

    L'activité Mathématiques manipulatrices « Ligne numérique, partie 1 » vous aidera à mieux comprendre le comptage des nombres et des nombres entiers.

    Notre système numérique est appelé système de valeurs de position, car la valeur d'un chiffre dépend de sa position dans un nombre. La figure\(\PageIndex{2}\) montre les valeurs de position. Les valeurs de position sont séparées en groupes de trois, appelés périodes. Les périodes sont des unes, des milliers, des millions, des milliards, des billions, etc. Dans un nombre écrit, des virgules séparent les points.

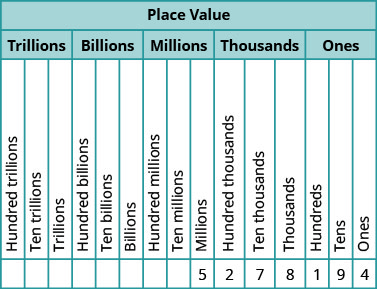
    Cette figure est un tableau illustrant le nombre 5 278 194 dans le système de valeurs de position. Le tableau est présenté avec une ligne d'en-tête, intitulée « Valeur de référence », divisée en une deuxième ligne d'en-tête intitulée « Trillions », « Billions », « Millions », « Millions », « Milliers » et « Unes ». Sous l'en-tête « Trillions » se trouvent trois colonnes étiquetées, écrites de bas en haut, sur lesquelles on peut lire « Cent billions », « Dix billions » et « Billions ». Sous l'en-tête « Billions » se trouvent trois colonnes étiquetées, écrites de bas en haut, sur lesquelles on peut lire « Cent milliards », « Dix milliards » et « Billions ». Sous l'en-tête « Millions » se trouvent trois colonnes étiquetées, écrites de bas en haut, sur lesquelles on peut lire « Cent millions », « Dix millions » et « Millions ». Sous l'en-tête « Milliers » se trouvent trois colonnes étiquetées, écrites de bas en haut, sur lesquelles on peut lire « Cent milliers », « Dix milliers » et « Milliers ». Sous l'en-tête « Un » se trouvent trois colonnes étiquetées, écrites de bas en haut, sur lesquelles on peut lire « Des centaines », « Des dizaines » et « Un ». De gauche à droite, sous les colonnes intitulées « Millions », « Cent milliers », « Dix milliers », « Des milliers », « Des centaines », « Des dizaines » et « Un », se trouvent les valeurs suivantes : 5, 2, 7, 8, 1, 9, 4. Cela signifie qu'il y en a 5 millions, 2 cents milliers, 7 dix mille, 8 000, 1 cent, 9 dizaines et 4 un au nombre de cinq millions deux cent soixante neuf mille cent nonante-quatre.
    Figure\(\PageIndex{2}\) : Le nombre\(5278194\) est indiqué sur le graphique. Le chiffre\(5\) est à la place des millions. Le chiffre\(2\) est à la centaine de milliers. Le chiffre\(7\) est à dix mille. Le chiffre\(8\) est à la place des milliers. Le chiffre\(1\) se trouve à la place des centaines. Le chiffre\(9\) se trouve à la dizaine. Le chiffre\(4\) est à la place d'un.
    Exercice\(\PageIndex{1}\)

    Dans le numéro\(63407218\), trouvez la valeur de position de chaque chiffre :

    1. \(7\)
    2. \(0\)
    3. \(1\)
    4. \(6\)
    5. \(3\)
    Réponse

    Placez le numéro dans le graphique des valeurs de position :

    Cette figure est un tableau illustrant le nombre 63 407 218 dans le système de valeurs de position. Le tableau est présenté avec une ligne d'en-tête, intitulée « Valeur de référence », divisée en une deuxième ligne d'en-tête intitulée « Trillions », « Billions », « Millions », « Millions », « Milliers » et « Unes ». Sous l'en-tête « Trillions » se trouvent trois colonnes étiquetées, écrites de bas en haut, sur lesquelles on peut lire « Cent billions », « Dix billions » et « Billions ». Sous l'en-tête « Billions » se trouvent trois colonnes étiquetées, écrites de bas en haut, sur lesquelles on peut lire « Cent milliards », « Dix milliards » et « Billions ». Sous l'en-tête « Millions » se trouvent trois colonnes étiquetées, écrites de bas en haut, sur lesquelles on peut lire « Cent millions », « Dix millions » et « Millions ». Sous l'en-tête « Milliers » se trouvent trois colonnes étiquetées, écrites de bas en haut, sur lesquelles on peut lire « Cent milliers », « Dix milliers » et « Milliers ». Sous l'en-tête « Un » se trouvent trois colonnes étiquetées, écrites de bas en haut, sur lesquelles on peut lire « Des centaines », « Des dizaines » et « Un ». De gauche à droite, sous les colonnes intitulées « Dix millions », « Millions », « Cent milliers », « Dix milliers », « Des milliers », « Des centaines », « Des dizaines » et « Un », se trouvent les valeurs suivantes : 6, 3, 4, 0, 7, 2, 1, 8. Cela signifie qu'il y en a 6 dix millions, 3 millions, 4 cents milliers, 10 000, 7 000, 2 cents, 1 dix et 8 sur un total de 63 millions, quatre cent sept mille, deux cent dix-huit.
    1. \(7\)Il y en a des milliers.
    2. \(0\)Il y en a dix mille.
    3. \(1\)Il se trouve à la dizaine.
    4. \(6\)Il est dans les dix millions.
    5. \(3\)Il y en a des millions.
    Exercice\(\PageIndex{2}\)

    Pour le numéro\(27493615\), trouvez la valeur de position de chaque chiffre :

    1. 2
    2. 1
    3. 4
    4. 7
    5. 5
    Réponse
    1. dix millions
    2. dizaines
    3. cent milliers
    4. millions
    5. uns
    Exercice\(\PageIndex{3}\)

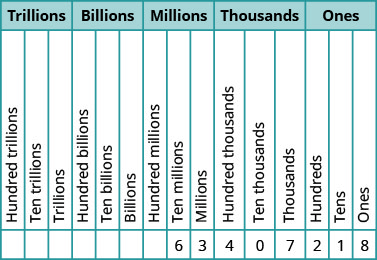
    Pour le numéro\(519711641328\), trouvez la valeur de position de chaque chiffre :

    1. 9
    2. 4
    3. 2
    4. 6
    5. 7
    Réponse
    1. milliards
    2. dix mille
    3. dizaines
    4. cent milliers
    5. cent millions

    Lorsque vous rédigez un chèque, vous écrivez le numéro en mots et en chiffres. Pour écrire un nombre en mots, inscrivez le nombre dans chaque période, suivi du nom de la période, sans le s à la fin. Commencez par la gauche, là où les périodes ont la plus grande valeur. La période des uns n'est pas nommée. Les virgules séparent les points. Ainsi, chaque fois qu'il y a une virgule dans le nombre, placez une virgule entre les mots (voir Figure\(\PageIndex{3}\)). Le nombre\(74218369\) s'écrit comme suit : soixante-quatorze millions, deux cent dix-huit mille, trois cent soixante-neuf.

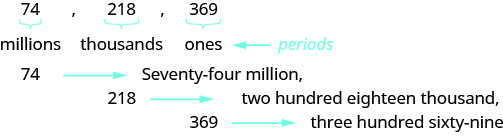
    Sur cette figure, les numéros 74, 218 et 369 sont listés dans une rangée, séparés par des virgules. Chaque chiffre comporte une parenthèse courbée en dessous avec le mot « millions » écrit sous le chiffre 74, « milliers » écrit sous le numéro 218 et « uns » écrit sous le chiffre 369. Une flèche orientée vers la gauche pointe vers ces trois mots, les qualifiant de « périodes ». Une rangée plus bas se trouve le chiffre « 74 », une flèche orientée vers la droite et les mots « 74 millions » suivis d'une virgule. La rangée suivante est le chiffre « 218 », une flèche orientée vers la droite et les mots « deux cent dix-huit mille » suivis d'une virgule. Sur la rangée du bas se trouvent le chiffre « 369 », une flèche orientée vers la droite et les mots « trois cent soixante-neuf ».
    Figurine\(\PageIndex{3}\)
    NOMMEZ UN NOMBRE ENTIER EN MOTS.
    1. Commencez par la gauche et nommez le numéro de chaque période, suivi du nom de la période.
    2. Mettez des virgules dans le nombre pour séparer les points.
    3. Ne nommez pas la période de ceux.
    Exercice\(\PageIndex{4}\)

    Nommez le numéro\(8165432098710\) en utilisant des mots.

    Réponse

    Nommez le numéro de chaque période, suivi du nom de la période.

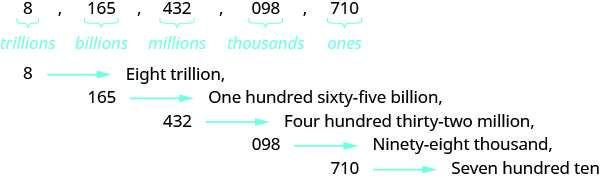
    Sur cette figure, les numéros 8, 165, 432, 098 et 710 sont listés dans une rangée, séparés par des virgules. Chaque chiffre a un crochet horizontal en dessous avec le mot « billions » écrit sous le chiffre 8, « milliards » écrit sous le chiffre 165, « millions » écrit sous le chiffre 432, « milliers » écrit sous le chiffre 098 et « uns » écrit sous le chiffre 710. Une rangée plus bas se trouve le chiffre 8, une flèche orientée vers la droite et les mots « Huit billions » suivis d'une virgule. Sur la rangée suivante se trouve le chiffre 165, une flèche orientée vers la droite et les mots « Cent soixante-cinq milliards » suivis d'une virgule. Sur la rangée suivante se trouve le chiffre 432, une flèche orientée vers la droite et les mots « Quatre cent trente-deux millions » suivis d'une virgule. Sur la rangée suivante se trouve le chiffre « 098 », une flèche orientée vers la droite et les mots « 98 000 » suivis d'une virgule. Sur la rangée du bas se trouvent le chiffre 710, une flèche orientée vers la droite et les mots « Sept cent dix ».

    Insérez des virgules pour séparer les points.

    Ainsi,\(8165432098710\) il est nommé comme huit billions, cent soixante-cinq milliards, quatre cent trente-deux millions, quatre-vingt-dix-huit mille, sept cent dix.

    Exercice\(\PageIndex{5}\)

    Nommez le numéro 9 258 137 904 0619 258 137 904 061 en utilisant des mots.

    Réponse

    neuf billions, deux cent 58 milliards, cent trente-sept millions, neuf cent quatre mille soixante et un

    Exercice\(\PageIndex{6}\)

    Nommez le numéro 17 864 325 619 00417 864 325 619 004 en utilisant des mots.

    Réponse

    dix-sept billions, huit cent soixante-quatre milliards, trois cent vingt-cinq millions, six cent dix-neuf mille quatre

    Nous allons maintenant inverser le processus en écrivant les chiffres du nom du numéro. Pour écrire le nombre en chiffres, nous cherchons d'abord les mots indices qui indiquent les points. Il est utile de dessiner trois espaces pour les périodes requises, puis de les remplir avec les chiffres, en séparant les points par des virgules.

    ÉCRIVEZ UN NOMBRE ENTIER À L'AIDE DE CHIFFRES.
    1. Identifiez les mots qui indiquent des périodes. (N'oubliez pas que la période des uns n'est jamais nommée.)
    2. Tracez trois blancs pour indiquer le nombre de places nécessaires pour chaque période. Séparez les points par des virgules.
    3. Nommez le numéro de chaque période et placez les chiffres à la bonne position.
    Exercice\(\PageIndex{7}\)

    Écrivez neuf milliards, deux cent quarante six millions, treize mille, cent quatre vingt neuf sous forme de nombre entier en utilisant des chiffres.

    Réponse

    Identifiez les mots qui indiquent des périodes.
    À l'exception de la première période, toutes les autres périodes doivent avoir trois places. Tracez trois blancs pour indiquer le nombre de places nécessaires pour chaque période. Séparez les points par des virgules.
    Écrivez ensuite les chiffres de chaque période.

    Une image comporte deux lignes de texte. Les lignes supérieures indiquent « neuf milliards », suivi d'une virgule, et « deux cent quarante six millions », également suivi d'une virgule. Les mots « milliard » et « million » sont soulignés et chaque phrase est entourée d'un crochet arrondi. Les lignes inférieures se lisent « 73 mille », suivi d'une virgule, et « cent quatre-vingt neuf ». Le mot « mille » est souligné et chaque phrase est encadrée d'un crochet.

    Le nombre est 9 246 073 189.
    Exercice\(\PageIndex{8}\)

    Écrivez le nombre deux milliards, quatre cent soixante-six millions, sept cent quatorze mille cinquante et un comme un nombre entier en utilisant des chiffres.

    Réponse

    2 466 714 051

    Exercice\(\PageIndex{9}\)

    Écrivez le nombre onze milliards, neuf cent vingt et un millions, huit cent trente mille, cent six comme un nombre entier en utilisant des chiffres.

    Réponse

    11 921 830 106

    En 2013, le Bureau du recensement des États-Unis a estimé la population de l'État de New York à 19 651 127 habitants. On pourrait dire que la population de New York était d'environ 20 millions d'habitants. Dans de nombreux cas, vous n'avez pas besoin de la valeur exacte ; un nombre approximatif suffit.

    Le processus d'approximation d'un nombre est appelé arrondi. Les nombres sont arrondis à une valeur décimale spécifique, en fonction de la précision requise. Dire que la population de New York est d'environ 20 millions d'habitants signifie que nous avons arrondi à des millions d'habitants.

    Exercice\(\PageIndex{10}\) How to Round Whole Numbers

    Arrondissez 23 658 à la centaine la plus proche.

    Réponse

    Cette figure est un tableau composé de trois colonnes et de quatre lignes. La première colonne est une colonne d'en-tête qui contient les noms et les numéros de chaque étape. La deuxième colonne contient d'autres instructions écrites. La troisième colonne contient les numéros correspondant aux étapes et aux instructions écrites. Dans la rangée supérieure, la première cellule indique : « Étape 1. Localisez la valeur de position donnée à l'aide d'une flèche. Tous les chiffres situés à gauche ne changent pas. » Dans la deuxième cellule, les instructions disent : « Localisez les centaines de places sur 23 658 ». Dans la troisième cellule, il y a le chiffre 23 658 avec une flèche pointant vers le chiffre 6, l'étiquetant « centaines de places ».Une ligne plus bas, les instructions de la première cellule indiquent : « Étape 2. Soulignez le chiffre situé à droite de la valeur de position donnée. » Dans la deuxième cellule, les instructions disent : « Soulignez le 5, qui se trouve à droite de la place des centaines ». Dans la troisième cellule, il y a à nouveau le chiffre 23 658, la même flèche pointant vers le chiffre 6, lui indiquant la centaine. Le 5 est également souligné dans cette case.Une ligne plus bas, la première cellule indique : « Étape 3. Ce chiffre est-il supérieur ou égal à 5 ? Oui : ajoutez 1 au chiffre dans la valeur de position donnée. Non, ne modifiez pas le chiffre dans la valeur de position spécifiée. » Dans la deuxième cellule, les instructions disent : « Ajoutez 1 aux 6 à la place des centaines, puisque 5 est supérieur ou égal à 5 ». La troisième cellule contient à nouveau le numéro 23 658, avec une flèche pointant vers le chiffre 6 et le texte « ajouter 1 ». Il y a également une parenthèse courbée sous les chiffres 5 et 8, avec une flèche pointant vers eux et le texte « remplacer par des 0 ».Dans la rangée du bas, la première cellule indique : « Étape 4. Remplacez tous les chiffres situés à droite de la valeur de position donnée par des zéros. Donc, 23 700 sont arrondis à la centaine la plus proche. » Dans la deuxième cellule, les instructions indiquent : « Remplacez tous les chiffres situés à droite de la centaine par des zéros ». La troisième cellule contient le nombre 23 700, que nous avons atteint en arrondissant le nombre 23 658 à la centaine la plus proche.

    Exercice\(\PageIndex{11}\)

    Arrondir à la centaine la plus proche : 17 852

    Réponse

    17 900

    Exercice\(\PageIndex{12}\)

    Arrondir à la centaine la plus proche : 468 751.

    Réponse

    468 800

    NOMBRES ENTIERS ARRONDIS.
    1. Localisez la valeur de position donnée et marquez-la avec une flèche. Tous les chiffres situés à gauche de la flèche ne changent pas.
    2. Soulignez le chiffre situé à droite de la valeur de position donnée.
    3. Ce chiffre est-il supérieur ou égal à 5 ?
      • Oui : ajoutez 11 au chiffre situé dans la valeur de position donnée.
      • Non : ne modifiez pas le chiffre dans la valeur de position spécifiée.
    4. Remplacez tous les chiffres situés à droite de la valeur de position donnée par des zéros.
    Exercice\(\PageIndex{13}\)

    Arrondissez 103 978 103 978 au plus proche :

    1. cent
    2. mille
    3. dix mille
    Réponse
    1.
    Localisez la centaine sur 103 978. .
    Soulignez le chiffre situé à droite de la place des centaines. .
    Puisque 7 est supérieur ou égal à 5, ajoutez 1 au 9. Remplacez tous les chiffres situés à droite de la centaine par des zéros. .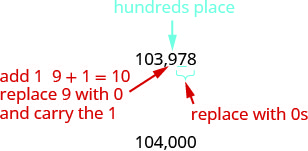
      Ainsi, 104 000 sont 103 978 arrondis à la centaine la plus proche.
    2.
    Repérez la place des milliers et soulignez le chiffre situé à droite de la place des milliers. .
    Puisque 9 est supérieur ou égal à 5, ajoutez 1 au 3. Remplacez tous les chiffres situés à droite de la centaine par des zéros. .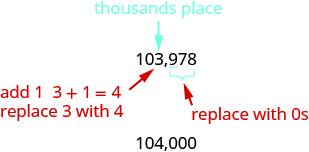
      Ainsi, 104 000 sont 103 978 arrondis au millier le plus proche.
    3.
    Repérez la place des dix mille et soulignez le chiffre situé à droite de la place des dix mille. .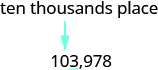
    Puisque 3 est inférieur à 5, nous laissons le 0 tel quel, puis nous remplaçons les chiffres à droite par des zéros. .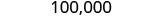
      Ainsi, 100 000 sont 103 978 arrondis à la dizaine de mille la plus proche.
    Exercice\(\PageIndex{14}\)

    Environ 206 981 au plus proche : 1 cent 2 mille 3 dix mille.

    Réponse
    1. 207 000
    2. 207 000
    3. 210 000
    Exercice\(\PageIndex{15}\)

    Environ 784 951 au plus proche : 1 cent 2 mille 3 dix mille.

    Réponse
    1. 785 000
    2. 785 000
    3. 780 000

    Identifier les multiples et appliquer des tests de divisibilité

    Les nombres 2, 4, 6, 8, 10 et 12 sont appelés multiples de 2. Un multiple de 2 peut être écrit comme le produit d'un nombre de comptage et de 2.

    Un diagramme composé de deux rangées de chiffres. La rangée du haut indique « 2, 4, 6, 8, 10, 12 », suivi d'une elipsis. En dessous de 2 est 2 fois 1, en dessous de 4 est 2 fois 2, en dessous de 6 est 2 fois 3, en dessous de 8 est 2 fois 4, en dessous de 10 est 2 fois 5 et en dessous de 12 est 2 fois 6.
    Figurine\(\PageIndex{4}\)

    De même, un multiple de 3 serait le produit d'un nombre de comptage et de 3.

    Un diagramme composé de deux rangées de chiffres. La rangée du haut indique « 3, 6, 9, 12, 15, 18 », suivi d'une elipsis. En dessous de 3 est 3 fois 1, en dessous de 6 est 3 fois 2, en dessous de 9 est 3 fois 3, en dessous de 12 est 3 fois 4, en dessous de 15 est 3 fois 5 et en dessous de 18 est 3 fois 6.
    Figurine\(\PageIndex{5}\)

    Nous pourrions trouver les multiples de n'importe quel nombre en continuant ce processus.

    Remarque

    L'activité « Multiples » des mathématiques manipulatrices vous aidera à mieux comprendre les multiples.

    Le tableau\(\PageIndex{1}\) montre les multiples de 2 à 9 pour les 12 premiers nombres de comptage.

    Nombre de comptage 1 2 3 4 5 6 7 8 9 10 11 12
    Multiples de 2 2 4 6 8 10 12 14 16 18 20 22 24
    Multiples de 3 3 6 9 12 15 18 21 24 27 30 33 36
    Multiples de 4 4 8 12 16 20 24 28 32 36 40 44 48
    Multiples de 5 5 10 15 20 25 30 35 40 45 50 55 60
    Multiples de 6 6 12 18 24 30 36 42 48 54 60 66 72
    Multiples de 7 7 14 21 28 35 42 49 56 63 70 77 84
    Multiples de 8 8 16 24 32 40 48 56 64 72 80 88 96
    Multiples de 9 9 18 27 36 45 54 63 72 81 90 99 108
    Multiples de 10 10 20 30 40 50 60 70 80 90 100 110 120
    Tableau\(\PageIndex{1}\)
    MULTIPLE D'UN NOMBRE

    Un nombre est un multiple de\(n\) s'il est le produit d'un nombre de comptage et\(n\).

    Une autre façon de dire que 15 est un multiple de 3 est de dire que 15 est divisible par 3. Cela signifie que lorsque nous divisons 3 en 15, nous obtenons un nombre de comptage. En fait,\(15\div 3\) c'est 5, donc 15 l'est\(5\cdot3\).

    DIVISIBLE PAR UN NOMBRE

    Si un nombre\(m\) est un multiple de\(n\), alors\(m\) est divisible par\(n\)

    Regardez les multiples de\(5\) dans le tableau\(\PageIndex{1}\). Ils se terminent tous par 5 ou 0. Les nombres dont le dernier chiffre est 5 ou 0 sont divisibles par 5. En recherchant d'autres modèles dans le tableau\(\PageIndex{1}\) qui montre des multiples des nombres 2 à 9, nous pouvons découvrir les tests de divisibilité suivants :

    TESTS DE DIVISIBILITÉ

    Un nombre est divisible par :

    • 2 si le dernier chiffre est 0, 2, 4, 6 ou 8.
    • 3 si la somme des chiffres est divisible par 3.
    • 5 si le dernier chiffre est 5 ou 0.
    • 6 s'il est divisible à la fois par 2 et par 3.
    • 10 s'il se termine par 0.
    Exercice\(\PageIndex{16}\)

    Est-ce que 5625 est divisible par 2 ? Par 3 ans ? D'ici 5 ans ? À 6 ans ? D'ici 10 ans ?

    Réponse

    \[\begin{array} {ll} {\text{Is 5625 divisible by 2?}} &{} \\ {\text{Does it end in 0, 2, 4, 6, or 8?}} &{\text{No.}} \\ {} &{\text{5625 is not divisible by 2.}} \end{array}\]

    \[\begin{array} {ll} {\text{Is 5625 divisible by 3?}} &{} \\ {\text{What is the sum of the digits?}} &{5 + 6 + 2 + 5 = 18} \\ {\text{Is the sum divisible by 3?}} &{\text{Yes, 5625 is divisible by 3.}} \end{array}\]

    \[\begin{array} {ll} {\text{Is 5625 divisible by 5 or 10?}} &{} \\ {\text{What is the last digit? It is 5.}} &{\text{5625 is divisible by 5 but not by 10.}} \end{array}\]

    \[\begin{array} {ll} {\text{Is 5625 divisible by 6?}} &{} \\ {\text{Is it divisible by both 2 and 3?}} &{\text{No, 5625 is not divisible by 2, so 5625 is }} \\ {} &{\text{not divisible by 6.}}\end{array}\]

    Exercice\(\PageIndex{17}\)

    Déterminez si 4 962 sont divisibles par 2, par 3, par 5, par 6 et par 10.

    Réponse

    par 2, 3 et 6

    Exercice\(\PageIndex{18}\)

    Déterminez si 3 765 sont divisibles par 2, par 3, par 5, par 6 et par 10.

    Réponse

    par 3 et 5

    Trouvez les factorisations principales et les multiples les moins courants

    En mathématiques, il existe souvent plusieurs manières de parler des mêmes idées. Jusqu'à présent, nous avons vu que\(m\) c'est un multiple de\(n\), on peut dire que\(m\) c'est divisible par\(n\). Par exemple, puisque 72 est un multiple de 8, nous disons que 72 est divisible par 8. Puisque 72 est un multiple de 9, on dit que 72 est divisible par 9. Nous pouvons exprimer cela d'une autre manière encore.

    Puisque\(8\cdot 9=72\), on dit que 8 et 9 sont des facteurs de 72. Lorsque nous écrivons\(72=8\cdot 9\), nous disons que nous avons pris en compte 72.

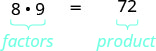
    Une image montre l'équation 8 fois 9 égale 72. En dessous de l'expression 8 fois 9 se trouve un crochet et le mot « facteurs » tandis qu'il est écrit en dessous de 72 se trouve un crochet horizontal et le mot « produit ».
    Figurine\(\PageIndex{6}\)

    Les autres moyens de factoriser 72 sont\(1\cdot 72\)\(2\cdot 36\),\(3\cdot 24\),\(4\cdot 18\) et\(6\cdot 12\). Soixante-douze ont de nombreux facteurs : 1, 2, 3, 4, 6, 8, 9, 12, 18, 36 et 72.

    FACTEURS

    Si\(a\cdot b=m\), alors\(a\) et\(b\) sont des facteurs de\(m\).

    Certains nombres, comme 72, ont de nombreux facteurs. Les autres chiffres n'ont que deux facteurs.

    Remarque

    L'activité de mathématiques manipulatrices « Multiplication et factorisation de modèles » vous aidera à mieux comprendre la multiplication et la factorisation.

    NOMBRE PREMIER ET NOMBRE COMPOSÉ

    Un nombre premier est un nombre de comptage supérieur à 1, dont les seuls facteurs sont 1 et lui-même.

    Un nombre composé est un nombre de comptage qui n'est pas premier. Un nombre composé possède des facteurs autres que 1 et lui-même.

    Remarque

    L'activité de mathématiques manipulatrices « Nombres premiers » vous aidera à mieux comprendre les nombres premiers.

    Les nombres de comptage de 2 à 19 sont répertoriés dans la figure\(\PageIndex{7}\), avec leurs facteurs. Assurez-vous d'être d'accord avec l'étiquette « principale » ou « composite » pour chacun d'entre eux !

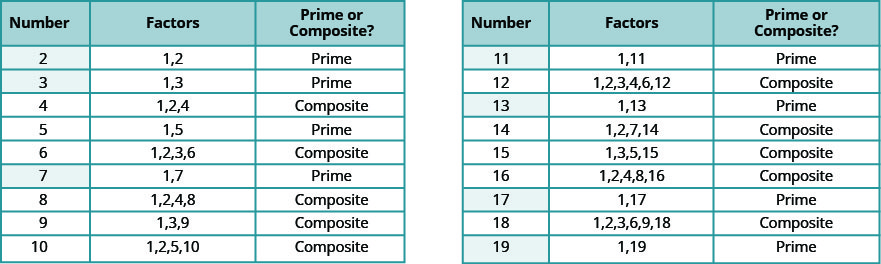
    Un tableau comportant onze lignes et sept colonnes est présenté. La première ligne est une ligne d'en-tête, et chaque cellule étiquette le contenu de la colonne située en dessous. Dans la ligne d'en-tête, les trois premières cellules se lisent de gauche à droite « Nombre », « Facteurs » et « Premier ou composite ? » La quatrième colonne est entièrement vide. Les trois dernières cellules se lisent de gauche à droite « Nombre », « Facteur » et « Premier ou composite ? » encore une fois. Dans chaque ligne suivante, la première cellule contient un nombre, la seconde contient ses facteurs et la troisième indique si le nombre est premier ou composite. Les trois colonnes à gauche de la colonne centrale vide contiennent ces informations pour les numéros 2 à 10, et les trois colonnes à droite de la colonne centrale vide contiennent ces informations pour les numéros 11 à 19. Sur le côté gauche de la colonne vide, dans la première ligne en dessous de la ligne d'en-tête, les cellules se lisent de gauche à droite : « 2 », « 1,2 » et « Prime ». Dans la rangée suivante, les cellules se lisent de gauche à droite : « 3 », « 1,3 » et « Prime ». Dans la rangée suivante, les cellules se lisent de gauche à droite : « 4 », « 1,2,4 » et « Composite ». Dans la rangée suivante, les cellules se lisent de gauche à droite : « 5 », « 1,5 » et « Prime ». Dans la rangée suivante, les cellules se lisent de gauche à droite : « 6 », « 1,2,3,6 » et « Composite ». Dans la rangée suivante, les cellules se lisent de gauche à droite : « 7 », « 1,7 » et « Prime ». Dans la rangée suivante, les cellules se lisent de gauche à droite : « 8 », « 1,2,4,8 » et « Composite ». Dans la rangée suivante, les cellules se lisent de gauche à droite : « 9 », « 1,3,9 » et « Composite ». Dans la rangée du bas, les cellules se lisent de gauche à droite : « 10 », « 1,2,5,10 » et « Composite ». Sur le côté droit de la colonne vide, dans la première ligne en dessous de la ligne d'en-tête, les cellules se lisent de gauche à droite : « 11 », « 1,11 » et « Prime ». Dans la rangée suivante, les cellules se lisent de gauche à droite : « 12 », « 1,2,3,4,6,12 » et « Composite ». Dans la rangée suivante, les cellules se lisent de gauche à droite : « 13 », « 1,13 » et « Prime ». Dans la rangée suivante, les cellules se lisent de gauche à droite « 14 », « 1,2,7,14 » et « Composite ». Dans la rangée suivante, les cellules se lisent de gauche à droite : « 15 », « 1,3,5,15 » et « Composite ». Dans la rangée suivante, les cellules se lisent de gauche à droite : « 16 », « 1,2,4,8,16 » et « Composite ». Dans la rangée suivante, les cellules se lisent de gauche à droite : « 17 », « 1,17 » et « Prime ». Dans la rangée suivante, les cellules se lisent de gauche à droite : « 18 », « 1,2,3,6,9,18 » et « Composite ». Dans la rangée du bas, les cellules se lisent de gauche à droite : « 19 », « 1,19 » et « Prime ».
    Figurine\(\PageIndex{7}\)

    Les nombres premiers s inférieurs à 20 sont 2, 3, 5, 7, 11, 13, 17 et 19. Notez que le seul nombre premier pair est 2.

    Un nombre composé peut être écrit comme un produit unique de nombres premiers. C'est ce que l'on appelle la factorisation première du nombre. Il sera utile de trouver la factorisation première d'un nombre composé plus loin dans ce cours.

    FACTORISATION PRIMAIRE

    La factorisation en nombres premiers d'un nombre est le produit des nombres premiers qui sont égaux au nombre.

    Pour déterminer la factorisation première d'un nombre composé, trouvez deux facteurs quelconques du nombre et utilisez-les pour créer deux branches. Si un facteur est premier, cette branche est complète. Encerclez ce prime !

    Si le facteur n'est pas premier, trouvez deux facteurs du nombre et poursuivez le processus. Une fois que toutes les branches ont encerclé des nombres premiers à la fin, la factorisation est terminée. Le nombre composé peut désormais être écrit comme un produit de nombres premiers.

    Exercice\(\PageIndex{19}\)

    Facteur 48.

    Réponse

    Cette figure est un tableau composé de trois colonnes et de quatre lignes. La première colonne est une colonne d'en-tête qui contient les noms et les numéros de chaque étape. La deuxième colonne contient d'autres instructions écrites et quelques calculs. La troisième colonne contient la plupart des travaux mathématiques correspondant aux étapes et aux instructions écrites. Dans la rangée supérieure, la première cellule indique : « Étape 1. Trouvez deux facteurs dont le produit est le nombre donné. Utilisez ces chiffres pour créer deux branches. » La deuxième cellule contient l'équation algébrique 48 égale 2 fois 24. Dans la troisième cellule, il y a un arbre de facteurs avec 48 en haut. Deux branches descendent de 48 et se terminent respectivement en 2 et 24.Une ligne plus bas, les instructions de la première cellule indiquent : « Étape 2. Si un facteur est premier, cette branche est complète. Encerclez le premier. » Dans la deuxième cellule, les instructions indiquent : « 2 est le premier. Encerclez le premier. » Dans la troisième cellule, l'arbre de facteurs de l'étape 1 est répété, mais le 2 au bas de l'arbre est maintenant encerclé.Une ligne plus bas, la première cellule indique : « Étape 3. Si un facteur n'est pas premier, écrivez-le comme le produit de deux facteurs et poursuivez le processus. » Dans la deuxième cellule, les instructions indiquent : « 24 n'est pas le premier. Divisez-le en deux autres facteurs. » La troisième cellule contient l'arbre factoriel d'origine, avec 48 en haut et deux branches pointant vers le bas se terminant par 2, qui est souligné, et 24. Deux autres branches descendent de 24 et se terminent respectivement à 4 et 6. Une ligne plus bas, les instructions au milieu de la cellule indiquent « 4 et 6 ne sont pas les premiers ». Divisez-les chacun en deux facteurs. » Dans la cellule de droite, l'arbre des facteurs est répété une fois de plus. Deux branches descendent de la 4 et se terminent en 2 et 2. Les deux 2 sont encerclés. Deux autres branches descendent de la 6 et se terminent en a 2 et en 3, qui sont toutes deux encerclées. Les instructions sur la gauche indiquent « 2 et 3 sont les meilleurs, alors encerclez-les ».Dans la rangée du bas, la première cellule indique : « Étape 4. Écrivez le nombre composé comme le produit de tous les nombres premiers encerclés. » La deuxième cellule est laissée vide. La troisième cellule contient l'équation algébrique 48 égale 2 fois 2 fois 2 fois 2 fois 2 fois 3.

    Nous disons que\(2\cdot 2\cdot 2\cdot 2\cdot 3\) c'est la factorisation première de 48. Nous écrivons généralement les nombres premiers par ordre croissant. N'oubliez pas de multiplier les facteurs pour vérifier votre réponse !

    Si nous avons d'abord factorisé 48 d'une manière différente, par exemple\(6\cdot 8\), le résultat serait toujours le même. Terminez la factorisation des matières premières et vérifiez-la par vous-même.

    Exercice\(\PageIndex{20}\)

    Détermine la factorisation première de 80.

    Réponse

    \(2\cdot 2\cdot 2\cdot 2\cdot 5\)

    Exercice\(\PageIndex{21}\)

    Détermine la factorisation première de 60.

    Réponse

    \(2\cdot 2\cdot 3\cdot 5\)

    TROUVEZ LA FACTORISATION PREMIÈRE D'UN NOMBRE COMPOSÉ.
    1. Trouvez deux facteurs dont le produit est le nombre donné et utilisez ces nombres pour créer deux branches.
    2. Si un facteur est premier, cette branche est complète. Encerclez la fleur, comme un bourgeon sur l'arbre.
    3. Si un facteur n'est pas premier, écrivez-le comme le produit de deux facteurs et poursuivez le processus.
    4. Écrivez le nombre composé comme le produit de tous les nombres premiers encerclés.
    Exercice\(\PageIndex{22}\)

    Trouvez la factorisation première de 252.

    Réponse
    Étape 1 Trouvez deux facteurs dont le produit est 252. 12 et 21 ne sont pas premiers.

    Divisez 12 et 21 en deux autres facteurs. Continuez jusqu'à ce que tous les nombres premiers soient pris en compte.    		 .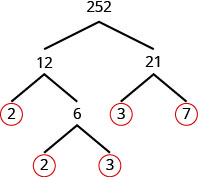
    Étape 2 Ecrivez 252 comme le produit de tous les nombres premiers encerclés.

    \(252=2\cdot 2\cdot 3\cdot 3\cdot 7\)
    Exercice\(\PageIndex{23}\)

    Détermine la factorisation première de 126.

    Réponse

    \(2\cdot 3\cdot 3\cdot 7\)

    Exercice\(\PageIndex{24}\)

    Trouvez la factorisation première de 294.

    Réponse

    \(2\cdot 3\cdot 7\cdot 7\)

    L'une des raisons pour lesquelles nous examinons les multiples et les nombres premiers est d'utiliser ces techniques pour trouver le multiple le moins courant de deux nombres. Cela sera utile lorsque nous additionnerons et soustrayons des fractions ayant des dénominateurs différents. Deux méthodes sont utilisées le plus souvent pour trouver le multiple le moins courant et nous les examinerons toutes les deux.

    La première méthode est la méthode Listing Multiples. Pour trouver le multiple le moins courant de 12 et 18, nous listons les premiers multiples de 12 et 18 :

    Deux rangées de chiffres sont affichées. La première ligne commence par 12, suivi de deux points, puis de 12, 24, 36, 48, 60, 72, 84, 96, 108 et d'un elipsis. 36, 72 et 108 sont en gras écrits en rouge. La deuxième rangée commence par 18, suivie d'un deux-points, puis de 18, 36, 54, 72, 90, 108 et d'un elipsis. Encore une fois, les chiffres 36, 72 et 108 sont écrits en gras en rouge. Sur la ligne ci-dessous se trouve l'expression « Multiples communs », deux points et les chiffres 36, 72 et 108, écrits en rouge. Une ligne ci-dessous se trouve la phrase « Multiple le moins commun », deux points et le chiffre 36, écrit en bleu.
    Figurine\(\PageIndex{8}\)

    Notez que certains numéros apparaissent dans les deux listes. Ce sont les multiples communs de 12 et 18.

    Nous voyons que les premiers multiples communs de 12 et 18 sont 36, 72 et 108. Comme 36 est le plus petit des multiples communs, nous l'appelons le plus petit multiple commun. Nous utilisons souvent l'abréviation LCM.

    MULTIPLE LE MOINS COURANT

    Le plus petit multiple commun (LCM) de deux nombres est le plus petit nombre qui est un multiple des deux nombres.

    L'encadré de procédure répertorie les étapes à suivre pour trouver le LCM en utilisant la méthode des facteurs premiers que nous avons utilisée ci-dessus pour 12 et 18.

    TROUVEZ LE MULTIPLE LE MOINS COURANT EN LISTANT LES MULTIPLES.
    1. Dressez la liste de plusieurs multiples de chaque numéro.
    2. Recherchez le plus petit nombre figurant sur les deux listes.
    3. Ce numéro est le LCM.
    Exercice\(\PageIndex{25}\)

    Trouvez le multiple le moins courant de 15 et 20 en listant les multiples.

    Réponse
    Faites des listes des premiers multiples de 15 et de 20, et utilisez-les pour trouver le multiple le moins courant. .
    Recherchez le plus petit nombre figurant dans les deux listes. Le premier chiffre qui apparaît sur les deux listes est 60, donc 60 est le multiple le moins courant de 15 et 20.

    Notez que 120 figure également dans les deux listes. C'est un multiple commun, mais ce n'est pas le multiple le moins courant.

    Exercice\(\PageIndex{26}\)

    Trouvez le multiple le moins courant en listant les multiples : 9 et 12.

    Réponse

    \(36\)

    Exercice\(\PageIndex{27}\)

    Trouvez le multiple le moins courant en listant les multiples : 18 et 24.

    Réponse

    \(72\)

    Notre deuxième méthode pour trouver le multiple le moins courant de deux nombres consiste à utiliser la méthode des facteurs premiers. Trouvons à nouveau le LCM de 12 et 18, cette fois en utilisant leurs facteurs premiers.

    Exercice\(\PageIndex{28}\)

    Déterminez le multiple le moins commun (LCM) de 12 et 18 à l'aide de la méthode des facteurs premiers.

    Réponse

    Cette figure est un tableau composé de trois colonnes et de quatre lignes. La première colonne est une colonne d'en-tête qui contient les noms et les numéros de chaque étape. La deuxième colonne contient d'autres instructions écrites et quelques calculs. La troisième colonne contient la plupart des travaux mathématiques correspondant aux étapes et aux instructions écrites. Dans la rangée supérieure, la première cellule indique : « Étape 1. Écrivez chaque nombre comme un produit de nombres premiers. » La deuxième cellule est laissée vide. Dans la troisième cellule, il y a deux arbres factoriels. Dans le premier arbre factoriel, deux branches descendent de 18 et se terminent respectivement en 3 et 6. Le 3 est premier et donc encerclé. Deux autres branches descendent de la 6 et se terminent en 2 et 3, toutes deux encerclées. Dans le second arbre factoriel, deux branches descendent de 12 et se terminent en 3 et 4. Le 3 est encerclé. Deux autres branches descendent de 4 et se terminent en 2 et 2, toutes deux encerclées.Une ligne plus bas, les instructions de la première cellule indiquent : « Étape 2. Répertoriez les nombres premiers de chaque nombre. Faites correspondre les nombres premiers verticalement si possible. » Dans la deuxième cellule, les instructions indiquent : « Listez les nombres premiers de 12. Listez les nombres premiers de 18. Alignez-vous avec les nombres premiers de 12 lorsque cela est possible. Sinon, créez une nouvelle colonne. » La troisième cellule contient la factorisation première de 12 exprimée comme suit : l'équation 12 est égale à 2 fois 2 fois 3. En dessous de cette équation se trouve une autre équation montrant la factorisation première de 18, écrite comme l'équation 18 est égale à 2 fois 3 fois 3. Les deux équations s'alignent verticalement au niveau du symbole égal. Le premier 2 de la factorisation première de 12 s'aligne sur le 2 de la factorisation première de 18. Sous le second 2 dans la factorisation première de 12, il y a un écart dans la factorisation première de 18. Sous le 3 dans la factorisation première de 12 se trouve le premier 3 dans la factorisation première de 18. Le second 3 de la factorisation première n'a aucun facteur supérieur à celui de la factorisation première de 12.Une ligne plus bas, les instructions de la première cellule indiquent : « Diminuez le nombre de chaque colonne ». La deuxième cellule est vide. La troisième cellule contient à nouveau les factorisations premières de 12 et 18, illustrées par deux équations alignées comme elles l'étaient auparavant. Cette fois, une ligne horizontale est tracée sous la factorisation première de 18. En dessous de cette droite se trouve l'équation LCM égale à 2 fois 2 fois 3 fois 3. Les flèches sont tracées verticalement depuis la factorisation première de 12 jusqu'à la factorisation première de 18 se terminant par l'équation LCM. La première flèche commence aux 2 premiers de la factorisation de 12 et continue vers le bas à travers les 2 de la factorisation des nombres premiers de 18, pour se terminer par les 2 premières du LCM. La deuxième flèche commence aux 2 suivants dans la factorisation des valeurs premières de 12 et continue vers le bas à travers l'écart de la factorisation des nombres premiers de 18, pour se terminer par les 2 secondes dans le LCM. La troisième flèche commence au 3 dans la factorisation première de 12 et continue vers le bas jusqu'aux 3 premières de la factorisation première de 18, pour se terminer par les 3 premières dans le LCM. La dernière flèche commence au deuxième 3 dans la factorisation première de 18 et pointe vers le bas jusqu'aux 3 secondes du LCM.Dans la rangée inférieure du tableau, la première cellule indique : « Étape 4 : Multipliez les facteurs ». La deuxième cellule est la banque. La troisième cellule contient l'équation LCM égale 36.

    Notez que les facteurs premiers\(12(2\cdot 2\cdot 3)\) et les facteurs premiers de\(18(2\cdot 3\cdot 3)\) sont inclus dans le LCM\((2\cdot 2\cdot 3\cdot 3)\). 36 est donc le multiple le moins courant de 12 et 18.

    En faisant correspondre les nombres premiers communs, chaque facteur premier commun n'est utilisé qu'une seule fois. De cette façon, vous êtes sûr que 36 est le multiple le moins courant.

    Exercice\(\PageIndex{29}\)

    Déterminez le LCM en utilisant la méthode des facteurs premiers : 9 et 12.

    Réponse

    \(36\)

    Exercice\(\PageIndex{30}\)

    Déterminez le LCM en utilisant la méthode des facteurs premiers : 18 et 24.

    Réponse

    \(72\)

    TROUVEZ LE MULTIPLE LE MOINS COURANT À L'AIDE DE LA MÉTHODE DES FACTEURS PREMIERS.
    1. Écrivez chaque nombre comme un produit de nombres premiers.
    2. Répertoriez les nombres premiers de chaque nombre. Faites correspondre les nombres premiers verticalement si possible.
    3. Abattez les colonnes.
    4. Multipliez les facteurs.
    Exercice\(\PageIndex{31}\)

    Déterminez le multiple le moins commun (LCM) de 24 et 36 à l'aide de la méthode des facteurs premiers.

    Réponse
    Détermine les nombres premiers de 24 et 36.
    Faites correspondre les nombres premiers verticalement si possible.

    Détruisez toutes les colonnes.    		 .
    Multipliez les facteurs. .
     

    Le LCM de 24 et 36 est de 72.
    Exercice\(\PageIndex{32}\)

    Déterminez le LCM en utilisant la méthode des facteurs premiers : 21 et 28.

    Réponse

    \(84\)

    Exercice\(\PageIndex{33}\)

    Déterminez le LCM en utilisant la méthode des facteurs premiers : 24 et 32.

    Réponse

    \(96\)

    Remarque

    Accédez à cette ressource en ligne pour obtenir des instructions supplémentaires et vous entraîner à utiliser des nombres entiers. Vous devez activer Java dans votre navigateur Web pour utiliser l'application.

    Concepts clés

    • Placez la valeur comme sur la figure.
    • Nommez un nombre entier en mots
      1. Commencez par la gauche et nommez le numéro de chaque période, suivi du nom de la période.
      2. Mettez des virgules dans le nombre pour séparer les points.
      3. Ne nommez pas la période de ceux.
    • Ecrire un nombre entier en utilisant des chiffres
      1. Identifiez les mots qui indiquent des périodes. (N'oubliez pas que la période de ceux qui ne sont jamais nommés.)
      2. Tracez 3 blancs pour indiquer le nombre de places nécessaires pour chaque période. Séparez les points par des virgules.
      3. Nommez le numéro de chaque période et placez les chiffres à la bonne position.
    • Nombres entiers ronds
      1. Localisez la valeur de position donnée et marquez-la avec une flèche. Tous les chiffres situés à gauche de la flèche ne changent pas.
      2. Soulignez le chiffre situé à droite de la valeur de position donnée.
      3. Ce chiffre est-il supérieur ou égal à 5 ?
        • Oui : ajoutez 1 au chiffre dans la valeur de position donnée.
        • Non : ne modifiez pas le chiffre dans la valeur de position spécifiée.
      4. Remplacez tous les chiffres situés à droite de la valeur de position donnée par des zéros.
    • Tests de divisibilité : Un nombre est divisible par :
      • 2 si le dernier chiffre est 0, 2, 4, 6 ou 8.
      • 3 si la somme des chiffres est divisible par 3.
      • 5 si le dernier chiffre est 5 ou 0.
      • 6 s'il est divisible à la fois par 2 et par 3.
      • 10 s'il se termine par 0.
    • Trouvez la factorisation première d'un nombre composé
      1. Trouvez deux facteurs dont le produit est le nombre donné et utilisez ces nombres pour créer deux branches.
      2. Si un facteur est premier, cette branche est complète. Encerclez la fleur, comme un bourgeon sur l'arbre.
      3. Si un facteur n'est pas premier, écrivez-le comme le produit de deux facteurs et poursuivez le processus.
      4. Écrivez le nombre composé comme le produit de tous les nombres premiers encerclés.
    • Trouvez le multiple le moins courant en listant les multiples
      1. Dressez la liste de plusieurs multiples de chaque numéro.
      2. Recherchez le plus petit nombre figurant sur les deux listes.
      3. Ce numéro est le LCM.
    • Trouvez le multiple le moins courant à l'aide de la méthode des facteurs premiers
      1. Écrivez chaque nombre comme un produit de nombres premiers.
      2. Répertoriez les nombres premiers de chaque nombre. Faites correspondre les nombres premiers verticalement si possible.
      3. Abattez les colonnes.
      4. Multipliez les facteurs.

    Lexique

    numéro composé
    Un nombre composé est un nombre de comptage qui n'est pas premier. Un nombre composé possède des facteurs autres que 1 et lui-même.
    compter les nombres
    Les nombres de comptage sont les nombres 1, 2, 3,...
    divisible par un nombre
    Si un nombre\(m\) est un multiple de\(n\), il\(m\) est divisible par\(n\). (Si 6 est un multiple de 3, alors 6 est divisible par 3.)
    facteurs
    Si\(a\cdot b=m\), alors\(a\) et\(b\) sont des facteurs de\(m\). Depuis\(3 \cdot 4 = 12\), 3 et 4 sont des facteurs de 12.
    multiple le moins courant
    Le plus petit multiple de deux nombres est le plus petit multiple des deux nombres.
    multiple d'un nombre
    Un nombre est un multiple de\(n\) s'il est le produit d'un nombre de comptage et\(n\).
    ligne numérique
    Une ligne numérique est utilisée pour visualiser les nombres. Les chiffres sur la ligne numérique grossissent lorsqu'ils vont de gauche à droite et diminuent lorsqu'ils vont de droite à gauche.
    origine
    L'origine est le point marqué 0 sur une ligne numérique.
    factorisation primaire
    La factorisation en nombres premiers d'un nombre est le produit des nombres premiers qui sont égaux au nombre.
    nombre premier
    Un nombre premier est un nombre de comptage supérieur à 1, dont les seuls facteurs sont 1 et lui-même.
    nombres entiers
    Les nombres entiers sont les nombres 0, 1, 2, 3,...