11.4 : Propriétés colligatives
- Page ID
- 193934
- Exprimer les concentrations des composants de la solution par fraction molaire et molalité
- Décrire l'effet de la concentration du soluté sur diverses propriétés de la solution (pression de vapeur, point d'ébullition, point de congélation et pression osmotique)
- Effectuer des calculs à l'aide des équations mathématiques qui décrivent ces différents effets colligatifs
- Décrire le processus de distillation et ses applications pratiques
- Expliquer le processus d'osmose et décrire comment il est appliqué dans l'industrie et dans la nature
Les propriétés d'une solution sont différentes de celles du ou des solutés purs ou du solvant. De nombreuses propriétés de la solution dépendent de l'identité chimique du soluté. Par rapport à l'eau pure, une solution de chlorure d'hydrogène est plus acide, une solution d'ammoniaque est plus basique, une solution de chlorure de sodium est plus dense et une solution de saccharose est plus visqueuse. Certaines propriétés de la solution dépendent toutefois uniquement de la concentration totale des espèces de solutés, quelle que soit leur identité. Ces propriétés colligatives incluent l'abaissement de la pression de vapeur, l'élévation du point d'ébullition, l'abaissement du point de congélation et la pression osmotique. Ce petit ensemble de propriétés est d'une importance capitale pour de nombreux phénomènes naturels et applications technologiques, comme cela sera décrit dans ce module.
Fraction molaire et molalité
Plusieurs unités couramment utilisées pour exprimer les concentrations des composants de la solution ont été présentées dans un chapitre précédent de ce texte, chacune présentant certains avantages pour une utilisation dans différentes applications. Par exemple, la molarité (M) est une unité pratique pour les calculs stœchiométriques, car elle est définie en termes de quantités molaires d'espèces de solutés :
\[M=\dfrac{\text{mol solute}}{\text{L solution}} \label{11.5.1} \]
Comme les volumes de solution varient en fonction de la température, les concentrations molaires peuvent également varier. Exprimée en molarité, la concentration d'une solution contenant un nombre identique d'espèces de soluté et de solvant sera différente à différentes températures, en raison de la contraction/de l'expansion de la solution. Les unités de concentration basées sur les taupes dont les valeurs ne dépendent pas de la température sont plus appropriées pour les calculs impliquant de nombreuses propriétés colligatives. Deux de ces unités sont la fraction molaire (présentée dans le chapitre précédent sur les gaz) et la molalité.
La fraction molaire d'un composant est le rapport entre sa quantité molaire et le nombre total de moles de tous les composants de la solution :\(\chi\)
\[\chi_\ce{A}=\dfrac{\text{mol A}}{\text{total mol of all components}} \label{11.5.2} \]
La molalité est une unité de concentration définie comme le rapport entre le nombre de moles de soluté et la masse du solvant en kilogrammes :
\[m=\dfrac{\text{mol solute}}{\text{kg solvent}} \label{11.5.3} \]
Comme ces unités sont calculées uniquement à l'aide de masses et de quantités molaires, elles ne varient pas en fonction de la température et sont donc mieux adaptées aux applications nécessitant des concentrations indépendantes de la température, y compris plusieurs propriétés colligatives, comme cela sera décrit dans ce module de chapitre.
L'antigel de la plupart des radiateurs automobiles est un mélange de volumes égaux d'éthylène glycol et d'eau, avec de petites quantités d'autres additifs qui empêchent la corrosion. Quelles sont (a) la fraction molaire et (b) la molalité de l'éthylène glycol, C 2 H 4 (OH) 2, dans une solution préparée à partir\(\mathrm{2.22 \times 10^3 \;g}\) d'éthylène glycol et\(\mathrm{2.00 \times 10^3\; g}\) d'eau (environ 2 L de glycol et 2 L d'eau) ?
Solution
(a) La fraction molaire d'éthylène glycol peut être calculée en déduisant d'abord les quantités molaires des deux composants de la solution, puis en les substituant dans la définition de l'unité.
\(\mathrm{mol\:H_2O=2000\:g×\dfrac{1\:mol\:H_2O}{18.02\:g\:H_2O}=111\:mol\:H_2O}\)
\(\chi_\mathrm{ethylene\:glycol}=\mathrm{\dfrac{35.8\:mol\:C_2H_4(OH)_2}{(35.8+111)\:mol\: total}=0.245}\)
Notez que la fraction molaire est une propriété sans dimension, c'est-à-dire le ratio de propriétés ayant des unités identiques (moles).
(b) Pour déterminer la molalité, il faut connaître les moles du soluté et la masse du solvant (en kg).
Tout d'abord, utilisez la masse donnée d'éthylène glycol et sa masse molaire pour trouver les moles de soluté :
\[\mathrm{2220\:g\:C_2H_4(OH)_2\left(\dfrac{mol\:C_2H_2(OH)_2}{62.07\:g}\right)=35.8\:mol\:C_2H_4(OH)_2} \nonumber \]
Ensuite, convertissez la masse de l'eau en grammes en kilogrammes :
\[\mathrm{2000\: g\:H_2O\left(\dfrac{1\:kg}{1000\:g}\right)=2\: kg\:H_2O} \nonumber \]
Enfin, calculez la molarité selon sa définition :
\ [\ begin {align*}
\ ce {molalité} &= \ mathrm {\ dfrac {mol \ : soluté} {kg \ : solvant}} \ \
\ ce {molalité} &= \ mathrm {\ dfrac {35,8 \ :mol \ :C_2H_4 (OH) _2} {2 \ :kg \ :H_2O}} \ \
\ {ce molalité} &=17,9 \ :m
\ end {align*} \ nonnumber \]
Quelles sont la fraction molaire et la molalité d'une solution contenant 0,850 g d'ammoniac, NH 3, dissous dans 125 g d'eau ?
- Réponse
-
7,14 × 10 −3 ; 0,399 m
Calculer la fraction molaire du soluté et du solvant dans une solution de 3,0 ml de chlorure de sodium.
Solution en solo
La conversion d'une unité de concentration à une autre s'effectue en comparant d'abord les deux définitions d'unités. Dans ce cas, les deux unités ont le même numérateur (moles de soluté) mais des dénominateurs différents. La concentration molale fournie peut être écrite comme suit :
\[\mathrm{\dfrac{3.0\;mol\; NaCl}{1.0\; kg\; H_2O}} \nonumber \]
Le numérateur de la fraction molaire de cette solution est donc de 3,0 mol de NaCl. Le dénominateur peut être calculé en dérivant la quantité molaire d'eau correspondant à 1,0 kg
\[\mathrm{1.0\:kg\:H_2O\left(\dfrac{1000\:g}{1\:kg}\right)\left(\dfrac{mol\:H_2O}{18.02\:g}\right)=55\:mol\:H_2O} \nonumber \]
puis en substituant ces quantités molaires dans la définition de la fraction molaire.
\ [\ begin {align*}
X_ \ mathrm {H_2O} &= \ mathrm {\ dfrac {mol \ :H_2O} {mol \ : NaCl + mol \ :H_2O}} \ \
X_ \ mathrm {H_2O} &= \ mathrm {\ dfrac {55 \ :mol \ :H_2O} {3.0 \ :mol \ : NaCl+55 \ :mol \ :H_2O}} \ \
X_ \ mathrm {H_2O} &=0,95 \ \
X_ \ mathrm {NaCl} &= \ mathrm {\ dfrac {mol \ : NaCl} { mol \ : NaCl+mol \ :H_2O}} \ \
X_ \ mathrm {NaCl} &= \ mathrm {\ dfrac {3.0 \ :mol \ :NaCl} {3.0 \ :mol \ : NaCl+55 \ :mol \ :H_2O}} \ \
X_ \ mathrm {NaCl} &=0,052
\ end {align*} \ aucun nombre \]
La fraction molaire d'iode\(\ce{I_2}\), dissoute dans du dichlorométhane\(\ce{CH_2Cl_2}\), est de 0,115. Quelle est la concentration molale, m, d'iode dans cette solution ?
- Réponse
-
1,50 m
Abaissement de la pression
Comme décrit dans le chapitre sur les liquides et les solides, la pression de vapeur d'équilibre d'un liquide est la pression exercée par sa phase gazeuse lorsque la vaporisation et la condensation se produisent à des taux égaux :
\[ \text{liquid} \rightleftharpoons \text{gas} \label{11.5.4} \]
La dissolution d'une substance non volatile dans un liquide volatil entraîne une baisse de la pression de vapeur du liquide. Ce phénomène peut être rationalisé en tenant compte de l'effet des molécules de soluté ajoutées sur les processus de vaporisation et de condensation du liquide. Pour se vaporiser, les molécules de solvant doivent être présentes à la surface de la solution. La présence de soluté réduit la surface disponible pour les molécules de solvant et réduit ainsi le taux de vaporisation du solvant. Comme la vitesse de condensation n'est pas affectée par la présence de soluté, le résultat net est que l'équilibre vaporisation-condensation est atteint avec moins de molécules de solvant en phase vapeur (c'est-à-dire à une pression de vapeur plus faible) (Figure\(\PageIndex{1}\)). Bien que cette interprétation cinétique soit utile, elle ne tient pas compte de plusieurs aspects importants de la nature colligative de l'abaissement de la pression de vapeur. Une explication plus rigoureuse concerne la propriété de l'entropie, sujet de discussion dans un chapitre de texte ultérieur sur la thermodynamique. Pour comprendre comment abaisser la pression de vapeur d'un liquide, il convient de noter que la plus grande entropie d'une solution par rapport à son solvant et à son soluté séparés permet de stabiliser efficacement les molécules de solvant et d'empêcher leur vaporisation. Il en résulte une pression de vapeur plus basse et un point d'ébullition proportionnellement plus élevé, comme décrit dans la section suivante de ce module.
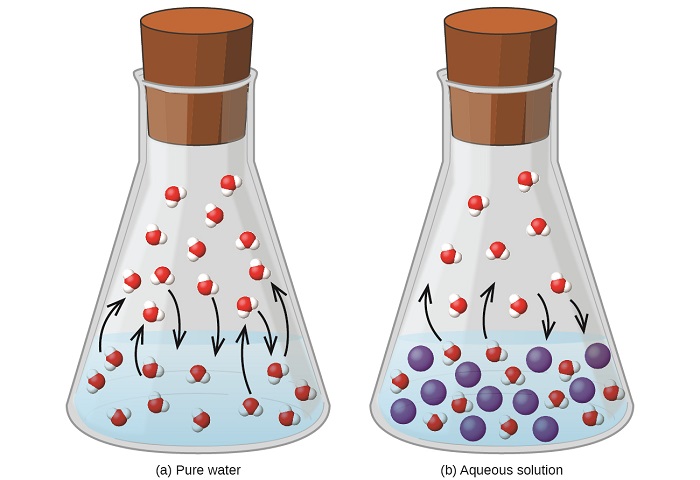
La relation entre les pressions de vapeur des composants de la solution et les concentrations de ces composants est décrite par la loi de Raoult : La pression partielle exercée par tout composant d'une solution idéale est égale à la pression de vapeur du composant pur multipliée par sa mole fraction dans la solution.
\[P_\ce{A}=X_\ce{A}P^\circ_\ce{A} \label{11.5.5} \]
où P A est la pression partielle exercée par le composant A dans la solution,\(P^\circ_\ce{A}\) est la pression de vapeur de A pur et X A est la fraction molaire de A dans la solution. (La fraction molaire est une unité de concentration introduite dans le chapitre sur les gaz.)
Rappelant que la pression totale d'un mélange gazeux est égale à la somme des pressions partielles pour tous ses composants (loi des pressions partielles de Dalton), la pression de vapeur totale exercée par une solution contenant i composants est
\[P_\ce{solution}=\sum_{i}P_i=\sum_{i}X_iP^\circ_i \label{11.5.6} \]
Une substance non volatile est une substance dont la pression de vapeur est négligeable (P° ≈ 0), de sorte que la pression de vapeur au-dessus d'une solution contenant uniquement des solutés non volatils est due uniquement au solvant :
\[P_\ce{solution}=X_\ce{solvent}P^\circ_\ce{solvent} \label{11.5.7} \]
Calculez la pression de vapeur d'une solution idéale contenant 92,1 g de glycérine, C 3 H 5 (OH) 3, et 184,4 g d'éthanol, C 2 H 5 OH, à 40 °C. La pression de vapeur de l'éthanol pur est de 0,178 atm à 40 °C. La glycérine est essentiellement non volatile à ce température.
Solution
Le solvant étant le seul composant volatil de cette solution, sa pression de vapeur peut être calculée selon la loi de Raoult comme suit :
\(P_\ce{solution}=X_\ce{solvent}P^\circ_\ce{solvent}\)
Tout d'abord, calculez les quantités molaires de chaque composant de la solution à l'aide des données de masse fournies.
\(\mathrm{92.1\cancel{g\:C_3H_5(OH)_3}×\dfrac{1\:mol\:C_3H_5(OH)_3}{92.094\cancel{g\:C_3H_5(OH)_3}}=1.00\:mol\:C_3H_5(OH)_3}\)
Ensuite, calculez la fraction molaire du solvant (éthanol) et utilisez la loi de Raoult pour calculer la pression de vapeur de la solution.
\(X_\mathrm{C_2H_5OH}=\mathrm{\dfrac{4.000\:mol}{(1.00\:mol+4.000\:mol)}=0.800}\)
\(P_\ce{solv}=X_\ce{solv}P^\circ_\ce{solv}=\mathrm{0.800×0.178\:atm=0.142\:atm}\)
Une solution contient 5,00 g d'urée, de CO (NH 2) 2 (un soluté non volatil) et 0,100 kg d'eau. Si la pression de vapeur de l'eau pure à 25 °C est de 23,7 torr, quelle est la pression de vapeur de la solution ?
- Réponse
-
23,4 torr
Élévation du point d'ébullition d'un solvant
Comme décrit dans le chapitre sur les liquides et les solides, le point d'ébullition d'un liquide est la température à laquelle sa pression de vapeur est égale à la pression atmosphérique ambiante. Comme la pression de vapeur d'une solution est abaissée en raison de la présence de solutés non volatils, il va de soi que le point d'ébullition de la solution sera ensuite augmenté. Par rapport à un solvant pur, une solution nécessitera donc une température plus élevée pour atteindre une pression de vapeur donnée, y compris une pression équivalente à celle de l'atmosphère environnante. L'augmentation du point d'ébullition observée lorsque le soluté non volatil est dissous dans un solvant est appelée élévation du point d'ébullition et est directement proportionnelle à la concentration molale des espèces de soluté :\(ΔT_b\)
\[ΔT_b=K_bm \label{11.5.8} \]
où
- \(K_\ce{b}\)est la constante d'élévation du point d'ébullition, ou la constante bullioscopique et
- \(m\)est la concentration molale (molalité) de toutes les espèces de solutés.
Les constantes d'élévation du point d'ébullition sont des propriétés caractéristiques qui dépendent de l'identité du solvant. Les valeurs de K b pour plusieurs solvants sont répertoriées dans le tableau\(\PageIndex{1}\).
| Solvant | Point d'ébullition (°C à 1 atm) | K b (Cm −1) | Point de congélation (°C à 1 atm) | K f (Cm −1) |
|---|---|---|---|---|
| eau | 100,0 | 0,512 | 0,0 | 1,86 |
| acétate d'hydrogène | 118.1 | 3,07 | 16,6 | 3.9 |
| benzène | 80,1 | 2,53 | 5.5 | 5.12 |
| chloroforme | 61,26 | 3,63 | −63,5 | 4,68 |
| nitrobenzène | 210,9 | 5,24 | 5,67 | 8.1 |
La mesure dans laquelle la pression de vapeur d'un solvant est abaissée et le point d'ébullition élevé dépend du nombre total de particules de soluté présentes dans une quantité donnée de solvant, et non de la masse, de la taille ou de l'identité chimique des particules. Une solution aqueuse de 1 m de saccharose (342 g/mol) et une solution aqueuse de 1 m d'éthylène glycol (62 g/mol) présenteront le même point d'ébullition car chaque solution contient une mole de particules de soluté (molécules) par kilogramme de solvant.
Quel est le point d'ébullition d'une solution à 0,33 m d'un soluté non volatil dans le benzène ?
Solution
Utilisez l'équation reliant l'élévation du point d'ébullition à la molalité du soluté pour résoudre ce problème en deux étapes.

- Calculez la variation du point d'ébullition.
\(ΔT_\ce{b}=K_\ce{b}m=2.53\:°\ce C\:m^{−1}×0.33\:m=0.83\:°\ce C\)
- Ajoutez l'élévation du point d'ébullition au point d'ébullition du solvant pur.
\(\mathrm{Boiling\: temperature=80.1\:°C+0.83\:°C=80.9\:°C}\)
Quel est le point d'ébullition de l'antigel décrit dans l'exemple\(\PageIndex{4}\) ?
- Réponse
-
109.2 °C
Déterminer le point d'ébullition d'une solution de 92,1 g d'iode\(\ce{I2}\), dans 800,0 g de chloroforme\(\ce{CHCl3}\), en supposant que l'iode n'est pas volatil et que la solution est idéale.
Solution
Nous pouvons résoudre ce problème en quatre étapes.

- Convertissez les grammes en moles\(\ce{I2}\) en utilisant la masse molaire de\(\ce{I2}\) dans le facteur de conversion unitaire.
Résultat : 0,363 mol
Déterminez la molalité de la solution à partir du nombre de moles de soluté et de la masse de solvant, en kilogrammes.
Résultat : 0,454 m
Utilisez la proportionnalité directe entre la variation du point d'ébullition et la concentration molale pour déterminer dans quelle mesure le point d'ébullition change.
Résultat : 1,65 °C
Déterminez le nouveau point d'ébullition à partir du point d'ébullition du solvant pur et de la modification.
Résultat : 62,91 °C
Vérifiez chaque résultat dans le cadre d'une auto-évaluation.
Quel est le point d'ébullition d'une solution de 1,0 g de glycérine dans 47,8 g d'eau ?\(\ce{C3H5(OH)3}\) Supposons que la solution soit idéale.
- Réponse
-
100.12 °C
Distillation des solutions
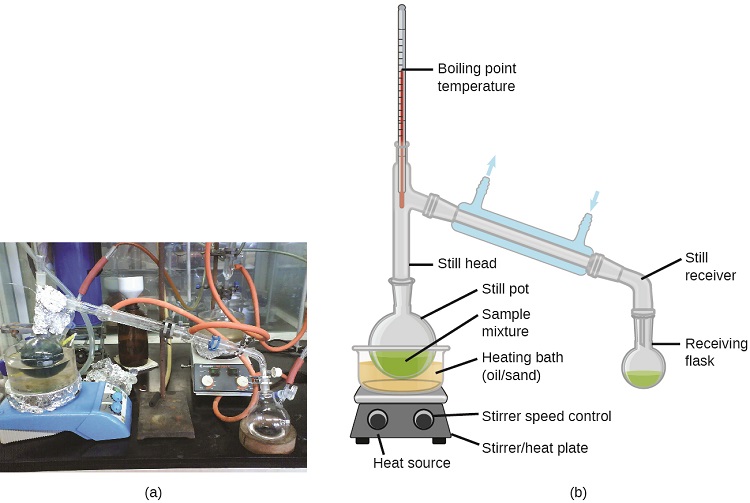
La distillation est une technique de séparation des composants des mélanges largement appliquée en laboratoire et en milieu industriel. Il est utilisé pour raffiner le pétrole, isoler les produits de fermentation et purifier l'eau. Cette technique de séparation implique le chauffage contrôlé d'un mélange d'échantillons pour vaporiser, condenser et collecter sélectivement un ou plusieurs composants d'intérêt. Un appareil typique pour les distillations en laboratoire est illustré à la figure\(\PageIndex{2}\).
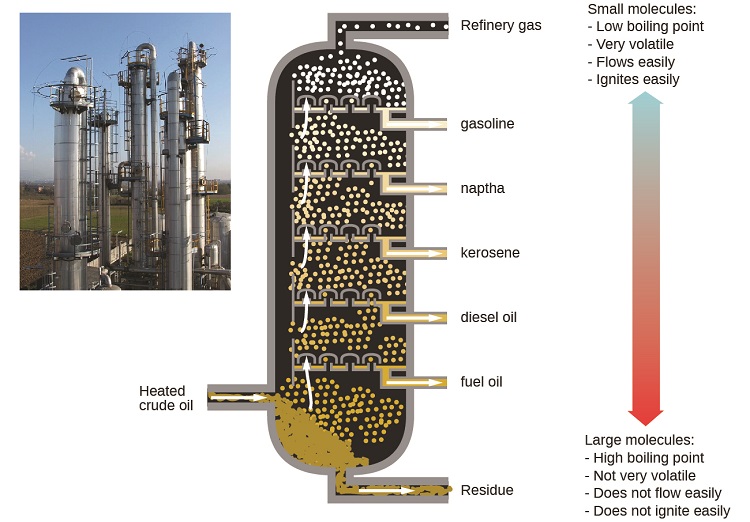
Les raffineries de pétrole utilisent la distillation fractionnée à grande échelle pour séparer les composants du pétrole brut. Le pétrole brut est chauffé à des températures élevées à la base d'une colonne de fractionnement haute, vaporisant de nombreux composants qui s'élèvent dans la colonne. Lorsque les composants vaporisés atteignent des zones suffisamment froides pendant leur remontée, ils se condensent et sont collectés. Les liquides collectés sont des mélanges plus simples d'hydrocarbures et d'autres composés pétroliers dont la composition est appropriée pour diverses applications (par exemple, carburant diesel, kérosène, essence), comme le montre la figure\(\PageIndex{3}\).
Abaissement du point de congélation d'un solvant
Les solutions gèlent à des températures plus basses que les liquides purs Ce phénomène est exploité dans les systèmes de « dégivrage » qui utilisent du sel (Figure\(\PageIndex{4}\)), du chlorure de calcium ou de l'urée pour faire fondre la glace sur les routes et les trottoirs, et dans l'utilisation de l'éthylène glycol comme « antigel » dans les radiateurs automobiles. L'eau de mer gèle à une température inférieure à celle de l'eau douce, de sorte que les océans Arctique et Antarctique restent dégelés même à des températures inférieures à 0 °C (tout comme les fluides corporels des poissons et autres animaux marins à sang froid qui vivent dans ces océans).

La diminution du point de congélation d'une solution diluée par rapport à celui du solvant pur, Δ T f, est appelée dépression du point de congélation et est directement proportionnelle à la concentration molale du soluté.
\[ΔT_\ce{f}=K_\ce{f}m \label{11.5.9} \]
où
- \(m\)est la concentration molale du soluté dans le solvant et
- \(K_f\)est appelée constante de dépression du point de congélation (ou constante cryoscopique).
Tout comme les constantes d'élévation du point d'ébullition, il s'agit de propriétés caractéristiques dont les valeurs dépendent de l'identité chimique du solvant. Les valeurs de K f pour plusieurs solvants sont répertoriées dans le tableau\(\PageIndex{1}\).
Quel est le point de congélation de la solution à 0,33 m d'un soluté non électrolytique non volatil dans le benzène décrite dans l'exemple\(\PageIndex{4}\) ?
Solution
Utilisez l'équation reliant l'abaissement du point de congélation à la molalité des solutés pour résoudre ce problème en deux étapes.

- Calculez la variation du point de congélation. \[ΔT_\ce{f}=K_\ce{f}m=5.12\:°\ce C\:m^{−1}×0.33\:m=1.7\:°\ce C \nonumber \]
- Soustrayez le changement de point de congélation observé du point de congélation du solvant pur. \[\mathrm{Freezing\: Temperature=5.5\:°C−1.7\:°C=3.8\:°C} \nonumber \]
Quel est le point de congélation d'une solution de 1,85 m d'un soluté non électrolytique non volatil dans du nitrobenzène ?
- Réponse
-
−9.3 °C
Le chlorure de sodium et ses analogues du groupe 2, le chlorure de calcium et de magnésium, sont souvent utilisés pour dégivrer les routes et les trottoirs, car une solution de l'un de ces sels aura un point de congélation inférieur à 0 °C, le point de congélation de l'eau pure. Les sels métalliques du groupe 2 sont fréquemment mélangés au chlorure de sodium (« sel gemme »), moins cher et plus facilement disponible pour une utilisation sur les routes, car ils ont tendance à être un peu moins corrosifs que le NaCl et ils réduisent davantage le point de congélation, car ils se dissocient pour produire trois particules par unité de formule, plutôt que deux particules comme le chlorure de sodium.
Comme ces composés ioniques ont tendance à accélérer la corrosion du métal, il ne serait pas judicieux de les utiliser comme antigel pour le radiateur de votre voiture ou pour dégivrer un avion avant le décollage. Pour ces applications, des composés covalents, tels que l'éthylène ou le propylène glycol, sont souvent utilisés. Les glycols utilisés dans le liquide de radiateur abaissent non seulement le point de congélation du liquide, mais ils élèvent également le point d'ébullition, ce qui rend le liquide utile en hiver et en été. Des glycols chauffés sont souvent pulvérisés sur la surface des avions avant le décollage par mauvais temps en hiver afin d'éliminer la glace qui s'est déjà formée et d'empêcher la formation de glace supplémentaire, ce qui serait particulièrement dangereux s'il se formait sur les gouvernes de l'avion (vidéo\(\PageIndex{1}\)).
Vidéo\(\PageIndex{1}\) : La dépression du point de congélation est exploitée pour retirer la glace des gouvernes des aéronefs.
Diagramme de phase pour une solution aqueuse d'un non-électrolyte
Les effets colligatifs sur la pression de vapeur, le point d'ébullition et le point de congélation décrits dans la section précédente sont résumés de manière pratique en comparant les diagrammes de phase d'un liquide pur et d'une solution dérivée de ce liquide. Les diagrammes de phase pour l'eau et une solution aqueuse sont présentés sur la figure\(\PageIndex{5}\).
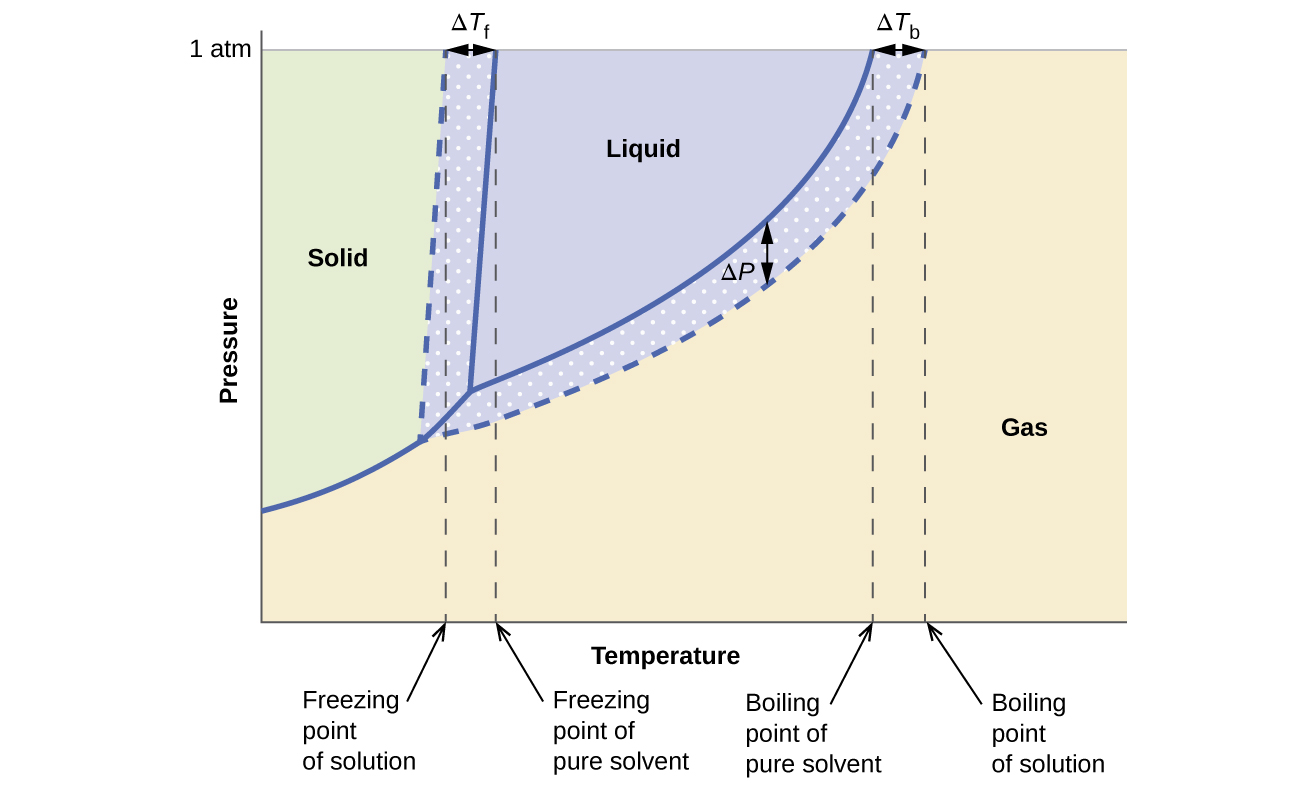
La courbe liquide-vapeur de la solution est située sous la courbe correspondante pour le solvant, représentant l'abaissement de la pression de vapeur, Δ P, qui résulte de la dissolution du soluté non volatil. Par conséquent, à toute pression donnée, le point d'ébullition de la solution est observé à une température supérieure à celle du solvant pur, reflétant l'élévation du point d'ébullition, Δ T b, associée à la présence d'un soluté non volatil. La courbe solide-liquide de la solution est décalée vers la gauche de celle du solvant pur, ce qui représente la dépression du point de congélation, Δ Tf, qui accompagne la formation de la solution. Enfin, notez que les courbes solide-gaz du solvant et de sa solution sont identiques. C'est le cas de nombreuses solutions comprenant des solvants liquides et des solutés non volatils. Tout comme pour la vaporisation, lorsqu'une solution de ce type est congelée, ce ne sont en fait que les molécules de solvant qui subissent la transition liquide-solide, formant un solvant solide pur qui exclut les espèces de solutés. Les phases solide et gazeuse sont donc composées uniquement de solvant, de sorte que les transitions entre ces phases ne sont pas soumises à des effets colligatifs.
Osmose et pression osmotique des solutions
Un certain nombre de matériaux naturels et synthétiques présentent une perméation sélective, ce qui signifie que seuls des molécules ou des ions d'une certaine taille, forme, polarité, charge, etc. peuvent traverser (pénétrer) le matériau. Les membranes cellulaires biologiques fournissent des exemples élégants de perméation sélective dans la nature, tandis que les tubes de dialyse utilisés pour éliminer les déchets métaboliques du sang constituent un exemple technologique plus simpliste. Quelle que soit la manière dont ils peuvent être fabriqués, ces matériaux sont généralement appelés membranes semi-perméables.
Prenons l'appareil illustré à la figure\(\PageIndex{6}\), dans lequel des échantillons de solvant pur et de solution sont séparés par une membrane que seules les molécules de solvant peuvent traverser. Les molécules de solvant se diffuseront à travers la membrane dans les deux sens. Comme la concentration de solvant est plus élevée dans le solvant pur que dans la solution, ces molécules diffuseront du côté solvant de la membrane vers le côté solution plus rapidement que dans le sens inverse. Il en résulte un transfert net de molécules de solvant du solvant pur vers la solution. Le transfert de molécules de solvant par diffusion à travers une membrane semi-perméable est un processus connu sous le nom d'osmose.
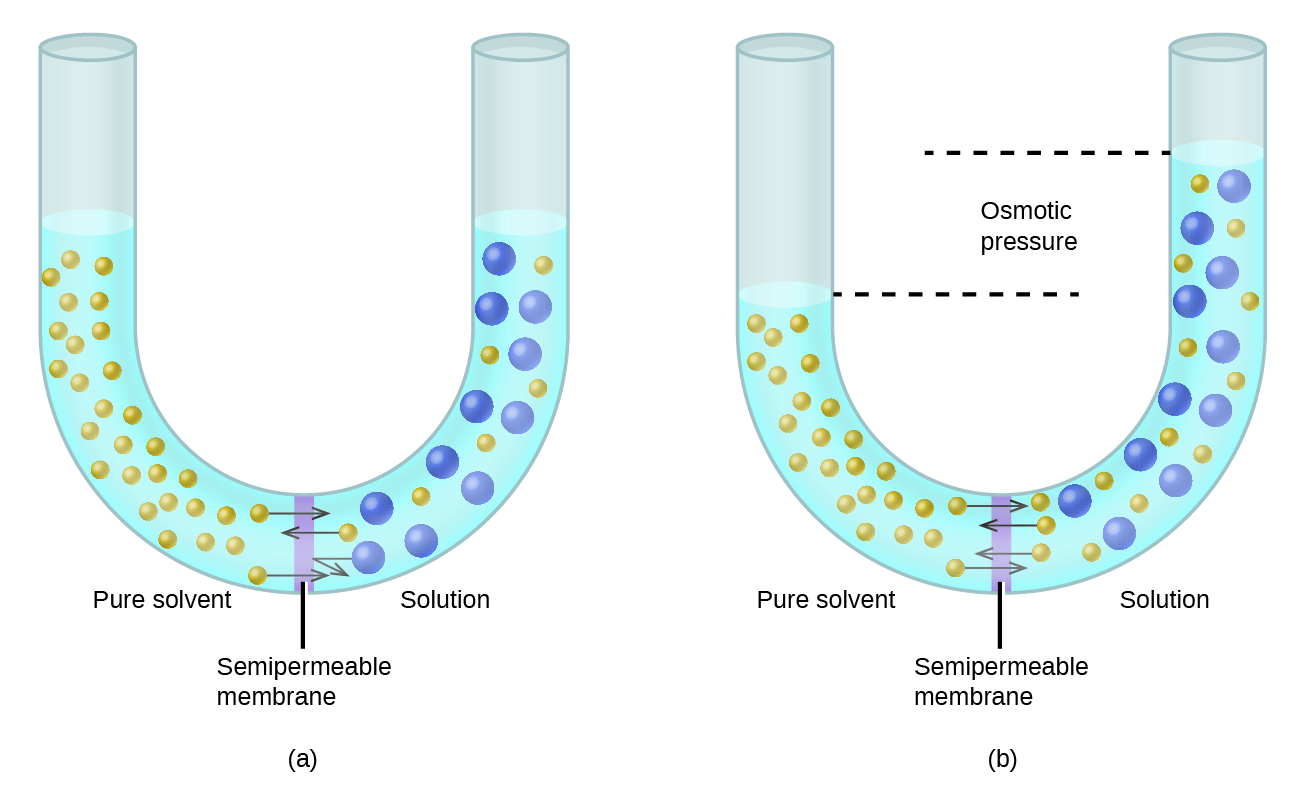
Lorsque l'osmose est réalisée dans un appareil tel que celui représenté sur la figure\(\PageIndex{6}\), le volume de la solution augmente à mesure qu'elle est diluée par accumulation de solvant. Cela provoque une augmentation du niveau de la solution, une augmentation de sa pression hydrostatique (due au poids de la colonne de solution dans le tube) et un transfert plus rapide des molécules de solvant vers le côté solvant pur. Lorsque la pression atteint une valeur qui donne un taux de transfert de solvant inverse égal au taux d'osmose, le transfert de solvant en vrac cesse. Cette pression est appelée pression osmotique (e\(\Pi\)) de la solution. La pression osmotique d'une solution diluée est liée à la molarité de son soluté, M, et à sa température absolue, T, selon l'équation
\[Π=MRT \label{11.5.10} \]
où\(R\) est la constante de gaz universelle.
Quelle est la pression osmotique (atm) d'une solution de glucose à 0,30 M dans de l'eau utilisée pour perfusion intraveineuse à la température corporelle, 37 °C ?
Solution
Nous pouvons déterminer la pression osmotique en utilisant l'équation \ ref {11.5.10}, où T est sur l'échelle Kelvin (310 K) et la valeur de R est exprimée en unités appropriées (0,08206 L atm/mol K).\(Π\)
\ [\ begin {align*}
π&=MRT \ \
&= \ mathrm {0,03 \ :mol/L×0,08206 \ : L \ : atm/mol \ : K × 310 \ : K} \ \
&= \ mathrm {7.6 \ :atm}
\ end {align*} \ nonnumber \]
Quelle est la pression osmotique (atm) d'une solution d'un volume de 0,750 L contenant 5,0 g de méthanol, CH 3 OH, dans de l'eau à 37 °C ?
- Réponse
-
5,3 atm
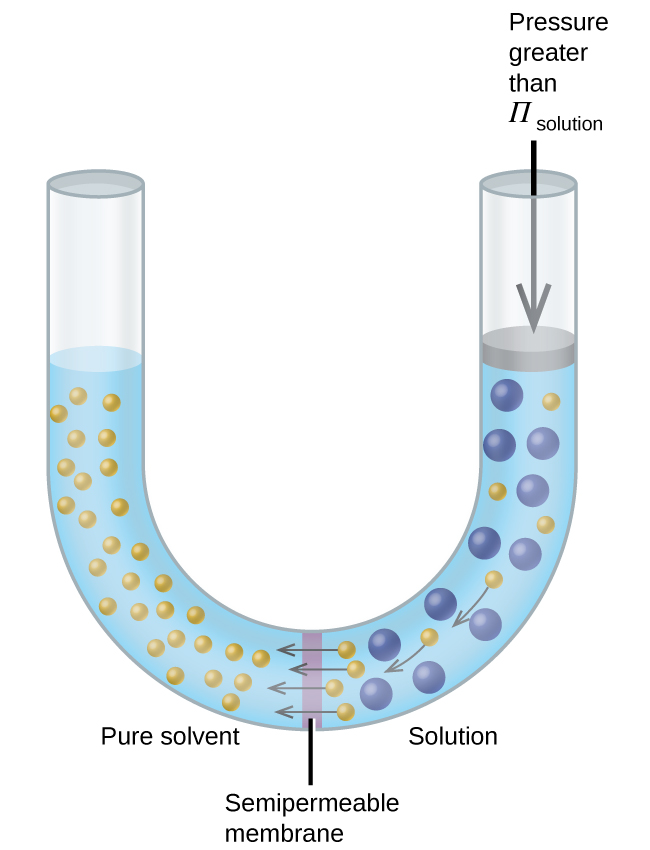
Si une solution est placée dans un appareil tel que celui illustré sur la figure\(\PageIndex{7}\), l'application d'une pression supérieure à la pression osmotique de la solution inverse l'osmose et pousse les molécules de solvant de la solution vers le solvant pur. Cette technique d'osmose inverse est utilisée pour le dessalement à grande échelle de l'eau de mer et, à plus petite échelle, pour produire de l'eau du robinet de haute pureté destinée à la consommation.
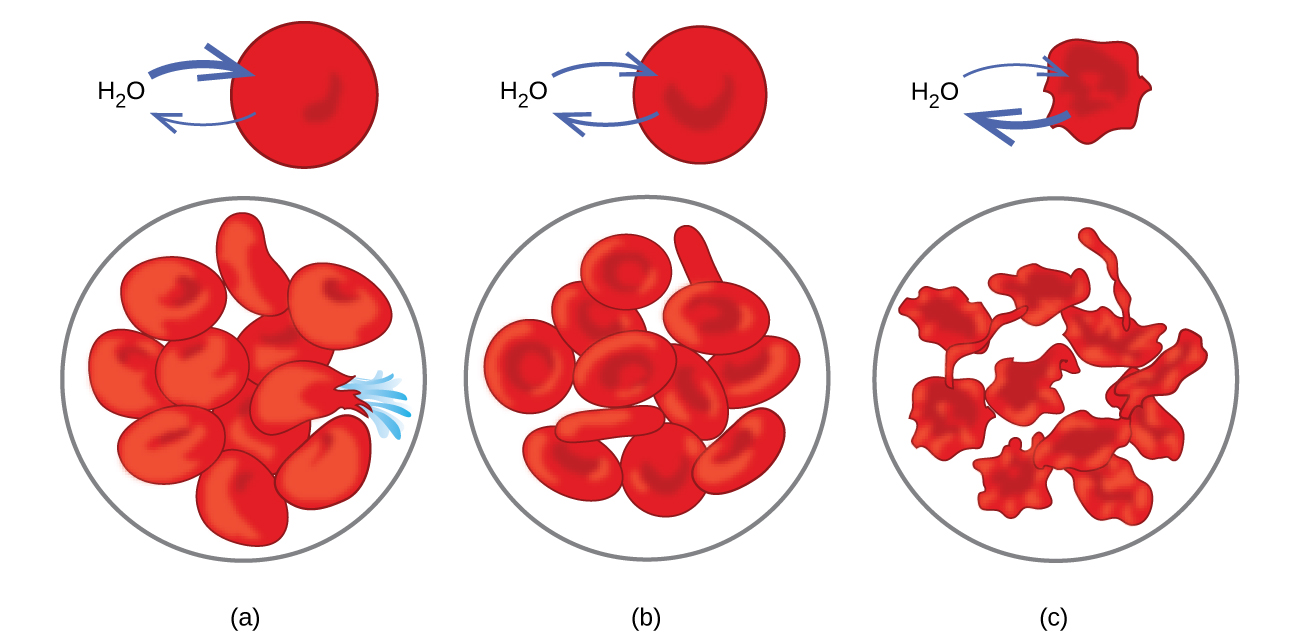
Des exemples d'osmose sont évidents dans de nombreux systèmes biologiques, car les cellules sont entourées de membranes semi-perméables. Les carottes et le céleri qui sont devenus mous parce qu'ils ont perdu de l'eau peuvent à nouveau être croustillants en les mettant dans de l'eau. L'eau pénètre dans les cellules de la carotte ou du céleri par osmose. Un concombre placé dans une solution saline concentrée perd de l'eau par osmose et absorbe un peu de sel pour se transformer en cornichon. L'osmose peut également affecter les cellules animales. Les concentrations de solutés sont particulièrement importantes lorsque les solutions sont injectées dans l'organisme. Les solutés présents dans les fluides cellulaires et le sérum sanguin confèrent à ces solutions une pression osmotique d'environ 7,7 atm. Les solutions injectées dans l'organisme doivent avoir la même pression osmotique que le sérum sanguin, c'est-à-dire qu'elles doivent être isotoniques avec le sérum sanguin. Si une solution moins concentrée, une solution hypotonique, est injectée en quantité suffisante pour diluer le sérum sanguin, l'eau du sérum dilué passe dans les cellules sanguines par osmose, provoquant l'expansion et la rupture des cellules. Ce processus s'appelle l'hémolyse. Lorsqu'une solution plus concentrée, une solution hypertonique, est injectée, les cellules perdent de l'eau au profit de la solution plus concentrée, se ratatinent et peuvent mourir au cours d'un processus appelé crénation (Figure 11.5.8).
Détermination des masses molaires
La pression osmotique et les variations du point de congélation, du point d'ébullition et de la pression de vapeur sont directement proportionnelles à la concentration du soluté présent. Par conséquent, nous pouvons utiliser la mesure de l'une de ces propriétés pour déterminer la masse molaire du soluté à partir des mesures.
On trouve qu'une solution de 4,00 g d'un non-électrolyte dissous dans 55,0 g de benzène gèle à 2,32 °C. Quelle est la masse molaire de ce composé ?
Solution
Nous pouvons résoudre ce problème en suivant les étapes suivantes.
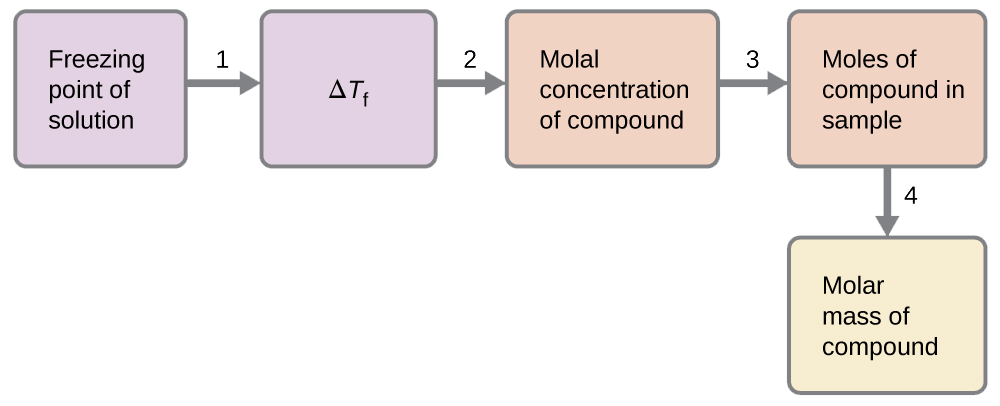
- Déterminer la variation du point de congélation par rapport au point de congélation observé et au point de congélation du benzène pur (tableau 11.5.1).
- Déterminer la concentration molale à partir de K f, de la constante de dépression du point de congélation pour le benzène (Tableau 11.5.1) et de Δ T f.
\(ΔT_\ce{f}=K_\ce{f}m\)
\(m=\dfrac{ΔT_\ce{f}}{K_\ce{f}}=\dfrac{3.2\:°\ce C}{5.12\:°\ce C m^{−1}}=0.63\:m\)
- Déterminer le nombre de moles de composé dans la solution à partir de la concentration molale et de la masse de solvant utilisée pour fabriquer la solution.
\(\mathrm{Moles\: of\: solute=\dfrac{0.62\:mol\: solute}{1.00\cancel{kg\: solvent}}×0.0550\cancel{kg\: solvent}=0.035\:mol}\)
- Déterminez la masse molaire à partir de la masse du soluté et du nombre de moles dans cette masse.
\(\mathrm{Molar\: mass=\dfrac{4.00\:g}{0.034\:mol}=1.2×10^2\:g/mol}\)
Une solution de 35,7 g d'un élément non électrolytique dans 220,0 g de chloroforme a un point d'ébullition de 64,5 °C. Quelle est la masse molaire de ce composé ?
- Réponse
-
1,8 × 10 2 g/mol
Un échantillon de 0,500 L d'une solution aqueuse contenant 10,0 g d'hémoglobine a une pression osmotique de 5,9 torr à 22 °C. Quelle est la masse molaire de l'hémoglobine ?
Solution
Voici une série d'étapes qui peuvent être utilisées pour résoudre le problème :

- \[\Pi=\mathrm{\dfrac{5.9\:torr×1\:atm}{760\:torr}=7.8×10^{−3}\:atm} \nonumber \]
\[\Pi=MRT \nonumber \]
\(M=\dfrac{Π}{RT}=\mathrm{\dfrac{7.8×10^{−3}\:atm}{(0.08206\:L\: atm/mol\: K)(295\:K)}=3.2×10^{−4}\:M}\)
- \(\mathrm{moles\: of\: hemoglobin=\dfrac{3.2×10^{−4}\:mol}{1\cancel{L\: solution}}×0.500\cancel{L\: solution}=1.6×10^{−4}\:mol}\)
- Déterminez la masse molaire à partir de la masse d'hémoglobine et du nombre de moles dans cette masse.
\(\mathrm{molar\: mass=\dfrac{10.0\:g}{1.6×10^{−4}\:mol}=6.2×10^4\:g/mol}\)
Quelle est la masse molaire d'une protéine si une solution de 0,02 g de protéine dans 25,0 ml de solution a une pression osmotique de 0,56 torr à 25 °C ?
- Réponse
-
2,7 × 10 4 g/mol
Propriétés colligatives des électrolytes
Comme indiqué précédemment dans ce module, les propriétés colligatives d'une solution dépendent uniquement du nombre, et non du type, d'espèces de solutés dissous. Par exemple, 1 mole de tout non-électrolyte dissous dans 1 kilogramme de solvant produit le même abaissement du point de congélation que 1 mole de tout autre non-électrolyte. Cependant, 1 mole de chlorure de sodium (un électrolyte) forme 2 moles d'ions lorsqu'elle est dissoute dans une solution. Chaque ion produit le même effet sur le point de congélation qu'une seule molécule.
La concentration en ions dans l'eau de mer est approximativement la même que celle d'une solution contenant 4,2 g de NaCl dissous dans 125 g d'eau. Supposons que chacun des ions de la solution de NaCl a le même effet sur le point de congélation de l'eau qu'une molécule non électrolytique, et déterminez la température de congélation de la solution (qui est approximativement égale à la température de congélation de l'eau de mer).
Solution
Nous pouvons résoudre ce problème en suivant les étapes suivantes.
- Convertir des grammes en moles de NaCl en utilisant la masse molaire de NaCl dans le facteur de conversion unitaire. Résultat : 0,072 mol de NaCl
- Déterminez le nombre de moles d'ions présentes dans la solution en utilisant le nombre de moles d'ions dans 1 mole de NaCl comme facteur de conversion (2 moles d'ions/1 mol de NaCl). Résultat : 0,14 mol d'ions
- Déterminez la molalité des ions dans la solution à partir du nombre de moles d'ions et de la masse de solvant, en kilogrammes. Résultat : 1,1 m
- Utilisez la proportionnalité directe entre la modification du point de congélation et la concentration molale pour déterminer dans quelle mesure le point de congélation change. Résultat : 2,0 °C
- Déterminez le nouveau point de congélation à partir du point de congélation du solvant pur et de la modification. Résultat : −2,0 °C
Vérifiez chaque résultat dans le cadre d'une auto-évaluation.
Supposons que chacun des ions du chlorure de calcium, CaCl 2, a le même effet sur le point de congélation de l'eau qu'une molécule non électrolytique. Calculer le point de congélation d'une solution de 0,724 g de CaCl 2 dans 175 g d'eau.
- Réponse
-
−0,208 °C
En supposant une dissociation complète, une solution aqueuse de 1 m de NaCl contient 2,0 moles d'ions (1,0 mol Na + et 1,0 mol Cl −) par kilogramme d'eau, et sa diminution du point de congélation devrait être
\[ΔT_\ce{f}=\mathrm{2.0\:mol\: ions/kg\: water×1.86\:°C\: kg\: water/mol\: ion=3.7\:°C.} \label{11.5.11} \]
Cependant, lorsque cette solution est réellement préparée et que son abaissement du point de congélation est mesuré, une valeur de 3,4 °C est obtenue. Des écarts similaires sont observés pour d'autres composés ioniques, et les différences entre les valeurs des propriétés colligatives mesurées et attendues deviennent généralement plus importantes à mesure que les concentrations de soluté augmentent. Ces observations suggèrent que les ions du chlorure de sodium (et d'autres électrolytes puissants) ne sont pas complètement dissociés en solution.
Pour en tenir compte et éviter les erreurs associées à l'hypothèse d'une dissociation totale, un paramètre mesuré expérimentalement nommé en l'honneur du chimiste allemand Jacobus Henricus van 't Hoff, lauréat du prix Nobel, est utilisé. Le facteur de Van 't Hoff (i) est défini comme le rapport entre les particules de soluté en solution et le nombre d'unités de formule dissoutes :
\[i=\dfrac{\textrm{moles of particles in solution}}{\textrm{moles of formula units dissolved}} \label{11.5.12} \]
Les valeurs des facteurs de Van 't Hoff mesurés pour plusieurs solutés, ainsi que les valeurs prédites en supposant une dissociation complète, sont présentées dans le tableau\(\PageIndex{2}\).
| électrolyte | Particules en solution | i (Prédit) | i (Mesuré) |
|---|---|---|---|
| HCl | H +, Cl − | 2 | 1,9 |
| NaCl | Na +, Cl − | 2 | 1,9 |
| MgSO 4 | Mg 2 +,\(\ce{SO4^2-}\) | 2 | 1.3 |
| MgCl 2 | Mg 2 +, 2 cl − | 3 | 2.7 |
| FéCl 3 | Fe 3 +, 3 Cl − | 4 | 3.4 |
| glucose (un produit non électrolytique) | C 12 H 22 O 11 | 1 | 1,0 |
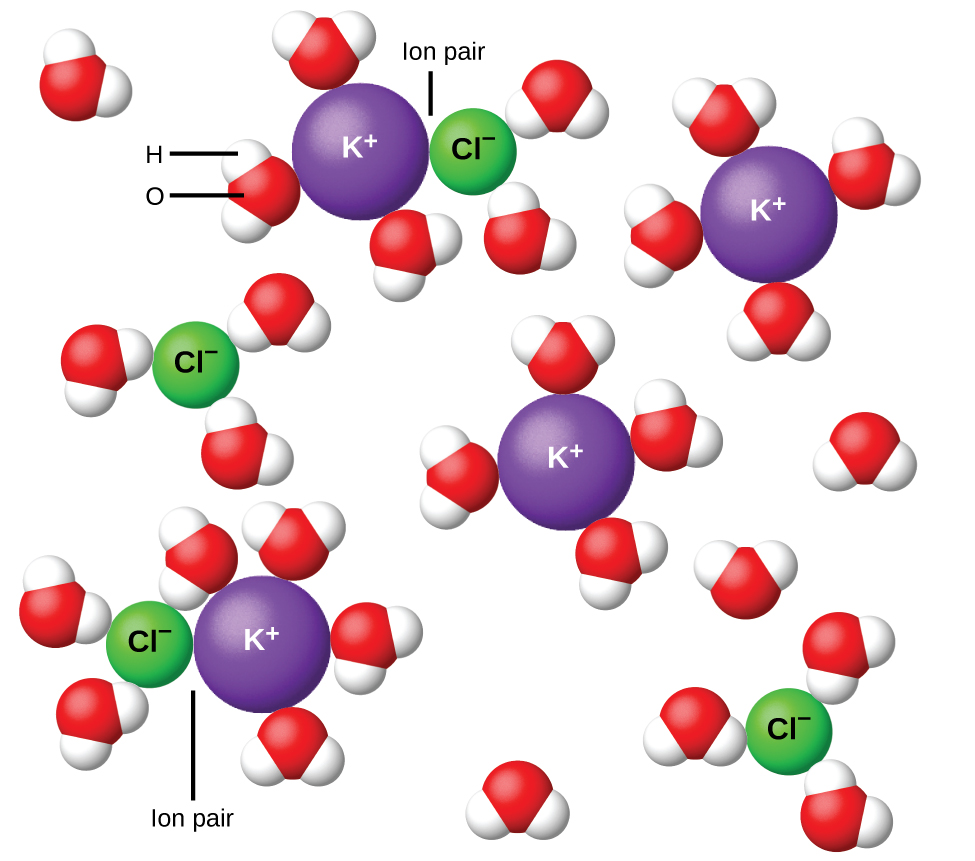
En 1923, les chimistes Peter Debye et Erich Hückel ont proposé une théorie pour expliquer l'ionisation apparemment incomplète des électrolytes forts. Ils ont suggéré que même si l'attraction interionique dans une solution aqueuse est très fortement réduite par la solvatation des ions et l'action isolante du solvant polaire, elle n'est pas complètement annulée. Les attractions résiduelles empêchent les ions de se comporter comme des particules totalement indépendantes (Figure\(\PageIndex{9}\)). Dans certains cas, un ion positif et un ion négatif peuvent réellement se toucher, donnant une unité solvatée appelée paire d'ions. Ainsi, l'activité, ou la concentration effective, d'un type particulier d'ion est inférieure à celle indiquée par la concentration réelle. Les ions se séparent de plus en plus à mesure que la solution se dilue, et les attractions interioniques résiduelles diminuent de moins en moins. Ainsi, dans les solutions extrêmement diluées, les concentrations effectives des ions (leurs activités) sont essentiellement égales aux concentrations réelles. Notez que les facteurs de Van 't Hoff pour les électrolytes du tableau\(\PageIndex{2}\) concernent des solutions de 0,05 m, à une concentration à laquelle la valeur de i pour le NaCl est de 1,9, par opposition à une valeur idéale de 2.
Résumé
Les propriétés d'une solution qui dépendent uniquement de la concentration des particules de soluté sont appelées propriétés colligatives. Ils incluent les modifications de la pression de vapeur, du point d'ébullition et du point de congélation du solvant dans la solution. L'ampleur de ces propriétés dépend uniquement de la concentration totale des particules de soluté en solution, et non du type de particules. La concentration totale de particules de soluté dans une solution détermine également sa pression osmotique. Il s'agit de la pression qui doit être appliquée à la solution pour empêcher la diffusion de molécules de solvant pur à travers une membrane semi-perméable dans la solution. Les composés ioniques peuvent ne pas se dissocier complètement en solution en raison des effets d'activité, auquel cas les effets colligatifs observés peuvent être inférieurs aux prévisions.
Équations clés
- \(\left(P_\ce{A}=X_\ce{A}P^\circ_\ce{A}\right)\)
- \(P_\ce{solution}=\sum_{i}P_i=\sum_{i}X_iP^\circ_i\)
- \(P_\ce{solution}=X_\ce{solvent}P^\circ_\ce{solvent}\)
- Δ T b = K b m
- Δ T f = K f m
- Π = MRT
Notes
- Un produit non électrolytique présenté à titre de comparaison.
Lexique
- élévation du point d'ébullition
- élévation du point d'ébullition d'un liquide par ajout d'un soluté
- constante d'élévation du point d'ébullition
- la constante de proportionnalité dans l'équation reliant l'élévation du point d'ébullition à la molalité du soluté ; également connue sous le nom de constante bullioscopique
- propriété collligative
- propriété d'une solution qui ne dépend que de la concentration d'une espèce de soluté
- crémation
- processus par lequel les cellules biologiques se ratatinent en raison de la perte d'eau par osmose
- dépression du point de congélation
- abaissement du point de congélation d'un liquide par ajout d'un soluté
- constante de dépression du point de congélation
- (également constante cryoscopique) constante de proportionnalité dans l'équation reliant l'abaissement du point de congélation à la molalité du soluté
- hémolyse
- rupture des globules rouges due à l'accumulation d'un excès d'eau par osmose
- hypertonique
- d'une pression osmotique plus élevée
- hypotonique
- de pression osmotique inférieure
- paire d'ions
- paire anion/cation solvatés maintenue ensemble par une attraction électrostatique modérée
- isotonique
- de pression osmotique égale
- molalité (m)
- une unité de concentration définie comme le rapport entre le nombre de moles de soluté et la masse du solvant en kilogrammes
- osmose
- diffusion de molécules de solvant à travers une membrane semi-perméable
- pression osmotique (Π)
- pression opposée requise pour empêcher le transfert massif des molécules de solvant à travers une membrane semi-perméable
- Loi de Raoult
- la pression partielle exercée par un composant de solution est égale au produit de la fraction molaire du composant dans la solution et de sa pression de vapeur d'équilibre à l'état pur
- membrane semi-perméable
- une membrane qui permet le passage sélectif de certains ions ou molécules
- Facteur Van 't Hoff (i)
- le rapport entre le nombre de moles de particules dans une solution et le nombre de moles d'unités de formule dissoutes dans la solution


