12.5 : Théorème binomial
- Page ID
- 194124
À la fin de cette section, vous serez en mesure de :
- Utiliser le triangle de Pascal pour développer un binôme
- Evaluer un coefficient binomial
- Utiliser le théorème binomial pour développer un binôme
Avant de commencer, répondez à ce questionnaire de préparation.
- Simplifiez :\(\frac{7 \cdot 6 \cdot 5 \cdot 4}{4 \cdot 3 \cdot 2 \cdot 1}\).
Si vous avez oublié ce problème, consultez l'exemple 1.25. - Agrandir :\((3 x+5)^{2}\).
Si vous avez oublié ce problème, consultez l'exemple 5.32. - Agrandir :\((x-y)^{2}\).
Si vous avez oublié ce problème, consultez l'exemple 5.32.
Utiliser le triangle de Pascal pour développer un binôme
Dans nos travaux précédents, nous avons quadrillé des binômes soit en utilisant FOIL, soit en utilisant le modèle de carrés binomiaux. Nous pouvons également dire que nous nous sommes développés\((a+b)^{2}\).
\((a+b)^{2}=a^{2}+2 a b+b^{2}\)
Pour nous développer\((a+b)^{3}\), nous reconnaissons que c'est le cas\((a+b)^{2}(a+b)\) et nous nous multiplions.
\((a+b)^{3}\)
\((a+b)^{2}(a+b)\)
\(\left(a^{2}+2 a b+b^{2}\right)(a+b)\)
\(a^{3}+2 a^{2} b+a b^{2}+a^{2} b+2 a b^{2}+b^{3}\)
\(a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\)
\((a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\)
Pour trouver une méthode moins fastidieuse qui fonctionnera pour les extensions supérieures, par exemple\((a+b)^{7}\), nous recherchons à nouveau des modèles dans certaines extensions.
| Nombre de termes | Premier mandat | Dernier mandat | |
|---|---|---|---|
| \((a+b)^{1}=a+b\) | \(2\) | \(a^{1}\) | \(b^{1}\) |
| \((a+b)^{2}=a^{2}+2 a b+b^{2}\) | \(3\) | \(a^{2}\) | \(b^{2}\) |
| \((a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\) | \(4\) | \(a^{3}\) | \(b^{3}\) |
| \((a+b)^{4}=a^{4}+4 a^{3} b+6 a^{2} b^{2}+4 a b^{3}+b^{4}\) | \(5\) | \(a^{4}\) | \(b^{4}\) |
| \((a+b)^{5}=a^{5}+5 a^{4} b+10 a^{3} b^{2}+10 a^{2} b^{3}+5 a b^{4}+b^{5}\) | \(6\) | \(a^{5}\) | \(b^{5}\) |
| \((a+b)^{n}\) | \(n\) | \(a^{n}\) | \(b^{n}\) |
Notez que le premier et le dernier terme n'indiquent qu'une seule variable. Souvenez-vous de cela\(a^{0}=1\), afin que nous puissions réécrire le premier et le dernier terme pour inclure les deux variables. Par exemple, nous pourrions l'étendre\((a+b)^{3}\) pour afficher chaque terme avec les deux variables.
En général, nous n'affichons pas les exposants nuls, comme nous l'\(x\)écrivons habituellement\(1x\).
Les tendances de l'expansion de\((a+b)^{n}\)
- Le nombre de termes est de\(n+1\).
- Le premier terme est\(a^{n}\) et le dernier terme est\(b^{n}\).
- Les exposants sur\(a\) diminuent d'un pour chaque terme, de gauche à droite.
- Les exposants\(b\) augmentent d'un pour chaque terme, de gauche à droite.
- La somme des exposants d'un terme est de\(n\).
Regardons un exemple pour mettre en évidence les trois derniers modèles.
À partir des modèles que nous avons identifiés, nous voyons les variables dans l'expansion de\((a+b)^{n}\), seraient
\((a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n}\).
Pour trouver les coefficients des termes, nous écrivons à nouveau nos extensions en nous concentrant sur les coefficients. Nous réécrivons les coefficients vers la droite pour former un tableau de coefficients.
Le tableau de droite s'appelle le triangle de Pascal. Notez que chaque nombre du tableau est la somme des deux nombres les plus proches de la ligne ci-dessus. Nous pouvons trouver la ligne suivante en commençant et en terminant par un, puis en ajoutant deux numéros adjacents.
Ce triangle donne les coefficients des termes lorsque nous développons des binômes.
Triangle de Pascal
Dans l'exemple suivant, nous utiliserons ce triangle et les motifs que nous avons reconnus pour développer le binôme.
Utilisez le triangle de Pascal pour l'agrandir\((x+y)^{6}\).
Solution :
Nous savons que les variables de cette extension suivront le modèle que nous avons identifié. Les exposants non nuls de\(x\) commenceront à six et diminueront à un. Les exposants non nuls de\(y\) commenceront à un et augmenteront jusqu'à six. La somme des exposants de chaque terme sera de six. Dans notre modèle,\(a=x\) et\(b=y\).
\(\begin{array}{l}{(a+b)^{n}=a^{n}+\_\_\_a^{n-1} b^{1}+\_\_\_a^{n-2} b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n}} \\ {(x+y)^{6}=x^{6}+\_\_\_x^{5} y^{1}+\_\_\_x^{4} y^{2}+\_\_\_x^{3} y^{3}+\_\_\_x^{2} y^{4}+\_\_\_x^{1} y^{5}+y^{6}}\end{array}\)
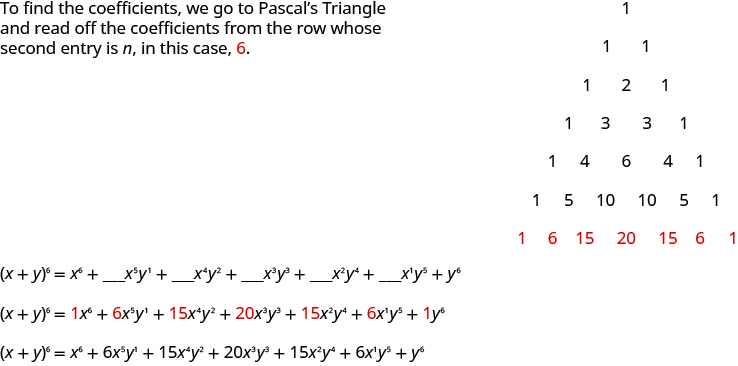
Utilisez le triangle de Pascal pour l'agrandir\((x+y)^{5}\).
- Réponse
-
\(\begin{array}{l}{x^{5}+5 x^{4} y+10 x^{3} y^{2}+10 x^{2} y^{3}} {+5 x y^{4}+y^{5}}\end{array}\)
Utilisez le triangle de Pascal pour l'agrandir\((p+q)^{7}\).
- Réponse
-
\(\begin{array}{c}{p^{7}+7 p^{6} q+21 p^{5} q^{2}+35 p^{4} q^{3}} {+35 p^{3} q^{4}+21 p^{2} q^{5}+7 p q^{6}+q^{7}}\end{array}\)
Dans l'exemple suivant, nous voulons développer un binôme avec une variable et une constante. Nous devons identifier le\(a\) et\(b\) appliquer soigneusement le modèle.
Utilisez le triangle de Pascal pour l'agrandir\((x+3)^{5}\).
Solution :
Nous identifions\(a\) la\(b\) fin du motif.
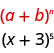
Dans notre modèle,\(a=x\) et\(b=3\).
Nous savons que les variables de cette extension suivront le modèle que nous avons identifié. La somme des exposants de chaque terme sera de cinq.
\((a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n} \)
\((x+3)^{5}=x^{5}+\_\_\_x^{4}\cdot3^{1}+\_\_\_x^{3}\cdot3^{2}+\_\_\_x^{2}\cdot3^{3}+\_\_\_x^{1}\cdot3^{4}+3^{5}\)

Utilisez le triangle de Pascal pour l'agrandir\((x+2)^{4}\).
- Réponse
-
\(x^{4}+8 x^{3}+24 x^{2}+32 x+16\)
Utilisez le triangle de Pascal pour l'agrandir\((x+1)^{6}\).
- Réponse
-
\(\begin{array}{l}{x^{6}+6 x^{5}+15 x^{4}+20 x^{3}+15 x^{2}} {+6 x+1}\end{array}\)
Dans l'exemple suivant, le binôme est une différence et le premier terme a une constante multipliée par la variable. Une fois que nous avons identifié la\(a\) fin\(b\) du motif, nous devons à nouveau appliquer le motif avec soin.
Utilisez le triangle de Pascal pour l'agrandir\((3x-2)^{4}\).
Solution :
Nous identifions\(a\) la\(b\) fin du motif.
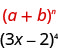
Dans notre modèle,\(a=3x\) et\(b=-2\).

\((a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n} \)
\((3 x-2 )^{4}=1 \cdot\left(\stackrel{3}{x}+4(3 x)^{3}(-2)^{1}+6(3 x)^{2}(-2)^{2}+4(3 x)^{1}(-2)^{3}+1 \cdot(-2)^{4}\right.\)
\((3 x-2)^{4}=81 x^{4}+4\left(27 x^{3}\right)(-2)+6\left(9 x^{2}\right)(4)+4(3 x)(-8)+1 \cdot 16\)
\((3 x-2 )^{4}=81 x^{4}-216 x^{3}+216 x^{2}-96 x+16\)
Utilisez le triangle de Pascal pour l'agrandir\((2x-3)^{4}\).
- Réponse
-
\(16 x^{4}-96 x^{3}+216 x^{2}-216 x+81\)
Utilisez le triangle de Pascal pour l'agrandir\((2x-1)^{6}\).
- Réponse
-
\(\begin{array}{l}{64 x^{6}-192 x^{5}+240 x^{4}-160 x^{3}} {+60 x^{2}-12 x+1}\end{array}\)
Évaluer un coefficient binomial
Bien que le Triangle de Pascal soit une méthode pour développer un binôme, nous examinerons également une autre méthode. Avant d'en arriver là, nous devons introduire une notation factorielle supplémentaire. Cette notation est utilisée non seulement pour étendre les binômes, mais également pour l'étude et l'utilisation des probabilités.
Pour trouver les coefficients des termes des binômes étendus, nous devrons être en mesure d'évaluer la notation\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) appelée coefficient binomial. Nous\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) entendons «\(n\) choisir\(r\) » ou «\(r\) à\(n\) prendre à la fois ».
Un coefficient binomial\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\), où\(r\) et\(b\) sont des nombres entiers avec\(0 \leq r \leq n\), est défini comme
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}\)
Nous\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) lisons «\(n\) choisir\(r\) » ou «\(n\) pris\(r\) à la fois ».
Évaluez :
- \(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)\)
- \(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)\)
- \(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)\)
- \(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)\)
Solution :
a. Nous utiliserons la définition d'un coefficient binomial,
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}\)
\(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)\)
Utilisez la définition\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), où\(n=5, r=1\).
\(\frac{5 !}{1 !(5-1) !}\)
Simplifiez.
\(\frac{5 !}{1 !(4) !}\)
Réécrire en\(5!\) tant que\(5\cdot 4!\)
\(\frac{5 \cdot 4 !}{1 ! \cdot 4 !}\)
Simplifiez en supprimant les facteurs communs.
\(\frac{5\cdot \cancel{4 !}}{1 ! \cdot \cancel{4 !}}\)
Simplifiez.
\(5\)
\(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)=5\)
b.\(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)\)
Utilisez la définition\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), où\(n=7, r=7\).
\(\frac{7 !}{7 !(7-7) !}\)
Simplifiez.
\(\frac{7 !}{7 !(0) !}\)
Simplifiez. N'oubliez pas\(0!=1\).
\(1\)
\(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)=1\)
c.\(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)\)
Utilisez la définition\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), où\(n=4, r=0\).
\(\frac{4 !}{0 !(4-0) !}\)
Simplifiez.
\(\frac{4 !}{0 !(4) !}\)
Simplifiez.
\(1\)
\(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)=1\)
d.\(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)\)
Utilisez la définition\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), où\(n=8, r=5\).
\(\frac{8 !}{5 !(8-5) !}\)
Simplifiez.
\(\frac{8 !}{5 !(3) !}\)
Réécrivez\(8!\) en fonction des facteurs courants\(8\cdot 7\cdot 6\cdot 5!\) et supprimez-les.
\(\frac{8\cdot7\cdot\cancel{6}\cdot\cancel{5!}}{\cancel{5!}\cdot\cancel{3}\cdot\cancel{2}\cdot1}\)
Simplifiez.
\(56\)
\(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)=56\)
Évaluez chaque coefficient binomial :
- \(\left( \begin{array}{l}{6} \\ {1}\end{array}\right)\)
- \(\left( \begin{array}{l}{8} \\ {8}\end{array}\right)\)
- \(\left( \begin{array}{l}{5} \\ {0}\end{array}\right)\)
- \(\left( \begin{array}{l}{7} \\ {3}\end{array}\right)\)
- Réponse
-
- \(6\)
- \(1\)
- \(1\)
- \(35\)
Évaluez chaque coefficient binomial :
- \(\left( \begin{array}{l}{2} \\ {1}\end{array}\right)\)
- \(\left( \begin{array}{l}{11} \\ {11}\end{array}\right)\)
- \(\left( \begin{array}{l}{9} \\ {0}\end{array}\right)\)
- \(\left( \begin{array}{l}{6} \\ {5}\end{array}\right)\)
- Réponse
-
- \(2\)
- \(1\)
- \(1\)
- \(6\)
Dans l'exemple précédent,,\((a)\)\((b)\),\((c)\) démontrez certaines propriétés spéciales des coefficients binomiaux.
Propriétés des coefficients binomiaux
\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n \quad \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1 \quad \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
Utiliser le théorème binomial pour développer un binôme
Nous sommes maintenant prêts à utiliser la méthode alternative d'extension des binômes. Le théorème binomial utilise le même modèle pour les variables, mais utilise le coefficient binomial pour le coefficient de chaque terme.
Théorème binomial
Pour tous les nombres réels\(a\) et\(b\) tous les entiers positifs\(n\),
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Utilisez le théorème binomial pour développer\((p+q)^{4}\).
Solution :
Nous identifions\(a\) la\(b\) fin du motif.
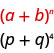
Dans notre modèle,\(a=p\) et\(b=q\).
Nous utilisons le théorème binomial.
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Remplacez par les valeurs\(a=p, b=q\) et\(n=4\).
\((p+q)^{4}=\left( \begin{array}{c}{4} \\ {0}\end{array}\right) p^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right) p^{4-1} q^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right) p^{4-2} q^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right) p^{4-3} q^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) q^{4}\)
Simplifiez les exposants.
\((p+q)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right) p^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right) p^{3} q+\left( \begin{array}{c}{4} \\ {2}\end{array}\right) p^{2} q^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right) p q^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) q^{4}\)
Évaluez les coefficients, souvenez-vous,\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
\((p+q)^{4}=1 p^{4}+4 p^{3} q^{1}+\frac{4 !}{2 !(2) !} p^{2} q^{2}+\frac{4 !}{3 !(4-3) !} p^{1} q^{3}+1 q^{4}\)
\((p+q)^{4}=p^{4}+4 p^{3} q+6 p^{2} q^{2}+4 p q^{3}+q^{4}\)
Utilisez le théorème binomial pour développer\((x+y)^{5}\).
- Réponse
-
\(\begin{array}{l}{x^{5}+5 x^{4} y+10 x^{3} y^{2}+10 x^{2} y^{3}} {+5 x y^{4}+y^{5}}\end{array}\)
Utilisez le théorème binomial pour développer\((m+n)^{6}\).
- Réponse
-
\(\begin{array}{l}{m^{6}+6 m^{5} n+15 m^{4} n^{2}+20 m^{3} n^{3}} {+15 m^{2} n^{4}+6 m n^{5}+n^{6}}\end{array}\)
Remarquez que lorsque nous avons développé\((p+q)^{4}\) le dernier exemple, en utilisant le théorème binomial, nous avons obtenu les mêmes coefficients que ceux obtenus en utilisant le triangle de Pascal.
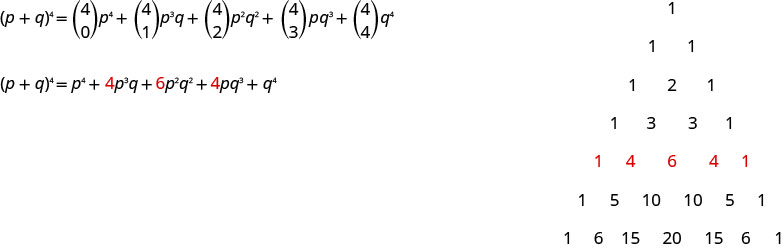
L'exemple suivant, le binôme est une différence. Lorsque le binôme est une différence, nous devons faire attention à identifier les valeurs que nous utiliserons dans le modèle.
Utilisez le théorème binomial pour développer\((x-2)^{5}\).
Solution :
Nous identifions\(a\) la\(b\) fin du motif.
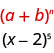
Dans notre modèle,\(a=x\) et\(b=-2\).
Nous utilisons le théorème binomial.
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Substituez les valeurs\(a=x, b=-2\), et\(n=5\).
\((x-2)^{5}=\left( \begin{array}{l}{5} \\ {0}\end{array}\right) x^{5}+\left( \begin{array}{c}{5} \\ {1}\end{array}\right) x^{5-1}(-2)^{1}+\left( \begin{array}{c}{5} \\ {2}\end{array}\right) x^{5-2}(-2)^{2}+\left( \begin{array}{c}{5} \\ {3}\end{array}\right) x^{5-3}(-2)^{3}+\left( \begin{array}{c}{5} \\ {4}\end{array}\right) x^{5-4}(-2)^{4}+\left( \begin{array}{c}{5} \\ {5}\end{array}\right)(-2)^{5}\)
Simplifiez les coefficients. N'oubliez pas,\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\).
\((x-2)^{5}=\left( \begin{array}{l}{5} \\ {0}\end{array}\right) x^{5}+\left( \begin{array}{c}{5} \\ {1}\end{array}\right) x^{4}(-2)+\left( \begin{array}{c}{5} \\ {2}\end{array}\right) x^{3}(-2)^{2}+\left( \begin{array}{c}{5} \\ {3}\end{array}\right) x^{2}(-2)^{3}+\left( \begin{array}{c}{5} \\ {4}\end{array}\right) x(-2)^{4}+\left( \begin{array}{c}{5} \\ {5}\end{array}\right)(-2)^{5}\)
\((x-2)^{5}=1 x^{5}+5(-2) x^{4}+\frac{5 !}{2 ! \cdot 3 !}(-2)^{2} x^{3}+\frac{5 !}{3 ! 2 !}(-2)^{3} x^{2}+\frac{5 !}{4 !1 !}(-2)^{4} x+1(-2)^{5}\)
\((x-2)^{5}=x^{5}+5(-2) x^{4}+10 \cdot 4 \cdot x^{3}+10(-8) x^{2}+5 \cdot 16 \cdot x+1(-32)\)
\((x-2)^{5}=x^{5}-10 x^{4}+40 x^{3}-80 x^{2}+80 x-32\)
Utilisez le théorème binomial pour développer\((x-3)^{5}\).
- Réponse
-
\(\begin{array}{l}{x^{5}-15 x^{4}+90 x^{3}-270 x^{2}} {+405 x-243}\end{array}\)
Utilisez le théorème binomial pour développer\((y-1)^{6}\).
- Réponse
-
\(\begin{array}{l}{y^{6}-6 y^{5}+15 y^{4}-20 y^{3}+15 y^{2}} {-6 y+1}\end{array}\)
Les choses peuvent devenir compliquées lorsque les deux termes ont un coefficient et une variable.
Utilisez le théorème binomial pour développer\((2x-3y)^{4}\).
Solution :
Nous identifions\(a\) la\(b\) fin du motif.
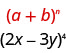
Dans notre modèle,\(a=2x\) et\(b=-3y\).
Nous utilisons le théorème binomial.
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Remplacez par les valeurs\(a=2x, b=-3y\) et\(n=4\).
\((2 x-3 y)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right)(2 x)^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right)(2 x)^{4-1}(-3 y)^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right)(2 x)^{4-2}(-3 y)^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right)(2 x)^{4-3}(-3 y)^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) (-3y)^{4}\)
Simplifiez les exposants.
\((2 x-3 y)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right)(2 x)^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right)(2 x)^{3}(-3 y)^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right)(2 x)^{2}(-3 y)^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right)(2 x)^{1}(-3 y)^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right)(-3 y)^{4}\)
Evaluez les coefficients. N'oubliez pas,\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
\((2 x-3 y)^{4}=1(2 x)^{4}+4(2 x)^{3}(-3 y)^{1}+\frac{4 !}{2 !(2 x) !}(2 x)^{2}+\frac{4 !}{3 !(4-3) !}(2 x)^{3}(-3 y)^{3}+1(-3 y)^{4}\)
\((2 x-3 y)^{4}=16 x^{4}+4 \cdot 8 x^{3}(-3 y)+6\left(4 x^{2}\right)\left(9 y^{2}\right)+4(2 x)\left(-27 y^{3}\right)+81 y^{4}\)
\((2 x-3 y)^{4}=16 x^{4}-96 x^{3} y+216 x^{2} y^{2}-216 x y^{3}+81 y^{4}\)
Utilisez le théorème binomial pour développer\((3x-2y)^{5}\).
- Réponse
-
\(\begin{array}{l}{243 x^{5}-810 x^{4} y+1080 x^{3} y^{2}} {-720 x^{2} y^{3}+240 x y^{4}-32 y^{5}}\end{array}\)
Utilisez le théorème binomial pour développer\((4x-3y)^{4}\).
- Réponse
-
\(\begin{array}{l}{256 x^{4}-768 x^{3} y+864 x^{2} y^{2}} {-432 x y^{3}+81 y^{4}}\end{array}\)
La vraie beauté du théorème binomial est qu'il donne une formule pour un terme particulier de l'expansion sans avoir à calculer la somme complète. Cherchons un modèle dans le théorème binomial.
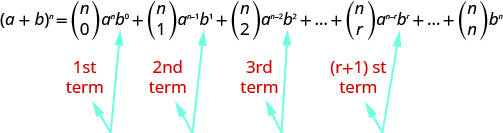
Notez que dans chaque cas, l'exposant sur le\(b\) est inférieur d'un au numéro du terme. Le\((r+1)^{st}\) terme est le terme où l'exposant de\(b\) est\(r\). Nous pouvons donc utiliser le format du\((r+1)^{st}\) terme pour trouver la valeur d'un terme spécifique.
Trouver un terme spécifique dans une extension binomiale
Le\((r+1)^{s t}\) terme utilisé dans l'extension de\((a+b)^{n}\) est
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}\)
Trouvez le quatrième terme de\((x+y)^{7}\).
Solution :
| Dans notre modèle,\(n=7, a=x\) et\(b=y\). | 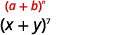 |
|
Nous sommes à la recherche d'un quatrième mandat. Depuis\(r+1=4\), alors\(r=3\). |
|
| Écrivez la formule | 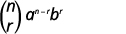 |
| Remplacez les valeurs par\(n=7, r=3, a=x\), et\(b=y\). | 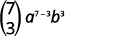 |
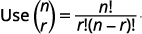 |
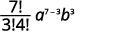 |
| Simplifiez. | 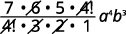 |
| Simplifiez. |  |
Trouvez le troisième terme de\((x+y)^{6}\).
- Réponse
-
\(15x^{4}y^{2}\)
Trouvez le cinquième mandat de\((a+b)^{8}\).
- Réponse
-
\(8ab^{7}\)
Détermine le coefficient du\(x^{6}\) terme de\((x+3)^{9}\).
Solution :
| Dans notre modèle, alors\(n=9, a=x\), et\(b=3\). |

|
| Nous cherchons le coefficient du\(x^{6}\) terme. Depuis\(a=x\), et\(x^{9-r}=x^{6}\), nous le savons\(r=3\). | |
| Écrivez la formule. |
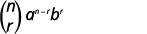
|
| Remplacez les valeurs par\(n=9, 4=3, a=x\), et\(b=3\). |
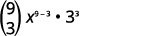
|
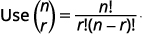
|
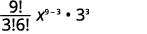
|
| Simplifiez. |
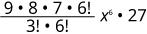
|
| Simplifiez. |
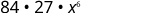
|
| Simplifiez. |

|
Détermine le coefficient du\(x^{5}\) terme de\((x+4)^{8}\).
- Réponse
-
\(7,168\)
Détermine le coefficient du\(x^{4}\) terme de\((x+2)^{7}\).
- Réponse
-
\(280\)
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner avec des séquences.
Concepts clés
- Modèles dans l'extension de \ ((a+b) ^ {n} \ (
- Le nombre de termes est de\(n+1\).
- Le premier terme est\(a^{n}\) et le dernier terme est\(b^{n}\).
- Les exposants sur\(a\) diminuent d'un pour chaque terme, de gauche à droite.
- Les exposants\(b\) augmentent d'un pour chaque terme, de gauche à droite.
- La somme des exposants d'un terme est de\(n\).
- Triangle de Pascal

- Coefficient binomial \(\left( \begin{array}{l}{\mathbf{n}} \\ {\mathbf{r}}\end{array}\right)\): Un coefficient binomial\(\left( \begin{array}{l}{\mathbf{n}} \\ {\mathbf{r}}\end{array}\right)\), où\(r\) et\(n\) sont des nombres entiers avec\(0≤r≤n\), est défini comme
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}\)
Nous\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) entendons «\(n\) choisir\(r\) » ou «\(r\) à\(n\) prendre à la fois ».
- Propriétés des coefficients binomiaux
\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n \quad \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1 \quad \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
- Théorème binomial :
Pour tous les nombres\(a\) réels\(b\) et les entiers positifs\(n\),
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)


