12.4 : Séquences et séries géométriques
- Page ID
- 194102
À la fin de cette section, vous serez en mesure de :
- Déterminer si une séquence est géométrique
- Trouvez le terme général (\(n\)le terme) d'une séquence géométrique
- Trouve la somme des premiers\(n\) termes d'une suite géométrique
- Trouvez la somme d'une série géométrique infinie
- Appliquez des séquences et des séries géométriques dans le monde réel
Avant de commencer, répondez à ce questionnaire de préparation.
- Simplifiez :\(\frac{24}{32}\).
Si vous avez oublié ce problème, consultez l'exemple 1.24. - Évaluer : a.\(3^{4}\)\(\left(\frac{1}{2}\right)^{4}\) b.
Si vous avez oublié ce problème, consultez l'exemple 1.19. - Si\(f(x)=4 \cdot 3^{x}\), trouvez un.\(f(1)\) b.\(f(2)\)\(f(3)\) c.
Si vous avez oublié ce problème, consultez l'exemple 3.49.
Déterminer si une séquence est géométrique
Nous sommes maintenant prêts à examiner le deuxième type spécial de séquence, la séquence géométrique.
Une séquence est appelée séquence géométrique si le rapport entre les termes consécutifs est toujours le même. Le rapport entre des termes consécutifs dans une séquence géométrique est\(r\) le rapport commun, où\(n\) est supérieur ou égal à deux.
Une séquence géométrique est une séquence dans laquelle le rapport entre des termes consécutifs est toujours le même.
Le rapport entre les termes consécutifs\(\frac{a_{n}}{a_{n-1}}\),\(r\), est le ratio commun. \(n\)est supérieur ou égal à deux.
Considérez ces séquences.
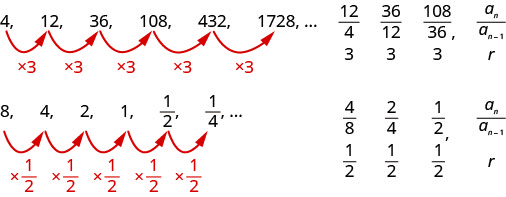
Déterminez si chaque séquence est géométrique. Dans l'affirmative, indiquez le ratio commun.
- \(4,8,16,32,64,128, \dots\)
- \(-2,6,-12,36,-72,216, \dots\)
- \(27,9,3,1, \frac{1}{3}, \frac{1}{9}, \ldots\)
Solution :
Pour déterminer si la séquence est géométrique, nous trouvons le ratio des termes consécutifs affichés.
a. Trouvez le ratio des termes consécutifs
\(\begin{aligned} 4, \quad& \:8, \quad 16, \quad 32, \quad 64, \quad 128, \dots \\ &\frac{8}{4} \quad\frac{16}{8}\quad\frac{32}{16}\quad\frac{64}{32}\quad\frac{128}{64} \\ &\:2 \quad\:\:\: 2 \quad\quad2\quad\quad2\quad\quad2 \end{aligned}\)
La séquence est géométrique. La ration courante est\(r=2\).
b. Trouvez le ratio des termes consécutifs
\(\begin{aligned}-\:2,\quad &\:\:\:6,\quad -12,\quad 36,\quad \:-72\quad \:\:216,\dots \\ & \frac{6}{-2}\quad\frac{-12}{6}\quad\frac{36}{-12}\quad\frac{-72}{36}\quad\frac{216}{-72} \\ & -3\quad -2\quad\:\: -3\quad \:\:\:-2\quad \:\:-3 \end{aligned}\)
La séquence n'est pas géométrique. Il n'existe pas de ratio commun.
c. Trouvez le ratio des termes consécutifs
\(\begin{aligned}27,\quad &\:\:9,\quad 3,\quad 1,\quad \frac{1}{3},\quad \frac{1}{9}, \ldots\\ & \frac{9}{27}\quad\frac{3}{9}\quad\frac{1}{3}\quad\frac{\frac{1}{3}}{1}\quad\frac{\frac{1}{9}}{\frac{1}{3}}\\ &\frac{1}{3}\quad\;\:\frac{1}{3}\quad\frac{1}{3}\quad\:\frac{1}{3}\quad\:\frac{1}{3}\end{aligned}\)
La séquence est géométrique. Le ratio commun est\(r=\frac{1}{3}\).
Déterminez si chaque séquence est géométrique. Dans l'affirmative, indiquez le ratio commun.
- \(7,21,63,189,567,1,701, \dots\)
- \(64,16,4,1, \frac{1}{4}, \frac{1}{16}, \dots\)
- \(2,4,12,48,240,1,440, \dots\)
- Réponse
-
- La séquence est géométrique avec un ratio commun\(r=3\).
- La séquence est géométrique avec un ratio commun\(d=\frac{1}{4}\).
- La séquence n'est pas géométrique. Il n'existe pas de ratio commun.
Déterminez si chaque séquence est géométrique. Dans l'affirmative, indiquez le ratio commun.
- \(-150,-30,-15,-5,-\frac{5}{2}, 0, \dots\)
- \(5,10,20,40,80,160, \dots\)
- \(8,4,2,1, \frac{1}{2}, \frac{1}{4}, \ldots\)
- Réponse
-
- La séquence n'est pas géométrique. Il n'existe pas de ratio commun.
- La séquence est géométrique avec un ratio commun\(r=2\).
- La séquence est géométrique avec un ratio commun\(r=\frac{1}{2}\).
Si nous connaissons le premier terme et le ratio commun\(r\), nous pouvons lister un nombre fini de termes de la séquence.\(a_{1}\)
Écrivez les cinq premiers termes de la séquence où le premier terme est\(3\) et le ratio commun est\(r=−2\).
Solution :
Nous commençons par le premier terme et le multiplions par le ratio commun. Ensuite, nous multiplions ce résultat par le ratio commun pour obtenir le terme suivant, et ainsi de suite.
\(\begin{array}{cccc}{a_{1}} & {a_{2}} & {a_{3}} & {a_{4}} & {a_{5}} \\ {3} & {3 \cdot(-2)} & {-6 \cdot(-2)} & {12 \cdot(-2)} & {-24 \cdot(-2)} \\& {-6} & {12} & {-24} & {48}\end{array}\)
Réponse :
La séquence est\(3,-6,12,-24,48, \dots\)
Écrivez les cinq premiers termes de la séquence où le premier terme est\(7\) et le ratio commun est\(r=−3\).
- Réponse
-
\(7,-21,63,-189,567\)
Écrivez les cinq premiers termes de la séquence où le premier terme est\(6\) et le ratio commun est\(r=−4\).
- Réponse
-
\(6,-24,96,-384,1536\)
Trouvez le terme général (\(n\)le terme) d'une séquence géométrique
Tout comme nous avons trouvé une formule pour le terme général d'une séquence et une séquence arithmétique, nous pouvons également trouver une formule pour le terme général d'une séquence géométrique.
Écrivons les premiers termes de la séquence où le premier terme est\(a_{1}\) et le ratio commun est\(r\). Nous chercherons ensuite un modèle.
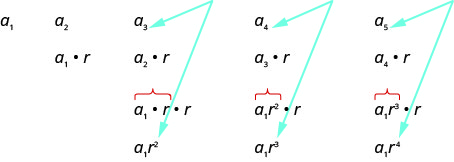
En recherchant un modèle dans les cinq termes ci-dessus, nous constatons que chacun des termes commence par\(a_{1}\).
Le premier terme,\(a_{1}\), n'est multiplié par aucun\(r\). Au second terme, le\(a_{1}\) est multiplié par\(r\). Au troisième terme, le\(a_{1}\) est multiplié par\(r\) deux (\(r⋅r\)ou\(r^{2}\)). Au quatrième terme, le\(a_{1}\) est multiplié par\(r\) trois (\(r⋅r⋅r\)ou\(r^{3}\)) et au cinquième terme,\(a_{1}\) il est multiplié par\(r\) quatre. Dans chaque terme, le nombre de fois\(a_{1}\) multiplié par\(r\) est inférieur d'un au nombre du terme. Cela nous amène à ce qui suit
\(a_{n}=a_{1} r^{n-1}\)
Le terme général d'une séquence géométrique avec un premier terme\(a_{1}\) et un ratio commun\(r\) est
\(a_{n}=a_{1} r^{n-1}\)
Nous utiliserons cette formule dans l'exemple suivant pour trouver le quatorzième terme d'une séquence.
Détermine le quatorzième terme d'une séquence où le premier terme est\(64\) et le ratio commun est\(r=\frac{1}{2}\).
Solution :
\(a_{n}=a_{1} r^{n-1}\)
Pour trouver le quatorzième terme\(a_{14}\), utilisez la formule avec\(a_{1}=64\) et\(r=\frac{1}{2}\).
\(a_{14}=64\left(\frac{1}{2}\right)^{14-1}\)
Substituez les valeurs.
\(a_{14}=64\left(\frac{1}{2}\right)^{13}\)
Simplifiez.
\(a_{14}=\frac{1}{128}\)
Détermine le treizième terme d'une séquence où le premier terme est\(81\) et le ratio commun est\(r=\frac{1}{3}\).
- Réponse
-
\(\frac{1}{6,561}\)
Détermine le douzième terme d'une séquence où le premier terme est\(256\) et le ratio commun est\(r=\frac{1}{4}\).
- Réponse
-
\(\frac{1}{16,384}\)
Parfois, nous ne connaissons pas le ratio commun et nous devons utiliser les informations fournies pour le trouver avant de trouver le terme demandé.
Trouvez le douzième terme de la séquence\(3, 6, 12, 24, 48, 96, …\) Trouvez le terme général de la séquence.
Solution :
Pour trouver le douzième terme, nous utilisons la formule\(a_{n}=a_{1} r^{n-1}\), et nous devons donc d'abord déterminer\(a_{1}\) et le ratio commun\(r\).
Le premier mandat est de trois.
\(3,6,12,24,48,96, \dots\)
\(a_{1}=3\)
Trouvez le ratio commun.
\(\begin{array}{l}{\frac{6}{3} \quad \frac{12}{6} \quad \frac{24}{12} \quad \frac{48}{24} \quad \frac{96}{48}} \\ {2 \:\:\:\quad 2 \quad \:\:2 \quad\:\:\: 2 \:\:\quad \:2} \\ {\text { The common ratio is } r=2}\end{array}\)
Pour trouver le douzième terme\(a_{12}\), utilisez la formule avec\(a_{1}=3\) et\(r=2\).
\(a_{n}=a_{1} r^{n-1}\)
Substituez les valeurs.
\(a_{12}=3 \cdot 2^{12-1}\)
Simplifiez.
\(a_{12}=3 \cdot 2^{11}\)
\(a_{12}=6,144\)
Trouvez le terme général. Nous utilisons la formule avec\(a_{1}=3\) et\(r=2\).
\(a_{n}=a_{1} r^{n-1}\)
\(a_{n}=3(2)^{n-1}\)
Trouvez le neuvième terme de la séquence\(6, 18, 54, 162, 486, 1,458, … \) Ensuite, trouvez le terme général de la séquence.
- Réponse
-
\(a_{9}=39,366 .\)Le terme général est\(a_{n}=6(3)^{n-1}\).
Trouvez le onzième terme de la séquence\(7, 14, 28, 56, 112, 224, …\) Ensuite, trouvez le terme général de la séquence.
- Réponse
-
\(a_{11}=7,168 .\)Le terme général est\(a_{n}=7(2)^{n-1}\).
Trouvez la somme des premiers\(n\) termes d'une séquence géométrique
Nous avons trouvé la somme des séquences générales et des séquences arithmétiques. Nous allons maintenant faire de même pour les séquences géométriques. La somme,\(S_{n}\), des premiers\(n\) termes d'une séquence géométrique s'écrit sous la forme\(S_{n}=a_{1}+a_{2}+a_{3}+\ldots+a_{n}\). Nous pouvons écrire cette somme en commençant par le premier terme\(a_{1}\), et continuer à la multiplier par\(r\) pour obtenir le terme suivant comme suit :
\(S_{n}=a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}\)
Multiplions également les deux côtés de l'équation par\(r\).
\(r S_{n}=a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n}\)
Ensuite, nous soustrayons ces équations. Nous verrons que lorsque nous soustrayons, tous les termes sauf le premier terme de l'équation supérieure et le dernier terme de l'équation inférieure se soustraient à zéro.
\(\begin{aligned} S_{n}&= a_{1}+a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n-1} \\ r S_{n} &= a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n-1}+a_{1} r^{n}\\\hline S_{n}-r S_{n} &= a_{1} -a_{1}r^{n} \end{aligned}\)
Nous prenons en compte les deux côtés.
\(S_{n}(1-r)=a_{1}\left(1-r^{n}\right)\)
Pour obtenir la formule de\(S_{n}\), divisez les deux côtés par\((1-r)\).
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
La somme\(S_{n}\) des premiers\(n\) termes d'une séquence géométrique est
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
où\(a_{1}\) est le premier terme et\(r\) le ratio commun, et n'\(r\)est pas égal à un.
Nous appliquons cette formule dans l'exemple suivant où les premiers termes de la séquence sont donnés. Notez que la somme d'une séquence géométrique devient généralement très importante lorsque le rapport commun est supérieur à un.
Trouve la somme des premiers\(20\) termes de la séquence géométrique\(7, 14, 28, 56, 112, 224, …\)
Solution :
Pour trouver la somme, nous utiliserons la formule\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\). Nous savons\(a_{1}=7\)\(r=2\), et\(n=20\),
Connaître\(a_{1}=7, r=2\) et\(n=20\) utiliser la formule de somme.
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
Substituez les valeurs.
\(S_{20}=\frac{7\left(1-2^{20}\right)}{1-2}\)
Simplifiez.
\(S_{20}=7,340,025\)
Trouve la somme des premiers\(20\) termes de la séquence géométrique\(3, 6, 12, 24, 48, 96, …\)
- Réponse
-
\(3,145,725\)
Trouve la somme des premiers\(20\) termes de la séquence géométrique\(6, 18, 54, 162, 486, 1,458, …\)
- Réponse
-
\(10,460,353,200\)
Dans l'exemple suivant, on nous donne la somme en notation de sommation. Bien qu'il soit possible d'ajouter tous les termes, le plus souvent, il est plus facile d'utiliser la formule pour trouver la somme des premiers\(n\) termes.
Pour utiliser la formule, nous avons besoin de\(r\). Nous pouvons le trouver en écrivant les premiers termes de la séquence et en trouvant leur ratio. Une autre option consiste à réaliser qu'en notation de sommation, une séquence est écrite sous la forme\(\sum_{i=1}^{k} a(r)^{i}\), où se\(r\) trouve le ratio commun.
Trouvez la somme :\(\sum_{i=1}^{15} 2(3)^{i}\).
Solution :
Pour trouver la somme, nous utiliserons la formule\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\), qui nécessite\(a_{1}\) et\(r\). Nous rédigerons quelques termes afin d'obtenir les informations nécessaires.
 |
|
| Écrivez les premiers termes. | 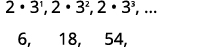 |
| Identifiez\(a_{1}\). |  |
| Trouvez le ratio commun. |  |
| Connaître\(a_{1}=6\)\(r=3\) et utiliser\(n=15\) la formule de somme. | 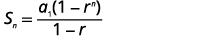 |
| Substituez les valeurs. | 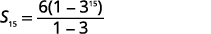 |
| Simplifiez. | 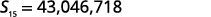 |
Trouvez la somme :\(\sum_{i=1}^{15} 6(2)^{i}\).
- Réponse
-
\(393,204\)
Trouvez la somme :\(\sum_{i=1}^{10} 5(2)^{i}\).
- Réponse
-
\(10,230\)
Trouvez la somme d'une série géométrique infinie
Si nous prenons une séquence géométrique et que nous ajoutons les termes, nous obtenons une somme appelée série géométrique. Une série géométrique infinie est une somme infinie dont le premier terme est\(a_{1}\) un ratio commun est\(r\) et est écrit
\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\ldots\)
Une série géométrique infinie est une somme infinie dont le premier terme est\(a_{1}\) un ratio commun est\(r\) et est écrit
\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\dots\)
Nous savons comment trouver la somme des premiers\(n\) termes d'une série géométrique à l'aide de la formule,\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\). Mais comment trouver la somme d'une somme infinie ?
Regardons la série géométrique infinie\(3+6+12+24+48+96+….\). Chaque terme s'agrandit de plus en plus, il est donc logique que la somme du nombre infini de termes augmente. Regardons quelques sommes partielles pour cette série. Nous voyons\(a_{1}=3\) et\(r=2\)
\(\begin{array}{lll}{S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}(1-r^{n})}{1-r}}\\ {S_{10}=\frac{3\left(1-2^{10}\right)}{1-2}} & {S_{30}=\frac{3\left(1-2^{30}\right)}{1-2}} & {S_{50}=\frac{3\left(1-2^{50}\right)}{1-2}} \\ {S_{10}=3,069} & {S_{30}=3,221,225,469} & {S_{50}\approx 3.38 \times 10^{15}}\end{array}\)
Au\(n\) fur et à mesure que la somme augmente, la somme augmente de plus en plus. C'est vrai quand\(|r|≥1\) et on qualifie la série de divergente. On ne peut pas trouver la somme d'une série géométrique infinie quand\(|r|≥1\).
Regardons une série géométrique infinie dont le rapport commun est une fraction inférieure à un,
\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\ldots\). Ici, les termes deviennent de plus en plus petits à mesure que l'on\(n\) grandit. Regardons quelques sommes limitées pour cette série. Nous voyons\(a_{1}=\frac{1}{2}\) et\(r=\frac{1}{2}\).
\(\begin{array}{lll}{S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}(1-r^{n})}{1-r}}\\ {S_{10}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{10}\right)}{1-\frac{1}{2}}} & {S_{20}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{20}\right)}{1-\frac{1}{2}}} & {S_{30}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{30}\right)}{1-\frac{1}{2}}} \\ {S_{10}\approx 0.9990234375} & {S_{20}\approx 0.9999990463} & {S_{30}\approx 0.9999999991}\end{array}\)
Remarquez que la somme augmente de plus en plus, mais qu'elle se rapproche de plus en plus d'un. Quand\(|r|<1\), l'expression\(r^{n}\) devient de plus en plus petite. Dans ce cas, nous appelons la série convergente. À mesure que l'infini s'\(n\)approche, (devient infiniment grand),\(r^{n}\) se rapproche de plus en plus de zéro. Dans notre formule de somme, nous pouvons\(r^{n}\) remplacer le par zéro, puis nous obtenons une formule pour la somme\(S\), pour une série géométrique infinie quand\(|r|<1\).
\(\begin{aligned} S_{n} &=\frac{a_{1}\left(1-r^{n}\right)}{1-r} \\ S &=\frac{a_{1}(1-0)}{1-r} \\ S &=\frac{a_{1}}{1-r} \end{aligned}\)
Cette formule nous donne la somme de la séquence géométrique infinie. Notez\(S\) que le n'a pas d'indice\(n\),\(S_{n}\) car nous n'ajoutons pas un nombre fini de termes.
Pour une série géométrique infinie dont le premier terme est\(a_{1}\) un ratio commun\(r\),
Si\(|r|<1\), la somme est
\(S=\frac{a_{1}}{1-r}\)
Si\(|r|≥1\), la série géométrique infinie n'a pas de somme. Nous disons que la série diverge.
Trouvez la somme des séries géométriques infinies\(54+18+6+2+\frac{2}{3}+\frac{2}{9}+\ldots\)
Solution :
Pour trouver la somme, nous devons d'abord vérifier que c'est le ratio commun,\(|r|<1\) puis nous pouvons utiliser la formule de somme\(S=\frac{a_{1}}{1-r}\).
Trouvez le ratio commun.
\(\begin{array}{ll}{r=\frac{18}{54}} & {r=\frac{6}{18} \dots} \\ {r=\frac{1}{3}} & {r=\frac{1}{3} \quad|r|<1}\end{array}\)
Identifiez\(a_{1}\).
\(a_{1}=54\)
Sachant\(a_{1}=54, r=\frac{1}{3}\), utilisez la formule de somme.
\(S=\frac{a_{1}}{1-r}\)
Substituez les valeurs.
\(S=\frac{54}{1-\frac{1}{3}}\)
Simplifiez.
\(S=81\)
Réponse :
\(S=80\)
Trouvez la somme des séries géométriques infinies\(48+24+12+6+3+\frac{3}{2}+\dots\)
- Réponse
-
\(96\)
Trouvez la somme des séries géométriques infinies\(64+16+4+1+\frac{1}{4}+\frac{1}{16}+\dots\)
- Réponse
-
\(\frac{256}{3}\)
Une utilisation intéressante des séries géométriques infinies consiste à écrire une décimale répétée sous forme de fraction.
Écrivez la décimale répétée\(0.5\) sous forme de fraction.
Solution :
Réécrivez l'\(0.5\)affichage des cinq répétitions. Utilisez la valeur de position pour la réécrire sous forme de somme. Il s'agit d'une série géométrique infinie.
0,5555555555555\(\ldots\)
\(0.5+0.05+0.005+0.0005+\dots\)
Trouvez le ratio commun.
\(\begin{array}{ll}{r=\frac{0.05}{0.5}} & {r=\frac{0.005}{0.05} \dots} \\ {r=0.1} & {r=0.1 \quad|r|<1}\end{array}\)
Identifiez\(a_{1}\)
\(a_{1}=0.5\)
Sachant\(a_{1}=0.5 ,r=0.1\), utilisez la formule de somme.
\(S=\frac{a_{1}}{1-r}\)
Substituez les valeurs.
\(S=\frac{0.5}{1-0.1}\)
Simplifiez.
\(S=\frac{0.5}{0.9}\)
Multipliez le numérateur et le dénominateur par\(10\).
\(S=\frac{5}{9}\)
On nous demande de trouver la forme de la fraction.
\(0.5 = \frac{5}{9}\)
Écrivez la décimale répétée\(0.4\) sous forme de fraction.
- Réponse
-
\(\frac{4}{9}\)
Écrivez la décimale répétée\(0.8\) sous forme de fraction.
- Réponse
-
\(\frac{8}{9}\)
Appliquer des séquences et des séries géométriques dans le monde réel
L'une des applications des séquences géométriques concerne les dépenses de consommation. Si une réduction d'impôt est accordée à chaque ménage, l'effet sur l'économie est plusieurs fois supérieur au montant de la réduction individuelle.
Le gouvernement a décidé d'accorder une réduction d'\(1,000\)impôt en dollars à chaque ménage afin de stimuler l'économie. Les statistiques gouvernementales indiquent que chaque ménage dépensera\(80\) % de la réduction en biens et services. Les entreprises et les particuliers qui ont bénéficié de ce\(80\) pourcentage dépenseront alors\(80\) % de ce qu'ils ont reçu, etc. Le résultat est appelé effet multiplicateur. Quel est l'effet global du rabais sur l'économie ?
Solution :
Chaque fois que de l'argent entre dans l'économie, le\(80\) pourcentage de cet argent est dépensé et est ensuite investi dans l'économie pour être dépensé. Encore une fois,\(80\) % de cet argent est à nouveau dépensé dans l'économie. Cette situation perdure et nous conduit ainsi à une série géométrique infinie.
\(1000+1000(0.8)+1000(0.8)^{2}+\ldots\)
Voici le premier terme\(1,000, a_{1}=1000\). Le ratio commun est\(0.8, r=0.8\). Nous pouvons évaluer cette somme depuis\(0.8<1\). Nous utilisons la formule de la somme sur une série géométrique infinie.
\(S=\frac{a_{1}}{1-r}\)
Substituez les valeurs,\(a_{1}=1,000\) et\(r=0.8\).
\(S=\frac{1,000}{1-0.8}\)
Évaluer.
\(S=5,000\)
Réponse :
L'effet total du dollar\(1,000\) reçu par chaque ménage sera une\(5,000\) croissance en dollars de l'économie.
Quel est l'effet total sur l'économie d'un remboursement d'impôt gouvernemental de dollars accordé\(1,000\) à chaque ménage afin de stimuler l'économie si chaque ménage consacre un\(90\) pourcentage de la réduction en biens et services ?
- Réponse
-
$\(10,000\)
Quel est l'effet total sur l'économie d'un remboursement d'impôt gouvernemental de dollars accordé\(500\) à chaque ménage afin de stimuler l'économie si chaque ménage consacre un\(85\) pourcentage de la réduction en biens et services ?
- Réponse
-
$\(3,333.33\)
Nous avons examiné une formule d'intérêt composé selon laquelle un capital est investi à un taux d'intérêt\(t\) pendant des années.\(P\)\(r\) Le nouveau solde\(A\), c'est\(A=P\left(1+\frac{r}{n}\right)^{n t}\) lorsque les intérêts sont composés\(n\) plusieurs fois par an. Cette formule s'applique lorsqu'une somme forfaitaire a été investie à l'avance et nous indique la valeur après un certain laps de temps.
Une rente est un investissement qui consiste en une séquence de dépôts périodiques égaux. Nous examinerons les rentes qui payent des intérêts au moment des dépôts. Au fur et à mesure que nous élaborerons la formule de la valeur d'une rente, nous allons la louer\(n=1\). Cela signifie qu'il y a un dépôt par an.
\(\begin{aligned} &A =P\left(1+\frac{r}{n}\right)^{n t} \\ \text { Let } n=1 .\quad & A=P\left(1+\frac{r}{1}\right)^{1 t} \\ \text { Simplify. }\quad & A=P(1+r)^{t} \end{aligned}\)
Supposons que des\(P\) dollars soient investis à la fin de chaque année. Un an plus tard, ce dépôt vaut des\(P(1+r)^{1}\) dollars et un an plus tard, il vaut des\(P(1+r)^{2}\) dollars. Après des\(t\) années, elle vaudra des\(P(1+r)^{t}\) dollars.
| Fin d'année\(1\) | Fin d'année\(2\) | Fin d'année\(3\) | |
|---|---|---|---|
| Premier dépôt à\(P\) la fin de l'année\(1\) | \ (1 \) « >\(P\) | \ (2 \) ">Montant un\(1\) an plus tard\(P(1+r)^{1}\) | \ (3 \) ">Montant des\(2\) années plus tard\(P(1+r)^{2}\) |
| \(2\)Dépôt final\(P\) à la fin de l'année\(2\) | \ (1 \) « > | \ (2 \) « >\(P\) | \ (3 \) ">Montant un\(1\) an plus tard\(P(1+r)^{1}\) |
| \(3\)3e dépôt à\(P\) la fin de l'année\(3\) | \ (1 \) « > | \ (2 \) « > | \ (3 \) « >\(P\) |
Après trois ans, la valeur de la rente est
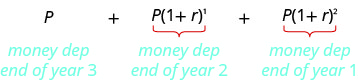
Il s'agit de la somme des termes d'une séquence géométrique où le premier terme est\(P\) et le ratio commun est\(1+r\). Nous substituons ces valeurs dans la formule de somme. Attention, nous avons deux utilisations différentes de\(r\). La formule\(r\) dans la somme est le ratio commun de la séquence. Dans ce cas, c'est\(1+r\) là que se\(r\) situe le taux d'intérêt.
\(\begin{aligned} &S_{t} =\frac{a_{1}\left(1-r^{t}\right)}{1-r} \\ \text { Substitute in the values. }\quad & S_{t}=\frac{P\left(1-(1+r)^{t}\right)}{1-(1+r)} \\ \text { Simplify. }\quad & S_{t} =\frac{P\left(1-(1+r)^{t}\right)}{-r} \\ &S_{t} =\frac{P\left((1+r)^{t}-1\right)}{r} \end{aligned}\)
N'oubliez pas que notre prémisse était qu'un dépôt était effectué à la fin de chaque année.
Nous pouvons adapter cette formule aux\(n\) dépôts effectués chaque année et les intérêts sont composés\(n\) plusieurs fois par an.
Pour un capital investi à la fin d'une période composée, avec un taux d'intérêt composé\(n\) plusieurs fois par an, le nouveau solde\(A\), après des\(t\) années, est\(P\)\(r\)
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
Les nouveaux parents décident d'investir $\(100\) par mois dans une rente pour leur petite fille. Le compte paiera un\(5\) % d'intérêt par an, composé mensuellement. Quel sera le montant sur le compte de l'enfant à son dix-huitième anniversaire ?
Solution :
Pour trouver la formule de la rente\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\), nous devons identifier\(P, r, n\), et\(t\).
Identifiez\(P\) le montant investi chaque mois.
\(P=100\)
Identifiez\(r\) le taux d'intérêt annuel, sous forme décimale.
\(r=0.05\)
Indiquez\(n\) le nombre de fois que le dépôt sera effectué et les intérêts composés chaque année.
\(n=12\)
Identifiez\(t\), le nombre d'années.
\(t=18\)
Connaître\(P=100, r=0.05, n=12\)\(t=18\) et utiliser la formule de somme.
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
Substituez les valeurs.
\(A_{t}=\frac{100\left(\left(1+\frac{0.05}{12}\right)^{12.18}-1\right)}{\frac{0.05}{12}}\)
Utilisez la calculatrice pour évaluer. Veillez à utiliser des parenthèses si nécessaire.
\(A_{t}=34.920 .20\)
Réponse :
L'enfant aura $\(34,920.20\)
Les nouveaux grands-parents décident d'investir $\(200\) par mois dans une rente pour leur petit-fils. Le compte paiera un\(5\) % d'intérêt par an, composé mensuellement. Quel sera le montant sur le compte de l'enfant à son vingt et unième anniversaire ?
- Réponse
-
$\(88,868.36\)
Arturo vient de décrocher son premier emploi à temps plein après avoir obtenu son diplôme universitaire à l'âge adulte\(27\). Il a décidé d'investir $\(200\) par mois dans un IRA (une rente). L'intérêt sur la rente est de\(8\) %, composé mensuellement. Quel sera le montant sur le compte d'Arturo lorsqu'il prendra sa retraite le jour de son soixante-septième anniversaire ?
- Réponse
-
$\(698,201.57\)
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner avec des séquences.
Concepts clés
- Terme général (\(n\)ème terme) d'une séquence géométrique : Le terme général d'une séquence géométrique avec le premier terme\(a_{1}\) et le ratio commun\(r\) est
\(a_{n}=a_{1} r^{n-1}\)
- Somme des premiers\(n\) termes d'une série géométrique : La somme des\(n\) termes d'une séquence géométrique est\(S_{n}\)
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
où\(a_{1}\) est le premier terme et\(r\) le ratio commun. Série géométrique infinie : Une série géométrique infinie est une somme infinie dont le premier terme est\(a_{1}\) un ratio commun est\(r\) et est écrit\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\ldots\)
- Somme d'une série géométrique infinie : Pour une série géométrique infinie dont le premier terme est\(a_{1}\) un ratio commun\(r\),
Si\(|r|<1\), la somme est
\(S=\frac{a_{1}}{1-r}\)
Nous disons que la série converge.
Si\(|r|≥1\), la série géométrique infinie n'a pas de somme. Nous disons que la série diverge.
- Valeur d'une rente avec intérêts composés \(n\)fois par an : Pour un capital\(P\), investi à la fin d'une période composée, avec un taux d'intérêt composé\(n\) fois par an, le nouveau solde\(A\), après\(r\) \(t\)ans, c'est
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
Lexique
- rente
- Une rente est un investissement qui consiste en une séquence de dépôts périodiques égaux.
- ratio commun
- Le rapport entre des termes consécutifs dans une séquence géométrique\(\frac{a_{n}}{a_{n-1}}\),\(r\), est le rapport commun, où il est\(r\) supérieur ou égal à deux.
- séquence géométrique
- Une séquence géométrique est une séquence dans laquelle le rapport entre des termes consécutifs est toujours le même
- série géométrique infinie
- Une série géométrique infinie est une séquence géométrique infinie à somme infinie.


