12.3 : Séquences arithmétiques
- Page ID
- 194122
À la fin de cette section, vous serez en mesure de :
- Déterminer si une séquence est arithmétique
- Trouve le terme général (\(n\)le terme) d'une suite arithmétique
- Trouve la somme des premiers\(n\) termes d'une suite arithmétique
Avant de commencer, répondez à ce questionnaire de préparation.
- \(4n−1\)Évaluez les nombres entiers\(1, 2, 3\), et\(4\).
Si vous avez oublié ce problème, consultez l'exemple 1.6. - Résolvez le système d'équations :\(\left\{\begin{array}{l}{x+y=7} \\ {3 x+4 y=23}\end{array}\right.\).
Si vous avez oublié ce problème, consultez l'exemple 4.9. - Si\(f(n)=\frac{n}{2}(3 n+5)\), trouvez\(f(1)+f(20)\).
Si vous avez oublié ce problème, consultez l'exemple 3.49.
Déterminer si une séquence est arithmétique
La dernière section a introduit les séquences et nous allons maintenant examiner deux types spécifiques de séquences qui ont chacune des propriétés spéciales. Dans cette section, nous examinerons les séquences arithmétiques et dans la section suivante, les séquences géométriques.
Une séquence arithmétique est une séquence dans laquelle la différence entre des termes consécutifs est constante. La différence entre des termes consécutifs dans une séquence arithmétique, a_ {n} -a_ {n-1}, est\(d\), la différence courante, pour un\(n\) nombre supérieur ou égal à deux.
Une suite arithmétique est une séquence dans laquelle la différence entre des termes consécutifs est toujours la même.
La différence entre des termes consécutifs, a_ {n} -a_ {n-1}\(d\), est la différence commune, pour un\(n\) nombre supérieur ou égal à deux.
Déterminez si chaque séquence est arithmétique. Dans l'affirmative, indiquez la différence commune.
- \(5,9,13,17,21,25, \dots\)
- \(4,9,12,17,20,25, \dots\)
- \(10,3,-4,-11,-18,-25, \dots\)
Solution :
Pour déterminer si la séquence est arithmétique, nous trouvons la différence entre les termes consécutifs affichés.
un.\(\begin{array}{cccccc}{5,} & {9,} & {13,} & {17} & {21,} & {25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {9-5} & {13-9} & {17-13} & {21-17} & {25-21} \\ & {4} & {4} & {4} & {4}&{4}\end{array}\)
La séquence est arithmétique. La différence commune est\(d=4\).
b.\(\begin{array}{cccccc}{4,} & {9,} & {12,} & {17} & {20,} & {25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {9-4} & {12-9} & {17-12} & {20-17} & {25-20} \\ & {2} & {3} & {5} & {3}&{5}\end{array}\)
La séquence n'est pas arithmétique car toutes les différences entre les termes consécutifs ne sont pas les mêmes. Il n'y a pas de différence commune.
c.\(\begin{array}{cccccc}{10,} & {3,} & {-4,} & {-11} & {-18,} & {-25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {3-10} & {-4-3} & {-11-(-4)} & {-18-(-11)} & {-25-(-18)} \\ & {-7} & {-7} & {-7} & {-7}&{-7}\end{array}\)
Réponse :
La séquence est arithmétique. La différence commune est\(d=-7\).
Déterminez si chaque séquence est arithmétique. Dans l'affirmative, indiquez la différence commune.
- \(9,20,31,42,53,64, \dots\)
- \(12,6,0,-6,-12,-18, \dots\)
- \(7,1,10,4,13,7, \dots\)
- Réponse
-
- La séquence est arithmétique avec des différences communes\(d=11\).
- La séquence est arithmétique avec des différences communes\(d=-6\).
- La séquence n'est pas arithmétique car toutes les différences entre les termes consécutifs ne sont pas les mêmes.
Déterminez si chaque séquence est arithmétique. Dans l'affirmative, indiquez la différence commune.
- \(-4,4,2,10,8,16, \dots\)
- \(-3,-1,1,3,5,7, \dots\)
- \(7,2,-3,-8,-13,-18, \dots\)
- Réponse
-
- La séquence n'est pas arithmétique car toutes les différences entre les termes consécutifs ne sont pas les mêmes.
- La séquence est arithmétique avec des différences communes\(d=2\).
- La séquence est arithmétique avec des différences communes\(d=−5\).
Si nous connaissons le premier terme et la différence commune\(d\), nous pouvons énumérer un nombre fini de termes de la séquence.\(a_{1}\)
Écrivez les cinq premiers termes de la séquence où se trouve le premier terme\(5\) et où se trouve la différence commune\(d=−6\).
Solution :
Nous commençons par le premier terme et ajoutons la différence commune. Ensuite, nous ajoutons la différence commune à ce résultat pour obtenir le terme suivant, et ainsi de suite.
\(\begin{array}{cccc}{a_{1}} & {a_{2}} & {a_{3}} & {a_{4}} & {a_{5}} \\ {5} & {5+(-6)} & {-1+(-6)} & {-7+(-6)} & {-13+(-6)} \\ {}&{-1} & {-7} & {-13} & {-19}\end{array}\)
Réponse :
La séquence est\(5,-1,-7,-13,-19, \dots\)
Écrivez les cinq premiers termes de la séquence où se trouve le premier terme\(7\) et où se trouve la différence commune\(d=−4\).
- Réponse
-
\(7,3,-1,-5,-9, \dots\)
Écrivez les cinq premiers termes de la séquence où se trouve le premier terme\(11\) et où se trouve la différence commune\(d=−8\).
- Réponse
-
\(11,3,-5,-13,-21, \dots\)
Trouver le terme général (\(n\)le terme) d'une suite arithmétique
Tout comme nous avons trouvé une formule pour le terme général d'une séquence, nous pouvons également trouver une formule pour le terme général d'une séquence arithmétique.
Écrivons les premiers termes d'une séquence où le premier terme est\(a_{1}\) et la différence commune est\(d\). Nous chercherons ensuite un modèle.
En recherchant un modèle, nous voyons que chaque terme commence par\(a_{1}\).
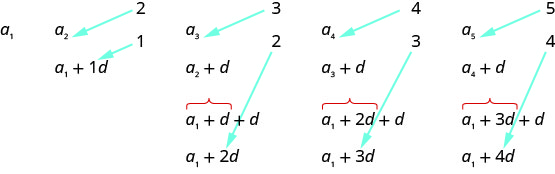
Le premier terme ajoute\(0d\)\(a_{1}\), le deuxième terme ajoute\(1d\), le troisième terme ajoute\(2d\), le quatrième terme ajoute\(3d\) et le cinquième terme ajoute\(4d\). Le nombre de ceux\(ds\) qui ont été ajoutés\(a_{1}\) est inférieur d'un au nombre du terme. Cela nous amène à ce qui suit
\(a_{n}=a_{1}+(n-1) d\)
Le terme général d'une suite arithmétique avec le premier terme\(a_{1}\) et la différence commune\(d\) est
\(a_{n}=a_{1}+(n-1) d\)
Nous utiliserons cette formule dans l'exemple suivant pour trouver le quinzième terme d'une séquence.
Détermine le quinzième terme d'une séquence où le premier terme est\(3\) et la différence commune est\(6\).
Solution :
\(\begin{array}{cc}{\text{To find the fifteenth term, }a_{15}\text{, use the formula with } a_{1}=3 \:\text{and} \:d=6.}&{a_{n}=a_{1}+(n-1) d} \\ {\text{Substitute in the values.}}&{a_{15}=3+(15-1) 6} \\{\text{Simplify.}}& {a_{15}=3+(14) 6} \\ {}&{a_{15}=87}\end{array}\)
Trouvez le vingt-septième terme d'une séquence où le premier terme est\(7\) et la différence commune est\(9\).
- Réponse
-
\(241\)
Trouvez le dix-huitième terme d'une séquence où le premier terme est\(13\) et la différence commune est\(−7\).
- Réponse
-
\(-106\)
Parfois, nous ne connaissons pas le premier terme et nous devons utiliser d'autres informations données pour le trouver avant de trouver le terme demandé.
Trouvez le douzième terme d'une séquence où le septième terme est\(10\) et la différence commune est\(−2\). Donnez la formule du terme général.
Solution :
Pour trouver d'abord le premier terme\(a_{1}\), utilisez la formule avec\(a_{7}=10\)\(n=7\), et\(d=−2\). Substituez les valeurs. Simplifiez.
\(a_{n}=a_{1}+(n-1) d\)
\(10=a_{1}+(7-1)(-2)\)
\(10=a_{1}+(6)(-2)\)
\(10=a_{1}-12\)
\(a_{1}=22\)
Trouvez le douzième terme\(a_{12}\), en utilisant la formule avec\(a_{1}=22\)\(n=12\), et\(d=-2\). Substituez les valeurs. Simplifiez.
\(a_{n}=a_{1}+(n-1) d\)
\(a_{12}=22+(12-1)(-2)\)
\(a_{12}=22+(11)(-2)\)
\(a_{12}=0\)
Le douzième terme de la séquence est\(0, a_{12}=0\)
Pour trouver le terme général, remplacez les valeurs dans la formule.
\(a_{n}=a_{1}+(n-1) d\)
\(a_{n}=22+(n-1)(-2)\)
\(a_{n}=22-2 n+2\)
Réponse :
Le terme général est\(a_{n}=-2 n+24\)
Trouvez le onzième terme d'une séquence où le neuvième terme est\(8\) et la différence commune est\(−3\). Donnez la formule du terme général.
- Réponse
-
\(a_{11}=2 .\)Le terme général est\(a_{n}=-3 n+35\)
Trouvez le dix-neuvième terme d'une séquence où le cinquième terme est\(1\) et la différence commune est\(−4\) .Donnez la formule du terme général.
- Réponse
-
\(a_{19}=-55 .\)Le terme général est\(a_{n}=-4 n+21\)
Parfois, les informations fournies nous mènent à deux équations dans deux inconnues. Nous utilisons ensuite nos méthodes pour résoudre des systèmes d'équations afin de trouver les valeurs nécessaires.
Déterminez le premier terme et la différence commune d'une séquence où le cinquième terme est\(19\) et le onzième terme est\(37\). Donnez la formule du terme général.
Solution :
Comme nous connaissons deux termes, nous pouvons créer un système d'équations en utilisant la formule du terme général.
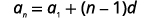 |
|
| Nous connaissons la valeur de\(a_{5}\) et\(a_{11}\), donc nous utiliserons\(n=5\) et\(n=11\). | 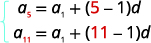 |
Substituez les valeurs,\(a_{5}=19\) et\(a_{11}=37\). |
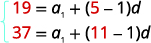 |
| Simplifiez. | 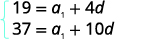 |
| Préparez-vous à éliminer le\(a_{1}\) terme en multipliant l'équation supérieure par\(−1\). Ajoutez les équations. |
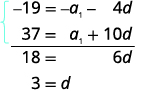 |
| \(d=3\)Remplacer dans la première équation. | 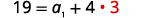 |
| Résolvez pour\(a_{1}\). |  |
| Utilisez la formule avec\(a_{1}=7\) et\(d=3\). | 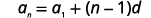 |
| Substituez les valeurs. | 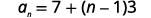 |
| Simplifiez. | 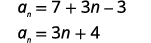 |
| Le premier terme est\(a_{1}=7\). La différence commune est\(d=3\). |
|
| Le terme général de la séquence est\(a_{n}=3n+4\). |
Réponse :
Le terme général de la séquence est\(a_{n}=3n+4\).
Déterminez le premier terme et la différence commune d'une séquence où le quatrième terme est\(17\) et le treizième terme est\(53\). Donnez la formule du terme général.
- Réponse
-
\(a_{1}=5, d=4 .\)Le terme général est\(a_{n}=4 n+1\).
Déterminez le premier terme et la différence commune d'une séquence où le troisième terme est\(2\) et le douzième terme est\(−25\). Donnez la formule du terme général.
- Réponse
-
\(a_{1}=8, d=-3 .\)Le terme général est\(a_{n}=-3 n+11\).
Trouvez la somme des premiers\(n\) termes d'une suite arithmétique
Comme pour les séquences générales, il est souvent utile de trouver la somme d'une séquence arithmétique. La somme des\(S_{n}\) premiers\(n\) termes de toute séquence arithmétique s'écrit sous la forme\(S_{n} =a_{1} +a_{2} +a_{3} +\ldots +a_{n}\). Trouver la somme en ajoutant simplement tous les termes peut être fastidieux. Nous pouvons donc également développer une formule pour trouver la somme d'une séquence en utilisant le premier et le dernier terme de la séquence.
Nous pouvons développer cette nouvelle formule en écrivant d'abord la somme en commençant par le premier terme\(a_{1}\), et en ajoutant un\(d\) pour obtenir le terme suivant comme suit :
\(S_{n}=a_{1}+\left(a_{1}+d\right)+\left(a_{1}+2 d\right)+\ldots+a_{n}\).
Nous pouvons également inverser l'ordre des termes et écrire la somme en commençant par\(a_{n}\) et en continuant\(d\) à soustraire pour obtenir le terme suivant comme
\(S_{n}=a_{n}+\left(a_{n}-d\right)+\left(a_{n}-2 d\right)+\ldots+a_{1}\).
Si nous ajoutons ces deux expressions pour la somme des premiers\(n\) termes d'une suite arithmétique, nous pouvons obtenir une formule pour la somme des premiers\(n\) termes de n'importe quelle série arithmétique.
\(\begin{aligned} &S_{n}= a_{1} \quad+\left(a_{1}+d\right)+\left(a_{1}+2 d\right)+\ldots+a_{n} \\+&S_{n} =a_{n} \quad+\left(a_{n}-d\right)+\left(a_{n}-2 d\right)+\ldots+a_{1} \\ \hline \\ &2S_{n}=(a_{1}+a_{n})+(a_{1}+a_{n})+(a_{1}+a_{n})+\dots+(a_{1}+a_{n}) \end{aligned}\)
Comme il y a des\(n\) sommes de\((a_{1}+a_{n})\) sur le côté droit de l'équation, nous réécrivons le côté droit comme\(n(a_{1}+a_{n})\).
\(2 S_{n}=n\left(a_{1}+a_{n}\right)\)
Nous divisons par deux pour résoudre\(S_{n}\).
\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)
Cela nous donne une formule générale pour la somme des premiers\(n\) termes d'une suite arithmétique.
La somme\(S_{n}\) des premiers\(n\) termes d'une suite arithmétique est
\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)
où\(a_{1}\) est le premier terme et\(a_{n}\) le\(n\) neuvième terme.
Nous appliquons cette formule dans l'exemple suivant où les premiers termes de la séquence sont donnés.
Trouvez la somme des premiers\(30\) termes de la suite arithmétique :\(8, 13, 18, 23, 28, …\)
Solution :
Pour trouver la somme, nous utiliserons la formule\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\). Nous le savons\(a_{1}=8, d=5\) et\(n=30\), mais nous devons trouver\(a_{n}\) pour utiliser la formule de somme.
Trouvez\(a_{n}\) où\(a_{1}=8, d=5\) et\(n=30\). Simplifiez.
\(\begin{aligned} a_{n} &=a_{1}+(n-1) d \\ a_{30} &=8+(30-1) 5 \\ a_{30} &=8+(29) 5 \\ a_{30} &=153 \end{aligned}\)
Connaître\(a_{1}=8, n=30\) et\(a_{30}=153\) utiliser la formule de somme. Substituez les valeurs. Simplifiez. Simplifiez.
\(\begin{aligned} S_{n} &=\frac{n}{2}\left(a_{1}+a_{n}\right) \\ S_{30} &=\frac{30}{2}(8+153) \\ S_{30} &=15(161) \\ S_{30} &=2,415 \end{aligned}\)
Trouvez la somme des premiers\(30\) termes de la suite arithmétique :\(5, 9, 13, 17, 21, …\)
- Réponse
-
\(1,890\)
Trouvez la somme des premiers\(30\) termes de la suite arithmétique :\(7, 10, 13, 16, 19, …\)
- Réponse
-
\(1,515\)
Dans l'exemple suivant, on nous donne le terme général de la séquence et on nous demande de trouver la somme des premiers\(50\) termes.
Détermine la somme des premiers\(50\) termes de la suite arithmétique dont le terme général est\(a_{n}=3n−4\).
Solution :
Pour trouver la somme, nous utiliserons la formule\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\). Nous\(n=50\) le savons, mais nous devons trouver\(a_{1}\) et\(a_{n}\) utiliser la formule de somme.
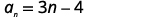 |
|
| Trouvez\(a_{1}\), en remplaçant\(n=1\). | 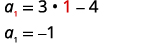 |
| Recherchez\(a_{n}\) en les remplaçant\(n=50\). | 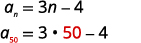 |
| Simplifiez. | 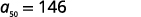 |
| Connaître\(n=50, a_{1}=−1,\) et\(a_{50}=146\) utiliser la formule de somme. | 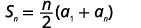 |
| Substituez les valeurs. | 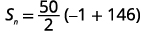 |
| Simplifiez. | 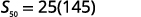 |
| Simplifiez. | 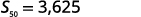 |
Détermine la somme des premiers\(50\) termes de la suite arithmétique dont le terme général est\(a_{n}=2n−5\).
- Réponse
-
\(2,300\)
Détermine la somme des premiers\(50\) termes de la suite arithmétique dont le terme général est\(a_{n}=4n+3\).
- Réponse
-
\(5,250\)
Dans l'exemple suivant, on nous donne la somme en notation de sommation. Ajouter tous les termes serait fastidieux, nous extrayons donc les informations nécessaires pour utiliser la formule afin de trouver la somme des premiers\(n\) termes.
Trouvez la somme :\(\sum_{i=1}^{25}(4 i+7)\).
Solution :
Pour trouver la somme, nous utiliserons la formule\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\). Nous\(n=25\) le savons, mais nous devons trouver\(a_{1}\) et\(a_{n}\) utiliser la formule de somme.
| Développez la notation de sommation. |
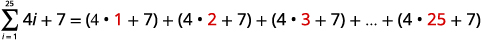
|
| Simplifiez. |
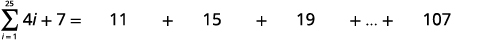
|
| Identifiez\(a_{1}\). |  |
| Identifiez\(a_{25}\). |

|
| Connaître\(n=25, a_{1}=11\) et\(a_{25} = 107\) utiliser la formule de somme. |  |
| Substituez les valeurs. |  |
| Simplifiez. |  |
| Simplifiez. |  |
Trouvez la somme :\(\sum_{i=1}^{30}(6 i-4)\).
- Réponse
-
\(2,670\)
Trouvez la somme :\(\sum_{i=1}^{35}(5 i-3)\).
- Réponse
-
\(3,045\)
Accédez à ces ressources en ligne pour des instructions et des exercices supplémentaires avec des séquences arithmétiques
Concepts clés
- Terme général (\(n\)e terme) d'une suite arithmétique
Le terme général d'une suite arithmétique avec le premier terme\(a_{1}\) et la différence commune\(d\) est\(a_{n}=a_{1}+(n-1) d\)
- Somme des premiers\(n\) termes d'une suite arithmétique
La somme\(S_{n}\),, des premiers \\(n\) termes d'une suite arithmétique, où\(a_{1}\) est le premier terme et\(a_{n}\) le\(n\) e terme est\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)
Lexique
- séquence arithmétique
- Une séquence arithmétique est une séquence dans laquelle la différence entre des termes consécutifs est constante.
- différence commune
- La différence entre des termes consécutifs dans une séquence arithmétique\(a_{n}−a_{n−1}\),\(d\), est la différence commune, pour un\(n\) nombre supérieur ou égal à deux.


