Skip to main content
Global

12.2 : Séquences

  1. Last updated
  2. Save as PDF
  • Page ID
    194103

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Écrivez les premiers termes d'une séquence
    • Trouvez une formule pour le terme général (nième terme) d'une séquence
    • Utiliser la notation factorielle
    • Trouvez la somme partielle
    • Utiliser la notation de sommation pour écrire une somme

    Avant de commencer, répondez à ce questionnaire de préparation.

    1. \(2n+3\)Évaluez les nombres entiers\(1, 2, 3\), et\(4\).
      Si vous avez oublié ce problème, consultez l'exemple 1.6.
    2. \((−1)^{n}\)Évaluez les nombres entiers\(1, 2, 3\), et\(4\).
      Si vous avez oublié ce problème, consultez l'exemple 1.19.
    3. Si\(f(n)=n^{2}+2\), trouvez\(f(1)+f(2)+f(3)\).
      Si vous avez oublié ce problème, consultez l'exemple 3.49.

    Écrire les premiers termes d'une séquence

    Examinons la fonction\(f(x)=2x\) et évaluons-la uniquement pour les nombres de comptage.

    \(f(x)=2x\)  
    \(x\) \(2x\)
    \(1\) \(2\)
    \(2\) \(4\)
    \(3\) \(6\)
    \(4\) \(8\)
    \(5\) \(10\)
    \(...\) \(...\)
    Tableau 12.1.1

    Si nous listons les valeurs des fonctions dans l'ordre suivant : et\(2, 4, 6, 8\)\(10\),..., nous avons une séquence. Une séquence est une fonction dont le domaine est le comptage des nombres.

    Définition\(\PageIndex{1}\)

    Une séquence est une fonction dont le domaine est le comptage des nombres.

    Une séquence peut également être vue comme une liste ordonnée de nombres et chaque numéro de la liste est un terme. Une séquence peut comporter un nombre infini de termes ou un nombre fini de termes. Notre séquence comporte trois points (points de suspension) à la fin, ce qui indique que la liste ne s'arrête jamais. Si le domaine est l'ensemble de tous les nombres de comptage, alors la séquence est une séquence infinie. Son domaine est de compter tous les nombres et il existe un nombre infini de nombres de comptage.

    \(2,4,6,8,10, \dots\)

    Si nous limitons le domaine à un nombre fini de nombres de comptage, alors la séquence est une séquence finie. Si nous n'utilisons que les quatre premiers nombres de comptage,\(1, 2, 3, 4\) notre séquence serait la séquence finie,

    \(2,4,6,8\)

    Souvent, lorsque nous travaillons avec des séquences, nous ne voulons pas écrire tous les termes. Nous voulons une manière plus compacte de montrer comment chaque terme est défini. Lorsque nous travaillions avec des fonctions, nous écrivions\(f(x)=2x\) et disions que l'expression\(2x\) était la règle qui définissait les valeurs de la plage. Bien qu'une séquence soit une fonction, nous n'utilisons pas la notation fonctionnelle habituelle. Au lieu d'écrire la fonction sous la forme\(f(x)=2x\), nous l'écririons sous la forme\(a_{n}=2n\). \(a_{n}\)C'est le\(n\) ème terme de la séquence, le terme situé en\(n\) ème position où se\(n\) trouve une valeur dans le domaine. La formule permettant d'écrire le\(n\) ième terme de la séquence est appelée terme général ou formule de la séquence.

    Définition\(\PageIndex{2}\)

    Le terme général de la séquence est trouvé à partir de la formule permettant d'écrire le\(n\) ième terme de la séquence. Le\(n\) e terme de la séquence,\(a_{n}\), est le terme situé en\(n\) ème position où se\(n\) trouve une valeur dans le domaine.

    Lorsque l'on nous donne le terme général de la séquence, nous pouvons trouver les termes en les\(n\) remplaçant par les nombres de comptage dans l'ordre. Pour\(a_{n}=2 n\),

    \(n\) \(1\) \(2\) \(3\) \(4\) \(5\) \(6\)
    \(a_{n}\) 2\(\cdot 1\) 2\(\cdot 2\) 2\(\cdot 3\) 2\(\cdot 4\) 2\(\cdot 5\) 2\(\cdot 6\)
      \(2\) \(4\) \(6\) \(8\) \(10\)  
    Tableau 12.1.2

    \(a_{1}, \quad a_{2}, \quad a_{3}, \quad a_{4}, \quad a_{5}, \ldots, \quad a_{n}, \dots\)

    \(2, \quad 4, \quad 6, \quad 8, \quad10, \dots\)

    Pour trouver les valeurs d'une séquence, nous les substituons par les nombres de comptage dans l'ordre du terme général de la séquence.

    Exemple\(\PageIndex{1}\)

    Écrivez les cinq premiers termes de la séquence dont le terme général est\(a_{n}=4 n-3\).

    Solution :

    Nous substituons les valeurs\(1, 2, 3, 4\), et\(5\) dans la formule\(a_{n}=4n−3\), dans l'ordre.

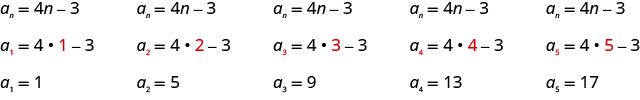
    Cette figure montre trois lignes et cinq colonnes. La première ligne indique que le nième terme est égal à 4 fois n moins 3 écrits cinq fois. La deuxième ligne indique qu'un sous 1 est égal à 4 fois g fois 1 moins 3, un sous-2 est égal à 4 fois g fois 2 moins 3, un sous 3 est égal à 4 fois g fois 3 moins 3, un sous-4 est égal à 4 fois g fois 4 fois moins 3, un sous 5 est égal à 4 fois g fois 5 moins 3. La troisième ligne se lit comme suit : un sous 1 est égal à 1, un sous 2 est égal à 5, un sous 3 est égal à 9, un sous-4 est égal à 13, un sous 5 est égal à 17.
    Graphique 12.1.1

    Réponse :

    Les cinq premiers termes de la séquence sont\(1, 5, 9, 13\), et\(17\).

    Exercice\(\PageIndex{1}\)

    Écrivez les cinq premiers termes de la séquence dont le terme général est\(a_{n}=3n-4\).

    Réponse

    \(-1,2,5,8,11\)

    Exercice\(\PageIndex{2}\)

    Écrivez les cinq premiers termes de la séquence dont le terme général est\(a_{n}=2n-5\).

    Réponse

    \(-3,-1,1,3,5\)

    Pour certaines séquences, la variable est un exposant.

    Exemple\(\PageIndex{2}\)

    Écrivez les cinq premiers termes de la séquence dont le terme général est\(a_{n}=2^{n}+1\).

    Solution :

    Nous substituons les valeurs\(1, 2, 3, 4\), et\(5\) dans la formule\(a_{n}=2^{n}+1\), dans l'ordre.

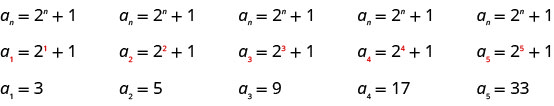
    Cette figure montre trois lignes et cinq colonnes. La première ligne indique « Le nième terme est égal à 2 à la nième puissance plus 1 » écrit cinq fois. La deuxième rangée se lit comme suit : « un sub 1 est égal à 2 fois 1 plus 1, un sub 2 est égal à 2 à la puissance de 2 plus 1, un sub 3 est égal à 2 à la puissance 3 plus 1, un sub 4 est égal à 2 à la puissance 4 plus 1, un sub 5 est égal à 2 à la puissance 5 plus 1 ». La dernière ligne se lit comme suit : « un sous 1 est égal à 3, un sous 2 est égal à 5, un sous 3 est égal à 9, un sous-4 est égal à 17, un sous 5 est égal à 33 ».
    Graphique 12.1.2

    Réponse :

    Les cinq premiers termes de la séquence sont\(3, 5, 9, 17\), et\(33\).

    Exercice\(\PageIndex{3}\)

    Écrivez les cinq premiers termes de la séquence dont le terme général est\(a_{n}=3^{n}+4\).

    Réponse

    \(7,13,31,85,247\)

    Exercice\(\PageIndex{4}\)

    Écrivez les cinq premiers termes de la séquence dont le terme général est\(a_{n}=2^{n}-5\).

    Réponse

    \(-3,-1,3,11,27\)

    Il n'est pas rare de voir les expressions\((−1)^{n}\) ou\((−1)^{n+1}\) le terme général désignant une séquence. Si nous évaluons chacune de ces expressions pour quelques valeurs, nous voyons que cette expression alterne le signe des termes.

    \(n\) \(1\) \(2\) \(3\) \(4\) \(5\)
    \ (n \) « >\((-1)^{n}\) \ (1 \) « >\((-1)^{1}\)
    \(-1\)    		 \ (2 \) « >\((-1)^{2}\)
    1    		 \ (3 \) « >\((-1)^{3}\)
    \(-1\)    		 \ (4 \) « >\((-1)^{4}\)
    \(1\)    		 \ (5 \) « >\((-1)^{5}\)
    \(-1\)
    \ (n \) « >\((-1)^{n+1}\) \ (1 \) « >\((-1)^{1+1}\)
    1    		 \ (2 \) « >\((-1)^{2+1}\)
    \(-1\)    		 \ (3 \) « >\((-1)^{3+1}\)
    1    		 \ (4 \) « >\((-1)^{4+1}\)
    \(-1\)    		 \ (5 \) « >\((-1)^{5+1}\)
    1
    Tableau 12.1.3

    \(a_{1}, \quad a_{2}, \quad a_{3}, \quad a_{4}, \quad a_{5}, \dots, \quad a_{n}, \dots\)

    \(\begin{array}{rrrr}{-1,} & {1,} & {-1,} & {1,} & {-1 \ldots} \\ {1,} & {-1,} & {1,} & {-1,} & {1 \ldots}\end{array}\)

    Exemple\(\PageIndex{3}\)

    Écrivez les cinq premiers termes de la séquence dont le terme général est\(a_{n}=(-1)^{n} n^{3}\).

    Solution :

    Nous substituons les valeurs\(1, 2, 3, 4\), et\(5\) dans la formule\(a_{n}=(-1)^{n} n^{3}\), dans l'ordre.

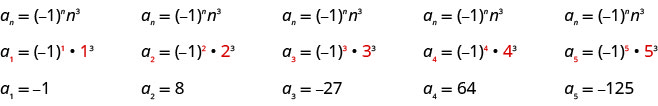
    Cette figure montre trois lignes et cinq colonnes. La première ligne se lit comme suit : « Le nième terme est égal à moins 1 à la nième puissance multipliée par n cubes » écrit cinq fois. La deuxième ligne indique : un sub 1 est égal à moins 1 à la puissance de 1 fois g fois 1 cube, un sub 2 est égal à moins 1 temps carré g fois 2 cubes, un sub 3 est égal à moins 1 cube fois g fois 23 cubes, un sub 4 est égal à moins 1 à la puissance de 4 fois g fois 4 cubes, un sub 5 est égal à moins 1 à la puissance de 5 4 fois 5 fois 5 en cubes. La dernière ligne se lit comme suit : « un sous 1 est égal à moins 1, un sous-2 est égal à 8, un sous-3 est égal à moins 27, un sous-4 est égal à 64 et un sous-5 est égal à moins 125.
    Graphique 12.1.3

    Réponse :

    Les cinq premiers termes de la séquence sont\(−1, 8, −27, 64, −1, 8, −27, 64\), et\(−125\).

    Exercice\(\PageIndex{5}\)

    Écrivez les cinq premiers termes de la séquence dont le terme général est\(a_{n}=(-1)^{n} n^{2}\).

    Réponse

    \(-1,4,-9,16,-25\)

    Exercice\(\PageIndex{6}\)

    Écrivez les cinq premiers termes de la séquence dont le terme général est\(a_{n}=(-1)^{n+1} n^{3}\).

    Réponse

    \(1,-8,27,-64,125\)

    Trouver une formule pour le terme général (\(n\)le terme) d'une séquence

    Parfois, nous avons quelques termes d'une séquence et il serait utile de connaître le terme général ou\(n\) le terme. Pour trouver le terme général, nous recherchons des modèles dans les termes. Souvent, les modèles impliquent des multiples ou des pouvoirs. Nous recherchons également un schéma dans les signes des termes.

    Exemple\(\PageIndex{4}\)

    Trouvez un terme général pour la séquence dont les cinq premiers termes sont affichés. \(4,8,12,16,20, \dots\)

    Solution :


      .
      .
    Nous cherchons un modèle dans les termes. .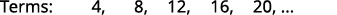
    Les nombres sont tous des multiples de\(4\). .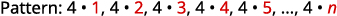
      Le terme général de la séquence est\(a_{n}=4n\).
    Tableau 12.1.4

    Réponse :

    Le terme général de la séquence est\(a_{n}=4n\).

    Exercice\(\PageIndex{7}\)

    Trouvez un terme général pour la séquence dont les cinq premiers termes sont affichés.

    \(3,6,9,12,15, \dots\)

    Réponse

    \(a_{n}=3 n\)

    Exercice\(\PageIndex{8}\)

    Trouvez un terme général pour la séquence dont les cinq premiers termes sont affichés.

    \(5,10,15,20,25, \dots\)

    Réponse

    \(a_{n}=5 n\)

    Exemple\(\PageIndex{5}\)

    Trouvez un terme général pour la séquence dont les cinq premiers termes sont affichés. \(2,-4,8,-16,32, \dots\)

    Solution :

     
    .
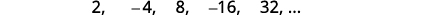
    Graphique 12.1.8
     
    .
    Graphique 12.1.9
    Nous cherchons un modèle dans les termes.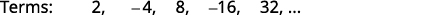
    .
    Graphique 12.1.10
    Les chiffres sont les pouvoirs de\(2\). Les signes sont alternés, voire\(n\) négatifs.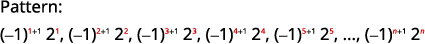
    .
    Graphique 12.1.11
      Le terme général de la séquence est\(a_{n}=(-1)^{n+1} 2^{n}\)
    Tableau 12.1.5

    Réponse :

    Le terme général de la séquence est\(a_{n}=(-1)^{n+1}2^{n}\).

    Exercice\(\PageIndex{9}\)

    Trouvez un terme général pour la séquence dont les cinq premiers termes sont affichés.

    \(-3,9,-27,81,-243, \dots\)

    Réponse

    \(a_{n}=(-1)^{n} 3^{n}\)

    Exercice\(\PageIndex{10}\)

    Trouvez un terme général pour la séquence dont les cinq premiers termes sont affichés

    \(1,-4,9,-16,25, \dots\)

    Réponse

    \(a_{n}=(-1)^{n+1} n^{2}\)

    Exemple\(\PageIndex{6}\)

    Trouvez un terme général pour la séquence dont les cinq premiers termes sont affichés. \(\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81}, \frac{1}{243}, \dots\)

    Solution :

     
    .
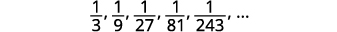
    Graphique 12.1.12
     
    .
    Graphique 12.1.13
    Nous cherchons un modèle dans les termes.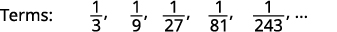
    .
    Graphique 12.1.14
    Les numérateurs sont tous\(1\).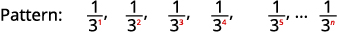
    .
    Graphique 12.1.15
    Les dénominateurs sont les pouvoirs de\(3\). Le terme général de la séquence est\(a_{n}=\frac{1}{3^{n}}\).
    Tableau 12.1.6

    Réponse :

    Le terme général de la séquence est\(a_{n}=\frac{1}{3^{n}}\).

    Exercice\(\PageIndex{11}\)

    Trouvez un terme général pour la séquence dont les cinq premiers termes sont affichés.

    \(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32}, \dots\)

    Réponse

    \(a_{n}=\frac{1}{2^{n}}\)

    Exercice\(\PageIndex{12}\)

    Trouvez un terme général pour la séquence dont les cinq premiers termes sont affichés.

    \(\frac{1}{1}, \frac{1}{4}, \frac{1}{9}, \frac{1}{16}, \frac{1}{25}, \dots\)

    Réponse

    \(a_{n}=\frac{1}{n^{2}}\)

    Utiliser la notation factorielle

    Les séquences contiennent souvent des termes qui sont des produits d'entiers consécutifs. Nous indiquons ces produits à l'aide d'une notation spéciale appelée notation factorielle. Par exemple\(5!\), lisez\(5\) factorielle, moyenne\(5⋅4⋅3⋅2⋅1\). Le point d'exclamation n'est pas la ponctuation ici ; il indique la notation factorielle.

    Définition\(\PageIndex{3}\)

    Si\(n\) est un entier positif, alors\(n!\) est

    \(n !=n(n-1)(n-2) \dots\)

    Nous définissons\(0!\) comme\(1\), donc\(0!=1\).

    Les valeurs de\(n!\) pour les premiers nombres entiers\(5\) positifs sont affichées.

    \(\begin{array}{ccccc}{1 !} & {2 !} & {3 !} & {4 !} & {5 !} \\ {1} & \quad{2 \cdot 1} & \quad {3 \cdot 2 \cdot 1} & \quad{4 \cdot 3 \cdot 2 \cdot 1} & \quad {5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \\ {1} & {2} & {6} & {24} & {120}\end{array}\)

    Exemple\(\PageIndex{7}\)

    Écrivez les cinq premiers termes de la séquence dont le terme général est\(a_{n}=\frac{1}{n !}\).

    Solution :

    Nous remplaçons les valeurs\(1, 2, 3, 4, 5\) dans la formule\(a_{n}=\frac{1}{n !}\), dans l'ordre.

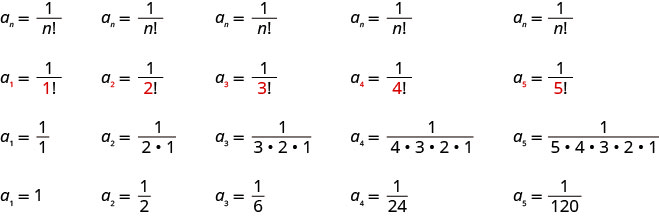
    Cette figure montre quatre lignes et cinq colonnes. La première ligne se lit comme suit : « Le nième terme est égal à un divisé par n factoriels » écrit cinq fois. La deuxième ligne se lit comme suit : « un sous 1 est égal à un divisé par 1 factoriel, un sous 2 est égal à 1 divisé par 2 factoriels, un sous 3 est égal à 1 divisé par 3 factoriels, un sous-4 est égal à 1 divisé par 4 factoriels, un sous 5 est égal à 1 divisé par 5 factoriels ». La troisième rangée se lit comme suit : « un sous 1 égal à 1 divisé », « un sous-ensemble 2 est égal à 1 divisé par 2 fois g fois 1 », « un sous-ensemble est égal à 1 divisé par 3 fois g fois 2 g fois 1 », « un sous-4 est égal à 1 divisé 4 fois g fois 3 fois g fois 3 fois g fois 2 fois », « un sous-ensemble 5 est égal à 1 divisé par 5 g fois 4 fois g fois 3 fois g fois 2 fois g fois 1 », « un sous 1 est égal à 1, un sous 2 est égal à la moitié », « un sous 3 est égal à un sixième », « un sous 4 est égal à 1 divisé par 24 », « un sous 5 est égal à 1 divisé par 120 ».
    Graphique 12.1.16

    Réponse :

    Les cinq premiers termes de la séquence sont\(1, \frac{1}{2}, \frac{1}{6}, \frac{1}{24}, \frac{1}{120}\).

    Exercice\(\PageIndex{13}\)

    Écrivez les cinq premiers termes de la séquence dont le terme général est\(a_{n}=\frac{2}{n !}\).

    Réponse

    \(2,1, \frac{1}{3}, \frac{1}{12}, \frac{1}{60}\)

    Exercice\(\PageIndex{14}\)

    Écrivez les cinq premiers termes de la séquence dont le terme général est\(a_{n}=\frac{3}{n !}\).

    Réponse

    \(3, \frac{3}{2}, \frac{1}{2}, \frac{1}{8}, \frac{1}{40}\)

    Lorsqu'il existe une fraction avec des factorielles au numérateur et au dénominateur, nous alignons les facteurs verticalement pour faciliter nos calculs.

    Exemple\(\PageIndex{8}\)

    Écrivez les cinq premiers termes de la séquence dont le terme général est\(a_{n}=\frac{(n+1) !}{(n-1) !}\).

    Solution :

    Nous remplaçons les valeurs\(1, 2, 3, 4, 5\) dans la formule\(a_{n}=\frac{(n+1) !}{(n-1) !}\), dans l'ordre.

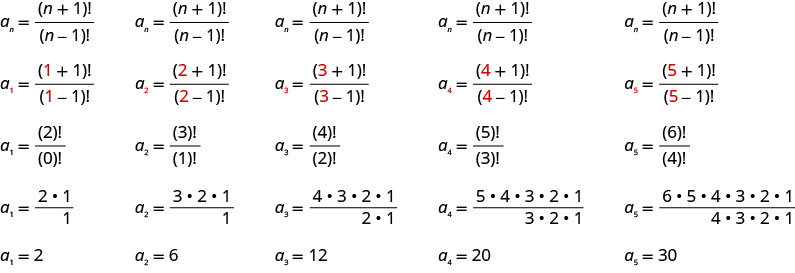
    Cette figure montre cinq colonnes et cinq lignes. La première ligne montre la séquence « Le nième terme est égal à n plus 1 fois factoriel divisé par n moins 1 fois factoriel » écrite cinq fois. La deuxième ligne est « un sous-1 est égal à 1 plus 1 fois factoriel divisé par 1 moins 1 fois factoriel », « un sous-ensemble 2 est égal à 2 plus 1 fois factoriel divisé par 2 moins 1 fois factoriel », « un sous-3 est égal à 3 plus 1 fois factoriel divisé par 3 moins 1 fois factoriel », « un sous-4 est égal à 4 plus 1 fois factoriel divisé par 4 moins 1 fois factoriel », « un sous-5 est égal à 5 plus 1 fois factoriel divisé par 5 moins 1 fois factoriel ». La troisième ligne se lit comme suit : « un sous-1 est égal à 2 fois factoriel divisé par 0 fois factoriel », « un sous-2 équivaut à 3 fois factoriel divisé par 1 fois factoriel », « un sous-3 est égal à 4 fois factoriel divisé par 2 fois factoriel », « un sous-3 est égal à 4 fois factoriel divisé par 2 fois factoriel », « un sous-4 est égal à 5 fois factoriel » divisé par 3 fois factoriel », « un sous-5 équivaut à 6 fois factoriel divisé par 4 fois factoriel ». La quatrième rangée se lit comme suit : « un sous-ensemble 1 est égal à 2 fois g temps 1 divisé par 1 », « un sous-ensemble 2 est égal à 3 fois g fois 2 fois g fois 1 divisé par 1 », « un sous-ensemble 3 est égal à 4 fois g fois 3 fois g fois 3 fois g fois 2 fois g fois 1 divisé par 2 fois g fois 1 », « un sous-ensemble 4 est égal à 5 fois g fois 4 fois g fois 3 fois g fois 2 fois g fois 1 divisé par 3 g fois 2 fois g fois 1 », et « un sous 5 est égal à 6 fois g fois 5 fois g fois 5 fois g fois 4 fois g fois 3 fois g fois 2 fois g fois 2 fois g fois 1 divisé par 4 fois g fois 3 fois g fois 3 fois g fois 2 fois g fois 1 ». La cinquième rangée se lit comme suit : « un sous 1 est égal à 2 », « un sous 2 est égal à 6 », « un sous 3 est égal à 12 », « un sous 4 est égal à 20 », « un sous 5 est égal à 30 ».
    Graphique 12.1.17

    Réponse :

    Les cinq premiers termes de la séquence sont\(2, 6, 12, 20\), et\(30\).

    Exercice\(\PageIndex{15}\)

    Écrivez les cinq premiers termes de la séquence dont le terme général est\(a_{n}=\frac{(n-1) !}{(n+1) !}\)

    Réponse

    \(\frac{1}{2}, \frac{1}{6}, \frac{1}{12}, \frac{1}{20}, \frac{1}{30}\)

    Exercice\(\PageIndex{16}\)

    Écrivez les cinq premiers termes de la séquence dont le terme général est\(a_{n}=\frac{n !}{(n+1) !}\).

    Réponse

    \(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}\)

    Trouvez la somme partielle

    Parfois, dans les applications, au lieu de simplement lister les termes, il est important pour nous d'ajouter les termes d'une séquence. Plutôt que de simplement relier les termes à des signes plus, nous pouvons utiliser la notation de sommation.

    Par exemple,\(a_{1}+a_{2}+a_{3}+a_{4}+a_{5}\) peut être écrit comme\(\sum_{i=1}^{5} a_{i}\). Nous lisons cela comme « la somme du\(a\) sous\(i\) de\(i\) est égale à un à cinq ». Le symbole\(∑\) signifie additionner et\(i\) est l'indice de sommation. Le nous\(1\) indique par où commencer (valeur initiale) et le\(5\) indique par où se terminer (valeur terminale).

    Définition\(\PageIndex{4}\)

    La somme des premiers\(n\) termes d'une séquence dont le\(n\) ième terme\(a_{n}\) est écrit en notation de sommation comme suit :

    \(\sum_{i=1}^{n} a_{i}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+\ldots+a_{n}\)

    \(i\)C'est l'indice de sommation qui nous\(1\) indique par où commencer et où terminer.\(n\)

    Lorsque nous ajoutons un nombre fini de termes, nous appelons la somme une somme partielle.

    Exemple\(\PageIndex{9}\)

    Développez la somme partielle et trouvez sa valeur :\(\sum_{i=1}^{5} 2 i\).

    Solution :

      \(\sum_{i=1}^{5} 2 i\)
    Nous substituons les valeurs\(1, 2, 3, 4, 5\) dans l'ordre. \(2 \cdot 1+2 \cdot 2+2 \cdot 3+2 \cdot 4 + 2 \cdot 5\)
    Simplifiez. \(2+4+6+8+10\)
    Ajoutez. \(\begin{array} {c} 30\\ \sum_{i=1}^{5} 2 i=30 \end{array}\)
    Tableau 12.1.7

    Réponse :

    \(\begin{array} {c} 30\\ \sum_{i=1}^{5} 2 i=30 \end{array}\)
    Exercice\(\PageIndex{17}\)

    Développez la somme partielle et trouvez sa valeur :\(\sum_{i=1}^{5} 3 i\).

    Réponse

    \(45\)

    Exercice\(\PageIndex{18}\)

    Développez la somme partielle et trouvez sa valeur :\(\sum_{i=1}^{5} 4 i\).

    Réponse

    \(60\)

    L'index ne doit pas toujours être :\(i\) nous pouvons utiliser n'importe quelle lettre, mais\(i\) nous\(k\) sommes couramment utilisés. L'indice ne doit pas nécessairement commencer par l'un\(1\) ou l'autre ; il peut commencer et se terminer par n'importe quel entier positif.

    Exemple\(\PageIndex{10}\)

    Développez la somme partielle et trouvez sa valeur :\(\sum_{k=0}^{3} \frac{1}{k !}\).

    Solution :

    \(\begin{array}{c c} {}&{\sum_{k=0}^{3} \frac{1}{k !}} \\ {We\:substitute\:the\:values\:0,1,2,3\:in\:order.}&{\frac{1}{1}+\frac{1}{1 !}+\frac{1}{2 !}+\frac{1}{3 !}} \\ {Evaluate\:the\:factorials.}& {\frac{1}{1}+\frac{1}{1}+\frac{1}{2 !}+\frac{1}{6}} \\ {Simplify.}&{1+1+\frac{3}{6}+\frac{1}{6}} \\{Simplify.}& {\frac{16}{6}} \\ {Simplify.}&{\frac{8}{3}} \\{}& {\sum_{k=0}^{3} \frac{1}{k !}=\frac{8}{3}}\end{array}\)

    Exercice\(\PageIndex{19}\)

    Développez la somme partielle et trouvez sa valeur :\(\sum_{k=0}^{3} \frac{2}{k !}\).

    Réponse

    \(\frac{16}{3}\)

    Exercice\(\PageIndex{20}\)

    Développez la somme partielle et trouvez sa valeur :\(\sum_{k=0}^{3} \frac{3}{k !}\).

    Réponse

    \(8\)

    Utiliser la notation de sommation pour écrire une somme

    Dans les deux derniers exemples, nous sommes passés de la notation de sommation à l'écriture de la somme. Nous allons maintenant commencer par une somme et la remplacer par une notation de sommation. Cela ressemble beaucoup à la recherche du terme général d'une séquence. Nous devrons examiner les termes et trouver un modèle. Souvent, les modèles impliquent des multiples ou des pouvoirs.

    Exemple\(\PageIndex{11}\)

    Écrivez la somme en utilisant la notation de sommation :\(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}\).

    Solution :

    \(\begin{array} {}&{ 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}} \\ {}&{n : 1,2,3,4,5} \\ {\text{We look for a pattern in the terms.}}&{\text { Terms: } 1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}} \\ {\text{The numerators are all one.}}&{\text { Pattern: } \frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \ldots \frac{1}{n}} \\ {\text{The denominators are the counting numbers from one to five.}}&{\text{The sum written in summation notation}} \\ {}&{1 + \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}=\sum^{5}_{n=1} \frac{1}{n}.} \end{array}\)

    Exercice\(\PageIndex{21}\)

    Écrivez la somme en utilisant la notation de sommation :\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\).

    Réponse

    \(\sum_{n=1}^{5} \frac{1}{2^{n}}\)

    Exercice\(\PageIndex{22}\)

    Écrivez la somme en utilisant la notation de sommation :\(1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}\)

    Réponse

    \(\sum_{n=1}^{5} \frac{1}{n^{2}}\)

    Lorsque les termes d'une somme ont des coefficients négatifs, nous devons analyser soigneusement la structure des signes.

    Exemple\(\PageIndex{12}\)

    Écrivez la somme en utilisant la notation de sommation :\(-1+8-27+64-125\).

    Solution :


     
    .
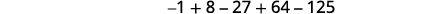
    Graphique 12.1.18
     
    .
    Graphique 12.1.19
    Nous cherchons un modèle dans les termes.
    .
    Graphique 12.1.20
    Les signes des termes alternent
    et les termes impairs sont négatifs.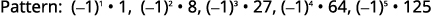
    .
    Graphique 12.1.21
    Les nombres sont les cubes des
    nombres de un à cinq.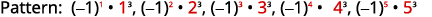
    .
    Graphique 12.1.22
     
    .
    Graphique 12.1.23
      La somme écrite en notation de sommation est
      \(-1+8-27+64-125=\sum_{n=1}^{5}(-1)^{n} \cdot n^{3}\)
    Tableau 12.1.8
    Exercice\(\PageIndex{23}\)

    Écrivez chaque somme en utilisant la notation de sommation :\(1-4+9-16+25\).

    Réponse

    \(\sum_{n=1}^{5}(-1)^{n+1} n^{2}\)

    Exercice\(\PageIndex{24}\)

    Écrivez chaque somme en utilisant la notation de sommation :\(-2+4-6+8-10\).

    Réponse

    \(\sum_{n=1}^{5}(-1)^{n} 2 n\)

    Accédez à cette ressource en ligne pour obtenir des instructions supplémentaires et vous entraîner avec les séquences.

    https://openstax.org/l/37serseqfindpat

    Concepts clés

    • Notation factorielle

    Si\(n\) est un entier positif, alors\(n!\) est

    \(n !=n(n-1)(n-2) \ldots(3)(2)(1)\)

    Nous définissons\(0!\) comme\(1\), donc\(0!=1\)

    • Notation de sommation

    La somme des premiers\(n\) termes d'une séquence dont le\(n\) ème terme\(a_{n}\) est écrit en notation sommative comme suit :

    \(\sum_{i=1}^{n} a_{i}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+\ldots+a_{n}\)

    \(i\)C'est l'indice de sommation qui nous\(1\) indique par où commencer et où terminer.\(n\)

    Lexique

    séquence finie
    Séquence dont le domaine est limité à un nombre fini de nombres de comptage.
    terme général d'une séquence
    Le terme général de la séquence est la formule permettant d'écrire le\(n\) ème terme de la séquence. Le\(n\) e terme de la séquence,\(a_{n}\), est le terme situé en\(n\) ème position où se\(n\) trouve une valeur dans le domaine.
    séquence infinie
    Une séquence dont le domaine est composé de nombres de comptage et dont le nombre est infini.
    somme partielle
    Lorsque nous ajoutons un nombre fini de termes d'une séquence, nous appelons la somme une somme partielle.
    séquence
    Une séquence est une fonction dont le domaine est le comptage des nombres.