10.5 : Utiliser les propriétés des logarithmes
- Page ID
- 194306
À la fin de cette section, vous serez en mesure de :
- Utiliser les propriétés des logarithmes
- Utiliser la formule de changement de base
Avant de commencer, répondez à ce questionnaire de préparation.
- Évaluer : a.\(a^{0}\)\(a^{1}\) b.
Si vous avez oublié ce problème, consultez l'exemple 5.14. - Écrivez avec un exposant rationnel :\(\sqrt[3]{x^{2} y}\).
Si vous avez oublié ce problème, consultez l'exemple 8.27. - Arrondir à la troisième décimale :\(2.5646415\).
Si vous avez oublié ce problème, consultez l'exemple 1.34.
Utiliser les propriétés des logarithmes
Maintenant que nous avons découvert les fonctions exponentielles et logarithmiques, nous pouvons introduire certaines des propriétés des logarithmes. Elles nous seront très utiles alors que nous continuons à résoudre des équations exponentielles et logarithmiques.
Les deux premières propriétés découlent de la définition des logarithmes. Depuis\(a^{0}=1\), nous pouvons le convertir en forme logarithmique et obtenir\(\log _{a} 1=0\). De plus, depuis\(a^{1}=a\), nous obtenons\(\log _{a} a=1\).
Propriétés des logarithmes
\(\log _{a} 1=0 \quad \log _{a} a=1\)
Dans l'exemple suivant, nous pourrions évaluer le logarithme en le convertissant sous forme exponentielle, comme nous l'avons fait précédemment, mais reconnaître puis appliquer les propriétés permet de gagner du temps.
Évaluez à l'aide des propriétés des logarithmes :
- \(\log _{8} 1\)
- \(\log _{6} 6\)
Solution :
un.
\(\log _{8} 1\)
Utilisez la propriété,\(\log _{a} 1=0\).
\(0 \quad \log _{8} 1=0\)
b.
\(\log _{6} 6\)
Utilisez la propriété,\(\log _{a} a=1\).
\(1 \quad \log _{6} 6=1\)
Évaluez à l'aide des propriétés des logarithmes :
- \(\log _{13} 1\)
- \(\log _{9} 9\)
- Réponse
-
- \(0\)
- \(1\)
Évaluez à l'aide des propriétés des logarithmes :
- \(\log _{5} 1\)
- \(\log _{7} 7\)
- Réponse
-
- \(0\)
- \(1\)
Les deux propriétés suivantes peuvent également être vérifiées en les convertissant de la forme exponentielle à la forme logarithmique, ou inversement.
L'équation exponentielle est\(a^{\log _{a} x}=x\) convertie en équation logarithmique\(\log _{a} x=\log _{a} x\), qui est une déclaration vraie pour les valeurs positives\(x\) uniquement.
L'équation logarithmique est\(\log _{a} a^{x}=x\) convertie en équation exponentielle\(a^{x}=a^{x}\), qui est également une déclaration vraie.
Ces deux propriétés sont appelées propriétés inverses parce que, lorsque nous avons la même base, le fait de passer à une puissance « annule » le journal et le fait de prendre le journal « annule » l'élévation à une puissance. Ces deux propriétés indiquent la composition des fonctions. Les deux ont abouti à la fonction d'identité qui montre à nouveau que les fonctions exponentielle et logarithmique sont des fonctions inverses.
Propriétés inverses des logarithmes
Pour\(a>0, x>0\) et\(a \neq 1\),
\(a^{\log _{a} x}=x \quad \log _{a} a^{x}=x\)
Dans l'exemple suivant, appliquez les propriétés inverses des logarithmes.
Évaluez à l'aide des propriétés des logarithmes :
- \(4^{\log _{4} 9}\)
- \(\log _{3} 3^{5}\)
Solution :
un.
\(4^{\log _{4} 9}\)
Utilisez la propriété,\(a^{\log _{a} x}=x\).
\(9 \quad 4^{\log _{4} 9}=9\)
b.
\(\log _{3} 3^{5}\)
Utilisez la propriété,\(a^{\log _{a} x}=x\).
\(5 \quad \log _{3} 3^{5}=5\)
Évaluez à l'aide des propriétés des logarithmes :
- \(5^{\log _{5} 15}\)
- \(\log _{7} 7^{4}\)
- Réponse
-
- \(15\)
- \(4\)
Évaluez à l'aide des propriétés des logarithmes :
- \(2^{\log _{2} 8}\)
- \(\log _{2} 2^{15}\)
- Réponse
-
- \(8\)
- \(15\)
Trois autres propriétés des logarithmes seront utiles dans notre travail. Nous savons que les fonctions exponentielles et les fonctions logarithmiques sont étroitement liées. Notre définition du logarithme nous montre qu'un logarithme est l'exposant de l'exponentielle équivalente. Les propriétés des exposants ont des propriétés connexes pour les exposants.
Dans la propriété de produit des exposants\(a^{m} \cdot a^{n}=a^{m+n}\), nous voyons que pour multiplier la même base, nous ajoutons les exposants. La propriété de produit des logarithmes nous\(\log _{a} M \cdot N=\log _{a} M+\log _{a} N\) indique de prendre le journal d'un produit, nous ajoutons le journal des facteurs.
Propriété de produit des logarithmes
Si\(M>0, N>0, \mathrm{a}>0\) et\(\mathrm{a} \neq 1,\) alors
\(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\)
Le logarithme d'un produit est la somme des logarithmes.
Nous utilisons cette propriété pour écrire le journal d'un produit sous la forme de la somme des logarithmes de chaque facteur.
Utilisez la propriété de produit des logarithmes pour écrire chaque logarithme sous la forme d'une somme de logarithmes. Simplifiez, si possible :
- \(\log _{3} 7 x\)
- \(\log _{4} 64 x y\)
Solution :
un.
\(\log _{3} 7 x\)
Utilisez la propriété du produit,\(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\).
\(\log _{3} 7+\log _{3} x\)
\(\log _{3} 7 x=\log _{3} 7+\log _{3} x\)
b.
\(\log _{4} 64 x y\)
Utilisez la propriété du produit,\(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\).
\(\log _{4} 64+\log _{4} x+\log _{4} y\)
Simplifiez en évaluant,\(\log _{4} 64\).
\(3+\log _{4} x+\log _{4} y\)
\(\log _{4} 64 x y=3+\log _{4} x+\log _{4} y\)
Utilisez la propriété de produit des logarithmes pour écrire chaque logarithme sous la forme d'une somme de logarithmes. Simplifiez, si possible :
- \(\log _{3} 3 x\)
- \(\log _{2} 8 x y\)
- Réponse
-
- \(1+\log _{3} x\)
- \(3+\log _{2} x+\log _{2} y\)
Utilisez la propriété de produit des logarithmes pour écrire chaque logarithme sous la forme d'une somme de logarithmes. Simplifiez, si possible :
- \(\log _{9} 9 x\)
- \(\log _{3} 27 x y\)
- Réponse
-
- \(1+\log _{9} x\)
- \(3+\log _{3} x+\log _{3} y\)
De même, dans la propriété du quotient des exposants\(\frac{a^{m}}{a^{n}}=a^{m-n}\), nous voyons que pour diviser la même base, nous soustrayons les exposants. La propriété du quotient des logarithmes nous\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\) indique que pour prendre le logarithme d'un quotient, nous soustrayons le logarithme du numérateur et du dénominateur.
Propriété du quotient des logarithmes
Si\(M>0, N>0, \mathrm{a}>0\) et\(\mathrm{a} \neq 1,\) alors
\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\)
Le logarithme d'un quotient est la différence des logarithmes.
Notez que\(\log _{a} M=\log _{a} N \not=\log _{a}(M-N)\).
Nous utilisons cette propriété pour écrire le logarithme d'un quotient sous forme de différence entre les logarithmes de chaque facteur.
Utilisez la propriété quotient des logarithmes pour écrire chaque logarithme sous la forme d'une différence de logarithmes. Simplifiez, si possible.
- \(\log _{5} \frac{5}{7}\)
- \(\log \frac{x}{100}\)
Solution :
un.
\(\log _{5} \frac{5}{7}\)
Utilisez la propriété Quotient,\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\).
\(\log _{5} 5-\log _{5} 7\)
Simplifiez.
\(1-\log _{5} 7\)
\(\log _{5} \frac{5}{7}=1-\log _{5} 7\)
b.
\(\log \frac{x}{100}\)
Utilisez la propriété Quotient,\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\).
\(\log x-\log 100\)
Simplifiez.
\(\log x-2\)
\(\log \frac{x}{100}=\log x-2\)
Utilisez la propriété quotient des logarithmes pour écrire chaque logarithme sous la forme d'une différence de logarithmes. Simplifiez, si possible.
- \(\log _{4} \frac{3}{4}\)
- \(\log \frac{x}{1000}\)
- Réponse
-
- \(\log _{4} 3-1\)
- \(\log x-3\)
Utilisez la propriété quotient des logarithmes pour écrire chaque logarithme sous la forme d'une différence de logarithmes. Simplifiez, si possible.
- \(\log _{2} \frac{5}{4}\)
- \(\log \frac{10}{y}\)
- Réponse
-
- \(\log _{2} 5-2\)
- \(1-\log y\)
La troisième propriété des logarithmes est liée à la propriété de puissance des exposants\(\left(a^{m}\right)^{n}=a^{m \cdot n}\), nous voyons que pour élever une puissance à une puissance, nous multiplions les exposants. La propriété de puissance des logarithmes nous\(\log _{a} M^{p}=p \log _{a} M\) indique de prendre le logarithme d'un nombre élevé à une puissance, nous multiplions la puissance par le logarithme du nombre.
Propriété de puissance des logarithmes
Si\(M>0, \mathrm{a}>0, \mathrm{a} \neq 1\) et\(p\) est un nombre réel alors,
\(\log _{a} M^{p}=p \log _{a} M\)
Le journal d'un nombre élevé à une puissance en tant que produit de la puissance multiplié par le logarithme du nombre.
Nous utilisons cette propriété pour écrire le journal d'un nombre élevé à une puissance en tant que produit de la puissance multiplié par le logarithme du nombre. Nous prenons essentiellement l'exposant et le plaçons devant le logarithme.
Utilisez la propriété Power des logarithmes pour écrire chaque logarithme sous la forme d'un produit de logarithmes. Simplifiez, si possible.
- \(\log _{5} 4^{3}\)
- \(\log x^{10}\)
Solution :
un.
\(\log _{5} 4^{3}\)
Utilisez la propriété Power,\(\log _{a} M^{p}=p \log _{a} M\).
3\(\log _{5} 4\)
\(\log _{5} 4^{3}=3 \log _{5} 4\)
b.
\(\log x^{10}\)
Utilisez la propriété Power,\(\log _{a} M^{p}=p \log _{a} M\).
\(10\log x\)
\(\log x^{10}=10 \log x\)
Utilisez la propriété Power des logarithmes pour écrire chaque logarithme sous la forme d'un produit de logarithmes. Simplifiez, si possible.
- \(\log _{7} 5^{4}\)
- \(\log x^{100}\)
- Réponse
-
- \(4\log _{7} 5\)
- 100\(\cdot \log x\)
Utilisez la propriété Power des logarithmes pour écrire chaque logarithme sous la forme d'un produit de logarithmes. Simplifiez, si possible.
- \(\log _{2} 3^{7}\)
- \(\log x^{20}\)
- Réponse
-
- \(7\log _{2} 3\)
- \(20\cdot \log x\)
Nous résumons les propriétés des logarithmes ici pour faciliter la consultation. Bien que les logarithmes naturels constituent un cas particulier de ces propriétés, il est souvent utile de montrer également la version logarithmique naturelle de chaque propriété.
Propriétés des logarithmes
Si\(M>0, \mathrm{a}>0, \mathrm{a} \neq 1\) et\(p\) est un nombre réel alors,
| Propriété | Base\(a\) | Base\(e\) |
|---|---|---|
| \ (a \) « >\(\log _{a} 1=0\) | \ (fr \) « >\(\ln 1=0\) | |
| \ (a \) « >\(\log _{a} a=1\) | \ (fr \) « >\(\ln e=1\) | |
| Propriétés inverses | \ (a \) « >\(a^{\log _{a} x}=x\) \(\log _{a} a^{x}=x\) |
\ (fr \) « >\(e^{\ln x}=x\) \(\ln e^{x}=x\) |
| Propriété de produit des logarithmes | \ (a \) « >\(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\) | \ (fr \) « >\(\ln (M \cdot N)=\ln M+\ln N\) |
| Propriété du quotient des logarithmes | \ (a \) « >\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\) | \ (fr \) « >\(\ln \frac{M}{N}=\ln M-\ln N\) |
| Propriété de puissance des logarithmes | \ (a \) « >\(\log _{a} M^{p}=p \log _{a} M\) | \ (fr \) « >\(\ln M^{p}=p \ln M\) |
Maintenant que nous avons les propriétés, nous pouvons les utiliser pour « développer » une expression logarithmique. Cela signifie écrire le logarithme sous forme de somme ou de différence et sans aucune puissance.
Nous appliquons généralement les propriétés du produit et du quotient avant d'appliquer la propriété de puissance.
Utilisez les propriétés des logarithmes pour développer le logarithme\(\log _{4}\left(2 x^{3} y^{2}\right)\). Simplifiez, si possible.
Solution :
Utilisez la propriété du produit,\(\log _{a} M \cdot N=\log _{a} M+\log _{a} N\).
Utilisez la propriété Power,\(\log _{a} M^{p}=p \log _{a} M\), sur les deux derniers termes. Simplifiez.
Utilisez les propriétés des logarithmes pour développer le logarithme\(\log _{2}\left(5 x^{4} y^{2}\right)\). Simplifiez, si possible.
- Réponse
-
\(\log _{2} 5+4 \log _{2} x+2 \log _{2} y\)
Utilisez les propriétés des logarithmes pour développer le logarithme\(\log _{3}\left(7 x^{5} y^{3}\right)\). Simplifiez, si possible.
- Réponse
-
\(\log _{3} 7+5 \log _{3} x+3 \log _{3} y\)
Lorsque nous avons un radical dans l'expression logarithmique, il est utile d'écrire d'abord son radical et comme un exposant rationnel.
Utilisez les propriétés des logarithmes pour développer le logarithme\(\log _{2} \sqrt[4]{\frac{x^{3}}{3 y^{2} z}}\). Simplifiez, si possible.
Solution
\(\log _{2} \sqrt[4]{\frac{x^{3}}{3 y^{2} z}}\)
Réécrivez le radical avec un exposant rationnel.
\(\log _{2}\left(\frac{x^{3}}{3 y^{2} z}\right)^{\frac{1}{4}}\)
Utilisez la propriété Power,\(\log _{a} M^{p}=p \log _{a} M\).
\(\frac{1}{4} \log _{2}\left(\frac{x^{3}}{3 y^{2} z}\right)\)
Utilisez la propriété Quotient,\(\log _{a} M \cdot N=\log _{a} M-\log _{a} N\).
\(\frac{1}{4}\left(\log _{2}\left(x^{3}\right)-\log _{2}\left(3 y^{2} z\right)\right)\)
Utilisez la propriété du produit\(\log _{a} M \cdot N=\log _{a} M+\log _{a} N\), au cours du second mandat.
\(\frac{1}{4}\left(\log _{2}\left(x^{3}\right)-\left(\log _{2} 3+\log _{2} y^{2}+\log _{2} z\right)\right)\)
Utilisez la propriété Power\(\log _{a} M^{p}=p \log _{a} M\), entre parenthèses.
\(\frac{1}{4}\left(3 \log _{2} x-\left(\log _{2} 3+2 \log _{2} y+\log _{2} z\right)\right)\)
Simplifiez en distribuant.
\(\frac{1}{4}\left(3 \log _{2} x-\log _{2} 3-2 \log _{2} y-\log _{2} z\right)\)
\(\log _{2} \sqrt[4]{\frac{x^{3}}{3 y^{2} z}}=\frac{1}{4}\left(3 \log _{2} x-\log _{2} 3-2 \log _{2} y-\log _{2} z\right)\)
Utilisez les propriétés des logarithmes pour développer le logarithme\(\log _{4} \sqrt[5]{\frac{x^{4}}{2 y^{3} z^{2}}}\). Simplifiez, si possible.
- Réponse
-
\(\frac{1}{5}\left(4 \log _{4} x-\frac{1}{2}-3 \log _{4} y-2 \log _{4} z\right)\)
Utilisez les propriétés des logarithmes pour développer le logarithme\(\log _{3} \sqrt[3]{\frac{x^{2}}{5 y z}}\). Simplifiez, si possible.
- Réponse
-
\(\frac{1}{3}\left(2 \log _{3} x-\log _{3} 5-\log _{3} y-\log _{3} z\right)\)
L'inverse de l'extension d'un logarithme est de condenser une somme ou une différence de logarithmes ayant la même base en un seul logarithme. Nous utilisons à nouveau les propriétés des logarithmes pour nous aider, mais en sens inverse.
Pour condenser des expressions logarithmiques ayant la même base en un seul logarithme, nous commençons par utiliser la propriété Power pour obtenir les coefficients des termes du logarithme à un, puis les propriétés du produit et du quotient selon les besoins.
Utilisez les propriétés des logarithmes pour condenser le logarithme\(\log _{4} 3+\log _{4} x-\log _{4} y\). Simplifiez, si possible.
Solution :
Les expressions du journal ont toutes la même base,\(4\).
Les deux premiers termes sont ajoutés, nous utilisons donc la propriété du produit,\(\log _{a} M+\log _{a} N=\log _{a} M : N\).
Comme les logs sont soustraits, nous utilisons la propriété du quotient,\(\log _{a} M-\log _{a} N=\log _{a} \frac{M}{N}\).
Utilisez les propriétés des logarithmes pour condenser le logarithme\(\log _{2} 5+\log _{2} x-\log _{2} y\). Simplifiez, si possible.
- Réponse
-
\(\log _{2} \frac{5 x}{y}\)
Utilisez les propriétés des logarithmes pour condenser le logarithme\(\log _{3} 6-\log _{3} x-\log _{3} y\). Simplifiez, si possible.
- Réponse
-
\(\log _{3} \frac{6}{x y}\)
Utilisez les propriétés des logarithmes pour condenser le logarithme\(2 \log _{3} x+4 \log _{3}(x+1)\). Simplifiez, si possible.
Solution :
Les expressions du journal ont la même base,\(3\).
\(2 \log _{3} x+4 \log _{3}(x+1)\)
Utilisez la propriété Power,\(\log _{a} M+\log _{a} N=\log _{a} M \cdot N\).
\(\log _{3} x^{2}+\log _{3}(x+1)^{4}\)
Les termes sont ajoutés, nous utilisons donc la propriété du produit,\(\log _{a} M+\log _{a} N=\log _{a} M \cdot N\).
\(\log _{3} x^{2}(x+1)^{4}\)
\(2 \log _{3} x+4 \log _{3}(x+1)=\log _{3} x^{2}(x+1)^{4}\)
Utilisez les propriétés des logarithmes pour condenser le logarithme\(3 \log _{2} x+2 \log _{2}(x-1)\). Simplifiez, si possible.
- Réponse
-
\(\log _{2} x^{3}(x-1)^{2}\)
Utilisez les propriétés des logarithmes pour condenser le logarithme\(2 \log x+2 \log (x+1)\). Simplifiez, si possible.
- Réponse
-
\(\log x^{2}(x+1)^{2}\)
Utiliser la formule de changement de base
Pour évaluer un logarithme avec n'importe quelle autre base, nous pouvons utiliser la formule de changement de base. Nous allons montrer comment cela est dérivé.
\(\begin{array} {l c} {\text{Suppose we want to evaluate} \log_{a}M} & {\log_{a}M} \\ {\text{Let} \:y =\log_{a}M. }&{y=\log_{a}M} \\ {\text{Rewrite the epression in exponential form. }}&{a^{y}=M } \\ {\text{Take the }\:\log_{b} \text{of each side.}}&{\log_{b}a^{y}=\log_{b}M}\\ {\text{Use the Power Property.}}&{y\log_{b}a=\log_{b}M} \\ {\text{Solve for}\:y. }&{y=\frac{\log_{b}M}{\log_{b}a}} \\ {\text{Substiture}\:y=\log_{a}M.}&{\log_{a}M=\frac{\log_{b}M}{\log_{b}a}} \end{array}\)
La formule de changement de base introduit une nouvelle base\(b\). Cela peut être n'importe quelle base où\(b\) nous voulons\(b>0,b≠1\). Comme nos calculateurs disposent de clés pour les logarithmes de base\(10\) et de base\(e\), nous allons réécrire la formule de changement de base avec la nouvelle base sous la forme\(10\) ou\(e\).
Formule de changement de base
Pour toutes les bases logarithmiques\(a, b\) et\(M>0\),
\(\begin{array}{lll}{\log _{a} M=\frac{\log _{b} M}{\log _{b} a}} & {\log _{a} M=\frac{\log M}{\log a}} & {\log _{a} M=\frac{\ln M}{\ln a}} \\ {\text { new base } b} & {\text { new base } 10} & {\text { new base } e}\end{array}\)
Lorsque nous utilisons une calculatrice pour trouver la valeur du logarithme, nous arrondissons généralement à trois décimales. Cela nous donne une valeur approximative et nous utilisons donc le symbole approximativement égal\((≈)\).
En arrondissant à la troisième décimale, c'est approximatif\(\log _{4} 35\).
Solution :
 |
|
| Utilisez la formule de changement de base. | 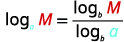 |
| Identifiez\(a\) et\(M\). Choisissez\(10\) pour\(b\). | 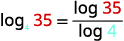 |
| Entrez l'expression\(\frac{\log 35}{\log 4}\) dans la calculatrice à l'aide du bouton journal comme base\(10\). Arrondir à la troisième décimale. | 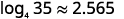 |
En arrondissant à la troisième décimale, c'est approximatif\(\log _{3} 42\).
- Réponse
-
\(3.402\)
En arrondissant à la troisième décimale, c'est approximatif\(\log _{5} 46\).
- Réponse
-
\(2.379\)
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à utiliser les propriétés des logarithmes.
Concepts clés
- \(\log _{a} 1=0 \quad \log _{a} a=1\)
- Propriétés inverses des logarithmes
- Pour\(a>0,x>0\) et\(a≠1\)
\(a^{\log _{a} x}=x \quad \log _{a} a^{x}=x\)
- Pour\(a>0,x>0\) et\(a≠1\)
- Propriété de produit des logarithmes
- Si\(M>0,N>0,a>0\) et\(a≠1\), alors,
\(\log _{a} M \cdot N=\log _{a} M+\log _{a} N\)
Le logarithme d'un produit est la somme des logarithmes.
- Si\(M>0,N>0,a>0\) et\(a≠1\), alors,
- Propriété du quotient des logarithmes
- Si\(M>0, N>0, \mathrm{a}>0\) et\(a≠1\), alors,
\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\)
Le logarithme d'un quotient est la différence des logarithmes.
- Si\(M>0, N>0, \mathrm{a}>0\) et\(a≠1\), alors,
- Propriété de puissance des logarithmes
- Si\(M>0,a>0,a≠1\) et\(p\) est un nombre réel alors,
\(\log _{a} M^{p}=p \log _{a} M\)
Le logarithme d'un nombre élevé à une puissance est le produit de la puissance par le logarithme du nombre.
- Si\(M>0,a>0,a≠1\) et\(p\) est un nombre réel alors,
- Résumé des propriétés des logarithmes
Si\(M>0,a>0,a≠1\) et\(p\) est un nombre réel alors,
| Propriété | Base\(a\) | Base\(e\) |
|---|---|---|
| \ (a \) « >\(\log _{a} 1=0\) | \ (fr \) « >\(\ln 1=0\) | |
| \ (a \) « >\(\log _{a} a=1\) | \ (fr \) « >\(\ln e=1\) | |
| Propriétés inverses | \ (a \) « >\(a^{\log _{a} x}=x\) \(\log _{a} a^{x}=x\) |
\ (fr \) « >\(e^{\ln x}=x\) \(\ln e^{x}=x\) |
| Propriété de produit des logarithmes | \ (a \) « >\(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\) | \ (fr \) « >\(\ln (M \cdot N)=\ln M+\ln N\) |
| Propriété du quotient des logarithmes | \ (a \) « >\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\) | \ (fr \) « >\(\ln \frac{M}{N}=\ln M-\ln N\) |
| Propriété de puissance des logarithmes | \ (a \) « >\(\log _{a} M^{p}=p \log _{a} M\) | \ (fr \) « >\(\ln M^{p}=p \ln M\) |
- Formule de changement de base
Pour toutes les bases logarithmiques\(a\) et\(b\), et\(M>0\),\(\begin{array}{ll}{\log _{a} M=\frac{\log _{b} M}{\log _{b} a}} & {\log _{a} M=\frac{\log M}{\log a}} & {\log _{a} M=\frac{\ln M}{\ln a}} \\ {\text { new base } b} & {\text { new base } 10} & {\text { new base } e}\end{array}\)


