10.4 : Évaluer et représenter graphiquement les fonctions logarithmiques
- Page ID
- 194322
À la fin de cette section, vous serez en mesure de :
- Convertir entre une forme exponentielle et une forme logarithmique
- Évaluer les fonctions logarithmiques
- Fonctions logarithmiques du graphe
- Résoudre des équations logarithmiques
- Utiliser des modèles logarithmiques dans les applications
Avant de commencer, répondez à ce questionnaire de préparation.
- Résoudre :\(x^{2}=81\).
Si vous avez oublié ce problème, consultez l'exemple 6.46. - Évaluez :\(3^{−2}\).
Si vous avez oublié ce problème, consultez l'exemple 5.15. - Résoudre :\(2^{4}=3x−5\).
Si vous avez oublié ce problème, consultez l'exemple 2.2.
Nous avons passé un certain temps à trouver l'inverse de nombreuses fonctions. Cela fonctionne bien pour « annuler » une opération par une autre. Soustraire « annule » l'addition, la multiplication « annule » la division, en prenant la racine carrée « annule » la mise au carré.
En étudiant la fonction exponentielle, nous avons constaté qu'elle est univoque car ses graphes passent le test de la ligne horizontale. Cela signifie qu'une fonction exponentielle possède un inverse. Si nous essayons notre méthode algébrique pour trouver un inverse, nous rencontrons un problème.
\(f(x)=a^{x}\)
Réécrivez avec\(y=f(x)\).
\(y=a^{x}\)
Échangez les variables\(x\) et\(y\).
\(x=a^{y}\)
Résolvez pour\(y\).
Oups ! Nous n'avons aucun moyen de le résoudre\(y\) !
Pour y remédier, nous définissons la fonction logarithme dont la base a est l'inverse de la fonction exponentielle\(f(x)=a^{x}\). Nous utilisons la notation\(f^{−1}(x)=log_{a}x\) et disons que la fonction inverse de la fonction exponentielle est la fonction logarithmique.
La fonction\(f(x)=\log_{a}x\) est la fonction logarithmique avec base\(a\)\(a>0,x>0\), où et\(a≠1\).
\(y=\log _{a} x\)est équivalent à\(x=a^{y}\)
Convertir entre une forme exponentielle et une forme logarithmique
Comme les équations\(y=\log _{a} x\) et\(x=a^{y}\) sont équivalentes, on peut faire des allers-retours entre elles. Ce sera souvent la méthode pour résoudre certaines équations exponentielles et logarithmiques. Pour vous aider à effectuer des conversions dans les deux sens, examinons de près les équations. Voir la Figure 10.3.1. Remarquez les positions de l'exposant et de la base.
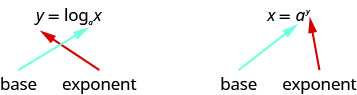
Si nous réalisons que le logarithme est l'exposant, cela facilite la conversion. Vous pouvez répéter : « en vous basant sur l'exposant, donnez-nous le nombre ».
Convertir au format logarithmique :
- \(2^{3}=8\)
- \(5^{\frac{1}{2}}=\sqrt{5}\)
- \(\left(\frac{1}{2}\right)^{x}=\frac{1}{16}\)
Solution :
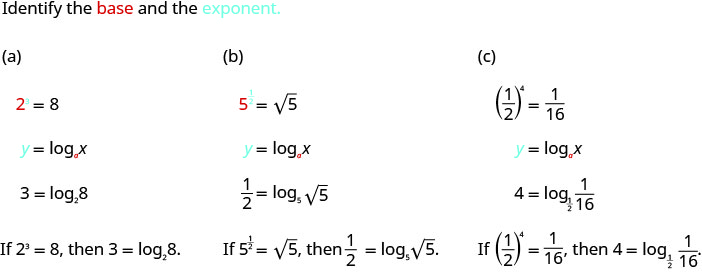
Convertir au format logarithmique :
- \(3^{2}=9\)
- \(7^{\frac{1}{2}}=\sqrt{7}\)
- \(\left(\frac{1}{3}\right)^{x}=\frac{1}{27}\)
- Réponse
-
- \(\log _{3} 9=2\)
- \(\log _{7} \sqrt{7}=\frac{1}{2}\)
- \(\log _{\frac{1}{3}} \frac{1}{27}=x\)
Convertir au format logarithmique :
- \(4^{3}=64\)
- \(4^{\frac{1}{3}}=\sqrt[3]{4}\)
- \(\left(\frac{1}{2}\right)^{x}=\frac{1}{32}\)
- Réponse
-
- \(\log _{4} 64=3\)
- \(\log _{4} \sqrt[3]{4}=\frac{1}{3}\)
- \(\log _{\frac{1}{2}} \frac{1}{32}=x\)
Dans l'exemple suivant, nous faisons l'inverse : convertir une forme logarithmique en forme exponentielle.
Convertir en forme exponentielle :
- \(2=\log _{8} 64\)
- \(0=\log _{4} 1\)
- \(-3=\log _{10} \frac{1}{1000}\)
Solution :
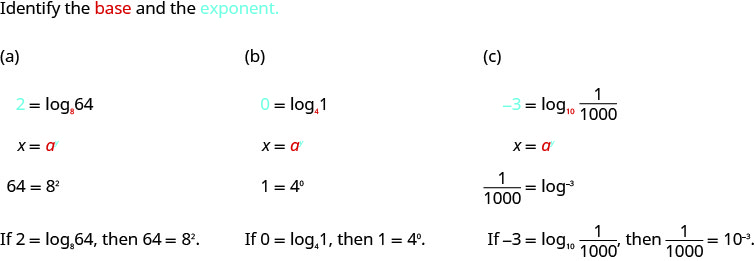
Convertir en forme exponentielle :
- \(3=\log _{4} 64\)
- \(0=\log _{x} 1\)
- \(-2=\log _{10} \frac{1}{100}\)
- Réponse
-
- \(64=4^{3}\)
- \(1=x^{0}\)
- \(\frac{1}{100}=10^{-2}\)
Convertir en forme exponentielle :
- \(3=\log _{3} 27\)
- \(0=\log _{x} 1\)
- \(-1=\log _{10} \frac{1}{10}\)
- Réponse
-
- \(27=3^{3}\)
- \(1=x^{0}\)
- \(\frac{1}{10}=10^{-1}\)
Évaluer les fonctions logarithmiques
Nous pouvons résoudre et évaluer des équations logarithmiques en utilisant la technique de conversion de l'équation en son équation exponentielle équivalente.
Trouvez la valeur de\(x\) :
- \(\log _{x} 36=2\)
- \(\log _{4} x=3\)
- \(\log _{\frac{1}{2}} \frac{1}{8}=x\)
Solution :
un.
\(\log _{x} 36=2\)
Convertir en forme exponentielle.
\(x^{2}=36\)
Résolvez le quadratique.
\(x=6, \quad \cancel{x=-6}\)
La base d'une fonction logarithmique doit être positive, donc on élimine\(x=−6\).
\(x=6 \quad\)Par conséquent,\(\log _{6} 36=2\)
b.
\(\log _{4} x=3\)
Convertir en forme exponentielle.
\(4^{3}=x\)
Simplifiez.
\(x=64 \quad\)Par conséquent\(, \log _{4} 64=3\)
c.
\(\log _{\frac{1}{2}} \frac{1}{8}=x\)
Convertir en forme exponentielle.
\(\left(\frac{1}{2}\right)^{x}=\frac{1}{8}\)
Réécrivez\(\frac{1}{8}\) en tant que\(\left(\frac{1}{2}\right)^{3}\).
\(\left(\frac{1}{2}\right)^{x}=\left(\frac{1}{2}\right)^{3}\)
Avec la même base, les exposants doivent être égaux.
\(x=3 \quad\)Par conséquent\(\log _{\frac{1}{2}} \frac{1}{8}=3\)
Trouvez la valeur de\(x\) :
- \(\log _{x} 64=2\)
- \(\log _{5} x=3\)
- \(\log _{\frac{1}{2}} \frac{1}{4}=x\)
- Réponse
-
- \(x=8\)
- \(x=125\)
- \(x=2\)
Trouvez la valeur de\(x\) :
- \(\log _{x} 81=2\)
- \(\log _{3} x=5\)
- \(\log _{\frac{1}{3}} \frac{1}{27}=x\)
- Réponse
-
- \(x=9\)
- \(x=243\)
- \(x=3\)
Lorsque vous voyez une expression telle que\(log_{3}27\), nous pouvons trouver sa valeur exacte de deux manières. Par inspection, nous nous rendons compte que cela signifie «\(3\) à quel pouvoir appartiendra-t-il\(27\) » ? Depuis\(3^{3}=27\), on le sait\(log_{3}27=3\). Une autre méthode consiste à définir l'expression comme égale à,\(x\) puis à la convertir en équation exponentielle.
Trouvez la valeur exacte de chaque logarithme sans utiliser de calculatrice :
- \(\log _{5} 25\)
- \(\log _{9} 3\)
- \(\log _{2} \frac{1}{16}\)
Solution :
un.
\(\log _{5} 25\)
\(5\)à quel pouvoir\(25\) appartiendra-t-il ?
\(\log _{5} 25=2\)
Ou
Définissez l'expression comme étant égale à\(x\).
\(\log _{5} 25=x\)
Passez à la forme exponentielle.
\(5^{x}=25\)
Réécrivez\(25\) en tant que\(5^{2}\).
\(5^{x}=5^{2}\)
Avec la même base, les exposants doivent être égaux.
\(x=2 \quad\)Par conséquent\(, \log _{5} 25=2\).
b.
\(\log _{9} 3\)
Définissez l'expression comme étant égale à\(x\).
\(\log _{9} 3=x\)
Passez à la forme exponentielle.
\(9^{x}=3\)
Réécrivez\(9\) en tant que\(3^{2}\).
\(\left(3^{2}\right)^{x}=3^{1}\)
Simplifiez les exposants.
\(3^{2 x}=3^{1}\)
Avec la même base, les exposants doivent être égaux.
\(2 x=1\)
Résolvez l'équation.
\(x=\frac{1}{2} \quad\)Par conséquent\(, \log _{9} 3=\frac{1}{2}\).
c.
\(\log _{2} \frac{1}{16}\)
Définissez l'expression comme étant égale à\(x\).
\(\log _{2} \frac{1}{16}=x\)
Passez à la forme exponentielle.
\(2^{x}=\frac{1}{16}\)
Réécrivez\(16\) en tant que\(2^{4}\).
\(2^{x}=\frac{1}{2^{4}}\)
\(2^{x}=2^{-4}\)
Avec la même base, les exposants doivent être égaux.
\(x=-4 \quad\)Par conséquent\(, \log _{2} \frac{1}{16}=-4\).
Trouvez la valeur exacte de chaque logarithme sans utiliser de calculatrice :
- \(\log _{12} 144\)
- \(\log _{4} 2\)
- \(\log _{2} \frac{1}{32}\)
- Réponse
-
- \(2\)
- \(\frac{1}{2}\)
- \(-5\)
Trouvez la valeur exacte de chaque logarithme sans utiliser de calculatrice :
- \(\log _{9} 81\)
- \(\log _{8} 2\)
- \(\log _{3} \frac{1}{9}\)
- Réponse
-
- \(2\)
- \(\frac{1}{3}\)
- \(-2\)
Fonctions logarithmiques du graphe
Pour représenter graphiquement une fonction logarithmique\(y=log_{a}x\), il est plus facile de convertir l'équation sous sa forme exponentielle,\(x=a^{y}\). Généralement, lorsque nous recherchons des paires ordonnées pour le graphe d'une fonction, nous choisissons généralement une\(x\) valeur, puis nous déterminons\(y\) la valeur correspondante. Dans ce cas, il peut être plus facile de choisir\(y\) des valeurs, puis de déterminer\(x\) la valeur correspondante.
Graphe\(y=\log _{2} x\).
Solution :
Pour représenter graphiquement la fonction, nous allons d'abord réécrire l'équation logarithmique\(y=\log _{2} x\), sous forme exponentielle\(2^{y}=x\).
Nous utiliserons le traçage par points pour représenter graphiquement la fonction. Il sera plus facile de commencer avec des valeurs de,\(y\) puis d'obtenir\(x\).
| \(y\) | \(2^{y}=x\) | \((x,y)\) |
|---|---|---|
| \ (y \) « >\(-2\) | \ (2^ {y} =x \) « >\(2^{-2}=\frac{1}{2^{2}}=\frac{1}{4}\) | \ ((x, y) \) « >\((\frac{1}{4},2)\) |
| \ (y \) « >\(-1\) | \ (2^ {y} =x \) « >\(2^{-1}=\frac{1}{2^{1}}=\frac{1}{2}\) | \ ((x, y) \) « >\((\frac{1}{2},-1)\) |
| \ (y \) « >\(0\) | \ (2^ {y} =x \) « >\(2^{0}=1\) | \ ((x, y) \) « >\((1,0)\) |
| \ (y \) « >\(1\) | \ (2^ {y} =x \) « >\(2^{1}=2\) | \ ((x, y) \) « >\((2,1)\) |
| \ (y \) « >\(2\) | \ (2^ {y} =x \) « >\(2^{2}=4\) | \ ((x, y) \) « >\((4,2)\) |
| \ (y \) « >\(3\) | \ (2^ {y} =x \) « >\(2^{3}=8\) | \ ((x, y) \) « >\((8,3)\) |
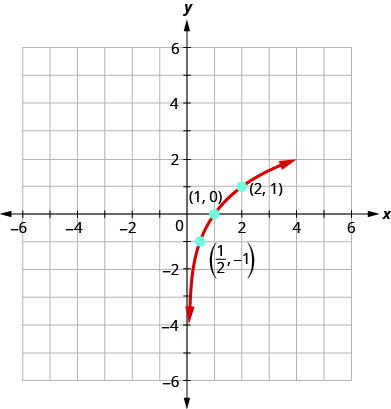
Graphique :\(y=\log _{3} x\).
- Réponse
-
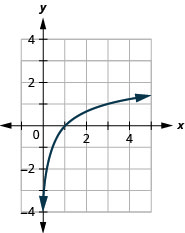
Graphique 10.3.5
Graphique :\(y=\log _{5} x\).
- Réponse
-
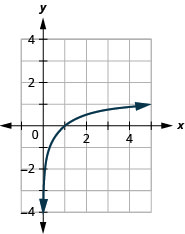
Graphique 10.3.6
Les graphes de\(y=\log _{2} x, y=\log _{3} x\) et\(y=\log _{5} x\) sont la forme que nous attendons d'une fonction logarithmique où\(a>1\).
On remarque que pour chaque fonction, le graphe contient le point\((1,0)\). Cela a du sens car c'est\(0=log_{a}1\) un moyen\(a^{0}=1\) qui est vrai pour tout le monde\(a\).
Le graphique de chaque fonction contient également le point\((a,1)\). Cela a du sens en tant que\(1=\log _{a} a\) moyen\(a^{1}=a\), ce qui est vrai pour tout le monde\(a\).
Notez également que le graphe de chaque fonction contient\(y=\log _{a} x\) également le point\(\left(\frac{1}{a},-1\right)\). Cela a du sens en tant que\(-1=\log _{a} \frac{1}{a}\) moyen\(a^{-1}=\frac{1}{a}\), ce qui est vrai pour tout le monde\(a\).
Examinez à nouveau chaque graphique. Nous allons maintenant voir que de nombreuses caractéristiques de la fonction logarithmique ne sont que des « images miroir » des caractéristiques de la fonction exponentielle correspondante.
Quel est le domaine de la fonction ? Le graphique n'atteint jamais l'\(y\)axe. Le domaine est composé uniquement de nombres positifs. Nous écrivons le domaine en notation par intervalles sous la forme\((0,∞)\).
Quelle est la plage pour chaque fonction ? Sur les graphiques, nous pouvons voir que la plage est l'ensemble de tous les nombres réels. Il n'y a aucune restriction quant à la portée. Nous écrivons la plage en notation par intervalles sous la forme\((−∞,∞)\).
Lorsque le graphe s'approche de très près de\(y\) l'axe -mais ne le franchit jamais, nous appelons la ligne\(x=0\), l'\(y\)axe -, une asymptote verticale.
| Domaine | \((0, \infty)\) |
| Gamme | \((-\infty, \infty)\) |
| \(x\)-intercepter | \((1,0)\) |
| \(y\)-intercepter | Aucune |
| Contient | \((a, 1),\left(\frac{1}{a},-1\right)\) |
| Asymptote | \(y\)-axe |
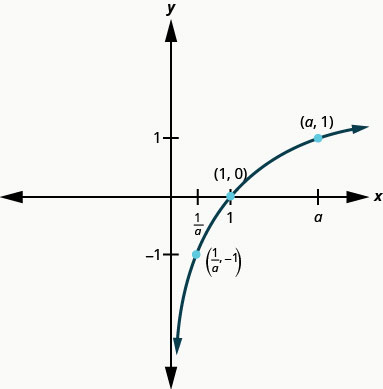
Notre exemple suivant examine le graphique indiquant\(y=log_{a}x\) quand\(0<a<1\).
Graphe\(y=\log _{\frac{1}{3}} x\).
Solution :
Pour représenter graphiquement la fonction, nous allons d'abord réécrire l'équation logarithmique\(y=\log _{\frac{1}{3}} x\), sous forme exponentielle\(\left(\frac{1}{3}\right)^{y}=x\).
Nous utiliserons le traçage par points pour représenter graphiquement la fonction. Il sera plus facile de commencer avec des valeurs de,\(y\) puis d'obtenir\(x\).
| \(y\) | \(\left(\frac{1}{3}\right)^{y}=x\) | \((x,y)\) |
|---|---|---|
| \ (y \) « >\(-2\) | \ (\ left (\ frac {1} {3} \ right) ^ {y} =x \) « >\(\left(\frac{1}{3}\right)^{-2}=3^{2}=9\) | \ ((x, y) \) « >\((9,-2)\) |
| \ (y \) « >\(-1\) | \ (\ left (\ frac {1} {3} \ right) ^ {y} =x \) « >\(\left(\frac{1}{3}\right)^{-1}=3^{1}=3\) | \ ((x, y) \) « >\((3,-1)\) |
| \ (y \) « >\(0\) | \ (\ left (\ frac {1} {3} \ right) ^ {y} =x \) « >\(\left(\frac{1}{3}\right)^{0}=1\) | \ ((x, y) \) « >\((1,0)\) |
| \ (y \) « >\(1\) | \ (\ left (\ frac {1} {3} \ right) ^ {y} =x \) « >\(\left(\frac{1}{3}\right)^{1}=\frac{1}{3}\) | \ ((x, y) \) « >\(\left(\frac{1}{3}, 1\right)\) |
| \ (y \) « >\(2\) | \ (\ left (\ frac {1} {3} \ right) ^ {y} =x \) « >\(\left(\frac{1}{3}\right)^{2}=\frac{1}{9}\) | \ ((x, y) \) « >\(\left(\frac{1}{9}, 2\right)\) |
| \ (y \) « >\(3\) | \ (\ left (\ frac {1} {3} \ right) ^ {y} =x \) « >\(\left(\frac{1}{3}\right)^{3}=\frac{1}{27}\) | \ ((x, y) \) « >\(\left(\frac{1}{27}, 3\right)\) |
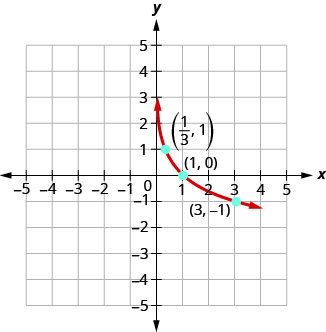
Graphique :\(y=\log _{\frac{1}{2}} x\).
- Réponse
-
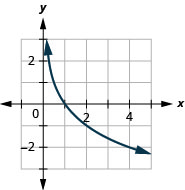
Graphique :\(y=\log _{\frac{1}{4}} x\).
- Réponse
-
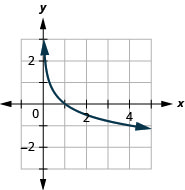
Maintenant, regardons les graphes\(y=\log _{\frac{1}{2}} x, y=\log _{\frac{1}{3}} x\) et\(y=\log _{\frac{1}{4}} x\), ainsi, nous pouvons identifier certaines des propriétés des fonctions logarithmiques où\(0<a<1\).
Les graphes ont tous la même forme de base. Bien que ce soit la forme que nous attendons d'une fonction logarithmique où\(0<a<1\).
Nous remarquons que pour chaque fonction, encore une fois, le graphique contient les points,\((1,0),(a, 1),\left(\frac{1}{a},-1\right)\). Cela a du sens pour les mêmes raisons que celles que nous avons expliquées ci-dessus.
Nous remarquons que le domaine et la plage sont également les mêmes : le domaine est\((0,∞)\) et la plage l'est\((−∞,∞)\). L'\(y\)axe -est à nouveau l'asymptote verticale.
Nous allons résumer ces propriétés dans le tableau ci-dessous. Ce qui inclut également quand\(a>1\).
| Quand\(a>1\) | Quand\(0<a<1\) | ||
|---|---|---|---|
| \ (a">1 \) ">Domaine | \((0, \infty)\) | \ (0<a<1 \) « >Domaine | \((0, \infty)\) |
| \ (a">1 \) « >Gamme | \((-\infty, \infty)\) | \ (0<a<1 \) « >Gamme | \((-\infty, \infty)\) |
| \ (a">1 \) « >\(x\) -intercepter | \((1,0)\) | \ (0<a<1 \) « >\(x\) -intercepter | \((1,0)\) |
| \ (a">1 \) « >\(y\) -intercepter | Aucune | \ (0<a<1 \) « >\(y\) -intercepter | Aucune |
| \ (a">1 \) « >Contient | \((a, 1),\left(\frac{1}{a},-1\right)\) | \ (0<a<1 \) « >Contient | \((a, 1),\left(\frac{1}{a},-1\right)\) |
| \ (a">1 \) « >Asymptote | \(y\)-axe | \ (0<a<1 \) « >Asymptote | \(y\)-axe |
| \ (a">1 \) ">Forme de base | En hausse | \ (0<a<1 \) « >Forme de base | Décroissant |

Nous avons parlé plus tôt de la façon dont la fonction logarithmique\(f^{-1}(x)=\log _{a} x\) est l'inverse de la fonction exponentielle\(f(x)=a^{x}\). Les graphiques de la Figure 10.3.12 montrent les fonctions exponentielle (bleue) et logarithmique (rouge) sur le même graphique pour\(a>1\) et\(0<a<1\).
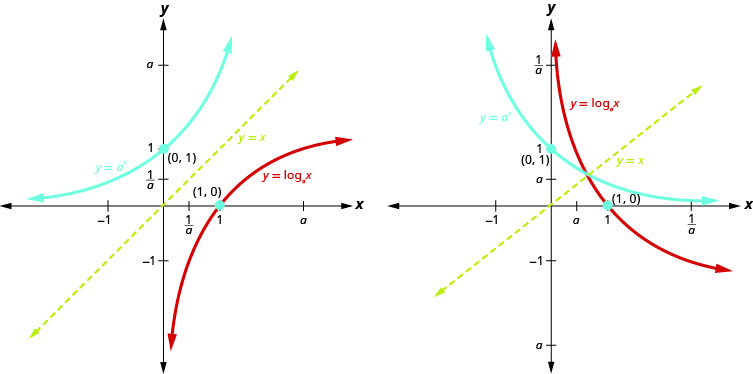
Remarquez comment les graphiques se reflètent les uns des autres à travers la ligne\(y=x\). Nous savons que c'est vrai pour les fonctions inverses. En gardant ces graphiques à l'esprit, vous pourrez vous souvenir du domaine et de la plage de chaque fonction. Notez que l'\(x\)axe -est l'asymptote horizontale pour les fonctions exponentielles et que l'\(y\)axe -est l'asymptote verticale pour les fonctions logarithmiques.
Résoudre des équations logarithmiques
Lorsque nous avons parlé de fonctions exponentielles, nous avons introduit le nombre\(e\). Tout comme\(e\) c'était une base pour une fonction exponentielle, elle peut également être utilisée comme base pour des fonctions logarithmiques. La fonction logarithmique avec base\(e\) est appelée fonction logarithmique naturelle. La fonction\(f(x)=\log _{e} x\) est généralement écrite\(f(x)=\ln x\) et nous la lisons comme « el en of »\(x\).
La fonction\(f(x)=\ln x\) est la fonction logarithmique naturelle avec base\(e\), où\(x>0\).
\(y=\ln x\)est équivalent à\(x=e^{y}\)
Lorsque la base de la fonction logarithmique est\(10\), nous l'appelons fonction logarithmique commune et la base n'est pas affichée. Si la base\(a\) d'un logarithme n'est pas affichée, nous supposons que c'est le cas\(10\).
La fonction\(f(x)=\log x\) est la fonction logarithmique commune avec base\(10\), où\(x>0\).
\(y=\log x\)est équivalent à\(x=10^{y}\)

Pour résoudre des équations logarithmiques, une stratégie consiste à transformer l'équation en une forme exponentielle, puis à résoudre l'équation exponentielle comme nous le faisions auparavant. Lorsque nous résolvons des équations logarithmiques\(y=log_{a}x\), nous devons nous en souvenir pour la base\(a\),\(a>0\) et\(a≠1\). De plus, le domaine est\(x>0\). Tout comme pour les équations radicales, nous devons vérifier nos solutions pour éliminer toute solution superflue.
Résoudre :
- \(\log _{a} 49=2\)
- \(\ln x=3\)
Solution :
un.
\(\log _{a} 49=2\)
Réécrivez sous forme exponentielle.
\(a^{2}=49\)
Résolvez l'équation en utilisant la propriété de racine carrée.
\(a=\pm 7\)
La base ne peut pas être négative, nous éliminons donc\(a=-7\).
\(a=7, \quad \cancel{a=-7}\)
Vérifiez. \(a=7\)
\(\begin{aligned} \log _{a} 49&=2 \\ \log_{7}49&\stackrel{?}{=}2 \\ 7^{2}&\stackrel{?}{=}49 \\ 49&=49 \end{aligned}\)
b.
\(\ln x=3\)
Réécrivez sous forme exponentielle.
\(e^{3}=x\)
Vérifiez. \(x=e^{3}\)
\(\begin{aligned} \ln x &=3 \\ \ln e^{3} & \stackrel{?}{=} 3 \\ e^{3} &=e^{3} \end{aligned}\)
Résoudre :
- \(\log _{a} 121=2\)
- \(\ln x=7\)
- Réponse
-
- \(a=11\)
- \(x=e^{7}\)
Résoudre :
- \(\log _{a} 64=3\)
- \(\ln x=9\)
- Réponse
-
- \(a=4\)
- \(x=e^{9}\)
Résoudre :
- \(\log _{2}(3 x-5)=4\)
- \(\ln e^{2 x}=4\)
Solution :
un.
\(\log _{2}(3 x-5)=4\)
Réécrivez sous forme exponentielle.
\(2^{4}=3 x-5\)
Simplifiez.
\(16=3 x-5\)
Résolvez l'équation.
\(21=3 x\)
\(7=x\)
Vérifiez. \(x=7\)
\(\begin{aligned} \log _{2}(3 x-5)&=4 \\ \log_{2}(3\cdot7-5)&\stackrel{?}{=}4\\ \log_{2}(16)&\stackrel{?}{=}4 \\ 2^{4}& \stackrel{?}{=}16 \\ 16&=16 \end{aligned}\)
b.
\(\ln e^{2 x}=4\)
Réécrivez sous forme exponentielle.
\(e^{4}=e^{2 x}\)
Comme les bases sont les mêmes, les exposants sont égaux.
\(4=2 x\)
Résolvez l'équation.
\(2=x\)
Vérifiez. \(x=2\)
\(\begin{aligned} \ln e^{2 x} &=4 \\ \ln e^{2 \cdot 2} & \stackrel{?}{=} 4 \\ \ln e^{4} &=4 \\ e^{4} &=e^{4} \end{aligned}\)
Résoudre :
- \(\log _{2}(5 x-1)=6\)
- \(\ln e^{3 x}=6\)
- Réponse
-
- \(x=13\)
- \(x=2\)
Résoudre :
- \(\log _{3}(4 x+3)=3\)
- \(\ln e^{4 x}=4\)
- Réponse
-
- \(x=6\)
- \(x=1\)
Utiliser des modèles logarithmiques dans les applications
De nombreuses applications sont modélisées par des équations logarithmiques. Nous allons d'abord examiner l'équation logarithmique qui donne le niveau sonore en décibels (dB). Les décibels vont de\(0\), ce qui est à peine audible\(160\), à, qui peut rompre un tympan. Le\(10^{−12}\) contenu de la formule représente l'intensité du son qui est à peine audible.
Niveau sonore en décibels
Le niveau de sonie\(D\), mesuré en décibels, d'un son d'intensité\(I\), mesuré en watts par pouce carré est
\(D=10 \log \left(\frac{I}{10^{-12}}\right)\)
Une exposition prolongée à un bruit de mesure en\(85\) dB peut endommager de façon permanente l'oreille interne et entraîner une perte auditive. Quel est le niveau de décibels de la musique émise par les écouteurs avec une intensité en\(10^{−2}\) watts par pouce carré ?
Solution :
 |
|
| Substituez le niveau d'intensité,\(I\). | 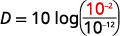 |
| Simplifiez. | 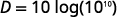 |
| Depuis\(\log 10^{10}=10\). |  |
| Multipliez. | 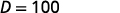 |
| Le niveau de décibels de la musique provenant des écouteurs est en\(100\) dB. |
Quel est le niveau de décibels de l'un des nouveaux lave-vaisselle silencieux d'une intensité en\(10^{−7}\) watts par pouce carré ?
- Réponse
-
Les lave-vaisselle silencieux ont un niveau de décibels en\(50\) dB.
Quel est le niveau de décibels du trafic urbain intense avec une intensité en\(10^{−3}\) watts par pouce carré ?
- Réponse
-
Le niveau de décibels d'un trafic intense est de\(90\) dB.
L'ampleur\(R\) d'un tremblement de terre est mesurée par une échelle logarithmique appelée échelle de Richter. Le modèle est\(R=\log I\), où\(I\) est l'intensité de l'onde de choc. Ce modèle permet de mesurer l'intensité des séismes.
L'ampleur\(R\) d'un tremblement de terre est mesurée par\(R=\log I\), où\(I\) est l'intensité de son onde de choc.
En 1906, San Francisco a connu un violent tremblement de terre d'une magnitude de\(7.8\) l'échelle de Richter. Plus de\(80\) % de la ville a été détruite par les incendies qui en ont résulté. En 2014, Los Angeles a connu un tremblement de terre modéré, d'une ampleur\(5.1\) sur l'échelle de Richter, qui a causé des dommages d'un\(108\) million de dollars. Comparez les intensités des deux tremblements de terre.
Solution :
Pour comparer les intensités, nous devons d'abord convertir les magnitudes en intensités à l'aide de la formule logarithmique. Ensuite, nous établirons un ratio pour comparer les intensités.
Convertissez les magnitudes en intensités.
\(R=\log I\)
Séisme de 1906
\(7.8=\log I\)
Convertir en forme exponentielle.
\(I=10^{7.8}\)
Séisme de 2014
\(5.1=\log I\)
Convertir en forme exponentielle.
\(I=10^{5.1}\)
Formez un ratio des intensités.
\(\frac{\text { Intensity for } 1906}{\text { Intensity for } 2014}\)
Substituez les valeurs.
\(\frac{10^{7.8}}{10^{5.1}}\)
Divisez en soustrayant les exposants.
\(10^{2.7}\)
Évaluer.
\(501\)
L'intensité du tremblement de terre de 1906 était environ deux\(501\) fois supérieure à celle du tremblement de terre de 2014.
En 1906, San Francisco a connu un violent tremblement de terre d'une magnitude de\(7.8\) l'échelle de Richter. En 1989, le tremblement de terre de Loma Prieta a également touché la région de San Francisco et a été mesuré\(6.9\) sur l'échelle de Richter. Comparez les intensités des deux tremblements de terre.
- Réponse
-
L'intensité du tremblement de terre de 1906 était environ deux\(8\) fois supérieure à celle du tremblement de terre de 1989.
En 2014, le Chili a connu un violent tremblement de terre d'une magnitude\(8.2\) de l'échelle de Richter. En 2014, Los Angeles a également connu un tremblement de terre mesuré\(5.1\) sur l'échelle de Richter. Comparez les intensités des deux tremblements de terre.
- Réponse
-
L'intensité du tremblement de terre au Chili était environ deux\(1,259\) fois supérieure à celle du tremblement de terre de Los Angeles.
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à évaluer et à représenter graphiquement des fonctions logarithmiques.
Concepts clés
- Propriétés du graphe de\(y=\log _{a} x\) :
| Quand\(a>1\) | Quand\(0<a<1\) | ||
|---|---|---|---|
| \ (a">1 \) ">Domaine | \((0, \infty)\) | \ (0<a<1 \) « >Domaine | \((0, \infty)\) |
| \ (a">1 \) « >Gamme | \((-\infty, \infty)\) | \ (0<a<1 \) « >Gamme | \((-\infty, \infty)\) |
| \ (a">1 \) « >\(x\) -intercepter | \((1,0)\) | \ (0<a<1 \) « >\(x\) -intercepter | \((1,0)\) |
| \ (a">1 \) « >\(y\) -intercepter | Aucune | \ (0<a<1 \) « >\(y\) -intercepter | Aucune |
| \ (a">1 \) « >Contient | \((a, 1),\left(\frac{1}{a},-1\right)\) | \ (0<a<1 \) « >Contient | \((a, 1),\left(\frac{1}{a},-1\right)\) |
| \ (a">1 \) « >Asymptote | \(y\)-axe | \ (0<a<1 \) « >Asymptote | \(y\)-axe |
| \ (a">1 \) ">Forme de base | En hausse | \ (0<a<1 \) « >Forme de base | Décroissant |

- Niveau sonore en décibels : Le niveau sonore\(D\), mesuré en décibels, d'un son d'intensité\(I\), mesuré en watts par pouce carré est de\(D=10 \log \left(\frac{I}{10^{-12}}\right)\).
- Intensité du tremblement\(R\) de terre : L'ampleur d'un tremblement de terre est mesurée par\(R=\log I\), où\(I\) est l'intensité de son onde de choc.
Lexique
- fonction logarithmique commune
- La fonction\(f(x)=\log x\) est la fonction logarithmique commune avec base\(10\), où\(x>0\).
\(y=\log x\)est équivalent à\(x=10^{y}\)
- fonction logarithmique
- La fonction\(f(x)=\log _{a} x\) est la fonction logarithmique avec base\(a\)\(a>0,x>0\), où et\(a≠1\).
\(y=\log _{a} x\)est équivalent à\(x=a^{y}\)
- fonction logarithmique naturelle
- La fonction\(f(x)=\ln x\) est la fonction logarithmique naturelle avec base\(e\), où\(x>0\).
\(y=\ln x\)est équivalent à\(x=e^{y}\)


