10.3 : Évaluer et représenter graphiquement les fonctions exponentielles
- Page ID
- 194305
À la fin de cette section, vous serez en mesure de :
- Fonctions exponentielles du graphe
- Résoudre des équations exponentielles
- Utiliser des modèles exponentiels dans les applications
Avant de commencer, répondez à ce questionnaire de préparation.
- Simplifiez :\(\left(\frac{x^{3}}{x^{2}}\right)\).
Si vous avez oublié ce problème, consultez l'exemple 5.13. - Évaluer : a.\(2^{0}\)\(\left(\frac{1}{3}\right)^{0}\) b.
Si vous avez oublié ce problème, consultez l'exemple 5.14. - Évaluer : a.\(2^{−1}\)\(\left(\frac{1}{3}\right)^{-1}\) b.
Si vous avez oublié ce problème, consultez l'exemple 5.15.
Fonctions exponentielles du graphe
Les fonctions que nous avons étudiées jusqu'à présent ne nous fournissent pas de modèle pour de nombreux phénomènes naturels. Qu'il s'agisse de la croissance des populations et de la propagation des virus, de la désintégration radioactive et de l'intérêt cumulé, les modèles sont très différents de ceux que nous avons étudiés jusqu'à présent. Ces modèles impliquent des fonctions exponentielles.
Une fonction exponentielle est une fonction de la forme\(f(x)=a^{x}\) où\(a>0\) et\(a≠1\).
Une fonction exponentielle, où\(a>0\) et\(a≠1\), est fonction de la forme
\(f(x)=a^{x}\)
Notez que dans cette fonction, la variable est l'exposant. Jusqu'à présent, les variables constituaient la base de nos fonctions.

Notre définition dit\(a≠1\). Si on laisse faire\(a=1\), alors ça\(f(x)=a^{x}\) devient\(f(x)=1^{x}\). Puisque\(1^{x}=1\) pour tous les nombres réels,\(f(x)=1\). Il s'agit de la fonction constante.
Notre définition le dit également\(a>0\). Si nous laissons une base négative, disons\(−4\), alors ce n'\(f(x)=(−4)^{x}\)est pas un vrai nombre quand\(x=\frac{1}{2}\).
\(\begin{aligned} f(x) &=(-4)^{x} \\ f\left(\frac{1}{2}\right) &=(-4)^{\frac{1}{2}} \\ f\left(\frac{1}{2}\right) &=\sqrt{-4} \text { not a real number } \end{aligned}\)
En fait, ne\(f(x)=(−4)^{x}\) serait pas un nombre réel à chaque fois\(x\) que c'est une fraction avec un dénominateur pair. Donc, notre définition l'exige\(a>0\).
En représentant graphiquement quelques fonctions exponentielles, nous serons en mesure de voir leurs propriétés uniques.
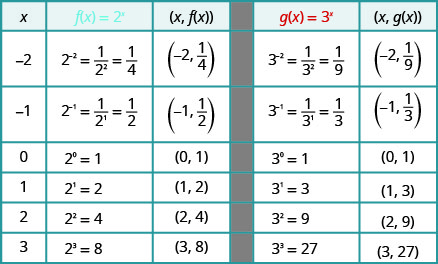
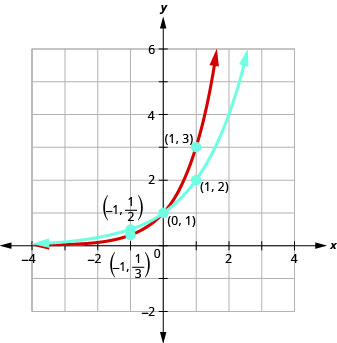
Sur le même graphique du système de coordonnées\(f(x)=2^{x}\) et\(g(x)=3^{x}\).
Solution :
Nous utiliserons le traçage par points pour représenter graphiquement les fonctions.
Graphique :\(f(x)=4^{x}\).
- Réponse
-
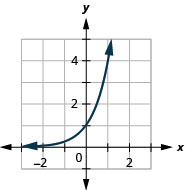
Graphique 10.2.4
Graphique :\(g(x)=5^{x}\)
- Réponse
-
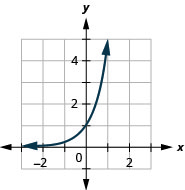
Graphique 10.2.5
Si nous examinons les graphiques de l'exemple 10.2.1 précédent et des exercices 10.2.1 et 10.2.2, nous pouvons identifier certaines des propriétés des fonctions exponentielles.
Les graphes de\(f(x)=2^{x}\) et\(g(x)=3^{x}\), ainsi que les graphes de\(f(x)=4^{x}\) et\(g(x)=5^{x}\), ont tous la même forme de base. C'est la forme que nous attendons d'une fonction exponentielle où\(a>1\).
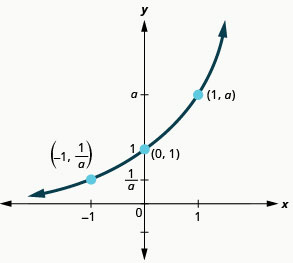
Nous remarquons que pour chaque fonction, le graphe contient le point\((0,1)\). Cela a du sens car\(a^{0}=1\) pour tout\(a\).
Le graphique de chaque fonction contient\(f(x)=a^{x}\) également le point\((1,a)\). Le graphique du\(f(x)=2^{x}\) contenu\((1,2)\) et le graphique du\(g(x)=3^{x}\) contenu\((1,3)\). Cela a du sens car\(a^{1}=a\).
Notez également que le graphe de chaque fonction contient\(f(x)=a^{x}\) également le point\((−1,\frac{1}{a})\). Le graphe du\(f(x)=2^{x}\) contenu\((−1,\frac{1}{2})\) et le graphique du\(g(x)=3^{x}\) contenu.\((−1,\frac{1}{3})\) Cela a du sens car\(a^{−1}=\frac{1}{a}\).
Quel est le domaine de chaque fonction ? Sur les graphiques, nous pouvons voir que le domaine est l'ensemble de tous les nombres réels. Il n'y a aucune restriction sur le domaine. Nous écrivons le domaine en notation par intervalles sous la forme\((−∞,∞)\).
Regardez chaque graphique. Quelle est la portée de cette fonction ? Le graphique n'atteint jamais l'\(x\)axe. La plage est composée uniquement de nombres positifs. Nous écrivons la plage en notation par intervalles sous la forme\((0,∞)\).
Chaque fois qu'un graphe d'une fonction s'approche d'une droite sans jamais la toucher, nous appelons cette droite une asymptote. Pour les fonctions exponentielles que nous examinons, le graphe s'approche de très près de\(x\) l'axe -mais ne le franchira jamais. Nous appelons la droite\(y=0\), l'\(x\)axe -, une asymptote horizontale.
Propriétés du graphe indiquant\(f(x)=a^{x}\) quand\(a>1\)
| Domaine | \((-\infty, \infty)\) |
| Gamme | \((0, \infty)\) |
| \(x\)-intercepter | Aucune |
| \(y\)-intercepter | \((0,1)\) |
| Contient | \((1, a),\left(-1, \frac{1}{a}\right)\) |
| Asymptote | \(x\)-axe, la ligne\(y=0\) |
Notre définition d'une fonction exponentielle le\(f(x)=a^{x}\) dit\(a>0\), mais les exemples et les discussions jusqu'à présent ont porté sur les fonctions où\(a>1\). Que se passera-t-il lorsque\(0<a<1\) l'exemple suivant explorera cette possibilité.
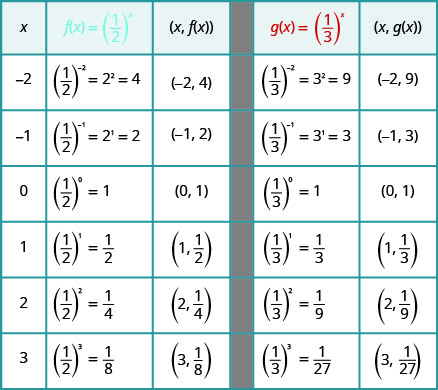
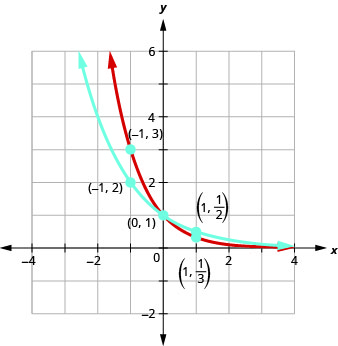
Sur le même système de coordonnées, tracez un graphique\(f(x)=\left(\frac{1}{2}\right)^{x}\) et\(g(x)=\left(\frac{1}{3}\right)^{x}\).
Solution :
Nous utiliserons le traçage par points pour représenter graphiquement les fonctions.
Graphique :\(f(x)=\left(\frac{1}{4}\right)^{x}\).
- Réponse
-
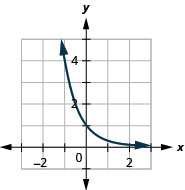
Graphique 10.2.9
Graphique :\(g(x)=\left(\frac{1}{5}\right)^{x}\).
- Réponse
-
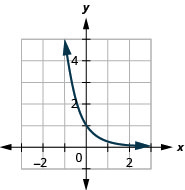
Graphique 10.2.10
Examinons maintenant les graphiques de l'exemple 10.2.2 précédent et des exercices 10.2.3 et 10.2.4 afin de pouvoir identifier certaines des propriétés des fonctions exponentielles où\(0<a<1\).
Les graphes de\(f(x)=\left(\frac{1}{2}\right)^{x}\) et\(g(x)=\left(\frac{1}{3}\right)^{x}\) ainsi que les graphes de\(f(x)=\left(\frac{1}{4}\right)^{x}\) et\(g(x)=\left(\frac{1}{5}\right)^{x}\) tous ont la même forme de base. Bien que ce soit la forme que nous attendons d'une fonction exponentielle où\(0<a<1\) les graphes descendent de gauche à droite alors que les graphes précédents, quand\(a>1\), allaient de haut en haut de gauche à droite.
On remarque que pour chaque fonction, le graphe contient toujours le point\((0, 1)\). Cela a du sens car\(a^{0}=1\) pour tout\(a\).
Comme précédemment, le graphe de chaque fonction contient également le point\((1,a)\).\(f(x)=a^{x}\) Le graphique du\(f(x)=\left(\frac{1}{2}\right)^{x}\) contenu\(\left(1, \frac{1}{2}\right)\) et le graphique du\(g(x)=\left(\frac{1}{3}\right)^{x}\) contenu\(\left(1, \frac{1}{3}\right)\). Cela a du sens car\(a^{1}=a\).
Notez également que le graphe de chaque fonction contient également le point\(\left(-1, \frac{1}{a}\right)\).\(f(x)=a^{x}\) Le graphique du\(f(x)=\left(\frac{1}{2}\right)^{x}\) contenu\((−1,2)\) et le graphique du\(g(x)=\left(\frac{1}{3}\right)^{x}\) contenu\((−1,3)\). Cela a du sens car\(a^{-1}=\frac{1}{a}\).
Quels sont le domaine et la plage de chaque fonction ? À partir des graphiques, nous pouvons voir que le domaine est l'ensemble de tous les nombres réels et nous écrivons le domaine en notation par intervalles sous la forme\((−∞,∞)\). Encore une fois, le graphique n'atteint jamais\(x\) l'axe. La plage est composée uniquement de nombres positifs. Nous écrivons la plage en notation par intervalles sous la forme\((0,∞)\).
Nous allons résumer ces propriétés dans le tableau ci-dessous. Ce qui inclut également quand\(a>1\).
Propriétés du graphe de\(f(x)=a^{x}\)
| Quand\(a>1\) | Quand\(0<a<1\) | ||
|---|---|---|---|
| \ (a">1 \) ">Domaine | \((-\infty, \infty)\) | \ (0<a<1 \) « >Domaine | \((-\infty, \infty)\) |
| \ (a">1 \) « >Gamme | \((0, \infty)\) | \ (0<a<1 \) « >Gamme | \((0, \infty)\) |
| \ (a">1 \) « >\(x\) -intercepter | aucune | \ (0<a<1 \) « >\(x\) -intercepter | aucune |
| \ (a">1 \) « >\(y\) -intercepter | \((0,1)\) | \ (0<a<1 \) « >\(y\) -intercepter | \((0,1)\) |
| \ (a">1 \) « >Contient | \((1, a),\left(-1, \frac{1}{a}\right)\) | \ (0<a<1 \) « >Contient | \((1, a),\left(-1, \frac{1}{a}\right)\) |
| \ (a">1 \) « >Asymptote |
\(x\)-axe, la ligne\(y=0\) |
\ (0<a<1 \) « >Asymptote | \(x\)-axe, la ligne\(y=0\) |
| \ (a">1 \) ">Forme de base | en augmentant | \ (0<a<1 \) « >Forme de base | décroissant |
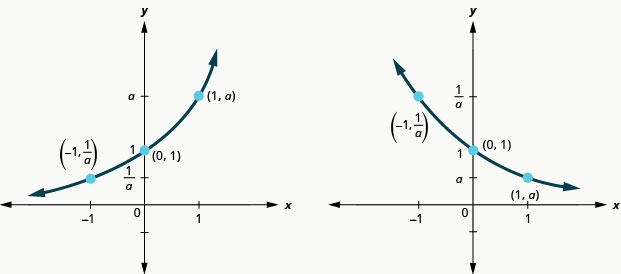
Il est important pour nous de noter que ces deux graphiques sont un à un, car ils passent tous les deux le test de la ligne horizontale. Cela signifie que la fonction exponentielle aura une inverse. Nous y reviendrons plus tard.
Lorsque nous avons représenté graphiquement des fonctions quadratiques, nous avons pu créer des graphes en utilisant la translation plutôt que de simplement tracer des points. Cela fonctionnera-t-il pour représenter graphiquement des fonctions exponentielles ?
Sur le même graphique du système de coordonnées\(f(x)=2^{x}\) et\(g(x)=2^{x+1}\).
Solution :
Nous utiliserons le traçage par points pour représenter graphiquement les fonctions.

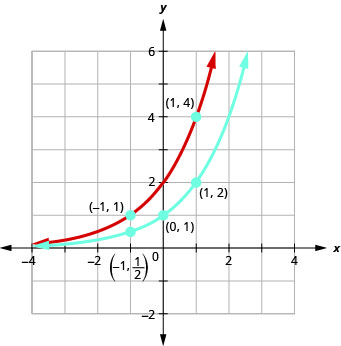
Sur le même système de coordonnées, tracez :\(f(x)=2^{x}\) et\(g(x)=2^{x-1}\).
- Réponse
-
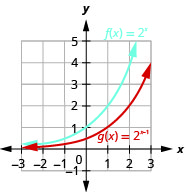
Graphique 10.2.14
Sur le même système de coordonnées, tracez un graphique\(f(x)=3^{x}\) et\(g(x)=3^{x+1}\).
- Réponse
-
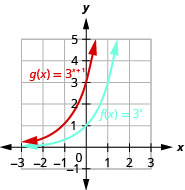
Graphique 10.2.15
En regardant les graphes des fonctions\(f(x)=2^{x}\) et\(g(x)=2^{x+1}\) dans le dernier exemple, nous voyons que l'ajout d'une fonction dans l'exposant a provoqué un décalage horizontal d'une unité vers la gauche. La reconnaissance de ce modèle nous permet de représenter graphiquement d'autres fonctions avec le même modèle par translation.
Examinons maintenant une autre situation qui pourrait être illustrée plus facilement par traduction, une fois que nous avons reconnu le modèle.
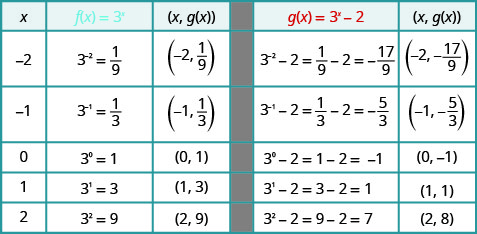
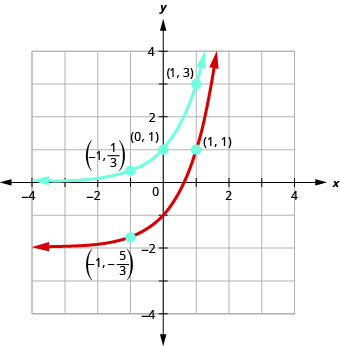
Sur le même graphique du système de coordonnées\(f(x)=3^{x}\) et\(g(x)=3^{x}-2\).
Solution :
Nous utiliserons le traçage par points pour représenter graphiquement les fonctions.
Sur le même système de coordonnées, tracez un graphique\(f(x)=3^{x}\) et\(g(x)=3^{x}+2\).
- Réponse
-
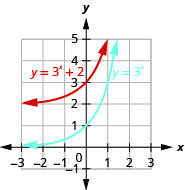
Graphique 10.2.18
Sur le même système de coordonnées, tracez un graphique\(f(x)=4^{x}\) et\(g(x)=4^{x}-2\).
- Réponse
-
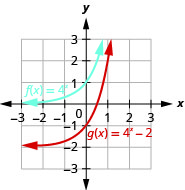
Graphique 10.2.19
En regardant les graphes des fonctions\(f(x)=3^{x}\) et\(g(x)=3^{x}−2\) dans le dernier exemple, nous voyons que la soustraction\(2\) a provoqué un décalage vertical de deux unités vers le bas. Notez que l'asymptote horizontale a également décalé les\(2\) unités vers le bas. La reconnaissance de ce modèle nous permet de représenter graphiquement d'autres fonctions avec le même modèle par translation.
Toutes nos fonctions exponentielles ont un entier ou un nombre rationnel comme base. Nous allons maintenant examiner une fonction exponentielle avec un nombre irrationnel comme base.
Avant de pouvoir examiner cette fonction exponentielle, nous devons définir le nombre irrationnel,\(e\). Ce nombre est utilisé comme base dans de nombreuses applications scientifiques et commerciales modélisées par des fonctions exponentielles. Le nombre est défini comme la valeur de «\(\left(1+\frac{1}{n}\right)^{n}\) as »\(n\) de plus en plus grande. Nous disons qu'il\(n\) s'approche de l'infini ou qu'il augmente sans limite. Le tableau indique la valeur de\(\left(1+\frac{1}{n}\right)^{n}\) pour plusieurs valeurs de\(n\).
| \(n\) | \(\left(1+\frac{1}{n}\right)^{n}\) |
|---|---|
| \ (n \) « >\(1\) | \ (\ left (1+ \ frac {1} {n} \ right) ^ {n} \) « >\(2\) |
| \ (n \) « >\(2\) | \ (\ left (1+ \ frac {1} {n} \ right) ^ {n} \) « >\(2.25\) |
| \ (n \) « >\(5\) | \ (\ left (1+ \ frac {1} {n} \ right) ^ {n} \) « >\(2.48832\) |
| \ (n \) « >\(10\) | \ (\ left (1+ \ frac {1} {n} \ right) ^ {n} \) « >\(2.59374246\) |
| \ (n \) « >\(100\) | \ (\ left (1+ \ frac {1} {n} \ right) ^ {n} \) « >\(2.704813829 \ldots\) |
| \ (n \) « >\(1,000\) | \ (\ left (1+ \ frac {1} {n} \ right) ^ {n} \) « >\(2.716923932 \ldots\) |
| \ (n \) « >\(10,000\) | \ (\ left (1+ \ frac {1} {n} \ right) ^ {n} \) « >\(2.718145927 \ldots\) |
| \ (n \) « >\(100,000\) | \ (\ left (1+ \ frac {1} {n} \ right) ^ {n} \) « >\(2.718268237 \ldots\) |
| \ (n \) « >\(1,000,000\) | \ (\ left (1+ \ frac {1} {n} \ right) ^ {n} \) « >\(2.718280469 \ldots\) |
| \ (n \) « >\(1,000,000,000\) | \ (\ left (1+ \ frac {1} {n} \ right) ^ {n} \) « >\(2.718281827 \ldots\) |
\(e \approx 2.718281827\)
Le nombre\(e\) est similaire au nombre\(π\) dans la mesure où nous utilisons un symbole pour le représenter, car sa représentation décimale ne s'arrête jamais ni ne se répète. Le nombre irrationnel\(e\) est appelé base naturelle.
Base naturelle\(e\)
Le nombre\(e\) est défini comme la valeur de\(\left(1+\frac{1}{n}\right)^{n}\), sous forme d'\(n\)augmentations sans limite. Nous disons qu'à mesure que l'infini\(n\) s'approche,
\(e \approx 2.718281827\)
La fonction exponentielle dont la base\(f(x)=e^{x}\) est\(e\) est appelée fonction exponentielle naturelle.
Fonction exponentielle naturelle
La fonction exponentielle naturelle est une fonction exponentielle dont la base est\(e\)
\(f(x)=e^{x}\)
Le domaine est\((−∞,∞)\) et la gamme est\((0,∞)\).
Reproduisons graphiquement la fonction\(f(x)=e^{x}\) sur le même système de coordonnées que\(g(x)=2^{x}\) et\(h(x)=3^{x}\).
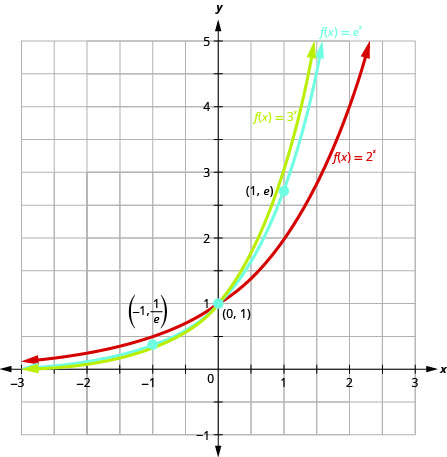
Remarquez que le graphique de\(f(x)=e^{x}\) se trouve « entre » les graphes de\(g(x)=2^{x}\) et\(h(x)=3^{x}\). Est-ce que cela a du sens\(2<e<3\) ?
Résoudre des équations exponentielles
Les équations qui incluent une expression exponentielle\(a^{x}\) sont appelées équations exponentielles. Pour les résoudre, nous utilisons une propriété qui dit aussi longtemps que\(a>0\) et\(a≠1\), si c'est\(a^{x}=a^{y}\) le cas, c'est vrai\(x=y\). En d'autres termes, dans une équation exponentielle, si les bases sont égales, les exposants sont égaux.
Propriété individuelle des équations exponentielles
Pour\(a>0\) et\(a≠1\),
Si\(a^{x}=a^{y}\), alors\(x=y\).
Pour utiliser cette propriété, nous devons nous assurer que les deux côtés de l'équation sont écrits avec la même base.
Résoudre :\(3^{2 x-5}=27\).
Solution :
| Étape 1 : Écrivez les deux côtés de l'équation avec la même base. | Puisque le côté gauche a une base\(3\), nous écrivons le côté droit avec base\(3\). \(27=3^{3}\) | \(3^{2 x-5}=27\) \(3^{2 x-5}=3^{3}\) |
| Étape 2 : Écrivez une nouvelle équation en mettant les exposants sur un pied d'égalité. | Les bases étant les mêmes, les exposants doivent être égaux. | \(2x-5=3\) |
| Étape 3 : Résolvez l'équation. |
Ajoutez\(5\) de chaque côté. Divisez par\(2\). |
\(\begin{aligned} 2 x &=8 \\ x &=4 \end{aligned}\) |
| Étape 4 : Vérifiez la solution. | \(x=4\)Substituez dans l'équation d'origine. | \(\begin{aligned} 3^{2 x-5} &=27 \\ 3^{2 \cdot \color{red}{4}\color{black}{-}5} & \stackrel{?}{=} 27 \\ 3^{3} &\stackrel{?}{=}27 \\ 27 &=27 \end{aligned}\) |
Résoudre :\(3^{3 x-2}=81\).
- Réponse
-
\(x=2\)
Résoudre :\(7^{x-3}=7\).
- Réponse
-
\(x=4\)
Les étapes sont résumées ci-dessous.
Comment résoudre une fonction exponentielle
- Écrivez les deux côtés de l'équation avec la même base, si possible.
- Écrivez une nouvelle équation en mettant les exposants sur un pied d'égalité.
- Résolvez l'équation.
- Vérifiez la solution.
Dans l'exemple suivant, nous utiliserons nos propriétés sur les exposants.
Résoudre\(\frac{e^{x^{2}}}{e^{3}}=e^{2 x}\).
Solution :
| \(\frac{e^{x^{2}}}{e^{3}}=e^{2 x}\) | |
| Utilisez la propriété des exposants :\(\frac{a^{m}}{a^{n}}=a^{m-n}\). | \(e^{x^{2}-3}=e^{2 x}\) |
| Écrivez une nouvelle équation en mettant les exposants sur un pied d'égalité. | \(x^{2}-3=2 x\) |
| Résolvez l'équation. | \(x^{2}-2 x-3=0\) |
| \((x-3)(x+1)=0\) | |
| \(x=3, x=-1\) | |
| Vérifiez les solutions. | |
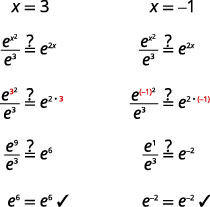 |
Résoudre :\(\frac{e^{x^{2}}}{e^{x}}=e^{2}\).
- Réponse
-
\(x=-1, x=2\)
Résoudre :\(\frac{e^{x^{2}}}{e^{x}}=e^{6}\).
- Réponse
-
\(x=-2, x=3\)
Utiliser des modèles exponentiels dans les applications
Les fonctions exponentielles modélisent de nombreuses situations. Si vous possédez un compte bancaire, vous avez fait l'expérience de l'utilisation d'une fonction exponentielle. Deux formules sont utilisées pour déterminer le solde du compte lorsque des intérêts sont gagnés. Si un capital est investi à un taux d'intérêt\(r\), pendant des\(t\) années, le nouveau solde dépendra de la fréquence à laquelle les intérêts sont composés.\(P\)\(A\) Si l'intérêt est composé\(n\) plusieurs fois par an, nous utilisons la formule\(A=P\left(1+\frac{r}{n}\right)^{n t}\). Si l'intérêt est composé en continu, nous utilisons la formule\(A=Pe^{rt}\). Ce sont les formules de l'intérêt composé.
Intérêt composé
Pour un capital investi à un taux d'intérêt\(r\), pendant des\(t\) années, le nouveau solde est :\(P\)\(A\)
\(\begin{array}{ll}{A=P\left(1+\frac{r}{n}\right)^{n t}} & {\text { when compounded } n \text { times a year. }} \\ {A=P e^{r t}} & {\text { when compounded continuously. }}\end{array}\)
Lorsque vous utilisez les formules d'intérêt, il est souvent utile d'identifier d'abord les valeurs des variables, puis de les remplacer dans la formule.
Un total de $\(10,000\) a été investi dans un fonds universitaire pour un nouveau petit-enfant. Si le taux d'intérêt est de\(5\) %, quel sera le montant du compte en\(18\) années selon chaque méthode de composition ?
- trimestriel composé
- mensuel composé
- composé en continu
Solution :
Identifiez les valeurs de chaque variable dans les formules. N'oubliez pas d'exprimer le pourcentage sous forme décimale.
\(\begin{aligned} A &=? \\ P &=\$ 10,000 \\ r &=0.05 \\ t &=18 \text { years } \end{aligned}\)
a. Pour la composition trimestrielle,\(n=4\). Il y a\(4\) des trimestres par an.
\(A=P\left(1+\frac{r}{n}\right)^{n t}\)
Remplacez les valeurs dans la formule.
\(A=10,000\left(1+\frac{0.05}{4}\right)^{4 \cdot 18}\)
Calculez le montant. Prenez soin de prendre en compte l'ordre des opérations lorsque vous saisissez l'expression dans votre calculatrice.
\(A=\$ 24,459.20\)
b. Pour la composition mensuelle,.\(n=12\) Il y a des\(12\) mois dans une année.
\(A=P\left(1+\frac{r}{n}\right)^{n t}\)
Remplacez les valeurs dans la formule.
\(A=10,000\left(1+\frac{0.05}{12}\right)^{12 \cdot 18}\)
Calculez le montant.
\(A=\$ 24,550.08\)
c. Pour la préparation en continu,
\(A=P e^{r t}\)
Remplacez les valeurs dans la formule.
\(A=10,000 e^{0.05 \cdot 18}\)
Calculez le montant.
\(A=\$ 24,596.03\)
Angela a investi $\(15,000\) dans un compte d'épargne. Si le taux d'intérêt est de\(4\) %, quel sera le montant du compte en\(10\) années selon chaque méthode de composition ?
- trimestriel composé
- mensuel composé
- composé en continu
- Réponse
-
- $\(22,332.96\)
- $\(22,362.49\)
- $\(22,377.37\)
Allan a investi $\(10,000\) dans un fonds commun de placement. Si le taux d'intérêt est de\(5\) %, quel sera le montant du compte en\(15\) années selon chaque méthode de composition ?
- trimestriel composé
- mensuel composé
- composé en continu
- Réponse
-
- $\(21,071.81\)
- $\(21,137.04\)
- $\(21,170.00\)
D'autres sujets modélisés par des fonctions exponentielles concernent la croissance et la décroissance. Les deux utilisent également la formule\(A=Pe^{rt}\) que nous avons utilisée pour la croissance de la monnaie. Pour la croissance et la décomposition, nous utilisons généralement\(A_{0}\), comme quantité initiale au lieu de l'appeler\(P\), le principal. Nous constatons que la croissance exponentielle a un taux de croissance positif et que la décroissance exponentielle a un taux de croissance négatif.
Croissance et décroissance exponentielles
Pour une quantité initiale\(A_{0}\), qui augmente ou diminue à un rythme donné\(r\), pendant un certain temps\(t\), la quantité finale est la suivante :\(A\)
\(A=A_{0} e^{r t}\)
La croissance exponentielle est généralement observée dans la croissance de populations d'humains, d'animaux ou de bactéries. L'exemple suivant porte sur la croissance d'un virus.
Chris est chercheur au Center for Disease Control and Prevention et tente de comprendre le comportement d'un nouveau virus dangereux. Il commence son expérience avec\(100\) le virus qui se développe à un taux de\(25\) % par heure. Il détectera le virus dans\(24\) quelques heures. Combien de virus trouvera-t-il ?
Solution :
Identifiez les valeurs de chaque variable dans les formules. Assurez-vous de saisir le pourcentage sous forme décimale. Assurez-vous que les unités correspondent : le taux est indiqué par heure et le temps est exprimé en heures.
\(\begin{aligned} A &=? \\ A_{0} &=100 \\ r &=0.25 / \text { hour } \\ t &=24 \text { hours } \end{aligned}\)
Remplacez les valeurs dans la formule :\(A=A_{0} e^{r t}\).
\(A=100 e^{0.25 \cdot 24}\)
Calculez le montant.
\(A=40,342.88\)
Arrondir au virus entier le plus proche.
\(A=40,343\)
Le chercheur découvrira des\(40,343\) virus.
Une autre chercheuse du Center for Disease Control and Prevention, Lisa, étudie la croissance d'une bactérie. Elle commence son expérience avec\(50\) la bactérie qui se développe à un taux de\(15\) % par heure. Il vérifiera la présence de la bactérie toutes les\(8\) heures. Combien de bactéries trouvera-t-il en\(8\) quelques heures ?
- Réponse
-
Elle trouvera des\(166\) bactéries.
Maria, biologiste, observe le schéma de croissance d'un virus. Elle commence par\(100\) le virus qui se développe à un taux de\(10\) % par heure. Elle détectera le virus dans\(24\) quelques heures. Combien de virus trouvera-t-elle ?
- Réponse
-
Elle va trouver des\(1,102\) virus.
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à évaluer et à représenter graphiquement des fonctions exponentielles.
Concepts clés
- Propriétés du graphe de\(f(x)=a^{x}\) :
| Quand\(a>1\) | Quand\(0<a<1\) | ||
|---|---|---|---|
| \ (a">1 \) ">Domaine | \((-\infty, \infty)\) | \ (0<a<1 \) « >Domaine | \((-\infty, \infty)\) |
| \ (a">1 \) « >Gamme | \((0, \infty)\) | \ (0<a<1 \) « >Gamme | \((0, \infty)\) |
| \ (a">1 \) « >\(x\) -intercepter | aucune | \ (0<a<1 \) « >\(x\) -intercepter | aucune |
| \ (a">1 \) « >\(y\) -intercepter | \((0,1)\) | \ (0<a<1 \) « >\(y\) -intercepter | \((0,1)\) |
| \ (a">1 \) « >Contient | \((1, a),\left(-1, \frac{1}{a}\right)\) | \ (0<a<1 \) « >Contient | \((1, a),\left(-1, \frac{1}{a}\right)\) |
| \ (a">1 \) « >Asymptote |
\(x\)-axe, la ligne\(y=0\) |
\ (0<a<1 \) « >Asymptote | \(x\)-axe, la ligne\(y=0\) |
| \ (a">1 \) ">Forme de base | en augmentant | \ (0<a<1 \) « >Forme de base | décroissant |
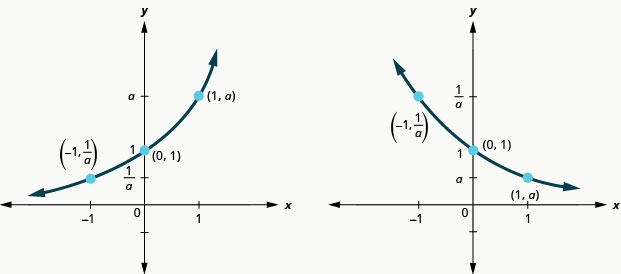
- Propriété individuelle des équations exponentielles :
pour\(a>0\) et\(a≠1\),\(A=A_{0} e^{r t}\)
- Comment résoudre une équation exponentielle
- Écrivez les deux côtés de l'équation avec la même base, si possible.
- Écrivez une nouvelle équation en mettant les exposants sur un pied d'égalité.
- Résolvez l'équation.
- Vérifiez la solution.
- Intérêt composé : Pour un principal\(P\), investi à un taux d'intérêt\(r\), pendant des\(t\) années\(A\), le nouveau solde est
\(\begin{array}{ll}{A=P\left(1+\frac{r}{n}\right)^{n t}} & {\text { when compounded } n \text { times a year. }} \\ {A=P e^{r t}} & {\text { when compounded continuously. }}\end{array}\) - Croissance et décroissance exponentielles : Pour une quantité initiale,\(A_{0}\) qui croît ou diminue à un rythme donné\(r\), pendant un certain temps\(t\), la quantité finale est de\(A=A_{0}e^{rt}\).\(A\)
Lexique
- asymptote
- Une droite qu'un graphe d'une fonction approche de près mais ne touche jamais.
- fonction exponentielle
- Une fonction exponentielle, où\(a>0\) et\(a≠1\), est fonction de la forme\(f(x)=a^{x}\).
- base naturelle
- Le nombre\(e\) est défini comme la valeur de\((1+\frac{1}{n})^{n}\), au fur\(n\) et à mesure que l'on grandit. Nous disons qu'à mesure qu'\(n\)elle augmente sans limite,\(e≈2.718281827...\)
- fonction exponentielle naturelle
- La fonction exponentielle naturelle est une fonction exponentielle dont la base est\(e\) :\(f(x)=e^{x}\). Le domaine est\((−∞,∞)\) et la gamme est\((0,∞)\).


