10.2 : Trouver des fonctions composites et inverses
- Page ID
- 194285
À la fin de cette section, vous serez en mesure de :
- Rechercher et évaluer des fonctions composites
- Déterminer si une fonction est biunivoque
- Trouvez l'inverse d'une fonction
Avant de commencer, répondez à ce questionnaire de préparation.
- Si\(f(x)=2 x-3\) et\(g(x)=x^{2}+2 x-3\), trouvez\(f(4)\).
Si vous avez oublié ce problème, consultez l'exemple 3.48. - Résolvez pour\(x\),\(3x+2y=12\).
Si vous avez oublié ce problème, consultez l'exemple 2.31. - Simplifiez :\(5 \frac{(x+4)}{5}-4\).
Si vous avez oublié ce problème, consultez l'exemple 1.25.
Dans ce chapitre, nous allons présenter deux nouveaux types de fonctions, les fonctions exponentielles et les fonctions logarithmiques. Ces fonctions sont largement utilisées dans les affaires et les sciences, comme nous le verrons.
Rechercher et évaluer des fonctions composites
Avant d'introduire les fonctions, nous devons examiner une autre opération sur les fonctions appelée composition. Dans la composition, la sortie d'une fonction est l'entrée d'une seconde fonction. Pour les fonctions\(f\) et\(g\), la composition est écrite\(f∘g\) et définie par\((f∘g)(x)=f(g(x))\).
Nous\(f(g(x))\) lisons «\(f\)\(g\) de »\(x\).
Pour faire une composition, la sortie de la première fonction devient l'entrée de la seconde fonction\(f\), et nous devons donc nous assurer qu'elle fait partie du domaine de\(f\).\(g(x)\)
La composition des fonctions\(f\)\(g\) est écrite\(f \cdot g\) et définie par
\((f \circ g)(x)=f(g(x))\)
Nous lisons\(f(g(x))\) à\(f\) partir\(g\) de\(x\).
Nous avons en fait utilisé la composition sans utiliser la notation à de nombreuses reprises auparavant. Lorsque nous avons représenté graphiquement des fonctions quadratiques à l'aide de traductions, nous composions des fonctions. Par exemple, si nous faisions d'abord un graphique\(g(x)=x^{2}\) sous forme de parabole, puis que nous la déplacions verticalement de quatre unités vers le bas, nous utilisions la composition définie par\((f∘g)(x)=f(g(x))\) où\(f(x)=x−4\).
Pour les fonctions\(f(x)=4x-5\) et\(g(x)=2x+3\), trouvez
- \((f \circ g)(x)\)
- \((g \circ f)(x)\)
- \((f \cdot g)(x)\)
Solution :
-
Utilisez la définition de\((f \circ g)(x)\). 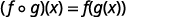

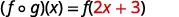

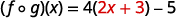
Distribuez. 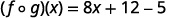
Simplifiez. 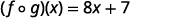
Tableau 10.1.1 -
Utilisez la définition de\((f \circ g)(x)\). 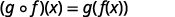

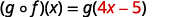

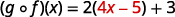
Distribuez. 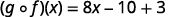
Simplifiez. 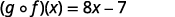
Tableau 10.1.2
Remarquez la différence entre le résultat dans la partie a. et dans la partie b.
c. Notez que c'\((f \cdot g)(x)\)est différent de\((f \circ g)(x)\). Dans la partie a. nous avons fait la composition des fonctions. Maintenant, dans la partie c., nous ne les composons pas, nous les multiplions.
Utilisez la définition de\((f \cdot g)(x)\).
\((f \cdot g)(x)=f(x) \cdot g(x)\)
Remplacer\(f(x)=4 x-5\) et\(g(x)=2 x+3\).
\((f \cdot g)(x)=(4 x-5) \cdot(2 x+3)\)
Multipliez.
\((f \cdot g)(x)=8 x^{2}+2 x-15\)
Pour les fonctions\(f(x)=3x-2\) et\(g(x)=5x+1\), trouvez
- \((f \circ g)(x)\)
- \((g \circ f)(x)\)
- \((f \cdot g)(x)\)
- Réponse
-
- \(15x+1\)
- \(15x-9\)
- \(15 x^{2}-7 x-2\)
Pour les fonctions et\(f(x)=4 x-3\)\(g(x)=6x-5\), trouvez
- \((f \circ g)(x)\)
- \((g \circ f)(x)\)
- \((f \cdot g)(x)\)
- Réponse
-
- \(24 x-23\)
- \(24 x-23\)
- \(24 x^{2}-38 x+15\)
Dans l'exemple suivant, nous allons évaluer une composition pour une valeur spécifique.
Pour les fonctions et\(f(x)=x^{2}-4\)\(g(x)=3 x+2\), trouvez :
- \((f \circ g)(-3)\)
- \((g \circ f)(-1)\)
- \((f \circ f)(2)\)
Solution :
-
Utilisez la définition de\((f \circ g)(-3)\). 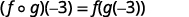

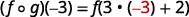
Simplifiez. 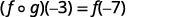

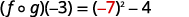
Simplifiez. 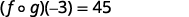
Tableau 10.1.3 -
Utilisez la définition de\((g \circ f)(-1)\). 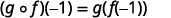

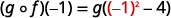
Simplifiez. 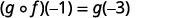

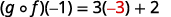
Simplifiez. 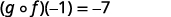
Tableau 10.1.4 -
Utilisez la définition de\((f \circ f)(2)\). 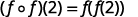

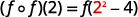
Simplifiez. 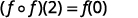

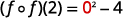
Simplifiez. 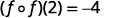
Tableau 10.1.5
Pour les fonctions et\(f(x)=x^{2}-9\)\(g(x)=2x+5\), trouvez
- \((f \circ g)(-2)\)
- \((g \circ f)(-3)\)
- \((f \circ f)(4)\)
- Réponse
-
- \(-8\)
- \(5\)
- \(40\)
Pour les fonctions et\(f(x)=x^{2}+1\)\(g(x)=3x-5\), trouvez
- \((f \circ g)(-1)\)
- \((g \circ f)(2)\)
- \((f \circ f)(-1)\)
- Réponse
-
- \(65\)
- \(10\)
- \(5\)
Déterminer si une fonction est univoque
Lorsque nous avons introduit les fonctions pour la première fois, nous avons dit qu'une fonction est une relation qui attribue à chaque élément de son domaine exactement un élément de la plage. Pour chaque paire ordonnée dans la relation, chaque\(x\) valeur est associée à une seule\(y\) valeur.
Nous avons utilisé l'exemple de l'anniversaire pour nous aider à comprendre la définition. Chaque personne a un anniversaire, mais personne n'a deux anniversaires et il est normal que deux personnes partagent un anniversaire. Comme chaque personne a exactement un anniversaire, cette relation est une fonction.

Une fonction est biunivoque si chaque valeur de la plage contient exactement un élément dans le domaine. Pour chaque paire ordonnée dans la fonction, chaque valeur y est associée à une seule\(x\) valeur.
Notre exemple de relation d'anniversaire n'est pas une fonction individuelle. Deux personnes peuvent partager le même anniversaire. La valeur de plage du 2 août correspond à l'anniversaire de Liz et de June, de sorte qu'une valeur de plage possède deux valeurs de domaine. Par conséquent, la fonction n'est pas individuelle.
Une fonction est biunivoque si chaque valeur de la plage correspond à un élément du domaine. Pour chaque paire ordonnée dans la fonction, chaque\(y\) valeur est associée à une seule\(x\) valeur. Il n'y a pas\(y\) de valeurs répétées.
Pour chaque ensemble de paires ordonnées, déterminez s'il représente une fonction et, dans l'affirmative, si la fonction est univoque.
- \(\{(-3,27),(-2,8),(-1,1),(0,0),(1,1),(2,8),(3,27)\}\)
- \(\{(0,0),(1,1),(4,2),(9,3),(16,4)\}\)
Solution :
- \(\{(-3,27),(-2,8),(-1,1),(0,0),(1,1),(2,8),(3,27)\}\)
Chaque\(x\) valeur est associée à une seule\(y\) valeur. Cette relation est donc une fonction.
Mais chaque\(y\) valeur n'est pas associée à une seule\(x\) valeur,\((−3,27)\) et\((3,27)\), par exemple. Cette fonction n'est donc pas individuelle.
- \(\{(0,0),(1,1),(4,2),(9,3),(16,4)\}\)
Chaque\(x\) valeur est associée à une seule\(y\) valeur. Cette relation est donc une fonction.
Comme chaque\(y\) valeur est associée à une seule\(x\) valeur, cette fonction est biunivoque.
Pour chaque ensemble de paires ordonnées, déterminez s'il représente une fonction et, dans l'affirmative, s'il s'agit d'une fonction univoque.
- \(\{(-3,-6),(-2,-4),(-1,-2),(0,0),(1,2),(2,4),(3,6)\}\)
- \(\{(-4,8),(-2,4),(-1,2),(0,0),(1,2),(2,4),(4,8)\}\)
- Réponse
-
- Fonction individuelle
- Fonction ; pas un à un
Pour chaque ensemble de paires ordonnées, déterminez s'il représente une fonction et, dans l'affirmative, s'il s'agit d'une fonction univoque.
- \(\{(27,-3),(8,-2),(1,-1),(0,0),(1,1),(8,2),(27,3)\}\)
- \(\{(7,-3),(-5,-4),(8,0),(0,0),(-6,4),(-2,2),(-1,3)\}\)
- Réponse
-
- Pas une fonction
- Fonction ; pas un à un
Pour nous aider à déterminer si une relation est une fonction, nous utilisons le test de la ligne verticale. Un ensemble de points dans un système de coordonnées rectangulaires est le graphe d'une fonction si chaque ligne verticale coupe le graphe en un point au plus. De même, si une ligne verticale coupe le graphe en plus d'un point, le graphique ne représente pas une fonction.
La ligne verticale représente une\(x\) valeur et nous vérifions qu'elle coupe le graphique en une seule\(y\) valeur. Alors c'est une fonction.
Pour vérifier si une fonction est biunivoque, nous utilisons un processus similaire. On utilise une ligne horizontale et on vérifie que chaque ligne horizontale croise le graphe en un seul point. La ligne horizontale représente une\(y\) valeur et nous vérifions qu'elle coupe le graphique en une seule\(x\) valeur. Si chaque ligne horizontale coupe le graphe d'une fonction en un point au plus, il s'agit d'une fonction biunivoque. Il s'agit du test de la ligne horizontale.
Test de ligne horizontale
Si chaque ligne horizontale coupe le graphe d'une fonction en un point au plus, il s'agit d'une fonction biunivoque.
Nous pouvons vérifier si le graphe d'une relation est une fonction en utilisant le test de la ligne verticale. Nous pouvons ensuite déterminer si la fonction est biunivoque en appliquant le test de la ligne horizontale.
Déterminer
- si chaque graphe est le graphe d'une fonction et, dans l'affirmative,
- si c'est en tête-à-tête
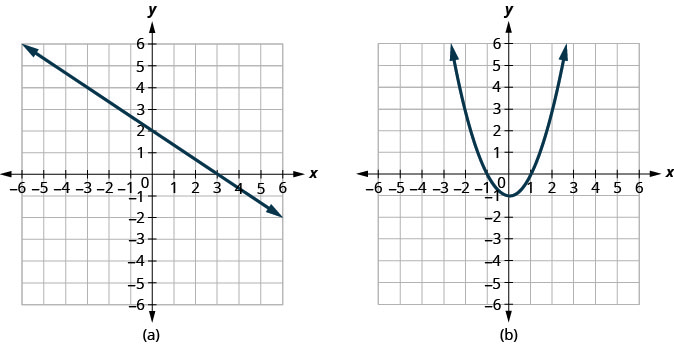
Solution :
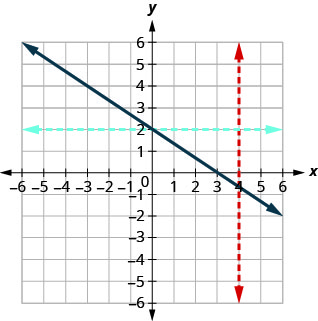
Graphique 10.1.40
Comme toute ligne verticale coupe le graphe en un point au plus, le graphe est le graphe d'une fonction. Comme toute ligne horizontale croise le graphe en un point au plus, le graphe est le graphe d'une fonction biunivoque.
b.
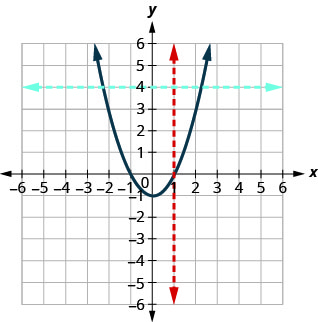
Comme toute ligne verticale coupe le graphe en un point au plus, le graphe est le graphe d'une fonction. La ligne horizontale représentée sur le graphique le coupe en deux points. Ce graphique ne représente pas une fonction biunivoque.
Déterminer
- si chaque graphe est le graphe d'une fonction et, dans l'affirmative,
- si c'est en tête-à-tête
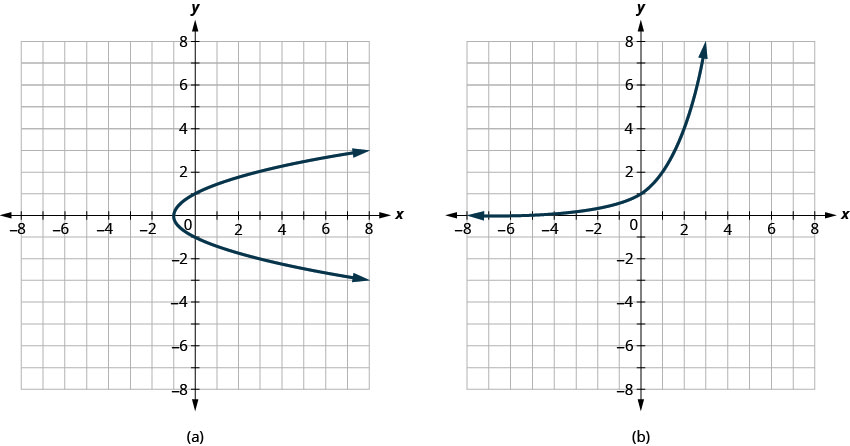
- Réponse
-
- Pas une fonction
- Fonction individuelle
Déterminer
- si chaque graphe est le graphe d'une fonction et, dans l'affirmative,
- si c'est en tête-à-tête
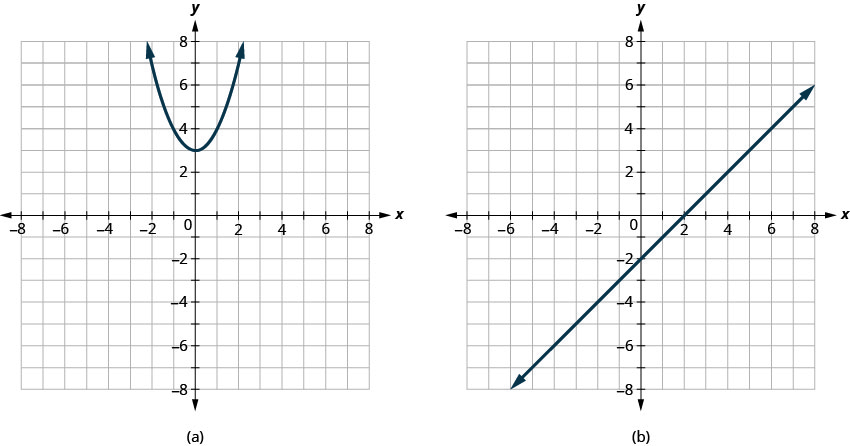
- Réponse
-
- Fonction ; pas un à un
- Fonction individuelle
Trouver l'inverse d'une fonction
Examinons une fonction biunivoque\(f\), représentée par les paires ordonnées\(\{(0,5),(1,6),(2,7),(3,8)\}\). Pour chaque\(x\) valeur,\(f\) ajoute\(5\) pour obtenir la\(y\) valeur. Pour « annuler » l'ajout de\(5\), nous\(5\) soustrayons de chaque\(y\) valeur et revenons à la\(x\) valeur initiale. Nous pouvons appeler cela « prendre l'inverse de\(f\) » et nommer la fonction\(f^{−1}\).
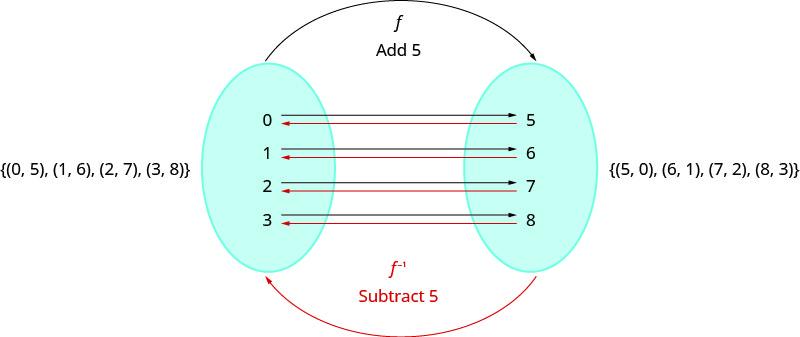
Notez que les paires ordonnées de\(f\) et\(f^{−1}\) ont leurs\(x\) valeurs -values et\(y\) -values inversées. Le domaine de\(f\) est la plage de\(f^{−1}\) et le domaine de\(f^{−1}\) est la plage de\(f\).
Inverse d'une fonction définie par des paires ordonnées
S'il s'\(f(x)\)agit d'une fonction biunivoque dont les paires ordonnées sont de la forme\((x,y)\), alors sa fonction inverse\(f^{−1}(x)\) est l'ensemble des paires ordonnées\((y,x)\).
Dans l'exemple suivant, nous trouverons l'inverse d'une fonction définie par des paires ordonnées.
Détermine l'inverse de la fonction\(\{(0,3),(1,5),(2,7),(3,9)\}\). Déterminez le domaine et la plage de la fonction inverse.
Solution :
Cette fonction est biunivoque puisque chaque\(x\) valeur est associée à exactement une\(y\) valeur.
Pour trouver l'inverse, nous inversons\(x\) les valeurs et\(y\) les valeurs -dans les paires ordonnées de la fonction.
\(\begin{array}{ll} {\text{Function}}&{\{(0,3),(1,5),(2,7),(3,9)\}} \\ {\text{Inverse Function}}& {\{(3,0), (5,1), (7,2), (9,3)\}} \\ {\text{Domain of Inverse Function}}&{\{3, 5, 7, 9\}} \\ {\text{Range of Inverse Function}}&{\{0, 1, 2, 3\}} \end{array}\)
Détermine l'inverse de\(\{(0,4),(1,7),(2,10),(3,13)\}\). Déterminez le domaine et la plage de la fonction inverse.
- Réponse
-
Fonction inverse :\(\{(4,0),(7,1),(10,2),(13,3)\}\). Domaine :\(\{4,7,10,13\}\). Gamme :\(\{0,1,2,3\}\).
Détermine l'inverse de\(\{(-1,4),(-2,1),(-3,0),(-4,2)\}\). Déterminez le domaine et la plage de la fonction inverse.
- Réponse
-
Fonction inverse :\(\{(4,-1),(1,-2),(0,-3),(2,-4)\}\). Domaine :\(\{0,1,2,4\}\). Gamme :\(\{-4,-3,-2,-1\}\).
Nous venons de noter que s'il s'\(f(x)\)agit d'une fonction biunivoque dont les paires ordonnées sont de la forme\((x,y)\), alors sa fonction inverse\(f^{−1}(x)\) est l'ensemble des paires ordonnées\((y,x)\).
Donc, si un point\((a,b)\) se trouve sur le graphe d'une fonction\(f(x)\), alors la paire ordonnée\((b,a)\) se trouve sur le graphique de\(f^{−1}(x)\). Voir la Figure 10.1.43.
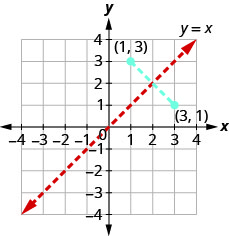
La distance entre deux paires\((a,b)\)\((b,a)\) est coupée de moitié par la ligne\(y=x\). Nous disons donc que les points sont des images miroir les uns des autres à travers la ligne\(y=x\).
Puisque chaque point du graphe d'une fonction\(f(x)\) est une image miroir d'un point sur le graphe de\(f^{−1}(x)\), nous disons que les graphes sont des images miroir les uns des autres sur la ligne\(y=x\). Nous utiliserons ce concept pour représenter graphiquement l'inverse d'une fonction dans l'exemple suivant.
Tracez, sur le même système de coordonnées, l'inverse de la fonction biunivoque affichée.
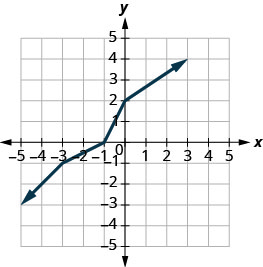
Solution :
Nous pouvons utiliser des points sur le graphique pour trouver des points sur le graphique inverse. Certains points du graphique sont :\((−5,−3),(−3,−1),(−1,0),(0,2),(3,4)\).
Ainsi, la fonction inverse contiendra les points :\((−3,−5),(−1,−3),(0,−1),(2,0),(4,3)\).
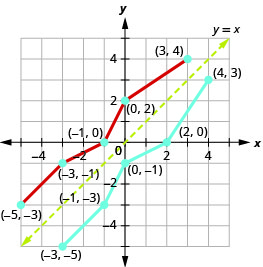
Remarquez que le graphe de la fonction d'origine et le graphe des fonctions inverses sont des images symétriques à travers la ligne\(y=x\).
Tracez, sur le même système de coordonnées, l'inverse de la fonction biunivoque.
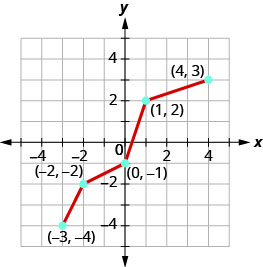
- Réponse
-
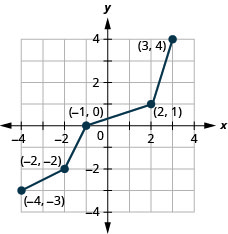
Graphique 10.1.49
Tracez, sur le même système de coordonnées, l'inverse de la fonction biunivoque.
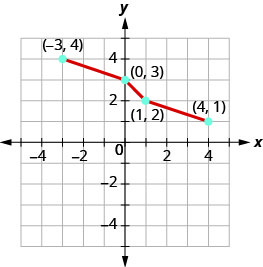
- Réponse
-
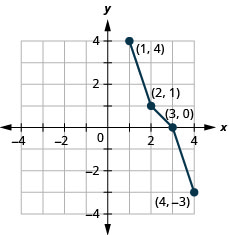
Graphique 10.1.51
Lorsque nous avons commencé notre discussion sur une fonction inverse, nous avons expliqué comment la fonction inverse « annule » ce que la fonction d'origine avait fait à une valeur de son domaine afin de revenir à la\(x\) valeur d'origine.

Fonctions inverses
\(f^{-1}(f(x))=x\), pour tous ceux\(x\) qui travaillent dans le domaine de\(f\)
\(f\left(f^{-1}(x)\right)=x\), pour tous ceux\(x\) qui travaillent dans le domaine de\(f^{-1}\)
Nous pouvons utiliser cette propriété pour vérifier que deux fonctions sont inversées l'une de l'autre.
Vérifiez cela\(f(x)=5x−1\) et\(g(x)=\frac{x+1}{5}\) sont des fonctions inverses.
Solution :
Les fonctions sont inverses l'une de l'autre si\(g(f(x))=x\) et\(f(g(x))=x\).
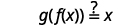 |
|
| Substitue\(5x-1\) à\(f(x)\). | 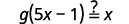 |
 |
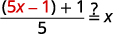 |
| Simplifiez. | 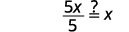 |
| Simplifiez. | 
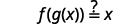
|
| Substitut\(\frac{x+1}{5}\) de\(g(x)\). | 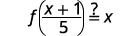 |
 |
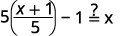 |
| Simplifiez. | 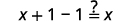 |
| Simplifiez. |  |
Puisque les deux\(g(f(x))=x\) et\(f(g(x))=x\) sont vrais, les fonctions\(f(x)=5x−1\) et\(g(x)=\frac{x+1}{5}\) sont des fonctions inverses. C'est-à-dire qu'ils sont inverses l'un de l'autre.
Vérifiez que les fonctions sont des fonctions inverses. \(f(x)=4 x-3\)et\(g(x)=\frac{x+3}{4}\).
- Réponse
-
\(g(f(x))=x\)\(f(g(x))=x\), et ce sont donc des inverses.
Vérifiez que les fonctions sont des fonctions inverses. \(f(x)=2 x+6\)et\(g(x)=\frac{x-6}{2}\)
- Réponse
-
\(g(f(x))=x,\)\(f(g(x))=x,\)ce sont donc des inverses.
Nous avons trouvé des inverses de fonction définis par des paires ordonnées et à partir d'un graphe. Nous allons maintenant voir comment trouver un inverse à l'aide d'une équation algébrique. La méthode utilise l'idée que s'il s'\(f(x)\)agit d'une fonction biunivoque avec des paires ordonnées\((x,y)\), alors sa fonction inverse\(f^{−1}(x)\) est l'ensemble des paires ordonnées\((y,x)\).
Si nous inversons le\(x\) et\(y\) dans la fonction, puis résolvons pour\(y\), nous obtenons notre fonction inverse.
Détermine l'inverse de\(f(x)=4 x+7\).
Solution :
| Étape 1. Substitut\(y\) de\(f(x)\). | Remplacez\(f(x)\) par\(y\). | \(\begin{aligned} f(x) &=4 x+7 \\ y &=4 x+7 \end{aligned}\) |
| Étape 2 : Échangez les variables\(x\) et\(y\). | Remplacez\(x\) par,\(y\) puis\(y\) par\(x\). | \(x=4y+7\) |
| Étape 3 : Résolvez pour\(y\). |
Soustrayez\(7\) de chaque côté. Divisez par\(4\). |
\(x-7=4 y\) \(\frac{x-7}{4}=y\) |
| Étape 4 : Remplacez\(f^{-1}(x)\) par\(y\). | Remplacez\(y\) par\(f^{-1}(x)\). | \(\frac{x-7}{4}=f^{-1}(x)\) |
| Étape 5 : Vérifiez que les fonctions sont inversées. |
Afficher\(f^{-1}(f(x))=x\) et\(f\left(f^{-1}(x)\right)=x\) |
\(\begin{aligned} f^{-1}(f(x)) & \stackrel{?}{=} x \\f^{-1}(4x+7)&\stackrel{?}{=}x\\ \frac{(4x+7)-7}{4}&\stackrel{?}{=}x \\ \frac{4x}{4}&\stackrel{?}{=}x\\x&=x \\ \\f(f^{-1}(x))&\stackrel{?}{=}x \\f \left(\frac{x-7}{4} \right)&\stackrel{?}{=}x \\ 4\left(\frac{x-7}{4} \right) + 7 &\stackrel{?}{=}x \\ x-7+7&\stackrel{?}{=}x \\x&=x \end{aligned}\) |
Détermine l'inverse de la fonction\(f(x)=5x-3\).
- Réponse
-
\(f^{-1}(x)=\frac{x+3}{5}\)
Détermine l'inverse de la fonction\(f(x)=8 x+5\).
- Réponse
-
\(f^{-1}(x)=\frac{x-5}{8}\)
Nous résumons les étapes ci-dessous.
Comment trouver l'inverse d'une fonction biunivoque
- Substitut\(y\) de\(f(x)\).
- Échangez les variables\(x\) et\(y\).
- Résolvez pour\(y\).
- Substitut\(f^{−1}(x)\) de\(y\).
- Vérifiez que les fonctions sont inversées.
Détermine l'inverse de\(f(x)=\sqrt[5]{2 x-3}\).
Solution :
\(f(x)=\sqrt[5]{2 x-3}\)
Substitut\(y\) de\(f(x)\).
\(y=\sqrt[5]{2 x-3}\)
Échangez les variables\(x\) et\(y\).
\(x=\sqrt[5]{2 y-3}\)
Résolvez pour\(y\).
\(\begin{aligned}(x)^{5} &=(\sqrt[5]{2 y-3})^{5} \\ x^{5} &=2 y-3 \\ x^{5}+3 &=2 y \\ \frac{x^{5}+3}{2} &=y \end{aligned}\)
Substitut\(f^{-1}(x)\) de\(y\).
\(f^{-1}(x)=\frac{x^{5}+3}{2}\)
Vérifiez que les fonctions sont inversées.
\(\begin{array}{rr} {f^{-1}(f(x)) \stackrel{?}{=} x} & {f\left(f^{-1}(x)\right) \stackrel{?}{=} x} \\ {f^{-1}(\sqrt[5]{2x-3})\stackrel{?}{=}x}&{f\left(\frac{x^{5}+3}{2} \right)}\stackrel{?}{=}x \\ {\frac{(\sqrt[5]{2x-3})^{5}+3}{2}\stackrel{?}{=}x}&{\sqrt[5]{2\left(\frac{x^{5}+3}{2} \right)-3}\stackrel{?}{=}x} \\ {\frac{2x-3+3}{2}\stackrel{?}{=}x}&{\sqrt[5]{x^{5}+3-3}\stackrel{?}{=}x}\\ {\frac{2x}{2}\stackrel{?}{=}x}&{\sqrt[5]{x^{5}}\stackrel{?}{=}x} \\ {x=x}&{x=x} \end{array}\)
Détermine l'inverse de la fonction\(f(x)=\sqrt[5]{3 x-2}\).
- Réponse
-
\(f^{-1}(x)=\frac{x^{5}+2}{3}\)
Détermine l'inverse de la fonction\(f(x)=\sqrt[4]{6 x-7}\).
- Réponse
-
\(f^{-1}(x)=\frac{x^{4}+7}{6}\)
Concepts clés
- Composition des fonctions : La composition des fonctions\(f\) et\(g\), est écrite\(f∘g\) et définie par
\((f \circ g)(x)=f(g(x))\)
Nous lisons\(f(g(x))\) à\(f\) partir\(g\) de\(x\). - Test de ligne horizontale : Si chaque ligne horizontale coupe le graphe d'une fonction en un point au plus, il s'agit d'une fonction biunivoque.
- Inverse d'une fonction définie par des paires ordonnées : s'il s'\(f(x)\)agit d'une fonction biunivoque dont les paires ordonnées sont de la forme\((x,y)\), alors sa fonction inverse\(f^{−1}(x)\) est l'ensemble des paires ordonnées\((y,x)\).
- Fonctions inverses : Pour chaque\(x\) élément du domaine de la fonction biunivoque\(f\) et\(f^{−1}\),
\(f^{-1}(f(x))=x\)
\(f\left(f^{-1}(x)\right)=x\) - Comment trouver l'inverse d'une fonction biunivoque :
- Substitut\(y\) de\(f(x)\).
- Échangez les variables\(x\) et\(y\).
- Résolvez pour\(y\).
- Substitut\(f^{−1}(x)\) de\(y\).
- Vérifiez que les fonctions sont inversées.
Lexique
- fonction un à un
- Une fonction est biunivoque si chaque valeur de la plage contient exactement un élément dans le domaine. Pour chaque paire ordonnée dans la fonction, chaque\(y\) valeur est associée à une seule\(x\) valeur.


