9.9 : Résoudre les inégalités quadratiques

Last updated

Nov 1, 2022
Page ID
194331
Save as PDF
- 9.8E : Exercices
- 9.9E : Exercices

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

Résoudre graphiquement les inégalités quadratiques
Résolvez les inégalités quadratiques de manière algébrique

Avant de commencer, répondez à ce questionnaire de préparation.

Résoudre : $2x−3=0$ .
Si vous avez oublié ce problème, consultez l'exemple 2.2.
Résoudre : $2y^{2}+y=15$ .
Si vous avez oublié ce problème, consultez l'exemple 6.45.
$\frac{1}{x^{2}+2 x-8}>0$
Résolu Si vous avez oublié ce problème, consultez l'exemple 7.56.

Nous avons déjà appris à résoudre les inégalités linéaires et les inégalités rationnelles. Certaines des techniques que nous avons utilisées pour les résoudre étaient les mêmes et d'autres étaient différentes. Nous allons maintenant apprendre à résoudre les inégalités qui ont une expression quadratique. Nous utiliserons certaines des techniques de résolution des inégalités linéaires et rationnelles ainsi que des équations quadratiques. Nous allons résoudre les inégalités quadratiques de deux manières, à la fois graphiquement et algébriquement.

Résoudre graphiquement les inégalités quadratiques

Une équation quadratique est sous forme standard lorsqu'elle est écrite sous la forme $ax^{2}+bx+c=0$ . Si nous remplaçons le signe égal par un signe d'inégalité, nous obtenons une inégalité quadratique sous forme standard.

Définition $\PageIndex{1}$ : Quadratic Inequality

Une inégalité quadratique est une inégalité qui contient une expression quadratique. La forme standard d'une inégalité quadratique s'écrit :

$\begin{array}{ll}{a x^{2}+b x+c<0} & {a x^{2}+b x+c \leq 0} \\ {a x^{2}+b x+c>0} & {a x^{2}+b x+c \geq 0}\end{array}$

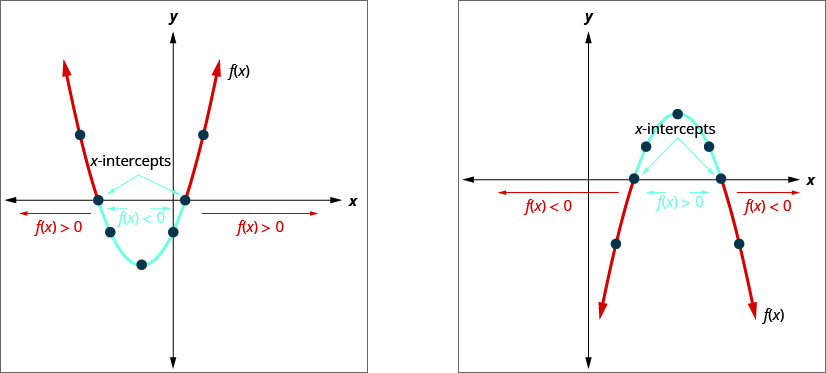
Le graphe d'une fonction quadratique $f(x)=a x^{2}+b x+c=0$ est une parabole. Lorsque nous demandons quand c'est le cas $a x^{2}+b x+c<0$ , nous nous demandons quand c'est le cas $f(x)<0$ . Nous voulons savoir quand la parabole se trouve en dessous de l' $x$ axe.

Lorsque nous demandons quand c'est le cas $a x^{2}+b x+c>0$ , nous nous demandons quand c'est le cas $f(x)>0$ . Nous voulons savoir quand la parabole se trouve au-dessus de l' $y$ axe.

Le premier graphe est une parabole orientée vers le haut, f de x, sur un plan de coordonnées x y. À gauche de la fonction, f de x est supérieur à 0. Entre les interceptions X, f de x est inférieur à 0. À droite de la fonction, f de x est supérieur à 0. Le second graphe est une parabole orientée vers le bas, f de x, sur un plan de coordonnées x y. À gauche de la fonction, f de x est inférieur à 0. Entre les interceptions X, f de x est supérieur à 0. À droite de la fonction, f de x est inférieur à 0. — Graphique 9.8.1

Exemple $\PageIndex{1}$ : How to Solve a Quadratic Inequality Graphically

Résolvez $x^{2}−6x+8<0$ graphiquement Écrivez la solution en notation par intervalles.

Solution :

Étape 1 : Écrivez l'inégalité quadratique sous forme standard.

L'inégalité se présente sous une forme standard.

$x^{2}-6 x+8<0$

Étape 2 : Représenter graphiquement la fonction $f(x)=a x^{2}+b x+c$ à l'aide de propriétés ou de transformations

Nous allons représenter graphiquement à l'aide des propriétés.

$f(x)=x^{2}-6 x+8$

Regardez $a$ dans l'équation.

$\color{red}{a=1, b=-6, c=8}$

$f(x)=x^{2}-6 x+8$

Puisque $a$ c'est positif, la parabole s'ouvre vers le haut.

La parabole s'ouvre vers le haut.

Capture d'écran (2) .png — Graphique 9.8.2

$f(x)=x^{2}-6 x+8$

L'axe de symétrie est la ligne $x=-\frac{b}{2 a}$ .

Axe de symétrie

$x=-\frac{b}{2 a}$

$\begin{array}{l}{x=-\frac{(-6)}{2 \cdot 1}} \\ {x=3}\end{array}$

L'axe de symétrie est la ligne $x=3$ .

Le sommet se trouve sur l'axe de symétrie. $x=3$ Substituez dans la fonction.

Sommet

$\begin{array}{l}{f(x)=x^{2}-6 x+8} \\ {f(3)=(\color{red}{3}\color{black}{)}^{2}-6(\color{red}{3}\color{black}{)}+8} \\ {f(3)=-1}\end{array}$

Le sommet est $(3,-1)$ .

Nous trouvons $f(0)$

$y$ -intercepter

$\begin{array}{l}{f(x)=x^{2}-6 x+8} \\ {f(0)=(\color{red}{0}\color{black}{)}^{2}-6(\color{red}{0}\color{black}{)}+8} \\ {f(0)=8}\end{array}$

Le $y$ -intercept est $(0.8)$ .

Nous utilisons l'axe de symétrie pour trouver un point symétrique à l' $y$ intersection. Le $y$ -intercept correspond aux $3$ unités situées à gauche de l'axe de symétrie, $x=3$ . Une $3$ unité ponctuelle située à droite de l'axe de symétrie possède $x=6$ .

Point symétrique par rapport à $y$ -intercept

Le fait est que $(6,8)$ .

Nous résolvons $f(x)=0$ .

$x$ -intercepte

Nous pouvons résoudre cette équation quadratique par factorisation.

$\begin{aligned} f(x) &=x^{2}-6 x+8 \\ \color{red}{0} &\color{black}{=}x^{2}-6 x+8 \\ \color{red}{0} &\color{black}{=}(x-2)(x-4) \\ x &=2 \text { or } x=4 \end{aligned}$

Les $x$ -intercepts sont $(2,0)$ et $(4,0)$ .

Nous représentons graphiquement le sommet, les interceptions et le point symétriquement par $y$ rapport à l'intersection. Nous relions ces $5$ points pour esquisser la parabole.

Capture d'écran (3) .png — Graphique 9.8.3

Étape 3 : Déterminez la solution à partir du graphique

$x^{2}-6 x+8<0$

L'inégalité demande des valeurs $x$ qui rendent la fonction inférieure à $0$ . Quelles valeurs de $x$ forment la parabole en dessous de l' $x$ axe.

Nous n'incluons pas les valeurs $2$ , $4$ car l'inégalité est inférieure à la limite.

La solution, en notation par intervalles, est $(2,4)$ .

Exercice $\PageIndex{1}$

Résoudre $x^{2}+2 x-8<0$ graphiquement
Ecrivez la solution en notation par intervalles

Réponse

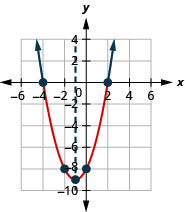
$Cette figure montre une parabole s'ouvrant vers le haut sur le plan de coordonnées x y. Il possède un sommet de (négatif 2, moins 9), une intersection y de (0, 8) et l'axe de symétrie indiqué en x est égal à moins 2.$
Graphique 9.8.4
$(-4,2)$

Exercice $\PageIndex{2}$

Résoudre $x^{2}-8 x+12 \geq 0$ graphiquement
Ecrivez la solution en notation par intervalles

Réponse

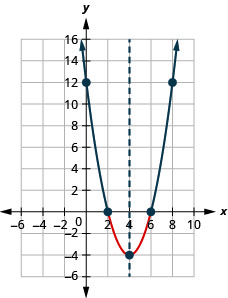
$Cette figure montre une parabole s'ouvrant vers le haut sur le plan de coordonnées x y. Il possède un sommet de (4, négatif 4) et des interceptions X de (2, 0) et (6, 0).$
Graphique 9.8.5
$(-\infty, 2] \cup[6, \infty)$

Nous listons graphiquement les étapes à suivre pour résoudre une inégalité quadratique.

Résolvez graphiquement une inégalité quadratique

Écrivez l'inégalité quadratique sous forme standard.
Tracez la fonction $f(x)=ax^{2}+bx+c$ .
Déterminez la solution à partir du graphique.

Dans le dernier exemple, la parabole s'ouvre vers le haut et dans l'exemple suivant, elle s'ouvre vers le bas. Dans les deux cas, nous cherchons la partie de la parabole située en dessous de l' $x$ axe -, mais nous remarquons comment la position de la parabole affecte la solution.

Exemple $\PageIndex{2}$

Résolvez $-x^{2}-8 x-12 \leq 0$ graphiquement Écrivez la solution en notation par intervalles.

Solution :

Tableau 9.8.1
L'inégalité quadratique sous forme standard.	$-x^{2}-8 x-12 \leq 0$
Tracez la fonction $f(x)=-x^{2}-8 x-12$	La parabole s'ouvre vers le bas. $.$ Graphique 9.8.6
Trouvez la ligne de symétrie.	$\begin{array}{l}{x=-\frac{b}{2 a}} \\ {x=-\frac{-8}{2(-1)}} \\ {x=-4}\end{array}$
Trouve le sommet.	$\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ f(-4) &=-(-4)^{2}-8(-4)-12 \\ f(-4) &=-16+32-12 \\ & f(-4)=4 \end{aligned}$ Sommet $(-4,4)$
Trouvez les $x$ -intercepts. Laissez $f(x)=0$ .	$\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ 0 &=-x^{2}-8 x-12 \end{aligned}$
Facteur : utilisez la propriété Zero Product.	$\begin{array}{l}{0=-1(x+6)(x+2)} \\ {x=-6 \quad x=-2}\end{array}$
Tracez la parabole.	$x$ -intercepte $(-6,0), (-2.0)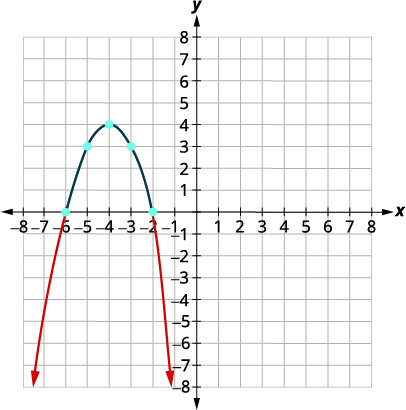$ $.$ Graphique 9.8.7
Déterminez la solution à partir du graphique. Nous incluons les $x$ -intercepts car l'inégalité est « inférieure ou égale à ».	$(-\infty,-6] \cup[-2, \infty)$

Exercice $\PageIndex{3}$

Résoudre $-x^{2}-6 x-5>0$ graphiquement
Ecrivez la solution en notation par intervalles

Réponse

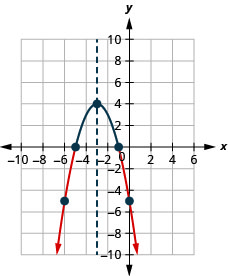
$Une parabole orientée vers le bas sur le plan de coordonnées x. Il possède un sommet de (négatif 3, 4), une intersection y à (0, moins 5) et un axe de symétrie indiqué en x est égal à moins 3.$
Graphique 9.8.8
$(-5,-1)$

Exercice $\PageIndex{4}$

Résoudre $−x^{2}+10x−16≤0$ graphiquement
Ecrivez la solution en notation par intervalles

Réponse

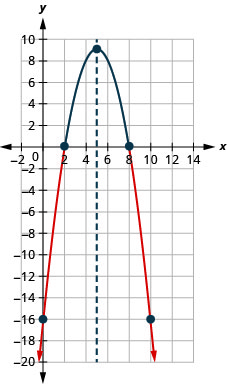
$Une parabole orientée vers le bas sur le plan de coordonnées x. Il possède un sommet de (5, 9), une intersection y à (0, moins 16) et un axe de symétrie de x égal à 5.$
Graphique 9.8.9
$(-\infty, 2] \cup[8, \infty)$

Résolvez les inégalités quadratiques de manière algébrique

La méthode algébrique que nous utiliserons est très similaire à celle que nous avons utilisée pour résoudre les inégalités rationnelles. Nous trouverons les points critiques de l'inégalité, qui seront les solutions à l'équation quadratique correspondante. N'oubliez pas qu'une expression polynomiale ne peut changer de signe que lorsque l'expression est nulle.

Nous utiliserons les points critiques pour diviser la droite numérique en intervalles, puis déterminerons si l'expression quadratique sera positive ou négative dans l'intervalle. Nous déterminons ensuite la solution à l'inégalité.

Exemple $\PageIndex{3}$ : How to Solve Quadratic Inequalities Algebraically

Résolvez $x^{2}-x-12 \geq 0$ algébriquement. Écrivez la solution en notation par intervalles.

Solution :

Tableau 9.8.2
Étape 1 : Écrivez l'inégalité quadratique sous forme standard.	L'inégalité se présente sous une forme standard.	$x^{2}-x-12 \geq 0$
Étape 2 : Déterminez les points critiques, c'est-à-dire les solutions à l'équation quadratique correspondante.	Remplacez le signe d'inégalité par un signe égal, puis résolvez l'équation.	$\begin{array}{c}{x^{2}-x-12=0} \\ {(x+3)(x-4)=0} \\ {x+3=0 \quad x-4=0} \\ {x=-3 \quad x=4}\end{array}$
Étape 3 : Utilisez les points critiques pour diviser la ligne numérique en intervalles.	Utilisez $-3$ et $4$ pour diviser la ligne numérique en intervalles.	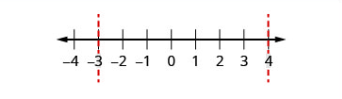$Capture d'écran (4) .png$
Étape 4 : Au-dessus de la ligne numérique, montrez le signe de chaque expression quadratique en utilisant les points de test de chaque intervalle substitués par l'inégalité d'origine.	Épreuve : $x=-5$ $x=0$ $x=5$	$\begin{array}{ccc}{x^{2}-x-12} & {x^{2}-x-12} & {x^{2}-x-12} \\ {(-5)^{2}-(-5)-12} & {0^{2}-0-12} & {5^{2}-5-12} \\ {18} & {-12} & {8}\end{array}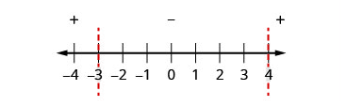$ $Capture d'écran (5) .png$ Graphique 9.8.11
Étape 5 : Déterminez les intervalles où l'inégalité est correcte. Écrivez la solution en notation par intervalles.	$x^{2}-x-12 \geq 0$ L'inégalité est positive dans le premier et le dernier intervalle et égale $0$ aux points $-4,3$ .	La solution, en notation par intervalles, est $(-\infty,-3] \cup[4, \infty)$ .

Exercice $\PageIndex{5}$

Résolvez $x^{2}+2x−8≥0$ algébriquement. Écrivez la solution en notation par intervalles.

Réponse: $(-\infty,-4] \cup[2, \infty)$

Exercice $\PageIndex{6}$

Résolvez $x^{2}−2x−15≤0$ algébriquement. Écrivez la solution en notation par intervalles.

Réponse: $[-3,5]$

Dans cet exemple, comme l'expression prend bien $x^{2}−x−12$ en compte, nous pouvons également trouver le signe dans chaque intervalle, un peu comme nous l'avons fait lorsque nous avons résolu des inégalités rationnelles. On retrouve le signe de chacun des facteurs, puis le signe du produit. Notre ligne numérique serait la suivante :

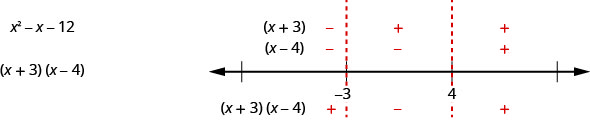
La figure montre l'expression x au carré moins x moins 12 multipliée par la quantité de x plus 3 fois la quantité de x moins 4. L'image montre une ligne numérique montrant des lignes pointillées sur les négatifs 3 et 4. Il montre que les signes de la quantité x plus 3 sont négatifs, positifs, positifs et que les signes de la quantité x moins 4 sont négatifs, négatifs, positifs. Sous la ligne numérique, il indique la quantité x plus 3 fois la quantité x moins 4 avec les signes positif, négatif et positif. — Graphique 9.8.12

Le résultat est le même que celui que nous avons trouvé en utilisant l'autre méthode.

Nous résumons les étapes ici.

Résolvez algébriquement une inégalité quadratique

Écrivez l'inégalité quadratique sous forme standard.
Déterminez les points critiques, c'est-à-dire les solutions à l'équation quadratique correspondante.
Utilisez les points critiques pour diviser la ligne numérique en intervalles.
Au-dessus de la ligne numérique, montrez le signe de chaque expression quadratique en utilisant les points de test de chaque intervalle substitués à l'inégalité d'origine.
Déterminez les intervalles où l'inégalité est correcte. Écrivez la solution en notation par intervalles.

Exemple $\PageIndex{4}$

Résolvez $x^{2}+6x−7≥0$ algébriquement. Écrivez la solution en notation par intervalles.

Solution :

Tableau 9.8.3
Écrivez l'inégalité quadratique sous forme standard.	$-x^{2}+6 x-7 \geq 0$
Multipliez les deux côtés de l'inégalité par $-1$ . N'oubliez pas d'inverser le signe d'inégalité.	$x^{2}-6 x+7 \leq 0$
Déterminez les points critiques en résolvant l'équation quadratique correspondante.	$x^{2}-6 x+7=0$
Écrivez la formule quadratique.	$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
Remplacez ensuite les valeurs de $a, b, c$ .	$x=\frac{-(-6) \pm \sqrt{(-6)^{2}-4 \cdot 1 \cdot(7)}}{2 \cdot 1}$
Simplifiez.	$x=\frac{6 \pm \sqrt{8}}{2}$
Simplifiez le radical.	$x=\frac{6 \pm 2 \sqrt{2}}{2}$
Supprimer le facteur commun, $2$ .	$\begin{array}{l}{x=\frac{2(3 \pm \sqrt{2})}{2}} \\ {x=3 \pm \sqrt{2}} \\ {x=3+\sqrt{2}} \quad x=3-\sqrt{2} \\ {x \approx 1.6}\quad\quad\:\:\: x\approx 4.4\end{array}$
Utilisez les points critiques pour diviser la ligne numérique en intervalles. Testez les nombres de chaque intervalle de l'inégalité d'origine.	$.$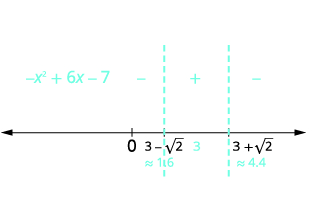
Déterminez les intervalles où l'inégalité est correcte. Écrivez la solution en notation par intervalles.	$-x^{2}+6 x-7 \geq 0$ dans l'intervalle moyen $[3-\sqrt{2}, 3+\sqrt{2}]$

Exercice $\PageIndex{7}$

Résolvez $−x^{2}+2x+1≥0$ algébriquement. Écrivez la solution en notation par intervalles.

Réponse: $[-1-\sqrt{2},-1+\sqrt{2}]$

Exercice $\PageIndex{8}$

Résolvez $−x^{2}+8x−14<0$ algébriquement. Écrivez la solution en notation par intervalles.

Réponse: $(-\infty, 4-\sqrt{2}) \cup(4+\sqrt{2}, \infty)$

Les solutions des inégalités quadratiques dans chacun des exemples précédents étaient soit un intervalle, soit l'union de deux intervalles. Cela s'explique par le fait que, dans chaque cas, nous avons trouvé deux solutions à l'équation quadratique correspondante $ax^{2}+bx+c=0$ . Ces deux solutions nous ont ensuite donné soit les deux $x$ interceptions pour le graphique, soit les deux points critiques pour diviser la ligne numérique en intervalles.

Cela correspond à notre discussion précédente sur le nombre et le type de solutions à une équation quadratique utilisant le discriminant.

Pour une équation quadratique de la forme $ax^{2}+bc+c=0, a≠0$ .

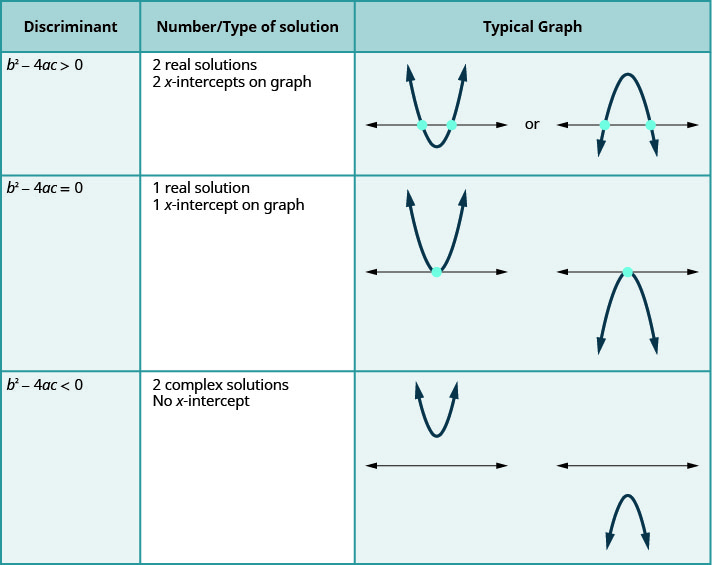
La figure est un tableau à 3 colonnes. La colonne 1 est étiquetée discriminante, la colonne 2 est Nombre/Type de solution et la colonne 3 est un graphique typique. Si l'on lit les colonnes, si b au carré moins 4 fois par c est supérieur à 0, il y aura 2 solutions réelles car il y a 2 interceptions X sur le graphique. L'image d'un graphe typique : une parabole ascendante ou descendante avec 2 interceptions en X. Si le discriminant b au carré moins 4 fois a fois c est égal à 0, alors il y a 1 solution réelle car il y a 1 intersection X sur le graphique. L'image du graphe type est une parabole orientée vers le haut ou vers le bas qui possède un sommet sur l'axe des abscisses au lieu de le traverser. Si le discriminant b au carré moins 4 fois a fois c est inférieur à 0, il existe 2 solutions complexes car il n'y a pas d'intersection X. L'image du graphique type montre une parabole orientée vers le haut ou vers le bas qui ne traverse pas l'axe des abscisses. — Graphique 9.8.14

La dernière ligne du tableau nous indique quand les paraboles ne croisent jamais l' $x$ axe. En utilisant la formule quadratique pour résoudre l'équation quadratique, le radicand est négatif. Nous avons deux solutions complexes.

Dans l'exemple suivant, les solutions d'inégalité quadratique résulteront de la complexité de la solution de l'équation quadratique.

Exemple $\PageIndex{5}$

Résolvez en écrivant n'importe quelle solution en notation par intervalles :

$x^{2}-3 x+4>0$
$x^{2}-3 x+4 \leq 0$

Solution :

un.

Tableau 9.8.4
Écrivez l'inégalité quadratique sous forme standard.	$-x^{2}-3 x+4>0$
Déterminez les points critiques en résolvant l'équation quadratique correspondante.	$x^{2}-3 x+4=0$
Écrivez la formule quadratique.	$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
Remplacez ensuite les valeurs de $a, b, c$ .	$x=\frac{-(-3) \pm \sqrt{(-3)^{2}-4 \cdot 1 \cdot(4)}}{2 \cdot 1}$
Simplifiez.	$x=\frac{3 \pm \sqrt{-7}}{2}$
Simplifiez le radicand.	$x=\frac{3 \pm \sqrt{7 i}}{2}$
Les solutions complexes nous indiquent que la parabole n'intercepte pas l' $x$ axe. De plus, la parabole s'ouvre vers le haut. Cela nous indique que la parabole est complètement au-dessus de l' $x$ axe.	Des solutions complexes 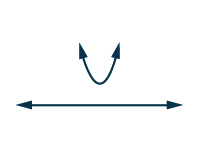$.$ Graphique 9.8.15

Nous devons trouver la solution à $x^{2}−3x+4>0$ . Comme toutes les valeurs $x$ du graphique se trouvent au-dessus de l' $x$ axe des -, toutes les valeurs $x$ de confirment l'inégalité. En notation par intervalles, nous écrivons $(−∞,∞)$ .

b. Écrivez l'inégalité quadratique sous forme standard.

$x^{2}-3 x+4 \leq 0$

Déterminez les points critiques en résolvant l'équation quadratique correspondante.

$x^{2}-3 x+4=0$

Puisque l'équation quadratique correspondante est la même que dans la partie (a), la parabole sera la même. La parabole s'ouvre vers le haut et se trouve complètement au-dessus de l' $x$ axe -; aucune partie de celle-ci ne se trouve en dessous de $x$ l'axe.

Nous devons trouver la solution à $x^{2}−3x+4≤0$ . Étant donné que toutes les valeurs $x$ du graphique ne sont jamais inférieures à l' $x$ axe Y, aucune valeur ne permet de $x$ confirmer l'inégalité. Il n'y a pas de solution à cette inégalité.

Exercice $\PageIndex{9}$

Résolvez et écrivez n'importe quelle solution en notation par intervalles :

$-x^{2}+2 x-4 \leq 0$
$-x^{2}+2 x-4 \geq 0$

Réponse

$(-\infty, \infty)$
aucune solution

Exercice $\PageIndex{10}$

Résolvez et écrivez n'importe quelle solution en notation par intervalles :

$x^{2}+3 x+3<0$
$x^{2}+3 x+3>0$

Réponse

aucune solution
$(-\infty, \infty)$

Concepts clés

Résolvez graphiquement une inégalité quadratique
1. Écrivez l'inégalité quadratique sous forme standard.
2. Tracez la fonction $f(x)=ax^{2}+bx+c$ en utilisant des propriétés ou des transformations.
3. Déterminez la solution à partir du graphique.
Comment résoudre algébriquement une inégalité quadratique
1. Écrivez l'inégalité quadratique sous forme standard.
2. Déterminez les points critiques, c'est-à-dire les solutions à l'équation quadratique correspondante.
3. Utilisez les points critiques pour diviser la ligne numérique en intervalles.
4. Au-dessus de la ligne numérique, montrez le signe de chaque expression quadratique en utilisant les points de test de chaque intervalle substitués à l'inégalité d'origine.
5. Déterminez les intervalles où l'inégalité est correcte. Écrivez la solution en notation par intervalles.

Lexique

inégalité quadratique: Une inégalité quadratique est une inégalité qui contient une expression quadratique.

Objectifs d'apprentissage

Résoudre graphiquement les inégalités quadratiques

Définition9.9.1\PageIndex{1}: Quadratic Inequality

Exemple9.9.1\PageIndex{1}: How to Solve a Quadratic Inequality Graphically

Exercice9.9.1\PageIndex{1}

Exercice9.9.2\PageIndex{2}

Résolvez graphiquement une inégalité quadratique

Exemple9.9.2\PageIndex{2}

Exercice9.9.3\PageIndex{3}

Exercice9.9.4\PageIndex{4}

Résolvez les inégalités quadratiques de manière algébrique

Exemple9.9.3\PageIndex{3}: How to Solve Quadratic Inequalities Algebraically

Exercice9.9.5\PageIndex{5}

Exercice9.9.6\PageIndex{6}

Résolvez algébriquement une inégalité quadratique

Exemple9.9.4\PageIndex{4}

Exercice9.9.7\PageIndex{7}

Exercice9.9.8\PageIndex{8}

Exemple9.9.5\PageIndex{5}

Exercice9.9.9\PageIndex{9}

Exercice9.9.10\PageIndex{10}

Concepts clés

Lexique

Définition $\PageIndex{1}$ : Quadratic Inequality

Exemple $\PageIndex{1}$ : How to Solve a Quadratic Inequality Graphically

Exercice $\PageIndex{1}$

Exercice $\PageIndex{2}$

Exemple $\PageIndex{2}$

Exercice $\PageIndex{3}$

Exercice $\PageIndex{4}$

Exemple $\PageIndex{3}$ : How to Solve Quadratic Inequalities Algebraically

Exercice $\PageIndex{5}$

Exercice $\PageIndex{6}$

Exemple $\PageIndex{4}$

Exercice $\PageIndex{7}$

Exercice $\PageIndex{8}$

Exemple $\PageIndex{5}$

Exercice $\PageIndex{9}$

Exercice $\PageIndex{10}$