Skip to main content
Global

9.4 : Résoudre des équations quadratiques à l'aide de la formule quadratique

  1. Last updated
  2. Save as PDF
  • Page ID
    194360

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Résolvez des équations quadratiques en utilisant la formule quadratique
    • Utilisez le discriminant pour prédire le nombre et le type de solutions d'une équation quadratique
    • Identifier la méthode la plus appropriée à utiliser pour résoudre une équation quadratique

    Avant de commencer, répondez à ce questionnaire de préparation.

    1. Évaluez\(b^{2}-4 a b\) quand\(a=3\) et\(b=−2\).
    2. Simplifiez\(\sqrt{108}\).
    3. Simplifiez\(\sqrt{50}\).

    Résolvez des équations quadratiques en utilisant la formule quadratique

    Lorsque nous avons résolu des équations quadratiques dans la dernière section en complétant le carré, nous avons suivi les mêmes étapes à chaque fois. À la fin de la série d'exercices, vous vous êtes peut-être demandé « n'y a-t-il pas un moyen plus simple de le faire ? » La réponse est « oui ». Les mathématiciens recherchent des modèles lorsqu'ils font des choses encore et encore afin de faciliter leur travail. Dans cette section, nous allons dériver et utiliser une formule pour trouver la solution d'une équation quadratique.

    Nous avons déjà vu comment résoudre une formule pour une variable spécifique « en général », de sorte que nous n'effectuions les étapes algébriques qu'une seule fois, puis que nous utilisions la nouvelle formule pour trouver la valeur de la variable spécifique. Nous allons maintenant passer par les étapes pour compléter le carré en utilisant la forme générale d'une équation quadratique pour résoudre une équation quadratique pour\(x\).

    Nous commençons par la forme standard d'une équation quadratique et la résolvons\(x\) en complétant le carré.

      \(ax^2 + bx + c = 0, \quad a \ne 0\)
    Isolez les termes variables d'un côté. \(ax^2 + bx \quad = -c\)
    Rendre le coefficient\(x^{2}\) égal à\(1\), en divisant par\(a\). \(\dfrac{ax^2}{a} + \dfrac{b}{a}x \quad = -\dfrac{c}{a}\)
    Simplifiez. \(x^2+ \dfrac{b}{a}x \quad = -\dfrac{c}{a}\)
    Pour compléter le carré, trouvez-le\(\left(\dfrac{1}{2} \cdot \dfrac{b}{a}\right)^{2}\) et ajoutez-le des deux côtés de l'équation.  
    \(\left(\dfrac{1}{2} \dfrac{b}{a}\right)^{2}=\dfrac{b^{2}}{4 a^{2}}\) \(x^2 + \dfrac{b}{a}x +{\color{red}{\dfrac{b^2}{4a^2}}}{\color{black}{ = -\dfrac{c}{a}\,+\,}}{\color{red}{\dfrac{b^2}{4a^2}}}\)
    Le côté gauche est un carré parfait, prenez-le en compte. \(\left( x + \dfrac{b}{2a}\right)^2 = -\dfrac{c}{a}+\dfrac{b^2}{4a^2}\)
    Trouvez le dénominateur commun du côté droit et écrivez des fractions équivalentes avec le dénominateur commun. \(\left( x + \dfrac{b}{2a}\right)^2 =\dfrac{b^2}{4a^2}-\dfrac{c\cdot\color{red}{4a}}{a\cdot\color{red}{4a}}\)
    Simplifiez. \(\left( x + \dfrac{b}{2a}\right)^2 =\dfrac{b^2}{4a^2}-\dfrac{4ac}{4a^2}\)
    Combinez jusqu'à obtenir une fraction. \(\left( x + \dfrac{b}{2a}\right)^2 =\dfrac{b^2-4ac}{4a^2}\)
    Utilisez la propriété de racine carrée. \(x + \dfrac{b}{2a}= \pm\sqrt{\dfrac{b^2-4ac}{4a^2}}\)
    Simplifiez le radical. \(x + \dfrac{b}{2a}= \pm\dfrac{\sqrt{b^2-4ac}}{2a}\)
    Ajoutez\(-\dfrac{b}{2a}\) les deux côtés de l'équation. \(x = -\dfrac{b}{2a} \pm\dfrac{\sqrt{b^2-4ac}}{2a}\)
    Combinez les termes sur le côté droit. \(x = \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\)

    L'équation finale s'appelle la « formule quadratique ».

    Définition\(\PageIndex{1}\): Quadratic Formula

    Les solutions d'une équation quadratique de la forme\(a x^{2}+b x+c=0\), où\(a≠0\) sont données par la formule :

    \[x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \label{quad}\]

    Pour utiliser la formule quadratique, nous substituons les valeurs de\(a,b\) et\(c\) de la forme standard dans l'expression située sur le côté droit de la formule. Ensuite, nous simplifions l'expression. Le résultat est la paire de solutions à l'équation quadratique.

    Notez que la formule quadratique (équation \ ref {quad}) est une équation. Assurez-vous d'utiliser les deux côtés de l'équation.

    Exemple\(\PageIndex{1}\) How to Solve a Quadratic Equation Using the Quadratic Formula

    Résolvez en utilisant la formule quadratique :\(2 x^{2}+9 x-5=0\).

    Solution :

    Étape 1 : Écrivez l'équation quadratique sous forme standard. Identifiez les\(a,b,c\) valeurs. Cette équation se présente sous forme standard. \(\begin{aligned} \color{red}{a x^{2}+b x+c =0} \\ 2 x^{2}+9 x-5 =0 \\ a=2, b =9, c=-5 \end{aligned}\)
    Étape 2 : Écrivez la formule quadratique. Remplacez ensuite les valeurs de\(a,b,c\). Substituer dans\(a=2, b=9, c=-5\) \(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
    \(x=\dfrac{-9 \pm \sqrt{9^{2}-4 \cdot 2 \cdot(-5)}}{2 \cdot 2}\)
    Étape 3 : Simplifiez la fraction et résolvez pour\(x\).   \(\begin{array}{l}{x=\dfrac{-9 \pm \sqrt{81-(-40)}}{4}} \\ {x=\dfrac{-9 \pm \sqrt{121}}{4}} \\ {x=\dfrac{-9 \pm 11}{4}} \\ {x=\dfrac{-9+11}{4}}\quad x=\dfrac{-9-11}{4} \\ {x=\dfrac{2}{4} \quad \quad\:\:\: x=\dfrac{-20}{4}}\\ {x=\dfrac{1}{2} \quad\quad\:\:\: x=-5}\end{array}\)
    Étape 4 : Vérifiez les solutions Mettez chaque réponse dans l'équation d'origine à vérifier. Substitut\(x=\color{red}{\dfrac{1}{2}}\) et\(x=\color{red}{-5}\).

    \(\begin{aligned}2 x^{2}+9 x-5&=0 \\ 2\color{black}{\left(\color{red}{\dfrac{1}{2}}\right)}^{2}+9 \cdot \color{red}{\dfrac{1}{2}}\color{black}{-}5 &\stackrel{?}{=} 0 \\ 2\cdot\dfrac{1}{4}+0\cdot\dfrac{1}{2}-5&\stackrel{?}{=}0 \\ 2\cdot\dfrac{1}{4}+9\cdot\dfrac{1}{2}-5&\stackrel{?}{=}0 \\ \dfrac{1}{2}+\dfrac{9}{2}-5&\stackrel{?}{=}0 \\ \dfrac{10}{2}-5&\stackrel{?}{=}0 \\5-5&\stackrel{?}{=}0\\0&=0\end{aligned}\)

    \(\begin{array}{r}{2 x^{2}+9 x-5=0} \\ {2(\color{red}{-5}\color{black}{)}^{2}+9(\color{red}{-5}\color{black}{)}-5\stackrel{?}{=}0} \\ {2 \cdot 25-45-5\stackrel{?}{=}0} \\ {50-45-5\stackrel{?}{=}0} \\ {0=0}\end{array}\)
    Exercice\(\PageIndex{1}\)

    Résolvez en utilisant la formule quadratique :\(3 y^{2}-5 y+2=0\).

    Réponse

    \(y=1, y=\dfrac{2}{3}\)

    Exercice\(\PageIndex{2}\)

    Résolvez en utilisant la formule quadratique :\(4 z^{2}+2 z-6=0\).

    Réponse

    \(z=1, z=-\dfrac{3}{2}\)

    Comment : résoudre une équation quadratique à l'aide de la formule quadratique
    1. Écrivez l'équation quadratique sous forme standard,\(a x^{2}+b x+c=0\). Identifiez les valeurs de\(a,b\), et\(c\).
    2. Écrivez la formule quadratique. Remplacez ensuite les valeurs de\(a,b\), et\(c\).
    3. Simplifiez.
    4. Vérifiez les solutions.

    Si vous dites la formule au fur et à mesure que vous l'écrivez dans chaque problème, vous la mémoriserez en un rien de temps ! Et n'oubliez pas que la formule quadratique est une ÉQUATION. Assurez-vous de commencer par «\(x=\) ».

    Exemple\(\PageIndex{2}\)

    Résolvez en utilisant la formule quadratique :\(x^{2}-6 x=-5\).

    Solution :

     

    \(x^{2}-6 x=-5\)
    Écrivez l'équation sous forme standard en l'ajoutant\(5\) de chaque côté.

    \(x^{2}-6 x+5=0\)
    Cette équation est maintenant sous forme standard.

    \({\color{red}{\small{ax^2+bx + c} = \small{0}}}\)
    \(x^2 - 6x + 5 = 0\)
    Identifiez les valeurs de\(\color{cyan}a\),\(\color{red}b\),\(\color{limegreen}c\). \({\color{cyan}a=1}\),\({\color{red}b=-6}\),\({\color{limegreen}c=5}\)
    Écrivez la formule quadratique.

    \(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
    Remplacez ensuite les valeurs de\(a, b, c\).

    \(x=\dfrac{-\color{red} (-6 ) \color{black} \pm \sqrt{\color{red}(-6) \color{black}^{2}-4 \cdot \color{cyan}1 \color{black} \cdot ( \color{limegreen}5 \color{black})}}{2 \cdot \color{cyan} 1} \)
    Simplifiez.

    \(x=\dfrac{6 \pm \sqrt{36-20}}{2}\)

    \(x=\dfrac{6 \pm \sqrt{16}}{2}\)

    \(x=\dfrac{6 \pm 4}{2}\)
    Réécrivez pour afficher deux solutions.

    \(x=\frac{6+4}{2}, \quad x=\frac{6-4}{2}\)
    Simplifiez.

    \(x=\frac{10}{2}, \quad x=\frac{2}{2}\)
      \(x=5, \quad x=1\)

    Vérifiez :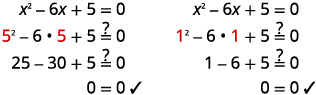

    .
    		  
    Exercice\(\PageIndex{3}\)

    Résolvez en utilisant la formule quadratique :\(a^{2}-2 a=15\).

    Réponse

    \(a=-3, a=5\)

    Exercice\(\PageIndex{4}\)

    Résolvez en utilisant la formule quadratique :\(b^{2}+24=-10 b\).

    Réponse

    \(b=-6, b=-4\)

    Lorsque nous résolvions des équations quadratiques à l'aide de la propriété de racine carrée, nous obtenions parfois des réponses contenant des radicaux. Cela peut également se produire lorsque vous utilisez la formule quadratique. Si nous obtenons un radical comme solution, la réponse finale doit avoir le radical dans sa forme simplifiée.

    Exemple\(\PageIndex{3}\)

    Résolvez en utilisant la formule quadratique :\(2 x^{2}+10 x+11=0\).

    Solution :

      .
    Cette équation se présente sous forme standard. .
    Identifiez les valeurs de\(a,b\) et\(c\). .
    Écrivez la formule quadratique.

    \(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
    Remplacez ensuite les valeurs de\(a, b\), et\(c\). .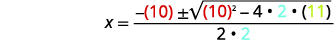
    Simplifiez.

    \(x=\dfrac{-10 \pm \sqrt{100-88}}{4}\)
     

    \(x=\dfrac{-10 \pm \sqrt{12}}{4}\)
    Simplifiez le radical.

    \(x=\dfrac{-10 \pm 2 \sqrt{3}}{4}\)
    Éliminez le facteur commun dans le numérateur.

    .

    \(x=\dfrac{\color{red}{2}(-5 \pm \sqrt{3})}{4}\)
    Supprimez les facteurs communs.

    \(x=\dfrac{-5 \pm \sqrt{3}}{2}\)
    Réécrivez pour afficher deux solutions.

    \(x=\dfrac{-5+\sqrt{3}}{2}, \quad x=\dfrac{-5-\sqrt{3}}{2}\)

    Vérifiez :

    Nous vous laissons le chèque !

    		  
    Exercice\(\PageIndex{5}\)

    Résolvez en utilisant la formule quadratique :\(3 m^{2}+12 m+7=0\).

    Réponse

    \(m=\dfrac{-6+\sqrt{15}}{3}, m=\dfrac{-6-\sqrt{15}}{3}\)

    Exercice\(\PageIndex{6}\)

    Résolvez en utilisant la formule quadratique :\(5 n^{2}+4 n-4=0\).

    Réponse

    \(n=\dfrac{-2+2 \sqrt{6}}{5}, n=\dfrac{-2-2 \sqrt{6}}{5}\)

    Lorsque nous la substituons\(a, b\), et\(c\) que la formule quadratique et que le radical est négatif, l'équation quadratique aura des solutions imaginaires ou complexes. Nous allons le voir dans l'exemple suivant.

    Exemple\(\PageIndex{4}\)

    Résolvez en utilisant la formule quadratique :\(3 p^{2}+2 p+9=0\).

    Solution :

      .
    Cette équation se présente sous forme standard. .
    Identifiez les valeurs de\(a,b,c\). .
    Écrivez la formule quadratique. .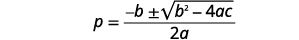
    Remplacez ensuite les valeurs de\(a,b,c\). .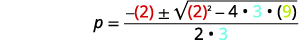
    Simplifiez. .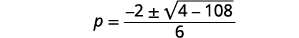
      .
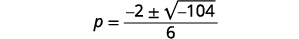    Simplifiez le radical en utilisant des nombres complexes. .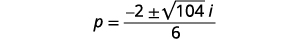
    Simplifiez le radical. .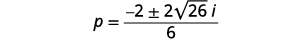
    Facturez le facteur commun dans le numérateur. .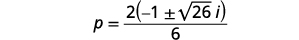
    Supprimez les facteurs communs. .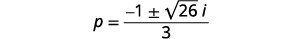
    Réécrivez sous\(a+bi\) forme standard. .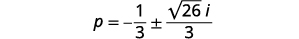
    Écrivez comme deux solutions. .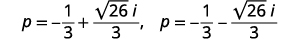
    Tableau 9.3.5
    Exercice\(\PageIndex{7}\)

    Résolvez en utilisant la formule quadratique :\(4 a^{2}-2 a+8=0\).

    Réponse

    \(a=\dfrac{1}{4}+\dfrac{\sqrt{31}}{4} i, \quad a=\dfrac{1}{4}-\dfrac{\sqrt{31}}{4} i\)

    Exercice\(\PageIndex{8}\)

    Résolvez en utilisant la formule quadratique :\(5 b^{2}+2 b+4=0\).

    Réponse

    \(b=-\dfrac{1}{5}+\dfrac{\sqrt{19}}{5} i, \quad b=-\dfrac{1}{5}-\dfrac{\sqrt{19}}{5} i\)

    N'oubliez pas que pour utiliser la formule quadratique, l'équation doit être écrite sous forme standard,\(a x^{2}+b x+c=0\). Parfois, nous devrons faire de l'algèbre pour obtenir la forme standard de l'équation avant de pouvoir utiliser la formule quadratique.

    Exemple\(\PageIndex{5}\)

    Résolvez en utilisant la formule quadratique :\(x(x+6)+4=0\).

    Solution :

    Notre première étape consiste à obtenir l'équation sous forme standard.

      .
    Distribuez pour obtenir l'équation sous forme standard. .
    Cette équation est maintenant sous forme standard. .
    Identifiez les valeurs de\(a,b,c\). .
    Écrivez la formule quadratique. .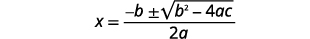
    Remplacez ensuite les valeurs de\(a,b,c\). .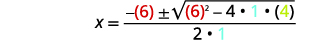
    Simplifiez. .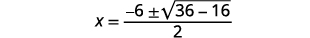
      .
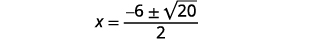    Simplifiez le radical. .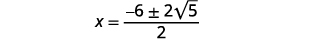
    Facturez le facteur commun dans le numérateur. .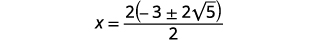
    Supprimez les facteurs communs. .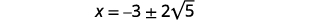
    Écrivez comme deux solutions. .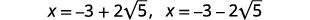

    Vérifiez :

    Nous vous laissons le chèque !

    		  
    Tableau 9.3.6
    Exercice\(\PageIndex{9}\)

    Résolvez en utilisant la formule quadratique :\(x(x+2)−5=0\).

    Réponse

    \(x=-1+\sqrt{6}, x=-1-\sqrt{6}\)

    Exercice\(\PageIndex{10}\)

    Résolvez en utilisant la formule quadratique :\(3y(y−2)−3=0\).

    Réponse

    \(y=1+\sqrt{2}, y=1-\sqrt{2}\)

    Lorsque nous résolvions des équations linéaires, si une équation comportait trop de fractions, nous supprimions les fractions en multipliant les deux côtés de l'équation par l'écran LCD. Cela nous a donné une équation équivalente, sans fractions, à résoudre. Nous pouvons utiliser la même stratégie avec des équations quadratiques.

    Exemple\(\PageIndex{6}\)

    Résolvez en utilisant la formule quadratique :\(\dfrac{1}{2} u^{2}+\dfrac{2}{3} u=\dfrac{1}{3}\).

    Solution :

    Notre première étape consiste à éliminer les fractions.

      .
    Multipliez les deux côtés par l'\(6\)écran LCD pour effacer les fractions. .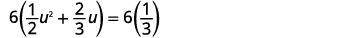
    Multipliez. .
    Soustrayez\(2\) pour obtenir l'équation sous forme standard. .
    Identifiez les valeurs de\(a, b\), et\(c\). .
    Écrivez la formule quadratique. .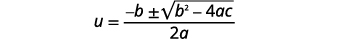
    Remplacez ensuite les valeurs de\(a, b,\) et\(c\). .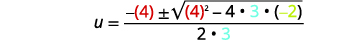
    Simplifiez. .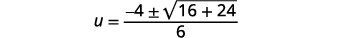
      .
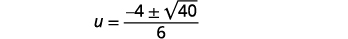    Simplifiez le radical. .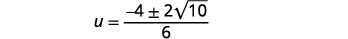
    Facturez le facteur commun dans le numérateur. .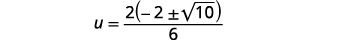
    Supprimez les facteurs communs. .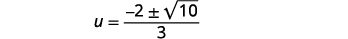
    Réécrivez pour afficher deux solutions. .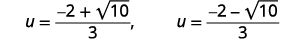

    Vérifiez :

    Nous vous laissons le chèque !

    		  
    Tableau 9.3.7
    Exercice\(\PageIndex{11}\)

    Résolvez en utilisant la formule quadratique :\(\dfrac{1}{4} c^{2}-\dfrac{1}{3} c=\dfrac{1}{12}\).

    Réponse

    \(c=\dfrac{2+\sqrt{7}}{3}, \quad c=\dfrac{2-\sqrt{7}}{3}\)

    Exercice\(\PageIndex{12}\)

    Résolvez en utilisant la formule quadratique :\(\dfrac{1}{9} d^{2}-\dfrac{1}{2} d=-\dfrac{1}{3}\).

    Réponse

    \(d=\dfrac{9+\sqrt{33}}{4}, d=\dfrac{9-\sqrt{33}}{4}\)

    Réfléchissez à l'équation\((x-3)^{2}=0\). Nous savons grâce à la propriété Zero Product que cette équation n'a qu'une seule solution,\(x=3\).

    Nous verrons dans l'exemple suivant comment l'utilisation de la formule quadratique pour résoudre une équation dont la forme standard est un trinôme carré parfait égal à\(0\) donne une seule solution. Notez qu'une fois que le radicand est simplifié, il devient\(0\), ce qui ne conduit qu'à une seule solution.

    Exemple\(\PageIndex{7}\)

    Résolvez en utilisant la formule quadratique :\(4 x^{2}-20 x=-25\).

    Solution :

      .
    Ajoutez\(25\) pour obtenir l'équation sous forme standard. .
    Identifiez les valeurs de\(a, b\), et\(c\). .
    Écrivez la formule quadratique. .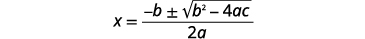
    Remplacez ensuite les valeurs de\(a, b\), et\(c\). .
    Simplifiez. .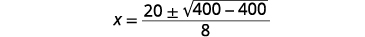
      .
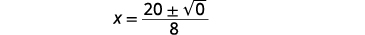    Simplifiez le radical. .
    Simplifiez la fraction. .

    Vérifiez :

    Nous vous laissons le chèque !

    		  
    Tableau 9.3.8

    Avez-vous reconnu que\(4 x^{2}-20 x+25\) c'est un trinôme carré parfait ? C'est équivalent à\((2 x-5)^{2}\) ? Si vous résolvez\(4 x^{2}-20 x+25=0\) en factorisant puis en utilisant la propriété Square Root, obtenez-vous le même résultat ?

    Exercice\(\PageIndex{13}\)

    Résolvez en utilisant la formule quadratique :\(r^{2}+10 r+25=0\).

    Réponse

    \(r=-5\)

    Exercice\(\PageIndex{14}\)

    Résolvez en utilisant la formule quadratique :\(25 t^{2}-40 t=-16\).

    Réponse

    \(t=\dfrac{4}{5}\)

    Utiliser le discriminant pour prédire le nombre et le type de solutions d'une équation quadratique

    Lorsque nous avons résolu les équations quadratiques des exemples précédents, nous avons parfois obtenu deux solutions réelles, une solution réelle et parfois deux solutions complexes. Existe-t-il un moyen de prédire le nombre et le type de solutions d'une équation quadratique sans réellement résoudre l'équation ?

    Oui, l'expression sous le radical de la formule quadratique nous permet de déterminer facilement le nombre et le type de solutions. Cette expression est appelée discriminant.

    Définition\(\PageIndex{2}\)

    Discriminant

    Dans la formule quadratique, x est égal au quotient de b négatif plus ou moins la racine carrée de b au carré moins 4 fois a fois c et 2 a, la valeur sous le radical, b au carré moins 4 fois a fois c, est appelée discriminant.
    Graphique 9.3.85

    Examinons le discriminant des équations dans certains exemples ainsi que le nombre et le type de solutions à ces équations quadratiques.

    Équation quadratique (sous forme standard) Discriminant\(b^{2}-4ac\) Valeur du discriminant Nombre et type de solutions
    \(2 x^{2}+9 x-5=0\) \ (b^ {2} -4 ac \) « >\(\begin{aligned} 9^{2}-& 4 \cdot 2(-5) \\ & 121 \end{aligned}\) \(+\) \(2\)réel
    \(4 x^{2}-20 x+25=0\) \ (b^ {2} -4 ac \) « >\((-20)^{2}-4 \cdot 4 \cdot 25\)
    \(0\)    		 \(0\) \(1\)réel
    \(3 p^{2}+2 p+9=0\) \ (b^ {2} -4 ac \) « >\(2^{2}-4 \cdot 3 \cdot 9\)
    \(-104\)    		 \(-\) \(2\)complexe
    Tableau 9.3.9
    Lorsque la valeur sous le radical dans la formule quadratique, le discriminant, est positive, l'équation a deux solutions réelles. Lorsque la valeur sous le radical dans la formule quadratique, le discriminant, est nulle, l'équation a une solution réelle. Lorsque la valeur sous le radical dans la formule quadratique, le discriminant, est négative, l'équation comporte deux solutions complexes.
    Graphique 9.3.86

    Utilisation du\(b^{2}-4ac\) discriminant pour déterminer le nombre et le type de solutions d'une équation quadratique

    Pour une équation quadratique de la forme\(ax^{2}+bx+c=0\)\(a \neq 0\),

    • Si\(b^{2}-4 a c>0\), l'équation a de\(2\) vraies solutions.
    • si\(b^{2}-4 a c=0\), l'équation a une\(1\) vraie solution.
    • si\(b^{2}-4 a c<0\), l'équation comporte des solutions\(2\) complexes.
    Exemple\(\PageIndex{8}\)

    Déterminez le nombre de solutions pour chaque équation quadratique.

    1. \(3 x^{2}+7 x-9=0\)
    2. \(5 n^{2}+n+4=0\)
    3. \(9 y^{2}-6 y+1=0\)

    Solution :

    Pour déterminer le nombre de solutions de chaque équation quadratique, nous examinerons son discriminant.

    un.

    \(3 x^{2}+7 x-9=0\)

    L'équation est sous forme standard\(a, b\), identifiez et\(c\).

    \(a=3, \quad b=7, \quad c=-9\)

    Écrivez le discriminant.

    \(b^{2}-4 a c\)

    Remplacez par les valeurs de\(a, b\), et\(c\).

    \((7)^{2}-4 \cdot 3 \cdot(-9)\)

    Simplifiez.

    \(49+108\)
    \(157\)

    Comme le discriminant est positif, il existe de\(2\) véritables solutions à l'équation.

    b.

    \(5 n^{2}+n+4=0\)

    L'équation est sous forme standard\(a, b\), identifiez et\(c\).

    \(a=5, \quad b=1, \quad c=4\)

    Écrivez le discriminant.

    \(b^{2}-4 a c\)

    Remplacez par les valeurs de\(a, b\), et\(c\).

    \((1)^{2}-4 \cdot 5 \cdot 4\)

    Simplifiez.

    \(1-80\)
    \(-79\)

    Comme le discriminant est négatif, il existe des solutions\(2\) complexes à l'équation.

    c.

    \(9 y^{2}-6 y+1=0\)

    L'équation est sous forme standard\(a, b\), identifiez et\(c\).

    \(a=9, \quad b=-6, \quad c=1\)

    Écrivez le discriminant.

    \(b^{2}-4 a c\)

    Remplacez par les valeurs de\(a, b\), et\(c\).

    \((-6)^{2}-4 \cdot 9 \cdot 1\)

    Simplifiez.

    \(36-36\)
    \(0\)

    Puisque le discriminant est\(0\), il existe une\(1\) vraie solution à l'équation.

    Exercice\(\PageIndex{15}\)

    Déterminez le nombre et le type de solutions pour chaque équation quadratique.

    1. \(8 m^{2}-3 m+6=0\)
    2. \(5 z^{2}+6 z-2=0\)
    3. \(9 w^{2}+24 w+16=0\)
    Réponse
    1. \(2\)solutions complexes
    2. \(2\)solutions réelles
    3. \(1\)solution réelle
    Exercice\(\PageIndex{16}\)

    Déterminez le nombre et le type de solutions pour chaque équation quadratique.

    1. \(b^{2}+7 b-13=0\)
    2. \(5 a^{2}-6 a+10=0\)
    3. \(4 r^{2}-20 r+25=0\)
    Réponse
    1. \(2\)solutions réelles
    2. \(2\)solutions complexes
    3. \(1\)solution réelle

    Identifier la méthode la plus appropriée à utiliser pour résoudre une équation quadratique

    Nous résumons ci-dessous les quatre méthodes que nous avons utilisées pour résoudre des équations quadratiques.

    Méthodes de résolution d'équations quadratiques

    1. Affacturage
    2. Propriété Square Root
    3. Compléter le carré
    4. Formule quadratique

    Étant donné que nous avons quatre méthodes à utiliser pour résoudre une équation quadratique, comment décidez-vous laquelle utiliser ? L'affacturage est souvent la méthode la plus rapide et nous l'essayons donc en premier. Si l'équation est\(ax^{2}=k\) ou si\(a(x−h)^{2}=k\) nous utilisons la propriété Square Root. Pour toute autre équation, il est probablement préférable d'utiliser la formule quadratique. N'oubliez pas que vous pouvez résoudre n'importe quelle équation quadratique en utilisant la formule quadratique, mais ce n'est pas toujours la méthode la plus simple.

    Qu'en est-il de la méthode de complétion du carré ? La plupart des gens trouvent cette méthode encombrante et préfèrent ne pas l'utiliser. Nous avons dû l'inclure dans la liste des méthodes parce que nous avons complété le carré en général pour obtenir la formule quadratique. Vous utiliserez également le processus de complétion du carré dans d'autres domaines de l'algèbre.

    Identifier la méthode la plus appropriée pour résoudre une équation quadratique

    1. Essayez d'abord le factoring. Si le quadratique prend facilement en compte, cette méthode est très rapide.
    2. Essayez ensuite la propriété Square Root. Si l'équation correspond à la forme\(ax^{2}=k\) ou\(a(x−h)^{2}=k\), elle peut être facilement résolue à l'aide de la propriété Square Root.
    3. Utilisez la formule quadratique. Toute autre équation quadratique est mieux résolue en utilisant la formule quadratique.

    L'exemple suivant utilise cette stratégie pour décider comment résoudre chaque équation quadratique.

    Exemple\(\PageIndex{9}\)

    Déterminez la méthode la plus appropriée à utiliser pour résoudre chaque équation quadratique.

    1. \(5 z^{2}=17\)
    2. \(4 x^{2}-12 x+9=0\)
    3. \(8 u^{2}+6 u=11\)

    Solution :

    un.

    \(5z^{2}=17\)

    Comme l'équation se trouve dans le\(ax^{2}=k\), la méthode la plus appropriée consiste à utiliser la propriété Square Root.

    b.

    \(4 x^{2}-12 x+9=0\)

    Nous reconnaissons que le côté gauche de l'équation est un trinôme carré parfait et que la factorisation sera donc la méthode la plus appropriée.

    c.

    \(8 u^{2}+6 u=11\)

    Mettez l'équation sous forme standard.

    \(8 u^{2}+6 u-11=0\)

    Bien que notre première idée soit d'essayer l'affacturage, le fait de réfléchir à toutes les possibilités de méthode par essais et erreurs nous amène à choisir la formule quadratique comme méthode la plus appropriée.

    Exercice\(\PageIndex{17}\)

    Déterminez la méthode la plus appropriée à utiliser pour résoudre chaque équation quadratique.

    1. \(x^{2}+6 x+8=0\)
    2. \((n-3)^{2}=16\)
    3. \(5 p^{2}-6 p=9\)
    Réponse
    1. Affacturage
    2. Propriété Square Root
    3. Formule quadratique
    Exercice\(\PageIndex{18}\)

    Déterminez la méthode la plus appropriée à utiliser pour résoudre chaque équation quadratique.

    1. \(8 a^{2}+3 a-9=0\)
    2. \(4 b^{2}+4 b+1=0\)
    3. \(5 c^{2}=125\)
    Réponse
    1. Formule quadratique
    2. Affacturage ou propriété à racine carrée
    3. Propriété Square Root

    Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à utiliser la formule quadratique.

    Concepts clés

    • Formule quadratique
      • Les solutions à une équation quadratique de la forme\(a x^{2}+b x+c=0, a \neq 0\) sont données par la formule :

        \(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)

    • Comment résoudre une équation quadratique à l'aide de la formule quadratique.
      1. Écrivez l'équation quadratique sous forme standard,\(a x^{2}+b x+c=0\). Identifiez les valeurs de\(a, b, c\).
      2. Écrivez la formule quadratique. Remplacez ensuite les valeurs de\(a, b, c\).
      3. Simplifiez.
      4. Vérifiez les solutions.
    • Utilisation du discriminant\(b^{2}-4 a c\), pour déterminer le nombre et le type de solutions d'une équation quadratique
      • Pour une équation quadratique de la forme\(a x^{2}+b x+c=0, a \neq 0\),
        • Si\(b^{2}-4 a c>0\), l'équation a de\(2\) vraies solutions.
        • Si\(b^{2}-4 a c=0\), l'équation a une\(1\) vraie solution.
        • Si\(b^{2}-4 a c<0\), l'équation comporte des solutions\(2\) complexes.
    • Méthodes pour résoudre des équations quadratiques :
      • Affacturage
      • Propriété Square Root
      • Compléter le carré
      • Formule quadratique
    • Comment identifier la méthode la plus appropriée pour résoudre une équation quadratique.
      1. Essayez d'abord le factoring. Si le quadratique prend facilement en compte, cette méthode est très rapide.
      2. Essayez ensuite la propriété Square Root. Si l'équation correspond à la forme\(a x^{2}=k\) ou\(a(x-h)^{2}=k\), elle peut être facilement résolue à l'aide de la propriété Square Root.
      3. Utilisez la formule quadratique. Toute autre équation quadratique est mieux résolue en utilisant la formule quadratique.

    Lexique

    discriminant
    Dans la formule quadratique\(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\), la quantité\(b^{2}-4 a c\) est appelée discriminant.