9.2 : Résoudre des équations quadratiques en utilisant la propriété de racine carrée
- Page ID
- 194330
À la fin de cette section, vous serez en mesure de :
- Résolvez les équations quadratiques du formulaire\(ax^{2}=k\) à l'aide de la propriété Square Root
- Résolvez les équations quadratiques du formulaire\(a(x–h)^{2}=k\) à l'aide de la propriété Square Root
Avant de commencer, répondez à ce questionnaire de préparation.
- Simplifiez :\(\sqrt{128}\).
Si vous avez oublié ce problème, consultez l'exemple 8.13. - Simplifiez :\(\sqrt{\frac{32}{5}}\).
Si vous avez oublié ce problème, consultez l'exemple 8.50. - Facteur :\(9 x^{2}-12 x+4\).
Si vous avez oublié ce problème, consultez l'exemple 6.23.
Une équation quadratique est une équation de la forme\(a x^{2}+b x+c=0\), où\(a≠0\). Les équations quadratiques diffèrent des équations linéaires en incluant un terme quadratique avec la variable portée à la deuxième puissance de la forme\(ax^{2}\). Nous utilisons des méthodes différentes pour résoudre des équations quadratiques que des équations linéaires, car le simple fait d'ajouter, de soustraire, de multiplier et de diviser des termes n'isolera pas la variable.
Nous avons vu que certaines équations quadratiques peuvent être résolues par factorisation. Dans ce chapitre, nous allons apprendre trois autres méthodes à utiliser dans le cas où une équation quadratique ne peut pas être factorisée.
Résolvez les équations quadratiques du formulaire\(ax^{2}=k\) à l'aide de la propriété Square Root
Nous avons déjà résolu certaines équations quadratiques par factorisation. Voyons comment nous avons utilisé la factorisation pour résoudre l'équation quadratique\(x^{2}=9\).
\(x^{2}=9\)
Mettez l'équation sous forme standard.
\(x^{2}-9=0\)
Facturez la différence entre les carrés.
\((x-3)(x+3)=0\)
Utilisez la propriété Zero Produce.
\(x-3=0 \quad x-3=0\)
Résolvez chaque équation.
\(x=3 \quad x=-3\)
Nous pouvons facilement utiliser la factorisation pour trouver les solutions d'équations similaires, comme\(x^{2}=16\) et\(x^{2}=25\) parce que\(16\) et\(25\) sont des carrés parfaits. Dans chaque cas, nous aurions deux solutions,\(x=4, x=-4\) et\(x=5, x=-5\)
Mais que se passe-t-il lorsque nous avons une équation comme celle-ci\(x^{2}=7\) ? Comme\(7\) il ne s'agit pas d'un carré parfait, nous ne pouvons pas résoudre l'équation par factorisation.
Auparavant, nous avons appris que puisque\(169\) est le carré de\(13\), on peut aussi dire que\(13\) c'est une racine carrée de\(169\). En outre\((-13)^{2}=169\), il en\(−13\) va de même pour la racine carrée de\(169\). Par conséquent, les deux\(13\) et\(−13\) sont des racines carrées de\(169\). Ainsi, chaque nombre positif a deux racines carrées : une positive et une négative. Nous avons précédemment défini la racine carrée d'un nombre de la manière suivante :
Si\(n^{2}=m\), alors\(n\) est une racine carrée de\(m\).
Comme ces équations sont toutes de la forme\(x^{2}=k\), la définition de la racine carrée nous indique que les solutions sont les deux racines carrées de\(k\). Cela mène à la propriété Square Root.
Propriété Square Root
Si\(x^{2}=k\), alors
\(x=\sqrt{k} \quad\)ou\(\quad x=-\sqrt{k} \quad\) ou\(\quad x=\pm \sqrt{k}\)
Notez que la propriété Square Root donne deux solutions à une équation de la forme\(x^{2}=k\), la racine carrée principale de\(k\) et son opposé. Nous pourrions également écrire la solution sous la forme\(x=\pm \sqrt{k}\). Nous lisons cela comme étant\(x\) égal, positif ou négatif, à la racine carrée de\(k\).
Nous allons maintenant résoudre\(x^{2}=9\) à nouveau l'équation, cette fois en utilisant la propriété Square Root.
\(\begin{aligned} &x^{2} =9 \\ \text { Use the Square Root Property. } \quad& x=\pm \sqrt{9} \\& x =\pm 3 \end{aligned}\)
Donc\(x=3\) ou\(x=-3\)
Que se passe-t-il lorsque la constante n'est pas un carré parfait ? Utilisons la propriété Square Root pour résoudre l'équation\(x^{2}=7\).
\(x^{2}=7\)
Utilisez la propriété Square Root. \(x=\sqrt{7}, \quad x=-\sqrt{7}\)
Nous ne pouvons pas simplifier\(\sqrt{7}\), nous laissons donc la réponse radicale.
Résoudre :\(x^{2}-50=0\).
Solution :
| Étape 1 : Isolez le terme quadratique et faites de son coefficient un. | Ajoutez\(50\) des deux côtés pour vous\(x^{2}\) débrouiller tout seul. | \(\begin{aligned} x^{2}-50 &=0 \\ x^{2} &=50 \end{aligned}\) |
| Étape 2 : Utilisez la propriété Square Root. | N'oubliez pas d'écrire le\(\pm\) symbole. | \(x=\pm \sqrt{50}\) |
| Étape 3 : Simplifiez le radical. | Réécrivez pour afficher deux solutions. | \(\begin{array}{l}{x=\pm \sqrt{25} \cdot \sqrt{2}} \\ {x=\pm 5 \sqrt{2}} \\ {}x=5\sqrt{2}, \:x=-5\sqrt{2}\end{array}\) |
| Étape 4 : Vérifiez les solutions. | Substituer par\(x=5 \sqrt{2}\) et\(x=-5 \sqrt{2}\) |
\(\begin{array}{r}{x^{2}-50=0} \\ {(\color{red}{5 \sqrt{2}}\color{black}{)}^{2}-50 \stackrel{?}{=} 0} \\ {25 \cdot 2-50 \stackrel{?}{=} 0} \\ {0=0}\end{array}\) \(\begin{array}{r}{x^{2}-50=0} \\ {(\color{red}{-5 \sqrt{2}}\color{black}{)}^{2}-50 \stackrel{?}{=} 0} \\ {25 \cdot 2-50 \stackrel{?}{=} 0} \\ {0=0}\end{array}\) |
Résoudre :\(x^{2}-48=0\).
- Réponse
-
\(x=4 \sqrt{3}, x=-4 \sqrt{3}\)
Résoudre :\(y^{2}-27=0\).
- Réponse
-
\(y=3 \sqrt{3}, y=-3 \sqrt{3}\)
Les étapes à suivre pour utiliser la propriété Square Root pour résoudre une équation quadratique sont répertoriées ici.
Résoudre une équation quadratique à l'aide de la propriété de racine carrée
- Isolez le terme quadratique et faites de son coefficient un.
- Utilisez la propriété Square Root.
- Simplifiez le radical.
- Vérifiez les solutions.
Pour utiliser la propriété Square Root, le coefficient du terme variable doit être égal à un. Dans l'exemple suivant, nous devons diviser les deux côtés de l'équation par le coefficient\(3\) avant d'utiliser la propriété Square Root.
Résoudre :\(3 z^{2}=108\).
Solution :
| \(3 z^{2}=108\) | |
| Le terme quadratique est isolé. Divisez par\(3\) pour obtenir son coefficient\(1\). | \(\frac{3 z^{2}}{3}=\frac{108}{3}\) |
| Simplifiez. | \(z^{2}=36\) |
| Utilisez la propriété Square Root. | \(z=\pm \sqrt{36}\) |
| Simplifiez le radical. | \(z=\pm 6\) |
| Réécrivez pour afficher deux solutions. | \(z=6, \quad z=-6\) |
|
Vérifiez les solutions : 
|
Résoudre :\(2x^{2}=98\).
- Réponse
-
\(x=7, x=-7\)
Résoudre :\(5m^{2}=80\).
- Réponse
-
\(m=4, m=-4\)
La propriété Square Root indique « Si »\(x^{2}=k\), que se passera-t-il si\(k<0\) ? Ce sera le cas dans l'exemple suivant.
Résoudre :\(x^{2}+72=0\).
Solution :
| \(x^{2}+72=0\) | |
| Isolez le terme quadratique. | \(x^{2}=-72\) |
| Utilisez la propriété Square Root. | \(x=\pm \sqrt{-72}\) |
| Simplifiez l'utilisation de nombres complexes | \(x=\pm \sqrt{72} i\) |
| Simplifiez le radical. | \(x=\pm 6 \sqrt{2} i\) |
| Réécrivez pour montrer deux solutions | \(x=6 \sqrt{2} i, x=-6 \sqrt{2} i\) |
|
Vérifiez les solutions : 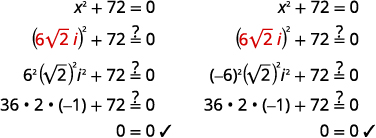
|
Résoudre :\(c^{2}+12=0\).
- Réponse
-
\(c=2 \sqrt{3} i, \quad c=-2 \sqrt{3} i\)
Résoudre :\(q^{2}+24=0\).
- Réponse
-
\(c=2 \sqrt{6} i, \quad c=-2 \sqrt{6} i\)
Notre méthode fonctionne également lorsque des fractions apparaissent dans l'équation, nous résolvons comme n'importe quelle équation avec des fractions. Dans l'exemple suivant, nous isolons d'abord le terme quadratique, puis nous rendons le coefficient égal à un.
Résoudre :\(\frac{2}{3} u^{2}+5=17\).
Solution :
| \(\frac{2}{3} u^{2}+5=17\) | |
| Isolez le terme quadratique. | 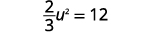 |
| Multipliez par\(\frac{3}{2}\) pour obtenir le coefficient\(1\). | 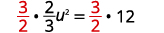 |
| Simplifiez. | 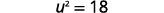 |
| Utilisez la propriété Square Root. | 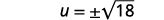 |
| Simplifiez le radical. | 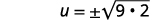 |
| Simplifiez. | 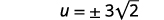 |
| Réécrivez pour afficher deux solutions. |  |
|
Vérifiez : 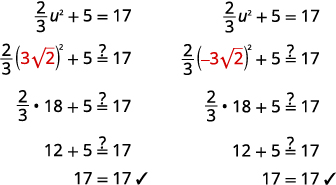
|
Résoudre :\(\frac{1}{2} x^{2}+4=24\).
- Réponse
-
\(x=2 \sqrt{10}, x=-2 \sqrt{10}\)
Résoudre :\(\frac{3}{4} y^{2}-3=18\).
- Réponse
-
\(y=2 \sqrt{7}, y=-2 \sqrt{7}\)
Les solutions de certaines équations peuvent avoir des fractions à l'intérieur des radicaux. Lorsque cela se produit, nous devons rationaliser le dénominateur.
Résoudre :\(2 x^{2}-8=41\).
Solution :
 |
|
| Isolez le terme quadratique. |  |
| Divisez par\(2\) pour obtenir le coefficient\(1\). | 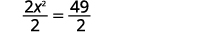 |
| Simplifiez. | 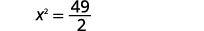 |
| Utilisez la propriété Square Root. | 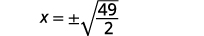 |
| Réécrivez le radical sous la forme d'une fraction de racines carrées. | 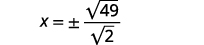 |
| Rationalisez le dénominateur. | 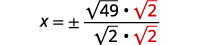 |
| Simplifiez. | 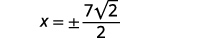 |
| Réécrivez pour afficher deux solutions. | 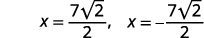 |
|
Vérifiez : Nous vous laissons le chèque. |
Résoudre :\(5 r^{2}-2=34\).
- Réponse
-
\(r=\frac{6 \sqrt{5}}{5}, \quad r=-\frac{6 \sqrt{5}}{5}\)
Résoudre :\(3 t^{2}+6=70\).
- Réponse
-
\(t=\frac{8 \sqrt{3}}{3}, \quad t=-\frac{8 \sqrt{3}}{3}\)
Résolvez l'équation quadratique de la forme\(a(x-h)^{2}=k\) à l'aide de la propriété de racine carrée
Nous pouvons également utiliser la propriété Square Root pour résoudre une équation de la\(a(x-h)^{2}=k\) forme. Notez que le terme quadratique,\(x\), dans sa forme originale\(ax^{2}=k\) est remplacé par\((x-h)\).
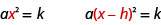
La première étape, comme précédemment, consiste à isoler le terme dont la variable est au carré. Dans ce cas, un binôme est mis au carré. Une fois que le binôme est isolé, en divisant chaque côté par le coefficient de\(a\), la propriété de racine carrée peut être utilisée sur\((x-h)^{2}\).
Résoudre :\(4(y-7)^{2}=48\).
Solution :
| \(4(y-7)^{2}=48\) | |
| Divisez les deux côtés par le coefficient\(4\). | \((y-7)^{2}=12\) |
| Utilisez la propriété Square Root sur le binôme. | \(y-7=\pm \sqrt{12}\) |
| Simplifiez le radical. | \(y-7=\pm 2 \sqrt{3}\) |
| Résolvez pour\(y\). | \(y=7 \pm 2 \sqrt{3}\) |
| Réécrivez pour afficher deux solutions. | \(y=7+2 \sqrt{3}\) \(y=7-2 \sqrt{3}\) |
|
Vérifiez : 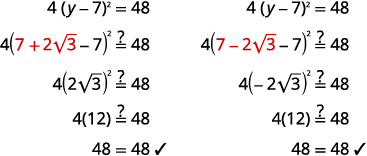
|
Résoudre :\(3(a-3)^{2}=54\).
- Réponse
-
\(a=3+3 \sqrt{2}, \quad a=3-3 \sqrt{2}\)
Résoudre :\(2(b+2)^{2}=80\).
- Réponse
-
\(b=-2+2 \sqrt{10}, \quad b=-2-2 \sqrt{10}\)
N'oubliez pas que lorsque nous prenons la racine carrée d'une fraction, nous pouvons prendre la racine carrée du numérateur et du dénominateur séparément.
Résoudre :\(\left(x-\frac{1}{3}\right)^{2}=\frac{5}{9}\).
Solution :
\(\left(x-\frac{1}{3}\right)^{2}=\frac{5}{9}\)
Utilisez la propriété Square Root.
\(x-\frac{1}{3}=\pm \sqrt{\frac{5}{9}}\)
Réécrivez le radical sous la forme d'une fraction de racines carrées.
\(x-\frac{1}{3}=\pm \frac{\sqrt{5}}{\sqrt{9}}\)
Simplifiez le radical.
\(x-\frac{1}{3}=\pm \frac{\sqrt{5}}{3}\)
Résolvez pour\(x\).
\(x=\frac{1}{3} \pm \frac{\sqrt{5}}{3}\)
Réécrivez pour afficher deux solutions.
\(x=\frac{1}{3}+\frac{\sqrt{5}}{3}, x=\frac{1}{3}-\frac{\sqrt{5}}{3}\)
Vérifiez :
Nous vous laissons le chèque.
Résoudre :\(\left(x-\frac{1}{2}\right)^{2}=\frac{5}{4}\).
- Réponse
-
\(x=\frac{1}{2}+\frac{\sqrt{5}}{2}, x=\frac{1}{2}-\frac{\sqrt{5}}{2}\)
Résoudre :\(\left(y+\frac{3}{4}\right)^{2}=\frac{7}{16}\).
- Réponse
-
\(y=-\frac{3}{4}+\frac{\sqrt{7}}{4}, y=-\frac{3}{4}-\frac{\sqrt{7}}{4}\)
Nous allons commencer la solution à l'exemple suivant en isolant le terme binomial.
Résoudre :\(2(x-2)^{2}+3=57\).
Solution :
\(2(x-2)^{2}+3=57\)
Soustrayez\(3\) des deux côtés pour isoler le terme binomial.
\(2(x-2)^{2}=54\)
Divisez les deux côtés par\(2\).
\((x-2)^{2}=27\)
Utilisez la propriété Square Root.
\(x-2=\pm \sqrt{27}\)
Simplifiez le radical.
\(x-2=\pm 3 \sqrt{3}\)
Résolvez pour\(x\).
\(x=2 \pm 3 \sqrt{3}\)
Réécrivez pour afficher deux solutions.
\(x=2+3 \sqrt{3}, x=2-3 \sqrt{3}\)
Vérifiez :
Nous vous laissons le chèque.
Résoudre :\(5(a-5)^{2}+4=104\).
- Réponse
-
\(a=5+2 \sqrt{5}, a=5-2 \sqrt{5}\)
Résoudre :\(3(b+3)^{2}-8=88\).
- Réponse
-
\(b=-3+4 \sqrt{2}, \quad b=-3-4 \sqrt{2}\)
Parfois, les solutions sont des nombres complexes.
Résoudre :\((2 x-3)^{2}=-12\).
Solution :
\((2 x-3)^{2}=-12\)
Utilisez la propriété Square Root.
\(2 x-3=\pm \sqrt{-12}\)
Simplifiez le radical.
\(2 x-3=\pm 2 \sqrt{3} i\)
Ajouter\(3\) des deux côtés.
\(2 x=3 \pm 2 \sqrt{3} i\)
Divisez les deux côtés par\(2\).
\(x=\frac{3 \pm 2 \sqrt{3 i}}{2}\)
Réécrivez sous forme standard.
\(x=\frac{3}{2} \pm \frac{2 \sqrt{3} i}{2}\)
Simplifiez.
\(x=\frac{3}{2} \pm \sqrt{3} i\)
Réécrivez pour afficher deux solutions.
\(x=\frac{3}{2}+\sqrt{3} i, x=\frac{3}{2}-\sqrt{3} i\)
Vérifiez :
Nous vous laissons le chèque.
Résoudre :\((3 r+4)^{2}=-8\).
- Réponse
-
\(r=-\frac{4}{3}+\frac{2 \sqrt{2} i}{3}, r=-\frac{4}{3}-\frac{2 \sqrt{2} i}{3}\)
Résoudre :\((2 t-8)^{2}=-10\).
- Réponse
-
\(t=4+\frac{\sqrt{10} i}{2}, t=4-\frac{\sqrt{10 i}}{2}\)
Les côtés gauches des équations des deux exemples suivants ne semblent pas être de la même forme\(a(x-h)^{2}\). Mais ce sont des trinômes carrés parfaits, nous allons donc les prendre en compte pour les mettre dans la forme dont nous avons besoin.
Résoudre :\(4 n^{2}+4 n+1=16\).
Solution :
Nous remarquons que le côté gauche de l'équation est un trinôme carré parfait. Nous allons d'abord en tenir compte.
| \(4 n^{2}+4 n+1=16\) | |
| Choisissez le trinôme carré parfait. | \((2 n+1)^{2}=16\) |
| Utilisez la propriété Square Root. | \(2 n+1=\pm \sqrt{16}\) |
| Simplifiez le radical. | \(2 n+1=\pm 4\) |
| Résolvez pour\(n\). | \(2 n=-1 \pm 4\) |
| Divisez chaque côté par\(2\). | \(\begin{aligned} \frac{2 n}{2} &=\frac{-1 \pm 4}{2} \\ n &=\frac{-1 \pm 4}{2} \end{aligned}\) |
| Réécrivez pour afficher deux solutions. | \(n=\frac{-1+4}{2}, n=\frac{-1-4}{2}\) |
| Simplifiez chaque équation. | \(n=\frac{3}{2}, \quad n=-\frac{5}{2}\) |
|
Vérifiez : 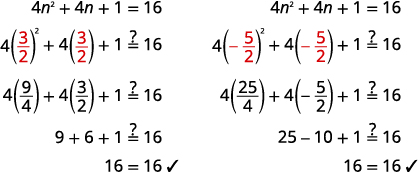
|
Résoudre :\(9 m^{2}-12 m+4=25\).
- Réponse
-
\(m=\frac{7}{3}, \quad m=-1\)
Résoudre :\(16 n^{2}+40 n+25=4\).
- Réponse
-
\(n=-\frac{3}{4}, \quad n=-\frac{7}{4}\)
Accédez à cette ressource en ligne pour obtenir des instructions supplémentaires et vous entraîner à utiliser la propriété Square Root pour résoudre des équations quadratiques.
Concepts clés
- Propriété Square Root
- Si\(x^{2}=k\), alors\(x=\sqrt{k}\) ou\(x=-\sqrt{k}\) ou\(x=\pm \sqrt{k}\)
- Isolez le terme quadratique et faites de son coefficient un.
- Utilisez la propriété Square Root.
- Simplifiez le radical.
- Vérifiez les solutions.


