Skip to main content
Global

Chapitre 8 Exercices de révision

  1. Last updated
  2. Save as PDF
  • Page ID
    194317

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Exercices de révision des

    Simplifiez les expressions grâce aux

    Exercice\(\PageIndex{1}\) Simplify Expressions with Roots

    Dans les exercices suivants, simplifiez.

      1. \(\sqrt{225}\)
      2. \(-\sqrt{16}\)
      1. \(-\sqrt{169}\)
      2. \(\sqrt{-8}\)
      1. \(\sqrt[3]{8}\)
      2. \(\sqrt[4]{81}\)
      3. \(\sqrt[5]{243}\)
      1. \(\sqrt[3]{-512}\)
      2. \(\sqrt[4]{-81}\)
      3. \(\sqrt[5]{-1}\)
    Réponse

    1.

    1. \(15\)
    2. \(-4\)

    3.

    1. \(2\)
    2. \(3\)
    3. \(3\)
    Exercice\(\PageIndex{2}\) Estimate and Approximate Roots

    Dans les exercices suivants, estimez chaque racine entre deux nombres entiers consécutifs.

      1. \(\sqrt{68}\)
      2. \(\sqrt[3]{84}\)
    Réponse

    1.

    1. \(8<\sqrt{68}<9\)
    2. \(4<\sqrt[3]{84}<5\)
    Exercice\(\PageIndex{3}\) Estimate and Approximate Roots

    Dans les exercices suivants, approximez chaque racine et arrondissez à deux décimales.

      1. \(\sqrt{37}\)
      2. \(\sqrt[3]{84}\)
      3. \(\sqrt[4]{125}\)
    Réponse

    1. Résolvez vous-même

    Exercice\(\PageIndex{4}\) Simplify Variable Expressions with Roots

    Dans les exercices suivants, simplifiez l'utilisation de valeurs absolues si nécessaire.

      1. \(\sqrt[3]{a^{3}}\)
      2. \(\sqrt[7]{b^{7}}\)
      1. \(\sqrt{a^{14}}\)
      2. \(\sqrt{w^{24}}\)
      1. \(\sqrt[4]{m^{8}}\)
      2. \(\sqrt[5]{n^{20}}\)
      1. \(\sqrt{121 m^{20}}\)
      2. \(-\sqrt{64 a^{2}}\)
      1. \(\sqrt[3]{216 a^{6}}\)
      2. \(\sqrt[5]{32 b^{20}}\)
      1. \(\sqrt{144 x^{2} y^{2}}\)
      2. \(\sqrt{169 w^{8} y^{10}}\)
      3. \(\sqrt[3]{8 a^{51} b^{6}}\)
    Réponse

    1.

    1. \(a\)
    2. \(|b|\)

    3.

    1. \(m^{2}\)
    2. \(n^{4}\)

    5.

    1. \(6a^{2}\)
    2. \(2b^{4}\)

    Simplifier les expressions

    Exercice\(\PageIndex{5}\) Use the Product Property to Simplify Radical Expressions

    Dans les exercices suivants, utilisez la propriété Product pour simplifier les expressions radicales.

    1. \(\sqrt{125}\)
    2. \(\sqrt{675}\)
      1. \(\sqrt[3]{625}\)
      2. \(\sqrt[6]{128}\)
    Réponse

    1. \(5\sqrt{5}\)

    3.

    1. \(5 \sqrt[3]{5}\)
    2. \(2 \sqrt[6]{2}\)
    Exercice\(\PageIndex{6}\) Use the Product Property to Simplify Radical Expressions

    Dans les exercices suivants, simplifiez l'utilisation des signes de valeur absolue selon vos besoins.

      1. \(\sqrt{a^{23}}\)
      2. \(\sqrt[3]{b^{8}}\)
      3. \(\sqrt[8]{c^{13}}\)
      1. \(\sqrt{80 s^{15}}\)
      2. \(\sqrt[5]{96 a^{7}}\)
      3. \(\sqrt[6]{128 b^{7}}\)
      1. \(\sqrt{96 r^{3} s^{3}}\)
      2. \(\sqrt[3]{80 x^{7} y^{6}}\)
      3. \(\sqrt[4]{80 x^{8} y^{9}}\)
      1. \(\sqrt[5]{-32}\)
      2. \(\sqrt[8]{-1}\)
      1. \(8+\sqrt{96}\)
      2. \(\frac{2+\sqrt{40}}{2}\)
    Réponse

    2.

    1. \(4\left|s^{7}\right| \sqrt{5 s}\)
    2. \(2 a \sqrt[5]{3 a^{2}}\)
    3. \(2|b| \sqrt[6]{2 b}\)

    4.

    1. \(-2\)
    2. pas réel
    Exercice\(\PageIndex{7}\) Use the Quotient Property to Simplify Radical Expressions

    Dans les exercices suivants, utilisez la propriété Quotient pour simplifier les racines carrées.

      1. \(\sqrt{\frac{72}{98}}\)
      2. \(\sqrt[3]{\frac{24}{81}}\)
      3. \(\sqrt[4]{\frac{6}{96}}\)
      1. \(\sqrt{\frac{y^{4}}{y^{8}}}\)
      2. \(\sqrt[5]{\frac{u^{21}}{u^{11}}}\)
      3. \(\sqrt[6]{\frac{v^{30}}{v^{12}}}\)
    3. \(\sqrt{\frac{300 m^{5}}{64}}\)
      1. \(\sqrt{\frac{28 p^{7}}{q^{2}}}\)
      2. \(\sqrt[3]{\frac{81 s^{8}}{t^{3}}}\)
      3. \(\sqrt[4]{\frac{64 p^{15}}{q^{12}}}\)
      1. \(\sqrt{\frac{27 p^{2} q}{108 p^{4} q^{3}}}\)
      2. \(\sqrt[3]{\frac{16 c^{5} d^{7}}{250 c^{2} d^{2}}}\)
      3. \(\sqrt[6]{\frac{2 m^{9} n^{7}}{128 m^{3} n}}\)
      1. \(\frac{\sqrt{80 q^{5}}}{\sqrt{5 q}}\)
      2. \(\frac{\sqrt[3]{-625}}{\sqrt[3]{5}}\)
      3. \(\frac{\sqrt[4]{80 m^{7}}}{\sqrt[4]{5 m}}\)
    Réponse

    1.

    1. \(\frac{6}{7}\)
    2. \(\frac{2}{3}\)
    3. \(\frac{1}{2}\)

    3. \(\frac{10 m^{2} \sqrt{3 m}}{8}\)

    5.

    1. \(\frac{1}{2|p q|}\)
    2. \(\frac{2 c d \sqrt[5]{2 d^{2}}}{5}\)
    3. \(\frac{|m n| \sqrt[6]{2}}{2}\)

    Simplifier les exposants rati

    Exercice\(\PageIndex{8}\) Simplify Expressions with \(a^{\frac{1}{n}}\)

    Dans les exercices suivants, écrivez comme une expression radicale.

      1. \(r^{\frac{1}{2}}\)
      2. \(s^{\frac{1}{3}}\)
      3. \(t^{\frac{1}{4}}\)
    Réponse

    1.

    1. \(\sqrt{r}\)
    2. \(\sqrt[3]{s}\)
    3. \(\sqrt[4]{t}\)
    Exercice\(\PageIndex{9}\) Simplify Expressions with \(a^{\frac{1}{n}}\)

    Dans les exercices suivants, écrivez avec un exposant rationnel.

      1. \(\sqrt{21p}\)
      2. \(\sqrt[4]{8q}\)
      3. \(4\sqrt[6]{36r}\)
    Réponse

    1. Résolvez vous-même

    Exercice\(\PageIndex{10}\) Simplify Expressions with \(a^{\frac{1}{n}}\)

    Dans les exercices suivants, simplifiez.

      1. \(625^{\frac{1}{4}}\)
      2. \(243^{\frac{1}{5}}\)
      3. \(32^{\frac{1}{5}}\)
      1. \((-1,000)^{\frac{1}{3}}\)
      2. \(-1,000^{\frac{1}{3}}\)
      3. \((1,000)^{-\frac{1}{3}}\)
      1. \((-32)^{\frac{1}{5}}\)
      2. \((243)^{-\frac{1}{5}}\)
      3. \(-125^{\frac{1}{3}}\)
    Réponse

    1.

    1. \(5\)
    2. \(3\)
    3. \(2\)

    3.

    1. \(-2\)
    2. \(\frac{1}{3}\)
    3. \(-5\)
    Exercice\(\PageIndex{11}\) Simplify Expressions with \(a^{\frac{m}{n}}\)

    Dans les exercices suivants, écrivez avec un exposant rationnel.

      1. \(\sqrt[4]{r^{7}}\)
      2. \((\sqrt[5]{2 p q})^{3}\)
      3. \(\sqrt[4]{\left(\frac{12 m}{7 n}\right)^{3}}\)
    Réponse

    1. Résolvez vous-même

    Exercice\(\PageIndex{12}\) Simplify Expressions with \(a^{\frac{m}{n}}\)

    Dans les exercices suivants, simplifiez.

      1. \(25^{\frac{3}{2}}\)
      2. \(9^{-\frac{3}{2}}\)
      3. \((-64)^{\frac{2}{3}}\)
      1. \(-64^{\frac{3}{2}}\)
      2. \(-64^{-\frac{3}{2}}\)
      3. \((-64)^{\frac{3}{2}}\)
    Réponse

    1.

    1. \(125\)
    2. \(\frac{1}{27}\)
    3. \(16\)
    Exercice\(\PageIndex{13}\) Use the Laws of Exponents to Simplify Expressions with Rational Exponents

    Dans les exercices suivants, simplifiez.

      1. \(6^{\frac{5}{2}} \cdot 6^{\frac{1}{2}}\)
      2. \(\left(b^{15}\right)^{\frac{3}{5}}\)
      3. \(\frac{w^{\frac{2}{7}}}{w^{\frac{9}{7}}}\)
      1. \(\frac{a^{\frac{3}{4}} \cdot a^{-\frac{1}{4}}}{a^{-\frac{10}{4}}}\)
      2. \(\left(\frac{27 b^{\frac{2}{3}} c^{-\frac{5}{2}}}{b^{-\frac{7}{3}} c^{\frac{1}{2}}}\right)^{\frac{1}{3}}\)
    Réponse

    1.

    1. \(6^{3}\)
    2. \(b^{9}\)
    3. \(\frac{1}{w}\)

    Ajouter, soustraire et multiplier des expressions radicales

    Exercice\(\PageIndex{14}\) add and Subtract Radical Expressions

    Dans les exercices suivants, simplifiez.

      1. \(7 \sqrt{2}-3 \sqrt{2}\)
      2. \(7 \sqrt[3]{p}+2 \sqrt[3]{p}\)
      3. \(5 \sqrt[3]{x}-3 \sqrt[3]{x}\)
      1. \(\sqrt{11 b}-5 \sqrt{11 b}+3 \sqrt{11 b}\)
      2. \(8 \sqrt[4]{11 c d}+5 \sqrt[4]{11 c d}-9 \sqrt[4]{11 c d}\)
      1. \(\sqrt{48}+\sqrt{27}\)
      2. \(\sqrt[3]{54}+\sqrt[3]{128}\)
      3. \(6 \sqrt[4]{5}-\frac{3}{2} \sqrt[4]{320}\)
      1. \(\sqrt{80 c^{7}}-\sqrt{20 c^{7}}\)
      2. \(2 \sqrt[4]{162 r^{10}}+4 \sqrt[4]{32 r^{10}}\)
    5. \(3 \sqrt{75 y^{2}}+8 y \sqrt{48}-\sqrt{300 y^{2}}\)
    Réponse

    1.

    1. \(4\sqrt{2}\)
    2. \(9\sqrt[3]{p}\)
    3. \(2\sqrt[3]{x}\)

    3.

    1. \(7\sqrt{3}\)
    2. \(7\sqrt[3]{2}\)
    3. \(3\sqrt[4]{5}\)

    5. \(37 y \sqrt{3}\)

    Exercice\(\PageIndex{15}\) Multiply Radical Expressions

    Dans les exercices suivants, simplifiez.

      1. \((5 \sqrt{6})(-\sqrt{12})\)
      2. \((-2 \sqrt[4]{18})(-\sqrt[4]{9})\)
      1. \(\left(3 \sqrt{2 x^{3}}\right)\left(7 \sqrt{18 x^{2}}\right)\)
      2. \(\left(-6 \sqrt[3]{20 a^{2}}\right)\left(-2 \sqrt[3]{16 a^{3}}\right)\)
    Réponse

    2.

    1. \(126 x^{2} \sqrt{2}\)
    2. \(48 a \sqrt[3]{a^{2}}\)
    Exercice\(\PageIndex{16}\) Use Polynomial Multiplication to Multiply Radical Expressions

    Dans les exercices suivants, multipliez.

      1. \(\sqrt{11}(8+4 \sqrt{11})\)
      2. \(\sqrt[3]{3}(\sqrt[3]{9}+\sqrt[3]{18})\)
      1. \((3-2 \sqrt{7})(5-4 \sqrt{7})\)
      2. \((\sqrt[3]{x}-5)(\sqrt[3]{x}-3)\)
    3. \((2 \sqrt{7}-5 \sqrt{11})(4 \sqrt{7}+9 \sqrt{11})\)
      1. \((4+\sqrt{11})^{2}\)
      2. \((3-2 \sqrt{5})^{2}\)
    5. \((7+\sqrt{10})(7-\sqrt{10})\)
    6. \((\sqrt[3]{3 x}+2)(\sqrt[3]{3 x}-2)\)
    Réponse

    2.

    1. \(71-22 \sqrt{7}\)
    2. \(\sqrt[3]{x^{2}}-8 \sqrt[3]{x}+15\)

    4.

    1. \(27+8 \sqrt{11}\)
    2. \(29-12 \sqrt{5}\)

    6. \(\sqrt[3]{9 x^{2}}-4\)

    Divisez les expressions

    Exercice\(\PageIndex{17}\) Divide Square Roots

    Dans les exercices suivants, simplifiez.

      1. \(\frac{\sqrt{48}}{\sqrt{75}}\)
      2. \(\frac{\sqrt[3]{81}}{\sqrt[3]{24}}\)
      1. \(\frac{\sqrt{320 m n^{-5}}}{\sqrt{45 m^{-7} n^{3}}}\)
      2. \(\frac{\sqrt[3]{16 x^{4} y^{-2}}}{\sqrt[3]{-54 x^{-2} y^{4}}}\)
    Réponse

    2.

    1. \(\frac{8 m^{4}}{3 n^{4}}\)
    2. \(-\frac{x^{2}}{2 y^{2}}\)
    Exercice\(\PageIndex{18}\) rationalize a One Term Denominator

    Dans les exercices suivants, rationalisez le dénominateur.

      1. \(\frac{8}{\sqrt{3}}\)
      2. \(\sqrt{\frac{7}{40}}\)
      3. \(\frac{8}{\sqrt{2 y}}\)
      1. \(\frac{1}{\sqrt[3]{11}}\)
      2. \(\sqrt[3]{\frac{7}{54}}\)
      3. \(\frac{3}{\sqrt[3]{3 x^{2}}}\)
      1. \(\frac{1}{\sqrt[4]{4}}\)
      2. \(\sqrt[4]{\frac{9}{32}}\)
      3. \(\frac{6}{\sqrt[4]{9 x^{3}}}\)
    Réponse

    2.

    1. \(\frac{\sqrt[3]{121}}{11}\)
    2. \(\frac{\sqrt[3]{28}}{6}\)
    3. \(\frac{\sqrt[3]{9 x}}{x}\)
    Exercice\(\PageIndex{19}\) Rationalize a Two Term Denominator

    Dans les exercices suivants, simplifiez.

    1. \(\frac{7}{2-\sqrt{6}}\)
    2. \(\frac{\sqrt{5}}{\sqrt{n}-\sqrt{7}}\)
    3. \(\frac{\sqrt{x}+\sqrt{8}}{\sqrt{x}-\sqrt{8}}\)
    Réponse

    1. \(-\frac{7(2+\sqrt{6})}{2}\)

    3. \(\frac{(\sqrt{x}+2 \sqrt{2})^{2}}{x-8}\)

    Résoudre des équations

    Exercice\(\PageIndex{20}\) Solve Radical Equations

    Dans les exercices suivants, résolvez.

    1. \(\sqrt{4 x-3}=7\)
    2. \(\sqrt{5 x+1}=-3\)
    3. \(\sqrt[3]{4 x-1}=3\)
    4. \(\sqrt{u-3}+3=u\)
    5. \(\sqrt[3]{4 x+5}-2=-5\)
    6. \((8 x+5)^{\frac{1}{3}}+2=-1\)
    7. \(\sqrt{y+4}-y+2=0\)
    8. \(2 \sqrt{8 r+1}-8=2\)
    Réponse

    2. aucune solution

    4. \(u=3, u=4\)

    6. \(x=-4\)

    8. \(r=3\)

    Exercice\(\PageIndex{21}\) Solve Radical Equations with Two Radicals

    Dans les exercices suivants, résolvez.

    1. \(\sqrt{10+2 c}=\sqrt{4 c+16}\)
    2. \(\sqrt[3]{2 x^{2}+9 x-18}=\sqrt[3]{x^{2}+3 x-2}\)
    3. \(\sqrt{r}+6=\sqrt{r+8}\)
    4. \(\sqrt{x+1}-\sqrt{x-2}=1\)
    Réponse

    2. \(x=-8, x=2\)

    4. \(x=3\)

    Exercice\(\PageIndex{22}\) Use Radicals in Applications

    Dans les exercices suivants, résolvez. Arrondissez les approximations à une décimale.

    1. Landscaping Reed veut avoir un terrain de jardin carré dans son jardin. Il dispose de suffisamment de compost pour couvrir une superficie de pieds\(75\) carrés. Utilisez la formule\(s=\sqrt{A}\) pour trouver la longueur de chaque côté de son jardin. Arrondissez vos réponses au dixième de pied le plus proche.
    2. Enquête sur un accident Un enquêteur a mesuré les marques de dérapage de l'un des véhicules impliqués dans un accident. La longueur des marques de dérapage était de\(175\) pieds. Utilisez la formule\(s=\sqrt{24d}\) pour déterminer la vitesse du véhicule avant que les freins ne soient actionnés. Arrondissez votre réponse au dixième le plus proche.
    Réponse

    2. \(64.8\)pieds

    Utiliser des radicaux dans les fonctions

    Exercice\(\PageIndex{23}\) Evaluate a Radical Function

    Dans les exercices suivants, évaluez chaque fonction.

    1. \(g(x)=\sqrt{6 x+1}\), trouvez
      1. \(g(4)\)
      2. \(g(8)\)
    2. \(G(x)=\sqrt{5 x-1}\), trouvez
      1. \(G(5)\)
      2. \(G(2)\)
    3. \(h(x)=\sqrt[3]{x^{2}-4}\), trouvez
      1. \(h(-2)\)
      2. \(h(6)\)
    4. Pour la fonction\(g(x)=\sqrt[4]{4-4 x}\), trouvez
      1. \(g(1)\)
      2. \(g(-3)\)
    Réponse

    2.

    1. \(G(5)=2 \sqrt{6}\)
    2. \(G(2)=3\)

    4.

    1. \(g(1)=0\)
    2. \(g(-3)=2\)
    Exercice\(\PageIndex{24}\) Find the Domain of a Radical Function

    Dans les exercices suivants, trouvez le domaine de la fonction et écrivez le domaine en notation par intervalles.

    1. \(g(x)=\sqrt{2-3 x}\)
    2. \(F(x)=\sqrt{\frac{x+3}{x-2}}\)
    3. \(f(x)=\sqrt[3]{4 x^{2}-16}\)
    4. \(F(x)=\sqrt[4]{10-7 x}\)
    Réponse

    2. \((2, \infty)\)

    4. \(\left[\frac{7}{10}, \infty\right)\)

    Exercice\(\PageIndex{25}\) graph Radical Functions

    Dans les exercices suivants,

    1. trouvez le domaine de la fonction
    2. représenter graphiquement la fonction
    3. utilisez le graphique pour déterminer la plage
    1. \(g(x)=\sqrt{x+4}\)
    2. \(g(x)=2 \sqrt{x}\)
    3. \(f(x)=\sqrt[3]{x-1}\)
    4. \(f(x)=\sqrt[3]{x}+3\)
    Réponse

    2.

    1. domaine :\([0, \infty)\)

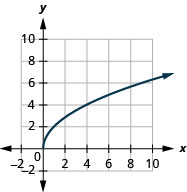
    2. La figure montre un graphe de fonction de racine carrée sur le plan de coordonnées x. L'axe X du plan va de 0 à 8. L'axe Y va de 0 à 8. La fonction a pour point de départ (0, 0) et passe par les points (1, 2) et (4, 4).
      Figure 8.E.1
    3. gamme :\([0, \infty)\)

    4.

    1. domaine :\((-\infty, \infty)\)

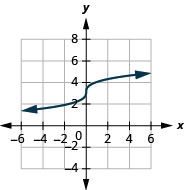
    2. La figure montre un graphe de la fonction racine cubique sur le plan de coordonnées x. L'axe X du plan va de moins 4 à 4. L'axe Y va de moins 2 à 6. La fonction a un point central en (0, 3) et passe par les points (moins 1, 2) et (1, 4).
      Graphique 8.E.2
    3. gamme :\((-\infty, \infty)\)

    Utiliser le système de numérotation complexe

    Exercice\(\PageIndex{26}\) evaluate the Square Root of a Negative Number

    Dans les exercices suivants, écrivez chaque expression en termes\(i\) et simplifiez-la si possible.

      1. \(\sqrt{-100}\)
      2. \(\sqrt{-13}\)
      3. \(\sqrt{-45}\)
    Réponse

    Résolvez vous-même

    Exercice\(\PageIndex{27}\) Add or Subtract Complex Numbers

    Dans les exercices suivants, ajoutez ou soustrayez.

    1. \(\sqrt{-50}+\sqrt{-18}\)
    2. \((8-i)+(6+3 i)\)
    3. \((6+i)-(-2-4 i)\)
    4. \((-7-\sqrt{-50})-(-32-\sqrt{-18})\)
    Réponse

    1. \(8 \sqrt{2} i\)

    3. \(8+5 i\)

    Exercice\(\PageIndex{28}\) Multiply Complex Numbers

    Dans les exercices suivants, multipliez.

    1. \((-2-5 i)(-4+3 i)\)
    2. \(-6 i(-3-2 i)\)
    3. \(\sqrt{-4} \cdot \sqrt{-16}\)
    4. \((5-\sqrt{-12})(-3+\sqrt{-75})\)
    Réponse

    1. \(23+14 i\)

    3. \(-6\)

    Exercice\(\PageIndex{29}\) Multiply Complex Numbers

    Dans les exercices suivants, multipliez en utilisant le modèle Product of Binomial Squares.

    1. \((-2-3 i)^{2}\)
    Réponse

    1. \(-5-12 i\)

    Exercice\(\PageIndex{30}\) Multiply Complex Numbers

    Dans les exercices suivants, multipliez en utilisant le modèle Product of Complex Conjugués.

    1. \((9-2 i)(9+2 i)\)
    Réponse

    Résolvez vous-même

    Exercice\(\PageIndex{31}\) divide Complex Numbers

    Dans les exercices suivants, divisez.

    1. \(\frac{2+i}{3-4 i}\)
    2. \(\frac{-4}{3-2 i}\)
    Réponse

    1. \(\frac{2}{25}+\frac{11}{25} i\)

    Exercice\(\PageIndex{32}\) Simplify Powers of \(i\)

    Dans les exercices suivants, simplifiez.

    1. \(i^{48}\)
    2. \(i^{255}\)
    Réponse

    1. \(1\)

    Test d'entraînement

    Exercice\(\PageIndex{33}\)

    Dans les exercices suivants, simplifiez l'utilisation de valeurs absolues si nécessaire.

    1. \(\sqrt[3]{125 x^{9}}\)
    2. \(\sqrt{169 x^{8} y^{6}}\)
    3. \(\sqrt[3]{72 x^{8} y^{4}}\)
    4. \(\sqrt{\frac{45 x^{3} y^{4}}{180 x^{5} y^{2}}}\)
    Réponse

    1. \(5x^{3}\)

    3. \(2 x^{2} y \sqrt[3]{9 x^{2} y}\)

    Exercice\(\PageIndex{34}\)

    Dans les exercices suivants, simplifiez. Supposons que toutes les variables sont positives.

      1. \(216^{-\frac{1}{4}}\)
      2. \(-49^{\frac{3}{2}}\)
    2. \(\sqrt{-45}\)
    3. \(\frac{x^{-\frac{1}{4}} \cdot x^{\frac{5}{4}}}{x^{-\frac{3}{4}}}\)
    4. \(\left(\frac{8 x^{\frac{2}{3}} y^{-\frac{5}{2}}}{x^{-\frac{7}{3}} y^{\frac{1}{2}}}\right)^{\frac{1}{3}}\)
    5. \(\sqrt{48 x^{5}}-\sqrt{75 x^{5}}\)
    6. \(\sqrt{27 x^{2}}-4 x \sqrt{12}+\sqrt{108 x^{2}}\)
    7. \(2 \sqrt{12 x^{5}} \cdot 3 \sqrt{6 x^{3}}\)
    8. \(\sqrt[3]{4}(\sqrt[3]{16}-\sqrt[3]{6})\)
    9. \((4-3 \sqrt{3})(5+2 \sqrt{3})\)
    10. \(\frac{\sqrt[3]{128}}{\sqrt[3]{54}}\)
    11. \(\frac{\sqrt{245 x y^{-4}}}{\sqrt{45 x^{4} y^{3}}}\)
    12. \(\frac{1}{\sqrt[3]{5}}\)
    13. \(\frac{3}{2+\sqrt{3}}\)
    14. \(\sqrt{-4} \cdot \sqrt{-9}\)
    15. \(-4 i(-2-3 i)\)
    16. \(\frac{4+i}{3-2 i}\)
    17. \(i^{172}\)
    Réponse

    1.

    1. \(\frac{1}{4}\)
    2. \(-343\)

    3. \(x^{\frac{7}{4}}\)

    5. \(-x^{2} \sqrt{3 x}\)

    7. \(36 x^{4} \sqrt{2}\)

    9. \(2-7 \sqrt{3}\)

    11. \(\frac{7 x^{5}}{3 y^{7}}\)

    13. \(3(2-\sqrt{3})\)

    15. \(-12+8i\)

    17. \(-i\)

    Exercice\(\PageIndex{35}\)

    Dans les exercices suivants, résolvez.

    1. \(\sqrt{2 x+5}+8=6\)
    2. \(\sqrt{x+5}+1=x\)
    3. \(\sqrt[3]{2 x^{2}-6 x-23}=\sqrt[3]{x^{2}-3 x+5}\)
    Réponse

    2. \(x=4\)

    Exercice\(\PageIndex{36}\)

    Dans l'exercice suivant,

    1. trouvez le domaine de la fonction
    2. représenter graphiquement la fonction
    3. utilisez le graphique pour déterminer la plage
    1. \(g(x)=\sqrt{x+2}\)
    Réponse

    1.

    1. domaine :\([-2, \infty)\)

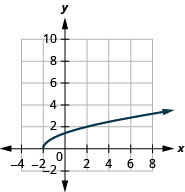
    2. La figure montre un graphe de fonction de racine carrée sur le plan de coordonnées x. L'axe X du plan va de moins 2 à 6. L'axe Y va de 0 à 8. La fonction a pour point de départ (négatif 2, 0) et passe par les points (négatif 1, 1) et (2, 2).
      Graphique 8.E.3
    3. gamme :\([0, \infty)\)