8.8 : Utiliser des radicaux dans les fonctions
- Page ID
- 194260
À la fin de cette section, vous serez en mesure de :
- Evaluer une fonction radicale
- Détermine le domaine d'une fonction radicale
- Fonctions radicales du graphe
Avant de commencer, répondez à ce questionnaire de préparation.
- Résoudre :\(1−2x≥0\).
Si vous avez oublié ce problème, consultez l'exemple 2.50. - Pour\(f(x)=3x−4\), évaluez\(f(2),f(−1),f(0)\).
Si vous avez oublié ce problème, consultez l'exemple 3.48. - Graphe\(f(x)=\sqrt{x}\). Indiquez le domaine et la plage de la fonction en notation par intervalles.
Si vous avez oublié ce problème, consultez l'exemple 3.56.
Évaluer une fonction radicale
Dans cette section, nous allons étendre nos travaux précédents sur les fonctions pour inclure les radicaux. Si une fonction est définie par une expression radicale, nous l'appelons fonction radicale.
- La fonction de racine carrée est\(f(x)=\sqrt{x}\).
- La fonction racine cubique est\(f(x)=\sqrt[3]{x}\).
Une fonction radicale est une fonction définie par une expression radicale.
Pour évaluer une fonction radicale, nous trouvons la valeur de\(f(x)\) pour une valeur donnée\(x\) exactement comme nous l'avons fait dans nos travaux précédents sur les fonctions.
Pour la fonction\(f(x)=\sqrt{2 x-1}\), trouvez
- \(f(5)\)
- \(f(-2)\)
Solution :
un.
\(f(x)=\sqrt{2 x-1}\)
Pour évaluer\(f(5)\), remplacez\(5\)\(x\).
\(f(5)=\sqrt{2 \cdot 5-1}\)
Simplifiez.
\(f(5)=\sqrt{9}\)
Prenez la racine carrée.
\(f(5)=3\)
b.
\(f(x)=\sqrt{2 x-1}\)
Pour évaluer\(f(-2)\), remplacez\(-2\)\(x\).
\(f(-2)=\sqrt{2(-2)-1}\)
Simplifiez.
\(f(-2)=\sqrt{-5}\)
Comme la racine carrée d'un nombre négatif n'est pas un nombre réel, la fonction n'a pas de valeur à\(x=-2\).
Pour la fonction\(f(x)=\sqrt{3 x-2}\), trouvez
- \(f(6)\)
- \(f(0)\)
- Réponse
-
- \(f(6)=4\)
- aucune valeur à\(x=0\)
Pour la fonction\(g(x)=\sqrt{5x+5}\), trouvez
- \(g(4)\)
- \(g(-3)\)
- Réponse
-
- \(g(4)=5\)
- aucune valeur à\(f(-3)\)
Nous suivons la même procédure pour évaluer les racines cubiques.
Pour la fonction\(g(x)=\sqrt[3]{x-6}\), trouvez
- \(g(14)\)
- \(g(-2)\)
Solution :
un.
\(g(x)=\sqrt[3]{x-6}\)
Pour évaluer\(g(14)\), remplacez\(14\)\(x\).
\(g(14)=\sqrt[3]{14-6}\)
Simplifiez.
\(g(14)=\sqrt[3]{8}\)
Prenez la racine cubique.
\(g(14)=2\)
b.
\(g(x)=\sqrt[3]{x-6}\)
Pour évaluer\(g(-2)\), remplacez\(-2\)\(x\).
\(g(-2)=\sqrt[3]{-2-6}\)
Simplifiez.
\(g(-2)=\sqrt[3]{-8}\)
Prenez la racine cubique.
\(g(-2)=-2\)
Pour la fonction\(g(x)=\sqrt[3]{3 x-4}\), trouvez
- \(g(4)\)
- \(g(1)\)
- Réponse
-
- \(g(4)=2\)
- \(g(1)=-1\)
Pour la fonction\(h(x)=\sqrt[3]{5 x-2}\), trouvez
- \(h(2)\)
- \(h(-5)\)
- Réponse
-
- \(h(2)=2\)
- \(h(-5)=-3\)
L'exemple suivant comporte une quatrième racine.
Pour la fonction\(f(x)=\sqrt[4]{5 x-4}\), trouvez
- \(f(4)\)
- \(f(-12)\)
Solution :
un.
\(f(x)=\sqrt[4]{5 x-4}\)
Pour évaluer\(f(4)\), remplacez\(4\)\(x\).
\(f(4)=\sqrt[4]{5 \cdot 4-4}\)
Simplifiez.
\(f(4)=\sqrt[4]{16}\)
Prenez la quatrième racine.
\(f(4)=2\)
b.
\(f(x)=\sqrt[4]{5 x-4}\)
Pour évaluer\(f(-12)\), remplacez\(-12\)\(x\).
\(f(-12)=\sqrt[4]{5(-12)-4}\)
Simplifiez.
\(f(-12)=\sqrt[4]{-64}\)
Comme la racine 4 d'un nombre négatif n'est pas un nombre réel, la fonction n'a pas de valeur à\(x=-12\).
Pour la fonction\(f(x)=\sqrt[4]{3 x+4}\), trouvez
- \(f(4)\)
- \(f(-1)\)
- Réponse
-
- \(f(4)=2\)
- \(f(-1)=1\)
Pour la fonction\(g(x)=\sqrt[4]{5 x+1}\), trouvez
- \(g(16)\)
- \(g(3)\)
- Réponse
-
- \(g(16)=3\)
- \(g(3)=2\)
Trouver le domaine d'une fonction radicale
Pour déterminer le domaine et la gamme des fonctions radicalaires, nous utilisons nos propriétés des radicaux. Pour un radical ayant un indice pair, nous avons dit que le radicand devait être supérieur ou égal à zéro, car les racines paires de nombres négatifs ne sont pas des nombres réels. Pour un indice impair, le radical peut être n'importe quel nombre réel. Nous reformulons les propriétés ici à titre de référence.
Propriétés de\(\sqrt[n]{a}\)
Quand\(n\) est un nombre pair et :
- \(a \geq 0\),\(\sqrt[n]{a}\) est donc un nombre réel.
- \(a<0\), n'\(\sqrt[n]{a}\)est donc pas un nombre réel.
Quand\(n\) est un nombre impair,\(\sqrt[n]{a}\) est un nombre réel pour toutes les valeurs de\(a\).
Ainsi, pour trouver le domaine d'une fonction radicale avec un indice pair, nous définissons le radical comme étant supérieur ou égal à zéro. Pour un radical d'indice impair, le radical peut être n'importe quel nombre réel.
Domaine d'une fonction radicale
Lorsque l'indice du radical est pair, le radical doit être supérieur ou égal à zéro.
Lorsque l'indice du radical est impair, le radical peut être n'importe quel nombre réel.
Trouvez le domaine de la fonction,\(f(x)=\sqrt{3 x-4}\). Écrivez le domaine en notation par intervalles.
Solution :
Puisque la fonction\(f(x)=\sqrt{3 x-4}\) a un radical avec un indice égal à\(2\), qui est pair, nous savons que le radical doit être supérieur ou égal à\(0\). Nous définissons le radical pour qu'il soit supérieur ou égal à,\(0\) puis nous résolvons pour trouver le domaine.
Résoudre.
\(\begin{aligned} 3 x-4 & \geq 0 \\ 3 x & \geq 4 \\ x & \geq \frac{4}{3} \end{aligned}\)
Le domaine de\(f(x)=\sqrt{3 x-4}\) est composé de toutes les valeurs\(x \geq \frac{4}{3}\) et nous l'écrivons en notation par intervalles sous la forme\(\left[\frac{4}{3}, \infty\right)\).
Trouvez le domaine de la fonction,\(f(x)=\sqrt{6 x-5}\). Écrivez le domaine en notation par intervalles.
- Réponse
-
\(\left[\frac{5}{6}, \infty\right)\)
Trouvez le domaine de la fonction,\(f(x)=\sqrt{4-5 x}\). Écrivez le domaine en notation par intervalles.
- Réponse
-
\(\left(-\infty, \frac{4}{5}\right]\)
Trouvez le domaine de la fonction,\(g(x)=\sqrt{\frac{6}{x-1}}\). Écrivez le domaine en notation par intervalles.
Solution :
Résolvez la fonction,\(g(x)=\sqrt{\frac{6}{x-1}}\) a un radical avec un indice de\(2\), qui est pair, nous savons que le radical et doit être supérieur ou égal à\(0\).
Le radical ne peut pas être nul puisque le numérateur n'est pas nul.
\(\frac{6}{x-1}\)Pour être supérieur à zéro, le dénominateur doit être positif puisque le numérateur est positif. Nous savons qu'un positif divisé par un positif est positif.
Nous définissons\(x-1>0\) et résolvons.
\(x-1>0\)
Résoudre.
\(x>1\)
De plus, comme le radicand est une fraction, il faut se rendre compte que le dénominateur ne peut pas être nul.
Nous nous\(x-1=0\) efforçons de trouver la valeur à éliminer du domaine.
\(x-1=0\)
Résoudre.
\(x=1\)donc\(x/neq 1\) dans le domaine.
En assemblant cela, nous obtenons le domaine\(x>1\) et nous l'écrivons comme\((1, \infty)\).
Trouvez le domaine de la fonction,\(f(x)=\sqrt{\frac{4}{x+3}}\). Écrivez le domaine en notation par intervalles.
- Réponse
-
\((-3, \infty)\)
Trouvez le domaine de la fonction,\(h(x)=\sqrt{\frac{9}{x-5}}\). Écrivez le domaine en notation par intervalles.
- Réponse
-
\((5, \infty)\)
L'exemple suivant implique une racine cubique et nécessitera donc une réflexion différente.
Trouvez le domaine de la fonction,\(f(x)=\sqrt[3]{2 x^{2}+3}\). Écrivez le domaine en notation par intervalles.
Solution :
Puisque la fonction\(f(x)=\sqrt[3]{2 x^{2}+3}\) a un radical avec un indice de\(3\), ce qui est étrange, nous savons que le radical peut être n'importe quel nombre réel. Cela nous indique que le domaine est un nombre réel. En notation par intervalles, nous écrivons\((-\infty, \infty)\).
Le domaine de\(f(x)=\sqrt[3]{2 x^{2}+3}\) est composé de tous les nombres réels et nous l'écrivons en notation par intervalles sous la forme\((-\infty, \infty)\).
Trouvez le domaine de la fonction,\(f(x)=\sqrt[3]{3 x^{2}-1}\). Écrivez le domaine en notation par intervalles.
- Réponse
-
\((-\infty, \infty)\)
Trouvez le domaine de la fonction,\(g(x)=\sqrt[3]{5 x-4}\). Écrivez le domaine en notation par intervalles.
- Réponse
-
\((-\infty, \infty)\)
Fonctions radicales du graphe
Avant de représenter graphiquement une fonction radicale, nous trouvons d'abord le domaine de la fonction. Pour la fonction\(f(x)=\sqrt{x}\), l'indice est pair, et le radical doit donc être supérieur ou égal à\(0\).
Cela nous indique que le domaine est\(x≥0\) et nous l'écrivons en notation par intervalles sous la forme\([0,∞)\).
Auparavant, nous utilisions le traçage par points pour représenter graphiquement la fonction,\(f(x)=\sqrt{x}\). Nous avons choisi\(x\) des valeurs, les avons remplacées puis créé un graphique. Notez que nous avons choisi des points qui sont des carrés parfaits afin de faciliter la prise de la racine carrée.
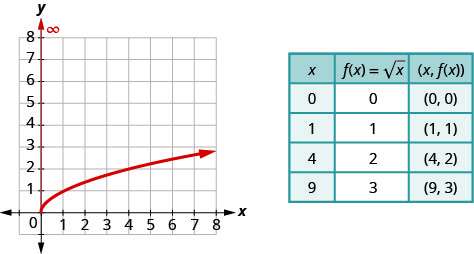
Une fois que nous voyons le graphique, nous pouvons trouver la plage de la fonction. Les\(y\) valeurs -de la fonction sont supérieures ou égales à zéro. La fourchette est alors\([0,∞)\).
Pour la fonction\(f(x)=\sqrt{x+3}\),
- trouvez le domaine
- représenter graphiquement la fonction
- utilisez le graphique pour déterminer la plage
Solution :
- Puisque le radical a un indice\(2\), nous savons que le radical doit être supérieur ou égal à zéro. Si\(x+3 \geq 0\), alors\(x \geq-3\). Cela nous indique que le domaine est composé de toutes les valeurs\(x \geq-3\) et est écrit en notation par intervalles sous la forme\([-3, \infty)\).
- Pour représenter graphiquement la fonction, nous choisissons des points dans l'intervalle\([-3, \infty)\) qui nous donneront également un radical dont il sera facile de prendre la racine carrée.
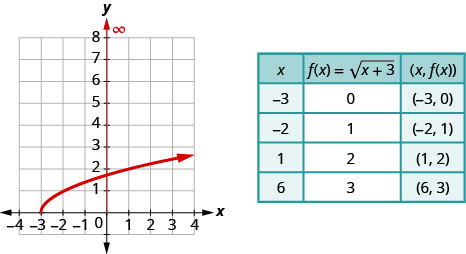
c. En regardant le graphique, nous voyons que les\(y\) valeurs -de la fonction sont supérieures ou égales à zéro. La fourchette est alors\([0, \infty)\).
Pour la fonction\(f(x)=\sqrt{x+2}\),
- trouvez le domaine
- représenter graphiquement la fonction
- utilisez le graphique pour déterminer la plage
- Réponse
-
- domaine :\([-2, \infty)\)
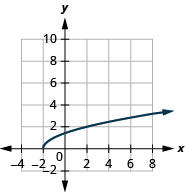
Graphique 8.7.3- gamme :\([0, \infty)\)
Pour la fonction\(f(x)=\sqrt{x-2}\),
- trouvez le domaine
- représenter graphiquement la fonction
- utilisez le graphique pour déterminer la plage
- Réponse
-
- domaine :\([2, \infty)\)
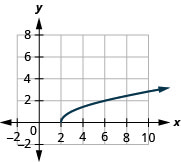
Graphique 8.7.4- gamme :\([0, \infty)\)
Dans nos travaux précédents sur les fonctions graphiques, nous avons représenté graphiquement la fonction,\(f(x)=x^{3}\) mais nous ne l'avons pas fait\(f(x)=\sqrt[3]{x}\). Nous allons le faire maintenant dans l'exemple suivant.
Pour la fonction\(f(x)=\sqrt[3]{x}\),
- trouvez le domaine
- représenter graphiquement la fonction
- utilisez le graphique pour déterminer la plage
Solution :
a. Comme le radical a un indice\(3\), nous savons que le radical peut être n'importe quel nombre réel. Cela nous indique que le domaine est composé uniquement de nombres réels et écrits en notation par intervalles comme\((-\infty, \infty)\)
b. Pour représenter graphiquement la fonction, nous choisissons des points dans l'intervalle\((-\infty, \infty)\) qui nous donneront également un radical dont il sera facile de prendre la racine cubique.

c. En regardant le graphique, nous voyons que les\(y\) valeurs -de la fonction sont toutes des nombres réels. La fourchette est alors\((-\infty, \infty)\).
Pour la fonction\(f(x)=-\sqrt[3]{x}\),
- trouvez le domaine
- représenter graphiquement la fonction
- utilisez le graphique pour déterminer la plage
- Réponse
-
- domaine :\((-\infty, \infty)\)
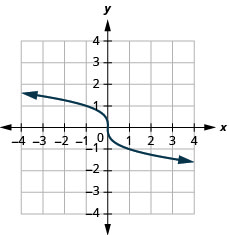
Graphique 8.7.6- gamme :\((-\infty, \infty)\)
Pour la fonction\(f(x)=\sqrt[3]{x-2}\),
- trouvez le domaine
- représenter graphiquement la fonction
- utilisez le graphique pour déterminer la plage
- Réponse
-
- domaine :\((-\infty, \infty)\)
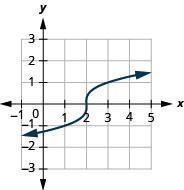
Graphique 8.7.7- gamme :\((-\infty, \infty)\)
Accédez à ces ressources en ligne pour des instructions et des exercices supplémentaires avec des fonctions radicales.
- Domaine d'une fonction radicale
- Domaine d'une fonction radicale 2
- Trouver le domaine d'une fonction radicale
Concepts clés
- Propriétés de\(\sqrt[n]{a}\)
- Quand\(n\) est un nombre pair et :
\(a≥0\), alors\(\sqrt[n]{a}\) est un nombre réel.
\(a<0\), n'\(\sqrt[n]{a}\)est donc pas un nombre réel. - Quand\(n\) est un nombre impair,\(\sqrt[n]{a}\) est un nombre réel pour toutes les valeurs de\(a\).
- Quand\(n\) est un nombre pair et :
- Domaine d'une fonction radicale
- Lorsque l'indice du radical est pair, le radical doit être supérieur ou égal à zéro.
- Lorsque l'indice du radical est impair, le radical peut être n'importe quel nombre réel.
Lexique
- fonction radicale
- Une fonction radicale est une fonction définie par une expression radicale.


