8.7 : Résolution d'équations radicales
- Page ID
- 194274
À la fin de cette section, vous serez en mesure de :
- Résoudre des équations
- Résoudre des équations radicales avec deux radicaux
- Utiliser des radicaux dans les applications
Avant de commencer, répondez à ce questionnaire de préparation.
- Simplifiez :\((y−3)^{2}\).
Si vous avez oublié ce problème, consultez l'exemple 5.31. - Résoudre :\(2x−5=0\).
Si vous avez oublié ce problème, consultez l'exemple 2.2. - Résoudre\(n^{2}−6n+8=0\).
Si vous avez oublié ce problème, consultez l'exemple 6.45.
Résoudre des équations
Dans cette section, nous allons résoudre des équations qui ont une variable dans le radical et dans une expression radicale. Une équation de ce type est appelée équation radicale.
Définition\(\PageIndex{1}\)
Une équation dans laquelle une variable se trouve dans le radical et dans une expression radicale est appelée équation radicale.
Comme d'habitude, lorsque nous résolvons ces équations, ce que nous faisons d'un côté d'une équation doit également être fait de l'autre côté. Une fois que nous aurons isolé le radical, notre stratégie sera de porter les deux côtés de l'équation à la puissance de l'indice. Cela éliminera le radical.
La résolution d'équations radicales contenant un indice pair en élevant les deux côtés à la puissance de l'indice peut introduire une solution algébrique qui ne serait pas une solution à l'équation radicale d'origine. Encore une fois, nous appelons cela une solution superflue, comme nous l'avons fait lorsque nous avons résolu des équations rationnelles.
Dans l'exemple suivant, nous verrons comment résoudre une équation radicale. Notre stratégie est basée sur l'élévation d'un radical avec un indice\(n\) de\(n^{th}\) puissance. Cela éliminera le radical.
Pour\(a \geq 0,(\sqrt[n]{a})^{n}=a\).
Résoudre :\(\sqrt{5 n-4}-9=0\).
Solution :
| Étape 1 : Isolez le radical d'un côté de l'équation. |
Pour isoler le radical, ajoutez-le\(9\) des deux côtés. Simplifiez. |
\(\begin{array}{c}{\sqrt{5 n-4}-9=0} \\ {\sqrt{5 n-4}-9\color{red}{+9}\color{black}{=}0\color{red}{+9}} \\ {\sqrt{5 n-4}=9}\end{array}\) |
| Étape 2 : Augmentez les deux côtés de l'équation à la puissance de l'indice. | Puisque l'indice d'une racine carrée est\(2\), nous mettons les deux côtés au carré. | \((\sqrt{5 n-4})^{2}=(9)^{2}\) |
| Étape 3 : Résolvez la nouvelle équation | N'oubliez pas,\((\sqrt{a})^{2}=a\). | \(\begin{aligned} 5 n-4 &=81 \\ 5 n &=85 \\ n &=17 \end{aligned}\) |
| Étape 4 : Vérifiez la réponse dans l'équation d'origine. |
Vérifiez la réponse. \(\begin{array}{r}{\sqrt{5 n-4}-9=0} \\ {\sqrt{5(\color{red}{17}\color{black}{)}-4}-9 \stackrel{?}{=} 0} \\ {\sqrt{85-4}-9 \stackrel{?}{=} 0} \\ {\sqrt{81}-9 \stackrel{?}{=} 0} \\ {9-9=0} \\ {0=0}\end{array}\) La solution est\(n=17\). |
Résoudre :\(\sqrt{3 m+2}-5=0\).
- Réponse
-
\(m=\frac{23}{3}\)
Résoudre :\(\sqrt{10 z+1}-2=0\).
- Réponse
-
\(z=\frac{3}{10}\)
Résolvez une équation radicale avec un radical
- Isolez le radical d'un côté de l'équation.
- Augmentez les deux côtés de l'équation à la puissance de l'indice.
- Résolvez la nouvelle équation.
- Vérifiez la réponse dans l'équation d'origine.
Lorsque nous utilisons un signe radical, il indique la racine principale ou positive. Si une équation possède un radical dont l'indice pair est égal à un nombre négatif, cette équation n'aura pas de solution.
Résoudre :\(\sqrt{9 k-2}+1=0\).
Solution :
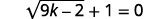 |
|
| Pour isoler le radical, soustrayez-le\(1\) des deux côtés. |  |
| Simplifiez. | 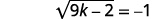 |
Comme la racine carrée est égale à un nombre négatif, l'équation n'a pas de solution.
Résoudre :\(\sqrt{2 r-3}+5=0\).
- Réponse
-
aucune solution
Résoudre :\(\sqrt{7 s-3}+2=0\).
- Réponse
-
aucune solution
Si l'un des côtés d'une équation avec une racine carrée est binomiale, nous utilisons le modèle du produit des carrés binomiaux lorsque nous la mettons au carré.
Définition\(\PageIndex{2}\)
Carrés binomiaux
\(\begin{array}{l}{(a+b)^{2}=a^{2}+2 a b+b^{2}} \\ {(a-b)^{2}=a^{2}-2 a b+b^{2}}\end{array}\)
N'oubliez pas le moyen terme !
Résoudre :\(\sqrt{p-1}+1=p\).
Solution :
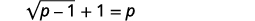 |
|
| Pour isoler le radical, soustrayez\(1\) des deux côtés. | 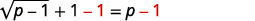 |
| Simplifiez. | 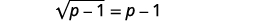 |
| Mettez les deux côtés de l'équation au carré. | 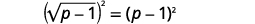 |
| Simplifiez en utilisant le modèle du produit des carrés binomiaux sur la droite, puis résolvez la nouvelle équation. | 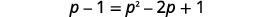 |
| C'est une équation quadratique, alors mettez zéro sur un côté. | 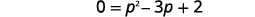 |
| Facteur du côté droit. | 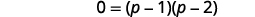 |
| Utilisez la propriété Zero Product. | 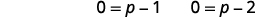 |
| Résolvez chaque équation. | 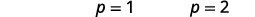 |
| Vérifiez les réponses. | |
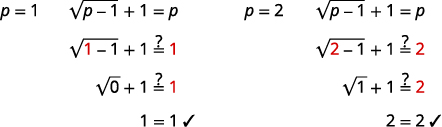 |
Les solutions sont\(p=1, p=2\).
Résoudre :\(\sqrt{x-2}+2=x\).
- Réponse
-
\(x=2, x=3\)
Résoudre :\(\sqrt{y-5}+5=y\).
- Réponse
-
\(y=5, y=6\)
Lorsque l'indice du radical est\(3\), nous coupons les deux côtés pour éliminer le radical.
\((\sqrt[3]{a})^{3}=a\)
Résoudre :\(\sqrt[3]{5 x+1}+8=4\).
Solution :
| \(\sqrt[3]{5 x+1}+8=4\) | |
| Pour isoler le radical, soustrayez\(8\) des deux côtés. | \(\sqrt[3]{5 x+1}=-4\) |
| Coupez les deux côtés de l'équation. | \((\sqrt[3]{5 x+1})^{3}=(-4)^{3}\) |
| Simplifiez. | \(5 x+1=-64\) |
| Résolvez l'équation. | \(5 x=-65\) |
| \(x=-13\) | |
| Vérifiez la réponse. | |
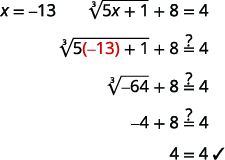 |
|
| La solution est\(x=-13\). |
Résoudre :\( \sqrt[3]{4 x-3}+8=5\)
- Réponse
-
\(x=-6\)
Résoudre :\(\sqrt[3]{6 x-10}+1=-3\)
- Réponse
-
\(x=-9\)
Parfois, une équation contient des exposants rationnels au lieu d'un radical. Nous utilisons les mêmes techniques pour résoudre l'équation que lorsque nous avons un radical. Nous élevons chaque côté de l'équation à la puissance du dénominateur de l'exposant rationnel. Puisque\(\left(a^{m}\right)^{^{n}}=a^{m \cdot n}\), par exemple, nous avons
\(\left(x^{\frac{1}{2}}\right)^{2}=x,\left(x^{\frac{1}{3}}\right)^{3}=x\)
N'oubliez pas,\(x^{\frac{1}{2}}=\sqrt{x}\) et\(x^{\frac{1}{3}}=\sqrt[3]{x}\).
Résoudre :\((3 x-2)^{\frac{1}{4}}+3=5\).
Solution :
| \((3 x-2)^{\frac{1}{4}}+3=5\) | |
| Pour isoler le terme avec l'exposant rationnel, soustrayez\(3\) des deux côtés. | \((3 x-2)^{\frac{1}{4}}=2\) |
| Portez chaque côté de l'équation à la quatrième puissance. | \(\left((3 x-2)^{\frac{1}{4}}\right)^{4}=(2)^{4}\) |
| Simplifiez. | \(3 x-2=16\) |
| Résolvez l'équation. | \(3x=18\) |
| \(x=6\) | |
| Vérifiez la réponse. | |
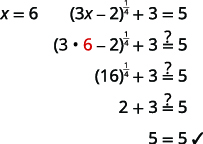 |
|
| La solution est\(x=6\). |
Résoudre :\((9 x+9)^{\frac{1}{4}}-2=1\)
- Réponse
-
\(x=8\)
Résoudre :\((4 x-8)^{\frac{1}{4}}+5=7\)
- Réponse
-
\(x=6\)
Parfois, la solution d'une équation radicale aboutit à deux solutions algébriques, mais l'une d'entre elles peut être une solution étrangère !
Résoudre :\(\sqrt{r+4}-r+2=0\).
Solution :
| \(\sqrt{r+4}-r+2=0\) | |
| Isolez le radical. | \(\sqrt{r+4}=r-2\) |
| Mettez les deux côtés de l'équation au carré. | \((\sqrt{r+4})^{2}=(r-2)^{2}\) |
| Simplifiez puis résolvez l'équation. | \(r+4=r^{2}-4 r+4\) |
| S'il s'agit d'une équation quadratique, mettez zéro sur un côté. | \(0=r^{2}-5 r\) |
| Facteur du côté droit. | \(0=r(r-5)\) |
| Utilisez la propriété Zero Product. | \(0=r \quad 0=r-5\) |
| Résolvez l'équation. | \(r=0 \quad r=5\) |
| Vérifiez votre réponse. | |
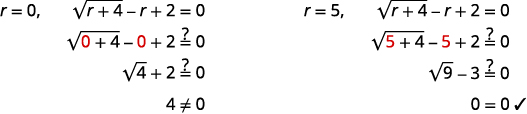 |
La solution est\(r=5\). |
| \(r=0\)est une solution extérieure. |
Résoudre :\(\sqrt{m+9}-m+3=0\)
- Réponse
-
\(m=7\)
Résoudre :\(\sqrt{n+1}-n+1=0\).
- Réponse
-
\(n=3\)
Lorsqu'il y a un coefficient devant le radical, nous devons également l'élever à la puissance de l'indice.
Résoudre :\(3 \sqrt{3 x-5}-8=4\).
Solution :
| \(3 \sqrt{3 x-5}-8=4\) | |
| Isolez le terme radical. | \(3 \sqrt{3 x-5}=12\) |
| Isolez le radical en divisant les deux côtés par\(3\). | \(\sqrt{3 x-5}=4\) |
| Mettez les deux côtés de l'équation au carré. | \((\sqrt{3 x-5})^{2}=(4)^{2}\) |
| Simplifiez, puis résolvez la nouvelle équation. | \(3 x-5=16\) |
| \(3x=21\) | |
| Résolvez l'équation. | \(x=7\) |
| Vérifiez la réponse. | |
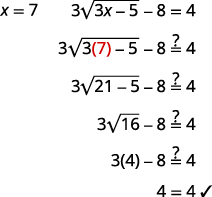 |
|
| La solution est\(x=7\). |
Résoudre :\(2 \sqrt{4 a+4}-16=16\).
- Réponse
-
\(a=63\)
Résoudre :\(3 \sqrt{2 b+3}-25=50\)
- Réponse
-
\(b=311\)
Résoudre des équations radicales avec deux radicaux
Si l'équation des radicaux comporte deux radicaux, on commence par isoler l'un d'entre eux. Il est souvent plus facile d'isoler d'abord le radical le plus complexe.
Dans l'exemple suivant, lorsqu'un radical est isolé, le second radical est également isolé.
Résoudre :\(\sqrt[3]{4 x-3}=\sqrt[3]{3 x+2}\).
Solution :
Les termes radicaux sont isolés.
\(\sqrt[3]{4 x-3}=\sqrt[3]{3 x+2}\)
Puisque l'indice est\(3\), cubez les deux côtés de l'équation.
\((\sqrt[3]{4 x-3})^{3}=(\sqrt[3]{3 x+2})^{3}\)
Simplifiez, puis résolvez la nouvelle équation.
\(\begin{aligned} 4 x-3 &=3 x+2 \\ x-3 &=2 \\ x &=5 \end{aligned}\)
La solution est\(x=5\).
Vérifiez la réponse.
Nous vous laissons le soin de montrer ces\(5\) chèques !
Résoudre :\(\sqrt[3]{5 x-4}=\sqrt[3]{2 x+5}\).
- Réponse
-
\(x=3\)
Résoudre :\(\sqrt[3]{7 x+1}=\sqrt[3]{2 x-5}\).
- Réponse
-
\(x=-\frac{6}{5}\)
Parfois, après avoir élevé les deux côtés d'une équation à une puissance, nous avons toujours une variable à l'intérieur d'un radical. Lorsque cela se produit, nous répétons les étapes 1 et 2 de notre procédure. Nous isolons le radical et élevons à nouveau les deux côtés de l'équation à la puissance de l'indice.
Résoudre :\(\sqrt{m}+1=\sqrt{m+9}\).
Solution :
| Étape 1 : Isolez l'un des termes radicaux d'un côté de l'équation. | Le radical de droite est isolé. | \(\sqrt{m}+1=\sqrt{m+9}\) |
| Étape 2 : Augmentez les deux côtés de l'équation à la puissance de l'indice. |
Nous quadrillons les deux côtés. Simplifiez : soyez très prudent lorsque vous multipliez ! |
\((\sqrt{m}+1)^{2}=(\sqrt{m+9})^{2}\) |
|
Étape 3 : Y a-t-il d'autres radicaux ? Si c'est le cas, répétez les étapes 1 et 2. Dans la négative, résolvez la nouvelle équation. |
Il y a toujours un radical dans l'équation. Nous devons donc répéter les étapes précédentes. Isolez le terme radical. Ici, on peut facilement isoler le radical en divisant les deux côtés par\(2\). Carrer les deux côtés. |
\(\begin{aligned} m+2 \sqrt{m}+1 &=m+9 \\ 2 \sqrt{m} &=8 \\ \sqrt{m} &=4 \\(\sqrt{m})^{2} &=(4)^{2} \\ m &=16 \end{aligned}\) |
| Étape 4 : Vérifiez la réponse dans l'équation d'origine. |
\(\begin{aligned}\sqrt{m}+1&=\sqrt{m+9} \\ \sqrt{\color{red}{16}}\color{black}{+}1& \stackrel{?}{=} \sqrt{\color{red}{16}\color{black}{+}9} \\ 4+1& \stackrel{?}{=} 5 \\ 5&=5\end{aligned}\) La solution est\(m=16\). |
Résoudre :\(3-\sqrt{x}=\sqrt{x-3}\).
- Réponse
-
\(x=4\)
Résoudre :\(\sqrt{x}+2=\sqrt{x+16}\).
- Réponse
-
\(x=9\)
Nous résumons les étapes ici. Nous avons ajusté nos étapes précédentes pour inclure plus d'un radical dans l'équation. Cette procédure fonctionne désormais pour toutes les équations radicales.
Résolvez une équation radicale
- Isolez l'un des termes radicaux d'un côté de l'équation.
- Augmentez les deux côtés de l'équation à la puissance de l'indice.
- Y a-t-il d'autres radicaux ?
Si c'est le cas, répétez les étapes 1 et 2.
Dans la négative, résolvez la nouvelle équation. - Vérifiez la réponse dans l'équation d'origine.
Faites attention lorsque vous mettez les binômes au carré dans l'exemple suivant. N'oubliez pas le motif dans\((a+b)^{2}=a^{2}+2 a b+b^{2}\) ou\((a-b)^{2}=a^{2}-2 a b+b^{2}\).
Résoudre :\(\sqrt{q-2}+3=\sqrt{4 q+1}\).
Solution :
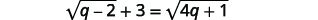 |
|
| Le radical de droite est isolé. Carrer les deux côtés. | 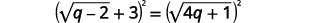 |
| Simplifiez. | 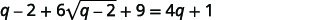 |
| Il y a toujours un radical dans l'équation, nous devons donc répéter les étapes précédentes. Isolez le radical. | 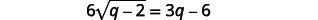 |
| Carrer les deux côtés. Il ne serait pas utile de diviser les deux camps\(6\). N'oubliez pas de mettre au carré le\(6\) et le\(\sqrt{q-2}\). | 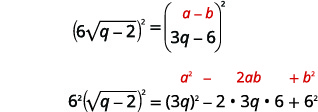 |
| Simplifiez, puis résolvez la nouvelle équation. | 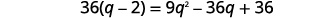 |
| Distribuez. | 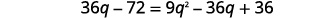 |
| C'est une équation quadratique, alors mettez zéro sur un côté. | 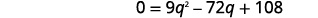 |
| Facteur du côté droit. | 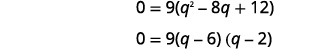 |
| Utilisez la propriété Zero Product. | 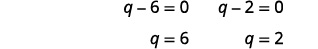 |
| Les chèques vous sont laissés. | Les solutions sont\(q=6\) et\(q=2\). |
Résoudre :\(\sqrt{x-1}+2=\sqrt{2 x+6}\)
- Réponse
-
\(x=5\)
Résoudre :\(\sqrt{x}+2=\sqrt{3 x+4}\)
- Réponse
-
\(x=0 x=4\)
Utiliser des radicaux dans les applications
Au fur et à mesure que vous progressez dans vos cours universitaires, vous rencontrerez des formules qui incluent des radicaux dans de nombreuses disciplines. Nous modifierons légèrement notre stratégie de résolution de problèmes pour les applications de géométrie afin de nous donner un plan de résolution des applications avec des formules issues de toutes les disciplines.
Utiliser une stratégie de résolution de problèmes pour les applications utilisant des formules
- Lisez le problème et assurez-vous que tous les mots et toutes les idées sont compris. Le cas échéant, dessinez une figure et étiquetez-la avec les informations fournies.
- Déterminez ce que nous recherchons.
- Nommez ce que vous recherchez en choisissant une variable pour le représenter.
- Traduisez en équation en écrivant la formule ou le modèle approprié à la situation. Remplacer dans les informations données.
- Résolvez l'équation en utilisant de bonnes techniques d'algèbre.
- Vérifiez la réponse au problème et assurez-vous qu'elle est logique.
- Répondez à la question par une phrase complète.
L'une des applications de radicaux concerne l'effet de la gravité sur les objets qui tombent. La formule nous permet de déterminer combien de temps il faudra à un objet tombé pour toucher le sol.
Définition\(\PageIndex{2}\)
Chute d'objets
Sur Terre, si un objet tombe d'une hauteur de\(h\) pieds, le temps en secondes qu'il faudra pour atteindre le sol est déterminé en utilisant la formule
\(t=\frac{\sqrt{h}}{4}\)
Par exemple, si un objet tombe d'une hauteur de\(64\) pieds, nous pouvons déterminer le temps qu'il faut pour atteindre le sol en le remplaçant\(h=64\) dans la formule.
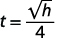 |
|
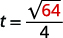 |
|
| Prenez la racine carrée de\(64\). | 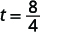 |
| Simplifiez la fraction. | 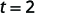 |
Il faudrait\(2\) quelques secondes pour qu'un objet tombé d'une hauteur de\(64\) pieds atteigne le sol.
Marissa a fait tomber ses lunettes de soleil d'un pont à\(400\) pieds au-dessus d'une rivière. Utilisez la formule\(t=\frac{\sqrt{h}}{4}\) pour déterminer le nombre de secondes qu'il a fallu aux lunettes de soleil pour atteindre la rivière.
Solution :
| Étape 1 : Lisez le problème | |
| Étape 2 : Identifiez ce que nous recherchons | Le temps qu'il faut aux lunettes de soleil pour atteindre la rivière. |
| Étape 3 : Nommez ce que nous recherchons. | Laissez (t= \) l'heure. |
| Étape 4 : Traduisez en équation en écrivant la formule appropriée. Remplacer dans les informations données. | 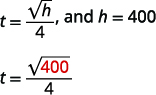 |
| Étape 5 : Résolvez l'équation |  |
 |
|
| Étape 6 : Vérifiez la réponse au problème et assurez-vous qu'elle est logique. | 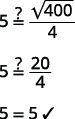 |
| Les\(5\) secondes semblent-elles être une durée raisonnable ? | Oui. |
| Étape 7 : Répondez à l'équation | Il faudra\(5\) quelques secondes pour que les lunettes de soleil atteignent la rivière. |
Un hélicoptère a largué un colis de secours d'une hauteur de\(1,296\) pieds. Utilisez la formule\(t=\frac{\sqrt{h}}{4}\) pour déterminer le nombre de secondes qu'il a fallu pour que le colis atteigne le sol.
- Réponse
-
\(9\)secondes
Un lave-vitres a fait tomber une raclette d'une plate-forme\(196\) située à pieds au-dessus du trottoir. Utilisez la formule\(t=\frac{\sqrt{h}}{4}\) pour déterminer le nombre de secondes qu'il a fallu à la raclette pour atteindre le trottoir.
- Réponse
-
\(3.5\)secondes
Les policiers qui enquêtent sur des accidents de voiture mesurent la longueur des marques de dérapage sur la chaussée. Ensuite, ils utilisent des racines carrées pour déterminer la vitesse, en miles par heure, qu'une voiture roulait avant d'appliquer les freins.
Définition\(\PageIndex{3}\)
Marques de dérapage et vitesse d'une voiture
Si la longueur des marques de dérapage est en\(d\) pieds, la vitesse de la voiture avant que les freins ne soient serrés peut être déterminée en utilisant la formule\(s\)
\(s=\sqrt{24 d}\)
Après un accident de voiture, les marques de dérapage d'une voiture mesuraient\(190\) les pieds. Utilisez la formule\(s=\sqrt{24d}\) pour déterminer la vitesse de la voiture avant que les freins ne soient serrés. Arrondissez votre réponse au dixième le plus proche.
Solution :
| Étape 1 : Lisez le problème | |
| Étape 2 : Identifiez ce que nous recherchons | La vitesse d'une voiture. |
| Étape 3 : Nommez ce que nous recherchons. | Laisse\(s=\) la vitesse. |
| Étape 4 : Traduisez en équation en écrivant la formule appropriée. Remplacer dans les informations données. | 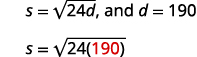 |
| Étape 5 : Résolvez l'équation | 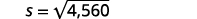 |
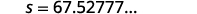 |
|
| Arrondir à la\(1\) décimale. |  |
 |
|
| La vitesse de la voiture avant que les freins ne soient serrés était de\(67.5\) milles à l'heure. |
Un enquêteur a mesuré les marques de dérapage de la voiture. La longueur des marques de dérapage était de\(76\) pieds. Utilisez la formule\(s=\sqrt{24d}\) pour déterminer la vitesse de la voiture avant que les freins ne soient serrés. Arrondissez votre réponse au dixième le plus proche.
- Réponse
-
\(42.7\)pieds
Les marques de dérapage d'un véhicule impliqué dans un accident\(122\) mesuraient des pieds. Utilisez la formule\(s=\sqrt{24d}\) pour déterminer la vitesse du véhicule avant que les freins ne soient actionnés. Arrondissez votre réponse au dixième le plus proche.
- Réponse
-
\(54.1\)pieds
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à résoudre des équations radicales.
- Résoudre une équation impliquant un seul radical
- Résolution d'équations avec des radicaux et des exposants rationnels
- Résoudre des équations
- Résoudre des équations
- Application de l'équation radicale
Concepts clés
- Carrés binomiaux
\(\begin{array}{l}{(a+b)^{2}=a^{2}+2 a b+b^{2}} \\ {(a-b)^{2}=a^{2}-2 a b+b^{2}}\end{array}\) - Résolvez une équation radicale
- Isolez l'un des termes radicaux d'un côté de l'équation.
- Augmentez les deux côtés de l'équation à la puissance de l'indice.
- Y a-t-il d'autres radicaux ?
Si c'est le cas, répétez les étapes 1 et 2.
Dans la négative, résolvez la nouvelle équation. - Vérifiez la réponse dans l'équation d'origine.
- Stratégie de résolution de problèmes pour les applications utilisant des formules
- Lisez le problème et assurez-vous que tous les mots et toutes les idées sont compris. Le cas échéant, dessinez une figure et étiquetez-la avec les informations fournies.
- Identifiez ce que nous recherchons.
- Nommez ce que vous recherchez en choisissant une variable pour le représenter.
- Traduisez en équation en écrivant la formule ou le modèle approprié à la situation. Remplacer dans les informations données.
- Résolvez l'équation en utilisant de bonnes techniques d'algèbre.
- Vérifiez la réponse au problème et assurez-vous qu'elle est logique.
- Répondez à la question par une phrase complète.
- Chute d'objets
- Sur Terre, si un objet tombe d'une hauteur de\(h\) pieds, le temps en secondes qu'il faudra pour atteindre le sol est déterminé à l'aide de la formule\(t=\frac{\sqrt{h}}{4}\).
- Marques de dérapage et vitesse d'une voiture
- Si la longueur des marques de dérapage est en\(d\) pieds, la vitesse de la voiture avant que les freins ne soient serrés peut être déterminée à l'aide de la formule\(s=\sqrt{24d}\).\(s\)
Lexique
- équation radicale
- Une équation dans laquelle une variable se trouve dans le radical et dans une expression radicale est appelée équation radicale.


