7.E : Exercices de révision du chapitre 7

Last updated
Save as PDF

Page ID: 194418

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Simplifier, multiplier et diviser les expressions rationnelles

Déterminer les valeurs pour lesquelles une expression rationnelle n'est pas définie

Dans les exercices suivants, déterminez les valeurs pour lesquelles l'expression rationnelle n'est pas définie.

1. $\dfrac{5 a+3}{3 a-2}$

Réponse: $a \neq \dfrac{2}{3}$

2. $\dfrac{b-7}{b^{2}-25}$

3. $\dfrac{5 x^{2} y^{2}}{8 y}$

Réponse: $y \neq 0$

4. $\dfrac{x-3}{x^{2}-x-30}$

Simplifier les expressions

Dans les exercices suivants, simplifiez.

5. $\dfrac{18}{24}$

Réponse: $\dfrac{3}{4}$

6. $\dfrac{9 m^{4}}{18 m n^{3}}$

7. $\dfrac{x^{2}+7 x+12}{x^{2}+8 x+16}$

Réponse: $\dfrac{x+3}{x+4}$

8. $\dfrac{7 v-35}{25-v^{2}}$

Multipliez les expressions

Dans les exercices suivants, multipliez.

9. $\dfrac{5}{8} \cdot \dfrac{4}{15}$

Réponse: $\dfrac{1}{6}$

10. $\dfrac{3 x y^{2}}{8 y^{3}} \cdot \dfrac{16 y^{2}}{24 x}$

11. $\dfrac{72 x-12 x^{2}}{8 x+32} \cdot \dfrac{x^{2}+10 x+24}{x^{2}-36}$

Réponse: $\dfrac{-3 x}{2}$

12. $\dfrac{6 y^{2}-2 y-10}{9-y^{2}} \cdot \dfrac{y^{2}-6 y+9}{6 y^{2}+29 y-20}$

Divisez les expressions

Dans les exercices suivants, divisez.

13. $\dfrac{x^{2}-4 x-12}{x^{2}+8 x+12} \div \dfrac{x^{2}-36}{3 x}$

Réponse: $\dfrac{3 x}{(x+6)(x+6)}$

14. $\dfrac{y^{2}-16}{4} \div \dfrac{y^{3}-64}{2 y^{2}+8 y+32}$

15. $\dfrac{11+w}{w-9} \div \dfrac{121-w^{2}}{9-w}$

Réponse: $\dfrac{1}{11+w}$

16. $\dfrac{3 y^{2}-12 y-63}{4 y+3} \div\left(6 y^{2}-42 y\right)$

17. $\dfrac{\dfrac{c^{2}-64}{3 c^{2}+26 c+16}}{\dfrac{c^{2}-4 c-32}{15 c+10}}$

Réponse: $\dfrac{5}{c+4}$

18. $\dfrac{8 a^{2}+16 a}{a-4} \cdot \dfrac{a^{2}+2 a-24}{a^{2}+7 a+10} \div \dfrac{2 a^{2}-6 a}{a+5}$

Multiplier et diviser les fonctions rationnelles

19. Trouvez$R(x)=f(x) \cdot g(x)$ où$f(x)=\dfrac{9 x^{2}+9 x}{x^{2}-3 x-4}$ et$g(x)=\dfrac{x^{2}-16}{3 x^{2}+12 x}$.

Réponse: $R(x)=3$

20. Trouvez$R(x)=\dfrac{f(x)}{g(x)}$ où$f(x)=\dfrac{27 x^{2}}{3 x-21}$ et$g(x)=\dfrac{9 x^{2}+54 x}{x^{2}-x-42} $.

Ajouter et soustraire des expressions rationnelles

Ajouter et soustraire des expressions rationnelles avec un dénominateur commun

Dans les exercices suivants, effectuez les opérations indiquées.

21. $\dfrac{7}{15}+\dfrac{8}{15}$

Réponse: $1$

22. $\dfrac{4 a^{2}}{2 a-1}-\dfrac{1}{2 a-1}$

23. $\dfrac{y^{2}+10 y}{y+5}+\dfrac{25}{y+5}$

Réponse: $y+5$

24. $\dfrac{7 x^{2}}{x^{2}-9}+\dfrac{21 x}{x^{2}-9}$

25. $\dfrac{x^{2}}{x-7}-\dfrac{3 x+28}{x-7}$

Réponse: $x+4$

26. $\dfrac{y^{2}}{y+11}-\dfrac{121}{y+11}$

27. $\dfrac{4 q^{2}-q+3}{q^{2}+6 q+5}-\dfrac{3 q^{2}-q-6}{q^{2}+6 q+5}$

Réponse: $\dfrac{q-3}{q+5}$

28. $\dfrac{5 t+4 t+3}{t^{2}-25}-\dfrac{4 t^{2}-8 t-32}{t^{2}-25}$

Additionner et soustraire des expressions rationnelles dont les dénominateurs sont opposés

Dans les exercices suivants, ajoutez et soustrayez.

29. $\dfrac{18 w}{6 w-1}+\dfrac{3 w-2}{1-6 w}$

Réponse: $\dfrac{15 w+2}{6 w-1}$

30. $\dfrac{a^{2}+3 a}{a^{2}-4}-\dfrac{3 a-8}{4-a^{2}}$

31. $\dfrac{2 b^{2}+3 b-15}{b^{2}-49}-\dfrac{b^{2}+16 b-1}{49-b^{2}}$

Réponse: $\dfrac{3 b-2}{b+7}$

32. $\dfrac{8 y^{2}-10 y+7}{2 y-5}+\dfrac{2 y^{2}+7 y+2}{5-2 y}$

Trouvez le plus petit dénominateur commun des expressions rationnelles

Dans les exercices suivants, trouvez l'écran LCD.

33. $\dfrac{7}{a^{2}-3 a-10}, \dfrac{3 a}{a^{2}-a-20}$

Réponse: $(a+2)(a-5)(a+4)$

34. $\dfrac{6}{n^{2}-4}, \dfrac{2 n}{n^{2}-4 n+4}$

35. $\dfrac{5}{3 p^{2}+17 p-6}, \dfrac{2 m}{3 p^{2}-23 p-8}$

Réponse: $(3 p+1)(p+6)(p+8)$

Ajouter et soustraire des expressions rationnelles avec des dénominateurs différents

Dans les exercices suivants, effectuez les opérations indiquées.

36. $\dfrac{7}{5 a}+\dfrac{3}{2 b}$

37. $\dfrac{2}{c-2}+\dfrac{9}{c+3}$

Réponse: $\dfrac{11 c-12}{(c-2)(c+3)}$

38. $\dfrac{3 x}{x^{2}-9}+\dfrac{5}{x^{2}+6 x+9}$

39. $\dfrac{2 x}{x^{2}+10 x+24}+\dfrac{3 x}{x^{2}+8 x+16}$

Réponse: $\dfrac{5 x^{2}+26 x}{(x+4)(x+4)(x+6)}$

40. $\dfrac{5 q}{p^{2} q-p^{2}}+\dfrac{4 q}{q^{2}-1}$

41. $\dfrac{3 y}{y+2}-\dfrac{y+2}{y+8}$

Réponse: $\dfrac{2\left(y^{2}+10 y-2\right)}{(y+2)(y+8)}$

42. $\dfrac{-3 w-15}{w^{2}+w-20}-\dfrac{w+2}{4-w}$

43. $\dfrac{7 m+3}{m+2}-5$

Réponse: $\dfrac{2 m-7}{m+2}$

44. $\dfrac{n}{n+3}+\dfrac{2}{n-3}-\dfrac{n-9}{n^{2}-9}$

45. $\dfrac{8 a}{a^{2}-64}-\dfrac{4}{a+8}$

Réponse: $\dfrac{4}{a-8}$

46. $\dfrac{5}{12 x^{2} y}+\dfrac{7}{20 x y^{3}}$

Ajouter et soustraire des fonctions rationnelles

Dans les exercices suivants, trouvez$R(x)=f(x)+g(x)$ où$f(x)$ et$g(x)$ recevez.

47. $f(x)=\dfrac{2 x^{2}+12 x-11}{x^{2}+3 x-10}, g(x)=\dfrac{x+1}{2-x}$

Réponse: $R(x)=\dfrac{x+8}{x+5}$

48. $f(x)=\dfrac{-4 x+31}{x^{2}+x-30}, g(x)=\dfrac{5}{x+6}$

Dans les exercices suivants, trouvez$R(x)=f(x)-g(x)$ où$f(x)$ et$g(x)$ recevez.

49. $f(x)=\dfrac{4 x}{x^{2}-121}, g(x)=\dfrac{2}{x-11}$

Réponse: $R(x)=\dfrac{2}{x+11}$

50. $f(x)=\dfrac{7}{x+6}, g(x)=\dfrac{14 x}{x^{2}-36}$

Simplifier les expressions rationnelles

Simplifiez une expression rationnelle complexe en l'écrivant sous forme de division

Dans les exercices suivants, simplifiez.

51. $\dfrac{\dfrac{7 x}{x+2}}{\dfrac{14 x^{2}}{x^{2}-4}}$

Réponse: $\dfrac{x-2}{2 x}$

52. $\dfrac{\dfrac{2}{5}+\dfrac{5}{6}}{\dfrac{1}{3}+\dfrac{1}{4}}$

53. $\dfrac{x-\dfrac{3 x}{x+5}}{\dfrac{1}{x+5}+\dfrac{1}{x-5}}$

Réponse: $\dfrac{(x-8)(x-5)}{2}$

54. $\dfrac{\dfrac{2}{m}+\dfrac{m}{n}}{\dfrac{n}{m}-\dfrac{1}{n}}$

Simplifiez une expression rationnelle complexe à l'aide de l'écran LCD

Dans les exercices suivants, simplifiez.

55. $\dfrac{\dfrac{1}{3}+\dfrac{1}{8}}{\dfrac{1}{4}+\dfrac{1}{12}}$

Réponse: $\dfrac{11}{8}$

56. $\dfrac{\dfrac{3}{a^{2}}-\dfrac{1}{b}}{\dfrac{1}{a}+\dfrac{1}{b^{2}}}$

57. $\dfrac{\dfrac{2}{z^{2}-49}+\dfrac{1}{z+7}}{\dfrac{9}{z+7}+\dfrac{12}{z-7}}$

Réponse: $\dfrac{z-5}{21 z+21}$

58. $\dfrac{\dfrac{3}{y^{2}-4 y-32}}{\dfrac{2}{y-8}+\dfrac{1}{y+4}}$

Résoudre des équations

Dans les exercices suivants, résolvez.

59. $\dfrac{1}{2}+\dfrac{2}{3}=\dfrac{1}{x}$

Réponse: $x=\dfrac{6}{7}$

60. $1-\dfrac{2}{m}=\dfrac{8}{m^{2}}$

61. $\dfrac{1}{b-2}+\dfrac{1}{b+2}=\dfrac{3}{b^{2}-4}$

Réponse: $b=\dfrac{3}{2}$

62. $\dfrac{3}{q+8}-\dfrac{2}{q-2}=1$

63. $\dfrac{v-15}{v^{2}-9 v+18}=\dfrac{4}{v-3}+\dfrac{2}{v-6}$

Réponse: aucune solution

64. $\dfrac{z}{12}+\dfrac{z+3}{3 z}=\dfrac{1}{z}$

Résoudre des équations rationnelles impliquant des fonctions

65. Pour un fonctionnement rationnel$f(x)=\dfrac{x+2}{x^{2}-6 x+8}$,

Trouvez le domaine de la fonction
Résoudre$f(x)=1$
Trouvez les points sur le graphique à cette valeur de fonction.

Réponse

Le domaine est composé uniquement de nombres réels, sauf$x \neq 2$ et$x \neq 4$
$x=1, x=6$
$(1,1),(6,1)$

66. Pour un fonctionnement rationnel$f(x)=\dfrac{2-x}{x^{2}+7 x+10}$,

Résoudre$f(x)=2$
Trouvez les points sur le graphique à cette valeur de fonction.

Résoudre une équation rationnelle pour une variable spécifique

Dans les exercices suivants, résolvez la variable indiquée.

67. $\dfrac{V}{l}=h w$pour$l$

Réponse: $l=\dfrac{V}{h w}$

68. $\dfrac{1}{x}-\dfrac{2}{y}=5$pour$y$

69. $x=\dfrac{y+5}{z-7}$pour$z$

Réponse: $z=\dfrac{y+5+7 x}{x}$

70. $P=\dfrac{k}{V}$pour$V$

Résoudre des applications avec des équations

Résoudre les proportions

Dans les exercices suivants, résolvez.

71. $\dfrac{x}{4}=\dfrac{3}{5}$

Réponse: $x = \dfrac{12}{5}$

72. $\dfrac{3}{y}=\dfrac{9}{5}$

73. $\dfrac{s}{s+20}=\dfrac{3}{7}$

Réponse: $s = 15$

74. $\dfrac{t-3}{5}=\dfrac{t+2}{9}$

Résolvez des applications en utilisant

Dans les exercices suivants, résolvez.

75. Rachael a mangé un shake aux fraises de 21 onces contenant 739 calories. Combien de calories y a-t-il dans un shake de 32 onces ?

Réponse: 1161 calories

76. Leo est allé au Mexique pendant les vacances de Noël et a changé 525 dollars en pesos mexicains. À cette époque, le taux de change était de 1 dollar américain, soit 16,25 pesos mexicains. Combien de pesos mexicains a-t-il reçu pour son voyage ?

Résoudre des applications de figures similaires

Dans les exercices suivants, résolvez.

77. $\Delta ABC$est similaire à$\Delta XYZ$. Les longueurs des deux côtés de chaque triangle sont indiquées sur la figure. Déterminez la longueur des troisièmes côtés.

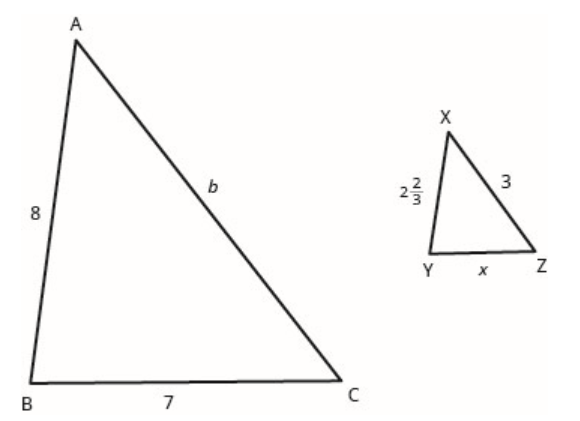
$clipboard_e3ea5ba04cf9cf3eca601a80313183f6d.png$

Réponse: $b=9 ; \; x=2 \dfrac{1}{3}$

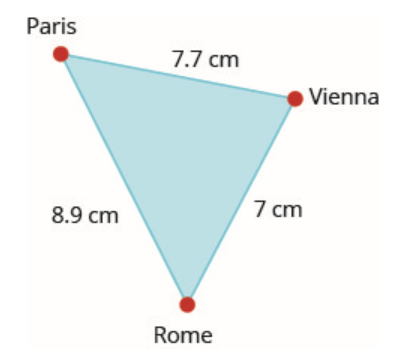
78. Sur une carte de l'Europe, Paris, Rome et Vienne forment un triangle dont les côtés sont illustrés dans la figure ci-dessous. Si la distance réelle entre Rome et Vienne est de 700 miles, trouvez la distance entre

Paris à Rome
Paris à Vienne

$clipboard_e52ae790b0233f8e2e5c50b849fb21443.png$

79. Francesca mesure 5,75 pieds. En fin d'après-midi, son ombre mesurait 8 pieds de long. Au même moment, l'ombre d'un arbre voisin mesurait 32 pieds de long. Trouve la hauteur de l'arbre.

Réponse: 23 pieds

80. La hauteur d'un phare de Pensacola, en Floride, est de 150 pieds. Debout à côté de la statue, Natasha, haute de 5,5 pieds, a jeté une ombre de 1,1 pied. Combien de temps durerait l'ombre du phare ?

Résolvez des applications de mouvements

Dans les exercices suivants, résolvez.

81. En faisant les 5 heures de route pour rentrer chez elle après avoir rendu visite à ses parents, Lolo a rencontré du mauvais temps. Elle a pu parcourir 176 milles par beau temps, mais elle a ensuite roulé 10 mi/h plus lentement et a parcouru 81 milles lorsqu'il a mal tourné. À quelle vitesse conduisait-elle par mauvais temps ?

Réponse: 45 mi/h

82. Mark est à bord d'un avion capable de parcourir 490 miles avec un vent arrière de 20 mi/h en même temps qu'il peut parcourir 350 miles contre un vent arrière de 20 mi/h. Quelle est la vitesse de l'avion ?

83. Josue peut faire du vélo 8 mph plus vite qu'Arjun ne peut faire du vélo. Luke met 3 heures de plus que Josue pour parcourir 48 miles. À quelle vitesse John peut-il faire du vélo ?

Réponse: 16 mi/h

84. Curtis s'entraînait pour un triathlon. Il a couru 8 kilomètres et parcouru 32 kilomètres à vélo en 3 heures au total. Sa vitesse de course était inférieure de 8 kilomètres à l'heure à celle de sa moto. Quelle était sa vitesse de course ?

Résoudre les applications professionnelles

Dans les exercices suivants, résolvez.

85. Brandy peut encadrer une pièce en 1 heure, tandis que Jake prend 4 heures. Combien de temps pourraient-ils encadrer une pièce en travaillant ensemble ?

Réponse: $\dfrac{4}{5}$heure

86. Prem met 3 heures pour tondre la pelouse tandis que sa cousine, Barb, prend 2 heures. Combien de temps leur faudra-t-il pour travailler ensemble ?

87. Jeffrey peut peindre une maison en 6 jours, mais s'il reçoit une aide, il peut le faire en 4 jours. Combien de temps faudrait-il à l'assistant pour peindre la maison seul ?

Réponse: 12 jours

88. Marta et Deb travaillent ensemble pour écrire un livre qui leur prend 90 jours. Si Sue travaillait seule, cela lui prendrait 120 jours. Combien de temps faudrait-il à Deb pour écrire le livre seule ?

Résoudre les problèmes de variation directe

Dans les exercices suivants, résolvez.

89. Cela$y$ varie directement selon le$x$ moment$y=9$ et$x=3$, trouvez$x$ quand$y=21$.

Réponse: $7$

90. Cela$y$ varie inversement selon le$x$ moment$y=20$ et le$x=2$ moment$y$ où$x=4$.

91. Vanessa est en voyage pour voir son fiancé. La distance varie directement avec la vitesse qu'$v$elle conduit.$d$ Si elle parcourt 258 miles à 60 mi/h, jusqu'où parcourrait-elle à 70 mi/h ?

Réponse: 301 mi/h

92. Si le coût d'une pizza varie directement en fonction de son diamètre, et si une pizza de 8 pouces de diamètre coûte 12$, combien coûterait une pizza de 6 pouces de diamètre ?

93. La distance à parcourir pour arrêter une voiture varie directement avec le carré de sa vitesse. Il faut 200 pieds pour arrêter une voiture qui roule à 50 km/h. Combien de pieds faudrait-il pour arrêter une voiture à 60 mi/h ?

Réponse: 288 pieds

Résoudre les problèmes de variation inverse

Dans les exercices suivants, résolvez.

94. Il$m$ varie inversement avec le carré de$n$, quand$m=4$ et$n=6$ trouve$m$ quand$n=2$.

95. Le nombre de billets pour une collecte de fonds musicale varie inversement en fonction du prix des billets. Si Madelyn a juste assez d'argent pour acheter 12 billets pour 6$, combien de billets Madelyn pourrait-elle se permettre d'acheter si le prix augmentait à 8$ ?

Réponse: 97 billets

96. Sur un instrument à cordes, la longueur d'une corde varie inversement avec la fréquence de ses vibrations. Si une corde de 11 pouces sur un violon a une fréquence de 360 cycles par seconde, quelle est la fréquence d'une corde de 12 pouces ?

Résolution des inégalités rationnelles

Dans les exercices suivants, résolvez chaque inégalité rationnelle et écrivez la solution en notation par intervalles.

97. $\dfrac{x-3}{x+4} \leq 0$

Réponse: $(-4,3]$

98. $\dfrac{5 x}{x-2}>1$

99. $\dfrac{3 x-2}{x-4} \leq 2$

Réponse: $[-6,4)$

100. $\dfrac{1}{x^{2}-4 x-12}<0$

101. $\dfrac{1}{2}-\dfrac{4}{x^{2}} \geq \dfrac{1}{x}$

Réponse: $(-\infty,-2] \cup[4, \infty)$

102. $\dfrac{4}{x-2}<\dfrac{3}{x+1}$

Résolvez une inégalité avec des fonctions rationnelles

Dans les exercices suivants, résolvez chaque inégalité de fonction rationnelle et écrivez la solution en notation par intervalles

103. En fonction de la fonction$R(x)=\dfrac{x-5}{x-2}$, trouvez les valeurs$x$ qui rendent la fonction supérieure ou égale à 0.

Réponse: $(-\infty, 2) \cup[5, \infty)$

104. En fonction de la fonction$R(x)=\dfrac{x+1}{x+3}$, trouvez les valeurs$x$ qui rendent la fonction supérieure ou égale à 0.

105. La fonction$C(x)=150 x+100,000$ représente le coût de production$x$, le nombre d'articles. Trouvez

La fonction de coût moyen,$c(x)$
Combien d'articles doivent être produits pour que le coût moyen soit inférieur à 160$.

Réponse

$c(x)=\dfrac{150 x+100000}{x}$
Plus de 10 000 articles doivent être produits pour maintenir le coût moyen en dessous de 160$ par article.

106. Tillman lance sa propre entreprise en vendant des tacos à la plage. Compte tenu du coût de son food truck et des ingrédients pour les tacos, la fonction$C(x)=2 x+6,000$ représente le coût de production des$x$ tacos pour Tillman. Trouvez

La fonction de coût moyen,$c(x)$ pour Tillman's Tacos
Combien de tacos Tillman devrait-il produire pour que le coût moyen soit inférieur à 4 dollars ?

Test d'entraînement

Dans les exercices suivants, simplifiez.

1. $\dfrac{4 a^{2} b}{12 a b^{2}}$

Réponse: $\dfrac{a}{3 b}$

2. $\dfrac{6 x-18}{x^{2}-9}$

Dans les exercices suivants, effectuez l'opération indiquée et simplifiez.

3. $\dfrac{4 x}{x+2} \cdot \dfrac{x^{2}+5 x+6}{12 x^{2}}$

Réponse: $\dfrac{x+3}{3 x}$

4. $\dfrac{2 y^{2}}{y^{2}-1} \div \dfrac{y^{3}-y^{2}+y}{y^{3}-1}$

5. $\dfrac{6 x^{2}-x+20}{x^{2}-81}-\dfrac{5 x^{2}+11 x-7}{x^{2}-81}$

Réponse: $\dfrac{x-3}{x+9}$

6. $\dfrac{-3 a}{3 a-3}+\dfrac{5 a}{a^{2}+3 a-4}$

7. $\dfrac{2 n^{2}+8 n-1}{n^{2}-1}-\dfrac{n^{2}-7 n-1}{1-n^{2}}$

Réponse: $\dfrac{3 n-2}{n-1}$

8. $\dfrac{10 x^{2}+16 x-7}{8 x-3}+\dfrac{2 x^{2}+3 x-1}{3-8 x}$

9. $\dfrac{\dfrac{1}{m}-\dfrac{1}{n}}{\dfrac{1}{n}+\dfrac{1}{m}}$

Réponse: $\dfrac{n-m}{m+n}$

Dans les exercices suivants, résolvez chaque équation.

10. $\dfrac{1}{x}+\dfrac{3}{4}=\dfrac{5}{8}$

11. $\dfrac{1}{z-5}+\dfrac{1}{z+5}=\dfrac{1}{z^{2}-25}$

Réponse: $z=\dfrac{1}{2}$

12. $\dfrac{z}{2 z+8}-\dfrac{3}{4 z-8}=\dfrac{3 z^{2}-16 z-16}{8 z^{2}+2 z-64}$

Dans les exercices suivants, résolvez chaque inégalité rationnelle et écrivez la solution en notation par intervalles.

13. $\dfrac{6 x}{x-6} \leq 2$

Réponse: $[-3,6)$

14. $\dfrac{2 x+3}{x-6}>1$

15. $\dfrac{1}{2}+\dfrac{12}{x^{2}} \geq \dfrac{5}{x}$

Réponse: $(-\infty, 0) \cup(0,4] \cup[6, \infty)$

Dans les exercices suivants, trouvez$R(x)$ donné$f(x)=\dfrac{x-4}{x^{2}-3 x-10}$ et$g(x)=\dfrac{x-5}{x^{2}-2 x-8}$.

16. $R(x)=f(x)-g(x)$

17. $R(x)=f(x) \cdot g(x)$

Réponse: $R(x)=\dfrac{1}{(x+2)(x+2)}$

18. $R(x)=f(x) \div g(x)$

19. En fonction de la fonction$R(x)=\dfrac{2}{2 x^{2}+x-15}$, trouvez les valeurs$x$ qui rendent la fonction inférieure ou égale à 0.

Réponse: $(2,5]$

Dans les exercices suivants, résolvez.

20. Cela$y$ varie directement avec$x$, et$x=5$ quand$y=30$, trouvez$x$ quand$y=42$.

21. Il$y$ varie inversement avec le carré de$x$ et$x=3$ quand$y=9$, trouvez$y$ quand$x=4$.

Réponse: $y=\dfrac{81}{16}$

22. Matheus peut parcourir 30 miles à vélo avec le vent en autant de temps qu'il peut parcourir 33 miles contre le vent. Si la vitesse du vent est de 6 mph, quelle est la vitesse de Matheus sur son vélo ?

23. Oliver peut diviser un camion de grumes en 8 heures, mais en travaillant avec son père, ils peuvent le faire en 3 heures. Combien de temps faudrait-il au père d'Oliver pour travailler seul pour partager les journaux ?

Réponse: Le père d'Oliver mettait des$4 \dfrac{4}{5}$ heures à partager les journaux lui-même.

24. Le volume d'un gaz dans un récipient varie inversement avec la pression sur le gaz. Si un réservoir d'azote a un volume de 29,5 litres à 2 000 psi, quel est le volume si le réservoir a une capacité nominale de 14,7 psi ? Arrondir au nombre entier le plus proche.

25.

Les villes de Dayton, Columbus et Cincinnati forment un triangle dans le sud de l'Ohio. Le diagramme indique les distances cartographiques entre ces villes en pouces.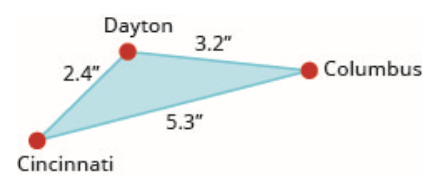

$clipboard_ed99a0bbb595e2e6dbfc06d21e311369b.png$

La distance réelle entre Dayton et Cincinnati est de 48 miles. Quelle est la distance réelle entre Dayton et Columbus ?

Réponse: La distance entre Dayton et Columbus est de 64 miles.