7.3 : Ajouter et soustraire des expressions rationnelles
- Page ID
- 194426
À la fin de cette section, vous serez en mesure de :
- Ajouter et soustraire des expressions rationnelles avec un dénominateur commun
- Additionner et soustraire des expressions rationnelles dont les dénominateurs sont opposés
- Trouvez le plus petit dénominateur commun des expressions rationnelles
- Ajouter et soustraire des expressions rationnelles avec des dénominateurs différents
- Ajouter et soustraire des fonctions rationnelles
Ajouter et soustraire des expressions rationnelles avec un dénominateur commun
Quelle est la première étape que vous effectuez lorsque vous ajoutez des fractions numériques ? Vous vérifiez s'ils ont un dénominateur commun. Si tel est le cas, vous ajoutez les numérateurs et placez la somme au-dessus du dénominateur commun. S'ils n'ont pas de dénominateur commun, vous en trouvez un avant de les additionner.
Il en va de même pour les expressions rationnelles. Pour ajouter des expressions rationnelles, elles doivent avoir un dénominateur commun. Lorsque les dénominateurs sont identiques, vous ajoutez les numérateurs et placez la somme au-dessus du dénominateur commun.
Si\(p\)\(q\), et\(r\) sont des polynômes où\(r\neq 0\), alors
\[\dfrac{p}{r}+\dfrac{q}{r}=\dfrac{p+q}{r} \quad \text{and} \quad \dfrac{p}{r}−\dfrac{q}{r}=\dfrac{p−q}{r}\nonumber\]
Pour ajouter ou soustraire des expressions rationnelles ayant un dénominateur commun, ajoutez ou soustrayez les numérateurs et placez le résultat au-dessus du dénominateur commun.
Nous simplifions toujours les expressions rationnelles. Assurez-vous de prendre en compte, si possible, après avoir soustrait les numérateurs afin de pouvoir identifier les facteurs communs.
N'oubliez pas non plus que nous n'autorisons pas les valeurs qui rendraient le dénominateur zéro. Quelle valeur de\(x\) doit être exclue dans l'exemple suivant ?
Ajoutez :\(\dfrac{11x+28}{x+4}+\dfrac{x^2}{x+4}\).
Solution
Puisque le dénominateur est\(x+4\), nous devons exclure la valeur\(x=−4\).
\(\begin{array} {ll} &\dfrac{11x+28}{x+4}+\dfrac{x^2}{x+4},\space x\neq −4 \\ \begin{array} {l} \text{The fractions have a common denominator,} \\ \text{so add the numerators and place the sum} \\ \text{over the common denominator.} \end{array} &\dfrac{11x+28+x^2}{x+4} \\ & \\ \text{Write the degrees in descending order.} &\dfrac{x^2+11x+28}{x+4} \\ & \\ \text{Factor the numerator.} &\dfrac{(x+4)(x+7)}{x+4} \\ & \\ \text{Simplify by removing common factors.} &\dfrac{\cancel{(x+4)}(x+7)}{\cancel{x+4}} \\ & \\ \text{Simplify.} &x+7 \end{array}\)
L'expression se simplifie en\(x+7\) mais l'expression d'origine en avait un dénominateur\(x\neq −4\).\(x+4\)
Simplifiez :\(\dfrac{9x+14}{x+7}+\dfrac{x^2}{x+7}\).
- Réponse
-
\(x+2\)
Simplifiez :\(\dfrac{x^2+8x}{x+5}+\dfrac{15}{x+5}\).
- Réponse
-
\(x+3\)
Pour soustraire des expressions rationnelles, elles doivent également avoir un dénominateur commun. Lorsque les dénominateurs sont identiques, vous soustrayez les numérateurs et placez la différence au-dessus du dénominateur commun. Faites attention aux signes lorsque vous soustrayez un binôme ou un trinôme.
Soustraire :\(\dfrac{5x^2−7x+3}{x^2−3x+18}−\dfrac{4x^2+x−9}{x^2−3x+18}\).
Solution
\(\begin{array} {ll} &\dfrac{5x^2−7x+3}{x^2−3x+18}−\dfrac{4x^2+x−9}{x^2−3x+18} \\ & \\ \begin{array} {l} \text{Subtract the numerators and place the} \\ \text{difference over the common denominator.} \end{array} &\dfrac{5x^2−7x+3−(4x^2+x−9)}{x^2−3x+18} \\ & \\ \text{Distribute the sign in the numerator.} &\dfrac{5x^2−7x+3−4x^2−x+9}{x^2−3x−18} \\ & \\ \text{Combine like terms.} &\dfrac{x^2−8x+12}{x^2−3x−18} \\ & \\ \text{Factor the numerator and the denominator.} &\dfrac{(x−2)(x−6)}{(x+3)(x−6)} \\ & \\ \text{Simplify by removing common factors.} &\dfrac{(x−2)\cancel{(x−6)}}{(x+3)\cancel{(x−6)}} \\ & \\ &(x−2)(x+3) \end{array}\)
Soustraire :\(\dfrac{4x^2−11x+8}{x^2−3x+2}−\dfrac{3x^2+x−3}{x^2−3x+2}\).
- Réponse
-
\(\dfrac{x−11}{x−2}\)
Soustraire :\(\dfrac{6x^2−x+20}{x^2−81}−\dfrac{5x^2+11x−7}{x^2−81}\).
- Réponse
-
\(\dfrac{x−3}{x+9}\)
Additionner et soustraire des expressions rationnelles dont les dénominateurs sont opposés
Lorsque les dénominateurs de deux expressions rationnelles sont opposés, il est facile d'obtenir un dénominateur commun. Il suffit de multiplier l'une des fractions par\(\dfrac{−1}{−1}\).
Voyons comment cela fonctionne.
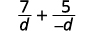 |
|
| Multipliez la deuxième fraction par\(\dfrac{−1}{−1}\). | 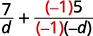 |
| Les dénominateurs sont les mêmes. | 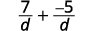 |
| Simplifiez. | 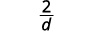 |
Faites attention aux signes lorsque vous travaillez avec les contraires lorsque vous soustrayez les fractions.
Soustraire :\(\dfrac{m^2−6m}{m^2−1}−\dfrac{3m+2}{1−m^2}\).
Solution
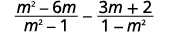 |
|
|
Les dénominateurs étant opposés, multipliez la |
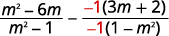 |
| Simplifiez la deuxième fraction. | 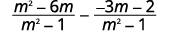 |
| Les dénominateurs sont les mêmes. Soustrayez les numérateurs. | 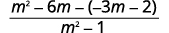 |
| Distribuez. | 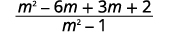 |
| Combinez les mêmes termes. | 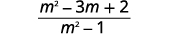 |
| Facturez le numérateur et le dénominateur. | 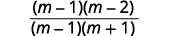 |
| Simplifiez en supprimant les facteurs courants. | 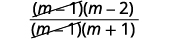 |
| Simplifiez. | 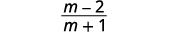 |
Soustraire :\(\dfrac{y^2−5y}{y^2−4}−\dfrac{6y−6}{4−y^2}\).
- Réponse
-
\(\dfrac{y+3}{y+2}\)
Soustraire :\(\dfrac{2n^2+8n−1}{n^2−1}−\dfrac{n^2−7n−1}{1−n^2}\).
- Réponse
-
\(\dfrac{3n−2}{n−1}\)
Trouvez le plus petit dénominateur commun des expressions rationnelles
Lorsque nous ajoutons ou soustrayons des expressions rationnelles ayant des dénominateurs différents, nous devons obtenir des dénominateurs communs. Si nous revoyons la procédure que nous avons utilisée avec les fractions numériques, nous saurons quoi faire avec les expressions rationnelles.
Regardons cet exemple :\(\dfrac{7}{12}+\dfrac{5}{18}\). Comme les dénominateurs ne sont pas les mêmes, la première étape a consisté à trouver le plus petit dénominateur commun (LCD).
Pour trouver l'écran LCD des fractions, nous avons factorisé 12 et 18 en nombres premiers, en alignant tous les nombres premiers courants dans des colonnes. Ensuite, nous avons « abaissé » un nombre premier de chaque colonne. Enfin, nous avons multiplié les facteurs pour trouver l'écran LCD.
Lorsque nous ajoutons des fractions numériques, une fois que nous avons trouvé l'écran LCD, nous avons réécrit chaque fraction en tant que fraction équivalente avec l'écran LCD en multipliant le numérateur et le dénominateur par le même nombre. Nous sommes maintenant prêts à ajouter.
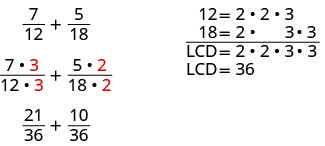
Nous faisons de même pour les expressions rationnelles. Cependant, nous laissons l'écran LCD sous forme pondérée.
- Facturez complètement chaque dénominateur.
- Énumérez les facteurs de chaque dénominateur. Faites correspondre les facteurs verticalement lorsque cela est possible.
- Réduisez les colonnes en incluant tous les facteurs, mais n'incluez pas deux fois les facteurs communs.
- Écrivez l'écran LCD comme le produit des facteurs.
N'oubliez pas que nous excluons toujours les valeurs qui rendraient le dénominateur zéro. Quelles valeurs de xx devons-nous exclure dans le prochain exemple ?
a. Trouvez l'écran LCD des expressions\(\dfrac{8}{x^2−2x−3}\),\(\dfrac{3x}{x^2+4x+3}\) et b. réécrivez-les en tant qu'expressions rationnelles équivalentes avec le plus petit dénominateur commun.
Solution
un.
| Trouvez l'écran LCD pour\(\dfrac{8}{x^2−2x−3}\),\(\dfrac{3x}{x^2+4x+3}\). | |
| Facturez complètement chaque dénominateur en alignant les facteurs communs. Abattez les colonnes. |
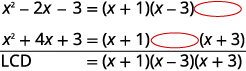 |
| Écrivez l'écran LCD comme le produit des facteurs. | 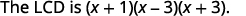 |
b.
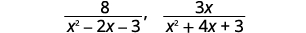 |
|
| Facturez chaque dénominateur. | 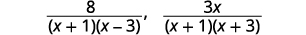 |
| Multipliez chaque dénominateur par le facteur LCD « manquant » et multipliez chaque numérateur par le même facteur. |
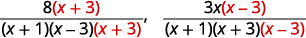 |
| Simplifiez les numérateurs. | 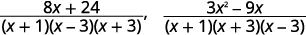 |
a. Trouvez l'écran LCD des expressions\(\dfrac{2}{x^2−x−12}\),\(\dfrac{1}{x^2−16}\) b. réécrivez-les en tant qu'expressions rationnelles équivalentes avec le plus petit dénominateur commun.
- Réponse
-
a.\((x−4)(x+3)(x+4)\)
b.\(\dfrac{2x+8}{(x−4)(x+3)(x+4)}\),
\(\dfrac{x+3}{(x−4)(x+3)(x+4)}\)
a. Trouvez l'écran LCD des expressions\(\dfrac{3x}{x^2−3x+10}\),\(\dfrac{5}{x^2+3x+2}\) b. réécrivez-les en tant qu'expressions rationnelles équivalentes avec le plus petit dénominateur commun.
- Réponse
-
a.\((x+2)(x−5)(x+1)\)
b.\(\dfrac{3x^2+3x}{(x+2)(x−5)(x+1)}\),
\(\dfrac{5x−25}{(x+2)(x−5)(x+1)}\)
Ajouter et soustraire des expressions rationnelles avec des dénominateurs différents
Nous avons maintenant toutes les étapes nécessaires pour ajouter ou soustraire des expressions rationnelles avec des dénominateurs différents.
Ajoutez :\(\dfrac{3}{x−3}+\dfrac{2}{x−2}\).
Solution



Ajoutez :\(\dfrac{2}{x−2}+\dfrac{5}{x+3}\).
- Réponse
-
\(\dfrac{7x−4}{(x−2)(x+3)}\)
Ajoutez :\(\dfrac{4}{m+3}+\dfrac{3}{m+4}\).
- Réponse
-
\(\dfrac{7m+25}{(m+3)(m+4)}\)
Les étapes utilisées pour ajouter des expressions rationnelles sont résumées ici.
- Déterminez si les expressions ont un dénominateur commun.
- Oui, passez à l'étape 2.
- Non — Réécrivez chaque expression rationnelle à l'aide de l'écran LCD.
- Trouvez l'écran LCD.
- Réécrivez chaque expression rationnelle en tant qu'expression rationnelle équivalente à l'aide de l'écran LCD.
- Ajoutez ou soustrayez les expressions rationnelles.
- Simplifiez, si possible.
Évitez la tentation de simplifier trop tôt. Dans l'exemple ci-dessus, il faut laisser la première expression rationnelle\(\dfrac{3x−6}{(x−3)(x−2)}\) pour pouvoir l'ajouter\(\dfrac{2x−6}{(x−2)(x−3)}\). Simplifiez uniquement après avoir combiné les numérateurs.
Ajoutez :\(\dfrac{8}{x^2−2x−3}+\dfrac{3x}{x^2+4x+3}\).
Solution
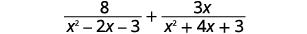 |
|
| Les expressions ont-elles un dénominateur commun ? | Non |
| Réécrivez chaque expression à l'aide de l'écran LCD. | |
| \(\begin{array} {ll} & \\ & \\ \text{Find the LCD.} &\begin{array} {l} \hspace{5mm} x^2−2x−3=(x+1)(x−3) \\ \underline{x^2+4x+3=(x+1)\quad (x+3)} \\ & \\ \qquad LCD=(x+1)(x−3)(x+3) \end{array} \end{array} \) | |
| Réécrivez chaque expression rationnelle en tant qu'expression rationnelle équivalente à l'aide de l'écran LCD. |
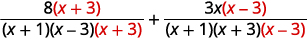 |
| Simplifiez les numérateurs. | 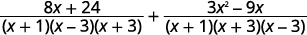 |
| Ajoutez les expressions rationnelles. | 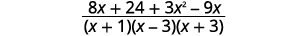 |
| Simplifiez le numérateur. | 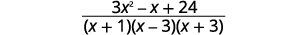 |
| Le numérateur est premier, il n'y a donc pas de facteurs communs. |
Ajoutez :\(\dfrac{1}{m^2−m−2}+\dfrac{5m}{m^2+3m+2}\).
- Réponse
-
\(\dfrac{5m^2−9m+2}{(m+1)(m−2)(m+2)}\)
Ajoutez :\(\dfrac{2n}{n^2−3n−10}+\dfrac{6}{n^2+5n+6}\).
- Réponse
-
\(\dfrac{2n^2+12n−30}{(n+2)(n−5)(n+3)}\)
Le processus que nous utilisons pour soustraire des expressions rationnelles avec différents dénominateurs est le même que pour l'addition. Il faut juste faire très attention aux signes lors de la soustraction des numérateurs.
Soustraire :\(\dfrac{8y}{y^2−16}−\dfrac{4}{y−4}\).
Solution
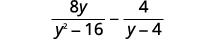 |
|
| Les expressions ont-elles un dénominateur commun ? | Non |
| Réécrivez chaque expression à l'aide de l'écran LCD. | |
| \(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} y^2−16=(y−4)(y+4) \\ \quad \underline{y−4=y−4} \\ LCD=(y−4)(y+4) \end{array} \end{array} \) | |
| Réécrivez chaque expression rationnelle en tant qu'expression rationnelle équivalente à l'aide de l'écran LCD. |
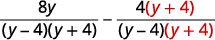 |
| Simplifiez les numérateurs. | 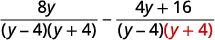 |
| Soustrayez les expressions rationnelles. | 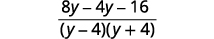 |
| Simplifiez le numérateur. | 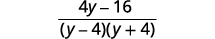 |
| Facturez le numérateur pour rechercher des facteurs communs. | 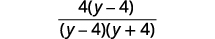 |
| Supprimer les facteurs courants | 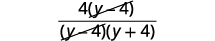 |
| Simplifiez. | 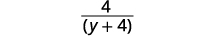 |
Soustraire :\(\dfrac{2x}{x^2−4}−\dfrac{1}{x+2}\).
- Réponse
-
\(\dfrac{1}{x−2}\)
Soustraire :\(\dfrac{3}{z+3}−\dfrac{6z}{z^2−9}\).
- Réponse
-
\(\dfrac{−3}{z−3}\)
Il y a beaucoup de signes négatifs dans l'exemple suivant. Fais très attention.
Soustraire :\(\dfrac{−3n−9}{n^2+n−6}−\dfrac{n+3}{2−n}\).
Solution
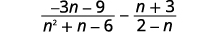 |
|
| Facturez le dénominateur. | 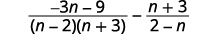 |
| Puisque\(n−2\) et\(2−n\) sont opposés, nous allons multiplier la deuxième expression rationnelle par\(\dfrac{−1}{−1}\). |
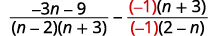 |
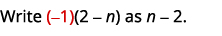 |
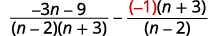 |
| Simplifiez. N'oubliez pas,\(a−(−b)=a+b\). | 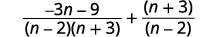 |
| Les expressions rationnelles ont-elles un dénominateur commun ? Non |
|
| \(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} n^2+n−6=(n−2)(n+3) \\ \quad\underline{n−2=(n−2)} \\ LCD=\quad (n−2)(n+3) \end{array} \end{array} \) | |
| Réécrivez chaque expression rationnelle en tant qu'expression rationnelle équivalente à l'aide de l'écran LCD. |
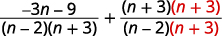 |
| Simplifiez les numérateurs. | 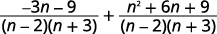 |
| Ajoutez les expressions rationnelles. | 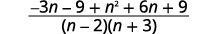 |
| Simplifiez le numérateur. | 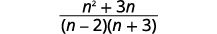 |
| Facturez le numérateur pour rechercher des facteurs communs. | 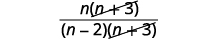 |
| Simplifiez. | 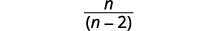 |
Soustraire :\(\dfrac{3x−1}{x^2−5x−6}−\dfrac{2}{6−x}\).
- Réponse
-
\(\dfrac{5x+1}{(x−6)(x+1)}\)
Soustraire :\(\dfrac{−2y−2}{y^2+2y−8}−\dfrac{y−1}{2−y}\).
- Réponse
-
\(\dfrac{y+3}{y+4}\)
Les choses peuvent devenir très compliquées lorsque les deux fractions doivent être multipliées par un binôme pour obtenir le dénominateur commun.
Soustraire :\(\dfrac{4}{a^2+6a+5}−\dfrac{3}{a^2+7a+10}\).
Solution
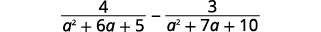 |
|
| Facturez les dénominateurs. | 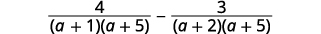 |
| Les expressions rationnelles ont-elles un dénominateur commun ? Non |
|
|
\(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} a^2+6a+5=(a+1)(a+5) \\ \underline{a^2+7a+10=(a+5)(a+2)} \\ LCD=(a+1)(a+5)(a+2) \end{array} \end{array} \) |
|
| Réécrivez chaque expression rationnelle en tant qu'expression rationnelle équivalente à l'aide de l'écran LCD. |
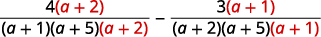 |
| Simplifiez les numérateurs. | 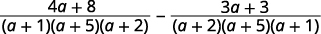 |
| Soustrayez les expressions rationnelles. | 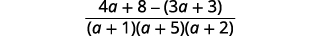 |
| Simplifiez le numérateur. | 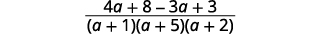 |
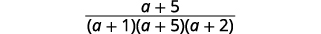 |
|
| Recherchez les facteurs communs. | 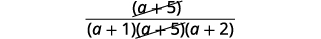 |
| Simplifiez. | 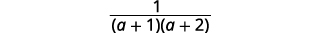 |
Soustraire :\(\dfrac{3}{b^2−4b−5}−\dfrac{2}{b^2−6b+5}\).
- Réponse
-
\(\dfrac{1}{(b+1)(b−1)}\)
Soustraire :\(\dfrac{4}{x^2−4}−\dfrac{3}{x^2−x−2}\).
- Réponse
-
\(\dfrac{1}{(x+2)(x+1)}\)
Nous suivons les mêmes étapes que précédemment pour trouver l'écran LCD lorsque nous avons plus de deux expressions rationnelles. Dans l'exemple suivant, nous allons commencer par factoriser les trois dénominateurs pour trouver leur écran LCD.
Simplifiez :\(\dfrac{2u}{u−1}+\dfrac{1}{u}−\dfrac{2u−1}{u^2−u}\).
Solution
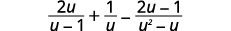 |
|
| Les expressions ont-elles un dénominateur commun ? Non Réécrivez chaque expression à l'aide de l'écran LCD. |
|
| \(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} u−1=(u−1) \\ u=u \\ \underline{u^2−u=u(u−1)} \\ LCD=u(u−1) \end{array} \end{array}\) | |
| Réécrivez chaque expression rationnelle en tant qu'expression rationnelle équivalente à l'aide de l'écran LCD. |
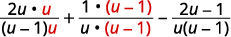 |
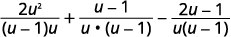 |
|
| Écrivez comme une expression rationnelle. | 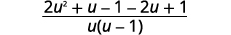 |
| Simplifiez. | 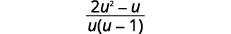 |
| Facturez le numérateur et supprimez les facteurs communs. |
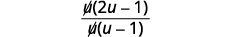 |
| Simplifiez. | 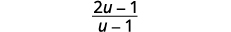 |
Simplifiez :\(\dfrac{v}{v+1}+\dfrac{3}{v−1}−\dfrac{6}{v^2−1}\).
- Réponse
-
\(\dfrac{v+3}{v+1}\)
Simplifiez :\(\dfrac{3w}{w+2}+\dfrac{2}{w+7}−\dfrac{17w+4}{w^2+9w+14}\).
- Réponse
-
\(\dfrac{3w}{w+7}\)
Ajouter et soustraire des fonctions rationnelles
Pour ajouter ou soustraire des fonctions rationnelles, nous utilisons les mêmes techniques que celles utilisées pour ajouter ou soustraire des fonctions polynomiales.
Trouvez\(R(x)=f(x)−g(x)\) où\(f(x)=\dfrac{x+5}{x−2}\) et\(g(x)=\dfrac{5x+18}{x^2−4}\).
- solution
-

Substitut dans les fonctions\(f(x)\),\(g(x)\). 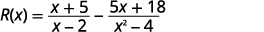
Facturez les dénominateurs. 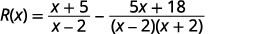
Les expressions ont-elles un dénominateur commun ? Non
Réécrivez chaque expression à l'aide de l'écran LCD.\(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} x−2=(x−2) \\ \underline{x^2−4=(x−2)(x+2)} \\ \hspace{4mm} LCD=(x−2)(x+2)\end{array} \end{array}\) Réécrivez chaque expression rationnelle en tant qu'expression rationnelle
équivalente à l'aide de l'écran LCD.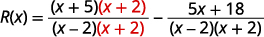
Écrivez comme une expression rationnelle. 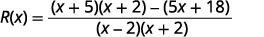
Simplifiez. 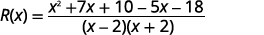
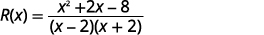
Facturez le numérateur et supprimez
les facteurs communs.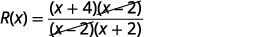
Simplifiez. 
Trouvez\(R(x)=f(x)−g(x)\) où\(f(x)=\dfrac{x+1}{x+3}\) et\(g(x)=\dfrac{x+17}{x^2−x−12}\).
- Réponse
-
\(\dfrac{x−7}{x−4}\)
Trouvez\(R(x)=f(x)+g(x)\) où\(f(x)=\dfrac{x−4}{x+3}\) et\(g(x)=\dfrac{4x+6}{x^2−9}\).
- Réponse
-
\(\dfrac{x^2−3x+18}{(x+3)(x−3)}\)
Accédez à cette ressource en ligne pour obtenir des instructions supplémentaires et vous entraîner à ajouter et à soustraire des expressions rationnelles.
- Ajouter et soustraire des expressions rationnelles, contrairement aux dénominateurs
Concepts clés
- Addition et soustraction d'expressions rationnelles
Si\(p\)\(q\), et\(r\) sont des polynômes où\(r\neq 0\), alors
\[\dfrac{p}{r}+\dfrac{q}{r}=\dfrac{p+q}{r} \quad \text{and} \quad \dfrac{p}{r}−\dfrac{q}{r}=\dfrac{p−q}{r}\nonumber\] - Comment trouver le plus petit dénominateur commun des expressions rationnelles.
- Facturez complètement chaque expression.
- Répertoriez les facteurs de chaque expression. Faites correspondre les facteurs verticalement lorsque cela est possible.
- Abattez les colonnes.
- Écrivez l'écran LCD comme le produit des facteurs.
- Comment ajouter ou soustraire des expressions rationnelles.
- Déterminez si les expressions ont un dénominateur commun.
- Oui, passez à l'étape 2.
- Non — Réécrivez chaque expression rationnelle à l'aide de l'écran LCD.
- Trouvez l'écran LCD.
- Réécrivez chaque expression rationnelle en tant qu'expression rationnelle équivalente à l'aide de l'écran LCD.
- Ajoutez ou soustrayez les expressions rationnelles.
- Simplifiez, si possible.
- Déterminez si les expressions ont un dénominateur commun.


