6.4 : Produits Factor Special
- Page ID
- 194239
À la fin de cette section, vous serez en mesure de :
- Facteur : trinômes carrés parfaits
- Différences factorielles des carrés
- Sommes factorielles et différences entre les cubes
Avant de commencer, répondez à ce questionnaire de préparation.
- Simplifiez :\((3x^2)^3\).
- Multipliez :\((m+4)^2\).
- Multipliez :\((x−3)(x+3)\).
Nous avons vu que certains binômes et trinômes résultent de produits spéciaux : la mise au carré des binômes et la multiplication des conjugués. Si vous apprenez à reconnaître ces types de polynômes, vous pouvez utiliser les modèles de produits spéciaux pour les factoriser beaucoup plus rapidement.
Trinômes carrés Factor Perfect
Certains trinômes sont des carrés parfaits. Ils résultent de la multiplication d'un binôme par lui-même. Nous avons quadrillé un binôme en utilisant le modèle des carrés binomiaux dans un chapitre précédent.
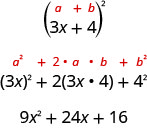
Le trinôme\(9x^2+24x+16\) est appelé trinôme carré parfait. C'est le carré du binôme\(3x+4\).
Dans ce chapitre, vous allez commencer par un trinôme carré parfait et le prendre en compte dans ses facteurs premiers. Vous pouvez factoriser ce trinôme en utilisant les méthodes décrites dans la dernière section, car il est de la forme\(ax^2+bx+c\). Mais si vous reconnaissez que le premier et le dernier terme sont des carrés et que le trinôme correspond parfaitement au modèle de trinôme carré, vous vous épargnerez beaucoup de travail. Voici le motif, l'inverse du schéma des carrés binomiaux.
Si\(a\) et\(b\) sont des nombres réels
\[a^2+2ab+b^2=(a+b)^2\nonumber\]
\[a^2−2ab+b^2=(a−b)^2\nonumber\]
Pour utiliser ce modèle, vous devez reconnaître qu'un trinôme donné lui convient. Vérifiez d'abord si le coefficient principal est un carré parfait,\(a^2\). Vérifiez ensuite que le dernier terme est un carré parfait,\(b^2\). Vérifiez ensuite le terme moyen : s'agit-il du produit,\(2ab\) ? Si tout se vérifie, vous pouvez facilement écrire les facteurs.
Facteur :\(9x^2+12x+4\).
- Réponse
-



Facteur :\(4x^2+12x+9\).
- Réponse
-
\((2x+3)^2\)
Facteur :\(9y^2+24y+16\).
- Réponse
-
\((3y+4)^2\)
Le signe du moyen terme détermine le modèle que nous utiliserons. Lorsque le moyen terme est négatif, nous utilisons le modèle\(a^2−2ab+b^2\), qui prend en compte\((a−b)^2\).
Les étapes sont résumées ici.
\(\begin{array} {lllll} \textbf{Step 1.} &\text{Does the trinomial fit the pattern?} &\quad &\hspace{7mm} a^2+2ab+b^2 &\hspace{7mm} a^2−2ab+b^2 \\ &\text{Are the first and last terms perfect squares?} &\quad & &\\ &\text{Write them as squares.} &\quad &\hspace{5mm}(a)^2\hspace{16mm} (b)^2 &\hspace{6mm}(a)^2\hspace{16mm} (b)^2 \\ &\text{Check the middle term. Is it }2ab? &\quad &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} \\ \textbf{Step 2.} &\text{Write the square of the binomial.} &\quad &\hspace{13mm} (a+b)^2 &\hspace{13mm} (a−b)^2 \\ \textbf{Step 3.} &\text{Check by multiplying.} & & & \end{array}\)
Nous allons maintenant en travailler un où le moyen terme est négatif.
Facteur :\(81y^2−72y+16\).
- Réponse
-
Le premier et le dernier terme sont des carrés. Voyez si le terme moyen correspond au modèle d'un trinôme carré parfait. Le terme moyen est négatif, donc le carré binomial le serait\((a−b)^2\).
\(81 y^{2}-72 y+16\) Le premier et le dernier trimestre sont-ils des carrés parfaits ? 
Vérifiez le moyen terme. 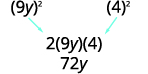
Est-ce que ça correspond\((a−b)^2\) ? Oui 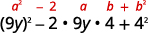
Écrivez comme le carré d'un binôme. \((9 y-4)^{2}\) Vérifiez en multipliant :
\[(9y−4)^2\nonumber\]\[(9y)^2−2·9y·4+4^2\nonumber\]\[81y^2−72y+16\checkmark\nonumber\]
Facteur :\(64y^2−80y+25\).
- Réponse
-
\((8y−5)^2\)
Facteur :\(16z^2−72z+81\).
- Réponse
-
\((4z−9)^2\)
L'exemple suivant sera un trinôme carré parfait avec deux variables.
Facteur :\(36x^2+84xy+49y^2\).
- Réponse
-
\(36 x^{2}+84 x y+49 y^{2}\) Testez chaque terme pour vérifier le schéma. 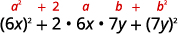
Facteur. \((6 x+7 y)^{2}\) Vérifiez en multipliant.
\[(6x+7y)^2\nonumber\]\[(6x)^2+2·6x·7y+(7y)^2\nonumber\]\[36x^2+84xy+49y^2\checkmark\nonumber\]
Facteur :\(49x^2+84xy+36y^2\).
- Réponse
-
\((7x+6y)^2\)
Facteur :\(64m^2+112mn+49n^2\).
- Réponse
-
\((8m+7n)^2\)
N'oubliez pas que la première étape de l'affacturage consiste à rechercher le plus grand facteur commun. Les trinômes carrés parfaits peuvent avoir un GCF dans les trois termes et il faut d'abord le prendre en compte. Et, parfois, une fois le GCF pris en compte, vous reconnaîtrez un trinôme carré parfait.
Facteur :\(100x^2y−80xy+16y\).
- Réponse
-
\(100 x^{2} y-80 x y+16 y\) Y a-t-il un GCF ? Oui\(4y\), alors prenez-le en compte. \(4 y\left(25 x^{2}-20 x+4\right)\) Est-ce un trinôme carré parfait ? Vérifiez le schéma. 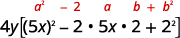
Facteur. \(4 y(5 x-2)^{2}\) N'oubliez pas : conservez le facteur 4 y dans le produit final. Vérifiez :
\[4y(5x−2)^2\nonumber\]\[4y[(5x)2−2·5x·2+22]\nonumber\]\[4y(25x2−20x+4)\nonumber\]100 x 2 ans − 80 xy+16 ans \ coche \]
Facteur :\(8x^2y−24xy+18y\).
- Réponse
-
\(2y(2x−3)^2\)
Facteur :\(27p^2q+90pq+75q\).
- Réponse
-
\(3q(3p+5)^2\)
Différences factorielles des carrés
L'autre produit spécial que vous avez vu dans le chapitre précédent était le modèle Product of Conjugués. Vous l'avez utilisé pour multiplier deux binômes qui étaient des conjugués. Voici un exemple :
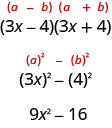
Une différence de facteurs carrés par rapport à un produit de conjugués.
Si\(a\) et\(b\) sont des nombres réels,
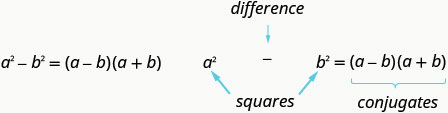
N'oubliez pas que la « différence » fait référence à la soustraction. Donc, pour utiliser ce modèle, vous devez vous assurer d'avoir un binôme dans lequel deux carrés sont soustraits.
Facteur :\(64y^2−1\).
- Réponse
-




Facteur :\(121m^2−1\).
- Réponse
-
\((11m−1)(11m+1)\)
Facteur :\(81y^2−1\).
- Réponse
-
\((9y−1)(9y+1)\)
\(\begin{array} {llll} \textbf{Step 1.} &\text{Does the binomial fit the pattern?} &\qquad &\hspace{5mm} a^2−b^2 \\ &\text{Is this a difference?} &\qquad &\hspace{2mm} \text{____−____} \\ &\text{Are the first and last terms perfect squares?} & & \\ \textbf{Step 2.} &\text{Write them as squares.} &\qquad &\hspace{3mm} (a)^2−(b)^2 \\ \textbf{Step 3.} &\text{Write the product of conjugates.} &\qquad &(a−b)(a+b) \\ \textbf{Step 4.} &\text{Check by multiplying.} & & \end{array}\)
Il est important de se rappeler que les sommes des carrés ne sont pas prises en compte dans le produit des binômes. Aucun facteur binomial ne se multiplie pour obtenir une somme de carrés. Après avoir supprimé tout GCF, l'expression\(a^2+b^2\) est première !
L'exemple suivant montre les variables dans les deux termes.
Facteur :\(144x^2−49y^2\).
- Réponse
-
\(\begin{array} {lll} &\quad &144x^2−49y^2 \\ \text{Is this a difference of squares? Yes.} &\quad &(12x)^2−(7y)^2 \\ \text{Factor as the product of conjugates.} &\quad &(12x−7y)(12x+7y) \\ \text{Check by multiplying.} &\quad &(12x−7y)(12x+7y) \\ \text{Check by multiplying.} &\quad & \\ &\quad & \\ &\quad & \\ \hspace{14mm} (12x−7y)(12x+7y) &\quad & \\ \hspace{21mm} 144x^2−49y^2\checkmark &\quad & \end{array}\)
Facteur :\(196m^2−25n^2\).
- Réponse
-
\((14m−5n)(14m+5n)\)
Facteur :\(121p^2−9q^2\).
- Réponse
-
\((11p−3q)(11p+3q)\)
Comme toujours, vous devez d'abord rechercher un facteur commun chaque fois que vous avez une expression à factoriser. Parfois, un facteur commun peut « masquer » la différence entre les carrés et vous ne reconnaîtrez pas les carrés parfaits tant que vous n'aurez pas pris en compte le GCF.
De plus, pour factoriser complètement le binôme dans l'exemple suivant, nous allons factoriser deux fois une différence de carrés !
Facteur :\(48x^4y^2−243y^2\).
- Réponse
-
\(\begin{array} {ll} &48x^4y^2−243y^2 \\ \text{Is there a GCF? Yes, }3y^2\text{—factor it out!} &3y^2(16x^4−81) \\ \text{Is the binomial a difference of squares? Yes.} &3y^2\left((4x^2)^2−(9)^2\right) \\ \text{Factor as a product of conjugates.} &3y^2(4x^2−9)(4x^2+9) \\ \text{Notice the first binomial is also a difference of squares!} &3y^2((2x)^2−(3)^2)(4x^2+9) \\ \text{Factor it as the product of conjugates.} &3y^2(2x−3)(2x+3)(4x^2+9) \end{array}\)
Le dernier facteur, la somme des carrés, ne peut pas être factorisé.
\(\begin{array} {l} \text{Check by multiplying:} \\ \hspace{10mm} 3y^2(2x−3)(2x+3)(4x^2+9) \\ \\ \\ \hspace{15mm} 3y^2(4x^2−9)(4x^2+9) \\ \hspace{20mm} 3y^2(16x^4−81) \\ \hspace{19mm} 48x^4y^2−243y^2\checkmark\end{array}\)
Facteur :\(2x^4y^2−32y^2\).
- Réponse
-
\(2y^2(x−2)(x+2)(x^2+4)\)
Facteur :\(7a^4c^2−7b^4c^2\).
- Réponse
-
\(7c^2(a−b)(a+b)(a^2+b^2)\)
L'exemple suivant comporte un polynôme à 4 termes. Jusqu'à présent, lorsque cela s'est produit, nous avons regroupé les termes par deux et pris en compte à partir de là. Nous remarquerons ici que les trois premiers termes forment un trinôme carré parfait.
Facteur :\(x^2−6x+9−y^2\).
- Réponse
-
Remarquez que les trois premiers termes forment un trinôme carré parfait.
\(x^{2}-6 x+9-y^{2}\) Facturez en regroupant les trois premiers termes. \(\underbrace{x^{2}-6 x+9} - y^{2}\) Utilisez le motif trinomial carré parfait. \((x-3)^{2}-y^{2}\) Est-ce une différence de carrés ? Oui Oui, écrivez-les sous forme de carrés. 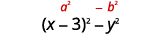
Facteur en tant que produit de conjugués. 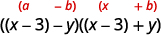
\((x-3-y)(x-3+y)\) Vous pouvez réécrire la solution sous la forme\((x−y−3)(x+y−3)\).
Facteur :\(x^2−10x+25−y^2\).
- Réponse
-
\((x−5−y)(x−5+y)\)
Facteur :\(x^2+6x+9−4y^2\).
- Réponse
-
\((x+3−2y)(x+3+2y)\)
Sommes factorielles et différences entre les cubes
Il existe un autre modèle spécial de factorisation, que nous n'avons pas utilisé lorsque nous avons multiplié des polynômes. C'est le modèle de la somme et de la différence des cubes. Nous allons d'abord écrire ces formules, puis les vérifier par multiplication.
\[a^3+b^3=(a+b)(a^2−ab+b^2\nonumber\]
\[a^3−b^3=(a−b)(a^2+ab+b^2)\nonumber\]
Nous allons vérifier le premier schéma et vous laisser le second.
| \(\color{red}(a+b) \color{black} \left(a^{2}-a b+b^{2}\right)\) | |
| Distribuez. | \(\color{red}a \color{black}\left(a^{2}-a b+b^{2}\right)+ \color{red}b \color{black}\left(a^{2}-a b+b^{2}\right)\) |
| Multipliez. | \(a^{3}-a^{2} b+a b^{2}+a^{2} b-a b^{2}+b^{3}\) |
| Combinez les mêmes termes. | \(a^{3}+b^{3}\) |
\[a^3+b^3=(a+b)(a^2−ab+b^2\nonumber\]\[a^3−b^3=(a−b)(a^2+ab+b^2)\nonumber\]
Les deux motifs se ressemblent beaucoup, n'est-ce pas ? Mais remarquez les signes dans les facteurs. Le signe du facteur binomial correspond au signe du binôme d'origine. Et le signe du terme moyen du facteur trinomial est l'opposé du signe du binôme original. Si vous reconnaissez le motif des signes, cela peut vous aider à les mémoriser.

Le facteur trinomial dans le schéma de somme et de différence des cubes ne peut pas être pris en compte.
Il est très utile d'apprendre à reconnaître les cubes des nombres entiers de 1 à 10, tout comme vous avez appris à reconnaître les carrés. Nous avons répertorié les cubes des nombres entiers de 1 à 10 dans le tableau.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(n^3\) | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1000 |
Facteur :\(x^3+64\).
- Réponse
-





Facteur :\(x^3+27\).
- Réponse
-
\((x+3)(x^2−3x+9)\)
Facteur :\(y^3+8\).
- Réponse
-
\((y+2)(y^2−2y+4)\)
- Le binôme correspond-il au modèle de somme ou de différence de cubes ?
S'agit-il d'une somme ou d'une différence ?
Le premier et le dernier trimestre sont-ils des cubes parfaits ? - Écrivez-les en cubes.
- Utilisez le modèle de somme ou de différence de cubes.
- Simplifiez entre parenthèses.
- Vérifiez en multipliant les facteurs.
Facteur :\(27u^3−125v^3\).
- Réponse
-
\(27 u^{3}-125 v^{3}\) Ce binôme fait la différence. Le premier et le dernier
terme sont des cubes parfaits.Écrivez les termes sous forme de cubes. 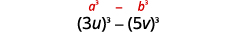
Utilisez la différence de motif de cubes. 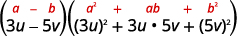
Simplifiez. 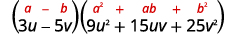
Vérifiez en multipliant. Nous vous laisserons le chèque.
Facteur :\(8x^3−27y^3\).
- Réponse
-
\((2x−3y)(4x^2+6xy+9y^2)\)
Facteur :\(1000m^3−125n^3\).
- Réponse
-
\((10m−5n)(100m^2+50mn+25n^2)\)
Dans l'exemple suivant, nous déduisons d'abord le GCF. Ensuite, nous pouvons reconnaître la somme des cubes.
Facteur :\(6x^3y+48y^4\).
- Réponse
-
\(6 x^{3} y+48 y^{4}\) Facteur le facteur commun. \(6 y\left(x^{3}+8 y^{3}\right)\) Ce binôme est une somme. Le premier et le dernier
terme sont des cubes parfaits.Écrivez les termes sous forme de cubes. 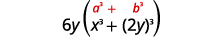
Utilisez le modèle de somme des cubes. 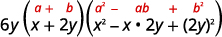
Simplifiez. 
Vérifiez :
Pour vérifier, il peut être plus facile de multiplier d'abord la somme des facteurs cubes, puis de multiplier ce produit par 6y.6y. Nous vous laissons la multiplication.
Facteur :\(500p^3+4q^3\).
- Réponse
-
\(4(5p+q)(25p^2−5pq+q^2)\)
Facteur :\(432c^3+686d^3\).
- Réponse
-
\(2(6c+7d)(36c^2−42cd+49d^2)\)
Le premier terme de l'exemple suivant est un binôme cubique.
Facteur :\((x+5)^3−64x^3\).
- Réponse
-
\((x+5)^{3}-64 x^{3}\) Ce binôme fait la différence. Le premier et le
dernier terme sont des cubes parfaits.Écrivez les termes sous forme de cubes. 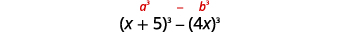
Utilisez la différence de motif de cubes. 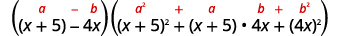
Simplifiez. \((x+5-4 x)\left(x^{2}+10 x+25+4 x^{2}+20 x+16 x^{2}\right)\) \((-3 x+5)\left(21 x^{2}+30 x+25\right)\) Vérifiez en multipliant. Nous vous laisserons le chèque.
Facteur :\((y+1)^3−27y^3\).
- Réponse
-
\((−2y+1)(13y^2+5y+1)\)
Facteur :\((n+3)^3−125n^3\).
- Réponse
-
\((−4n+3)(31n^2+21n+9)\)
Accédez à cette ressource en ligne pour obtenir des instructions et des exercices supplémentaires sur l'affacturage de produits spéciaux
Concepts clés
- Modèle parfait de trinômes carrés : si a et b sont des nombres réels,
\[\begin{array} {l} a^2+2ab+b^2=(a+b)^2 \\ a^2−2ab+b^2=(a−b)^2\end{array} \nonumber\]
- Comment factoriser des trinômes carrés parfaits.
\(\begin{array} {lllll} \textbf{Step 1.} &\text{Does the trinomial fit the pattern?} &\quad &\hspace{7mm} a^2+2ab+b^2 &\hspace{7mm} a^2−2ab+b^2 \\ &\text{Are the first and last terms perfect squares?} &\quad & &\\ &\text{Write them as squares.} &\quad &\hspace{5mm}(a)^2\hspace{16mm} (b)^2 &\hspace{6mm}(a)^2\hspace{16mm} (b)^2 \\ &\text{Check the middle term. Is it }2ab? &\quad &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} \\ \textbf{Step 2.} &\text{Write the square of the binomial.} &\quad &\hspace{13mm} (a+b)^2 &\hspace{13mm} (a−b)^2 \\ \textbf{Step 3.} &\text{Check by multiplying.} & & & \end{array}\) - Modèle de différence de carrés : si a, ba, b sont des nombres réels,
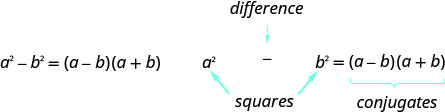
- Comment factoriser les différences entre les carrés.
\(\begin{array} {llll} \textbf{Step 1.} &\text{Does the binomial fit the pattern?} &\qquad &\hspace{5mm} a^2−b^2 \\ &\text{Is this a difference?} &\qquad &\hspace{2mm} \text{____−____} \\ &\text{Are the first and last terms perfect squares?} & & \\ \textbf{Step 2.} &\text{Write them as squares.} &\qquad &\hspace{3mm} (a)^2−(b)^2 \\ \textbf{Step 3.} &\text{Write the product of conjugates.} &\qquad &(a−b)(a+b) \\ \textbf{Step 4.} &\text{Check by multiplying.} & & \end{array}\) - Modèle de somme et de différence de cubes
\(\begin{array} {l} a^3+b3=(a+b)(a^2−ab+b^2) \\ a^3−b^3=(a−b)(a^2+ab+b^2) \end{array} \) - Comment factoriser la somme ou la différence de cubes.
- Le binôme correspond-il au modèle de somme ou de différence de cubes ?
S'agit-il d'une somme ou d'une différence ?
Le premier et le dernier trimestre sont-ils des cubes parfaits ? - Écrivez-les en cubes.
- Utilisez le modèle de somme ou de différence de cubes.
- Simplifier entre parenthèses
- Vérifiez en multipliant les facteurs.
- Le binôme correspond-il au modèle de somme ou de différence de cubes ?


