6.3 : Trinômes factoriels
- Page ID
- 194209
À la fin de cette section, vous serez en mesure de :
- Trinômes factoriels de la forme\(x^2+bx+c\)
- Facteur des trinômes du\(ax^2+bx+c\) formulaire par essais et erreurs
- Factorez les trinômes du formulaire\(ax^2+bx+c\) en utilisant la méthode\(ac\) « »
- Facteur utilisant la substitution
Avant de commencer, répondez à ce questionnaire de préparation.
Les trinômes factoriels de la forme\(x^2+bx+c\)
Vous avez déjà appris à multiplier des binômes à l'aide de FOIL. Vous devez maintenant « annuler » cette multiplication. Facturer le trinôme signifie commencer par le produit et terminer par les facteurs.
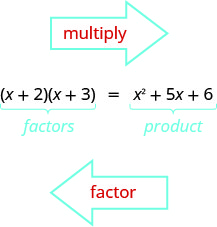
Pour comprendre comment nous factoriserions un trinôme de la forme\(x^2+bx+c\), tel que\(x^2+5x+6\) et le factoriserions\((x+2)(x+3)\), commençons par deux binômes généraux de la forme\((x+m)\) et\((x+n)\).
| \((x+m)(x+n)\) | |
| Feuilletez pour trouver le produit. | \(x^{2}+m x+n x+m n\) |
| Facturez le GCF à partir des termes intermédiaires. | \(x^{2}+(m+n) x+m n\) |
| Notre trinôme est de la forme\(x^2+bx+c\). | \(\overbrace{x^{2}+(m+n) x+m n}^{\color{red}x^{2}+b x+c}\) |
Cela nous indique que pour factoriser un trinôme de la forme\(x^2+bx+c\), nous avons besoin de deux facteurs\((x+m)\) et\((x+n)\) où les deux nombres\(n\) se multiplient\(m\)\(c\) et s'additionnent\(b\).
Facteur :\(x^2+11x+24\).
- Réponse
-




Facteur :\(q^2+10q+24\).
- Réponse
-
\((q+4)(q+6)\)
Facteur :\(t^2+14t+24\).
- Réponse
-
\((t+2)(t+12)\)
Résumons les étapes que nous avons utilisées pour trouver les facteurs.
- Écrivez les facteurs sous forme de deux binômes avec les premiers termes x. \(\quad \begin{array} {l} x^2+bx+c \\ (x\quad)(x\quad) \end{array} \)
- Trouve deux chiffres\(m\) et\(n\) ça
- multipliez jusqu'à\(c\),\(m·n=c\)
- ajouter à\(b\),\(m+n=b\)
- Utilisez\(m\) et\(n\) comme dernier terme des facteurs. \(\quad (x+m)(x+n)\)
- Vérifiez en multipliant les facteurs.
Dans le premier exemple, tous les termes du trinôme étaient positifs. Que se passe-t-il lorsqu'il y a des termes négatifs ? Eh bien, cela dépend du terme négatif. Examinons d'abord les trinômes dont seul le moyen terme est négatif.
Comment obtenir un produit positif et une somme négative ? Nous utilisons deux nombres négatifs.
Facteur :\(y^2−11y+28\).
- Réponse
-
Encore une fois, avec le dernier terme positif et le moyen terme négatif\(−11y\), nous avons besoin de deux facteurs négatifs.\(28\) Trouvez deux nombres qui se multiplient\(28\) et s'additionnent\(−11\).
\(\begin{array} {ll} &y^2−11y+28 \\ \text{Write the factors as two binomials with first terms }y. &( y \quad )( y \quad ) \\ \text{Find two numbers that: multiply to }28\text{ and add to }−11.\end{array}\)Facteurs de\(28\) Somme des facteurs \ (28 \) » validation des données = « top">\(−1,\space −28\)
\(−2,\space −14\)
\(−4,\space −7\)\(−1+(−28)=−29\)
\(−2+(−14)=−16\)
\(−4+(−7)=−11^∗\)\(\begin{array} {ll} \text{Use }−4,\space −7\text{ as the last terms of the binomials.} &(y−4)(y−7) \\ \text{Check:} & \\ \hspace{30mm} (y−4)(y−7) & \\ \hspace{25mm} y^2−7y−4y+28 & \\ \hspace{30mm} y^2−11y+28\checkmark & \end{array} \)
Facteur :\(u^2−9u+18\).
- Réponse
-
\((u−3)(u−6)\)
Facteur :\(y^2−16y+63\).
- Réponse
-
\((y−7)(y−9)\)
Et si le dernier terme du trinôme est négatif ? Pensez à FOIL. Le dernier terme est le produit des derniers termes des deux binômes. Un produit négatif résulte de la multiplication de deux nombres par des signes opposés. Vous devez également faire très attention à choisir les facteurs pour vous assurer d'obtenir le bon signe pour le moyen terme.
Comment obtenir un produit négatif et une somme positive ? Nous utilisons un nombre positif et un nombre négatif.
Lorsque nous prenons en compte les trinômes, les termes doivent être écrits par ordre décroissant, du degré le plus élevé au degré le plus bas.
Facteur :\(2x+x^2−48\).
- Réponse
-
\(\begin{array} {ll} &2x+x^2−48 \\ \text{First we put the terms in decreasing degree order.} &x^2+2x−48 \\ \text{Factors will be two binomials with first terms }x. &(x\quad)(x\quad) \end{array} \)
Facteurs de −48−48 Somme des facteurs \(−1,\space 48\)
\(−2,\space 24\)
\(−3,\space 16\)
\(−4,\space 12\)
\(−6,\space 8\)\(−1+48=47\)
\(−2+24=22\)
\(−3+16=13\)
\(−4+12=8\)
\(−6+8=2^∗\)\(\begin{array} {ll} \text{Use }−6,\space 8\text{ as the last terms of the binomials.} &(x−6)(x+8) \\ \text{Check:} & \\ \hspace{30mm} (x−6)(x+8) & \\ \hspace{25mm} x^2−6q+8q−48 & \\ \hspace{30mm} x^2+2x−48\checkmark & \end{array} \)
Facteur :\(9m+m^2+18\).
- Réponse
-
\((m+3)(m+6)\)
Facteur :\(−7n+12+n^2\).
- Réponse
-
\((n−3)(n−4)\)
Parfois, vous aurez besoin de factoriser les trinômes du formulaire\(x^2+bxy+cy^2\) avec deux variables, telles que\(x^2+12xy+36y^2\). Le premier terme,\(x^2\), est le produit des premiers termes des facteurs binomiaux,\(x·x\). Le\(y^2\) dans le dernier terme signifie que les deuxièmes termes des facteurs binomiaux doivent chacun contenir\(y\). Pour obtenir les coefficients\(b\) et\(c\), vous utilisez le même processus résumé dans How To Factor trinomials.
Facteur :\(r^2−8rs−9s^2\).
- Réponse
-
Nous\(r\) en avons besoin au premier terme de chaque binôme et\(s\) au second terme. Le dernier terme du trinôme est négatif, de sorte que les facteurs doivent avoir des signes opposés.
\(\begin{array} {ll} &r^2−8rs−9s^2 \\ \text{Note that the first terms are }r,\text{last terms contain }s. &(r\quad s)(r\quad s) \\ \text{Find the numbers that multiply to }−9\text{ and add to }−8. \end{array}\)Facteurs de\(−9\) Somme des facteurs \ (−9 \) » validation des données ="top">\(1,\space −9\) \(−1+9=8\) \ (−9 \) » validation des données ="top">\(−1,\space 9\) \(1+(−9)=−8^∗\) \ (−9 \) » validation des données ="top">\(3,\space −3\) \(3+(−3)=0\) \(\begin{array} {ll} \text{Use }1,\space -9\text{ as coefficients of the last terms.} &(r+s)(r−9s) \\ \text{Check:} & \\ \hspace{30mm} (r−9s)(r+s) & \\ \hspace{25mm} r^2+rs−9rs−9s^2 & \\ \hspace{30mm} r^2−8rs−9s^2\checkmark & \end{array} \)
Facteur :\(a^2−11ab+10b^2\).
- Réponse
-
\((a−b)(a−10b)\)
Facteur :\(m^2−13mn+12n^2\).
- Réponse
-
\((m−n)(m−12n)\)
Certains trinômes sont excellents. La seule façon de s'assurer qu'un trinôme est excellent est d'énumérer toutes les possibilités et de montrer qu'aucune d'entre elles ne fonctionne.
Facteur :\(u^2−9uv−12v^2\).
- Réponse
-
Nous\(u\) en avons besoin au premier terme de chaque binôme et\(v\) au second terme. Le dernier terme du trinôme est négatif, de sorte que les facteurs doivent avoir des signes opposés.
\(\begin{array} {ll} &u^2−9uv−12v^2 \\ \text{Note that the first terms are }u,\text{ last terms contain }v. &(u\quad v)(u\quad v) \\ \text{Find the numbers that multiply to }−12\text{ and add to }−9. & \end{array} \)Facteurs de\(−12\) Somme des facteurs \ (−12 \) » validation des données ="top">\(1,−12\)
\(−1,12\)
\(2,−6\)
\(−2,6\)
\(3,−4\)
\(−3,4\)\(1+(−12)=−11\)
\(−1+12=11\)
\(2+(−6)=−4\)
\(−2+6=4\)
\(3+(−4)=−1\)
\(−3+4=1\)Notez qu'aucune paire de facteurs ne nous\(−9\) donne une somme. Le trinôme est primordial.
Facteur :\(x^2−7xy−10y^2\).
- Réponse
-
fleur
Facteur :\(p^2+15pq+20q^2\).
- Réponse
-
fleur
Résumons la méthode que nous venons de développer pour factoriser les trinômes du formulaire\(x^2+bx+c\).
Lorsque nous factorisons un trinôme, nous examinons d'abord les signes de ses termes pour déterminer les signes des facteurs binomiaux.
| \( x^{2}+b x+c \) | ||
| \( (x+m)(x+n) \) | ||
| Quand\( c \) est positif\( m \) et\( n \) porte le même signe. | ||
| \( b \)positif | \( b \)négatif | |
| \( m,n \)positif | \( m,n \)négatif | |
| \( x^{2}+5 x+6 \) | \( x^{2}-6 x+8 \) | |
| \( (x+2)(x+3) \) | \( (x-4)(x-2) \) | |
| mêmes signes | mêmes signes | |
| Quand\( c \) est négatif,\( m \) et\( n \) avoir le signe opposé. | ||
| \( x^{2}+x-12 \) | \( x^{2}-2 x-15 \) | |
| \( (x+4)(x-3) \) | \( (x-5)(x+3) \) | |
| signes opposés | signes opposés | |
Notez que, dans le cas où\(m\) et\(n\) ont des signes opposés, le signe de celui dont la valeur absolue est la plus grande correspond au signe de\(b\).
Trinômes factoriels de la forme ax 2 + bx + c en utilisant des essais et des erreurs
Notre prochaine étape consiste à factoriser les trinômes dont le coefficient principal n'est pas 1, les trinômes de la forme\(ax^2+bx+c\).
N'oubliez pas de toujours vérifier d'abord s'il y a un GCF ! Parfois, après avoir factorisé le GCF, le coefficient principal du trinôme devient\(1\) et vous pouvez le factoriser selon les méthodes que nous avons utilisées jusqu'à présent. Faisons un exemple pour voir comment cela fonctionne.
Facteur complètement :\(4x^3+16x^2−20x\).
- Réponse
-
\(\begin{array} {lll} \text{Is there a greatest common factor?} &\qquad &4x^3+16x^2−20x \\ \quad \text{Yes, }GCF=4x.\text{ Factor it.} & &4x(x^2+4x−5) \\ & & \\ & & \\ \text{Binomial, trinomial, or more than three terms?} & & \\ \quad \text{It is a trinomial. So “undo FOIL.”} & &4x(x\quad)(x\quad) \\ & & \\ & & \\ \text{Use a table like the one shown to find two numbers that} & &4x(x−1)(x+5) \\ \text{multiply to }−5\text{ and add to }4. & & \\ & & \\ & & \end{array} \)
Facteurs de\(−5\) Somme des facteurs \ (−5 \) » validation des données ="top">\(−1,5\)
\(1,−5\)\(−1+5=4^∗\)
\(1+(−5)=−4\)\(\begin{array} {l} \text{Check:}\\ \hspace{27mm}4x(x−1)(x+5) \\ \hspace{25mm} 4x(x^2+5x−x−5) \\ \hspace{30mm} 4x(x^2+4x−5) \\ \hspace{25mm} 4x^3+16x2−20x\checkmark \end{array} \)
Facteur complètement :\(5x^3+15x^2−20x\).
- Réponse
-
\(5x(x−1)(x+4)\)
Facteur complètement :\(6y^3+18y^2−60y\).
- Réponse
-
\(6y(y−2)(y+5)\)
Que se passe-t-il lorsque le coefficient principal ne l'est pas\(1\) et qu'il n'y a pas de GCF ? Plusieurs méthodes peuvent être utilisées pour factoriser ces trinômes. Nous allons d'abord utiliser la méthode des essais et des erreurs.
Prenons en compte le trinôme\(3x^2+5x+2\).
D'après nos travaux antérieurs, nous nous attendons à ce que cela soit pris en compte dans deux binômes.
\[3x^2+5x+2\nonumber\]\[(\quad)(\quad)\nonumber\]
Nous savons que les premiers termes des facteurs binomiaux se multiplieront pour nous donner\(3x^2\). Les seuls facteurs\(3x^2\) sont\(1x,\space 3x\). Nous pouvons les placer dans les binômes.
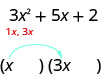
Vérifiez : Est-ce que\(1x·3x=3x^2\) ?
Nous savons que les derniers termes des binômes se multiplieront en\(2\). Comme ce trinôme contient tous des termes positifs, il suffit de prendre en compte les facteurs positifs. Les seuls facteurs\(2\) sont\(1\) et\(2\). Mais nous avons maintenant deux cas à considérer car cela fera une différence si nous écrivons\(1\),\(2\) ou\(2\),\(1\).

Quels sont les facteurs corrects ? Pour en décider, nous multiplions les termes intérieurs et extérieurs.
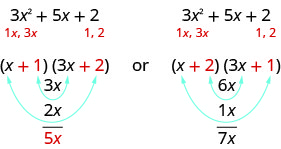
Puisque le terme moyen du trinôme est\(5x\), les facteurs du premier cas fonctionneront. Utilisons FOIL pour vérifier.
\[(x+1)(3x+2)\nonumber\]\[3x^2+2x+3x+2\nonumber\]\[3x^2+5x+2\checkmark\nonumber\]
Notre résultat de l'affacturage est le suivant :
\[3x^2+5x+2\nonumber\]\[(x+1)(3x+2)\nonumber\]
Factoriez complètement en utilisant des essais et des erreurs :\(3y^2+22y+7\).
- Réponse
-






Factoriez complètement en utilisant des essais et des erreurs :\(2a^2+5a+3\).
- Réponse
-
\((a+1)(2a+3)\)
Factoriez complètement en utilisant des essais et des erreurs :\(4b^2+5b+1\).
- Réponse
-
\((b+1)(4b+1)\)
- Écrivez le trinôme par ordre décroissant de degrés selon les besoins.
- Tenez compte de tout GCF.
- Trouvez toutes les paires de facteurs du premier terme.
- Trouvez toutes les paires de facteurs du troisième terme.
- Testez toutes les combinaisons possibles de facteurs jusqu'à ce que le bon produit soit trouvé.
- Vérifiez en multipliant.
N'oubliez pas que lorsque le terme moyen est négatif et que le dernier terme est positif, les signes des binômes doivent tous deux être négatifs.
Factoriez complètement en utilisant des essais et des erreurs :\(6b^2−13b+5\).
- Réponse
-
Le trinôme est déjà dans l'ordre décroissant. 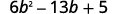
Déterminez les facteurs du premier mandat. 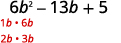
Trouvez les facteurs du dernier trimestre. Tenez compte des signes.
Puisque le dernier terme,\(5\), est positif, ses facteurs doivent être à la fois
positifs ou négatifs. Le coefficient du
moyen terme étant négatif, nous utilisons les facteurs négatifs.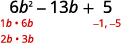
Tenez compte de toutes les combinaisons de facteurs.
\(6b^2−13b+5\) Facteurs possibles Produit \ (6b^2−13b+5 \) Facteurs possibles » data-valign="top">\((b−1)(6b−5)\) \ (6b^2−13b+5 \) Produit » data-valign="top">\(6b^2−11b+5\) \ (6b^2−13b+5 \) Facteurs possibles » data-valign="top">\((b−5)(6b−1)\) \ (6b^2−13b+5 \) Produit » data-valign="top">\(6b^2−31b+5\) \ (6b^2−13b+5 \) Facteurs possibles » data-valign="top">\((2b−1)(3b−5)\) \ (6b^2−13b+5 \) Produit » data-valign="middle">\(6b^2−13b+5^∗\) \ (6b^2−13b+5 \) Facteurs possibles » data-valign="top">\((2b−5)(3b−1)\) \ (6b^2−13b+5 \) Produit » data-valign="middle">\(6b^2−17b+5\) \(\begin{array} {ll} \text{The correct factors are those whose product} & \\ \text{is the original trinomial.} &(2b−1)(3b−5) \\ \text{Check by multiplying:} & \\ \hspace{50mm} (2b−1)(3b−5) & \\ \hspace{47mm} 6b^2−10b−3b+5 & \\ \hspace{50mm} 6b^2−13b+5\checkmark & \end{array} \)
Factoriez complètement en utilisant des essais et des erreurs :\(8x^2−14x+3\).
- Réponse
-
\((2x−3)(4x−1)\)
Factoriez complètement en utilisant des essais et des erreurs :\(10y^2−37y+7\).
- Réponse
-
\((2y−7)(5y−1)\)
Lorsque nous factorisons une expression, nous cherchons toujours d'abord le plus grand facteur commun. Si l'expression n'a pas de plus grand facteur commun, il ne peut pas non plus y en avoir un dans ses facteurs. Cela peut nous aider à éliminer certaines des combinaisons de facteurs possibles.
Factoriez complètement en utilisant des essais et des erreurs :\(18x^2−37xy+15y^2\).
- Réponse
-
Le trinôme est déjà dans l'ordre décroissant. 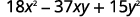
Déterminez les facteurs du premier mandat. 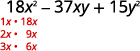
Trouvez les facteurs du dernier trimestre. Tenez compte des signes.
Comme 15 est positif et que le coefficient du moyen
terme est négatif, nous utilisons les facteurs négatifs.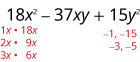
Tenez compte de toutes les combinaisons de facteurs.

\(\begin{array} {ll} \text{The correct factors are those whose product is} & \\ \text{the original trinomial.} &(2x−3y)(9x−5y) \\ \text{Check by multiplying:} & \\ & \\ & \\ & \\ \hspace{50mm} (2x−3y)(9x−5y) & \\ \hspace{45mm}18x^2−10xy−27xy+15y^2 & \\ \hspace{47mm}18x^2−37xy+15y^2\checkmark & \end{array} \)
Factorez complètement par essais et erreurs\(18x^2−3xy−10y^2\).
- Réponse
-
\((3x+2y)(6x−5y)\)
Factoriez complètement en utilisant des essais et des erreurs :\(30x^2−53xy−21y^2\).
- Réponse
-
\((3x+y)(10x−21y)\)
N'oubliez pas de rechercher d'abord un GCF et de vous rappeler si le coefficient principal est négatif, il en va de même pour le GCF.
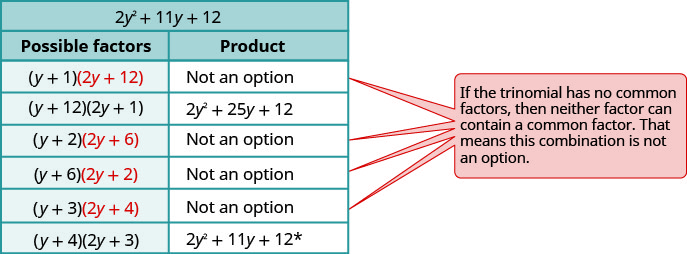
Factoriez complètement en utilisant des essais et des erreurs :\(−10y^4−55y^3−60y^2\).
- Réponse
-
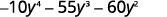
Remarquez le plus grand facteur commun, alors considérez-le d'abord. 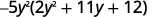
Tenez compte du trinôme. 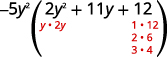
Tenez compte de toutes les combinaisons.
-
\(\begin{array} {ll} \text{The correct factors are those whose product} & \\ \text{is the original trinomial. Remember to include} & \\ \text{the factor }−5^y2. &−5y^2(y+4)(2y+3) \\ \text{Check by multiplying:} & \\ \hspace{50mm} −5y^2(y+4)(2y+3) & \\ \hspace{45mm} −5y^2(2y^2+8y+3y+12) & \\ \hspace{47mm}−10y^4−55y^3−60y^2\checkmark & \end{array} \)
Factoriez complètement en utilisant des essais et des erreurs :\(15n^3−85n^2+100n\).
- Réponse
-
\(5n(n−4)(3n−5)\)
Factoriez complètement en utilisant des essais et des erreurs :\(56q^3+320q^2−96q\).
- Réponse
-
\(8q(q+6)(7q−2)\)
Facteur des trinômes du formulaire\(ax^2+bx+c\) en utilisant la méthode «\(ac\) »
Une autre façon de factoriser les trinômes de la forme\(ax^2+bx+c\) est la méthode «\(ac\) ». (La méthode «\(ac\) » est parfois appelée méthode de regroupement.) La méthode «\(ac\) » est en fait une extension des méthodes que vous avez utilisées dans la dernière section pour factoriser les trinômes dont le coefficient principal est un. Cette méthode est très structurée (c'est-à-dire étape par étape), et elle fonctionne toujours !
Facteur utilisant la méthode «\(ac\) » :\(6x^2+7x+2\).
- Réponse
-






Facteur utilisant la méthode «\(ac\) » :\(6x^2+13x+2\).
- Réponse
-
\((x+2)(6x+1)\)
Facteur utilisant la méthode «\(ac\) » :\(4y^2+8y+3\).
- Réponse
-
\((2y+1)(2y+3)\)
La méthode «\(ac\) » est résumée ici.
- Tenez compte de tout GCF.
- Trouvez le produit\(ac\).
- Trouvez deux nombres\(m\) et\(n\) cela :
\(\begin{array} {ll} \text{Multiply to }ac &m·n=a·c \\ \text{Add to }b &m+n=b \\ &ax^2+bx+c \end{array} \) - Divisez le moyen terme en utilisant\(m\) et\(n\). \(ax^2+mx+nx+c\)
- Facteur par regroupement.
- Vérifiez en multipliant les facteurs.
N'oubliez pas de rechercher un facteur commun !
Facteur utilisant la méthode « \(ac\)» :\(10y^2−55y+70\).
- Réponse
-
Y a-t-il un plus grand facteur commun ? Oui. Le GCF est\(5\). 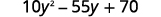
Tenez-le en compte. 
Le trinôme entre parenthèses a un coefficient
principal qui ne l'est pas\(1\).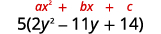
Trouvez le produit\(ac\). \(ac=28\) Trouvez deux nombres qui se multiplient par\(ac\) \((−4)(−7)=28\) et ajoutez-le à\(b\). \(−4(−7)=−11\) Divisez le moyen terme. 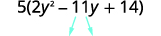
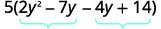
Facturez le trinôme en le regroupant. 
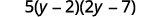
Vérifiez en multipliant les trois facteurs.
\(\hspace{50mm} 5(y−2)(2y−7)\)\(\hspace{45mm} 5(2y^2−7y−4y+14)\)
\(\hspace{48mm} 5(2y^2−11y+14)\)
\(\hspace{49mm} 10y^2−55y+70\checkmark\)
Facteur utilisant la méthode «\(ac\) » :\(16x^2−32x+12\).
- Réponse
-
\(4(2x−3)(2x−1)\)
Facteur utilisant la méthode «\(ac\) » :\(18w^2−39w+18\).
- Réponse
-
\(3(3w−2)(2w−3)\)
Facteur utilisant la substitution
Parfois, un trinôme ne semble pas figurer dans le\(ax^2+bx+c\) formulaire. Cependant, nous pouvons souvent effectuer une substitution réfléchie qui nous permettra de l'adapter à la\(ax^2+bx+c\) forme. C'est ce que l'on appelle la factorisation par substitution. Il est standard à utiliser\(u\) pour la substitution.
Dans le\(ax^2+bx+c\), le terme moyen a une variable\(x\), et son carré\(x^2\), est la partie variable du premier terme. Recherchez cette relation lorsque vous essayez de trouver une substitution.
Facteur par substitution :\(x^4−4x^2−5\).
- Réponse
-
La partie variable du terme moyen est\(x^2\) et son carré,\(x^4\), est la partie variable du premier terme. (Nous savons\((x^2)^2=x^4)\). Si nous le laissons faire\(u=x^2\), nous pouvons mettre notre trinôme sous la\(ax^2+bx+c\) forme dont nous avons besoin pour le prendre en compte.
\(x^4−4x^2−5\) Réécrivez le trinôme pour préparer la substitution. \((x^2)^2−4(x^2)-5\) Laisser\(u=x^2\) et remplacer. \((u)^2−4(u)-5\) Tenez compte du trinôme. \((u+1)(u-5)\) Remplacez\(u\) par\(x^2\). \((x^2+1)(x^2-5)\) Vérifiez :
\(\begin{array} {l} \hspace{37mm} (x^2+1)(x^2−5) \\ \hspace{35mm}x^4−5x^2+x^2−5 \\ \hspace{40mm}x^4−4x^2−5\checkmark\end{array}\)
Facteur par substitution :\(h^4+4h^2−12\).
- Réponse
-
\((h^2−2)(h^2+6)\)
Facteur par substitution :\(y^4−y^2−20\).
- Réponse
-
\((y^2+4)(y^2−5)\)
Parfois, l'expression à substituer n'est pas un monomial.
Facteur par substitution :\((x−2)^2+7(x−2)+12\)
- Réponse
-
Le binôme au moyen terme\((x−2)\) est mis au carré au premier terme. Si nous le laissons\(u=x−2\) et le remplaçons, notre trinôme sera en\(ax^2+bx+c\) forme.
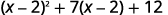
Réécrivez le trinôme pour préparer la substitution. 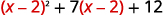
Laisser\(u=x−2\) et remplacer. 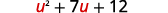
Tenez compte du trinôme. 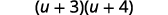
Remplacez\(u\) par\(x−2\). 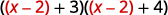
Simplifiez entre parenthèses. 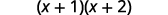
Cela pourrait également être pris en compte en multipliant d'abord le\((x−2)^2\) et le,\(7(x−2)\) puis en combinant des termes similaires, puis en factorisant. La plupart des étudiants préfèrent la méthode de substitution.
Facteur par substitution :\((x−5)^2+6(x−5)+8\).
- Réponse
-
\((x−3)(x−1)\)
Facteur par substitution :\((y−4)^2+8(y−4)+15\).
- Réponse
-
\((y−1)(y+1)\)
Regardez cette vidéo pour obtenir des instructions supplémentaires et vous entraîner à l'affacturage.
Concepts clés
- Comment factoriser les trinômes de la forme\(x^2+bx+c\).
- Écrivez les facteurs sous forme de deux binômes avec les premiers termes x. \(\quad \begin{array} (l) x^2+bx+c \\ (x\quad)(x\quad)\end{array}\)
- Trouve deux chiffres\(m\) et\(n\) ça
\(\begin{array} {ll} \text{multiply to} &c,\space m·n=c \\ \text{add to} &b,\space m+n=b\end{array}\) - Utilisez\(m\) et\(n\) comme dernier terme des facteurs. \(\qquad (x+m)(x+n)\)
- Vérifiez en multipliant les facteurs.
- Stratégie de factorisation des trinômes de la forme\(x^2+bx+c\) : Lorsque nous factorisons un trinôme, nous examinons d'abord les signes de ses termes pour déterminer les signes des facteurs binomiaux.
Pour les trinômes de la forme :\(x^2+bx+c = (x+m)(x+n)\)
Quand\(c\) est positif\(m\) et\(n\) doit avoir le même signe (et ce sera le signe de\(b\) ).
Exemples :\(x^2+5x+6=(x+2)(x+3)\),\(x^2−6x+8 = (x−4)(x−2)\)
Quand\(c\) est négatif\(m\) et\(n\) a des signes opposés. Le plus grand de\(m\) et\(n\) portera le signe de\(b\).
Exemples :\(x^2+x−12=(x+4)(x−3)\),\(x^2−2x−15=(x−5)(x+3)\)
Notez que, dans le cas où\(m\) et\(n\) ont des signes opposés, le signe de celui dont la valeur absolue est la plus grande correspond au signe de\(b\). - Comment factoriser les trinômes du\(ax^2+bx+c\) formulaire par essais et erreurs.
- Écrivez le trinôme par ordre décroissant de degrés selon les besoins.
- Tenez compte de tout GCF.
- Trouvez toutes les paires de facteurs du premier terme.
- Trouvez toutes les paires de facteurs du troisième terme.
- Testez toutes les combinaisons possibles de facteurs jusqu'à ce que le bon produit soit trouvé.
- Vérifiez en multipliant.
- Comment factoriser les trinômes de la forme à\(ax^2+bx+c\) l'aide de la méthode «\(ac\) ».
- Tenez compte de tout GCF.
- Trouvez le produit\(ac\).
- Trouvez deux nombres\(m\) et\(n\) cela :
\(\begin{array} {ll} \text{Multiply to }ac. &m·n=a·c \\ \text{Add to }b. &m+n=b \\ &ax^2+bx+c\end{array}\) - Divisez le moyen terme en utilisant\(m\) et\(n\). \(\quad ax^2+mx+nx+c\)
- Facteur par regroupement.
- Vérifiez en multipliant les facteurs.


