Chapitre 3 Exercices de révision

Exercices de révision des

Tracez des équations linéaires à deux variables

Tracer des points dans un système de coordonnées rectangulaires

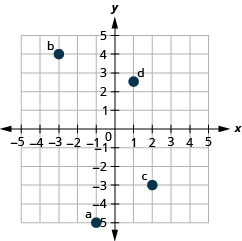
Dans les exercices suivants, tracez chaque point dans un système de coordonnées rectangulaires.

1. ⓐ$(−1,−5)$
ⓑ$(−3,4)$
ⓒ$(2,−3)$
ⓓ$(1,\frac{5}{2})$

Réponse

2. ⓐ$(−2,0)$
ⓑ$(0,−4)$
ⓒ$(0,5)$
ⓓ$(3,0)$

Dans les exercices suivants, déterminez quelles paires ordonnées sont des solutions aux équations données.

3. $5x+y=10$;

ⓐ$(5,1)$
ⓑ$(2,0)$
ⓒ$(4,−10)$

Réponse

ⓑ, ⓒ

4. $y=6x−2$;

ⓐ$(1,4)$
ⓑ$(13,0)$
ⓒ$(6,−2)$

Tracez une équation linéaire en traçant des points

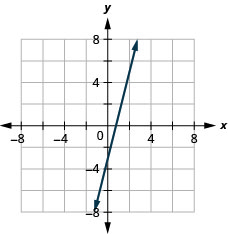
Dans les exercices suivants, tracez un graphique en traçant des points.

5. $y=4x−3$

Réponse

6. $y=−3x$

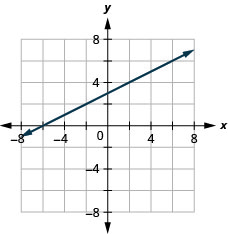
7. $y=\frac{1}{2}x+3$

Réponse

8. $y=−\frac{4}{5}|x−1$

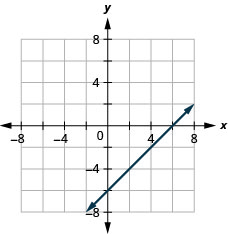
9. $x−y=6$

Réponse

10. $2x+y=7$

11. $3x−2y=6$

Réponse

Tracez des lignes verticales et horizontales

Dans les exercices suivants, tracez chaque équation.

12. $y=−2$

13. $x=3$

Réponse

Dans les exercices suivants, tracez chaque paire d'équations dans le même système de coordonnées rectangulaires.

14. $y=−2x$et$y=−2$

15. $y=\frac{4}{3}x$et$y=\frac{4}{3}$

Réponse

Trouvez les interceptions x et y

Dans les exercices suivants, trouvez les points d'intersection x et y.

16.

17.

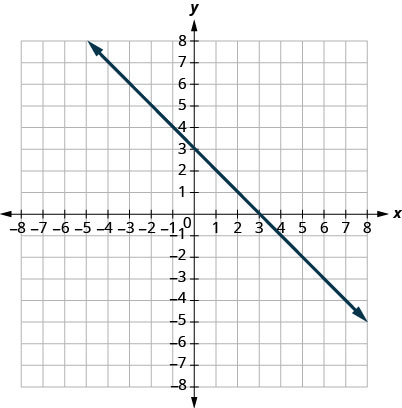
Réponse

$(0,3)(3,0)$

Dans les exercices suivants, trouvez les points d'intersection de chaque équation.

18. $x−y=−1$

19. $x+2y=6$

Réponse

$(6,0),\space (0,3)$

20. $2x+3y=12$

21. $y=\frac{3}{4}x−12$

Réponse

$(16,0),\space (0,−12)$

22. $y=3x$

Tracez une ligne à l'aide des interceptions

Dans les exercices suivants, tracez un graphique à l'aide des interceptions.

23. $−x+3y=3$

Réponse

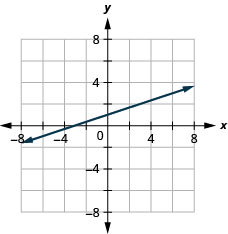
24. $x−y=4$

25. $2x−y=5$

Réponse

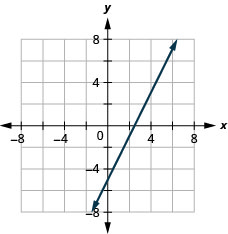
26. $2x−4y=8$

27. $y=4x$

Réponse

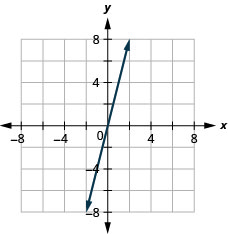
Pente d'une ligne

Trouvez la pente d'une ligne

Dans les exercices suivants, déterminez la pente de chaque ligne affichée.

28.

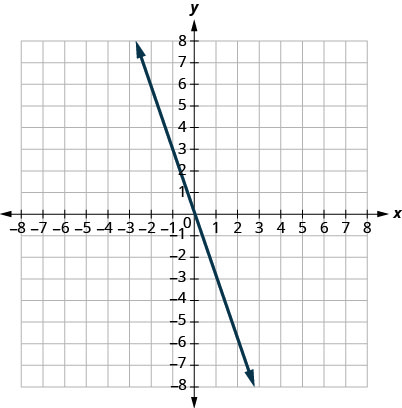
29.

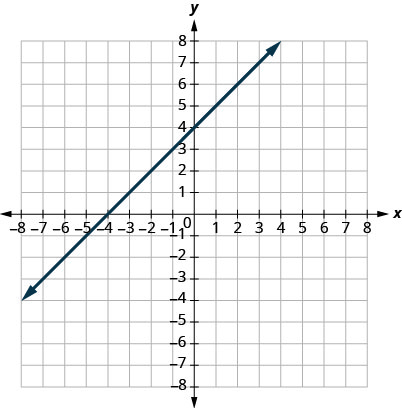
Réponse

1

30.

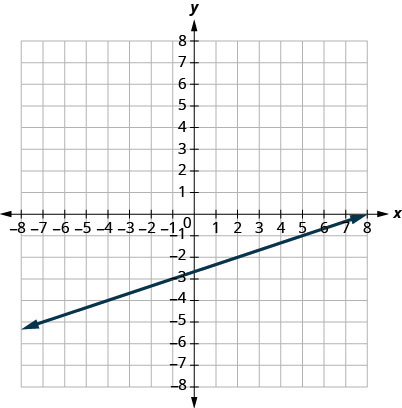
31.

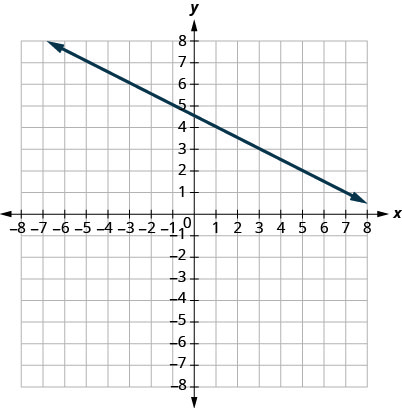
Réponse

$−12$

Dans les exercices suivants, déterminez la pente de chaque ligne.

32. $y=2$

33. $x=5$

Réponse

indéfini

34. $x=−3$

35. $y=−1$

Réponse

0

Utilisez la formule de pente pour déterminer la pente d'une droite entre deux points

Dans les exercices suivants, utilisez la formule de pente pour déterminer la pente de la ligne entre chaque paire de points.

36. $(−1,−1),(0,5)$

37. $(3.5),(4,−1)$

Réponse

$−6$

38. $(−5,−2),(3,2)$

39. $(2,1),(4,6)$

Réponse

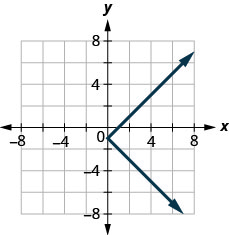
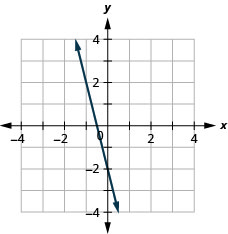
$52$

Tracez une droite en fonction d'un point et de la pente

Dans les exercices suivants, tracez chaque ligne avec le point et la pente donnés.

40. $(2,−2);\space m=52$

41. $(−3,4);\space m=−13$

Réponse

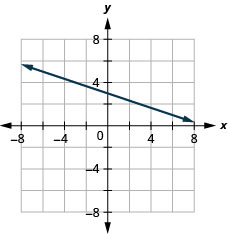
42. $x$-intercepter$−4; m=3$

43. $y$-intercepter$1; m=−34$

Réponse

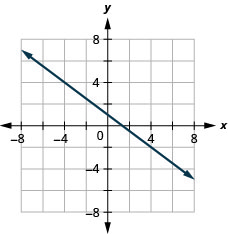
Tracez une ligne en utilisant sa pente et son intersection

Dans les exercices suivants, identifiez la pente et l'$y$intersection de chaque ligne.

44. $y=−4x+9$

45. $y=53x−6$

Réponse

$m=53;\space (0,−6)$

46. $5x+y=10$

47. $4x−5y=8$

Réponse

$m=\frac{4}{5};\space (0,−\frac{8}{5})$

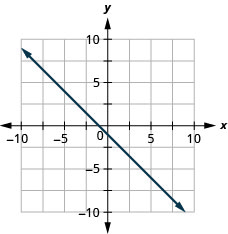
Dans les exercices suivants, tracez la droite de chaque équation en utilisant sa pente et son intersection y.

48. $y=2x+3$

49. $y=−x−1$

Réponse

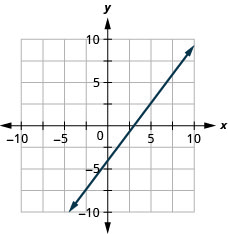
50. $y=−25x+3$

51. $4x−3y=12$

Réponse

Dans les exercices suivants, déterminez la méthode la plus pratique pour représenter graphiquement chaque ligne.

52. $x=5$

53. $y=−3$

Réponse

ligne horizontale

54. $2x+y=5$

55. $x−y=2$

Réponse

intercepte

56. $y=22x+2$

57. $y=34x−1$

Réponse

points de traçage

Applications graphiques et interprétatives de Slope-Intercept

58. Katherine est chef privée. L'équation$C=6.5m+42$ modélise la relation entre son coût hebdomadaire, C, en dollars et le nombre de repas, m, qu'elle sert.

ⓐ Trouvez le coût de Katherine pour une semaine lorsqu'elle ne sert aucun repas.
ⓑ Trouvez le coût pour une semaine lorsqu'elle sert 14 repas.
ⓒ Interprétez la pente et l'intersection C de l'équation.
ⓓ Tracez l'équation.

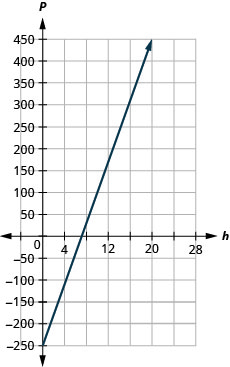
59. Marjorie enseigne le piano. L'équation$P=35h−250$ modélise la relation entre son bénéfice hebdomadaire, P, en dollars et le nombre de leçons qu'elle donne aux étudiants.

ⓐ Trouvez le profit de Marjorie pendant une semaine lorsqu'elle ne donne aucun cours aux élèves.
ⓑ Trouvez le profit d'une semaine lorsqu'elle donne des cours à 20 élèves.
ⓒ Interprétez la pente et l'intersection P de l'équation.
ⓓ Tracez l'équation.

Réponse

ⓐ$−$250$
ⓑ$$450$
ⓒ La pente, 35, signifie que le bénéfice hebdomadaire de Marjorie, P, augmente de 35$ pour chaque leçon supplémentaire qu'elle donne à un élève.
L'intercept P signifie que lorsque le nombre de leçons est de 0, Marjorie perd 250$.
ⓓ

Utiliser les pentes pour identifier les lignes parallèles et perpendiculaires

Dans les exercices suivants, utilisez les pentes et$y$ les interceptions pour déterminer si les lignes sont parallèles, perpendiculaires ou aucune des deux.

60. $4x−3y=−1;\quad y=43x−3$

61. $y=5x−1;\quad 10x+2y=0$

Réponse

ni

62. $3x−2y=5;\quad 2x+3y=6$

63. $2x−y=8;\quad x−2y=4$

Réponse

pas parallèle

Trouvez l'équation d'une droite

Trouvez une équation de la droite en fonction de la pente et de l'intersection y

Dans les exercices suivants, trouvez l'équation d'une droite avec une pente et une intersection y données. Écrivez l'équation sous forme de pente et d'intersection.

64. Pente$\frac{1}{3}$ et$y$ intersection$(0,−6)$

65. Pente$−5$ et$y$ intersection$(0,−3)$

Réponse

$y=−5x−3$

66. Pente$0$ et$y$ intersection$(0,4)$

67. Pente$−2$ et$y$ intersection$(0,0)$

Réponse

$y=−2x$

Dans les exercices suivants, trouvez l'équation de la droite affichée sur chaque graphique. Écrivez l'équation sous forme de pente et d'intersection.

68.

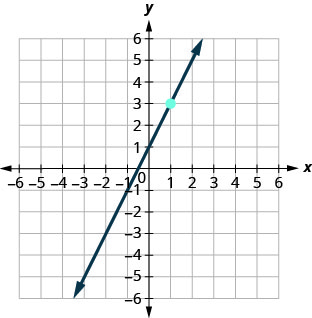
69.

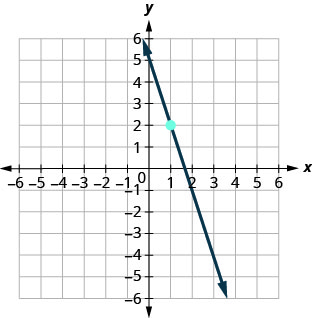
Réponse

$y=−3x+5$

70.

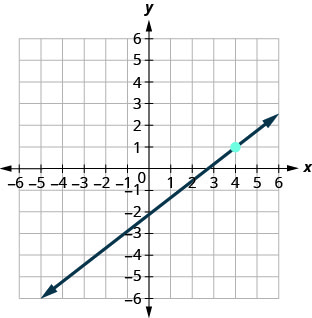
71.

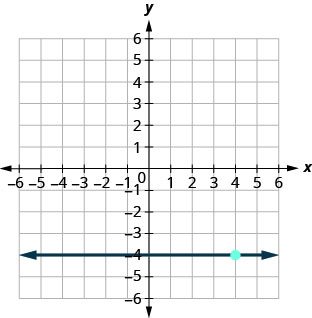
Réponse

$y=−4$

Trouvez une équation de la droite en fonction de la pente et d'un point

Dans les exercices suivants, trouvez l'équation d'une droite avec une pente donnée et contenant le point donné. Écrivez l'équation sous forme de pente et d'intersection.

72. $m=−\frac{1}{4}$, point$(−8,3)$

73. $m=\frac{3}{5}$, point$(10,6)$

Réponse

$y=\frac{3}{5}x$

74. Ligne horizontale contenant$(−2,7)$

75. $m=−2$, point$(−1,−3)$

Réponse

$y=−2x−5$

Trouvez une équation de la droite à partir de deux points

Dans les exercices suivants, trouvez l'équation d'une droite contenant les points donnés. Écrivez l'équation sous forme de pente et d'intersection.

76. $(2,10)$et$(−2,−2)$

77. $(7,1)$et$(5,0)$

Réponse

$y=\frac{1}{2}x−\frac{5}{2}$

78. $(3,8)$et$(3,−4)$

79. $(5,2)$et$(−1,2)$

Réponse

$y=2$

Trouver l'équation d'une droite parallèle à une droite donnée

Dans les exercices suivants, trouvez l'équation d'une droite parallèle à la droite donnée et contenant le point donné. Écrivez l'équation sous forme de pente et d'intersection.

80. ligne$y=−3x+6$, point$(1,−5)$

81. ligne$2x+5y=−10$, point$(10,4)$

Réponse

$y=−\frac{2}{5}x+8$

82. Ligne$x=4$, point$(−2,−1)$

83. ligne$y=−5$, point$(−4,3)$

Réponse

$y=3$

Trouver l'équation d'une droite perpendiculaire à une droite donnée

Dans les exercices suivants, trouvez l'équation d'une droite perpendiculaire à la droite donnée et contenant le point donné. Écrivez l'équation sous forme de pente et d'intersection.

84. ligne$y=−\frac{4}{5}x+2$, point$(8,9)$

85. ligne$2x−3y=9$, point$(−4,0)$

Réponse

$y=−\frac{3}{2}x−6$

86. ligne$y=3$, point$(−1,−3)$

87.$x=−5$ point de ligne$(2,1)$

Réponse

$y=1$

Représenter graphiquement les inégalités linéaires dans deux variables

Vérifier les solutions à une inégalité entre deux variables

Dans les exercices suivants, déterminez si chaque paire ordonnée est une solution à l'inégalité donnée.

88. Déterminez si chaque paire ordonnée est une solution à l'inégalité$y<x−3$ :

ⓐ$(0,1)$ ⓑ$(−2,−4)$ ⓒ$(5,2)$ ⓓ$(3,−1)$
ⓔ$(−1,−5)$

89. Déterminez si chaque paire ordonnée est une solution à l'inégalité$x+y>4$ :

ⓐ$(6,1)$ ⓑ$(−3,6)$ ⓒ$(3,2)$ ⓓ$(−5,10)$ ⓔ$(0,0)$

Réponse

ⓐ oui ⓑ non ⓒ oui ⓓ oui ; ⓔ nom

Reconnaître la relation entre les solutions d'une inégalité et son graphe

Dans les exercices suivants, écrivez l'inégalité indiquée par la région ombrée.

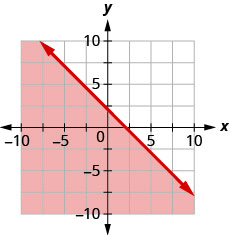
90. Écrivez l'inégalité indiquée par le graphique avec la ligne de démarcation$y=−x+2.$

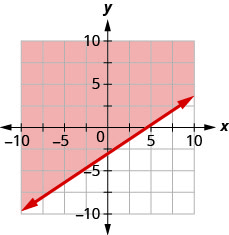
91. Écrivez l'inégalité indiquée par le graphique avec la ligne de démarcation$y=\frac{2}{3}x−3$.

Réponse

$y>\frac{2}{3}x−3$

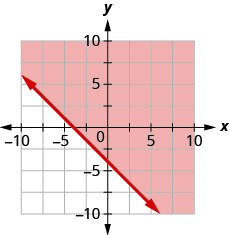
92. Écrivez l'inégalité indiquée par la région ombrée dans le graphique avec la ligne de démarcation$x+y=−4$.

93. Écrivez l'inégalité indiquée par la région ombrée dans le graphique avec la ligne de démarcation$x−2y=6$.

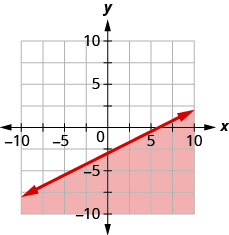
Réponse

$x−2y\geq 6$

Représenter graphiquement les inégalités linéaires dans deux variables

Dans les exercices suivants, représentez graphiquement chaque inégalité linéaire.

94. Tracez l'inégalité linéaire$y>\frac{2}{5}x−4$.

95. Tracez l'inégalité linéaire$y\leq −\frac{1}{4}x+3$.

Réponse

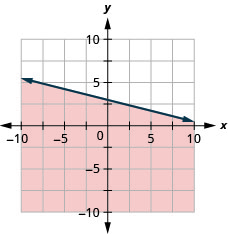
96. Tracez l'inégalité linéaire$x−y\leq 5$.

97. Représenter graphiquement l'inégalité linéaire$3x+2y>10.$

Réponse

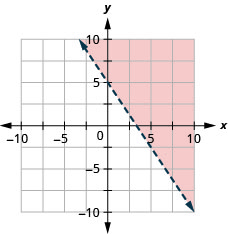
98. Tracez l'inégalité linéaire$y\leq −3x$.

99. Représenter graphiquement l'inégalité linéaire$y<6.$

Réponse

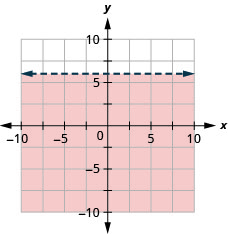
Résolvez des applications en utilisant des inégalités linéaires dans deux variables

100. Shanthie doit gagner au moins 500$ par semaine pendant ses vacances d'été pour payer ses études universitaires. Elle a deux emplois. L'un en tant que moniteur de natation payant 10 dollars de l'heure et l'autre en tant que stagiaire dans un cabinet d'avocats pour 25 dollars de l'heure. Combien d'heures Shanthie doit-elle travailler pour chaque emploi pour gagner au moins 500$ par semaine ?

ⓐ Soit x le nombre d'heures pendant lesquelles elle enseigne la natation et y le nombre d'heures pendant lesquelles elle travaille en tant que stagiaire. Écrivez une inégalité qui modéliserait cette situation.
ⓑ Représenter graphiquement l'inégalité.
ⓒ Trouvez trois paires ordonnées$(x,y)$ qui seraient des solutions à l'inégalité. Ensuite, expliquez ce que cela signifie pour Shanthie.

101. Au sushi, il doit faire suffisamment d'exercice pour brûler des$600$ calories chaque jour. Il préfère courir ou faire du vélo et brûle des$20$ calories par minute en courant et des$15$ calories par minute en faisant du vélo.

ⓐ Si x est le nombre de minutes pendant lesquelles Atsushi court et y le nombre de minutes pendant lesquelles il fait du vélo, trouvez l'inégalité qui modélise la situation.
ⓑ Représenter graphiquement l'inégalité.
ⓒ Énumérez trois solutions à l'inégalité. Quelles options les solutions offrent-elles à Atsushi ?

Réponse

ⓐ$20x+15y\geq 60020x+15y\geq 600$
ⓑ

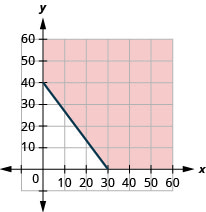
ⓒ Les réponses peuvent varier.

Relations et fonctions

Trouvez le domaine et l'étendue d'une relation

Dans les exercices suivants, pour chaque relation, ⓐ trouvez le domaine de la relation ⓑ trouvez la plage de la relation.

102. ${\{(5,−2),\,(5,−4),\,(7,−6),\,(8,−8),\,(9,−10)}\}$

103. ${\{(−3,7),\,(−2,3),\,(−1,9), \,(0,−3),\,(−1,8)}\}$

Réponse

ⓐ$D: {−3, −2, −1, 0}$
ⓑ$R: {7, 3, 9, −3, 8}$

Dans l'exercice suivant, utilisez le mappage de la relation pour ⓐ répertorier les paires ordonnées de la relation ⓑ trouver le domaine de la relation ⓒ trouver la plage de la relation.

104. La cartographie ci-dessous montre le poids moyen d'un enfant en fonction de son âge.

Dans l'exercice suivant, utilisez le graphe de la relation pour ⓐ répertorier les paires ordonnées de la relation ⓑ trouver le domaine de la relation ⓒ trouver la plage de la relation.

105.

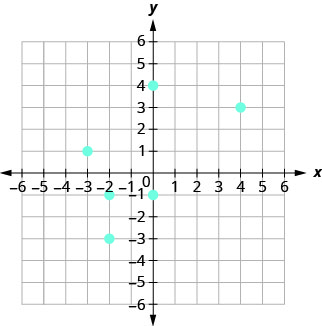
Réponse

ⓐ$(4, 3), \,(−2, −3), \,(−2, −1), \,(−3, 1), \,(0, −1), \,(0, 4)$
ⓑ$D: {−3, −2, 0, 4}$
ⓒ$R: {−3, −1, 1, 3, 4}$

Déterminer si une relation est une fonction

Dans les exercices suivants, utilisez l'ensemble de paires ordonnées pour ⓐ déterminer si la relation est une fonction ⓑ trouver le domaine de la relation ⓒ trouver la plage de la relation.

106. ${\{(9,−5),\,(4,−3),\,(1,−1),\,(0,0),\,(1,1),\,(4,3),\,(9,5)}\}$

107. ${\{(−3,27),\,(−2,8),\,(−1,1),\,(0,0),\,(1,1),\,(2,8),\,(3,27)}\}$

Réponse

ⓐ Oui ⓑ${−3, −2, −1, 0, 1, 2, 3}$
ⓒ${0, 1, 8, 27}$

Dans les exercices suivants, utilisez le mappage pour ⓐ déterminer si la relation est une fonction ⓑ trouver le domaine de la fonction ⓒ trouver la plage de la fonction.

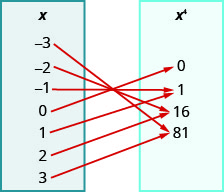
108.

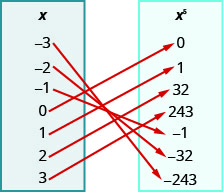
109.

Réponse

ⓐ${−3, −2, −1, 0, 1, 2, 3}$
ⓑ${−3, −2, −1, 0, 1, 2, 3}$
ⓒ${−243, −32, −1, 0, 1, 32, 243}$

Dans les exercices suivants, déterminez si chaque équation est une fonction.

110. $2x+y=−3$

111. $y=x^2$

Réponse

oui

112. $y=3x−5$

113. $y=x^3$

Réponse

oui

114. $2x+y2=4$

Trouver la valeur d'une fonction

Dans les exercices suivants, évaluez la fonction :

ⓐ$f(−2)$ ⓑ$f(3)$ ⓒ$f(a)$.

115. $f(x)=3x−4$

Réponse

ⓐ$f(−2)=−10$ ⓑ$f(3)=5$ ⓒ$f(a)=3a−4$

116. $f(x)=−2x+5$

117. $f(x)=x^2−5x+6$

Réponse

ⓐ$f(−2)=20$ ⓑ$f(3)=0$ ⓒ$f(a)=a^2−5a+6$

118. $f(x)=3x^2−2x+1$

Dans les exercices suivants, évaluez la fonction.

119. $g(x)=3x2−5x;\space g(2)$

Réponse

$2$

120. $F(x)=2x2−3x+1;\space F(−1)$

121. $h(t)=4|t−1|+2;\space h(t)=4$

Réponse

$18$

122. $f(x)=x+2x−1;\space f(3)$

Graphiques des fonctions

Utiliser le test de la ligne verticale

Dans les exercices suivants, déterminez si chaque graphique est le graphe d'une fonction.

123.

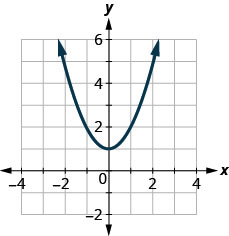
Réponse

oui

124.

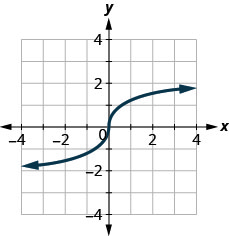
125.

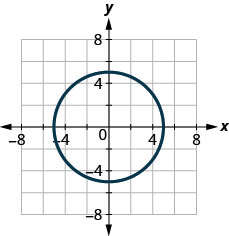
Réponse

non

126.

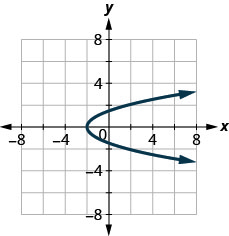
127.

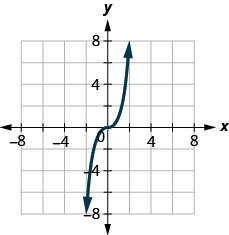
Réponse

oui

128.

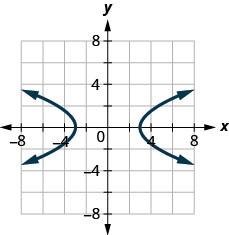
129.

Réponse

non

Identifier les graphes des fonctions de base

Dans les exercices suivants, ⓐ représente graphiquement chaque fonction ⓑ indiquez son domaine et sa plage. Écrivez le domaine et la plage en notation par intervalles.

130. $f(x)=5x+1$

131. $f(x)=−4x−2$

Réponse

ⓐ

ⓑ$D: (-\inf ,\inf ), R: (-\inf ,\inf )$

132. $f(x)=\frac{2}{3}x−1$

133. $f(x)=−6$

Réponse

ⓐ

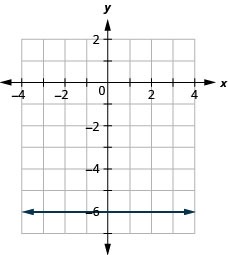
ⓑ$D: (-\inf ,\inf ), R: (-\inf ,\inf )$

134. $f(x)=2x$

135. $f(x)=3x^2$

Réponse

ⓐ

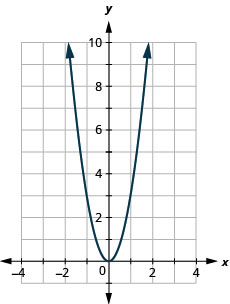
ⓑ$D: (-\inf ,\inf ), R: (-\inf ,0]$

136. $f(x)=−12x^2$

137. $f(x)=x^2+2$

Réponse

ⓐ

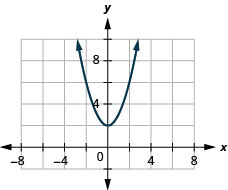
ⓑ$D: (-\inf ,\inf ), R: (-\inf ,\inf )$

138. $f(x)=x^3−2$

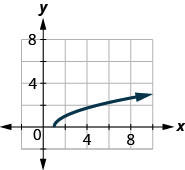
139. $f(x)=\sqrt{x+2}$

Réponse

ⓐ

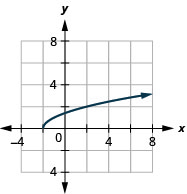
ⓑ$D: [−2,−2, \inf ), \space R: [0,\inf )$

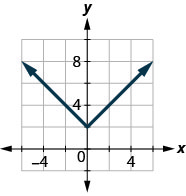
140. $f(x)=−|x|$

141. $f(x)=|x|+1$

Réponse

ⓐ

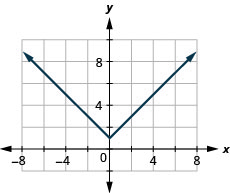
ⓑ$D: (-\inf ,\inf ), \space R: [1,\inf )$

Lire des informations à partir du graphe d'une fonction

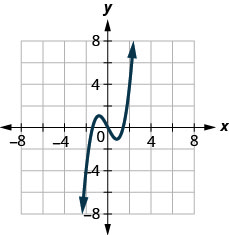
Dans les exercices suivants, utilisez le graphique de la fonction pour déterminer son domaine et sa plage. Écrivez le domaine et la plage en notation par intervalles

142.

143.

Réponse

$D: (-\inf ,\inf ), R: [2,\inf )$

144.

Dans les exercices suivants, utilisez le graphique de la fonction pour trouver les valeurs indiquées.

145.

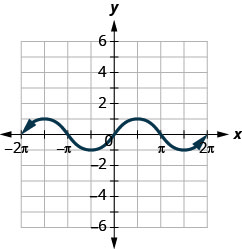
ⓐ Trouvez$f(0)$.
ⓑ Trouvez$f(12\pi )$.
ⓒ Trouvez$f(−32\pi )$.
ⓓ Trouvez les valeurs pour savoir$x$ quand$f(x)=0$.
ⓔ Trouvez les$x$ -intercepts.
ⓕ Trouvez le ou les$y$ -intercept (s).
ⓖ Trouvez le domaine. Écrivez-le en notation par intervalles.
ⓗ Trouvez la gamme. Écrivez-le en notation par intervalles.

Réponse

ⓐ$f(x)=0$ ⓑ$f(\pi /2)=1$
ⓒ$f(−3\pi /2)=1$ ⓓ$f(x)=0$ pour$x=−2\pi ,−\pi ,0,\pi ,2\pi$
ⓔ$(−2\pi ,0), (−\pi ,0), (0,0), (\pi ,0), (2\pi ,0)$ ⓕ$(0,0)$
ⓖ$[−2\pi ,2\pi ]$ ⓗ$[−1,1]$

146.

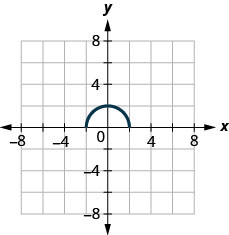
ⓐ Trouvez$f(0)$.
ⓑ Trouvez les valeurs pour savoir$x$ quand$f(x)=0$.
ⓒ Trouvez les$x$ -intercepts.
ⓓ Trouvez le ou les$y$ -intercept (s).
ⓔ Trouvez le domaine. Écrivez-le en notation par intervalles.
ⓕ Trouvez la gamme. Écrivez-le en notation par intervalles.

Test d'entraînement

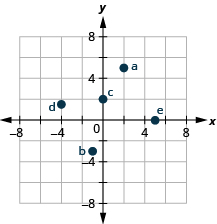
1. Tracez chaque point dans un système de coordonnées rectangulaires.

ⓐ$(2,5)$
ⓑ$(−1,−3)$
ⓒ$(0,2)$
ⓓ$(−4,32)$
ⓔ$(5,0)$

Réponse

2. Parmi les paires ordonnées données, lesquelles sont des solutions à l'équation$3x−y=6$ ?

ⓐ$(3,3)$ ⓑ$(2,0)$ ⓒ$(4,−6)$

3. Déterminez la pente de chaque ligne affichée.

ⓐ

ⓑ

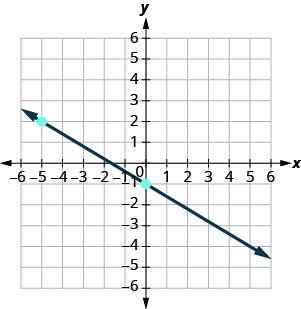
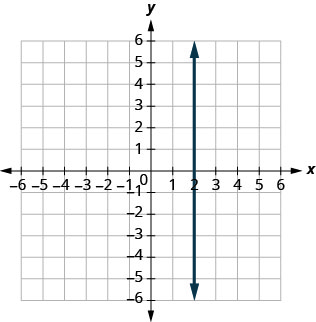
Réponse

ⓐ$−\frac{3}{5}$ ⓑ indéfini

4. Détermine la pente de la ligne entre les points$(5,2)$ et$(−1,−4)$.

5. Tracez la ligne avec la pente$\frac{1}{2}$ contenant le point$(−3,−4)$.

Réponse

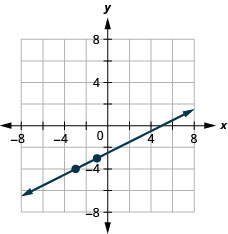
6. Trouvez les points d'intersection$4x+2y=−8$ et tracez un graphique.

Tracez la droite pour chacune des équations suivantes.

7. $y=\frac{5}{3}x−1$

Réponse

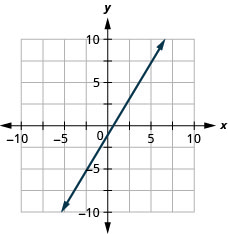
8. $y=−x$

9. $y=2$

Réponse

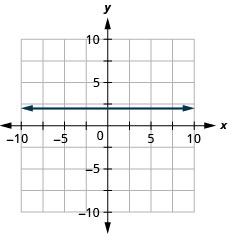
Trouvez l'équation de chaque droite. Écrivez l'équation sous forme d'intersection de pente.

10. pente$−\frac{3}{4}$ et$y$ intersection$(0,−2)$

11. $m=2$, point$(−3,−1)$

Réponse

$y=2x+5$

12. contenant$(10,1)$ et$(6,−1)$

13. perpendiculaire à la ligne$y=\frac{5}{4}x+2$, contenant le point$(−10,3)$

Réponse

$y=−\frac{4}{5}x−5$

14. Écrivez l'inégalité indiquée par le graphique avec la ligne de démarcation$y=−x−3$.

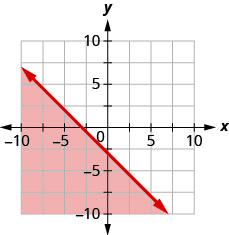
Tracez chaque inégalité linéaire.

15. $y>\frac{3}{2}x+5$

Réponse

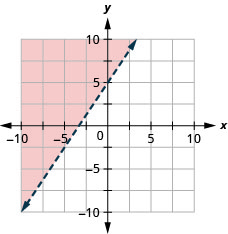
16. $x−y\geq −4$

17. $y\leq −5x$

Réponse

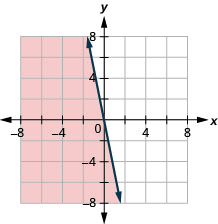
18. Hiro occupe deux emplois à temps partiel afin de gagner suffisamment d'argent pour s'acquitter de ses obligations d'au moins 450$ par semaine. Son travail au centre commercial rapporte 10 dollars de l'heure et son emploi d'assistante administrative sur le campus rapporte 15 dollars de l'heure. Combien d'heures Hiro a-t-il besoin pour travailler à chaque poste pour gagner au moins 450$ ?

ⓐ Soit x le nombre d'heures pendant lesquelles elle travaille au centre commercial et y le nombre d'heures pendant lesquelles elle travaille en tant qu'assistante administrative. Écrivez une inégalité qui modéliserait cette situation.
ⓑ Représenter graphiquement l'inégalité.
ⓒ Trouvez trois paires ordonnées$(x,y)$ qui seraient des solutions à l'inégalité. Expliquez ensuite ce que cela signifie pour Hiro.

19. Utilisez l'ensemble de paires ordonnées pour ⓐ déterminer si la relation est une fonction, ⓑ trouver le domaine de la relation et ⓒ trouver la plage de la relation.

\ ({\ {(−3,27), (−2,8), (−1,1), (0,0),
(1,1), (2,8), (3,27)} \} \)

Réponse

ⓐ Oui ⓑ${\{−3,−2,−1,0,1,2,3}\}$ ⓒ${\{0, 1, 8, 27}\}$

20. Évaluez la fonction : ⓐ$f(−1)$ ⓑ$f(2)$ ⓒ$f(c)$.

$f(x)=4x^2−2x−3$

21. Pour$h(y)=3|y−1|−3$, évaluez$h(−4)$.

Réponse

$12$

22. Déterminez si le graphe est le graphe d'une fonction. Expliquez votre réponse.

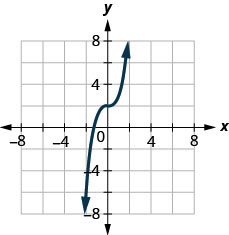
Dans les exercices suivants, ⓐ représente graphiquement chaque fonction ⓑ indiquez son domaine et sa plage.
Écrivez le domaine et la plage en notation par intervalles.

23. $f(x)=x^2+1$

Réponse

ⓐ

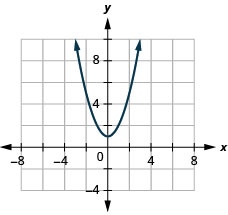
ⓑ$D: (-\inf ,\inf ), R: [1,\inf )$

24. $f(x)=\sqrt{x+1}$

ⓑ Trouvez les$y$ -intercepts.
ⓒ Trouvez$f(−1)$.
ⓓ Trouvez$f(1)$.
ⓔ Trouvez le domaine. Écrivez-le en notation par intervalles.
ⓕ Trouvez la gamme. Écrivez-le en notation par intervalles.

Réponse

ⓐ$x=−2,2$ ⓑ$y=−4$
ⓒ$f(−1)=−3$ ⓓ$f(1)=−3$
ⓔ$D: (-\inf ,\inf )$ ⓕ$R: [−4, \inf)$