3.7E : Exercices

Last updated
Save as PDF

Page ID: 194146

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La pratique permet de perfectionner

Utiliser le test de la ligne verticale

Dans les exercices suivants, déterminez si chaque graphique est le graphe d'une fonction.

1. ⓐ

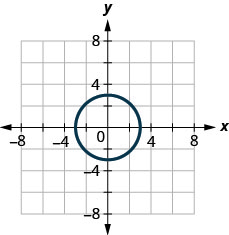
$La figure présente un cercle représenté sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 6 à 6. Le cercle passe par les points (moins 3, 0), (3, 0), (0, moins 3) et (0, 3).$

ⓑ

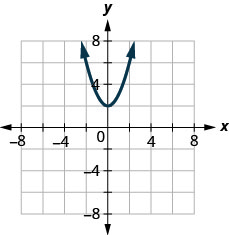
$La figure possède une parabole s'ouvrant graphiquement sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 4 à 8. La parabole passe par les points (négatif 2, 6), (1, 3), (0, 2), (1, 3) et (2, 6).$

Réponse: ⓐ non ⓑ oui

2. ⓐ

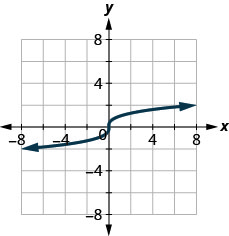
$La figure présente une ligne incurvée en forme de S tracée sur le plan de coordonnées x y. L'axe X va de moins 6 à 6. L'axe Y va de moins 6 à 6. La ligne courbe en forme de S passe par les points (négatif 1, 1), (0, 0) et (1, 1).$

ⓑ

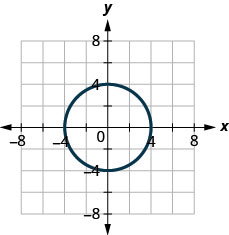
$La figure présente un cercle représenté sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 6 à 6. Le cercle passe par les points (moins 4, 0), (4, 0), (0, moins 4) et (0, 4).$

3. ⓐ

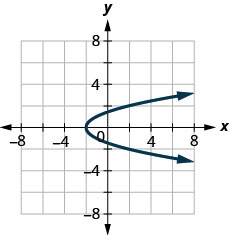
$La figure possède une ouverture parabolique tracée à droite sur le plan de coordonnées x y. L'axe X va de moins 6 à 6. L'axe Y va de moins 6 à 6. La parabole passe par les points (négatif 2, 0), (négatif 1, 1), (négatif 1, négatif 1), (négatif 2, 2) et (2, 2).$

ⓑ

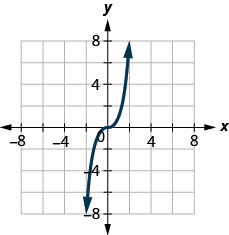
$La figure possède une fonction cubique représentée sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 6 à 6. La ligne courbe passe par les points (négatif 1, négatif 1), (0, 0) et (1, 1).$

Réponse: ⓐ non ⓑ oui

4. ⓐ

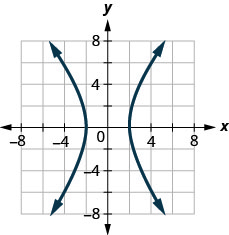
$La figure comporte deux lignes courbes tracées sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 6 à 6. La ligne courbe sur la gauche passe par les points (moins 2, 0), (moins 4, 5) et (moins 4, moins 5). La ligne courbe sur la droite passe par les points (2, 0), (4, 5) et (4, moins 5).$

ⓑ

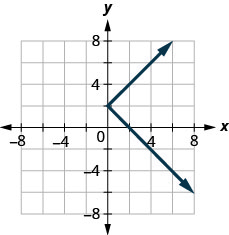
$La figure possède une fonction de valeur absolue orientée latéralement sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 6 à 6. La ligne se courbe au point (0, 2) et va vers la droite. La ligne passe par les points (1, 3), (2, 4), (1, 1) et (2, 0).$

Identifier les graphes des fonctions de base

Dans les exercices suivants, ⓐ représente graphiquement chaque fonction ⓑ indiquez son domaine et sa plage. Écrivez le domaine et la plage en notation par intervalles.

5. $f(x)=3x+4$

Réponse

ⓐ

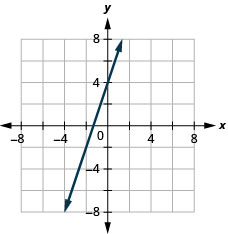
$La figure possède une fonction linéaire représentée sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 6 à 6. La ligne passe par les points (négatif 2, négatif 2), (négatif 1, 1) et (0, 4).$

ⓑ$ D:(-\inf ,\inf ),\space R:(-\inf ,\inf ) $

6. $f(x)=2x+5$

7. $f(x)=−x−2$

Réponse

ⓐ

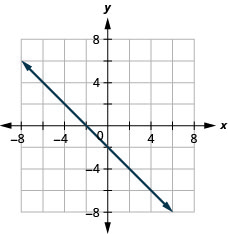
$La figure possède une fonction linéaire représentée sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 6 à 6. La ligne passe par les points (moins 2, 0), (0, moins 2) et (2, moins 4).$

ⓑ$D:(-\inf ,\inf ),\space R:(-\inf ,\inf )$

8. $f(x)=−4x−3$

9. $f(x)=−2x+2$

Réponse

ⓐ

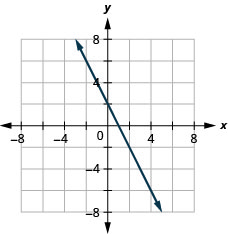
$La figure possède une fonction linéaire représentée sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 6 à 6. La ligne passe par les points (négatif 2, 2), (négatif 1, 0) et (0, moins 2).$

ⓑ$D:(-\inf ,\inf ),\space R:(-\inf ,\inf )$

10. $f(x)=−3x+3$

11. $f(x)=\frac{1}{2}x+1$

Réponse

ⓐ

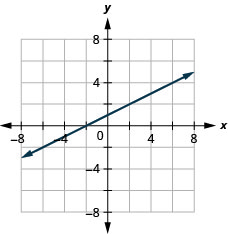
$La figure possède une fonction linéaire représentée sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 6 à 6. La ligne passe par les points (moins 2, 0), (0, 1) et (2, 2).$

ⓑ$D:(-\inf ,\inf ),\space R:(-\inf ,\inf )$

12. $f(x)=\frac{2}{3}x−2$

13. $f(x)=5$

Réponse

ⓐ

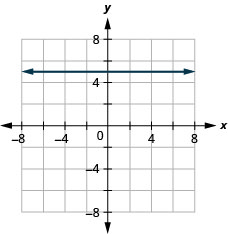
$La figure possède une fonction constante représentée graphiquement sur le plan de coordonnées x. L'axe X va de moins 8 à 8. L'axe Y va de moins 8 à 8. La ligne passe par les points (moins 2, 5), (moins 1, 5) et (0, 5).$

ⓑ$D:(-\inf ,\inf ), R:{5}$

14. $f(x)=2$

15. $f(x)=−3$

Réponse

ⓐ

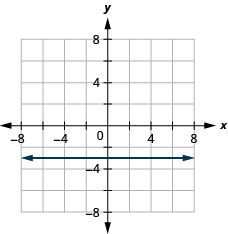
$La figure possède une fonction constante représentée graphiquement sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 6 à 6. La ligne passe par les points (0, moins 3), (1, moins 3) et (2, moins 3).$

ⓑ$D:(-\inf ,\inf ),\space R: {−3}$

16. $f(x)=−1$

17. $f(x)=2x$

Réponse

ⓐ

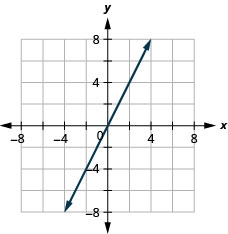
$La figure possède une fonction linéaire représentée sur le plan de coordonnées x. L'axe X va de moins 8 à 8. L'axe Y va de moins 8 à 8. La ligne passe par les points (0, 0), (2, 4) et (moins 2, moins 4).$

ⓑ$D:(-\inf ,\inf ),\space R:(-\inf ,\inf )$

18. $f(x)=3x$

19. $f(x)=−2x$

Réponse

ⓐ

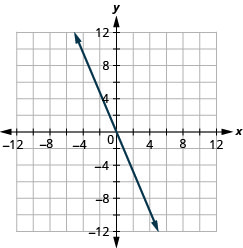
$La figure possède une fonction linéaire représentée sur le plan de coordonnées x. L'axe X va de moins 12 à 12. L'axe Y va de moins 12 à 12. La ligne passe par les points (0, 0), (1, moins 2) et (négatif 1, 2).$

ⓑ$D:(-\inf ,\inf ), R:(-\inf ,\inf )$

20. $f(x)=−3x$

21. $f(x)=3x^2$

Réponse

ⓐ

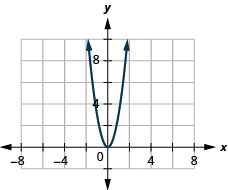
$La figure possède une fonction carrée représentée sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 2 à 10. La parabole passe par les points (moins 1, 3), (0, 0) et (1, 3). Le point le plus bas du graphique est (0, 0).$

ⓑ$D:(-\inf ,\inf ),\space R:[0,\inf )$

22. $f(x)=2x^2$

23. $f(x)=−3x^2$

Réponse

ⓐ

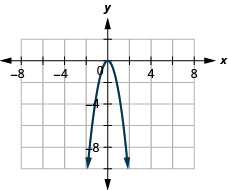
$La figure possède une fonction carrée représentée sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 10 à 2. La parabole passe par les points (négatif 1, négatif 3), (0, 0) et (1, négatif 3). Le point le plus élevé du graphique est (0, 0).$

ⓑ$ D: (-\inf ,\inf ),\space R:(-\inf ,0]$

24. $f(x)=−2x^2$

25. $f(x)=12x^2$

Réponse

ⓐ

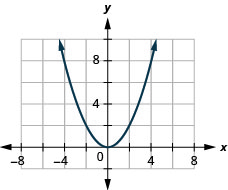
$La figure possède une fonction carrée représentée sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 2 à 10. La parabole passe par les points (négatif 4, 8), (négatif 2, 2), (0, 0), (2, 2) et (4, 8). Le point le plus bas du graphique est (0, 0).$

ⓑ$D: (-\inf ,\inf ),\space R:[-\inf ,0)$

26. $f(x)=\frac{1}{3}x^2$

27. $f(x)=x^2−1$

Réponse

ⓐ

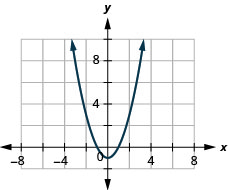
$La figure possède une fonction carrée représentée sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 2 à 10. La parabole passe par les points (négatif 2, 3), (négatif 1, 0), (0, négatif 1), (1, 0) et (2, 3). Le point le plus bas du graphique est (0, moins 1).$

ⓑ$D: (-\inf ,\inf ),\space R:[−1, \inf )$

28. $f(x)=x^2+1$

29. $f(x)=−2x^3$

Réponse

ⓐ

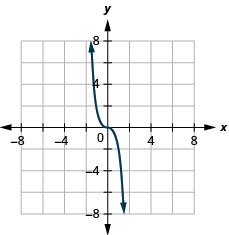
$La figure possède une fonction cubique représentée sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 6 à 6. La ligne courbe passe par les points (moins 1, 2), (0, 0) et (1, moins 2).$

ⓑ$D:(-\inf ,\inf ),\space R:(-\inf ,\inf )$

30. $f(x)=2x^3$

31. $f(x)=x^3+2$

Réponse

ⓐ

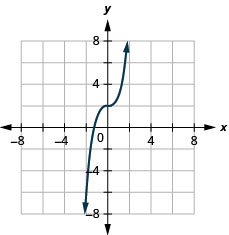
$La figure possède une fonction cubique représentée sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 6 à 6. La ligne courbe passe par les points (moins 1, 1), (0, 2) et (1, 3).$

ⓑ$D:(-\inf ,\inf ), R:(-\inf ,\inf )$

32. $f(x)=x^3−2$

33. $f(x)=2\sqrt{x}$

Réponse

ⓐ

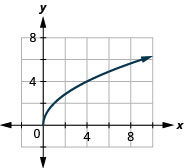
$La figure possède une fonction de racine carrée représentée graphiquement sur le plan de coordonnées x. L'axe X s'étend de 0 à 10. L'axe Y s'étend de 0 à 10. La demi-ligne commence au point (0, 0) et passe par les points (1, 2) et (4, 4).$

ⓑ$D:[0,\inf ), R:[0,\inf )$

34. $f(x)=−2\sqrt{x}$

35. $f(x)=\sqrt{x-1}$

Réponse

ⓐ

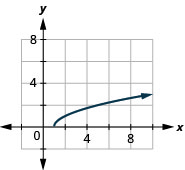
ⓑ$D:[1,\inf ), R:[0,\inf )$

36. $f(x)=\sqrt{x+1}$

37. $f(x)=3|x|$

Réponse

ⓐ

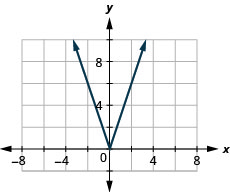
$La figure possède une fonction de valeur absolue représentée graphiquement sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 2 à 10. Le sommet se trouve au point (0, 0). La ligne passe par les points (moins 1, 3) et (1, 3).$

ⓑ$D:[ −1,−1, \inf ), R:[−\inf ,\inf )$

38. $f(x)=−2|x|$

39. $f(x)=|x|+1$

Réponse

ⓐ

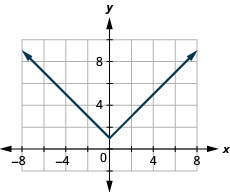
$La figure possède une fonction de valeur absolue représentée graphiquement sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 2 à 10. Le sommet se trouve au point (0, 1). La ligne passe par les points (moins 1, 2) et (1, 2).$

ⓑ$D:(-\inf ,\inf ), R:[1,\inf )$

40. $f(x)=|x|−1$

Lire des informations à partir du graphe d'une fonction

Dans les exercices suivants, utilisez le graphique de la fonction pour déterminer son domaine et sa plage. Écrivez le domaine et la plage en notation par intervalles.

41.
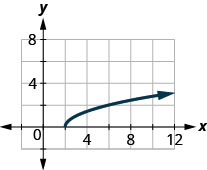
$La figure possède une fonction de racine carrée représentée graphiquement sur le plan de coordonnées x. L'axe X va de moins 2 à 8. L'axe Y va de moins 2 à 8. La demi-ligne commence au point (2, 0) et passe par les points (3, 1) et (6, 2).$

Réponse: $D: [2,\inf ),\space R: [0,\inf )$

42.
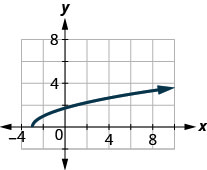
$La figure possède une fonction de racine carrée représentée graphiquement sur le plan de coordonnées x. L'axe X va de moins 2 à 8. L'axe Y va de moins 2 à 10. La demi-ligne commence au point (moins 3, 0) et passe par les points (moins 2, 1) et (1, 2).$

43.
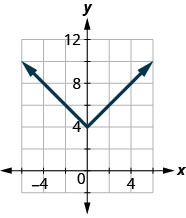
$La figure possède une fonction de valeur absolue représentée graphiquement sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y s'étend de 0 à 12. Le sommet se trouve au point (0, 4). La ligne passe par les points (moins 2, 6) et (2, 6).$

Réponse: $D: (-\inf ,\inf ),\space R: [4,\inf )$

44.
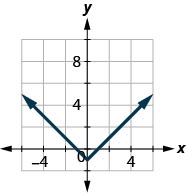
$La figure possède une fonction de valeur absolue représentée graphiquement sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 4 à 8. Le sommet se trouve au point (0, moins 1). La ligne passe par les points (moins 1, 0) et (1, 0).$

45.
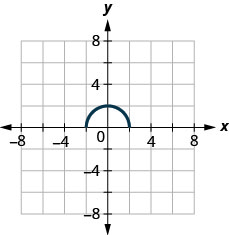
$La figure comporte un demi-cercle tracé sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 6 à 6. Le segment de ligne courbe commence au point (négatif 2, 0). La ligne passe par le point (0, 2) et se termine au point (2, 0).$

Réponse: $D: [−2,2],\space R: [0, 2]$

46.
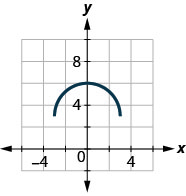
$La figure comporte un demi-cercle tracé sur le plan de coordonnées x. L'axe X va de moins 6 à 6. L'axe Y va de moins 2 à 10. Le segment de ligne courbe commence au point (négatif 3, 3). La ligne passe par le point (0, 6) et se termine au point (3, 3).$

Dans les exercices suivants, utilisez le graphique de la fonction pour trouver les valeurs indiquées.

47.
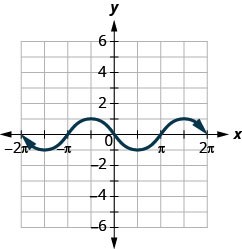
$Cette figure présente une ligne incurvée ondulée tracée sur le plan de coordonnées x. L'axe X va de 2 fois pi à 2 fois pi et 2 fois pi. L'axe Y va de moins 6 à 6. Le segment de ligne courbe passe par les points (négatif 2 fois pi, 0), (négatif 3 divisé par 2 fois pi, négatif 1), (négatif pi, 0), (négatif 1 divisé par 2 fois pi, 1), (0, 0), (1 divisé par 2 fois pi, négatif 1), (pi, 0), (3 divisé par 2 fois pi, 1) et (2 fois pi, 0). Les points (moins 3 divisé par 2 fois pi, moins 1) et (1 divisé par 2 fois pi, moins 1) sont les points les plus bas du graphique. Les points (moins 1 divisé par 2 fois pi, 1) et (3 divisé par 2 fois pi, 1) sont les points les plus élevés du graphique. Le motif s'étend à l'infini vers la gauche et la droite.$

ⓐ Trouvez :$f(0)$.
ⓑ Trouvez :$f(12\pi)$.
ⓒ Trouvez :$f(−32\pi)$.
ⓓ Trouvez les valeurs pour savoir$x$ quand$f(x)=0$.
ⓔ Trouvez les$x$ -intercepts.
ⓕ Trouvez les$y$ -intercepts.
ⓖ Trouvez le domaine. Écrivez-le en notation par intervalles.
ⓗ Trouvez la gamme. Écrivez-le en notation par intervalles.

Réponse: ⓐ$f(0)=0$ ⓑ$(\pi/2)=−1$
ⓒ$f(−3\pi/2)=−1$ ⓓ$f(x)=0$ pour$x=−2\pi,-\pi,0,\pi,2\pi$
ⓔ$(−2\pi,0),(−\pi,0),$$(0,0),(\pi,0),(2\pi,0)$$(f)(0,0)$
ⓖ$[−2\pi,2\pi]$ ⓗ$[−1,1]$

48.
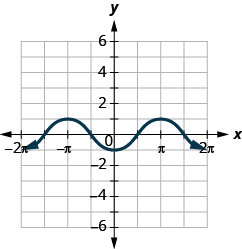
$Int_Alg_Section03_07_Exercise_48.jpeg$

ⓐ Trouvez :$f(0)$.
ⓑ Trouvez :$f(\pi)$.
ⓒ Trouvez :$f(−\pi)$.
ⓓ Trouvez les valeurs pour savoir$x$ quand$f(x)=0$.
ⓔ Trouvez les$x$ -intercepts.
ⓕ Trouvez les$y$ -intercepts.
ⓖ Trouvez le domaine. Écrivez-le en notation par intervalles.
ⓗ Trouvez la gamme. Écrivez-le en notation par intervalles

49.
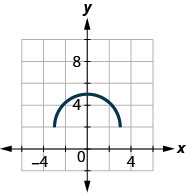
$La moitié supérieure d'un cercle de la figure est tracée sur le plan de coordonnées x y. L'axe X va de moins 6 à 6. L'axe Y va de moins 4 à 8. Le segment de ligne courbe commence au point (négatif 3, 2). La ligne passe par le point (0, 5) et se termine au point (3, 2). Le point (0, 5) est le point le plus haut du graphique. Les points (moins 3, 2) et (3, 2) sont les points les plus bas du graphique.$

ⓐ Trouvez :$f(0)$.
ⓑ Trouvez :$f(−3)$.
ⓒ Trouvez :$f(3)$.
ⓓ Trouvez les valeurs pour savoir$x$ quand$f(x)=0$.
ⓔ Trouvez les$x$ -intercepts.
ⓕ Trouvez les$y$ -intercepts.
ⓖ Trouvez le domaine. Écrivez-le en notation par intervalles.
ⓗ Trouvez la gamme. Écrivez-le en notation par intervalles.

50.
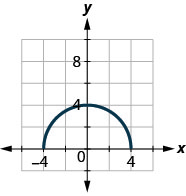
$La moitié supérieure d'un cercle de la figure est tracée sur le plan de coordonnées x y. L'axe X va de moins 6 à 6. L'axe Y va de moins 4 à 8. Le segment de ligne courbe commence au point (négatif 4, 0). La ligne passe par le point (0, 4) et se termine au point (4, 0). Le point (0, 4) est le point le plus haut du graphique. Les points (moins 4, 0) et (4, 0) sont les points les plus bas du graphique.$

ⓐ Trouvez :$f(0)$.
ⓑ Trouvez les valeurs pour savoir$x$ quand$f(x)=0$.
ⓒ Trouvez les$x$ -intercepts.
ⓓ Trouvez les$y$ -intercepts.
ⓔ Trouvez le domaine. Écrivez-le en notation par intervalles.
ⓕ Trouvez la gamme. Écrivez-le en notation par intervalles

Exercices d'écriture

51. Expliquez avec vos propres mots comment trouver le domaine à partir d'un graphique.

52. Expliquez avec vos propres mots comment déterminer la plage à partir d'un graphique.

53. Expliquez avec vos propres mots comment utiliser le test de la ligne verticale.

54. Dessinez une esquisse des fonctions de carré et de cube. Quelles sont les similitudes et les différences entre les graphiques ?

Auto-vérification

ⓐ Une fois les exercices terminés, utilisez cette liste de contrôle pour évaluer votre maîtrise des objectifs de cette section.

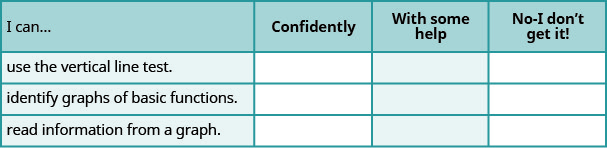
$La figure montre un tableau composé de quatre lignes et de quatre colonnes. La première ligne est une ligne d'en-tête et elle étiquette chaque colonne. L'en-tête de la première colonne est « Je peux... », le second est « En toute confiance », le troisième est « avec de l'aide », « non moins, je ne comprends pas ! ». Dans la première colonne se trouvent les phrases « utiliser le test de la ligne verticale », « identifier les graphes des fonctions de base » et « lire des informations à partir d'un graphique ». Sous les deuxième, troisième et quatrième colonnes se trouvent des espaces vides où l'apprenant peut vérifier le niveau de maîtrise qu'il a atteint$

ⓑ Après avoir examiné cette liste de contrôle, que ferez-vous pour atteindre tous les objectifs en toute confiance ?