3.7 : Graphiques des fonctions
- Page ID
- 194139
À la fin de cette section, vous serez en mesure de :
- Utiliser le test de la ligne verticale
- Identifier les graphes des fonctions de base
- Lire des informations à partir du graphique d'une fonction
Avant de commencer, répondez à ce questionnaire de préparation.
Utiliser le test de la ligne verticale
Dans la dernière section, nous avons appris comment déterminer si une relation est une fonction. Les relations que nous avons examinées étaient exprimées sous la forme d'un ensemble de paires ordonnées, d'une cartographie ou d'une équation. Nous allons maintenant voir comment déterminer si un graphe est celui d'une fonction.
Une paire ordonnée\((x,y)\) est la solution d'une équation linéaire, si l'équation est une déclaration vraie lorsque les valeurs x et y de la paire ordonnée sont substituées dans l'équation.
Le graphique d'une équation linéaire est une ligne droite où chaque point de la droite est une solution de l'équation et chaque solution de cette équation est un point sur cette droite.
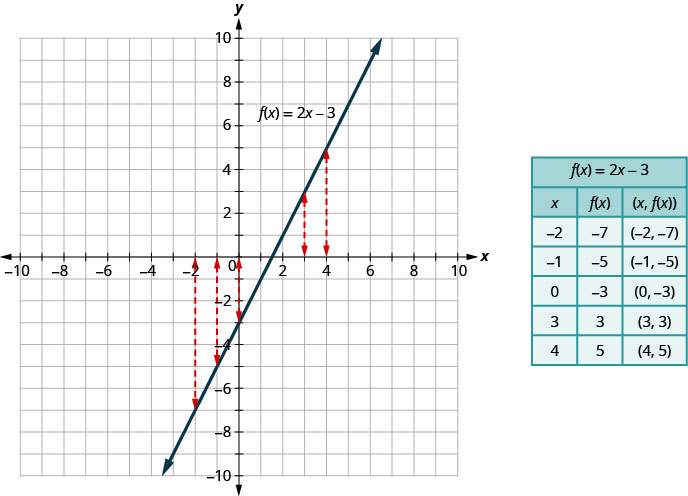
Sur la figure, nous pouvons voir que, dans le graphique de l'équation\(y=2x−3\), pour chaque valeur x, il n'y a qu'une seule valeur y, comme indiqué dans le tableau ci-joint.
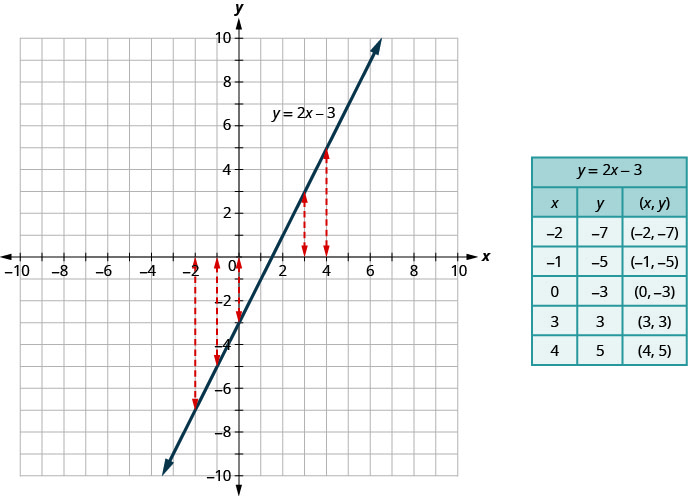
Une relation est une fonction si chaque élément du domaine possède exactement une valeur dans la plage. La relation définie par l'équation\(y=2x−3\) est donc une fonction.
Si nous examinons le graphique, chaque ligne pointillée verticale ne croise la ligne qu'en un point. Cela est logique car dans une fonction, pour chaque valeur x, il n'y a qu'une seule valeur y.
Si la ligne verticale touchait le graphique deux fois, la valeur x serait mappée à deux valeurs y, de sorte que le graphique ne représenterait pas une fonction.
Cela nous amène au test de la ligne verticale. Un ensemble de points dans un système de coordonnées rectangulaires est le graphe d'une fonction si chaque ligne verticale coupe le graphe en un point au plus. Si une ligne verticale coupe le graphe en plus d'un point, le graphique ne représente pas une fonction.
Un ensemble de points dans un système de coordonnées rectangulaires est le graphe d'une fonction si chaque ligne verticale coupe le graphe en un point au plus.
Si une ligne verticale coupe le graphe en plus d'un point, le graphique ne représente pas une fonction.
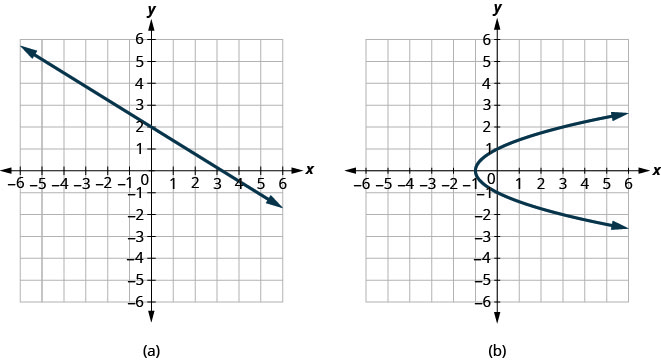
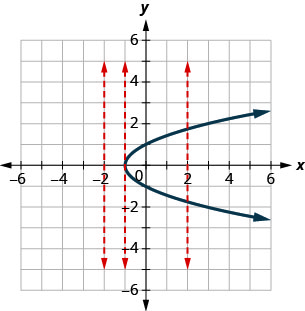
Déterminez si chaque graphique est le graphe d'une fonction.
- Réponse
-
ⓐ Comme toute ligne verticale coupe le graphe en un point au plus, le graphe est le graphe d'une fonction.
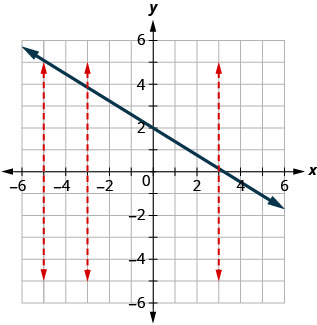
ⓑ L'une des lignes verticales affichées sur le graphique le coupe en deux points. Ce graphique ne représente pas une fonction.
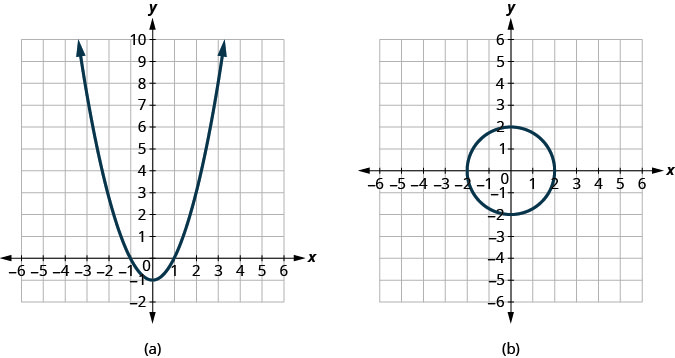
Déterminez si chaque graphique est le graphe d'une fonction.
- Réponse
-
ⓐ Oui ⓑ Non
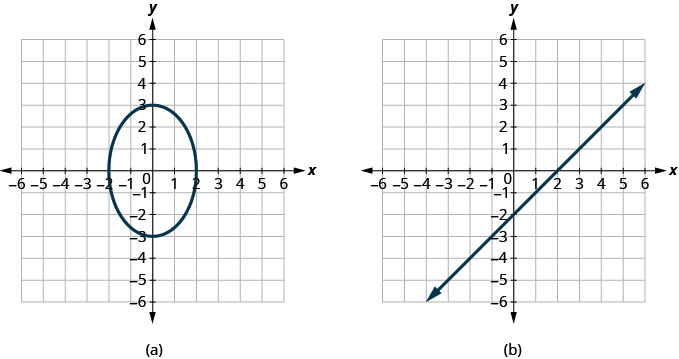
Déterminez si chaque graphique est le graphe d'une fonction.
- Réponse
-
ⓐ non ⓑ oui
Identifier les graphes des fonctions de base
Nous avons utilisé l'équation\(y=2x−3\) et son graphique pour développer le test de la ligne verticale. Nous avons dit que la relation définie par l'équation\(y=2x−3\) est une fonction.
Nous pouvons l'écrire comme dans la notation des fonctions comme\(f(x)=2x−3\). Cela signifie toujours la même chose. Le graphe de la fonction est le graphe de toutes les paires ordonnées\((x,y)\) où\(y=f(x)\). Nous pouvons donc écrire les paires ordonnées sous la forme\((x,f(x))\). Cela semble différent mais le graphique sera le même.
Comparez le graphique de la figure\(y=2x−3\) précédente avec le graphique de la\(f(x)=2x−3\) figure. Rien n'a changé à part la notation.
Le graphe d'une fonction est le graphe de toutes ses paires ordonnées, (x, y) (x, y) ou en utilisant la notation des fonctions, (x, f (x)) (x, f (x)) où y=f (x) .y=f (x).
\[\begin{array} {ll} {f} &{\text{name of function}} \\ {x} &{\text{x-coordinate of the ordered pair}} \\ {f(x)} &{\text{y-coordinate of the ordered pair}} \\ \nonumber \end{array}\]
Au fur et à mesure que nous avançons dans notre étude, il est utile de se familiariser avec les graphiques de plusieurs fonctions de base et de pouvoir les identifier.
Grâce à nos travaux antérieurs, nous nous sommes familiarisés avec les graphes d'équations linéaires. Le processus que nous avons utilisé pour décider s'il s'\(y=2x−3\)agit d'une fonction s'appliquerait à toutes les équations linéaires. Toutes les équations linéaires non verticales sont des fonctions. Les lignes verticales ne sont pas des fonctions car la valeur x possède une infinité de valeurs y.
Nous avons écrit des équations linéaires sous plusieurs formes, mais il nous sera très utile d'utiliser ici la forme d'intersection de pente de l'équation linéaire. La forme d'intersection de pente d'une équation linéaire est\(y=mx+b\). En notation de fonction, cette fonction linéaire devient\(f(x)=mx+b\) où m est la pente de la droite et b est l'intersection y.
Le domaine est l'ensemble de tous les nombres réels, et la plage est également l'ensemble de tous les nombres réels.
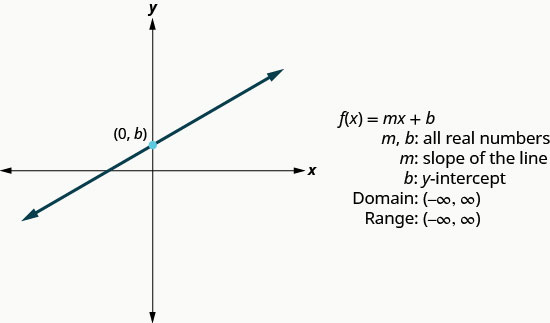
Nous utiliserons les techniques de représentation graphique que nous avons utilisées précédemment pour représenter graphiquement les fonctions de base.
Graphique :\(f(x)=−2x−4\).
- Réponse
-
\(f(x)=−2x−4\) Nous reconnaissons qu'il s'agit d'une fonction linéaire. Déterminez la pente et l'intersection y. \(m=−2\)
\(b=−4\)Tracez en utilisant l'intersection de la pente. 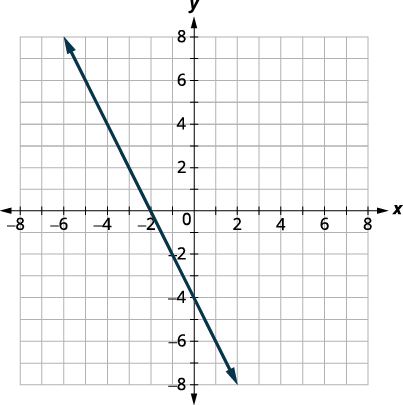
Graphique :\(f(x)=−3x−1\)
- Réponse
-
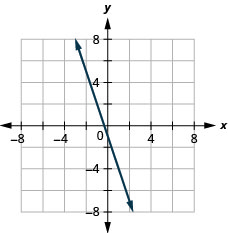
Graphique :\(f(x)=−4x−5\)
- Réponse
-
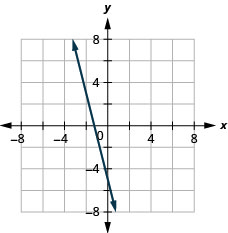
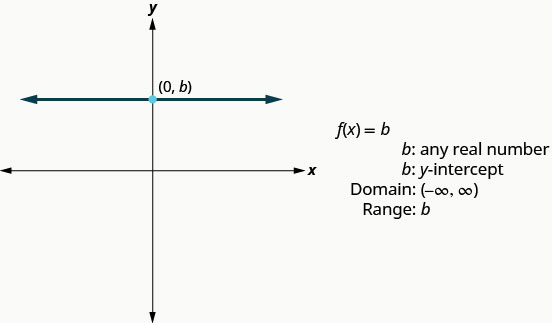
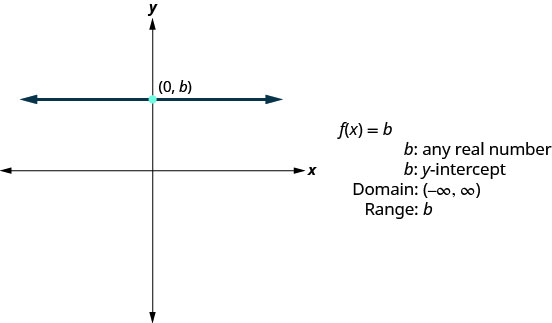
La fonction suivante dont nous allons examiner le graphique est appelée fonction constante et son équation est de la forme\(f(x)=b\), où b est un nombre réel quelconque. Si nous les\(f(x)\) remplaçons par y, nous obtenons\(y=b\). Nous reconnaissons qu'il s'agit de la ligne horizontale dont l'intersection y est b. Le graphe de la fonction\(f(x)=b\) est également la ligne horizontale dont l'intersection y est b.
Notez que pour tout nombre réel que nous mettons dans la fonction, la valeur de la fonction sera b. Cela nous indique que la plage n'a qu'une seule valeur, b.
Graphique :\(f(x)=4\).
- Réponse
-
\(f(x)=4\) Nous reconnaissons qu'il s'agit d'une fonction constante. Le graphique sera traversé par une ligne horizontale\((0,4)\). 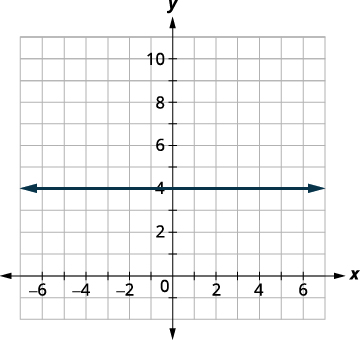
Graphique :\(f(x)=−2\).
- Réponse
-
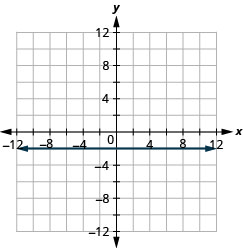
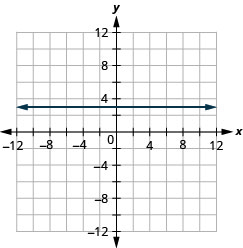
Graphique :\(f(x)=3\).
- Réponse
-
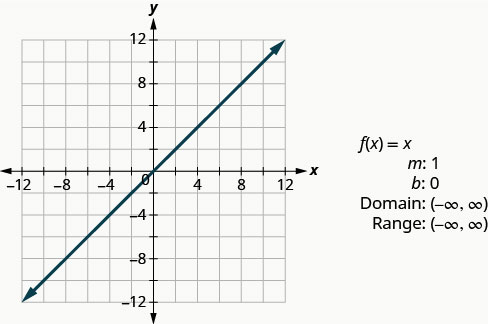
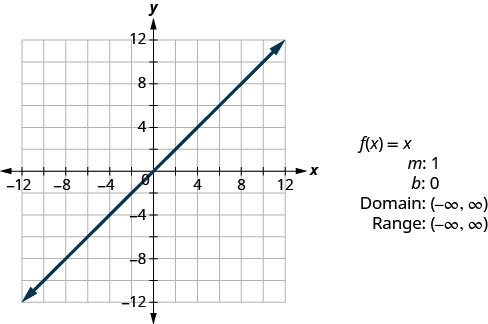
La fonction d'identité\(f(x)=x\) est un cas particulier de la fonction linéaire. Si nous l'écrivons sous forme de fonction linéaire\(f(x)=1x+0\), nous voyons que la pente est de 1 et que l'intersection y est de 0.
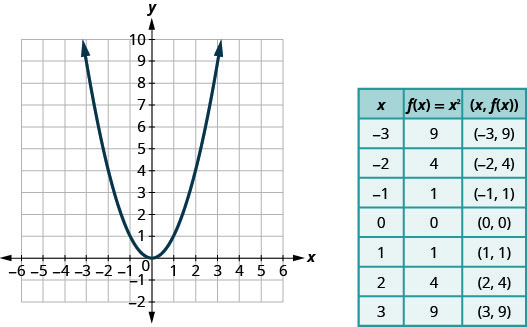
La fonction suivante que nous allons examiner n'est pas une fonction linéaire. Le graphique ne sera donc pas une ligne. La seule méthode dont nous disposons pour représenter graphiquement cette fonction est le traçage par points. Comme il s'agit d'une fonction peu familière, nous nous assurons de choisir plusieurs valeurs positives et négatives ainsi que 0 pour nos valeurs X.
Graphique :\(f(x)=x^2\).
- Réponse
-
Nous choisissons des valeurs x. Nous les remplaçons puis créons un graphique comme indiqué.
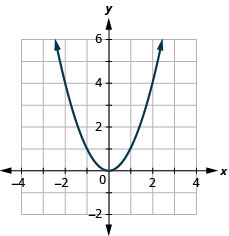
Graphique :\(f(x)=x^2\).
- Réponse
-
\(f(x)=−x^2\)
- Réponse
-
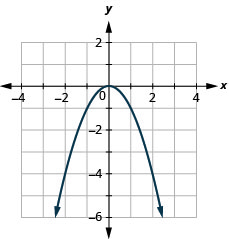
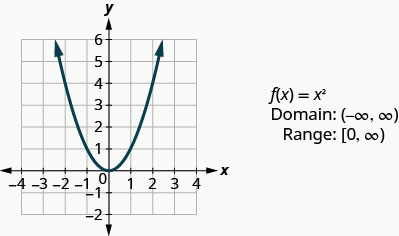
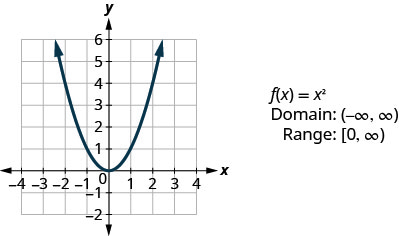
En regardant le résultat dans Example, nous pouvons résumer les caractéristiques de la fonction carrée. Nous appelons ce graphe une parabole. Lorsque nous examinons le domaine, notez que n'importe quel nombre réel peut être utilisé comme valeur x. Le domaine est composé uniquement de vrais nombres.
La gamme ne comprend pas uniquement des nombres réels. Notez que le graphique se compose de valeurs de y qui ne descendent jamais en dessous de zéro. Cela est logique car le carré d'un nombre ne peut pas être négatif. Ainsi, la plage de la fonction carrée est composée de tous les nombres réels non négatifs.
La fonction suivante que nous examinerons n'est pas non plus une fonction linéaire, donc le graphique ne sera pas une ligne. Encore une fois, nous utiliserons le traçage par points et veillerons à choisir plusieurs valeurs positives et négatives ainsi que 0 pour nos valeurs x.
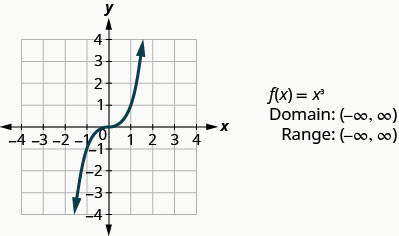
Graphique :\(f(x)=x^3\).
- Réponse
-
Nous choisissons des valeurs x. Nous les remplaçons puis créons un graphique.
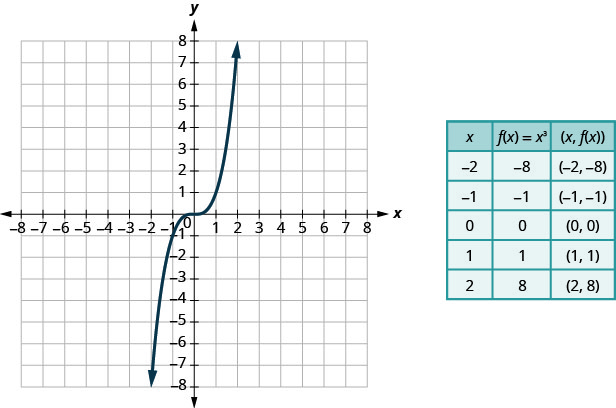
Graphique :\(f(x)=x^3\).
- Réponse
-
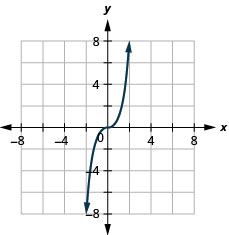
Graphique :\(f(x)=−x^3\).
- Réponse
-
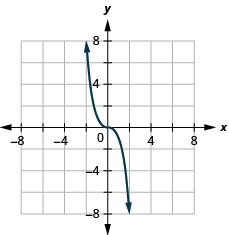
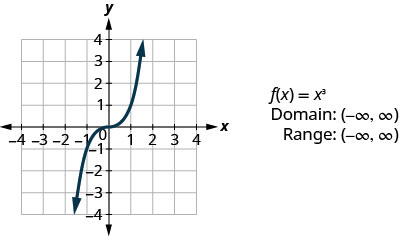
En regardant le résultat dans Example, nous pouvons résumer les fonctionnalités de la fonction cube. Lorsque nous examinons le domaine, notez que n'importe quel nombre réel peut être utilisé comme valeur x. Le domaine est composé uniquement de vrais nombres.
La plage est composée uniquement de nombres réels. Cela est logique car le cube de tout nombre différent de zéro peut être positif ou négatif. Ainsi, la plage de la fonction cube est constituée uniquement de nombres réels.
La fonction suivante que nous allons examiner ne met pas en carré ou en cube les valeurs d'entrée, mais prend plutôt la racine carrée de ces valeurs.
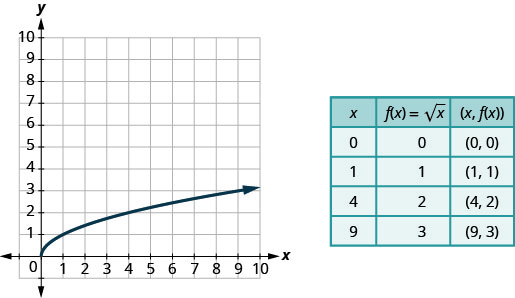
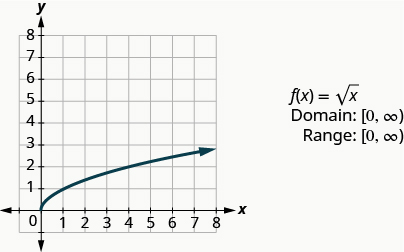
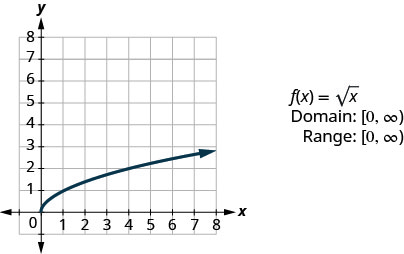
Reproduisons la fonction sous\(f(x)=\sqrt{x}\) forme graphique, puis résumons les caractéristiques de la fonction. N'oubliez pas que nous ne pouvons prendre que la racine carrée des nombres réels non négatifs, donc notre domaine sera constitué des nombres réels non négatifs.
\(f(x)=\sqrt{x}\)
- Réponse
-
Nous choisissons des valeurs x. Comme nous allons prendre la racine carrée, nous choisissons des nombres qui sont des carrés parfaits, afin de faciliter notre travail. Nous les remplaçons puis créons un graphique.
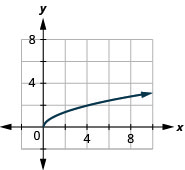
Graphique :\(f(x)=x\).
- Réponse
-
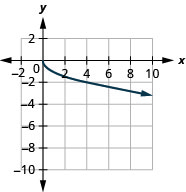
Graphique :\(f(x)=−\sqrt{x}\).
- Réponse
-
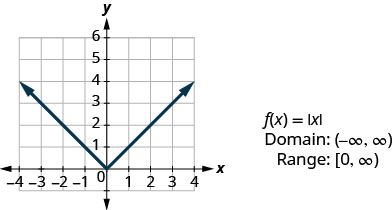
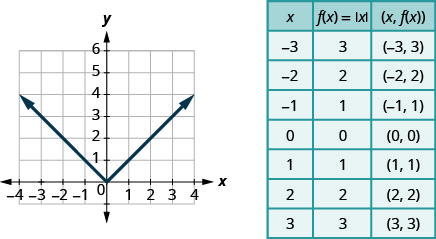
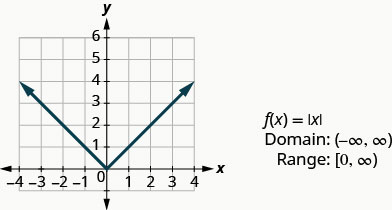
Notre dernière fonction de base est la fonction de valeur absolue,\(f(x)=|x|\). N'oubliez pas que la valeur absolue d'un nombre est sa distance par rapport à zéro. Comme nous ne mesurons jamais la distance comme un nombre négatif, nous n'obtiendrons jamais de nombre négatif dans la plage.
Graphique :\(f(x)=|x|\).
- Réponse
-
Nous choisissons des valeurs x. Nous les remplaçons puis créons un graphique.
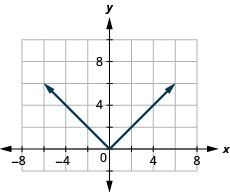
Graphique :\(f(x)=|x|\).
- Réponse
-
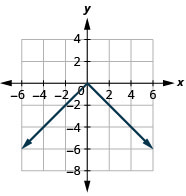
Graphique :\(f(x)=−|x|\).
- Réponse
-
Lire des informations à partir du graphe d'une fonction
Dans les sciences et les affaires, les données sont souvent collectées puis représentées graphiquement. Le graphique est analysé, des informations sont obtenues à partir du graphique, puis souvent des prédictions sont faites à partir des données.
Nous allons commencer par lire le domaine et la plage d'une fonction à partir de son graphe.
N'oubliez pas que le domaine est l'ensemble de toutes les valeurs x dans les paires ordonnées de la fonction. Pour trouver le domaine, nous examinons le graphique et trouvons toutes les valeurs de x qui ont une valeur correspondante sur le graphique. Suivez la valeur x verticalement vers le haut ou vers le bas. Si vous cliquez sur le graphique de la fonction, alors x se trouve dans le domaine.
N'oubliez pas que la plage est l'ensemble de toutes les valeurs y dans les paires ordonnées de la fonction. Pour trouver la plage, nous examinons le graphique et trouvons toutes les valeurs de y qui ont une valeur correspondante sur le graphique. Suivez la valeur y à gauche ou à droite horizontalement. Si vous cliquez sur le graphique de la fonction, alors y se trouve dans la plage.
Utilisez le graphique de la fonction pour trouver son domaine et sa plage. Écrivez le domaine et la plage en notation par intervalles.
![Cette figure présente un segment de ligne incurvé représenté sur le plan de coordonnées x y. L'axe X va de moins 4 à 4. L'axe Y va de moins 4 à 4. Le segment de ligne courbe passe par les points (négatif 3, négatif 1), (1,5, 3) et (3, 1). L'intervalle [négatif 3, 3] est marqué sur l'axe horizontal. L'intervalle [négatif 1, 3] est marqué sur l'axe vertical.](https://math.libretexts.org/@api/deki/files/22958/CNX_IntAlg_Figure_03_06_021_img_new.jpg)
- Réponse
-
Pour trouver le domaine, nous examinons le graphique et trouvons toutes les valeurs de x qui correspondent à un point du graphique. Le domaine est surligné en rouge sur le graphique. Le domaine est\([−3,3]\).
Pour trouver la plage, nous examinons le graphique et trouvons toutes les valeurs de y qui correspondent à un point du graphique. La plage est surlignée en bleu sur le graphique. La gamme est\([−1,3]\).
Utilisez le graphique de la fonction pour trouver son domaine et sa plage. Écrivez le domaine et la plage en notation par intervalles.
![Cette figure présente un segment de ligne incurvé représenté sur le plan de coordonnées x y. L'axe X va de moins 6 à 6. L'axe Y va de moins 6 à 6. Le segment de ligne courbe passe par les points (moins 5, moins 4), (0, moins 3) et (1, 2). L'intervalle [négatif 5, 1] est marqué sur l'axe horizontal. L'intervalle [négatif 4, 2] est marqué sur l'axe vertical.](https://math.libretexts.org/@api/deki/files/22776/CNX_IntAlg_Figure_03_06_022_img_new.jpg)
- Réponse
-
Le domaine est\([−5,1]\). La gamme est\([−4,2]\).
Utilisez le graphique de la fonction pour trouver son domaine et sa plage. Écrivez le domaine et la plage en notation par intervalles.
![Cette figure présente un segment de ligne incurvé représenté sur le plan de coordonnées x y. L'axe X va de moins 4 à 5. L'axe Y va de moins 6 à 4. Le segment de ligne courbe passe par les points (moins 2, 1), (0, 3) et (4, moins 5). L'intervalle [négatif 2, 4] est marqué sur l'axe horizontal. L'intervalle [négatif 5, 3] est marqué sur l'axe vertical.](https://math.libretexts.org/@api/deki/files/22921/CNX_IntAlg_Figure_03_06_023_img_new.jpg)
- Réponse
-
Le domaine est\([−2,4]\). La gamme est\([−5,3]\).
Nous allons maintenant lire les informations du graphique que vous pourrez voir dans les prochains cours de mathématiques.
Utilisez le graphique de la fonction pour trouver les valeurs indiquées.

ⓐ Trouvez :\(f(0)\).
ⓑ Trouvez :\(f(32\pi)\).
ⓒ Trouvez :\(f(−12\pi)\).
ⓓ Trouvez les valeurs de x quand\(f(x)=0\).
ⓔ Trouvez les x -intercepts.
ⓕ Trouvez les y -intercepts.
ⓖ Trouvez le domaine. Écrivez-le en notation par intervalles.
ⓗ Trouvez la gamme. Écrivez-le en notation par intervalles.
- Réponse
-
ⓐ Lorsque\(x=0\), la fonction croise l'axe y à 0. Donc,\(f(0)=0\).
ⓑ Quand\(x=32\pi\), la valeur y de la fonction est\(−1\). Donc,\(f(32\pi)=−1\).
ⓒ Quand\(x=−12\pi\), la valeur y de la fonction est\(−1\). Donc,\(f(−12\pi)=−1\).
ⓓ La fonction est 0 aux points,\((−2\pi,0), (−\pi,0), (0,0),(\pi,0),(2\pi,0)\). Les valeurs x lorsque\(f(x)=0\) sont\(−2\pi,−\pi,0,\pi,2\pi\).
ⓔ Les interceptions x se produisent lorsque\(y=0\). Les x -intercepts se produisent donc lorsque\(f(x)=0\). Les x -intercepts sont\((−2\pi,0),(−\pi,0),(0,0),(\pi,0),(2\pi,0)\).
ⓕ Les interceptions y se produisent lorsque x=0,x=0. Les y -intercepts se produisent donc à\(f(0)\). L'intersection y est\((0,0)\).
ⓖ Cette fonction a une valeur lorsque x est compris entre\(−2\pi\) et\(2\pi\). Par conséquent, le domaine de la notation par intervalles est\([−2\pi,2\pi]\).
ⓗ Les valeurs de cette fonction, ou les valeurs y, vont de 1\(−1\) à 1. Par conséquent, la plage, en notation par intervalles, est\([−1,1]\).
Utilisez le graphique de la fonction pour trouver les valeurs indiquées.
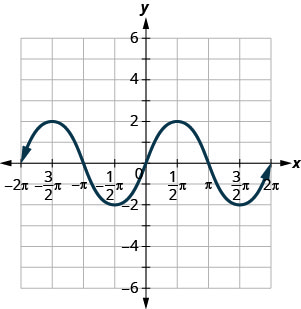
ⓐ Rechercher : f (0) .f (0).
ⓑ Trouvez : f (12 \ pi) .f (12 \ pi).
ⓒ Rechercher : f (−32 \ pi) .f (−32 \ pi).
ⓓ Trouvez les valeurs de x lorsque f (x) =0,f (x) =0.
ⓔ Trouvez les x -intercepts.
ⓕ Trouvez les y -intercepts.
ⓖ Trouvez le domaine. Écrivez-le en notation par intervalles.
ⓗ Trouvez la gamme. Écrivez-le en notation par intervalles.
- Réponse
-
ⓐ\(f(0)=0\) ⓑ\(f=(\pi2)=2\) ⓒ\(f=(−3\pi2)=2\) ⓓ\(f(x)=0\) pour\(x=−2\pi,−\pi,0,\pi,2\pi\) ⓔ\((−2\pi,0),(−\pi,0),(0,0),(\pi,0),(2\pi,0)\) ⓕ (0,0) (0,0) ⓖ\([−2\pi,2\pi]\) ⓗ\([−2,2]\)
Utilisez le graphique de la fonction pour trouver les valeurs indiquées.
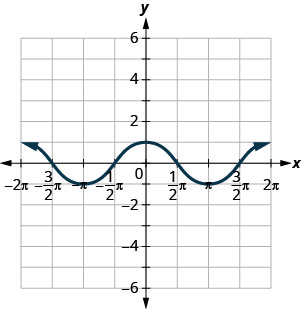
ⓐ Trouvez :\(f(0)\).
ⓑ Trouvez :\(f(\pi)\).
ⓒ Trouvez :\(f(−\pi)\).
ⓓ Trouvez les valeurs de x quand\(f(x)=0\).
ⓔ Trouvez les x -intercepts.
ⓕ Trouvez les y -intercepts.
ⓖ Trouvez le domaine. Écrivez-le en notation par intervalles.
ⓗ Trouvez la gamme. Écrivez-le en notation par intervalles.
- Réponse
-
ⓐ\(f(0)=1\) ⓑ\(f(\pi)=−1\) ⓒ\(f(−\pi)=−1\) ⓓ\(f(x)=0\) pour\(x=−3\pi2,−\pi2,\pi2,3\pi2\) ⓔ\((−2pi,0),(−pi,0),(0,0),(pi,0),(2pi,0)\) ⓕ\((0,1)\) ⓖ\([−2pi,2pi]\) ⓗ\([−1,1]\)
Accédez à cette ressource en ligne pour obtenir des instructions et des exercices supplémentaires grâce à des graphiques de fonctions.
Concepts clés
- Test de ligne verticale
- Un ensemble de points dans un système de coordonnées rectangulaires est le graphe d'une fonction si chaque ligne verticale coupe le graphe en un point au plus.
- Si une ligne verticale coupe le graphe en plus d'un point, le graphique ne représente pas une fonction.
- Graphe d'une fonction
- Le graphe d'une fonction est le graphe de toutes ses paires ordonnées, (x, y) (x, y) ou en utilisant la notation des fonctions, (x, f (x)) (x, f (x)) où y=f (x) .y=f (x).
fxf (x) nom de la fonction x coordonnée de la paire ordonnée coordonnée de la paire ordonnée nom de la fonction xx coordonnée de la paire ordonnée coordonnée y de la paire ordonnée
- Le graphe d'une fonction est le graphe de toutes ses paires ordonnées, (x, y) (x, y) ou en utilisant la notation des fonctions, (x, f (x)) (x, f (x)) où y=f (x) .y=f (x).
- Fonction linéaire
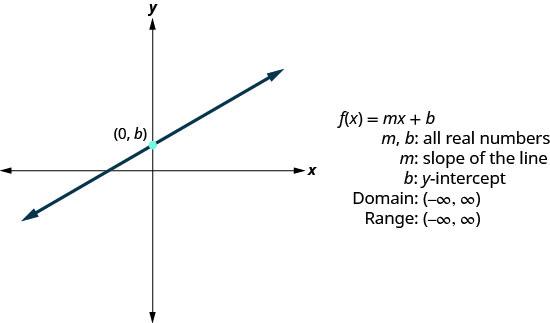
- Fonction constante
- Fonction d'identité
- Fonction carrée
- Fonction cubique
- Fonction de racine carrée
- Fonction de valeur absolue