Skip to main content
Global

3.6E : Exercices

  1. Last updated
  2. Save as PDF
  • Page ID
    194145

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    La pratique rend parfait

    Trouvez le domaine et l'étendue d'une relation

    Dans les exercices suivants, pour chaque relation a. trouvez le domaine de la relation b. trouvez la plage de la relation.

    1. \({\{(1,4),(2,8),(3,12),(4,16),(5,20)}\}\)

    Réponse

    a.\({\{1, 2, 3, 4, 5}\}\) b.\({\{4, 8, 12, 16, 20}\}\)

    2. \({\{(1,−2),(2,−4),(3,−6),(4,−8),(5,−10)}\}\)

    3. \({\{(1,7),(5,3),(7,9),(−2,−3),(−2,8)}\}\)

    Réponse

    a.\({\{1, 5, 7, −2}\}\) b.\({\{7, 3, 9, −3, 8}\}\)

    4. \({\{(11,3),(−2,−7),(4,−8),(4,17),(−6,9)}\}\)

    Dans les exercices suivants, utilisez le mappage de la relation avec a. répertoriez les paires ordonnées de la relation, b. trouvez le domaine de la relation et c. trouvez la plage de la relation.

    5.
    Cette figure montre deux tableaux comportant chacun une colonne. Le tableau de gauche contient l'en-tête « Nom » et répertorie les noms « Rebecca », « Jennifer », « John », « Hector », « Luis », « Ebony », « Raphael », « Meredith », « Karen » et « Joseph ». Le tableau de droite comporte l'en-tête « Anniversaire » et indique les dates « 18 janvier », « 15 février », « 1er avril », « 7 avril », « 23 juin », « 30 juillet », « 19 août » et « 6 novembre ». Des flèches commencent par des noms dans le tableau des noms et pointent vers des dates dans le tableau des anniversaires. La première flèche va de Rebecca au 18 janvier. La deuxième flèche va de Jennifer au 1er avril. La troisième flèche va de John au 18 janvier. La quatrième flèche va d'Hector au 23 juin. La cinquième flèche va de Luis au 15 février. La sixième flèche va d'Ebony au 7 avril. La septième flèche va de Raphaël au 6 novembre. La huitième flèche va de Meredith au 19 août. La neuvième flèche va de Karen au 19 août. La dixième flèche va de Joseph au 30 juillet.

    Réponse

    a. (Rebecca, 18 janvier), (Jennifer, 1er avril), (John, 18 janvier), (Hector, 23 juin), (Luis, 15 février), (Ebony, 7 avril), (Raphael, 6 novembre), (Meredith, 19 août), (Karen, 19 août), (Joseph, 30 juillet)
    b. {Rebecca, Jennifer, John, Hector, Luis, Ebony, Raphael El, Meredith, Karen, Joseph}
    c. {18 janvier, 1er avril, 23 juin, 15 février, 7 avril, 6 novembre, 19 août, 30 juillet}

    6.
    Cette figure montre deux tableaux comportant chacun une colonne. Le tableau de gauche contient l'en-tête « Nom » et répertorie les noms « Amy », « Carol », « Devon », « Harrison », « Jackson », « Labron », « Mason », « Natalie », « Paul » et « Sylvester ». Le tableau de droite comporte l'en-tête « Anniversaire » et indique les dates « 5 janvier », « 7 janvier », « 14 février », « 1er mars », « 7 avril », « 30 mai », « 20 juillet », « 1er août », « 13 novembre » et « 26 novembre ». Des flèches commencent par des noms dans le tableau des noms et pointent vers des dates dans le tableau des anniversaires. La première flèche va d'Amy au 14 février. La deuxième flèche va de Carol au 30 mai. La troisième flèche va du Devon au 5 janvier. La quatrième flèche va de Harrison au 7 janvier. La cinquième flèche va de Jackson au 26 novembre. La sixième flèche va de Labron au 7 avril. La septième flèche va de Mason au 20 juillet. La huitième flèche va de Natalie au 1er mars. La neuvième flèche va de Paul au 1er août. La dixième flèche va de Sylvester au 13 novembre.

    7. Pour une femme de grande taille,\(5'4''\) la carte ci-dessous montre l'indice de masse corporelle (IMC) correspondant. L'indice de masse corporelle est une mesure de la graisse corporelle basée sur la taille et le poids. Un IMC de\(18.5–24.9\) est considéré comme sain.

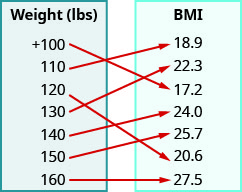
    Cette figure montre deux tableaux comportant chacun une colonne. Le tableau de gauche contient l'en-tête « Poids (livres) » et répertorie les nombres plus 100, 110, 120, 130, 140, 150 et 160. Le tableau de droite contient l'en-tête « IMC » et répertorie les numéros 18, 9, 22, 3, 17, 2, 24, 0, 25, 7, 20, 6 et 27, 5. Des flèches commencent par des nombres dans le tableau de poids et pointent vers des chiffres dans le tableau de l'IMC. La première flèche va de plus 100 à 17. 2. La deuxième flèche va de 110 à 18. 9. La troisième flèche va de 120 à 20. 6. La quatrième flèche va de 130 à 22. 3. La cinquième flèche va de 140 à 24. 0. La sixième flèche va de 150 à 25. 7. La septième flèche va de 160 à 27. 5.

    Réponse

    a.\((+100, 17. 2), (110, 18.9), (120, 20.6), (130, 22.3), (140, 24.0), (150, 25.7), (160, 27.5)\) b.\({\{+100, 110, 120, 130, 140, 150, 160,}\}\) c.\({\{17.2, 18.9, 20.6, 22.3, 24.0, 25.7, 27.5}\}\)

    8. Pour un homme de grande taille,\(5'11''\) la carte ci-dessous montre l'indice de masse corporelle (IMC) correspondant. L'indice de masse corporelle est une mesure de la graisse corporelle basée sur la taille et le poids. Un IMC de\(18.5–24.9\) est considéré comme sain.

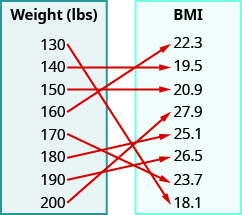
    Cette figure montre deux tableaux comportant chacun une colonne. Le tableau de gauche contient l'en-tête « Poids (livres) » et répertorie les chiffres 130, 140, 150, 160, 170, 180, 190 et 200. Le tableau de droite porte l'en-tête « IMC » et répertorie les nombres 22,3, 19,5, 20,9, 27,9, 25,1, 26,5, 23,7 et 18.1. Des flèches commencent par des nombres dans le tableau de poids et pointent vers des chiffres dans le tableau de l'IMC. La première flèche va de 130 à 18. 1. La deuxième flèche va de 140 à 19. 5. La troisième flèche va de 150 à 20. 9. La quatrième flèche va de 160 à 22. 3. La cinquième flèche va de 170 à 23. 7. La sixième flèche va de 180 à 25. 1. La septième flèche va de 190 à 26. 5. La huitième flèche va de 200 à 27. 9.

    Dans les exercices suivants, utilisez le graphe de la relation avec a. Listez les paires ordonnées de la relation b. trouvez le domaine de la relation c. trouvez la plage de la relation.

    9.
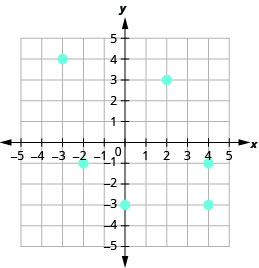
    La figure montre le graphique de certains points sur le plan de coordonnées x. Les axes x et y vont de moins 6 à 6. Les points (négatif 3, 4), (négatif 3, négatif 1), (0, négatif 3), (2, 3), (4, négatif 1) et (4, négatif 3).

    Réponse

    a.\((2, 3), (4, −3), (−2, −1), (−3, 4), (4, −1), (0, −3)\) b.\({\{−3, −2, 0, 2, 4}\}\)
    c.\({\{−3, −1, 3, 4}\}\)

    10.
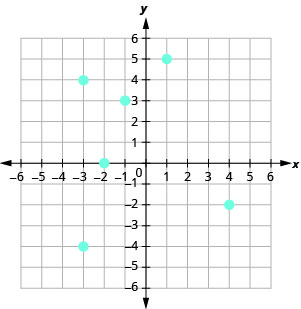
    La figure montre le graphique de certains points sur le plan de coordonnées x. Les axes x et y vont de moins 6 à 6. Les points (négatif 3, 4), (négatif 3, négatif 4), (négatif 2, 0), (négatif 1, 3), (1, 5) et (4, négatif 2).

    11.
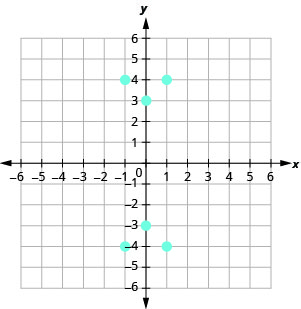
    La figure montre le graphique de certains points sur le plan de coordonnées x. Les axes x et y vont de moins 6 à 6. Les points (négatif 1, 4), (négatif 1, négatif 4), (0, 3), (0, négatif 3), (1, 4) et (1, négatif 4).

    Réponse

    a.\((1, 4), (1, −4), (−1, 4), (−1, −4), (0, 3), (0, −3)\) b.\({\{−1, 0, 1}\}\) c.\({\{−4, −3, 3,4}\}\)

    12.
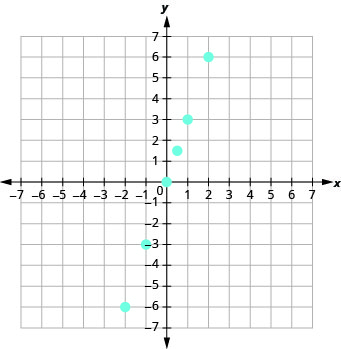
    La figure montre le graphique de certains points sur le plan de coordonnées x. Les axes x et y vont de moins 10 à 10. Les points (négatif 2, négatif 6), (négatif 2, négatif 3), (0, 0), (0,5, 1,5), (1, 3) et (3, 6).

    Déterminer si une relation est une fonction

    Dans les exercices suivants, utilisez l'ensemble de paires ordonnées pour a. déterminer si la relation est une fonction, b. trouver le domaine de la relation et c. déterminer la plage de la relation.

    13. \( {\{(−3,9),(−2,4),(−1,1), (0,0),(1,1),(2,4),(3,9)}\}\)

    Réponse

    a. oui b.\({\{−3, −2, −1, 0, 1, 2, 3}\}\) c.\({\{9, 4, 1, 0}\}\)

    14. \({\{(9,−3),(4,−2),(1,−1),(0,0),(1,1),(4,2),(9,3)}\}\)

    15. \({\{(−3,27),(−2,8),(−1,1), (0,0),(1,1),(2,8),(3,27)}\}\)

    Réponse

    a. oui b.\({\{−3, −2, −1, 0, 1, 2, 3}\}\) c.\({\{0, 1, 8, 27}\}\)

    16. \({\{(−3,−27),(−2,−8),(−1,−1), (0,0),(1,1),(2,8),(3,27)}\}\)

    Dans les exercices suivants, utilisez le mappage pour a. déterminer si la relation est une fonction, b. trouver le domaine de la fonction et c. déterminer la plage de la fonction.

    17.
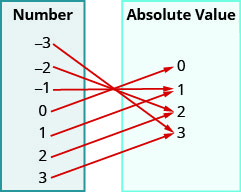
    Cette figure montre deux tableaux comportant chacun une colonne. Le tableau de gauche contient l'en-tête « Numéro » et répertorie les nombres négatifs 3, moins 2, moins 1, 0, 1, 2 et 3. Le tableau de droite contient l'en-tête « Valeur absolue » et répertorie les nombres 0, 1, 2 et 3. Des flèches commencent par des nombres dans la table des nombres et pointent vers des nombres dans la table des valeurs absolues. La première flèche va de moins 3 à 3. La deuxième flèche va de moins 2 à 2. La troisième flèche va de moins 1 à 1. La quatrième flèche va de 0 à 0. La cinquième flèche va de 1 à 1. La sixième flèche va de 2 à 2. La septième flèche va de 3 à 3.

    Réponse

    a. oui b.\({\{−3, −2, −1, 0, 1, 2, 3}\}\) c.\({\{0, 1, 2, 3}\}\)

    18.
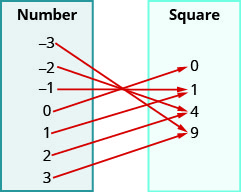
    Cette figure montre deux tableaux comportant chacun une colonne. Le tableau de gauche contient l'en-tête « Numéro » et répertorie les nombres négatifs 3, moins 2, moins 1, 0, 1, 2 et 3. Le tableau de droite comporte l'en-tête « Carré » et répertorie les chiffres 0, 1, 4 et 9. Des flèches commencent par des nombres dans le tableau des nombres et pointent vers des nombres dans le tableau carré. La première flèche va de moins 3 à 9. La deuxième flèche va de moins 2 à 4. La troisième flèche va de moins 1 à 1. La quatrième flèche va de 0 à 0. La cinquième flèche va de 1 à 1. La sixième flèche va de 2 à 4. La septième flèche va de 3 à 9.

    19.
    Cette figure montre deux tableaux comportant chacun une colonne. Le tableau de gauche contient l'en-tête « Nom » et répertorie les noms « Jenny », « R and y », « Dennis », « Emily » et « Raul ». Le tableau de droite contient l'en-tête « Email » et répertorie les adresses e-mail RHern et ez @state. edu, JKim@gmail.com, Raul@gmail.com, eSmith @state. edu, DBrown@aol.com, jenny@aol.com et R et y@gmail.com. Des flèches commencent par des noms dans la table des noms et pointent vers des adresses dans la table des e-mails. La première flèche va de Jenny à JKim@gmail.com. La deuxième flèche va de Jenny à jenny@aol.com. La troisième flèche va de R et y à R et y@gmail.com. La quatrième flèche va de Dennis à DBrown@aol.com. La cinquième flèche va d'Emily à eSmith @state. edu. La sixième flèche va de Raul à RHern et ez @state. edu. La septième flèche va de Raul à Raul@gmail.com.

    Réponse

    a. no b. {Jenny, R et y, Dennis, Emily, Raul} c. {RHern et ez@state.edu, JKim@gmail.com, Raul@gmail.com, ESmith@state.edu, DBroen@aol.com, jenny@aol.cvom, R et y@gmail.com}

    20.
    Cette figure montre deux tableaux comportant chacun une colonne. Le tableau de gauche contient l'en-tête « Nom » et répertorie les noms « Jon », « Rachel », « Matt », « Leslie », « Chris », « Beth » et « Liz ». Le tableau de droite contient l'en-tête « E-mail » et répertorie les adresses e-mail chrisg@gmail.com, lizzie@aol.com, jong@gmail.com, mattg@gmail.com, Rachel @state. edu, leslie@aol.com et bethc@gmail.com. Des flèches commencent par des noms dans la table des noms et pointent vers des adresses dans la table des e-mails. La première flèche va de Jon à jong@gmail.com. La deuxième flèche va de Rachel à Rachel @state. edu. La troisième flèche va de Matt à mattg@gmail.com. La quatrième flèche va de Leslie à leslie@aol.com. La cinquième flèche va de Chris à chrisg@gmail.com. La sixième flèche va de Beth à bethc@gmail.com. La septième flèche va de Liz à lizzie@aol.com.

    Dans les exercices suivants, déterminez si chaque équation est une fonction.

    21. a.\(2x+y=−3\)
    b.\(y=x^2\)
    c.\(x+y^2=−5\)

    Réponse

    a. oui b. oui c. non

    22. a.\(y=3x−5\)
    b.\(y=x^3\)
    c.\(2x+y^2=4\)

    23. a.\(y−3x^3=2\)
    b.\(x+y^2=3\)
    c.\(3x−2y=6\)

    Réponse

    a. oui b. non c. oui

    24. a.\(2x−4y=8\)
    b.\(−4=x^2−y\)
    c.\(y^2=−x+5\)

    Trouver la valeur d'une fonction

    Dans les exercices suivants, évaluez la fonction : a.\(f(2)\)\(f(a)\) b.\(f(−1)\) c.

    25. \(f(x)=5x−3\)

    Réponse

    a.\(f(2)=7\) b.\(f(−1)=−8\) c.\(f(a)=5a−3\)

    26. \(f(x)=3x+4\)

    27. \(f(x)=−4x+2\)

    Réponse

    a.\(f(2)=−6\) b.\(f(−1)=6\) c.\(f(a)=−4a+2\)

    28. \(f(x)=−6x−3\)

    29. \(f(x)=x^2−x+3\)

    Réponse

    a.\(f(2)=5\) b.\(f(−1)=5\)
    c.\(f(a)=a^2−a+3\)

    30. \(f(x)=x^2+x−2\)

    31. \(f(x)=2x^2−x+3\)

    Réponse

    a.\(f(2)=9\) b.\(f(−1)=6\)
    c.\(f(a)=2a^2−a+3\)

    32. \(f(x)=3x^2+x−2\)

    Dans les exercices suivants, évaluez la fonction : a.\(g(h^2)\)\(g(x)+g(2)\) b.\(g(x+2)\) c.

    33. \(g(x)=2x+1\)

    Réponse

    a.\(g(h^2)=2h^2+1\)
    b.\(g(x+2)=4x+5\)
    c.\(g(x)+g(2)=2x+6\)

    34. \(g(x)=5x−8\)

    35. \(g(x)=−3x−2\)

    Réponse

    a.\(g(h^2)=−3h^2−2\)
    b.\(g(x+2)=−3x−8\)
    c.\(g(x)+g(2)=−3x−10\)

    36. \(g(x)=−8x+2\)

    37. \(g(x)=3−x\)

    Réponse

    a.\(g(h^2)=3−h^2\)
    b.\(g(x+2)=1−x\)
    c.\(g(x)+g(2)=4−x\)

    38. \(g(x)=7−5x\)

    Dans les exercices suivants, évaluez la fonction.

    39. \(f(x)=3x^2−5x\);\(f(2)\)

    Réponse

    2

    40. \(g(x)=4x^2−3x\);\(g(3)\)

    41. \(F(x)=2x^2−3x+1\);\(F(−1)\)

    Réponse

    6

    42. \(G(x)=3x^2−5x+2\);\(G(−2)\)

    43. \(h(t)=2|t−5|+4\);\(f(−4)\)

    Réponse

    22

    44. \(h(y)=3|y−1|−3\);\(h(−4)\)

    45. \(f(x)=x+2x−1\);\(f(2)\)

    Réponse

    4

    46. \(g(x)=x−2x+2\);\(g(4)\)

    Dans les exercices suivants, résolvez.

    47. Le nombre d'émissions non regardées dans le DVR de Sylvia est de 85. Ce nombre augmente de 20 émissions non regardées par semaine. La fonction\(N(t)=85+20t\) représente la relation entre le nombre d'émissions non regardées, N, et l'heure, t, mesurée en semaines.

    a. Déterminez la variable indépendante et la variable dépendante.

    b. Trouvez\(N(4)\). Expliquez ce que signifie ce résultat

    Réponse

    a. t IND ; N DEP
    b.\(N(4)=165\) le nombre d'émissions non regardées dans le DVR de Sylvia à la quatrième semaine.

    48. Chaque jour, un nouveau puzzle est téléchargé sur le compte de Ken. À l'heure actuelle, il a 43 puzzles sur son compte. La fonction\(N(t)=43+t\) représente la relation entre le nombre de puzzles, N, et le temps, t, mesuré en jours.

    a. Déterminez la variable indépendante et la variable dépendante.

    b. Trouvez\(N(30)\). Expliquez ce que signifie ce résultat.

    49. Le coût quotidien d'impression d'un livre pour l'imprimerie est modélisé par la fonction\(C(x)=3.25x+1500\) où C est le coût quotidien total et x est le nombre de livres imprimés.

    a. Déterminez la variable indépendante et la variable dépendante.

    b. Trouvez\(N(0)\). Expliquez ce que signifie ce résultat.

    c. Trouvez\(N(1000)\). Expliquez ce que signifie ce résultat.

    Réponse

    a. x IND ; C DEP
    b.\(N(0)=1500\) le coût quotidien si aucun livre n'est imprimé
    c.\(N(1000)=4750\) le coût quotidien de l'impression de 1 000 livres

    50. Le coût quotidien pour l'entreprise de fabrication est modélisé par la fonction\(C(x)=7.25x+2500\) où\(C(x)\) est le coût quotidien total et x est le nombre d'articles fabriqués.

    a. Déterminez la variable indépendante et la variable dépendante.

    b. Trouvez\(C(0)\). Expliquez ce que signifie ce résultat.

    c. Trouvez\(C(1000)\). Expliquez ce que signifie ce résultat.

    Exercices d'écriture

    51. Expliquez avec vos propres mots la différence entre une relation et une fonction.

    52. Dans vos propres mots, expliquez ce que l'on entend par domaine et par plage.

    53. Chaque relation est-elle une fonction ? Est-ce que chaque fonction est une relation ?

    54. Comment trouvez-vous la valeur d'une fonction ?

    Auto-vérification

    a. Une fois les exercices terminés, utilisez cette liste de contrôle pour évaluer votre maîtrise des objectifs de cette section.

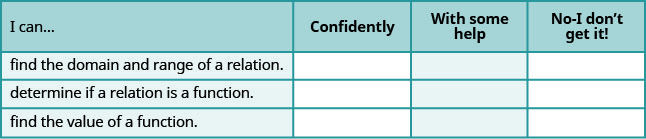
    La figure montre un tableau à quatre lignes et quatre colonnes. La première ligne est une ligne d'en-tête et elle étiquette chaque colonne. L'en-tête de la première colonne est « Je peux... », le second est « En toute confiance », le troisième est « avec de l'aide », « non moins, je ne comprends pas ! ». Sous la première colonne se trouvent les phrases « trouver le domaine et la plage d'une relation », « déterminer si une relation est une fonction » et « trouver la valeur d'une fonction ». Sous les deuxième, troisième et quatrième colonnes se trouvent des espaces vides où l'apprenant peut vérifier le niveau de maîtrise qu'il a atteint.

    b. Après avoir examiné la liste de contrôle, pensez-vous être bien préparé pour la section suivante ? Pourquoi ou pourquoi pas ?