3.6 : Relations et fonctions

Last updated
Save as PDF

Page ID: 194138

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

Trouvez le domaine et l'étendue d'une relation
Déterminer si une relation est une fonction
Trouve la valeur d'une fonction

Avant de commencer, répondez à ce questionnaire de préparation.

Évaluez$3x−5$ quand$x=−2$.
Si vous avez oublié ce problème, consultez [lien].
Évaluez$2x^2−x−3$ quand$x=a$.
Si vous avez oublié ce problème, consultez [lien].
Simplifiez :$7x−1−4x+5$.
Si vous avez oublié ce problème, consultez [lien].

Trouvez le domaine et l'étendue d'une relation

Dans notre vie quotidienne, de nombreux éléments de données ou quantités sont associés à nos noms. Notre numéro de sécurité sociale, notre numéro d'étudiant, notre adresse e-mail, notre numéro de téléphone et notre date de naissance correspondent à notre nom. Il existe un lien entre notre nom et chacun de ces éléments.

Lorsque votre professeur obtient sa liste de classe, les noms de tous les étudiants de la classe sont répertoriés dans une colonne, puis le numéro d'identification de l'étudiant est susceptible de figurer dans la colonne suivante. Si nous considérons la correspondance comme un ensemble de paires ordonnées, où le premier élément est le nom d'un étudiant et le second est le numéro d'identification de cet étudiant, nous appelons cela une relation.

\[(\text{Student name}, \text{ Student ID #})\nonumber \]

L'ensemble des noms des étudiants de la classe est appelé le domaine de la relation et l'ensemble de tous les numéros d'identification des étudiants associés à ces étudiants constitue la plage de la relation.

Il existe de nombreuses situations similaires où une variable est associée ou mise en correspondance avec une autre. L'ensemble de paires ordonnées qui enregistre cette correspondance est une relation.

Définition : Relation

Une relation est un ensemble de paires ordonnées,$(x,y)$. Toutes les valeurs x des paires ordonnées constituent ensemble le domaine. Toutes les valeurs y des paires ordonnées constituent ensemble la plage.

Exemple$\PageIndex{1}$

Pour la relation${(1,1),(2,4),(3,9),(4,16),(5,25)}$ :

Trouvez le domaine de la relation.
Déterminez l'étendue de la relation.

Réponse: \[\begin{array} {ll} {} &{ {\{(1,1), (2,4), (3,9), (4,16), (5,25) }\} } \\ {ⓐ\text{ The domain is the set of all x-values of the relation.}} &{ {\{1,2,3,4,5}\} } \\ {ⓑ\text{ The range is the set of all y-values of the relation.}} &{ {\{1,4,9,16,25}\} } \\ \nonumber \end{array}\]

Exemple$\PageIndex{2}$

Pour la relation${\{(1,1),(2,8),(3,27),(4,64),(5,125)}\}$ :

Trouvez le domaine de la relation.
Déterminez l'étendue de la relation.

Répondez à une: ${\{1,2,3,4,5}\}$
Réponse b: ${\{1,8,27,64,125}\}$

Exemple$\PageIndex{3}$

Pour la relation${\{(1,3),(2,6),(3,9),(4,12),(5,15)}\}$ :

Trouvez le domaine de la relation.
Déterminez l'étendue de la relation.

Répondez à une: ${\{1,2,3,4,5}\}$
Réponse b: ${\{3,6,9,12,15}\}$

MAPPAGE

Un mappage est parfois utilisé pour montrer une relation. Les flèches indiquent l'appariement des éléments du domaine avec les éléments de la gamme.

Exemple$\PageIndex{4}$

Utilisez le mappage de la relation indiquée pour

lister les paires ordonnées de la relation,
trouver le domaine de la relation, et
trouvez l'étendue de la relation.

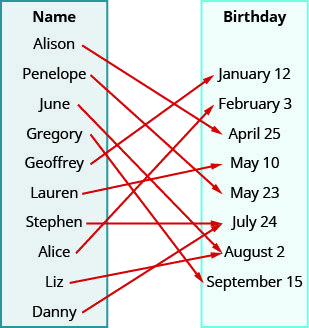
$Cette figure montre deux tableaux comportant chacun une colonne. Le tableau de gauche contient l'en-tête « Nom » et répertorie les noms « Alison », « Penelope », « June », « Gregory », « Geoffrey », « Lauren », « Stephen », « Alice », « Liz », « Danny ». Le tableau de droite comporte l'en-tête « Anniversaire » et indique les dates « 12 janvier », « 3 février », « 25 avril », « 10 mai », « 23 mai », « 24 juillet », « 2 août » et « 15 septembre ». Il y a une flèche pour chaque nom dans le tableau des noms qui commence par le nom et pointe vers une date dans le tableau des anniversaires. Alors que la plupart des dates n'ont qu'une seule flèche pointant vers elles, il y a deux flèches pointant vers le 24 juillet : une de Stephen et une de Liz.$

Réponse

ⓐ La flèche indique la date de naissance de la personne. Nous créons des paires ordonnées avec le nom de la personne comme valeur x et sa date de naissance comme valeur y.

{(Alison, 25 avril), (Pénélope, 23 mai), (juin, 2 août), (Gregory, 15 septembre), (Geoffrey, 12 janvier), (Lauren, 10 mai), (Stephen, 24 juillet), (Alice, 3 février), (Liz, 2 août), (Danny, 24 juillet)}

ⓑ Le domaine est l'ensemble de toutes les valeurs x de la relation.

{Alison, Pénélope, June, Gregory, Geoffrey, Lauren, Stephen, Alice, Liz, Danny}

{12 janvier, 3 février, 25 avril, 10 mai, 23 mai, 24 juillet, 2 août, 15 septembre}

Exemple$\PageIndex{5}$

Utilisez le mappage de la relation indiquée pour

liste les paires ordonnées de la relation
trouvez le domaine de la relation
trouvez l'étendue de la relation.

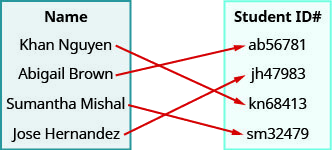
$Cette figure montre deux tableaux comportant chacun une colonne. Le tableau de gauche contient l'en-tête « Nom » et répertorie les noms « Khanh Nguyen », « Abigail Brown », « Sumantha Mishal » et « Jose Hern et ez ». Le tableau de droite contient l'en-tête « Numéro d'identification de l'étudiant » et répertorie les codes « a b 56781 », « j h 47983 », « k n 68413 » et « s m 32479 ». Dans le tableau des noms, il y a une flèche qui commence par le nom et pointe vers un code dans le tableau des identifiants des étudiants. La première flèche va de Khanh Nguyen au k n 68413. La deuxième flèche part d'Abigail Brown et prend la direction a b 56781. La troisième flèche va de Sumantha Mishal au m 32479. La quatrième flèche part de Jose Hern et ez jusqu'au j h 47983.$

Réponse

ⓐ (Khanh Nguyen, n° 68413), (Abigail Brown, ab56781), (Sumantha Mishal, sm32479), (Jose Hern et Ez, jh47983)

ⓑ {Khanh Nguyen, Abigail Brown, Sumantha Mishal, José Hern et ez}

Exemple$\PageIndex{6}$

Utilisez le mappage de la relation indiquée pour

liste les paires ordonnées de la relation
trouvez le domaine de la relation
trouvez l'étendue de la relation.

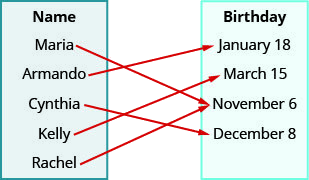
$Cette figure montre deux tableaux comportant chacun une colonne. Le tableau de gauche contient l'en-tête « Nom » et répertorie les noms « Maria », « Arm and o », « Cynthia », « Kelly » et « Rachel ». Le tableau de droite comporte l'en-tête « Anniversaire » et indique les dates « 18 janvier », « 15 mars », « 6 novembre » et « 8 décembre ». Il y a une flèche pour chaque nom dans le tableau des noms qui commence par le nom et pointe vers une date dans le tableau des anniversaires. La première flèche va de Maria au 6 novembre. La deuxième flèche va de Arm et O à un 18 janvier. La troisième flèche va de Cynthia au 8 décembre. La quatrième flèche va de Kelly au 15 mars. La cinquième flèche va de Rachel au 6 novembre.$

Réponse

ⓐ (Maria, 6 novembre), (Arm and o, 18 janvier), (Cynthia, 8 décembre), (Kelly, 15 mars), (Rachel, 6 novembre)

ⓑ {Maria, bras et autres, Cynthia, Kelly, Rachel}

Un graphe est un autre moyen de représenter une relation. L'ensemble des paires ordonnées de tous les points tracés constitue la relation. L'ensemble de toutes les coordonnées x est le domaine de la relation et l'ensemble de toutes les coordonnées y est la plage. En général, nous écrivons les nombres par ordre croissant pour le domaine et la plage.

Exemple$\PageIndex{7}$

Utilisez le graphique de la relation avec

liste les paires ordonnées de la relation
trouvez le domaine de la relation
trouvez l'étendue de la relation.

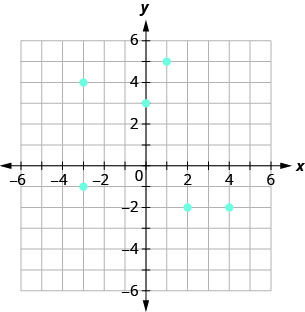
$La figure montre le graphique de certains points sur le plan de coordonnées x. Les axes x et y vont de moins 6 à 6. Les points (négatif 3, 4), (négatif 3, négatif 1), (0, 3), (1, 5), (2, négatif 2) et (4, négatif 2).$

Réponse

ⓐ Les paires ordonnées de la relation sont les suivantes :\[{\{(1,5),(−3,−1),(4,−2),(0,3),(2,−2),(−3,4)}\}.\nonumber\]

ⓑ Le domaine est l'ensemble de toutes les valeurs x de la relation :$\quad {\{−3,0,1,2,4}\}$.

Notez que lorsqu'il est$−3$ répété, il n'est répertorié qu'une seule fois.

Notez que lorsqu'il est$−2$ répété, il n'est répertorié qu'une seule fois.

Exemple$\PageIndex{8}$

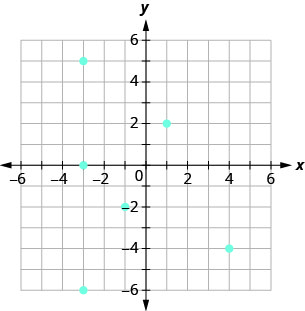
Utilisez le graphique de la relation avec

liste les paires ordonnées de la relation
trouvez le domaine de la relation
trouvez l'étendue de la relation.
$La figure montre le graphique de certains points sur le plan de coordonnées x. Les axes x et y vont de moins 6 à 6. Les points (négatif 3, 3), (négatif 2, 2), (négatif 1, 0), (0, négatif 1), (2, négatif 2) et (4, négatif 4).$

Réponse: ⓐ$(−3,3),(−2,2),(−1,0),$
$(0,−1),(2,−2),(4,−4)$
ⓑ${\{−3,−2,−1,0,2,4}\}$
ⓒ${\{3,2,0,−1,−2,−4}\}$

Exemple$\PageIndex{9}$

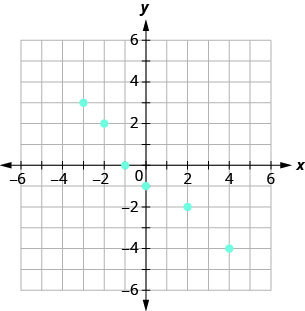
Utilisez le graphique de la relation avec

liste les paires ordonnées de la relation
trouvez le domaine de la relation
trouvez l'étendue de la relation.

$La figure montre le graphique de certains points sur le plan de coordonnées x. Les axes x et y vont de moins 6 à 6. Les points (négatif 3, 5), (négatif 3, 0), (négatif 3, négatif 6), (négatif 1, négatif 2), (1, 2) et (4, négatif 4).$

Réponse: ⓐ$(−3,0),(−3,5),(−3,−6),$
$(−1,−2),(1,2),(4,−4)$
ⓑ${\{−3,−1,1,4}\}$
ⓒ${\{−6,0,5,−2,2,−4}\}$

Déterminer si une relation est une fonction

Un type particulier de relation, appelé fonction, est très répandu en mathématiques. Une fonction est une relation qui attribue à chaque élément de son domaine exactement un élément de la plage. Pour chaque paire ordonnée dans la relation, chaque valeur x est associée à une seule valeur y.

Définition : Fonction

Une fonction est une relation qui attribue à chaque élément de son domaine exactement un élément de la plage.

L'exemple d'anniversaire tiré d'Example nous aide à comprendre cette définition. Chaque personne a un anniversaire, mais personne n'en a deux. Il est normal que deux personnes partagent un anniversaire. ^{Il est normal que Danny et Stephen partagent le 24 juillet comme ^anniversaire et que June et Liz partagent le 2 août.} Comme chaque personne a exactement une date de naissance, la relation dans l'exemple est une fonction.

La relation illustrée par le graphique de l'exemple inclut les paires ordonnées$(−3,−1)$ et$(−3,4)$. Est-ce que ça va dans une réception ? Non, car c'est comme si une personne avait deux anniversaires différents.

Exemple$\PageIndex{10}$

Utilisez l'ensemble de paires ordonnées pour (i) déterminer si la relation est une fonction (ii) trouver le domaine de la relation (iii) trouver la plage de la relation.

${\{(−3,27),(−2,8),(−1,1),(0,0),(1,1),(2,8),(3,27)}\}$
${\{(9,−3),(4,−2),(1,−1),(0,0),(1,1),(4,2),(9,3)}\}$

Réponse

ⓐ${\{(−3,27),(−2,8),(−1,1),(0,0),(1,1),(2,8),(3,27)}\}$

(i) Chaque valeur x est associée à une seule valeur y. Cette relation est donc une fonction.

(ii) Le domaine est l'ensemble de toutes les valeurs x de la relation.
Le domaine est :${\{−3,−2,−1,0,1,2,3}\}$.

(iii) La plage est l'ensemble de toutes les valeurs y de la relation. Notez que nous ne listons pas deux fois les valeurs de plage.
La gamme est de :${\{27,8,1,0}\}$.

ⓑ${\{(9,−3),(4,−2),(1,−1),(0,0),(1,1),(4,2),(9,3)}\}$

(i) La valeur x 9 est mise en correspondance avec deux valeurs y, à la fois 3 et$−3$. Cette relation n'est donc pas une fonction.

(ii) Le domaine est l'ensemble de toutes les valeurs x de la relation. Notez que nous ne listons pas les valeurs de domaine deux fois.
Le domaine est :${\{0,1,2,4,9}\}$.

(iii) La plage est l'ensemble de toutes les valeurs y de la relation.
La gamme est de :${\{−3,−2,−1,0,1,2,3}\}$.

Exemple$\PageIndex{11}$

Utilisez l'ensemble de paires ordonnées pour (i) déterminer si la relation est une fonction (ii) trouver le domaine de la relation (iii) trouver la plage de la fonction.

${\{(−3,−6),(−2,−4),(−1,−2),(0,0),(1,2),(2,4),(3,6)}\}$
${\{(8,−4),(4,−2),(2,−1),(0,0),(2,1),(4,2),(8,4)}\}$

Réponse: ⓐ Oui${\{−3,−2,−1,0,1,2,3}\}$ ;
${\{−6,−4,−2,0,2,4,6}\}$
ⓑ Non${\{0,2,4,8}\}$ ;
${\{−4,−2,−1,0,1,2,4}\}$

Exemple$\PageIndex{12}$

Utilisez l'ensemble de paires ordonnées pour (i) déterminer si la relation est une fonction (ii) trouver le domaine de la relation (iii) trouver la plage de la relation.

${\{(27,−3),(8,−2),(1,−1),(0,0),(1,1),(8,2),(27,3)}\}$
${\{(7,−3),(−5,−4),(8,−0),(0,0),(−6,4),(−2,2),(−1,3)}\}$

Réponse: ⓐ Non${\{0,1,8,27}\}$ ;
${\{−3,−2,−1,0,2,2,3}\}$
ⓑ Oui${\{7,−5,8,0,−6,−2,−1}\}$ ;
${\{−3,−4,0,4,2,3}\}$

Exemple$\PageIndex{13}$

Utilisez le mappage pour

déterminer si la relation est une fonction
trouvez le domaine de la relation
trouvez l'étendue de la relation.

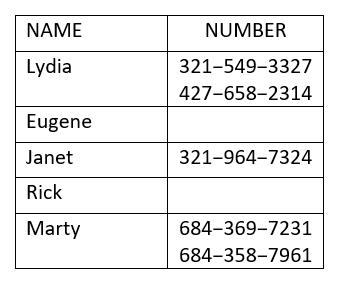
$clipboard_e358fef1793647353f09157074f4029e0.png$

Réponse

ⓐ Lydia et Marty ont deux numéros de téléphone. Ainsi, chaque valeur x n'est pas associée à une seule valeur y. Cette relation n'est donc pas une fonction.

ⓑ Le domaine est l'ensemble de toutes les valeurs x de la relation. Le domaine est : {Lydia, Eugene, Janet, Rick, Marty}

${\{321-549-3327, 427-658-2314, 321-964-7324, 684-358-7961, 684-369-7231, 798-367-8541}\}$

Exemple$\PageIndex{14}$

Utilisez le mappage pour ⓐ déterminer si la relation est une fonction ⓑ trouver le domaine de la relation ⓒ trouver la plage de la relation.

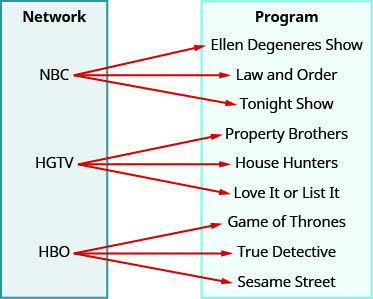
$Cette figure montre deux tableaux comportant chacun une colonne. Le tableau de gauche contient l'en-tête « Réseau » et répertorie les chaînes de télévision « NBC », « HGTV » et « HBO ». Le tableau de droite contient l'en-tête « Programme » et répertorie les émissions télévisées « Ellen Degeneres Show », « Law and Order », « Tonight Show », « Property Brothers », « House Hunters », « Love it or List it », « Game of Thrones », « True Detective » et « Sesame Street ». Certaines flèches commencent par un réseau dans le premier tableau et pointent vers un programme dans le second tableau. La première flèche va de NBC à Ellen Degeneres Show. La deuxième flèche va de NBC à Law and Order. La troisième flèche va de NBC à Tonight Show. La quatrième flèche va de HGTV à Property Brothers. La cinquième flèche va de HGTV à House Hunters. La sixième flèche va de HGTV à Love it ou List it. La septième flèche va de HBO à Game of Thrones. La huitième flèche va de HBO à True Detective. La neuvième flèche va de HBO à Sesame Street.$

Réponse: ⓐ no ⓑ {NBC, HGTV, HBO} ⓒ {Ellen Degeneres Show, Law and Order, Tonight Show, Property Brothers, House Hunters, Aimez-le ou Listez-le, Game of Thrones, True Detective, Sesame Street}

Exemple$\PageIndex{15}$

Utilisez le mappage pour

déterminer si la relation est une fonction
trouvez le domaine de la relation
trouvez l'étendue de la relation.

Réponse: ⓐ Non ⓑ {Neal, Krystal, Kelvin, George, Christa, Mike} ⓒ {123-567-4839 travail, 231-378-5941 cellule, 743-469-9731, 567-534-2970 travail, 684-369-7231 cellule, 798-367-8541 cellule, 639-847-6971 cellule}

En algèbre, le plus souvent, les fonctions seront représentées par une équation. Il est plus facile de voir si l'équation est une fonction lorsqu'elle est résolue pour y. Si chaque valeur de x ne donne qu'une seule valeur de y, alors l'équation définit une fonction.

Exemple$\PageIndex{16}$

Déterminez si chaque équation est une fonction.

$2x+y=7$
$y=x^2+1$
$x+y^2=3$

Réponse

ⓐ$2x+y=7$

Pour chaque valeur de x, nous la multiplions par$−2$ puis ajoutons 7 pour obtenir la valeur y

	$.$
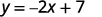
Par exemple, si$x=3$ :	$.$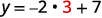
	$.$

C'est ce que nous aurons$x=3$, alors$y=1$. Cela fonctionnerait de la même manière pour n'importe quelle valeur de x. Comme chaque valeur de x correspond à une seule valeur de y, l'équation définit une fonction.

ⓑ$y=x^2+1$

Pour chaque valeur de x, nous la mettons au carré puis ajoutons 1 pour obtenir la valeur y.

	$.$
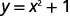
Par exemple, si$x=2$ :	$.$
	$.$

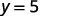
C'est ce que nous aurons$x=2$, alors$y=5$. Cela fonctionnerait de la même manière pour n'importe quelle valeur de x. Comme chaque valeur de x correspond à une seule valeur de y, l'équation définit une fonction.

ⓒ

	$.$
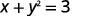
Isolez le terme y.	$.$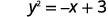
Remplaçons$x=2$.	$.$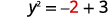
	$.$
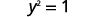
Cela nous donne deux valeurs pour y.	$y=1\space y=−1$

Nous avons montré que quand$x=2$, alors$y=1$ et$y=−1$. Cela fonctionnerait de la même manière pour n'importe quelle valeur de x. Comme chaque valeur de x ne correspond pas à une seule valeur de y, l'équation ne définit pas de fonction.

Exemple$\PageIndex{17}$

Déterminez si chaque équation est une fonction.

$4x+y=−3$
$x+y^2=1$
$y−x^2=2$

Réponse: ⓐ oui ⓑ non ⓒ oui

Exemple$\PageIndex{18}$

Déterminez si chaque équation est une fonction.

$x+y^2=4$
$y=x^2−7$
$y=5x−4$

Réponse: ⓐ non ⓑ oui ⓒ oui

Trouver la valeur d'une fonction

Il est très pratique de nommer une fonction et le plus souvent nous la nommons f, g, h, F, G ou H. Dans n'importe quelle fonction, pour chaque valeur x du domaine, nous obtenons une valeur y correspondante dans la plage. Pour la fonction$f$, nous écrivons cette valeur de plage$y$ sous la forme$f(x)$. C'est ce que l'on appelle la notation$f$ des$x$ fonctions et on lit la valeur de$f$ at$x$. Dans ce cas, les parenthèses n'indiquent pas une multiplication.

Définition : Notation des fonctions

Pour la fonction$y=f(x)$

\[\begin{array} {l} {f\text{ is the name of the function}} \\{x \text{ is the domain value}} \\ {f(x) \text{ is the range value } y \text{ corresponding to the value } x} \\ \nonumber \end{array}\]

Nous lisons$f(x)$ à$f$ partir de$x$ ou la valeur de$f$ at$x$.

Nous appelons x la variable indépendante car il peut s'agir de n'importe quelle valeur du domaine. Nous appelons y la variable dépendante car sa valeur dépend de x.

VARIABLES INDÉPENDANTES ET DÉPENDANTES

Pour la fonction$y=f(x)$,

\[\begin{array} {l} {x \text{ is the independent variable as it can be any value in the domain}} \\ {y \text{ the dependent variable as its value depends on } x} \\ \nonumber \end{array}\]

Tout comme lorsque vous avez rencontré la variable x pour la première fois, la notation des fonctions peut être assez troublante. Cela semble étrange parce que c'est nouveau. Vous vous sentirez plus à l'aise avec la notation lorsque vous l'utiliserez.

Regardons l'équation$y=4x−5$. Pour trouver la valeur de y quand$x=2$, nous savons qu'il faut la remplacer$x=2$ dans l'équation, puis la simplifier.

	$.$
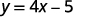Soit x = 2.	$.$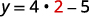
	$.$

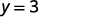La valeur de la fonction at$x=2$ est 3.

Nous faisons la même chose en utilisant la notation des fonctions, l'équation$y=4x−5$ peut être écrite sous la forme$f(x)=4x−5$. Pour trouver la valeur à quel moment$x=2$, nous écrivons :

	$.$
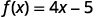Soit x = 2.	$.$
	$.$

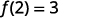La valeur de la fonction at$x=2$ est 3.

Ce processus de recherche de la valeur de$f(x)$ pour une valeur donnée de x est appelé évaluation de la fonction.

Exemple$\PageIndex{19}$

Pour la fonction$f(x)=2x^2+3x−1$, évaluez-la.

$f(3)$
$f(−2)$
$f(a)$

Réponse

ⓐ

	$.$
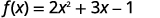
Pour évaluer$f(3)$, remplacez 3 par x.	$.$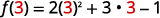
Simplifiez.	$.$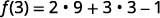
	$.$
	$.$

ⓑ

		$.$
$.$		$.$
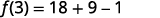
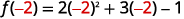
Simplifiez.		$.$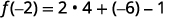
		$.$
		$.$

ⓒ

	$.$
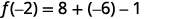
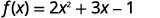
Pour évaluer f (a), f (a), remplacez x par a.	$.$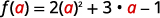
Simplifiez.	$.$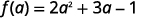

Exemple$\PageIndex{20}$

Pour la fonction$f(x)=3x^2−2x+1$, évaluez-la.

$f(3)$
$f(−1)$
$f(t)$

Exemple$\PageIndex{21}$

Pour la fonction$f(x)=2x^2+4x−3$, évaluez-la.

$f(2)$
$f(−3)$
$f(h)$

Dans le dernier exemple, nous avons trouvé$f(x)$ une valeur constante de x. Dans l'exemple suivant, on nous demande de rechercher$g(x)$ des valeurs de x qui sont des variables. Nous suivons toujours la même procédure et remplaçons les variables par le x.

Exemple$\PageIndex{22}$

Pour la fonction$g(x)=3x−5$, évaluez-la.

$g(h^2)$
$g(x+2)$
$g(x)+g(2)$

Réponse

ⓐ

			$.$
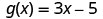
Pour évaluer$g(h^2)$, remplacez$h^2$ x.			$.$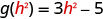
			$.$

ⓑ

	$.$
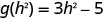
Pour évaluer$g(x+2)$, remplacez$x+2$ x.	$.$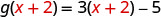
Simplifiez.	$.$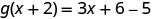
	$.$

ⓒ

		$.$
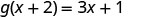
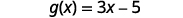
Pour évaluer$g(x)+g(2)$, trouvez d'abord$g(2)$.		$.$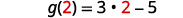
		$.$
$.$		$.$
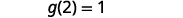
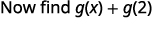
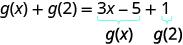
Simplifiez.		$.$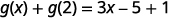
		$.$

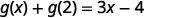
Remarquez la différence entre la partie ⓑ et la partie ⓒ. Nous obtenons$g(x+2)=3x+1$ et$g(x)+g(2)=3x−4$. C'est ce que nous voyons$g(x+2)\neq g(x)+g(2)$.

Exemple$\PageIndex{23}$

Pour la fonction$g(x)=4x−7$, évaluez-la.

$g(m^2)$
$g(x−3)$
$g(x)−g(3)$

Exemple$\PageIndex{24}$

Pour la fonction$h(x)=2x+1$, évaluez-la.

$h(k^2)$
$h(x+1)$
$h(x)+h(1)$

De nombreuses situations quotidiennes peuvent être modélisées à l'aide de fonctions.

Exemple$\PageIndex{25}$

Le nombre de courriels non lus sur le compte de Sylvia est de 75. Ce nombre augmente de 10 e-mails non lus par jour. La fonction$N(t)=75+10t$ représente la relation entre le nombre d'e-mails, N, et l'heure, t, mesurée en jours.

Déterminez la variable indépendante et dépendante.
Trouve$N(5)$. Expliquez ce que signifie ce résultat.

Réponse

ⓐ Le nombre d'e-mails non lus est fonction du nombre de jours. Le nombre de courriels non lus, N, dépend du nombre de jours, t. Par conséquent, la variable N est la variable dépendante et la variable tt est la variable indépendante.

ⓑ Trouvez$N(5)$. Expliquez ce que signifie ce résultat.

	$.$
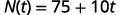
Remplacer par t=5.t=5.	$.$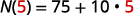
Simplifiez.	$.$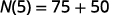
	$.$

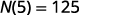
Puisque 5 est le nombre de jours,$N(5)$, est le nombre d'e-mails non lus après 5 jours. Au bout de 5 jours, le compte contient 125 e-mails non lus.

Exemple$\PageIndex{26}$

Le nombre d'e-mails non lus sur le compte de Bryan est de 100. Ce nombre augmente de 15 e-mails non lus par jour. La fonction$N(t)=100+15t$ représente la relation entre le nombre d'e-mails, N, et l'heure, t, mesurée en jours.

Déterminez la variable indépendante et dépendante.
Trouve$N(7)]$. Expliquez ce que signifie ce résultat.

Réponse: ⓐ t IND ; N DEP ⓑ 205 ; le nombre de courriels non lus sur le compte de Bryan au septième jour.

Exemple$\PageIndex{27}$

Le nombre d'e-mails non lus sur le compte d'Anthony est de 110. Ce nombre augmente de 25 e-mails non lus par jour. La fonction$N(t)=110+25t$ représente la relation entre le nombre d'e-mails, N, et l'heure, t, mesurée en jours.

Déterminez la variable indépendante et dépendante.
Trouve$N(14)$. Expliquez ce que signifie ce résultat.

Réponse: ⓐ t IND ; N DEP ⓑ 460 ; le nombre de courriels non lus sur le compte d'Anthony au quatorzième jour

Accédez à cette ressource en ligne pour obtenir des instructions et des exercices supplémentaires concernant les relations et les fonctions.

Présentation des fonctions

Concepts clés

Notation de fonction : Pour la fonction$y=f(x)$
- f est le nom de la fonction
- x est la valeur du domaine
- $f(x)$est la valeur de plage y correspondant à la valeur x
  On lit$f(x)$ f de x ou la valeur de f à x.
Variables indépendantes et dépendantes : pour la fonction$y=f(x)$,
- x est la variable indépendante car il peut s'agir de n'importe quelle valeur du domaine
- y est la variable dépendante car sa valeur dépend de x

Lexique

domaine d'une relation: Le domaine d'une relation est constitué de toutes les valeurs x des paires ordonnées de la relation.

fonction: Une fonction est une relation qui attribue à chaque élément de son domaine exactement un élément de la plage.

cartographie: Un mappage est parfois utilisé pour montrer une relation. Les flèches indiquent l'appariement des éléments du domaine avec les éléments de la gamme.

étendue d'une relation: La plage d'une relation est constituée de toutes les valeurs y dans les paires ordonnées de la relation.

relation: Une relation est un ensemble de paires ordonnées (x, y). (x, y). Toutes les valeurs x des paires ordonnées constituent ensemble le domaine. Toutes les valeurs y des paires ordonnées constituent ensemble la plage.

Définition : Relation

Exemple\(\PageIndex{1}\)

Exemple\(\PageIndex{2}\)

Exemple\(\PageIndex{3}\)

MAPPAGE

Exemple\(\PageIndex{4}\)

Exemple\(\PageIndex{5}\)

Exemple\(\PageIndex{6}\)

Exemple\(\PageIndex{7}\)

Exemple\(\PageIndex{8}\)

Exemple\(\PageIndex{9}\)

Définition : Fonction

Exemple\(\PageIndex{10}\)

Exemple\(\PageIndex{11}\)

Exemple\(\PageIndex{12}\)

Exemple\(\PageIndex{13}\)

Exemple\(\PageIndex{14}\)

Exemple\(\PageIndex{15}\)

Exemple\(\PageIndex{16}\)

Exemple\(\PageIndex{17}\)

Exemple\(\PageIndex{18}\)

Définition : Notation des fonctions

VARIABLES INDÉPENDANTES ET DÉPENDANTES

Exemple\(\PageIndex{19}\)

Exemple\(\PageIndex{20}\)

Exemple\(\PageIndex{21}\)

Exemple\(\PageIndex{22}\)

Exemple\(\PageIndex{23}\)

Exemple\(\PageIndex{24}\)

Exemple\(\PageIndex{25}\)

Exemple\(\PageIndex{26}\)

Exemple\(\PageIndex{27}\)

	$.$
Isolez le terme y.	$.$
Remplaçons\(x=2\).	$.$
	$.$
Cela nous donne deux valeurs pour y.	\(y=1\space y=−1\)

	$.$
Pour évaluer\(f(3)\), remplacez 3 par x.	$.$
Simplifiez.	$.$
	$.$
	$.$

	$.$
Pour évaluer\(g(x+2)\), remplacez\(x+2\) x.	$.$
Simplifiez.	$.$
	$.$

		$.$
Pour évaluer\(g(x)+g(2)\), trouvez d'abord\(g(2)\).		$.$
		$.$
$.$		$.$
Simplifiez.		$.$
		$.$