1.2E : Exercices

Last updated
Save as PDF

Page ID: 194247

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La pratique rend parfait

Identifier les multiples et les facteurs

Dans les exercices suivants, utilisez les tests de divisibilité pour déterminer si chaque nombre est divisible par 2, par 3, par 5, par 6 et par 10.

1. $84$

Réponse: Divisible par 2, 3, 6

2. $96$

3. $896$

Réponse: Divisible par 2

4. $942$

5. $22,335$

Réponse: Divisible par 3, 5

6. $39,075$

Trouvez les factorisations principales et les multiples les moins courants

Dans les exercices suivants, déterminez la factorisation principale.

7. $86$

Réponse: $2⋅43$

8. $78$

9. $455$

Réponse: $5⋅7⋅13$

10. $400$

11. $432$

Réponse: $2⋅2⋅2⋅2⋅3⋅3⋅3$

12. $627$

Dans les exercices suivants, trouvez le multiple le moins courant de chaque paire de nombres à l'aide de la méthode des facteurs premiers.

13. $8,\; 12$

Réponse: $24$

14. $12,\; 16$

15. $28,\; 40$

Réponse: $280$

16. $84, \;90$

17. $55, \;88$

Réponse: $440$

18. $60, \;72$

Simplifier les expressions en utilisant l'ordre des opérations

Dans les exercices suivants, simplifiez chaque expression.

19. $2^3−12÷(9−5)$

Réponse: $5$

20. $3^2−18÷(11−5)$

21. $2+8(6+1)$

Réponse: $58$

22. $4+6(3+6)$

23. $20÷4+6(5−1)$

Réponse: $29$

24. $33÷3+4(7−2)$

25. $3(1+9⋅6)−4^2$

Réponse: $149$

26. $5(2+8⋅4)−7^2$

27. $2[1+3(10−2)]$

Réponse: $50$

28. $5[2+4(3−2)]$

29. $8+2[7−2(5−3)]−3^2$

Réponse: $5$

30. $10+3[6−2(4−2)]−2^4$

Évaluer une expression

Dans les exercices suivants, évaluez les expressions suivantes.

31. Quand$x=2$,

un.$x^6$

b.$4^x$

c.$2x^2+3x−7$

Réponse: a. 64
b. 16
c. 7

32. Quand$x=3$,

un.$x^5$

b.$5x$

c.$3x^2−4x−8$

33. Quand$x=4$ et$y=1$

$x^2+3xy−7y^2$

Réponse: $21$

34. Quand$x=3$ et$y=2$

$6x^2+3xy−9y^2$

35. Quand$x=10$ et$y=7$

$(x−y)^2$

Réponse: $9$

36. Quand$a=3$ et$b=8$

$a^2+b^2$

Simplifiez les expressions en combinant des termes similaires

Dans les exercices suivants, simplifiez les expressions suivantes en combinant des termes similaires.

37. $7x+2+3x+4$

Réponse: $10x+6$

38. $8y+5+2y−4$

39. $10a+7+5a−2+7a−4$

Réponse: $22a+1$

40. $7c+4+6c−3+9c−1$

41. $3x^2+12x+11+14x^2+8x+5$

Réponse: $17x^2+20x+16$

42. $5b^2+9b+10+2b^2+3b−4$

Traduire une phrase anglaise en une expression algébrique

Dans les exercices suivants, traduisez les phrases en expressions algébriques.

43. a. la différence entre$5x^2$ et$6xy$

b. le quotient de$6y^2$ et$5x$

c. Vingt et un de plus que$y^2$

d.$6x$ inférieur à$81x^2$

Réponse

a.$5x^2−6xy$ b.$\frac{6y^2}{5x}$

$y^2+21$c.d.$81x^2−6x$

44. a. la différence entre$17x^2$ et$17x^2$ et$5xy$

b. le quotient de$8y^3$ et$3x$

c. Dix-huit de plus que$a^2$ ;

d.$11b$ inférieur à$100b^2$

45. a. la somme de$4ab^2$ et$3a^2b$

b. le produit de$4y^2$ et$5x$

c. Quinze de plus que$m$

d.$9x$ inférieur à$121x^2$

Réponse

a.$4ab^2+3a^2b$ b.$20xy^2$

$m+15$c.d.$121x^2−9x$$9x<121x^2$

46. a. la somme de$3x^2y$ et$7xy^2$

b. le produit de$6xy^2$ et$4z$

c. Douze de plus que$3x^2$

d.$7x^2$ inférieur à$63x^3$

47. a. huit fois la différence$y$ et neuf

b. la différence de huit fois$y$ et$9$

Réponse: a.$8(y−9)$
b.$8y−9$

48. a. sept fois la différence de$y$ et un

b. la différence de sept fois$y$ et$1$

49. a. cinq fois la somme de$3x$ et$y$

b. la somme de cinq fois$3x$ et$y$

Réponse: a.$5(3x+y)$
b.$15x+y$

50. a. Onze fois la somme de$4x2$ et$5x$

b. la somme de onze fois$4x^2$ et$5x$

51. Eric a des chansons rock et country sur sa playlist. Le nombre de chansons rock est de 14, soit plus du double du nombre de chansons country. Soit c le nombre de chansons country. Ecrivez une expression pour le nombre de chansons rock.

Réponse: $14>2c$

52. Le nombre de femmes dans un cours de statistique est de 8, soit plus du double du nombre d'hommes. $m$Représente le nombre d'hommes. Écrivez une expression pour le nombre de femmes.

53. Greg a de l'argent et des sous en poche. Le nombre de centimes est inférieur de sept cents à trois cents. Soit n le nombre de nickels. Écrivez une expression pour le nombre de centimes.

Réponse: $3n-7$

54. Jeannette a$$5$ des$$10$ factures dans son portefeuille. Le nombre de cinq est trois fois plus que six fois supérieur à celui des dizaines. $t$Représentez le nombre de dizaines. Écrivez une expression pour le nombre de cinq.

Exercices d'écriture

55. Expliquez avec vos propres mots comment déterminer la factorisation première d'un nombre composé.

Réponse: Les réponses peuvent varier.

56. Pourquoi est-il important d'utiliser l'ordre des opérations pour simplifier une expression ?

57. Expliquez comment identifier les termes similaires dans l'expression$8a^2+4a+9−a^2−1.$

Réponse: Les réponses peuvent varier.

58. Expliquez la différence entre les phrases « 4 fois la somme de x et y » et « la somme de 4 fois x et y ».

Auto-vérification

a. Utilisez cette liste de contrôle pour évaluer votre maîtrise des objectifs de cette section.

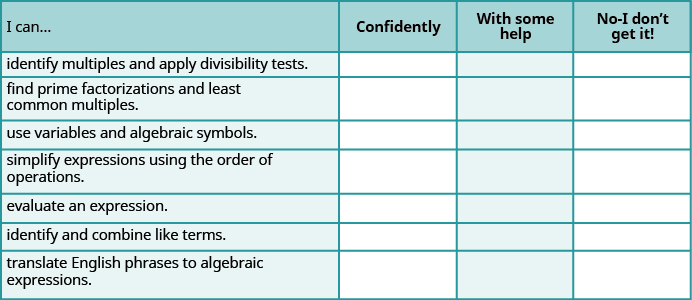
$Ce tableau comporte 4 colonnes, 7 lignes et une ligne d'en-tête. La ligne d'en-tête étiquette chaque colonne que je peux, en toute confiance, avec de l'aide et non, je ne comprends pas. La première colonne contient les instructions suivantes : identifier les multiples et appliquer des tests de divisibilité, trouver des factorisations premières et des multiples les moins courants, utiliser des variables et des symboles algébriques, simplifier les expressions en utilisant l'ordre des opérations, évaluer une expression, identifier et combiner des termes similaires, traduire l'anglais des phrases à des expressions algébriques. Les colonnes restantes sont vides.$

b. Si la plupart de vos chèques étaient :

... en toute confiance. Félicitations ! Vous avez atteint les objectifs de cette section. Réfléchissez aux compétences d'étude que vous avez utilisées afin de pouvoir continuer à les utiliser. Qu'avez-vous fait pour avoir confiance en votre capacité à faire ces choses ? Soyez précis.

... avec de l'aide. Cela doit être abordé rapidement car les sujets que vous ne maîtrisez pas deviennent des nids-de-poule sur votre chemin vers le succès. En mathématiques, chaque sujet s'appuie sur des travaux antérieurs. Il est important de vous assurer d'avoir une base solide avant de passer à autre chose. À qui pouvez-vous demander de l'aide ? Vos camarades de classe et votre instructeur sont de bonnes ressources. Y a-t-il un endroit sur le campus où des professeurs de mathématiques sont disponibles ? Vos compétences d'étude peuvent-elles être améliorées ?

... non, je ne comprends pas ! Il s'agit d'un signe d'avertissement et vous ne devez pas l'ignorer. Vous devriez obtenir de l'aide immédiatement, sinon vous serez rapidement dépassé. Consultez votre instructeur dès que possible pour discuter de votre situation. Ensemble, vous pouvez élaborer un plan pour obtenir l'aide dont vous avez besoin.